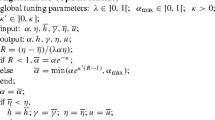Constant-Time Algorithms for Continuous Optimization Problems

Abstract

In this chapter, we consider constant-time algorithms for continuous optimization problems. Specifically, we consider quadratic function minimization and tensor decomposition, both of which have numerous applications in machine learning and data mining. The key component in our analysis is graph limit theory, which was originally developed to study graphs analytically.

1 Introduction

In this chapter, we turn our attention to constant-time algorithms for continuous optimization problems. Specifically, we consider quadratic function minimization and tensor decomposition, both of which have numerous applications in machine learning and data mining. The key component in our analysis is graph limit theory, which was originally developed to study graphs analytically.

We introduce graph limit theory in Sect. 3.2, and then discuss quadratic function minimization and tensor decomposition in Sects. 3.3 and 3.4, respectively. Throughout this chapter, we assume the real RAM model, in which we can perform basic algebraic operations on real numbers in one step. For a positive integer n, let [n] denote the set $\{1,2,\ldots ,n\}$. For real values $a,b,c \in \mathbb {R}$, $a = b \pm c$ is used as shorthand for $b - c \le a \le b + c$. The algorithms and analysis presented in this chapter are based on [5, 6].

2 Graph Limit Theory

This section reviews the basic concepts of graph limit theory. For further details, refer to the book by Lovász [7].

We call a (measurable) function $\mathcal {W}:{[0,1]}^K \rightarrow \mathbb {R}$ a dikernel of order K. We define

$$\begin{aligned} {\vert \mathcal {W}\vert }_F&= \sqrt{\int _{{[0,1]}^K} {\mathcal {W}(\boldsymbol{x})}^2 \mathrm {d} \boldsymbol{x}}, \qquad \qquad \qquad \qquad \quad \quad \qquad \qquad \qquad \qquad \quad \quad {\text {(Frobenius norm)}} \\ {\vert \mathcal {W}\vert }_{\max }&= \max _{\boldsymbol{x} \in {[0,1]}^K}|\mathcal {W}(\boldsymbol{x})|, \qquad \qquad \qquad \quad \qquad \quad \quad \qquad \qquad \qquad \qquad \qquad {\text {(Max norm)}} \\ {\vert \mathcal {W}\vert }_\square&= \sup _{S_1,\ldots ,S_K\subseteq [0,1]}\Bigl |\int _{S_1 \times \cdots \times S_K} \mathcal {W}(\boldsymbol{x}) \mathrm {d} \boldsymbol{x}. \Bigr | \qquad \qquad \qquad \qquad \quad \quad \qquad \qquad \qquad \qquad \qquad {\text {(Cut norm)}} \end{aligned}$$

We note that these norms satisfy the triangle inequality. For two dikernels $\mathcal {W}$ and $\mathcal {W}'$, we define their inner product as $\langle \mathcal {W}, \mathcal {W}'\rangle = \int _{{[0,1]}^K}\mathcal {W}(\boldsymbol{x})\mathcal {W}'(\boldsymbol{x})\mathrm {d} \boldsymbol{x}$. For a dikernel $\mathcal {W}:[0,1]^2 \rightarrow \mathbb {R}$ and a function $f:[0,1] \rightarrow \mathbb {R}$, we define a function $\mathcal {W} f:[0,1] \rightarrow \mathbb {R}$ as $(\mathcal {W} f)(x) = \langle \mathcal {W}(x,\cdot ),f\rangle$.

Let $\lambda$ be a Lebesgue measure. A map $\pi : [0, 1] \rightarrow [0, 1]$ is said to be measure-preserving if the pre-image $\pi ^{-1}(X)$ is measurable for every measurable set X, and $\lambda (\pi ^{-1}(X)) = \lambda (X)$. A measure-preserving bijection is a measure-preserving map whose inverse map exists and is also measurable (and, in turn, also measure-preserving). For a measure-preserving bijection $\pi :[0,1] \rightarrow [0,1]$ and a dikernel $\mathcal {W}:{[0,1]}^K {\rightarrow } \mathbb {R}$, we define a dikernel $\pi (\mathcal {W}):{[0,1]}^K \rightarrow \mathbb {R}$ as $\pi (\mathcal {W})(x_1,\ldots ,x_K) = \mathcal {W}(\pi (x_1),\ldots ,\pi (x_K))$.

A partition $\mathcal {P} = (V_1,\ldots ,V_p)$ of the interval [0, 1] is called an equipartition if $\lambda (V_i) = 1/p$ for every $i \in [p]$. For a dikernel $\mathcal {W}:{[0,1]}^K \rightarrow \mathbb {R}$ and an equipartition $\mathcal {P} = (V_1,\ldots , V_p)$ of [0, 1], we define $\mathcal {W}_\mathcal {P}:{[0,1]}^K \rightarrow \mathbb {R}$ as the dikernel obtained by averaging each $V_{i_1} \times \cdots \times V_{i_K}$ for $i_1,\ldots ,i_K \in [p]$. More formally, we define

$$\begin{aligned} \mathcal {W}_\mathcal {P}(\boldsymbol{x}) = \frac{1}{\prod _{k \in [K]}\lambda (V_{i_k})}\int _{V_{i_1} \times \cdots \times V_{i_K}}\mathcal {W}(\boldsymbol{x}')\mathrm {d} \boldsymbol{x}' = p^K\int _{V_{i_1} \times \cdots \times V_{i_K}}\mathcal {W}(\boldsymbol{x}')\mathrm {d} \boldsymbol{x}', \end{aligned}$$

where $i_k$ is the unique index such that $x_k \in V_{i_k}$ for each $k \in [K]$. The following lemma states that any dikernel $\mathcal {W}:{[0,1]}^K \rightarrow \mathbb {R}$ can be well approximated by $\mathcal {W}_\mathcal {P}$ for some equipartition $\mathcal {P}$ into a small number of parts.

Lemma 3.1

(Weak regularity lemma for dikernels [4]) Let $\mathcal {W}^1,\ldots ,\mathcal {W}^T:{[0,1]}^K \rightarrow \mathbb {R}$ be dikernels. Then, for any $\epsilon > 0$, there exists an equipartition $\mathcal {P}$ into $|\mathcal {P}| \le 2^{O(T/\epsilon ^{2K})}$ parts, such that for every $t \in [T]$,

$$\begin{aligned} \vert \mathcal {W}^t -\mathcal {W}^t_\mathcal {P}\vert _\square \le \epsilon \vert \mathcal {W}^t\vert _F. \end{aligned}$$

We can construct the dikernel $\mathcal {X}:{[0,1]}^K \rightarrow \mathbb {R}$ from a tensor $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$ as follows. For an integer $n \in \mathbb {N}$, let $I^n_1 = [0,\frac{1}{n}], I^n_2 = (\frac{1}{n},\frac{2}{n}], \ldots , I^n_n = (\frac{n-1}{n},\ldots ,1]$. For $x \in [0,1]$, we define $i_n(x) \in [n]$ as the unique integer such that $x \in I^n_i$. We then define $\mathcal {X}(x_1,\ldots ,x_K) = X_{i_{N_1}(x_1) \cdots i_{N_K}(x_K)}$. The main motivation of creating a dikernel from a tensor is that, in doing so, we can define the distance between two tensors X and Y of different sizes via the cut norm—that is, $\vert \mathcal {X} - \mathcal {Y}\vert _\square$, where $\mathcal {X}$ and $\mathcal {Y}$ are dikernels corresponding to X and Y, respectively.

Let $\mathcal {W}:{[0,1]}^K \rightarrow \mathbb {R}$ be a dikernel and $S_k = (x^k_1,\ldots ,x^k_s)$ for $k \in [K]$ be sequences of elements in [0, 1]. Then, we define a dikernel $\mathcal {W}|_{S_1,\ldots ,S_K}:{[0,1]}^K \rightarrow \mathbb {R}$ as follows: We first extract a tensor $W \in \mathbb {R}^{s \times \cdots \times s}$ by setting $W_{i_1\cdots i_K} {=} \mathcal {W}(x^1_{i_1},\ldots ,x^K_{i_K})$. Next, we define $\mathcal {W}|_{S_1,\ldots ,S_K}$ as the dikernel corresponding to $W|_{S_1,\ldots ,S_K}$. The following is the key technical lemma in the analysis of the algorithms given in the subsequent sections.

Lemma 3.2

Let $\mathcal {W}^1,\ldots ,\mathcal {W}^T: {[0,1]}^K \rightarrow [-L,L]$ be dikernels. Let $S_1,\ldots ,S_K$ be sequences of s elements uniformly and independently sampled from [0, 1]. Then, with probability at least $1 - \exp (-\Omega _K(s^2 {(T/ \log s)}^{1/K}))$, there exists a measure-preserving bijection $\pi :[0,1] \rightarrow [0,1]$ such that, for every $t \in [T]$, we have

$$\begin{aligned} \vert \mathcal {W}^t - \pi (\mathcal {W}^t|_{S_1,\ldots ,S_K})\vert _{\square } = L \cdot {O_K\left( \frac{T}{\log s}\right) }^{1/2K}, \end{aligned}$$

where $O_K(\cdot )$ and $\Omega _K(\cdot )$ hide factors depending on K.

3 Quadratic Function Minimization

Background

Quadratic functions are one of the most important function classes in machine learning, statistics, and data mining. Many fundamental problems such as linear regression, k-means clustering, principal component analysis, support vector machines, and kernel methods can be formulated as a minimization problem of a quadratic function. See, e.g., [8] for more details.

In some applications, it is sufficient to compute the minimum value of a quadratic function rather than its solution. For example, Yamada et al. [13] proposed an efficient method for estimating the Pearson divergence, which provides useful information about data, such as the density ratio [10]. They formulated the estimation problem as the minimization of a squared loss and showed that the Pearson divergence can be estimated from the minimum value. Least-squares mutual information [9] is another example that can be computed in a similar manner.

Despite its importance, minimization of quadratic functions suffers from the issue of scalability. Let $n\in \mathbb {N}$ be the number of variables. In general, this kind of minimization problem can be solved by quadratic programming (QP), which requires $\mathrm {poly}(n)$ time. If the problem is convex and there are no constraints, then the problem is reduced to solving a system of linear equations, which requires $O(n^3)$ time. Both methods easily become infeasible, even for medium-scale problems of, say, $n>10000$.

Although several techniques have been proposed to accelerate quadratic function minimization, they require at least linear time in n. This is problematic when handling large-scale problems, where even linear time is slow or prohibitive. For example, stochastic gradient descent (SGD) is an optimization method that is widely used for large-scale problems. A nice property of this method is that, if the objective function is strongly convex, it outputs a point that is sufficiently close to an optimal solution after a constant number of iterations [1]. Nevertheless, each iteration needs at least $\Omega (n)$ time to access the variables. Another popular technique is low-rank approximation such as Nyström’s method [12]. The underlying idea is to approximate the input matrix by a low-rank matrix, which drastically reduces the time complexity. However, we still need to compute the matrix vector product of size n, which requires $\Omega (n)$ time. Clarkson et al. [2] proposed sublinear-time algorithms for special cases of quadratic function minimization. However, these are “sublinear” with respect to the number of pairwise interactions of the variables, which is $\Theta (n^2)$, and the algorithms require $O(n \log ^c n)$ time for some $c \ge 1$.

Constant-time algorithm for quadratic function minimization

Let $A \in \mathbb {R}^{n \times n}$ be a matrix and $\boldsymbol{d},\boldsymbol{b} \in \mathbb {R}^n$ be vectors. Then, we consider the following quadratic problem:

(3.1)

where $\langle \cdot ,\cdot \rangle$ denotes the inner product and $\mathrm {diag}(\boldsymbol{d})$ denotes a diagonal matrix in which the diagonal entries are specified by $\boldsymbol{d}$. Note that although a constant term can be included in (3.1), it is omitted here because it is irrelevant when optimizing (3.1), and hence we omit it.

Let $z^* \in \mathbb {R}$ be the optimal value of (3.1) and let $\epsilon , \delta \in (0,1)$ be parameters. Then, our goal is then to compute z with $|z - z^*| = O(\epsilon n^2)$ with probability at least $1-\delta$ in constant time. We further assume that we have query access to A, $\boldsymbol{b}$, and $\boldsymbol{d}$, with which we can obtain their entry by specifying an index. We note that $\boldsymbol{z}^*$ is typically $\Theta (n^2)$ because $\langle \boldsymbol{v}, A\boldsymbol{v}\rangle$ consists of $\Theta (n^2)$ terms, and $\langle \boldsymbol{v}, \mathrm {diag}(\boldsymbol{d})\boldsymbol{v}\rangle$ and $\langle \boldsymbol{b},\boldsymbol{v}\rangle$ consist of $\Theta (n)$ terms. Hence, we can regard the error of $\Theta (\epsilon n^2)$ as an error of $\Theta (\epsilon )$ for each term, which is reasonably small in typical situations.

Let $\cdot |_S$ be an operator that extracts a submatrix (or subvector) specified by an index set $S\subset \mathbb {N}$. Our algorithm is then given by Algorithm 1, where the parameter $s := s(\epsilon ,\delta )$ is determined later. In other words, we sample a constant number of indices from the set [n], and then solve the problem (3.1) restricted to these indices. Note that the number of queries and the time complexity are $O(s^2)$ and $\mathrm {poly}(s)$, respectively.

The goal of the rest of this section is to show the following approximation guarantee of Algorithm 1.

Theorem 3.1

Let $\boldsymbol{v}^*$ and $z^*$ be an optimal solution and the optimal value, respectively, of problem (3.1). By choosing $s(\epsilon ,\delta ) = 2^{\Theta (1/\epsilon ^2)}+\Theta (\log \frac{1}{\delta }\log \log \frac{1}{\delta })$, with probability at least $1-\delta$, a sequence S of s indices independently and uniformly sampled from [n] satisfies the following: Let $\tilde{\boldsymbol{v}}^*$ and $\tilde{z}^*$ be an optimal solution and the optimal value, respectively, of the problem $\min _{\boldsymbol{v} \in \mathbb {R}^s}p_{s,A|_S,\boldsymbol{d}|_S,\boldsymbol{b}|_S}(\boldsymbol{v})$. Then, we have

$$\begin{aligned} \Bigl |\frac{n^2}{s^2}\tilde{z}^* - z^*\Bigr | \le \epsilon LM^2n^2, \end{aligned}$$

where

$$\begin{aligned} L = \max \left\{ \max _{i,j}|A_{ij}|,\max _i |d_i|, \max _i |b_i|\right\} \text { and } M = \max \left\{ \max _{i \in [n]}|v^*_i|, \max _{i \in [n]}|\tilde{v}^*_i|\right\} . \end{aligned}$$

We can show that M is bounded when A is symmetric and full rank. To see this, we first note that we can assume $A + n\mathrm {diag}(\boldsymbol{d})$ is positive-definite, as otherwise $p_{n,A,\boldsymbol{d},\boldsymbol{b}}$ is not bounded and the problem is uninteresting. Then, for any set $S \subseteq [n]$ of s indices, $(A+n\mathrm {diag}(\boldsymbol{d}))|_S$ is again positive-definite because it is a principal submatrix. Hence, we have $\boldsymbol{v}^* = (A+n\mathrm {diag}(\boldsymbol{d}))^{-1}n\boldsymbol{b}/2$ and $\tilde{\boldsymbol{v}}^* = (A|_S+n\mathrm {diag}(\boldsymbol{d}|_S))^{-1}n\boldsymbol{b}|_S/2$, which means that M is bounded.

3.1 Proof of Theorem 3.1

To use dikernels in our analysis, we first introduce a continuous version of $p_{n,A,\boldsymbol{d},\boldsymbol{b}}$. The real-valued function $P_{n,A,\boldsymbol{d},\boldsymbol{b}}$ on the functions $f:[0,1]\rightarrow \mathbb {R}$ is defined as

$$\begin{aligned} P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f) = \langle f,\mathcal {A} f\rangle + \langle f^2,\mathcal {D} 1\rangle + \langle f,\mathcal {B} 1\rangle , \end{aligned}$$

where $\mathcal {D}$ and $\mathcal {B}$ are the dikernels corresponding to $\boldsymbol{d} \boldsymbol{1}^\top$ and $\boldsymbol{b} \boldsymbol{1}^\top$, respectively, $f^2:[0,1]\rightarrow \mathbb {R}$ is a function such that $f^2(x) = f(x)^2$ for every $x \in [0,1]$ and $1:[0,1] \rightarrow \mathbb {R}$ is a constant function that has a value of 1 everywhere. The following lemma states that the minimizations of $p_{n,A,\boldsymbol{d},\boldsymbol{b}}$ and $P_{n,A,\boldsymbol{d},\boldsymbol{b}}$ are equivalent:

Lemma 3.3

Let $A \in \mathbb {R}^{n \times n}$ be a matrix and $\boldsymbol{d},\boldsymbol{b} \in \mathbb {R}^{n \times n}$ be vectors. Then, we have

$$\begin{aligned} \min _{\boldsymbol{v} \in {[-M,M]}^n}p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v}) = n^2 \cdot \inf _{f:[0,1] \rightarrow [-M,M]}P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f). \end{aligned}$$

for any $M > 0$.

Proof

First, we show that $n^2 \cdot \inf _{f:[0,1] \rightarrow [-M,M]}P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f) \le \min _{\boldsymbol{v} \in {[-M,M]}^n}p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v})$. Given a vector $\boldsymbol{v} \in {[-M,M]}^n$, we define $f: [0,1] \rightarrow [-M,M]$ as $f(x) = v_{i_n(x)}$. Then,

$$\begin{aligned} \langle f,\mathcal {A}f\rangle&= \sum _{i,j \in [n]} \int _{I^n_i}\int _{I^n_j}A_{ij} f(x)f(y) \mathrm {d} x \mathrm {d} y = \frac{1}{n^2}\sum _{i,j \in [n]} A_{ij}v_i v_j = \frac{1}{n^2}\langle \boldsymbol{v},A\boldsymbol{v}\rangle , \\ \langle f^2,\mathcal {D} 1\rangle&= \sum _{i,j \in [n]} \int _{I^n_i}\int _{I^n_j}d_i {f(x)}^2 \mathrm {d} x \mathrm {d} y = \sum _{i \in [n]} \int _{I^n_i}d_i {f(x)}^2 \mathrm {d} x \\&= \frac{1}{n}\sum _{i \in [n]}d_i v_i^2 = \frac{1}{n}\langle \boldsymbol{v},\mathrm {diag}(\boldsymbol{d}) \boldsymbol{v}\rangle , \\ \langle f,\mathcal {B}1\rangle&= \sum _{ i,j \in [n]} \int _{I^n_i}\int _{I^n_j}b_i f(x) \mathrm {d} x \mathrm {d} y = \sum _{ i \in [n]} \int _{I^n_i}b_i f(x) \mathrm {d} x = \frac{1}{n}\sum _{i \in [n]}b_i v_i = \frac{1}{n}\langle \boldsymbol{v},\boldsymbol{b}\rangle . \end{aligned}$$

Hence, we have $n^2 P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f) \le p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v})$.

Next, we show that $\min _{\boldsymbol{v} \in [-M,M]^n}p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v}) \le n^2 \cdot \inf _{f:[0,1] \rightarrow [-M,M]}P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f)$. Let $f:[0,1] \rightarrow [-M,M]$ be a measurable function. For $x \in [0,1]$, we then have

$$\begin{aligned}&\frac{\partial P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f(x))}{\partial f(x)} \\&= \sum _{i \in [n]}\int _{I^n_i}A_{i i_n(x)}f(y)\mathrm {d} y + \sum _{j \in [n]}\int _{I^n_j}A_{i_n(x)j}f(y)\mathrm {d} y + 2d_{i_n(x)}f(x) + b_{i_n(x)}. \end{aligned}$$

Note that the form of this partial derivative depends on only $i_n(x)$. Hence, in the optimal solution $f^*:[0,1] \rightarrow [-M,M]$, we can assume $f^*(x) = f^*(y)$ if $i_n(x) = i_n(y)$. In other words, $f^*$ is constant on each of the intervals $I^n_1,\ldots ,I^n_n$. For such $f^*$, we define the vector $\boldsymbol{v}\in \mathbb {R}^n$ as $v_i = f^*(x)$, where $x \in [0,1]$ is any element in $I^n_i$. Then, we have

$$\begin{aligned} \langle \boldsymbol{v},A\boldsymbol{v}\rangle&= \sum _{i,j\in [n]}A_{ij}v_i v_j = n^2\sum _{i,j\in [n]}\int _{I^n_i}\int _{I^n_j}A_{ij}f^*(x)f^*(y)\mathrm {d} x \mathrm {d} y = n^2\langle f^*,\mathcal {A}f^*\rangle , \\ \langle \boldsymbol{v},\mathrm {diag}(\boldsymbol{d}) \boldsymbol{v}\rangle&= \sum _{i\in [n]}d_i v_i^2 = n\sum _{i\in [n]}\int _{I^n_i}d_i {f^*(x)}^2\mathrm {d} x = n\langle {(f^*)}^2,\mathcal {D}1\rangle ,\\ \langle \boldsymbol{v},\boldsymbol{b}\rangle&= \sum _{i\in [n]}b_i v_i = n\sum _{i\in [n]}\int _{I^n_i}b_i f^*(x)\mathrm {d} x = n\langle f^*,\mathcal {B}1\rangle . \end{aligned}$$

Hence, we have $p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v}) \le n^2 P_{n,A,\boldsymbol{d},\boldsymbol{b}}(f^*)$.

Proof

(of Theorem 3.1) We instantiate Lemma 3.2 with $s = 2^{\Theta (1/\epsilon ^2)}+\Theta (\log \frac{1}{\delta }\log \log \frac{1}{\delta })$ and the dikernels $\mathcal {A}$, $\mathcal {D}$, and $\mathcal {B}$. Then, with probability at least $1-\delta$, there exists a measure-preserving bijection $\pi :[0,1]\rightarrow [0,1]$ such that

$$\begin{aligned} \max \Bigl \{ |\langle f,(\mathcal {A} - \pi (\mathcal {A}|_S))f\rangle |, |\langle f^2,(\mathcal {D} - \pi (\mathcal {D}|_S))1\rangle | , |\langle f,(\mathcal {B} - \pi (\mathcal {B}|_S))1\rangle |\Bigr \} \le \frac{\epsilon LM^2}{3} \end{aligned}$$

for any function $f:[0,1]\rightarrow [-M,M]$. Conditioned on this event, we have

$$\begin{aligned} \tilde{z}^*&= \min _{\boldsymbol{v} \in \mathbb {R}^s}p_{s,A|_S,\boldsymbol{d}|_S,\boldsymbol{b}|_S}(\boldsymbol{v}) = \min _{\boldsymbol{v} \in {[-M,M]}^s}p_{s,A|_S,\boldsymbol{d}|_S,\boldsymbol{b}|_S}(\boldsymbol{v})\\&= s^2 \cdot \inf _{f:[0,1]\rightarrow [-M,M]} P_{s,A|_S,\boldsymbol{d}|_S,\boldsymbol{b}|_S} (f) \qquad \qquad \quad \quad {\text {(By Lemma~3)}} \\&= s^2 \cdot \inf _{f:[0,1]\rightarrow [-M,M]}\Bigl (\langle f,(\pi (\mathcal {A}|_S) - \mathcal {A})f\rangle + \langle f,\mathcal {A} f\rangle + \langle f^2,(\pi (\mathcal {D}|_S) - \mathcal {D})1\rangle + \\&\qquad \qquad \qquad \qquad \langle f^2,\mathcal {D}1\rangle + \langle f,(\pi (\mathcal {B}|_S) - \mathcal {B})1\rangle + \langle f,\mathcal {B}1\rangle \Bigr )\\&\le s^2 \cdot \inf _{f:[0,1]\rightarrow [-M,M]} \Bigl (\langle f,\mathcal {A} f\rangle +\langle f^2,\mathcal {D}1 \rangle +\langle f,\mathcal {B}1 \rangle \pm \epsilon LM^2 \Bigr )\\&= \frac{s^2}{n^2} \cdot \min _{\boldsymbol{v} \in [-M,M]^n} p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v}) \pm \epsilon LM^2\,s^2. \quad \quad \quad \quad {\text {(By Lemma~3)}} \\&= \frac{s^2}{n^2} \cdot \min _{\boldsymbol{v} \in \mathbb {R}^n} p_{n,A,\boldsymbol{d},\boldsymbol{b}}(\boldsymbol{v}) \pm \epsilon LM^2\,s^2 = \frac{s^2}{n^2}z^* \pm \epsilon LM^2\,s^2. \end{aligned}$$

Rearranging the inequality, we obtain the desired result.

4 Tensor Decomposition

Background

We say that a tensor (or a multidimensional array) is of order K if it is a K-dimensional array. Each dimension is called a mode in tensor terminology. Tensor decomposition, which approximates the input tensor by a number of smaller tensors, is a fundamental tool for dealing with large tensors because it drastically reduces memory usage.

Among the many existing tensor decomposition methods, Tucker decomposition [11] is a popular choice. To some extent, Tucker decomposition is analogous to singular-value decomposition (SVD). Whereas SVD decomposes a matrix into left and right singular vectors that interact via singular values, Tucker decomposition of an order-K tensor consists of K factor matrices that interact via the so-called core tensor. The key difference between SVD and Tucker decomposition is that, in the latter, the core tensor does not need to be diagonal and its “rank” can differ for each mode. We refer to the size of the core tensor, which is a K-tuple, as the Tucker rank of a Tucker decomposition.

We are usually interested in obtaining factor matrices and a core tensor to minimize the residual error—the error between the input and low-rank approximated tensors. Sometimes, however, knowing the residual error itself is a task of interest. The residual error tells us how suitable a low-rank approximation is to approximate the input tensor in the first place, and is also useful to predetermine the Tucker rank. In real applications, Tucker ranks are not explicitly given, and we must select them by considering the tradeoff between space usage and approximation accuracy. For example, if the selected Tucker rank is too small, we risk losing essential information in the input tensor, whereas if the selected Tucker rank is too large, the computational cost of computing the Tucker decomposition (even if we allow for approximation methods) increases considerably along with space usage. As with the case of the matrix rank, one might think that a reasonably good Tucker rank can be found using a grid search. Unfortunately, grid search for an appropriate Tucker rank is challenging because, for an order-K tensor, the Tucker rank consists of K free parameters and the search space grows exponentially in K. Hence, we want to evaluate each grid point as quickly as possible.

Although several practical algorithms have been proposed, such as the higher order orthogonal iteration (HOOI) [3], they are not sufficiently scalable. For each mode, HOOI iteratively applies SVD to an unfolded tensor—a matrix that is reshaped from the input tensor. Given an $N_1\times \cdots \times N_K$ tensor, the computational cost is hence $O(K \max _k N_k \cdot \prod _k N_k)$, which crucially depends on the input size $N_1,\dots ,N_K$. Although there are several approximation algorithms, their computational costs are still intensive.

Constant-time algorithm for the Tucker fitting problem

The problem of computing the residual error is formalized as the following Tucker fitting problem: Given an order-K tensor $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$ and integers $R_k \le N_k\;(k = 1,\dots ,K)$, we want to compute the following normalized residual error:

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(X) := \mathop {\text {min}}_{G \in \mathbb {R}^{R_1 \times \cdots \times R_K}, {\{U^{(k)} \in \mathbb {R}^{N_k \times R_k}\}}_{k \in [K]}} \frac{\Bigl \vert {X} - [[G; U^{(1)},\ldots ,U^{(K)} ]]\Bigr \vert _F^2}{\prod _{k \in [K]}N_k }, \end{aligned}$$

(3.2)

where $[[G; U^{(1)},\ldots ,U^{(K)}]]\in \mathbb {R}^{N_1 \times \cdots \times N_K}$ is an order-K tensor, defined as

$$\begin{aligned}{}[[G; U^{(1)},\ldots ,U^{(K)}]]_{i_1\cdots i_K} = \sum _{r_1 \in [R_1], \ldots , r_K \in [R_K]} G_{r_1\cdots r_K} \prod _{k \in [K]} U^{(k)}_{i_k r_k} \end{aligned}$$

for every $i_1 \in [N_1],\ldots ,i_K \in [N_K]$. Here, G is the core tensor, and $U^{(1)},\ldots ,U^{(K)}$ are the factor matrices. Note that we are not concerned with computing the minimizer, but only want to compute the minimum value. In addition, we do not need the exact minimum. Indeed, a rough estimate still helps to narrow down promising rank candidates. The question here is how quickly we can compute the normalized residual error $\ell _{R_1,\ldots ,R_K}(X)$ with moderate accuracy.

In this section, we consider the following simple sampling algorithm, and show that it can be used to approximately solve the Tucker fitting problem. First, given an order-K tensor $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$, Tucker rank $(R_1,\ldots ,R_K)$, and sample size $s\in \mathbb {N}$, we sample a sequence of indices $S_k = (x^{k}_1,\ldots ,x^{k}_s)$ uniformly and independently from $[N_k]$ for each mode $k\in [K]$. We then construct a mini-tensor $X|_{S_1,\ldots ,S_K}\in \mathbb {R}^{s \times \cdots \times s}$, where ${(X|_{S_1,\ldots ,S_K})}_{i_1,\ldots ,i_K} = X_{x^{1}_{i_1}\ldots ,x^{K}_{i_K}}$. Finally, we compute $\ell _{R_1,\ldots ,R_K}(X|_{S_1,\ldots ,S_K})$ using an arbitrary solver, such as HOOI, and output the obtained value. The details are provided in Algorithm 2. Note that the time complexity for computing $\ell _{R_1,\ldots ,R_K}(X|_{S_1,\ldots ,S_K})$ does not depend on the input size $N_1,\dots ,N_K$ but rather on the sample size s, meaning that the algorithm runs in constant time, regardless of the input size.

The goal of the rest of this section is to show the following approximation guarantee of Algorithm 2.

Theorem 3.2

Let $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$ be a tensor, $R_1,\ldots ,R_K$ be integers, and $\epsilon ,\delta \in (0,1)$. For $s(\epsilon ,\delta ) = 2^{\Theta (1/\epsilon ^{2K-2})}+\Theta (\log \frac{1}{\delta }\log \log \frac{1}{\delta })$, we have the following. Let $S_1,\ldots ,S_K$ be sequences of indices as defined in Algorithm 2. Let $(G^*,U^*_1,\ldots ,U^*_K)$ and $(\tilde{G}^*,\tilde{U}^*_1,\ldots ,\tilde{U}^*_K )$ be minimizers of problem (3.2) on X and $X|_{S_1,\ldots ,S_K}$ for which the factor matrices are orthonormal, respectively. Then we have

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(X|_{S_1,\ldots ,S_K}) = \ell _{R_1,\ldots ,R_K}(X) \pm O(\epsilon L^2 (1+2MR)), \end{aligned}$$

with probability at least $1-\delta$, where $L = \vert {X}\vert _{\max }$, $M = \max \{\vert {G}^*\vert _{\max }, \vert \tilde{G}^*\vert _{\max }\}$, and $R=\prod _{k \in [K]}R_k$.

We remark that, for the matrix case (i.e., $K=2$), $\vert {G}^*\vert _{\max }$ and $\vert \tilde{G}^*\vert _{\max }$ are equal to the maximum singular values of the original and sampled matrices, respectively.

4.1 Preliminaries

Let $X \in \mathbb {R}^{N_1 \times \cdots N_K}$ be a tensor. We define

$$\begin{aligned} \vert {X}\vert _F&= \sqrt{\sum _{i_1,\ldots ,i_K} X_{i_1\cdots i_K}^2}, \qquad \qquad \quad \quad {\text {(Frobenius norm)}} \\ \vert {X}\vert _{\max }&= \max \limits _{i_1 \in [N_1],\ldots ,i_K \in [N_K]}|X_{i_1\cdots i_K}|,\qquad \qquad \quad \quad {\text {(Max norm)}} \\ \vert {X}\vert _\square&= \max \limits _{S_1 \subseteq [N_1],\ldots ,S_K \subseteq [N_K] }\left| \sum \limits _{i_1 \in S_1,\ldots ,i_K \in S_K} X_{i_1 \cdots i_K}\right| . \quad \quad \quad \quad {\text {(Cut norm)}} \end{aligned}$$

We note that these norms satisfy the triangle inequality.

For a vector $\boldsymbol{v} \in \mathbb {R}^n$ and a sequence $S = (x_1,\ldots ,x_s)$ of indices in [n], we define the restriction $\boldsymbol{v}|_S \in \mathbb {R}^s$ of $\boldsymbol{v}$ as ${(\boldsymbol{v}|_S)}_i = v_{x_i}$ for $i \in [s]$. Let $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$ be a tensor, and $S_k = (x^{k}_1,\ldots ,x^{k}_s)$ be a sequence of indices in $[N_k]$ for each mode $k \in [K]$. Then, we define the restriction $X|_{S_1,\ldots ,S_K} \in \mathbb {R}^{s \times \cdots \times s}$ of X to $S_1 \times \cdots \times S_K$ as ${(X|_{S_1,\ldots ,S_K})}_{i_1 \cdots i_K} = X_{x^{1}_{i_1},\ldots , x^{K}_{i_K}}$ for each $i_1 \in [N_1],\ldots ,i_K \in [N_k]$.

For a tensor $G {\in } \mathbb {R}^{R_1 \times \cdots \times R_K}$ and vector-valued functions ${\{F^{(k)}:[0,1] {\rightarrow } \mathbb {R}^{R_k} \}}_{k \in [K]}$, we define an order-K dikernel $[[G; F^{(1)},\ldots ,F^{(K)} ]]: {[0,1]}^K \rightarrow \mathbb {R}$ as

$$\begin{aligned}{}[[G; F^{(1)},\ldots ,F^{(K)} ]](x_1,\ldots ,x_K) = \sum _{r_1 \in [R_1],\ldots ,r_K \in [R_K]} G_{r_1,\ldots ,r_K} \prod _{k \in [K]} F^{(k)}{(x_k)}_{r_k} \end{aligned}$$

We note that $[[G; F^{(1)},\ldots ,F^{(K)} ]]$ is a continuous analogue of Tucker decomposition.

4.2 Proof of Theorem 3.2

To prove Theorem 3.2, we first consider the dikernel counterpart to the Tucker fitting problem, in which we want to minimize the following:

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(\mathcal {X}) := \inf _{G \in \mathbb {R}^{R_1 \times \cdots \times R_K}, {\{f^{(k)}: [0,1] \rightarrow \mathbb {R}^{R_k}\}}_{k \in [K]}} \Bigl \vert \mathcal {X} - [[G; f^{(1)},\ldots ,f^{(K)} ]]\Bigr \vert _F^2, \end{aligned}$$

(3.3)

The following lemma, which is proved in Sect. 3.4.3, states that the Tucker fitting problem and its dikernel counterpart have the same optimum values.

Lemma 3.4

Let $X \in \mathbb {R}^{N_1 \times \cdots \times N_K}$ be a tensor, and let $R_1,\ldots ,R_K \in \mathbb {N}$ be integers. Then, we have

$$\begin{aligned}&\ell _{R_1,\ldots ,R_K}(X) = \ell _{R_1,\ldots ,R_K}(\mathcal {X}). \end{aligned}$$

For a set of vector-valued functions $F = \{f^{(k)}:[0,1] \rightarrow \mathbb {R}^{R_k}\}_{k \in [K]}$, we define $\vert {F}\vert _{\max } = \max _{k \in [K], r \in [R_k],x \in [0,1]}f^{(k)}_{r}(x)$. For a dikernel $\mathcal {X}:{[0,1]}^K \rightarrow \mathbb {R}$, we define a dikernel $\mathcal {X}^2:{[0,1]}^K \rightarrow \mathbb {R}$ as $\mathcal {X}^2(\boldsymbol{x}) = {\mathcal {X}(\boldsymbol{x})}^2$ for every $\boldsymbol{x} \in {[0,1]}^K$. The following lemma, which is proved in Sect. 3.4.4, states that if $\mathcal {X}$ and $\mathcal {Y}$ are close in the cut norm, then the optimum values when the Tucker fitting problem is applied to them are also close.

Lemma 3.5

Let $\mathcal {X},\mathcal {Y}:{[0,1]}^K \rightarrow \mathbb {R}$ be dikernels with $\vert \mathcal {X} - \mathcal {Y}\vert _\square \le \epsilon$ and $\vert \mathcal {X}^2 - \mathcal {Y}^2\vert _\square \le \epsilon$. For $R_1,\ldots ,R_K \in \mathbb {N}$, we have

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(\mathcal {X}) = \ell _{R_1,\ldots ,R_K}(\mathcal {Y}) \pm 2\epsilon \Bigl (1 + R\bigl (\vert {G}_{\mathcal {X}}\vert _{\max } \vert {F}_{\mathcal {X}}\vert _{\max }^K + \vert {G}_{\mathcal {Y}}\vert _{\max } \vert {F}_{\mathcal {Y}}\vert _{\max }^K \bigr ) \Bigr ), \end{aligned}$$

where $(G_{\mathcal {X}},F_{\mathcal {X}} = \{f^{(k)}_{\mathcal {X}}\}_{k \in [K]})$ and $(G_{\mathcal {Y},}F_{\mathcal {Y} }= \{f^{(k)}_{\mathcal {Y}}\}_{k \in [K]})$ are solutions to problem (3.3) on $\mathcal {X}$ and $\mathcal {Y}$, respectively, which have objective values exceeding the infima by at most $\epsilon$, and $R = \prod _{k \in [K]}R_k$.

Proof

(of Theorem 3.2) We apply Lemma 3.2 to $\mathcal {X}$ and $\mathcal {X}^2$. Thus, with probability at least $1-\delta$, there exists a measure-preserving bijection $\pi :[0,1]\rightarrow [0,1]$ such that

$$\begin{aligned} \vert \mathcal {X} - \pi (\mathcal {X}|_{S_1,\ldots ,S_K})\vert _\square \le \epsilon L \quad \text {and} \quad \vert \mathcal {X}^2 - \pi (\mathcal {X}^2|_{S_1,\ldots ,S_K})\vert _\square \le \epsilon L^2. \end{aligned}$$

In the following, we assume that this has happened. By Lemma 3.5 and the fact that $\ell _{R_1,\ldots ,R_K}(\mathcal {X}|_{S_1,\ldots ,S_K}) = \ell _{R_1,\ldots ,R_K}(\pi (\mathcal {X}|_{S_1,\ldots ,S_K}))$, we have

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(\mathcal {X}|_{S_1,\ldots ,S_K}) = \ell _{R_1,\ldots ,R_K}(\mathcal {X}) \pm \epsilon L^2 \Bigl ( 1 + 2R (\vert {G}\vert _{\max } \vert {F}\vert _{\max }^K + \vert \tilde{G}\vert _{\max } \vert \tilde{F}\vert _{\max }^K ) \Bigr ), \end{aligned}$$

where $(G,F= \{f^{(k)}\}_{k \in [K]})$ and $(\tilde{G},\tilde{F}= \{\tilde{f}^{(k)}\}_{k \in [K]})$ are as in the statement of Lemma 3.5. From the proof of Lemma 3.4, we can assume that $\vert {G}\vert _{\max } = \vert {G}^*\vert _{\max }$, $\vert \tilde{G}\vert _{\max } = \vert \tilde{G}^*\vert _{\max }$, $\vert {F}\vert _{\max } \le 1$, and $\vert \tilde{F}\vert _{\max } \le 1$ (owing to the orthonormality of $U^*_1,\ldots ,U^*_K$ and $\tilde{U}^*_1,\ldots ,\tilde{U}^*_K$). It follows that

$$\begin{aligned} \ell _{R_1,\ldots ,R_K}(\mathcal {X}|_{S_1,\ldots ,S_K}) = \ell _{R_1,\ldots ,R_K}(\mathcal {X}) \pm \epsilon L^2 \Bigl ( 1 + 2 R (\vert {G}^*\vert _{\max } + \vert \tilde{G}^*\vert _{\max } ) \Bigr ). \end{aligned}$$

(3.4)

Then, we have

$$\begin{aligned}&\ell _{R_1,\ldots ,R_K}(X|_{S_1,\ldots ,S_K}) = \ell _{R_1,\ldots ,R_K}(\mathcal {X}|_{S_1,\ldots ,S_K}) \qquad \qquad \qquad \quad {\text {(By Lemma~4)}} \\&= \ell _{R_1,\ldots ,R_K}(\mathcal {X}) \pm \epsilon L^2 \Bigl (1 + 2R (\vert {G}^*\vert _{\max } + \vert \tilde{G}^*\vert _{\max } ) \Bigr ) \qquad \quad \quad {\text {(By~4)}} \\&= \ell _{R_1,\ldots ,R_K}(X) \pm \epsilon L^2 \Bigl (1 + 2R (\vert {G}^*\vert _{\max } + \vert \tilde{G}^*\vert _{\max } ) \Bigr ). \quad \quad \quad \quad {\text {(By Lemma~4)}} \end{aligned}$$

Hence, the proof is complete.

4.3 Proof of Lemma 3.4

We say that a vector-valued function $f:[0,1] \rightarrow \mathbb {R}^{R}$ is orthonormal if $\langle f_r,f_r \rangle = 1$ for every $r\in [R]$ and $\langle f_r,f_{r'}\rangle =0$ if $r \ne r'$. First, we calculate the partial derivatives of the objective function. We omit the proof because it is a straightforward (but tedious) calculation.

Lemma 3.6

Let $\mathcal {X} \in [0,1]^K \rightarrow \mathbb {R}$ be a dikernel, $G \in \mathbb {R}^{R_1 \times \cdots R_K}$ be a tensor, and $\{f^{(k)}:[0,1] \rightarrow \mathbb {R}^{R_k}\}_{k \in [K]}$ be a set of orthonormal vector-valued functions. Then, we have

$$\begin{aligned}&\frac{\partial }{\partial f^{(k_0)}_{r_0}(x_0)} \Bigl \vert \mathcal {X} - [[G; f^{(1)},\ldots ,f^{(K)} ]]\Bigr \vert _F^2 \\&= 2 \sum _{r_1,\ldots ,r_K:r_{k_0}=r_0}G_{r_1 \cdots r_K} \int _{{[0,1]}^K:x_{k_0}=x_0} \mathcal {X}(\boldsymbol{x}) \prod _{k \in [K] \setminus \{k_0\}}f^{(k)}_{r_k}(x_k) \mathrm {d}\boldsymbol{x} \\&\qquad - 2 \sum _{r_1,\ldots ,r_K}G_{r_1\cdots r_K} G_{r_1 \cdots r_{k_0-1} r_0 r_{k_0+1} \cdots r_K}f^{(k_0)}_{r_{k_0}}(x_0). \end{aligned}$$

Proof

(of Lemma 3.4) First, we show that (LHS) $\le$ (RHS). Consider a sequence of solutions for the continuous problem (3.3) for which the objective values attain the infimum. For Tucker decompositions, it is well known that there exists a minimizer for which the factor matrices $U^{(1)},\ldots ,U^{(K)}$ are orthonormal. By similar reasoning, we can show that the vector-valued functions $f^{(1)},\ldots ,f^{(K)}$ in each solution of the sequence are orthonormal. As the objective function is coercive with respect to tensor G, we can take a subsequence for which G converges. Let $G^*$ be the limit. Now, for any $\delta >0$, we can create a matrix $\tilde{G}$ by perturbing $G^*$ so that (i) by fixing G to $\tilde{G}$ in the continuous problem, the infimum increases only by $\delta$, and (ii) a matrix constructed from $\tilde{G}$ is invertible and has a condition number at least $\delta '=\delta '(\delta )>0$.

Now, consider a sequence of solutions for the continuous problem (3.3) with G fixed to $\tilde{G}$ for which the objective values attain the infimum. We can show that the partial derivatives converge to zero almost everywhere. For any $\epsilon > 0$, there then exists a solution $(\tilde{G}, f^{(1)},\ldots ,f^{(K)})$ in the sequence such that the partial derivatives are at most $\epsilon$ almost everywhere.

Then by Lemma 3.6, for any $k_0 \in [K]$, $r_0 \in [R_k]$, and almost all $x \in [0,1]$, we have

$$\begin{aligned}&\sum _{r_1,\ldots ,r_K}\tilde{G}_{r_1\cdots r_K} \tilde{G}_{r_1 \cdots r_{k_0-1} r_0 r_{k_0+1} \cdots r_K}f^{(k_0)}_{r_{k_0}}(x_0) \nonumber \\&= \sum _{r_1,\ldots ,r_K:r_{k_0}=r_0}\tilde{G}_{r_1 \cdots r_K} \int _{{[0,1]}^K:x_{k_0}=x_0} \mathcal {X}(\boldsymbol{x}) \prod _{k \in [K] \setminus \{k_0\}}f^{(k)}_{r_k}(x_k) \mathrm {d}\boldsymbol{x} \pm \epsilon (k_0,r_0,x), \end{aligned}$$

(3.5)

where $\epsilon (k_0,r_0,x)=O(\epsilon )$. Now, we consider a system of linear equations consisting of (3.5) for $r_0=1,\ldots ,R_{k_0}$, where the variables are $f_{1}^{k_0}(x_0),\ldots ,f_{R_{k_0}}^{k_0}(x_0)$. We can assume that the matrix involved in this system is invertible and has a positive condition number. For any $k \in [K]$, $r \in [R_k]$ and almost every pair $x,x' \in [0,1]$ with $i_{N_k}(x) = i_{N_k}(x')$, we then have $f^{(k_0)}_{r_0}(x) = f^{(k_0)}_{r_0}(x') \pm O(\epsilon / \delta ' )$. For each $k\in [K]$, we can define a matrix $U^{(k)} \in \mathbb {R}^{N_k \times R_k}$ as $U^{(k)}_{ir} = f^{(k)}_r(x)$, where $x \in [0,1]$ is an arbitrary value with $i_{N_k}(x) = i$. Then, we have

$$\begin{aligned}&\frac{1}{N}\Bigl \vert {X} - [[\tilde{G}; U^{(1)},\ldots ,U^{(K)}]]\Bigr \vert _F^2 = \frac{1}{N}\sum _{i_1,\ldots ,i_K} \Bigl (X_{i_1 \cdots i_K} - [[\tilde{G}; U^{(1)},\ldots ,U^{(K)}]]_{i_1\cdots i_K}\Bigr )^2 \\&= \sum _{i_1,\ldots ,i_K}\int _{I^{N_1}_{i_1} \times \cdots \times I^{N_K}_{i_K}} \Bigl (\mathcal {X}(\boldsymbol{x}) - [[\tilde{G}; f^{(1)},\ldots ,f^{(K)}]](\boldsymbol{x}) \pm O(\epsilon /\delta ')\Bigr )^2 \mathrm {d} \boldsymbol{x}\\&= \Bigl \vert \mathcal {X} - [[\tilde{G}; f^{(1)},\ldots ,f^{(K)}]]\Bigr \vert _F^2 \pm O(\epsilon ^2N/(\delta ')^2) \end{aligned}$$

for $N= \prod _{k \in [K]}N_k$. As the choice of $\epsilon$ and $\delta$ are arbitrary, we obtain (LHS) $\le$ (RHS).

Second, we show that (RHS) $\le$ (LHS). Let $U^{(k)} \in \mathbb {R}^{N_k \times R_k}\;(k \in [K])$ be matrices. We define a vector-valued function $f^{(k)} : [0,1] \rightarrow \mathbb {R}^{R_k}$ as $f^{(k)}_r(x) = U^{(k)}_{i_{N_k}(x)r}$ for each $k \in [K]$ and $r \in [R_k]$. Then, we have

$$\begin{aligned}&\Bigl \vert \mathcal {X} - [[G; f^{(1)},\ldots ,f^{(K)}]]\Bigr \vert _F^2 = \int _{{[0,1]}^K} \Bigl (\mathcal {X}(\boldsymbol{x}) - [[G; f^{(1)},\ldots ,,f^{(K)}]](\boldsymbol{x})\Bigr )^2 \mathrm {d} \boldsymbol{x} \\&= \sum _{i_1,\ldots ,i_K}\int _{\prod _{k \in [K]} I^{N_k}_{i_k}} \Bigl (\mathcal {X}(\boldsymbol{x}) - [[G; f^{(1)},\ldots ,f^{(K)}]](\boldsymbol{x})\Bigr )^2 \mathrm {d} \boldsymbol{x}\\&= \frac{1}{N}\sum _{i_1,\ldots ,i_K} \Bigl (X_{i_1 \cdots i_K} - [[G; U^{(1)},\ldots ,U^{(K)}]]_{i_1\cdots i_K} \Bigr )^2 \\&= \frac{1}{N}\Bigl \vert {X} - [G; U^{(1)}, \ldots ,U^{(K)}] \Bigr \vert _F^2, \end{aligned}$$

from which the claim follows.

4.4 Proof of Lemma 3.5

For a sequence of functions $f^{(1)},\ldots ,f^{(K)}$, we define their tensor product $\bigotimes _{k \in [K]}f^{(k)} \in {[0,1]}^K \rightarrow \mathbb {R}$ as $\bigotimes _{k \in [K]}f^{(k)}(x_1,\ldots ,x_K) = \prod _{k \in [K]}f^{(k)}(x_k)$, which is a dikernel of order-K.

The cut norm is useful for bounding the absolute value of the inner product between a tensor and a tensor product:

Lemma 3.7

Let $\epsilon \ge 0$ and $\mathcal {W}:{[0,1]}^K\rightarrow \mathbb {R}$ be a dikernel with $\vert \mathcal {W}\vert _\square \le \epsilon$. Then, for any functions $f^{(1)},\ldots ,f^{(K)}:[0,1] \rightarrow [-L,L]$, we have $|\langle \mathcal {W}, \bigotimes _{k\in [K]} f^{(k)}\rangle | \le \epsilon L^K$.

Proof

For $\tau \in \mathbb {R}$ and the function $h:[0,1]\rightarrow \mathbb {R}$, let $L_\tau (h) := \{ x \in [0,1] \mid h(x) = \tau \}$ be the level set of h at $\tau$. For $f'^{(i)} = f^{(i)}/L$, we have

$$\begin{aligned}&\left| \left\langle \mathcal {W}, \bigotimes _{k \in [K]} f^{(k)} \right\rangle \right| = L^K \left| \left\langle \mathcal {W}, \bigotimes _{k \in [K]} f'^{(k)} \right\rangle \right| \\&= L^K\left| \int _{{[-1,1]}^K}\prod _{k \in [K]}\tau _k \int _{\prod _{k \in [K]}L_{\tau _k}(f'^{(k)})} \mathcal {W}(\boldsymbol{x}) \mathrm {d} \boldsymbol{x} \mathrm {d} \boldsymbol{\tau } \right| \\&\le L^K\int _{{[-1,1]}^K}\prod _{k \in [K]}|\tau _k| \left| \int _{\prod _{k \in [K]}L_{\tau _k}(f'^{(k)})} \mathcal {W}(\boldsymbol{x}) \mathrm {d} \boldsymbol{x} \mathrm {d} \boldsymbol{\tau } \right| \\&\le \epsilon L^K \int _{{[-1,1]}^K} \prod _{k\in [K]}|\tau _k| \mathrm {d} \boldsymbol{\tau } = \epsilon L^K. \end{aligned}$$

Thus, we have the following:

Lemma 3.8

Let $\mathcal {X},\mathcal {Y}:{[0,1]}^K \rightarrow \mathbb {R}$ be dikernels with $\vert \mathcal {X} - \mathcal {Y}\vert _\square \le \epsilon$ and $\vert \mathcal {X}^2 - \mathcal {Y}^2\vert _\square \le \epsilon$, where $\mathcal {X}^2(\boldsymbol{x}) = {\mathcal {X}(\boldsymbol{x})}^2$ and $\mathcal {Y}^2(\boldsymbol{x}) = {\mathcal {Y}(\boldsymbol{x})}^2$ for every $\boldsymbol{x} \in {[0,1]}^K$. Then, for any tensor $G \in \mathbb {R}^{R_1 \times \cdots \times R_K}$ and a set of vector-valued functions $F = \{f^{(k)}:[0,1] \rightarrow \mathbb {R}^{R_k}\}_{k \in [K]}$, we have

$$\begin{aligned} \Bigl \vert \mathcal {X} - [[G; f^{(1)},\ldots ,f^{(K)} ]]\Bigr \vert _F^2 = \Bigl \vert \mathcal {Y} - [[G; f^{(1)},\ldots ,f^{(K)} ]]\Bigr \vert _F^2 \pm \epsilon \Bigl (1 + 2 R \vert {G}\vert _{\max } \vert {F}\vert _{\max }^K \Bigr ), \end{aligned}$$

where $R = \prod _{k \in [K]}R_K$.

Proof

We have

$$\begin{aligned}&\left| \bigl \vert \mathcal {X} - [[G; f^{(1)},\ldots ,f^{(K)}]]\bigr \vert _F^2 - \bigl \vert \mathcal {Y} - [[G; f^{(1)},\ldots ,f^{(K)} ]]\bigr \vert _F^2\right| \\&= \Biggl |\int _{{[0,1]}^K} {\Bigl (\mathcal {X}(\boldsymbol{x}) - [[G; f^{(1)},\ldots ,f^{(K)} ]](\boldsymbol{x})\Bigr )}^2 \mathrm {d} \boldsymbol{x} \\&\qquad - \int _{{[0,1]}^K} {\Bigl (\mathcal {Y}(\boldsymbol{x}) - [[G; f^{(1)},\ldots ,f^{(K)} ]](\boldsymbol{x})\Bigr )}^2 \mathrm {d} \boldsymbol{x} \Biggr |\\&= \left| \int _{{[0,1]}^K} \Bigl ({\mathcal {X}(\boldsymbol{x})}^2 - {\mathcal {Y}(\boldsymbol{x})}^2\Bigr ) \mathrm {d} \boldsymbol{x} - 2 \int _{{[0,1]}^K} (\mathcal {X}(\boldsymbol{x}) - \mathcal {Y}(\boldsymbol{x})) [[G; f^{(1)},\ldots ,f^{(K)}]](\boldsymbol{x}) \mathrm {d} \boldsymbol{x} \right| \\&\le \vert \mathcal {X}^2 - \mathcal {Y}^2\vert _\square + 2\sum _{r_1 \in [R_1],\ldots , r_k \in [R_k] } |G_{r_1 \cdots r_K}| \cdot \left| \left\langle \mathcal {X} - \mathcal {Y}, \bigotimes _{k \in [K]} f^{(k)}_{r_k} \right\rangle \right| \\&\le \epsilon + 2 \epsilon R \vert {G}\vert _{\max } \vert {F}\vert _{\max }^K \end{aligned}$$

by Lemma 3.7.

Proof

(of Lemma 3.5) By Lemma 3.8, we have

$$\begin{aligned}&\Bigl \vert \mathcal {Y} - [[G_{\mathcal {Y}}; f^{(1)}_{\mathcal {Y}},\ldots ,f^{(K)}_{\mathcal {Y}}]]\Bigr \vert _F^2 \le \Bigl \vert \mathcal {Y} - [[G_{\mathcal {X}}; f^{(1)}_{\mathcal {X}},\ldots ,f^{(K)}_{\mathcal {X}}]]\Bigr \vert _F^2 + \epsilon \\&\le \Bigl \vert \mathcal {X} - [[G_{\mathcal {X}}; f^{(1)}_{\mathcal {X}},\ldots ,f^{(K)}_{\mathcal {X}}]]\Bigr \vert _F^2 + \Bigl (2\epsilon + 2 \epsilon R\vert {G}_{\mathcal {X}}\Vert _{\max } \Vert F_{\mathcal {X}}\Vert _{\max }^K \Bigr ). \end{aligned}$$

Similarly, we have

$$\begin{aligned}&\Bigl \Vert \mathcal {X} - [[G_{\mathcal {X}}; f^{(1)}_{\mathcal {X}},\ldots ,f^{(K)}_{\mathcal {X}}]]\Bigr \Vert _F^2 \le \Bigl \Vert \mathcal {X} - [[G_{\mathcal {Y}}; f^{(1)}_{\mathcal {Y}},\ldots ,f^{(K)}_{\mathcal {Y}}]]\Bigr \Vert _F^2 + \epsilon \\&\le \Bigl \Vert \mathcal {Y} - [[G_{\mathcal {Y}}; f^{(1)}_{\mathcal {Y}},\ldots ,f^{(K)}_{\mathcal {Y}}]]\Bigr \Vert _F^2 + \Bigl (2\epsilon + 2 \epsilon R\Vert G_{\mathcal {Y}}\Vert _{\max } \Vert F_{\mathcal {Y}}\Vert _{\max }^K \Bigr ). \end{aligned}$$

Hence, the claim follows.