Optimization of Evacuation and Walking-Home Routes from Osaka City After a Nankai Megathrust Earthquake Using Road Network Big Data

Abstract

When a disaster such as a large earthquake occurs, the resulting breakdown in public transportation leaves urban areas with many people who are struggling to return home. With people from various surrounding areas gathered in the city, unusually heavy congestion may occur on the roads when the commuters start to return home all at once on foot. In this chapter, it is assumed that a large earthquake caused by the Nankai Trough occurs at 2 p.m. on a weekday in Osaka City, where there are many commuters. We then assume a scenario in which evacuation from a resulting tsunami is carried out in the flooded area and people return home on foot in the other areas. At this time, evacuation and returning-home routes with the shortest possible travel times are obtained by solving the evacuation planning problem. However, the road network big data for Osaka City make such optimization difficult. Therefore, we propose methods for simplifying the large network while keeping those properties necessary for solving the optimization problem and then recovering the network. The obtained routes are then verified by large-scale pedestrian simulation, and the effect of the optimization is verified.

1 Introduction

When a disaster such as a large earthquake occurs, the resulting breakdown in public transportation leaves urban areas with many people who are struggling to return home. With people from various surrounding areas gathered in the city, unusually heavy congestion may occur on the roads when the commuters start to return home all at once on foot. In Japan, the Great East Japan Earthquake on March 11, 2011 left many people in central Tokyo unable to return home, and roads were flooded with pedestrians attempting to do so. After the Osaka North Earthquake on June 18, 2018, the Shin-Yodogawa Bridge and its surroundings were extremely congested by displaced people crossing the Yodo River from Umeda.

From reflecting on such confusion, many local governments have already decided on countermeasures for people who are struggling to return home [16]. Common among these countermeasures is that people who need to return home from their places of work are urged not to do so immediately after the disaster but rather to remain in place. Meanwhile, although it is known empirically that great confusion arises when difficulties in returning home occur, the associated countermeasures tend to be approximate because it is not known how much congestion occurs and where until after the disaster has occurred. Pedestrian simulation of the whole city would seem useful in such cases, but this has not been attempted until recently because doing so requires large-scale and detailed data and a high-speed calculation environment. However, Hiroi et al. carried out a simulation of mass returning-home behavior on foot after a large earthquake for an area within 40 km from Tokyo Station [3].

In the case of western Japan, such as Osaka City, an earthquake originating from the Nankai Trough is the most dangerous. In Osaka City, the resulting tsunami is predicted to reach the shore in 1 h and 50 minutes and flood about half of the city [14]. One of the major problems with the tsunami is that it will travel up the Yodo River in the northern part of Osaka City and spread to the coastal area. As mentioned above, people returning home after the 2018 Northern Osaka Earthquake became congested around bridges crossing the Yodo River, a phenomena that Kawagishi and Takizawa predicted by means of a large-scale simulation of returning home from Osaka City [7].

However, if the timings of the tsunami flooding and the movement of people overlap, a large-scale secondary disaster may occur. Therefore, in Osaka City, it is necessary to consider risks such as delayed escape from tsunami along with the countermeasures for people who are struggling to return home, but it is difficult to say that the current countermeasures consider such risks. The purpose of the study by Kawagishi and Takizawa [7] was to investigate how a Nankai Trough earthquake would affect the return home of commuters in Osaka City. The results confirmed that bridges over the Yodo River from the center of Osaka City would be congested for a long time with people crossing, and that there would be a danger of delayed escape from tsunami by remaining in the vicinity. However, that study did not consider evacuation behavior from tsunami, and it assumed that people who walk home take the shortest route to do so. Therefore, problems remained, such as excessive concentration of pedestrians on specific roads and bridges.

In the present study, it is assumed that a large earthquake caused by the Nankai Trough occurs at 2 p.m. on a weekday in Osaka City, where there are many commuters. We then assume a scenario in which evacuation from tsunami is carried out in the flooded area and people return home on foot in the other areas. At this time, the evacuation and returning-home routes with the shortest possible travel times are obtained by solving the evacuation planning problem [8, 19]. However, the road network big data for Osaka City make such optimization difficult. Therefore, we propose methods for simplifying the large network while keeping those properties that are necessary for solving the optimization problem and then recovering the network. The obtained routes are then verified by large-scale pedestrian simulation, and the effect of the optimization is verified.

The remainder of this chapter is organized as follows. The next section explains the evacuation planning model. Next, the pedestrian simulation model for a large-scale network model is described. Then, the results are discussed, and conclusions and suggestions for future work are presented.

2 Quickest Evacuation Planning Problem

This section describes the quickest evacuation planning problem based on a dynamic network in which the flow rate changes over time. Meanwhile, a network in which the flow rate does not change over time is called a static network.

2.1 Dynamic Network

We define a directed graph $D = (V,E)$ for vertex set V and edge set E. In V, the sources (i.e., the starting vertices of the flow) and sinks (i.e., the destinations) are given. A directed edge with a start vertex $u \in V$ and an end vertex $v \in V$ is expressed as $e = (u,v)$, and the start vertex of e is expressed as tail(e) and the end vertex is expressed as head(e). For vertex $v \in V$, $\delta _{D}^{+}(v) \subset E$ is defined as a set of edges going out of v and $\delta _{D}^{-}(v) \subset E$ is a set of edges going toward v. For each edge $e \in E$, we define a travel time function $\tau : E \rightarrow \mathbb {Z}_+$ that denotes the time required to flow on e from tail(e) to head(e). The maximum value of the flow on e is denoted by the capacity function $c: E \rightarrow \mathbb {R}_+$. For each vertex $v \in V$, we define a supply function $b: V \rightarrow \mathbb {R}_+$ that denotes the amount of supply at that vertex, and the set of vertices with one or more supplies as $S^+ \subseteq V$. Furthermore, the sink set $S^- \subseteq V$ is also defined.

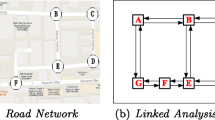
Using the above definitions, a dynamic network $N = (D, c, \tau , b, S^+, S^-)$ is defined, and Fig. 15.1 shows an example of N. Assuming application to evacuation planning, the flow denotes the movement of evacuees, a sink denotes an evacuation site, and the flow reaching a sink denotes the accommodation of evacuees at that evacuation site. An evacuee who arrives at a vertex moves on an edge and is deemed evacuated upon reaching a sink. The total number of evacuees at point $v \in V$ is regarded as the supply at that point b(v).

Fig. 15.1

Example of a dynamic network N

Next, we define a dynamic flow $f: E \times \mathbb {Z}_+ \rightarrow \mathbb {R}_+$ on dynamic network N as the flow rate entering the edge $e \in E$ at discrete time $\theta \in \mathbb {Z}_+$, and it is expressed as $f(e, \theta )$. Note that the flow that enters tail(e) of edge e at time $\theta$ arrives at head(e) at time $\theta + \tau (e)$.

On the dynamic flow, the following three constraints are defined. First, the capacity constraint is given by

$$\begin{aligned} 0 \le f(e,\theta ) \le c(e) \;\; (\forall e \in E, \theta \in \mathbb {Z}_+), \end{aligned}$$

(15.1)

then the flow conservation law is given by

$$\begin{aligned} \sum _{e \in \delta _{D}^{+}(v)} \sum _{\theta = 0}^{\Theta }f(e,\theta ) - \sum _{e \in \delta _{D}^{-}(v)}^{} \sum _{\theta = 0}^{\Theta - \tau (e)}f(e,\theta ) \le b(v) \;\; (\forall v \in V, \forall \Theta \in \mathbb {Z}_+), \end{aligned}$$

(15.2)

and the demand constraint is given by

$$\begin{aligned} \sum _{s \in S^-}^{} \sum _{e \in \delta _{D}^{-}(s)}^{} \sum _{\theta = 0}^{\Theta - \tau (e)} f(e,\theta ) = \sum _{v \in V} b(v) \;\; (\exists \Theta \in \mathbb {Z}_+). \end{aligned}$$

(15.3)

A dynamic flow that satisfies these three constraints is said to be feasible, and the feasible dynamic flow that achieves the minimum time $\Theta *$ is called the quickest flow. The quickest evacuation planning problem is to find the minimum evacuation completion time $\Theta *$.

Considering application to an actual evacuation planning problem, there is an upper limit on the number of evacuees that can be accepted at each sink, which is an evacuation center. As defined by Kamiyama et al. [6], it is assumed that the capacity function $l: S^- \rightarrow \mathbb {Z}_ +$ pertains to each sink, and the feasible flow f satisfies

$$\begin{aligned} \sum _{e \in \delta _{D}^{-}(s)} \sum _{\theta = 0}^{\Theta }f(e,\theta ) \le l(s) \;\; (\forall s \in S^-, \forall \Theta \in \mathbb {Z}_+). \end{aligned}$$

(15.4)

2.2 Time-Expanded Network

Ford and Fulkerson [1, 2] proposed the time-expanded network to obtain the quickest flow. This is a static network corresponding to dynamic network N with time constraint $\Theta$, and it is designated as $N(\Theta )$. The set of vertices for $N(\Theta )$ is defined by

$$\begin{aligned} \{v(\theta )| v \in V, \theta \in \{0,\dots ,\Theta \}\}. \end{aligned}$$

(15.5)

That is, for vertex v of the original network, vertex $v(\theta )$ is provided corresponding to each time $\theta \in \{0,\dots ,\Theta \}$ (see Fig. 15.2).

The edge set of $N (\Theta )$ consists of two parts. First, for each edge $e = (u, v) \in E$ and each time $\theta \in \{0,\dots ,\Theta - \tau (e)\}$, we have edge $e(\theta ) = (u(\theta ), v(\theta + \tau (e)))$ of capacity c(e). Second, for each vertex $v \in V$ and time $\theta \in \{0,\dots ,\Theta - 1\}$, we add stagnant edges $(v(\theta ), v(\theta + 1))$ of capacity $+\infty$ (the horizontal edges in Fig. 15.2). For each vertex $v \in V$, the supply of v(0) is defined as b(v). The supply of $v(\theta )$ for $\theta \in \{1,\dots ,\Theta \}$ is set to zero. Let the sink set of $N(\Theta )$ be $\{s(\theta ) | s \in S^-, \theta \in \{0,\dots ,\Theta \}\}$.

Fig. 15.2

Time-expanded network N(4) of Fig. 15.1 with super sink st

2.3 Algorithm for Solving Quickest Evacuation Planning Problem

Ford and Fulkerson [1, 2] showed that for the evacuation completion time to be less than $\Theta$ in dynamic network $N(\Theta )$, the necessary and sufficient condition is that there exists a flow of size $\sum _{s \in S^+}^{} b(s)$ from source set $\{s(0) | s \in S^+\}$ to the sink set. The existence of such a feasible flow can be examined by obtaining the maximum flow of $N(\Theta )$. To consider the sink capacity for evaluation sites, we add a super sink st and edges of capacity l(s) from $s(\theta )$ to st for $s \in S^-$ and $\theta \in \Theta$. Then, the necessary and sufficient condition for the evacuation completion time to be less than or equal to $\Theta$ in dynamic network N is that the aforementioned feasible flow exists in the time-expanded network $N(\Theta )$.

In this way, it is possible to obtain the quickest flow of evacuation planning in pseudo-polynomial time using the time-expanded network, but as the size of the actual network increases, so does that of the time-expanded one. Moreover, Hoppe and Tardos [4, 5] proposed the quickest transport algorithm without using a time-expanded network. However, although it is a polynomial-time algorithm, it is necessary to minimize the sub-modular function iteratively, and currently this algorithm is inefficient for a large-scale network such as the one in the present study.

Generally, there is more than one quickest flow, of which the one for which the cumulative number of evacuees who have so far been evacuated is the largest at each time before the evacuation completion time $\Theta$ is called the universal quickest flow. This is obtained by first finding the evacuation completion time $\Theta$ and then finding the flow known as the lexicographic maximum flow [9] on the corresponding time-expanded network. When the sinks are subjected to the capacity constraint, the universal quickest flow does not always exist. However, when this constraint is imposed, the obtained flow is experimentally similar to the universal quickest flow [19].

3 Pedestrian Simulation Model

Because both the travel time and time interval of a dynamic network model are approximate, pedestrian simulations are carried out for the obtained route to improve the accuracy, and the travel time and congestion are confirmed. Because the present study deals with a large-scale road network, we use the one-dimensional pedestrian model with high computational efficiency developed by Yamashita et al. [20]. In this model, pedestrians walking in the same direction move in a row on an edge. This row is called a lane, and the number of lanes is determined according to the width of the sidewalk as determined in Sect. 15.4.1. As illustrated in Fig. 15.3, it is assumed that pedestrians move in their specified lane and do not overtake. A discrete-time simulation is performed to determine the speed of each pedestrian in a lane at the next time step from their current speed and the distance between each pedestrian and the one walking immediately in front.

Fig. 15.3

Movement of pedestrians in a lane according to one-dimensional pedestrian model

In a lane as illustrated in Fig. 15.3, the leading pedestrian is defined as the one closest to the target node. Let $x_i(t)$ be the distance of the i-th pedestrian from the beginning of the edge from the starting vertex at time t. The velocity $\dot{x}_i(t+\delta t)$ of pedestrian i in the lane at time $t+\delta t$ is considered to depend on the current velocity of the pedestrian and the distance to the pedestrian walking immediately in front, and it is determined by

$$\begin{aligned} \dot{x}_i(t+\delta t)=\dot{x}_i(t)+\left( a_1(v_0-\dot{x}_i(t))-a_2\exp \left( \frac{r-(x_{i-1}(t)-x_i(t)}{a_3}\right) \right) \delta (t), \end{aligned}$$

(15.6)

where $v_0$ is the free walking speed, r is the radius of the pedestrian, and $a_1$, $a_2$, and $a_3$ are parameters. According to a previous study [20], we set $v_0 = 1.023$ [m/s], $r = 0.522$ [m], $a_1 = 0.962$, $a_2 = 0.869$, and $a_3 = 0.214$.

4 Data Preparation

The geographic information system (GIS) datasets used in this study are listed in Table 15.1, and Fig. 15.4 shows the city of Osaka covered by this study, the 20-km zone within which people walk home, and the flooded area. In the following, we explain the data preparation.

Table 15.1 GIS datasets used for optimization and simulation

4.1 Road Network

Based on the approach of the Cabinet Office of Japan for people struggling to return home [10], the road network was calculated from the roads in Osaka City except for the expressways, and the range of the buffer was 20 km. Consequently, a large-scale road network comprising 815 739 edges and 621 670 nodes was obtained. Simplification of this large-scale road network is described in the next section. In the case of an earthquake due to the Nankai Trough, a seismic intensity of a 6-lower is assumed in Osaka City. There is expected to be little major damage to roads and buildings at this seismic intensity, therefore in this study buildings and roads are assumed to be undamaged.

We assume that pedestrians move on sidewalks, but there are no sidewalk data for this road network. Therefore, referring to the regulations of the Ministry of Land, Infrastructure and Transport [12], we sampled the sidewalk width every 10 blocks using the distance-measuring function of Google Maps for each of six road types obtained from the road network data, and we unified the sidewalk width by each road type.

Fig. 15.4

Osaka City and its 20-km surrounding area

Next, a sidewalk along which only one person could pass at a time was made to be a lane, and the lane width was made to be uniformly 0.75 m. The number of lanes was set as an even value that did not exceed the determined width of the sidewalk divided by the width of a lane. This was done so that edges opposite to each other had the same number of lanes. For each road type, the maximum and minimum numbers of lanes obtained under these conditions were eight and two, respectively.

Fig. 15.5

Tsunami evacuation buildings and passable bridges

4.2 Tsunami Evacuation Buildings

As tsunami evacuation buildings, we used 649 buildings designated by Osaka City in 2016. These were inputted as GIS point data, and each point was connected to the nearest road edge by a straight line. The capacity of tsunami evacuees was set for each tsunami evacuation building. In total, 560 816 people could be accommodated in all the tsunami evacuation buildings. Figure 15.5 shows the tsunami evacuation buildings that were used. As described in Sect. 15.6, when we optimize and simulate the routes including the bridges over the Yodo River, the bridges in the flooded area are set to be impassable.

4.3 Daytime Population

The daytime population was calculated from mobile spatial statistics generated from the travel histories of users of mobile phones. As shown in Fig. 15.6, we used 500-m mesh data of the population at 2 p.m. on a weekday in Osaka City in April 2015. There were 2 696 546 residents and commuters in Osaka City during this period, but note that mobile spatial statistics cover only the population between 15 and 79 years of age. We allocated the daytime population equally to nodes of the road network in each mesh, and this became the initial arrangement of evacuees and stranded people. Because the mobile spatial statistics also contain the population of each residential area, we chose the node of the home place for each pedestrian randomly according to this information.

Fig. 15.6

Distribution of commuters in Osaka City at 2 p.m. on a weekday in April 2015

4.4 Decisions on Number of People Struggling to Return Home and Number of Evacuees

The polygons of the tsunami-flooded area were superimposed on the road network, and the flooded nodes and edges were determined. For each visitor, the action of evacuate, walk home, or remain in place was chosen according to the flooded condition of the present node, the flooded condition of the home node, and the distance to the home node. Whether or not to return home on foot was determined by the method used by the Cabinet Office to estimate the number of people struggling to return home [10].

Let R denote the set of commuters struggling to return home. In this approach, the probability $P_r$ of resident $r \in R$ deciding to return home on foot is determined by the following equation based on the distance $d_r$ [km] from the current place to the returning place:

$$\begin{aligned} P_i = {\left\{ \begin{array}{ll} 1 &{} (d_r< 10), \\ \frac{20-d_r}{10} &{} (10 \le d_r < 20), \\ 0 &{} (20 \le d_r). \end{array}\right. } \end{aligned}$$

(15.7)

In this study, the return distance of each visitor is the length of the shortest path from their present node to their home node obtained on the road network before simplification. In the case of resident r whose return distance is $10 \le d_r <20$, the action is decided probabilistically according to $P_r$ with uniform distribution. The conditions for each action are summarized in Table 15.2.

Table 15.2 Decision rules for each action

Table 15.3 lists the breakdown of the number of people for each activity classified according to these rules. Of the people who return home on foot, approximately 150 000 cross bridges over the Yodo River, and they become the objects for route optimization. Everyone else returning on foot was deemed to take the shortest route.

Table 15.3 Breakdown of numbers of people involved in each activity

5 Simplifying and Restoring Large Road Network for Route Optimization

Computing the quickest flow depends greatly on the scale of the network. Although the main part of the quickest-flow algorithm is computing the maximum flow, the effect of parallelization on this algorithm is limited. Therefore, it is difficult to apply this algorithm to a large network, even by using a recent central processing unit with many cores. In this study, we simplify the large-scale road network and optimize the routes for evacuation and returning home using the quickest flow. We also develop a method for restoring the optimized routes to the original road network. The proposed method is outlined below and illustrated in Fig. 15.7.

Fig. 15.7

Simplification and restoration of road network

5.1 Simplification of Road Network

The basic idea is to construct a simplified road network by dividing the space by polygons of the sub-regions of the area and connecting their centers of gravity with straight lines between adjacent sub-regions. At this time, the sum of the numbers of lanes of the original edges crossing the line segments shared by two polygons is made to be the number of lanes of a simplified edge. If no original edges crossed between two sub-regions, then the two polygons are not connected by a simplified edge. The length of a simplified edge is the Euclidean distance between centers of gravity, and commuters assigned to nodes in a polygon are aggregated on its center of gravity.

The following procedures were carried out using GIS software to simplify the original road network: recognizing adjacent polygons, decomposing polygons into line segments, generating the centers of gravity of the sub-region polygons, extracting the road edge that crosses the line segment of each pair of adjacent polygons, and generating the simplified road network. Consequently, there were 36 276 edges and 15 853 vertices, these being approximately 4% and 3%, respectively, of those of the original road network.

5.2 Restoring Optimized Routes on Original Road Network

Let A be a set of sub-regions traversed by an origin–destination (OD) path in the set of optimized OD paths on a simplified road network. In this study, we refer to the OD path in the original road network being obtained as the shortest path in the road network in A as route restoration. However, with this method, the destination may not be reachable using only the road network in A (see Fig. 15.7d2). In that case, the route obtained by the optimization is not used and is replaced by the shortest path in the whole road network. Then, the extent to which the original OD path could be restored from the route in A is evaluated as the reproduction rate.

6 Route Optimization Settings

Thus, the routes for evacuation and returning home can be optimized. To prioritize human life, we first secure evacuation routes for tsunami evacuees and then optimize the routes for people walking home. The procedure and settings are described below.

6.1 Optimization Steps

First, we explain the concept of optimization for tsunami evacuees. As mentioned in Sect. 15.4, in Osaka City, there are many tsunami evacuation buildings in the expected flooded area, and the plan is to evacuate to those buildings. However, many areas may continue to be flooded for several days even after drainage is carried out, and it is feared that many tsunami evacuation buildings will be isolated by flooding.

In the event of a tsunami disaster in a large city, it is reasonable to suppose that not many evacuees will use the tsunami evacuation buildings, given the limited resources for rescuing evacuees from such buildings. Therefore, it is necessary to clarify which areas contain evacuees who can only evacuate to a tsunami evacuation building. In this study, we optimize the destinations and routes of evacuees in the following three steps.

Step 1

In the simplified road network, the destinations of evacuees are set not as the tsunami evacuation buildings but as the intersections of the boundaries of the flooded-area polygons and the intersecting edges. Then, they are connected to one super sink, the route is optimized by the universal quickest flow, and the evacuation completion time for each evacuee is calculated.

Step 2

For evacuees whose evacuation completion time determined in step 1 exceeds 1 h and 50 minutes, their evacuation routes are optimized again using the universal quickest flow to evacuate to tsunami evacuation buildings. At this time, the optimization is executed by using the residual network of the time-expanded network used in step 1 except for that of evacuees in step 2.

Step 3

The routes of approximately 150 000 commuters walking home across passable four bridges over the Yodo River shown in Fig. 15.5 are optimized using the universal quickest flow. We refer to such pedestrians as “bridge passers.” In this case, sinks are set to nodes on the north side of each bridge and are connected by one super sink. In addition, the residual network used in the optimization up to step 2 is used. People in areas other than the flooded area return home via the shortest route, this being because there is less congestion than on the bridges, and the optimization problem in this case becomes a general multi-commodity flow problem, which is more difficult than the quickest-flow problem.

6.2 Computational Conditions

The time unit of the quickest flow was set to 10 s considering the computational time and available memory. The walking speed of a pedestrian was set to 1 m/s. Meanwhile, the free walking speed in the one-dimensional pedestrian model was set to 1.023 m/s, which is similar to that in the original model [20]. The optimization and simulation code was implemented using Visual C++ 2015, and LEDA 6.4 was also used as a network library to solve the maximum-flow problem. The optimization and simulation were carried out on a personal computer (PC) with Windows 10 Professional 64 bit, an Intel Core i7-6700k, and 32 GB of memory.

7 Results of Route Optimization

The optimization results are shown below, where the evacuation completion time is the result of each pedestrian walking along the designated route using the one-dimensional pedestrian model on the original road network.

7.1 Computational Times

The computational times for the route optimization for the two types of pedestrian are listed in Table 15.4. Even though the PC that was used was of an older specification dating back several generations, the computation took only a matter of days. In other words, the problem could be computed even with such a low-specification PC. Although there were fewer bridge passers, their optimization took longer, probably because their routes were longer.

Table 15.4 Computational time for each optimization

7.2 Reproducibility of Restored Routes

We analyze the reproducibility of the routes optimized by the simplified network after they are restored to the original network. The reproducibility is evaluated by the difference in the length of a route before and after the restoration and the selectivity of the route described above. Table 15.5 lists the mean route lengths before and after network restoration for each type of pedestrian. In the case of evacuees, the mean route length increases after restoration, whereas it decreases for bridge passers. However, the restoration does not cause an extremely large difference in either case.

Table 15.6 lists the selection ratio, which is the percentage of each type of pedestrian using the routes obtained by the universal quickest flow after network restoration. Although the selection ratio for evacuees exceeded 80%, that for bridge passers was only 64%. Because the route became longer for the latter, this is thought to have increased the number of cases in which a route cannot be constructed within the limited range.

Table 15.5 Mean route lengths for each type of pedestrian before and after network restoration

Table 15.6 Selection ratios for optimized routes

7.3 Optimization Results

Here, we assess by how much the optimization shortened the travel time compared with that of the shortest route.

First, regarding the movement by evacuation, Fig. 15.8 shows how the cumulative number of evacuees for each type of route varies with time, and Table 15.7 lists the mean evacuation time and evacuation completion time. Although the cumulative numbers of evacuees for both types of route vary similarly, the effect of the optimization is evident because it shortens the evacuation completion time by approximately 1 h compared with that of the shortest route. However, the evacuation completion time is over 7 h, which is too long to avoid the impact of the tsunami. This is considered to be a result of interference between the routes of evacuees and people returning home. At the time of optimization, priority was given to evacuees, but this assumption may have collapsed upon restoring the routes. Regardless, it is suggested that evacuees should avoid evacuating outside the flooded area by using the tsunami evacuation buildings as much as possible.

Fig. 15.8

Cumulative number of arriving evacuees for each route type

Table 15.7 Comparison of travel times of evacuees for both route types

Next, we perform a similar verification for bridge passers. Figure 15.9 shows how the cumulative number of arriving people varies with time, and Table 15.8 compares the mean travel times and travel completion times for both route types. In the case of the shortest route, pedestrian bridge congestion begins early, after which the slope of the straight line of the accumulated number of arriving people is relatively low. As a result, the completion time of returning home was drastically shortened by about 3 h and 20 min by the optimization with consideration of securing routes for tsunami evacuees.

The effect of the optimization was demonstrated, especially for bridge passers. To understand the changes concretely, the total numbers of pedestrians passing along each road for both route types are visualized in Fig. 15.10. In the case of the shortest route, people returning home are concentrated on the Nagara Bridge, but when the route is optimized, two bridges upstream from the Nagara Bridge are used.

People generally use the Shin-Yodogawa Bridge to travel to the north of the Yodo River from Osaka City, but in this case that bridge cannot be used because it is in the tsunami-flooded area. Therefore, with no restrictions, most people returning home would cross the Nagara Bridge, which is the next one upstream of the Shin-Yodogawa Bridge. Bridges further upstream than the Nagara Bridge are not usually used for transportation from Osaka City because they are located more than 3 km away. However, the optimization means that these bridges are also used for returning home, and congestion is reduced.

Fig. 15.9

Cumulative number of arriving bridge passers for each route type

Table 15.8 Comparison of travel times of bridge passers for both route types

Fig. 15.10

Total number of pedestrians passing at each road edge for each route

8 Conclusion

In this study, we proposed a method for network simplification and restoration to optimize the traveling routes of more than 2 million pedestrians with a large-scale and detailed road network in Osaka City and its surrounding area. We then showed that such route optimization worked well.