Analysis of the Hydrological Behavior of Watersheds in the Context of Climate Change (Northwestern Algeria)

Abstract

The aim of this work is to study the temporal evolution of the rainfall-runoff relations of four basins in northwestern Algeria: the Tafna Maritime, Isser Sikkak, downstream Mouilah and Upper Tafna basins. The adopted approach consists of analyzing hydroclimatic variables using statistical methods and testing the nonstationarity of the rainfall-runoff relation by the cross-simulation method using the GR2M model. The results of the different statistical methods applied to the series of rainfall and hydrometric variables show a decrease due to a break in stationarity detected since the mid-1970s and the beginning of the 1980s. The annual rainfall deficits reached average values of 34.6% during the period of 1941–2006 and 29.1% during the period of 1970–2010. The average annual wadi flows showed average deficits of 61.1% between 1912 and 2000 and 53.1% between 1973 and 2009. The GR2M conceptual model simulated the observed hydrographs in an acceptable manner by providing calculated runoff values in the calibration and validation periods greater or less than the observed runoff values. The application of the cross-simulation method highlighted the nonstationarity of the rainfall-runoff relations in three of the four studied basins, indicating downward trends of monthly runoff.

1 Introduction

Water is a common and vital good, and its access, security and control are major challenges. In addition to these challenges, there are other challenges linked to probable changes in extreme climatic events, particularly periods of drought, which are predicted to become intense and persistent over time (Vervier et al. 2004). For all these reasons, the quantification of water resources is of great importance for scientists and water managers around the world (Milano et al. 2013). The importance of research lies in the major challenges represented by meteorological variability and its effect on the hydrological cycle (Goula et al. 2006).

In Algeria, the majority of productive watersheds, representing approximately 75% of the annual flow of surface water, are found in the eastern part of the country along the Mediterranean coast. Much of the rest of the land is subjected to desert conditions in which water scarcity is acute (PNUD-FEM 2003). In addition to the unfavorable geographic position of the country, the population explosion has worsened the situation. Indeed, the available water resources per inhabitant per year, which was 1,500 m³ in 1962, dropped to 720 m³ in 1990, 630 m³ in 1998 and 430 m³ now, thus reflecting pressure from population growth (Mozas and Ghosn 2013; Safar-Zitoun 2019). Therefore, Algeria is already in a situation of water scarcity (Benblidia and Thivet 2010) that could be amplified by the intensity and pace of climate change (Barnett et al. 2001; Frich et al. 2002). In fact, with regard to estimates of sectoral needs, climate change will place the country in an uncomfortable situation since the maximum volume of water that can be mobilized will reach the limit of the water needs of the country (Rousset and Arrus 2006).

Current climate disturbances are reflected in irregular rainfall and a drought that has become established over several years. This climatic variability, manifested by a drop in rainfall, has been the subject of numerous studies. In 1993, following an analysis of data from 120 rainfall stations, Laborde (1993) was able to highlight a succession of four rainfall phases, including a long deficit phase established at the end of 1973. The most pronounced rainfall deficit was recorded in the western part of the country, where the rainfall hardly exceeded 350 mm on average (Matari et al. 1999; Medejerab and Henia, 2011; Belarbi et al. 2013; Achite et al. 2014; Belarbi et al. 2016, 2019; Khedimallah et al. 2020). According to Aït Mouhoub (1998), while this reduction was on the order of 30% in eastern Algeria, it amounted to more than 50% in the central and western regions of the country. Meddi and Meddi (2009) estimated the deficit at 20% in the central region and more than 36% in the far western region, resulting in a drastic decrease in surface flows. Meddi and Hubert (2003) estimated this reduction at nearly 55% for the basins in the central region and between 37 and 44% in the eastern region, while the deficit varied from 61 to 71% for the basins in the far west.

The objective of this study is to analyze trends in the rainfall-runoff relation, taking four basins in northwestern Algeria as the study area: the Maritime Tafna, Isser Sikkak, downstream Mouilah and Upper Tafna basins. These four basins are of important socioeconomic interest because they supply water to the populations of many municipalities and provide the needs of the agricultural and industrial sectors, which are very active in the region (Kettab 2001). The methodological approach consists, first, of a characterization of hydrometeorological variability using nonparametric statistical tests for trend analysis and, second, of an application of the cross-simulation method starting from the lumped conceptual hydrologic monthly model GR2M over several subperiods.

2 Methods and Materials

2.1 Study Area

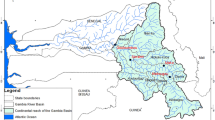
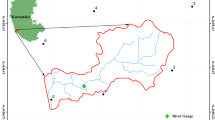
The four basins, which are subbasins of the Tafna basin, occupy the extreme northwest of Algeria (Fig. 5.1).

Fig. 5.1

Geographic location of the study area

The Upper Tafna basin (1604) (Fig. 5.1) covers an area of 256 km² and has a perimeter of 78 km (Ghenim 2001). Bounded to the north by the plains of Maghnia and Hennaya and to the south by the high Oran plains, this basin is occupied mainly by mountains of the Alpine orogeny formation whose summits culminate at 1465 m above sea level (Tlemcen Mountains). This basin is characterized by steep relief, and 49% of its surface has a slope greater than 25% (Megnounif et al. 2003). The watershed is well-drained with a poorly organized hydrographic network (Rc < 2) (Bouanani 2004). Its mainstream, Oued Sebdou, drains the basin over a length of 28 km (Ghenim et al. 2010). Oued Sebdou begins in Ouled Ouriach at Ghar Boumaaza, at an altitude of 1300 m, but is clearly distinct only around the town of Sebdou at an altitude of 900 m. From Sebdou and up to Sidi Medjahed, the course of Oued Sebdou follows a steep valley established in limestones and dolomites of the Jurassic period. It then follows a southeast/northwest direction until it reaches the Beni-Bahdel dam (Ghenim et al. 2010).

The downstream Mouilah basin (1602) (Fig. 5.1) covers an area of 2650 km² and has a perimeter of 230 km. A large portion of its surface is in Moroccan territory. The fairly varied relief in this basin consists of very heterogeneous zones formed by mountains (the Traras Mountains in the northwest and the Tlemcen Mountains in the south), plains and valleys. The slopes are generally very accentuated in the mountains (exceeding 20%) and gentler (between 0 and 10%) on either side of the watercourse (Ghenim et al. 2008). The stream begins in the El Abed region at an altitude of 1250 m, enters Morocco (40 km north of Oujda) and takes the name Oued Isly. Oued Isly becomes permanent downstream near Oujda and is then called Oued Bou-Naïm; Oued Bou-Naïm enters Algeria around Maghnia under the name Oued Mouilah. The confluence of Oued Mouilah with Oued Tafna is located at an altitude of 285 m upstream of the Hammam Boughrara dam at the level of Sidi Belkheir (Dahmani et al. 2006). Oued Mouilah receives on its right bank Oued Ouerdeffou, which forms the meeting of Oued Abbes, Oued Aouina and Oued Mehaguene (Terfous et al. 2001), and on its left bank, it receives Oued Bou-Selit, Oued Ben-Saria and Oued El Aouedj.

The Isser Sikkak basin (1607) (Fig. 5.1) covers an area of 460 km² with a perimeter of 116 km. The average altitude in this basin is 475 m. The Isser Sikkak watercourse originates at an altitude of 1190 m on the Terny plateau south of Tlemcen at the source of Aïn-Rhanous. The length of its main thalweg is 55.7 km. This thalweg is reformed from the sources of the El-Ourit waterfalls at an altitude of 800 m and takes the name Oued Saf-Saf downstream from the village of Saf-Saf and then the name Oued Sikkak from the commune of Chetouane. It first follows a deep and steep valley and then continues on the plains of Hennaya.

The Tafna Maritime basin (1608) (Fig. 5.1) has an area of 392 km² with a maximum altitude of 713 m and a perimeter of 116 km (ABHOCC 2006). It is the lowest region in the large Tafna watershed and is the region all the waters of Oued Tafna and its tributaries collect.

The types of geological formations that are observed in outcrops in the basins influence the distribution of superficial flows. Following his study, Bouanani (2004) found that almost the entire area of the basins is occupied by permeable to semipermeable formations, which promote the infiltration of surface water. However, the relative abundance of karst carbonate formations, represented by the Tlemcen and de Terny dolomites in the Upper Tafna (1604) and Isser Sikkak (1607) basins, undoubtedly differentiates the hydrological behavior of these two basins from that of the downstream Mouilah basin (1602), more than half of the surface of which is occupied by Plio-Quarternary alluvium surmounting marl and Miocene sandstone at the level of the Maghnia plain.

The region is characterized by a semiarid climate with two predominant seasons. A cool, wet season extends from October to May with fairly irregular rains; the other season, which is dry and warmer, extends from June to September with low rainfall (ABHOCC 2006).

2.2 Data Description

Rainfall, temperature and hydrometric data were obtained from the two organizations that are responsible for the hydrometeorological network, namely, the National Agency for Hydraulic Resources (NAHR) and the National Office for Meteorology (NOM).

We needed to select a homogeneous observation period to ensure the statistical consistency of the results. Following quality control and homogeneity tests of the rainfall, hydrometric and temperature data, we selected six rainfall stations arranged over two periods: the first period begins in 1941 and runs until 2006, and the second period begins in 1970 and runs until 2010. The data were represented by observations from four stations arranged over two study periods: First period began in 1912 and ended in 2000, and the second period began in 1973 and ended in 2006. The temperature data were collected from four stations and covered a single study period from 1976 to 2007.

It should also be mentioned that, for the statistical analysis of the hydrometeorological data, a hydrological year beginning on September 1 of year M and ending on August 31 of year (M + 1) was adopted. This decision is justified by the fact that in the Mediterranean area, the rainy season begins in the month of September and ends in May. The maximum rainfall rates are often recorded during winter in the months of November, December and January. It follows that the hydrological year reflects the natural climatic conditions (Sebbar et al. 2011).

The geographic coordinates and the main statistical parameters characterizing the distributions of rainfall data (mm) from the different stations selected are shown in Table 5.1.

Table 5.1 Geographic coordinates and statistical parameters of the selected rainfall stations

Table 5.1 shows that the average annual rainfall over the 1941–2006 period varies between 424.8 (Bensekrane station) and 521.7 mm (Zenata station), with a general average of 470.3 mm. Over the 1970–2010 period, the annual averages fluctuate between 325.5 (Pierre du Chat station) and 565.0 mm (Mefrouche station), with a general average of 409.8 mm. The table also shows that the decade of the 1980s had the highest rainfall deficit in the region. The coefficient of variation (C_v) is quite important. The highest variability is noted at Zenata station, with a coefficient of variation equal to 0.406 (1941–2006).

The geographic location, catchment area and various statistical parameters of the mean annual flows are presented in Table 5.2.

Table 5.2 Geographic location and statistical characteristics of the selected hydrometric stations

According to Table 5.2, the results of the mean annual flow analysis show a high standard deviation and coefficient of variation. Across all stations, the runoff depth varies enormously from year to year. In addition, these results show that the decade of the 1990s was the driest decade. On the other hand, the decades of the 1930s (1912–2000) and the 1970s (1973–2009) were periods of surplus. The coefficient of variation, C_v, varies between 64% and 77%, which means that the variability of the hydrometric series is considered to be very high.

The results of the descriptive analyses of the two quantiles (the minimum and the maximum), mean, standard deviation and coefficient of variation of the temperature time series are shown in Table 5.3.

Table 5.3 Temperature stations and their statistical characteristics (℃)

The long-term averages of the mean annual temperatures range from 17.3 ℃ (Mefrouche station) to 18.2 ℃ (Beni-Bahdel station), with an average across all stations of 17.7 ℃. The coefficient of variation, C_v, does not exceed 8%, which means that the variability of the temperature time series is considered to be low (Table 5.3).

Potential evapotranspiration is an essential input of the GR2M model. Potential evapotranspiration expresses the evaporative losses of a basin and is used in the production function of the model (Kouassi et al. 2008). The potential evapotranspiration values, which were calculated according to the Thornthwaite formula, cover the period from 1976 to 2007.

2.3 Methodological Approach to Structural Break Detection

The literature on statistical approaches to time series of hydrometeorological variables is particularly abundant. In this study, we opted for the nonparametric Pettitt and Mann-Kendall (MK) tests. The Pettitt test is renowned for its robustness; it allows the detection of breaks in a time series (a break at time “t” can be defined, generally, by a change or shift in the central tendency of a time series variable) (Braud 2011). To complement the results of the Pettitt test, we used the Mann-Kendall test. This test makes it possible to analyze the existence of a linear trend (upward or downward) in a time series. The robustness of this statistical test has been approved by several comparison tests carried out by Yue and Wang (2004). These two tests were programmed in the Turbo Pascal language. In addition, the results of the applications were represented by the selection of a significance level of 5%.

Pettitt Test

Pettitt (1979) defines the variable U_t,n as follows:

$$U_{t,n} = \mathop \sum \limits_{i = 1}^{t} \mathop \sum \limits_{j = t + 1}^{n} D_{ij}$$

(1)

or

$$D_{i,j} = \text{sgn} \left( {x_{i} - x_{j} } \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{si}}\;\;x_{i} > x_{j} } \hfill \\ 0 \hfill & {{\text{si}}\;\;x_{i} = x_{j} } \hfill \\ { - 1} \hfill & {{\text{si}}\;\;x_{i} < x_{j} } \hfill \\ \end{array} } \right.$$

(2)

Pettitt proposed testing the null hypothesis using the K_n statistic, which is defined by the maximum absolute value of U_t,n for values of t varying from 1 to n−1. From rank theory, k denotes the value of K_n taken over the studied series; under the null hypothesis, the probability of exceeding the value k is given approximately as follows:

$$\Pr \left( {K_{n} > k} \right) \approx 2 \exp \left[ {\frac{{ - 6k^{2} }}{{\left( {n^{3} + n^{2} } \right)}}} \right]$$

(3)

For a given risk (significance level) α, if the estimated probability of exceedance is less than α, the null hypothesis, H₀, is rejected. The series then includes a localized break at the time when it is observed as $\hbox{max} \left| {U_{t,n} } \right|_{t = 1, \ldots , n - 1}$ (Belarbi et al. 2012).

Mann-Kendall Test

If we consider each element x_i in a time series with (i = 1, …, n), we can calculate the trend statistic, $t^{\prime}$, of the test, given as follows by Mann (1945), Kendall (1975) and Paturel and Servat (Paturel and Servat 1996):

$$t^{\prime} = \mathop \sum \limits_{i = 1}^{n} n_{i}$$

(4)

The mean and variance of the test statistic are calculated, respectively, as follows:

$$E\left( {t'} \right) = \frac{{n\left( {n - 1} \right)}}{4}$$

(5)

$$V\left( {t^{\prime}} \right) = \frac{{n\left( {n - 1} \right)\left( {2n + 5} \right)}}{72}$$

(6)

The reduced test statistic is given as follows:

$$u\left( {t^{\prime}} \right) = \frac{{\left[ {t^{\prime} - E\left( {t^{\prime}} \right)} \right]}}{{\sqrt {V\left( {t^{\prime}} \right)} }}$$

(7)

We seek the probability, $\alpha_{1}$, using the reduced centered normal law such that $\alpha_{1} = P\left( {\left| u \right| > \left| {u\left( {t^{\prime}} \right)} \right|} \right)$, and the null hypothesis is accepted or rejected at level α depending on whether $\alpha_{1} > \alpha$ or $\alpha_{1} < \alpha .$

When the values of $u\left( {t^{\prime}} \right)$ are significant, we conclude that there is an increasing or decreasing trend depending on whether $u\left( {t^{\prime}} \right) > 0$ or $u\left( {t^{\prime}} \right) < 0$, respectively (Sneyers 1975).

To locate the period when a trend appeared, the test statistic lends itself better to the progressive and retrograde calculations necessary for this purpose. By reversing the direction of the calculation, the obtained variable, $u\left( {t^{\prime}} \right)$, is called a retrograde series. The point of intersection of $- u\left( {t^{\prime}} \right)$ with $u\left( {t^{\prime}} \right)$ indicates the beginning of the trend (Meddi et al. 2005).

2.3.1 Analysis of Variability of Meteorological Observations

The moving average method aims to reduce the influence of accidental variations and to eliminate the effect of very short-term fluctuations. This method makes it possible to smoothen random and periodic components without affecting the general movement of the series (Belarbi et al. 2012). The principle of this method is to replace the original series with a series of moving average values defined, in the simplest case, as follows:

$$y_{k} = \frac{1}{2n + 1}\mathop \sum \limits_{i = - n}^{n} \left( {y_{k + i} } \right)$$

(8)

In addition, to assess the evolution of an annual time series of a meteorological variable, it is advisable to take into account any deviation from the average that corresponds to the surplus or deficit for the year in question compared to the observed long-term average (Bodian 2011). This deficit is calculated as follows:

$$E_{i} = \frac{{\left( {Y_{i} - {\text{Mean}}} \right)}}{\text{Mean}} \times 100$$

(9)

where E_i denotes the deviation from the average (percent); Y_i represents the annual average of the variable recorded during year i; and Y_mean indicates the interannual average of the variable recorded over the study period.

2.3.2 Hydrological Modeling and Rainfall-Runoff Relation

Modeling the rainfall-runoff relation has become an essential tool for the management of water resources. A number of studies carried out in Algeria using conceptual models have been presented in the hydrological literature. Several models (GR1A, GR2M, GR3M, GR4J, SWAT or even neuro-fuzzy) have been used in the works of these authors.

For this research, we chose the GR2M model developed in the GR (Rural Engineering) model series from CEMAGREF. This global conceptual model has undergone several revisions, proposed successively by Kabouya and Michel (1991), Makhlouf and Michel (1994), Mouelhi (2003) and Mouelhi et al. (2006), which allowed the gradual improvement of the performance of the model.

Indeed, the advantage of using GR2M comes from the small amount of data required (rain, evapotranspiration and flow) for the calibration and simulations. These input data are expressed in depth of runoff (mm). GR2M simulates the flow at the outlet of a watershed using precipitation and evapotranspiration data.

2.3.3 Description of the GR2M Model

The GR2M model consists of a production tank that governs the production function, characterized by its maximum capacity, and a reservoir (gravity water) that governs the transfer function (Kouassi et al. 2012). This monthly water balance model contains two free parameters that require calibration (X₁ and X₂). The first parameter (X₁) represents the maximum capacity of the tank (soil). The second parameter (X₂) represents the exchange parameter at the underground reservoir level (gravity water) (Perrin et al. 2007). Two free parameters in a global conceptual model are sufficient to represent the rainfall-runoff relation at the monthly time step (Mouelhi 2003; Makhlouf and Michel 1994).

2.3.4 Mathematical Criterion for Optimizing the Model (Nash-Sutcliffe Criterion)

The performance of a model is measured according to the objectives that are set. The same model can be assessed in several ways, the only constraint being the objective of the assessment (Djellouli et al. 2013).

The best-known and best-performing criterion for conceptual models is the Nash-Sutcliffe criterion (Perrin et al. 2007). Indeed, several comparative studies among different forms of criteria have been carried out and have shown that the Nash-Sutcliffe criterion imposes itself as that which, overall, allows the best calibration (Mouelhi 2003). This dimensionless criterion makes it possible to judge the quality of an adjustment and facilitates the comparison of adjustments among different basins whose flows correspond to different orders of magnitude (Kouassi 2007). The criterion is defined by Nash and Sutcliffe (1970) as follows:

$${\text{Nash}} = \left[ {1 - \frac{{\sum \left( {Q_{0}^{i} - Q_{C}^{i} } \right)^{2} }}{{\sum \left( {Q_{0}^{i} - Q_{m} } \right)^{2} }}} \right] \cdot 100$$

(10)

where $Q_{0}^{i}$ represents the monthly observed discharge; $Q_{C}^{i}$ is the monthly calculated discharge; and Q_m is the average flow observed over the whole observation period without gaps.

The estimation of the Nash-Sutcliffe criterion ranges between $- \infty$ and 100%. The model is considered effective when the estimated streams approach the observed streams, i.e., when the value of the Nash-Sutcliffe criterion is close to 100%. Thus, a performance greater than or equal to 60% can be viewed as acceptable (Perrin 2000). The version of the GR2M model used in this study is available on the CEMAGREF Web site (http://webgr.irstea.fr/modeles/mensuel-gr2m/).

2.3.5 Evaluation of the Robustness of the GR2M Model

One of the most commonly utilized methods to assess the robustness of a model is the double-sample technique. This method makes it possible to test the adaptability of models regardless of their complexities (Kouassi et al. 2011).

In the case where there are observations presenting themselves as time series (e.g., monthly or annual time series), it suffices to subdivide the observation period of each watershed into subperiods and perform a calibration over one period and a validation over the rest of the observations while making sure to reserve a period for the model warm-up (Kouassi 2007). This task is repeated such that the model calibrates successively on all the subperiods. The robustness of a model is evaluated by the difference between the value of the Nash criterion in the calibration phase and that in the validation phase (Perrin 2000).

2.3.6 Cross-Simulation Approach: Trend Analysis of the Rainfall-Runoff Relation

While many methods to detect trends in hydrological variables such as rainfall and flows are available, there are very few methods capable of detecting trends in rainfall-runoff behavior (Aït-Mesbah 2012). Among these methods, the cross-simulation approach is used because of its robustness for the study of trends in rainfall-runoff relations (Kouamé et al. 2013).

The description of the methodology of this approach is based on the work of Andréassian et al. (2003) and Kouassi et al. (2012).

The methodology begins with the division of the study period into n successive periods of equal lengths. This approach is based on the principle that calibrating a model makes it possible to characterize the hydrologic behavior of the model over the calibration period (of n subperiods). Then, applying the calibrated model to all the other subperiods while keeping the same parameters, we obtain the flow that would have resulted had the basin remained under the conditions of the calibration period. By renewing this operation after each control, we thus build a trend matrix. In the interpretation of the simulation matrices, each value is replaced by a sign, indicating an increasing or decreasing evolution of the hydrological variable over time. For this study, the target variable that is considered is the monthly average flow, transformed into a measure of the depth of runoff (mm). For this purpose, each value in the matrix is replaced by a (+) or a (−), depending on whether the value is greater or less than the value of the diagonal. The value located on the diagonal represents, for each line, the best reference insofar as it is the closest value to the value that was actually observed (because it is predicted by the model calibrated on the period in question). The comparison is carried out line by line because it is necessary to ensure conditions of equal rainfall. If the (+) values represent the majority, this means that the hydrological variable simulated in the matrix tends to increase over time. If (−) values represent the majority, the opposite is true (Renard Renard 2006; Belarbi et al. 2017).

3 Results and Discussions

3.1 Results

3.1.1 Detection of Breaks in the Rainfall Time Series

The application of the two tests (Mann-Kendall and Pettitt) at a significance level of 5% made it possible to identify a breakpoint in the rainfall time series. The identification of this breakpoint makes it possible to distinguish two periods, a surplus period and a deficit period, in the basins (Table 5.4).

Table 5.4 Statistical tests applied to the time series of annual rainfall totals

The Pettitt test, when applied to annual rainfall totals during the 1941–2006 period, confirmed the occurrence of significant breakpoints in the mid-1970s (Table 5.4; Fig. 5.2). However, during the 1970–2010 study period, breakpoints were identified in 1980/81 (Table 5.4; Fig. 5.3).

Fig. 5.2

Application of the Pettitt test to the annual rainfall time series data for the period 1941–2006

Fig. 5.3

Application of the Pettitt test to the annual rainfall time series data over the 1970–2010 period

This break is identified by a peak in the evolution of the Pettitt indices. Over the period from 1941 to 2006 (Fig. 5.2), the Pettitt indices correspond to 646 for the Bensekrane station, 692 for the Beni-Bahdel station and 1013 for the Zenata station. During the period 1970–2010, indices have values of 203 for the Pierre du Chat station, 221 for the Mefrouche station and 203 for the Maghnia station (Fig. 5.3).

By applying the Mann-Kendall test, we detected the existence of a very significant downward break in the time series of the annual rainfall totals of the Bensekrane, Beni-Bahdel and Zenata stations. This abrupt change occurred in the mid- and late 1970s (Table 5.4; Fig. 5.4). During the 1970–2010 study period, a break was identified in the mid-1970s in the rainfall totals from the Mefrouche station (Fig. 5.5). However, the trend in the annual rainfall totals of the Pierre du Chat and Maghnia stations is not significant (the null hypothesis that there is no trend is accepted) (Table 5.4).

Fig. 5.4

Application of the Mann-Kendall test to the annual rainfall time series data for the period 1941–2006

Fig. 5.5

Application of the Mann-Kendall test to the annual rainfall time series data over the 1970–2010 period

A rainfall deficit indicates a negative change or a decrease in the mean annual rainfall, while a surplus means an increase in the mean annual rainfall observed in the time series before and after a breakpoint. The deficits are −50.82% for the Zenata station, −27.76% for the Beni-Bahdel station and −25.16% for the Bensekrane station (period 1941–2006) (Table 5.5). During the period 1970–2006, the deficits exceeded -26% for the Pierre du Chat station and −30% for the Mefrouche and Maghnia stations. Furthermore, the linear regression between the precipitation values and time, which is used to quantitatively describe the possibility of a linear downward or upward trend in the time series, confirms that annual rainfall totals experienced an average decrease. The rainfall totals reached −8.04 mm annually at Zenata station (study period 1941–2006) (Fig. 5.4) and −6.83 mm annually at Mefrouche station (study period 1970–2010) (Fig. 5.5).

Table 5.5 Rainfall deficits at the various stations studied

These observations corroborate the results of a number of studies, among which we can cite Laborde (1993), Matari et al. (1999), Meddi and Hubert (2003), Meddi and Meddi (2009), Belarbi et al. (2013, 2016, 2017), and Sebaibi (2014), which place most of the breakpoints during the 1970s in Algeria, particularly in the western part of the country.

3.1.2 Detection of Breakpoints in the Runoff Time Series

The results of the two tests, at a significance level of 5%, on the mean annual flow time series of the Pierre du Chat, Remchi, Pont RN7/A and Beni-Bahdel stations are shown in Table 5.6.

Table 5.6 Statistical tests applied to the mean annual flow time series

The mean annual flow time series of the Pierre du Chat and Remchi stations analyzed over the period from 1912 to 2000 show a significant break in the mid-1970s (Table 5.6). The results show that the test statistic reached a maximum in 1975/76 for the time series from Pierre du Chat station and in 1974/75 for that of Remchi station (Fig. 5.6).

Fig. 5.6

Trends of mean annual flows determined using the Pettitt test

During the 1973–2009 study period, a break in the mean annual flow time series was identified in the mid-1980s for the Beni-Bahdel station (Table 5.6; Fig. 5.6). No break was detected in the discharge time series of the RN7/A Pont station (Table 5.6).

The identification of these structural breaks is an expected consequence following a very significant downward trend in annual average flows during the twentieth century in general and in particular since the mid-1970s and 1980. In addition, the linear regression between the annual average flows and time indicated downward trends in the flows. The average annual drop reached −0.27 mm at the Pierre du Chat station during the study period of 1912–2000 and −1.57 mm at the Beni-Bahdel station during the period from 1973 to 2009 (Fig. 5.7).

Fig. 5.7

Trends of mean annual flows determined using the Mann-Kendall test

The flow deficits calculated before and after the date of the break of each mean annual flow time series were quite significant (Table 5.7).

Table 5.7 Hydrometric deficits of the different stations studied

3.1.3 Study of Interannual Rainfall Variability

Rainfall is very variable from year to year and from one station to another. A very rainy year can be suddenly followed by a dry year without a transition period. This is the case for the Bensekrane station, which received a total rainfall of 725 mm in 1964/65 and only 205.8 mm in 1965/66 (Fig. 5.8). Similarly, the Pierre du Chat station recorded 494.2 mm and 135.4 mm in the 1980/81 and 1981/82 seasons, respectively (Fig. 5.9).

Fig. 5.8

Interannual variability in annual rainfall totals for the period 1941–2006

Fig. 5.9

Interannual variability in annual rainfall totals over the period 1970–2010

The seven-year moving average curve highlights the excess, normal and deficit periods. The rainfall evolution of the Bensekrane station is characterized by excess, normal and deficit periods (Table 5.8; Fig. 5.8). The surplus period from 1941/42 to 1967/68 had an average rainfall of 485.3 mm, which was 14% higher than the total annual average of 424.8 mm. This surplus was followed by a normal period from 1967/68 to 1977/78; the average rainfall during this period (449.6 mm) was close to the total annual average (424.8 mm). The deficit period began in 1977/78 and ran until 2005/06. During this period, the total annual average rainfall was 358.9 mm.

Table 5.8 Different trends at the studied rainfall stations

For the Beni-Bahdel station (Table 5.8; Fig. 5.8), only one excess period was observed, ranging from 1941/42 to 1975/76 with an average annual rainfall of 531.5 mm, followed by the first period of deficit beginning in 1975/76 and running until 1990/91. During this period of deficit, a minimum total rainfall value of 187.7 mm was recorded (1987/88). The period between 1990/91 and 1997/98 was a normal period with an average rainfall of 442.6 mm, which was close to the total annual average (464.8 mm). Again, a succession of dry years followed this normal period. The second deficit period began in 1997/98 and continued until 2005/06.

For the Zenata station, two contrasting periods were identified (Table 5.8; Fig. 5.8). The first is a surplus period from 1941/42 to 1973/74. During this period, the total rainfall reached a maximum of 986 mm (1963/64). This surplus period was followed by a deficit period that began at the end of the excess period and ran until 2005/06. The total annual average rainfall was 350.6 mm.

The application of the seven-year moving average method highlighted two distinct periods at all the analyzed stations during the 1970-2010 study period. For the Pierre du Chat and Mefrouche stations (Table 5.8; Fig. 5.9), excess periods were observed between 1970/71 and 1977/78, with interannual averages of 412.8 mm for the Pierre du Chat station and 834.8 mm for the Mefrouche station. The other period was a deficit period that began in 1977/78 and ran until 2007/08. The total annual average rainfall values recorded during this period were 295.3 mm and 542.4 mm for the Pierre du Chat and Mefrouche stations, respectively.

The analysis of rainfall data from the Maghnia station (Table 5.8; Fig. 5.9) showed an excess phase that began in 1970/71 and ended in 1980/81. During this phase, the total maximum rainfall between the beginning and the mid-1970s reached 586.6 mm. The deficit phase began at the end of the excess period and ran until 2007/08. During this phase, the average annual rainfall was 294.5 mm.

The results obtained following calculations of the deviations from the means highlight the succession of dry and wet periods.

During the period 1941–2006 (Fig. 5.10), the wettest years corresponded to 1964/65 for the Bensekrane station, 1967/68 for the Beni-Bahdel station and 1963/64 for the Zenata station, with deviations from the mean of 70.7%, 62.7% and 88.9%, respectively. The driest years were 1944/45 for the Bensekrane station, 1987/88 for the Beni-Bahdel station and 1982/83 for the Zenata station.

Fig. 5.10

Relative average deviations in annual rainfall for the period 1941–2006

Over the period of analysis (1970–2010) (Fig. 5.11), the driest years were 1981/82 for the Pierre du Chat station, 1999/00 for the Mefrouche station and 1982/83 for the Maghnia station.

Fig. 5.11

Relative average deviations in annual rainfall over the 1970–2010 period

3.1.4 Study of Interannual Hydrometric Variability

The depth of runoff over the basins is marked by high temporal variability. Indeed, the transition from a wet year to a dry year can be very abrupt. For example, for the years 1933/34 and 1934/35, the Pierre du Chat station recorded runoff depths of 90.3 mm and 11.71 mm, respectively. The same case applies for Remchi station, which recorded a water depth of 157.7 mm in 1935/36 and a depth of only 28.1 mm in 1936/37 (Fig. 5.12).

Fig. 5.12

Interannual variability in annual average station flows for the period 1912–2000

An analysis of the evolution of the average annual flows using seven-year moving averages better illustrates the variability at all the stations (Table 5.9; Fig. 5.12). Figure 5.12 shows that the evolution of flows at the Pierre du Chat station is characterized by alternating periods of rainfall deficits and excesses. A dry period was identified between 1912/13 and 1926/27. The average flow during this period was 5.6 m³/s with a minimum of 0.8 m³/s in 1919/20. A wet period followed, lasting from 1926/27 to 1940/41. During this period, the average annual flow reached a value of 11.5 m³/s. A second dry period occurred between 1940/41 and 1949/50 with a mean annual flow of 4.2 m³/s. This short deficit phase was limited in time by a sequence of wet years beginning in 1949/50 and extending until 1975/76. The average flow during this period was 8.8 m³/s. From 1975/76 to 1999/00, a long phase of dry years was established with a maximum flow of 9.3 m³/s in 1979/80 and a minimum of 0.2 m³/s in 1999/00.

Table 5.9 Different trends at the studied hydrometric stations

The evolution of the interannual variability in the mean annual flow at the Remchi station includes three hydrometeorological periods (Table 5.9; Fig. 5.12), starting with an initial dry period between 1912/13 and 1928/29. Over this period, the average annual flow was 2.9 m³/s, with a minimum of 4.9 m³/s in 1922/23. The second period was a long sequence of wet years between 1928/29 and 1975/76. During this period, the maximum flow reached a value of 9.7 m³/s in 1935–1936. The third period was marked by a more intense and more severe drought than the first; this dry period was established in 1975/76 and lasted until 1999/00. The average annual flow dropped to 1.04 m³/s with a minimum of 0.07 m³/s in 1999/00.

During the 1973–2009 study period, successions of dry and wet periods were observed at the two studied stations. For the Beni-Bahdel station (Table 5.9; Fig. 5.13), a sequence of wet years was detected during the period from 1973/74 to 1980/81. During this period, the average annual flow was 1.5 m³/s with a maximum of 2.7 m³/s in 1973/74. The second period observed at this station was a dry period beginning in 1980/81 and ending in 2007/08; the average annual flow was 0.7 m³/s with a minimum of 0.3 m³/s in 2004/05.

Fig. 5.13

Interannual variability in the annual average station flows over the 1973–2009 period

On the other hand, the interannual flow variability of the Pont RN7/A station (Table 5.9; Fig. 5.13) was characterized by an initial dry period from 1973/74 to 2000/01 followed by a wet period from 2000/01 to 2008/09. During this wet period, the average annual flow was 1.3 m³/s.

Figures 5.14 and 5.15 show the deviations of the annual average flows from the mean. For the four stations, the wettest years correspond to 1932/33 for the Pierre du Chat station, 1935/36 for the Remchi station, 1973/74 for the Beni-Bahdel station and 1979/80 for the Pont RN7/A station, with deviations from the mean of 235.3%, 198.5%, 220.4% and 116.8%, respectively.

Fig. 5.14

Relative average deviations of annual average flows for the period 1912–2000

Fig. 5.15

Relative average deviations of annual average flows for the period 1973–2009

The driest year corresponded to 1999/00 for both the Pierre du Chat and Remchi stations (Fig. 5.14), 2004/05 for the Beni-Bahdel station and 1992/93 for the Pont RN7/A station (Fig. 5.15). The analysis results also show that the 1930s and 1970s stood out as surplus phases in the region.

3.1.5 Evaluation of the GR2M Model Applied to the Four Basins

The breaks in stationarity in the mid-1970s and early 1980s detected during the analysis of the rainfall series introduced a modification of the hydrological functioning of the four basins. Therefore, the choice of calibration periods becomes essential for the specification of the model parameters. In this study, to represent the modeling results in the calibration and validation phases, we used 2/3 of the data for calibration and 1/3 for validation.

For hydrological modeling of the Tafna Maritime basin (1608), we used potential evapotranspiration data from the Zenata station and rainfall data from the Pierre du Chat station. Potential evapotranspiration data from the Mefrouche station and areal rainfall time series calculated from the Mefrouche and Bensekrane stations were used to model the Isser Sikkak basin (1607). The Upper Tafna basin (1604) was represented by rainfall data and potential evapotranspiration data from the Beni-Bahdel station. Finally, rainfall data series and potential evapotranspiration from the Maghnia station were adopted to represent the downstream Mouilah basin (1602).

The monthly flow simulation results for the four basins are shown in Tables 5.10 and 5.11.

Table 5.10 Results of the calibration (1976–1992) and validation (1992–2000) of the GR2M model at the Tafna maritime (1608) and Isser Sikkak (1607) basins for the period 1976–2000

Table 5.11 Results of the calibration (1976–1996) and validation (1996–2006) of the GR2M model at the Upper Tafna (1604) and downstream Mouilah (1602) basins for the period 1976–2006

According to Tables 5.10 and 5.11, the X₁ parameter varied between 492.75 and 699.24 mm, with an average of approximately 596.0 mm, during the 1976–2000 period and between 88.68 and 295.27 mm, with an average of 192 mm, for the 1976–2006 period. The parameter X₂ oscillated between 0.72 and 0.88 during the 1976–2000 period, with an average of 0.8, and between 0.42 and 0.74 in the 1976–2006 period, with an average of 0.6. These values are less than 1, which indicates that groundwater inflows to the different rivers. Indeed, when X₂ is greater than 1, there is a loss of water from the reservoirs to other watersheds, and vice versa. In the case of the four studied basins, the reservoirs contribute water to the rivers (Koffi 2007).

In general, for the calibration phase, the values of the Nash-Sutcliffe criteria were satisfactory for all four basins. The average performance of the Nash-Sutcliffe criterion was 75.4% for the studied basins during the 1976–2000 period and 77.2% for those analyzed over the 1976–2006 period. For the validation phase, the average values of the obtained Nash-Sutcliffe criteria were 81.5% for the basins modeled during the 1976–2000 study period and 78.7% for those analyzed over the 1976 to 2006 period. Regarding the coefficient of determination (R²), the values obtained were as follows: the maximum was 0.833 (1976–2006), and the minimum was 0.718 (1976–2000). In the validation phase, the maximum R² was obtained during the 1976–2000 period with a value of 0.938, and the minimum value was 0.689, obtained during the 1976–2006 period.

The different average performance values obtained for the calibration and validation phases of the GR2M model are shown in Table 5.12.

Table 5.12 Average performance and robustness criterion of the GR2M model

According to the double-sample method, the performance values obtained from the calibration and validation stages, which define the robustness criterion of the model, are acceptable. The range was between −0.4 and −5.9%, with an average of −3.2% for the basins analyzed during the 1976–2000 period. The values varied between −4.6 and +1.9%, with an average of −1.3%, for the basins analyzed over the period from 1979 to 2006. The absolute values of the robustness criterion obtained when the Nash-Sutcliffe criterion was used were less than 10%, which reflects the robustness of the GR2M model Mouelhi version applied to the Tafna Maritime (1608), Isser Sikkak (1607), Upper Tafna (1604) and downstream Mouilah (1602) basins.

Figures 5.16 and 5.17 indicate the hydrographs of the observed and simulated phases for the calibration and validation stages.

Fig. 5.16

Hydrographs of observed and simulated flows during the calibration phase of the GR2M model

Fig. 5.17

Hydrographs of observed and simulated flows during the validation phase of the GR2M model

Figures 5.16 and 5.17 show that the dynamics of the simulated flows in the calibration and validation phases were fairly consistent with the observed flows. Indeed, the mean monthly runoff depths captured the seasonal variations of the calibration sample (Fig. 5.16). On the other hand, floods were poorly simulated, particularly after 1978, a period marked by the intensification of degradation phenomena in hydrometeorological conditions. These conditions also affected the parameters that constituted the forcing variables of the GR2M model. In the validation phase, the GR2M model underestimated the highest peak flows except in the Upper Tafna basin (1604), where the peak flows were overestimated (Fig. 5.17). On the other hand, the model generated very low flows during the period from 1987 to 1992 in the Tafna Maritime (1608) and Isser Sikkak (1607) basins and from 1988 to 1996 in the Upper Tafna (1604) and downstream Mouilah (1602) basins. These periods coincided with periods of drought.

3.1.6 Study of the Trend of the Rainfall-Runoff Relation

A matrix of cross-simulations was applied to the simulated annual average water depths, which made it possible to correctly present the rain-runoff relations in the four basins. The constituted periods, of which there were 4 in the 1976–2000 period and 5 in the 1976–2006 period, were in steps of 6 years. The results of this application are shown in Tables 5.13, 5.14, 5.15 and 5.16.

Table 5.13 Matrix of cross-simulations of runoff depth (mm) in the Tafna Maritime basin (1608) for the 1976–2000 period

Table 5.14 Matrix of cross-simulations of runoff depth (mm) for the Isser Sikkak basin (1607) for the 1976–2000 period

Table 5.15 Matrix of cross-simulations of runoff depth (mm) for the Upper Tafna basin (1604) for the 1976–2006 period

Table 5.16 Matrix of cross-simulations of runoff depth (mm) the downstream Mouilah basin (1602) for the 1976–2006 period

The matrices of cross-simulations were transformed into matrices of standardized simulations and then into sign matrices, as shown in Tables 5.17, 5.18, 5.19 and 5.20. Recall that the gains and losses are indicated in these matrices by “+” and “−” signs, respectively. As we studied the annual average flows in the direction of the progressive evolution of time, the half of each standardized matrix above the diagonal has been taken into account.

Table 5.17 Sign matrix for the Tafna Maritime basin (1608) for the 1976–2000 period

Table 5.18 Sign matrix for the Isser Sikkak basin (1607) for the 1976–2000 period

Table 5.19 Sign matrix for the Upper Tafna basin (1604) for the 1976–2006 period

Table 5.20 Sign matrix the downstream Mouilah basin (1602) for the 1976–2006 period

In the Tafna Maritime basin (1608), a total of 9 negative signs were recorded versus 3 positive signs. In the Isser Sikkak basin (1607), 11 negative signs were recorded versus 1 positive sign. In the Upper Tafna basin (1604), 14 negative signs were recorded versus 6 positive signs. In the downstream Mouilah basin (1602), 4 negative signs were recorded versus 16 positive signs.

From the results for all the studied basins, it is apparent that the negative signs constitute the majority compared to the positive signs except in the downstream Mouilah basin (1602).

The two study periods (1976–2000 and 1976–2006) are both characterized by high hydrometeorological variability. The assumption of the stationarity of the annual runoff time series in the Tafna Maritime (1608), Isser Sikkak (1607) and Upper Tafna (1604) basins can be rejected. Thus, this implies a nonstationarity of the rainfall-runoff relations, manifested by downward trends in the hydrological behavior of these basins. For the downstream Mouilah basin (1602), the stationarity hypothesis is accepted.

3.2 Discussions

During the last four decades, 1970–1980, 1980–1990, 1990–2000 and 2000–2010, a persistent decline in rainfall was experienced. The results of the application of the Pettitt and Mann-Kendall tests programmed in the Turbo Pascal language established that there was a significant downward trend at a significance level of 5% that manifested itself during the mid-1970s and intensified during the 1980s. The rainfall deficit reached an average value of 34.6% during the period from 1941 to 2006; it fluctuated between 26.7 and 30.5% during the 1970–2010 study period. These results confirm the drought that plagues the countries of the southern shores of the Mediterranean. Thus, Sebbar (2013) estimated the rainfall deficit in Morocco to be between 17.8% and 20%. Bahir et al. (2020) estimated this deficit in the upstream part of the Essaouira basin (Morocco) at approximately 14% (1940–2015). In Algeria, Meddi et al. (2009) indicated that since the mid-1970s, deficit years are consistent, and these authors estimated rainfall deficits of 38% in Ain Fekane, 40% in Ras El Ma and 39% in Ben Badis. By analyzing the data of 16 rainfall stations located in the Tafna watershed, Ghenim and Megnounif (2013) found that the breakpoint seen from the middle to the end of the 1970s was sudden and substantial. In their study, observed rainfall deficit was estimated to be between 23 and 36%. Belarbi (2017), who studied the same watershed, showed that in addition to the downward trend and the timing of the breakpoint, the winter and spring rains greatly decreased. The analysis of the various results obtained by the seven-year moving average method confirms that the period after the break is dominated by deficit years beginning from the end of the twentieth century and extending into the early twenty-first century. Of the six stations used for the study of rainfall variability, five stations showed sudden drops in rainfall from 1981 to 1988. This period was marked by a severe drought in the region. This result was confirmed by the work of Meddi and Meddi (2009), who found that the 1980s were defined by the most abrupt and significant fluctuation (in the statistical sense of the term) observed in the northwest region of Algeria; the drop in rainfall amounted to more than 36% over the west of the country. This drop led to a reduction in the runoff contributions of the watersheds and was marked by a significant break in the stationarity of the runoff time series detected in the mid-1970s for the period 1912–2000 and in the mid-1980s for Beni-Bahdel hydrometric station during the period 1973–2009. Indeed, the characteristic synchronization of the breakpoints identified in the rainfall and flow time series underlines the indisputable link that exists between drops in rainfall and decreases in surface runoff (Kouassi et al. 2008). The average hydrometric deficit was estimated at 69.1% over the period 1912–2000 and was estimated to exceed 53% for the Beni-Bahdel station during the period 1973–2009. The runoff deficit was greater than the rainfall deficit, which reflects the intensification of meteorological drought at the level of runoff. The results of the time series analysis of runoff depth using the seven-year moving average method support the results found by change point detection tests. Indeed, the dry periods detected during the 1970s and 1980s coincided with the breaks in stationarity identified by the two statistical tests applied to the runoff time series data at the Pierre du Chat, Remchi and Beni-Bahdel stations. Similarly, an analysis of the results shows that the 1930s and 1970s stand out as surplus phases in the region.

The GR2M model was used to model monthly flows in the Tafna Maritime, Isser Sikkak, Upper Tafna and downstream Mouilah basins. The results show that this model is efficient and robust when applied to these basins. The performance of the model during calibration and validation attained NSE values over 60%. Similarly, the values of the robustness criteria were less than 10% in absolute value. These results corroborate those previously found. Following these conclusions (performance and robustness), the GR2M model was used to analyze trends in the rainfall-runoff relation by applying the cross-simulation approach. This approach allows the testing of the expression of a stationarity behavior (such as in cases of progressive evolution, cases of sudden disturbances and cases of presumed stability) in rainfall-runoff relations. In our case, the results indicated decreases in the monthly runoff depth in two periods: 1976–2000 and 1976–2006. These results highlighted the nonstationarity of the hydrological response of the Tafna Maritime (1608), Isser Sikkak (1607) and Upper Tafna (1604) basins. This nonstationarity can be attributed to various causes. In some basins, nonstationarity results from the physiographic character of the basin (soils, relief, vegetation, etc.). In other basins, the change is probably due to rainfall variability, which is manifested by decreases in the frequency and quantity of rainfall depths.

4 Conclusions

An analysis of the variability of hydrometeorological observations allowed the characterization of the main modifications that the Tafna Maritime, Isser Sikkak, Upper Tafna and downstream Mouilah basins have experienced. Generally, for the four basins, rainfall deficits started in 1974/75 and continue to this day. The severities of these deficits vary from one year to another. However, the repercussions of this reduction in rainfall depth were identifiable in the runoff depth values, which showed clear downward trends detected in the mid-1980s.

Given its performance and robustness, the GR2M model was applied to analyze the trends in the rainfall-runoff relations of the Tafna Maritime and Isser Sikkak basins over the period from 1975 to 2000 and the downstream Mouilah and Upper Tafna basins over the 1976–2006 period. Nonstationarity was observed in the rainfall-runoff relations, characterized by downward trends in the hydrometric behavior of the Tafna Maritime (1608), Isser Sikkak (1607) and Upper Tafna (1604) basins. This decrease was attributed to the modification of the rainfall regime experienced in the region over the past 40 years and to the change in land use following the geographic and morphological modifications of each basin. These modifications, characterized by downward trends, motivate us to pay more attention to the proper functioning of completed or planned projects and challenge us to attain sustainable management of water resources in the region to mitigate persistent drought.