Information Criteria

Abstract

Until now, from the observed data, we have considered the following cases:

• Build a statistical model and estimate the parameters contained in it.

• Estimate the statistical model.

In this chapter, we consider the latter for linear regression. The act of finding rules from observational data is not limited to data science and statistics. However, many scientific discoveries are born through such processes. For example, the writing of the theory of elliptical orbits, the law of constant area velocity, and the rule of harmony in the theory of planetary motion published by Kepler in 1596 marked the transition from the dominant theory to the planetary motion theory. While the explanation by the planetary motion theory was based on countless theories based on philosophy and thought, Kepler’s law solved most of the questions at the time with only three laws. In other words, as long as it is a law of science, it must not only be able to explain phenomena (fitness), but it must also be simple (simplicity). In this chapter, we will learn how to derive and apply the AIC and BIC, which evaluate statistical models of data and balance fitness and simplicity.

Appendices

Appendix: Proof of Propositions

Proposition 18

For covariates x ₁, …, x _N , if the responses are z ₁, …, z _N , the likelihood $\displaystyle -\sum _{i=1}^N\log f(z_i|x_i,\gamma )$ of $\gamma \in {\mathbb R}^{p+1}$ is

$$\displaystyle \begin{aligned} \frac{N}{2}\log 2\pi\sigma^2 +\frac{1}{2\sigma^2}\|z-X\beta\|{}^2 -\frac{1}{\sigma^2}(\gamma-\beta)^TX^T(z-X\beta)+\frac{1}{2\sigma^2}(\gamma-\beta)^TX^TX(\gamma-\beta) \end{aligned} $$

(5.15)

for an arbitrary $\beta \in {\mathbb R}^{p+1}$.

Proof

In fact, for $u\in {\mathbb R}$ and $x\in {\mathbb R}^{p+1}$, we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} \log f(u|x,\gamma)& =&\displaystyle -\frac{1}{2}\log 2\pi\sigma^2-\frac{1}{2\sigma^2}(u-x\gamma)^2\\ (u-x\gamma)^2& =&\displaystyle \{(u-x\beta)-x(\gamma-\beta)\}^2\\ & =&\displaystyle (u-x\beta)^2-2(\gamma-\beta)^Tx^T(u-x\beta)+(\gamma-\beta)^Tx^Tx(\gamma-\beta)\\ \log f(u|x,\gamma)& =&\displaystyle -\frac{1}{2}\log 2\pi\sigma^2 -\frac{1}{2\sigma^2}(u-x\beta)^2\\ & &\displaystyle +\frac{1}{\sigma^2}(\gamma-\beta)^Tx^T(u-x\beta)-\frac{1}{2\sigma^2}(\gamma-\beta)^Tx^Tx(\gamma-\beta) \end{array} \end{aligned} $$

and, if we sum over (x, u) = (x ₁, z ₁), …, (x _n, z _n), we can write

$$\displaystyle \begin{aligned} \begin{array}{rcl} -\sum_{i=1}^N\log f(z_i|x_i,\gamma)& =&\displaystyle \frac{N}{2}\log 2\pi\sigma^2 +\frac{1}{2\sigma^2}\|z-X\beta\|{}^2\\ & &\displaystyle -\frac{1}{\sigma^2}(\gamma-\beta)^TX^T(z-X\beta)+\frac{1}{2\sigma^2}(\gamma-\beta)^TX^TX(\gamma-\beta)\ , \end{array} \end{aligned} $$

where we have used z = [z ₁, …, z _N]^T and $\displaystyle \|z-X\beta \|{ }^2=\sum _{i=1}^N(z_i-x_i\beta )^2,\ \displaystyle X^TX=\sum _{i=1}^Nx_i^Tx_i,\ X^T(z-X\beta )=\sum _{i=1}^Nx_i^T(z_i-x_i\beta )$. □

Proposition 19

Let k(S) be the cardinality of S. Then, we have ⁴

$$\displaystyle \begin{aligned}E[\log \hat{\sigma}^2(S)]=\log\sigma^2(S)-\frac{k(S)+2}{N}+O\left(\frac{1}{N^2}\right)\ .\end{aligned}$$

Proof

Let m ≥ 1, $U\sim \chi ^2_m$, V ₁, …, V _m ∼ N(0, 1). For i = 1, …, m, we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} Ee^{tV_i^2}& =&\displaystyle \int_{-\infty}^\infty e^{tv_i^2}\frac{1}{\sqrt{2\pi}}e^{-v_i^2/2}dv_i= \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} \exp\left\{-\frac{(1-2t)v_i^2}{2}\right\} dv_i= (1-2t)^{-1/2}\\ Ee^{tU}& =&\displaystyle \int_{-\infty}^\infty e^{t(v_1^2+\cdots+v_{m}^2)}\frac{1}{\sqrt{2\pi}} e^{-(v_1^2+\cdots+v_{m}^2)/2}\, dv_1\cdots dv_{m} =(1-2t)^{-m/2}\ , \end{array} \end{aligned} $$

which means that for n = 1, 2, …,

$$\displaystyle \begin{aligned} \begin{array}{rcl} EU^n& =&\displaystyle \frac{d^nEe^{tU}}{dt^n}\bigg|{}_{t=0}=m(m+2)\cdots(m+2n-2) \ ,{} \end{array} \end{aligned} $$

(5.16)

where $\displaystyle Ee^{tU}=1+tE[U]+\frac {t^2}{2}E[U^2]+\cdots$ has been used. Moreover, from the Taylor expansion, we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} E\left[\log \frac{U}{m}\right]& =&\displaystyle E\left(\frac{U}{m}-1\right)-\frac{1}{2}E\left(\frac{U}{m}-1\right)^2+\cdots\ . {} \end{array} \end{aligned} $$

(5.17)

If we let (5.16) for n = 1, 2, where EU = m and EU ² = m(m + 2), the first and second terms of (5.17) are zero and

$$\displaystyle \begin{aligned}-\frac{1}{2m^2}(EU^2-2mEU+m^2)=-\frac{1}{2m^2}\{m(m+2)-2m^2+m^2\}=-\frac{1}{m}\ ,\end{aligned}$$

respectively.

Next, we show that each term in (5.17) for n ≥ 3 is at most O(1∕m ²). From the binomial theorem and (5.16), we have that

$$\displaystyle \begin{aligned} E(U-m)^n &= \sum_{j=0}^n \left( \begin{array}{c} n\\j \end{array} \right) EU^j(-m)^{n-j} \\ &= \sum_{j=0}^n(-1)^{n-j} \left( \begin{array}{c} n\\j \end{array} \right) m^{n-j}m(m+2)\cdots(m+2j-2)\ . \end{aligned} $$

(5.18)

If we regard

$$\displaystyle \begin{aligned}m^{n-j}m(m+2)\cdots(m+2j-2)\end{aligned}$$

as a polynomial w.r.t. m, the coefficients of the highest and (n − 1)-th terms are one and 2{1 + 2 + ⋯ + (j − 1)} = j(j − 1), respectively. Hence, the coefficients of the n-th and (n − 1)-th terms in (5.18) are

$$\displaystyle \begin{aligned}\displaystyle \sum_{j=0}^n\left( \begin{array}{c} n\\j \end{array} \right) (-1)^{n-j}= \sum_{j=0}^n\left( \begin{array}{c} n\\j \end{array} \right) (-1)^j1^{n-j}=(-1+1)^n= 0\end{aligned}$$

and

$$\displaystyle \begin{aligned}\sum_{j=0}^n \left( \begin{array}{c} n\\j \end{array} \right)(-1)^jj(j-1) &= \sum_{j=2}^n \frac{n!}{(n-j)!(j-2)!} (-1)^{j-2} \\ &= n(n-1) \sum_{i=0}^{n-2} \left( \begin{array}{c} n-2\\i \end{array} \right)(-1)^{i}=0\ , \end{aligned} $$

respectively. Thus, we have shown that for n ≥ 3,

$$\displaystyle \begin{aligned}E\left(\frac{U}{m}-1\right)^n=O\left(\frac{1}{m^2}\right)\ .\end{aligned}$$

Finally, from $\displaystyle \frac {RSS(S)}{\sigma ^2(S)}= \frac {N\hat {\sigma }^2(S)}{{\sigma }^2(S)}\sim \chi ^2_{N-k(S)-1}$ and (5.17), if we apply m = N − k(S) − 1, then we have that

$$\displaystyle \begin{aligned}\log\frac{N}{N-k(S)-1}=\frac{k(S)+1}{N-k(S)-1}+O\left(\left(\frac{1}{N-k(S)-1}\right)^2\right)\end{aligned}$$

$$\displaystyle \begin{aligned}E\left[\log \left(\frac{\hat{\sigma}^2(S)}{N-k(S)-1}\bigg/\frac{{\sigma}^2}{N}\right)\right]=-\frac{1}{N-k(S)-1}+O\left(\frac{1}{N^2}\right) =-\frac{1}{N}+O\left(\frac{1}{N^2}\right)\end{aligned}$$

and

$$\displaystyle \begin{aligned}E\left[\log \frac{\hat{\sigma}^2(S)}{\sigma^2}\right] =-\frac{1}{N}-\frac{k(S)+1}{N}+O\left(\frac{1}{N^2}\right) =-\frac{k(S)+2}{N}+O\left(\frac{1}{N^2}\right)\ . \end{aligned}$$

□

Exercises 40–48

In the following, we define

$$\displaystyle \begin{aligned}X= \left[ \begin{array}{c} {x_1}\\ \vdots\\ x_N \end{array} \right]\in {\mathbb R}^{N\times (p+1)} ,\ y= \left[ \begin{array}{c} y_1\\ \vdots\\ y_N \end{array} \right]\in {\mathbb R}^N ,\ z= \left[ \begin{array}{c} z_1\\ \vdots\\ z_N \end{array} \right]\in {\mathbb R}^N ,\ \beta= \left[ \begin{array}{c} \beta_0\\ \beta_1\\ \vdots\\ \beta_p \end{array} \right]\in {\mathbb R}^{p+1}\ , \end{aligned}$$

where x ₁, …, x _N are row vectors. We assume that X ^T X has an inverse matrix and denote by E[⋅] the expectation w.r.t.

$$\displaystyle \begin{aligned}f(y_i|x_i,\beta):=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{\|y_i-x_i\beta\|{}^2}{2\sigma^2}\right\}\ .\end{aligned}$$

• 40. For $X \in {\mathbb R}^{N\times (p+1)}$ and $y\in {\mathbb R}^N$, show each of the following:

  • (a) If the variance σ ² > 0 is known, the $\beta \in {\mathbb R}^{p+1}$ that maximizes $\displaystyle l:=\sum _{i=1}^N \log f(y_i|x_i,\beta )$ coincides with the least squares solution. Hint:

    $$\displaystyle \begin{aligned}{l}=-\frac{N}{2}\log (2\pi\sigma^2)-\frac{1}{2\sigma^2}\|y-X\beta\|{}^2.\end{aligned}$$

  • (b) If both $\beta \in {\mathbb R}^{p+1}$ and σ ² > 0 are unknown, the maximum likelihood estimate of σ ² is given by

    $$\displaystyle \begin{aligned}\hat{\sigma}^2=\frac{1}{N}\|y-X\hat{\beta}\|{}^2.\end{aligned}$$

    Hint: If we partially differentiate l with respect to σ ², we have

    $$\displaystyle \begin{aligned}\displaystyle \frac{\partial l}{\partial \sigma^2}=- \frac{N}{2\sigma^2}+\frac{\|y-X\beta\|{}^2}{2(\sigma^2)^2} =0.\end{aligned}$$

  • (c) For probabilistic density functions f and g over $\mathbb R$, the Kullback–Leibler divergence is nonnegative, i.e.,

    $$\displaystyle \begin{aligned}\displaystyle D(f\|g):=\int_{-\infty}^\infty f(x)\log \frac{f(x)}{g(x)}dx\geq 0.\end{aligned}$$

• 41. Let $f^N(y|x,\beta ):=\prod _{i=1}^Nf(y_i|x_i,\beta )$. By showing (a) through (d), prove

  $$\displaystyle \begin{aligned}J=\frac{1}{N}E(\nabla l)^2=-\frac{1}{N}E\nabla^2 l.\end{aligned} $$

  • (a) $\displaystyle {\nabla l}=\frac {\nabla f^N(y|x,\beta )}{f^N(y|x,\beta )}$;

  • (b) $\displaystyle \int \nabla f^N(y|x,\beta )dy=0$;

  • (c) E∇l = 0;

  • (d) ∇E[∇l] = E[∇² l] + E[(∇l)²].

• 42. Let $\tilde {\beta }\in {\mathbb R}^{p+1}$ be an arbitrary unbiased estimate β. By showing (a) through (c), prove Cramer–Rao’s inequality

  $$\displaystyle \begin{aligned}V(\tilde{\beta})\geq (NJ)^{-1}.\end{aligned} $$

  • (a) $E[(\tilde {\beta }-\beta )(\nabla l)^T]=I$.

  • (b) The covariance matrix of the vector combining $\tilde {\beta }-\beta$ and ∇l of size 2(p + 1)

    $$\displaystyle \begin{aligned} \left[ \begin{array}{c@{\quad }c} V(\tilde{\beta})&I\\ I&NJ \end{array} \right]\ . \end{aligned}$$

  • (c) Both sides of

    $$\displaystyle \begin{aligned}\left[ \begin{array}{c@{\quad }c} V(\tilde{\beta})-(NJ)^{-1}&0\\ 0&NJ \end{array} \right]= \left[ \begin{array}{c@{\quad }c} I&-(NJ)^{-1}\\ 0&I \end{array} \right] \left[ \begin{array}{c@{\quad }c} V(\tilde{\beta})&I\\ I&NJ \end{array} \right] \left[ \begin{array}{c@{\quad }c} I&0\\ -(NJ)^{-1}&I \end{array} \right] \end{aligned}$$

    are nonnegative definite.

• 43. By showing (a) through (c), prove $E\|X(\tilde {\beta }-\beta )\|{ }^2\geq \sigma ^2(p+1)$.

  • (a) $E[(\tilde {\beta }-\beta )^T\nabla {l}]=p+1$;

  • (b) E∥X(X ^T X)⁻¹∇l∥² = (p + 1)∕σ ²;

  • (c) $\{E(\tilde {\beta }-\beta )^T\nabla {l}\}^2\leq E\|X(X^TX)^{-1}\nabla l\|{ }^2E\|X(\tilde {\beta }-\beta )\|{ }^2$. Hint: For random variables $U,V\in {\mathbb R}^m$ (m ≥ 1), prove {E[U ^T V ]}² ≤ E[∥U∥²]E[∥V ∥²] (Schwarz’s inequality).

• 44. Prove the following statements:

  • (a) For covariates x ₁, …, x _N, if we obtain the responses z ₁, …, z _N, then the likelihood $\displaystyle -\sum _{i=1}^N\log f(z_i|x_i,\gamma )$ of the parameter $\gamma \in {\mathbb R}^{p+1}$ is

    $$\displaystyle \begin{aligned}\frac{N}{2}\log 2\pi\sigma^2 +\frac{1}{2\sigma^2}\|z-X\beta\|{}^2 -\frac{1}{\sigma^2}(\gamma-\beta)^TX^T(z-X\beta)+\frac{1}{2\sigma^2}(\gamma-\beta)^TX^TX(\gamma-\beta) \end{aligned}$$

    for an arbitrary $\beta \in {\mathbb R}^{p+1}$.

  • (b) If we take the expectation of (a) w.r.t. z ₁, …, z _N, it is

    $$\displaystyle \begin{aligned}\frac{N}{2}\log (2\pi\sigma^2e)+\frac{1}{2\sigma^2}\|X(\gamma-\beta)\|{}^2\ .\end{aligned}$$

  • (c) If we estimate β and choose an estimate γ of β, the minimum value of (b) on average is

    $$\displaystyle \begin{aligned}\frac{N}{2}\log (2\pi\sigma^2e)+\frac{1}{2}(p+1),\end{aligned}$$

    and the minimum value is realized by the least squares method.

  • (d) Instead of choosing all the p covariates, we choose 0 ≤ k ≤ p covariates from p. Minimizing

    $$\displaystyle \begin{aligned}\frac{N}{2}\log (2\pi\sigma_k^2e)+\frac{1}{2}(k+1)\end{aligned}$$

    w.r.t. k is equivalent to minimizing ${N}\log \sigma ^2_k+k$ w.r.t. k, where $\sigma ^2_k$ is the minimum variance when we choose k covariates.

• 45. By showing (a) through (f), prove

  $$\displaystyle \begin{aligned}E\log \frac{\hat{\sigma}^2(S)}{\sigma^2} =-\frac{1}{N}-\frac{k(S)+1}{N}+O\left(\frac{1}{N^2}\right) =-\frac{k(S)+2}{N}+O\left(\frac{1}{N^2}\right)\ .\end{aligned}$$

  Use the fact that the moment of $U\sim \chi ^2_m$ is

  $$\displaystyle \begin{aligned}EU^n=m(m+2)\cdots(m+2n-2)\ \end{aligned}$$

  without proving it.

  • (a) $\displaystyle E\log \frac {U}{m}=E\left (\frac {U}{m}-1\right )-\frac {1}{2}E\left (\frac {U}{m}-1\right )^2+\cdots$

  • (b) $\displaystyle E\left (\frac {U}{m}-1\right )=0$ and $\displaystyle E\left (\frac {U}{m}-1\right )^2=\frac {2}{m}$.

  • (c) $\displaystyle \sum _{j=0}^n(-1)^{n-j} \left ( \begin {array}{c} n\\j \end {array} \right )=0$.

  • (d) If we regard $\displaystyle E(U-m)^n= \sum _{j=0}^n(-1)^{n-j} \left ( \begin {array}{c} n\\j \end {array} \right ) m^{n-j}m(m+2)\cdots (m+2j-2)$ as a polynomial of degree m, the sum of the terms of degree n is zero. Hint: Use (c).

  • (e) The sum of the terms of degree n − 1 is zero. Hint: Derive that the coefficient of degree n − 1 is 2{1 + 2 + ⋯ + (j − 1)} = j(j − 1) for each j and that $\displaystyle \sum _{j=0}^n \left ( \begin {array}{c} n\\j \end {array} \right )(-1)^jj(j-1)=0$.

  • (f) $\displaystyle E\log \left (\frac {\hat {\sigma }^2(S)}{N-k(S)-1}\bigg /\frac {{\sigma }^2}{N}\right )=-\frac {1}{N}+O\left (\frac {1}{N^2}\right ).$

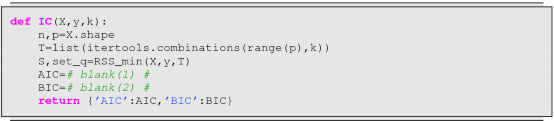
• 46. The following procedure produces the AIC value. Fill in the blanks and execute the procedure.

  

• 47. Instead of AIC, we consider a criterion that minimizes the following quantity (Bayesian Information Criterion (BIC)):

  $$\displaystyle \begin{aligned}N\log \hat{\sigma}^2+k\log N.\end{aligned}$$

  Replace the associated lines of the AIC procedure above, and name the function BIC. For the same data, execute BIC. Moreover, construct a procedure to choose the covariate set that maximizes

  $$\displaystyle \begin{aligned}AR^2:=1-\frac{RSS/(N-k-1)}{TSS/(N-1)}\end{aligned}$$

  (adjusted coefficient of determination), and name the function AR2. For the same data, execute AR2.

• 48. We wish to visualize the k that minimizes AIC and BIC. Fill in the blanks and execute the procedure.