Abstract
So far we have studied the quantum formalism in the abstract (Chap. 2) and in the context of rotational dynamics (Chap. 3). In this chapter we work with the spatial motion of point particles, which represents a kind of mechanics that is much closer to our everyday experience. Here, quantum states are called wavefunctions and depend on the spatial coordinate(s). This apparent difference to the material covered in the previous chapters disappears when we express all wavefunctions in a basis set. We develop numerical methods for studying spatial dynamics that stay as close to a real-space description as quantum mechanics allows.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
To be exact, the Dirac position basis set spans a space that is much larger than the Hilbert space of square-integrable smooth functions used in quantum mechanics. This can be seen by noting that this basis set has an uncountably infinite number of elements \(|x\rangle \), while the dimension of the Hilbert space in question is only countably infinite [see Eq. (4.5) for a countably infinite basis set]. The underlying problem of the continuum, which quantum mechanics attempts to resolve, is discussed with some of its philosophical origins and implications by Erwin Schrödinger in his essay “Science and Humanism” (Cambridge University Press, 1951, ISBN 978-0521575508).
- 2.
This eigenvalue equation is tricky: remember that \(\hat{x}\) is an operator, \(|x\rangle \) is a state, and x is a real number.
- 3.
- 4.
- 5.
See https://en.wikipedia.org/wiki/Discrete_sine_transform and https://en.wikipedia.org/wiki/Fast_Fourier_transform. The precise meaning of the DST-I can be seen from its equivalent definition through a standard discrete Fourier transform of doubled length: for a complex vector
 , we can substitute
, we can substitute 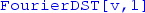 by
by 
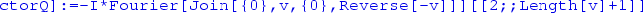 . In this sense it is the discrete Fourier transform of a list
. In this sense it is the discrete Fourier transform of a list  augmented with (i) zero boundary conditions and (ii) reflection anti-symmetry at the boundaries. Remember that the
augmented with (i) zero boundary conditions and (ii) reflection anti-symmetry at the boundaries. Remember that the 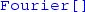 transform assumes periodic boundary conditions, which are incorrect in the present setup, and need to be modified into a DST-I.
transform assumes periodic boundary conditions, which are incorrect in the present setup, and need to be modified into a DST-I. - 6.
See https://en.wikipedia.org/wiki/Finite_difference_coefficient for explicit forms of higher-order finite-differences expressions that can be used to approximate derivatives.
- 7.
- 8.
This procedure works for situations other than the usual \(x_{\text {min}}=0\) and \(x_{\text {max}}=a\).
- 9.
- 10.
A functional is an operation that calculates a number from a given function. For example, \(E[\psi ]:L^2\rightarrow \mathbb {R}\) converts a wavefunction \(\psi \in L^2\) into an energy \(E\in \mathbb {R}\). See https://en.wikipedia.org/wiki/Functional_(mathematics).
- 11.
- 12.
- 13.
For simplicity we assume here that the ground state is non-degenerate.
- 14.
- 15.
- 16.
The eigenvectors of Hermitian operators can always be chosen to have real coefficients. Proof: Suppose that \(\varvec{H}\cdot \varvec{\vec {\psi }}=E\varvec{\vec {\psi }}\) for a vector \(\varvec{\vec {\psi }}\) with complex entries. Complex-conjugate the eigenvalue equation, \(\varvec{H}^{\dagger }\cdot \varvec{\vec {\psi }}^*=E^*\varvec{\vec {\psi }}^*\); but \(\varvec{H}^{\dagger }=\varvec{H}\) and \(E^*=E\), and hence \(\varvec{\vec {\psi }}^*\) is also an eigenvector of \(\varvec{H}\) with eigenvalue E. Thus we can introduce two real-valued vectors \(\varvec{\vec {\psi }}_{\text {r}}=\varvec{\vec {\psi }}+\varvec{\vec {\psi }}^*\) and \(\varvec{\vec {\psi }}_{\text {i}}=\text {i}(\varvec{\vec {\psi }}-\varvec{\vec {\psi }}^*)\), representing the real and imaginary parts of \(\varvec{\vec {\psi }}\), respectively, which are both eigenvectors of \(\varvec{H}\) with eigenvalue E. Mathematica (as well as most other matrix diagonalization algorithms) automatically detect Hermitian matrices and return eigenvectors with real coefficients.
Author information
Authors and Affiliations
Corresponding author
4.1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Schmied, R. (2020). Quantum Motion in Real Space. In: Using Mathematica for Quantum Mechanics. Springer, Singapore. https://doi.org/10.1007/978-981-13-7588-0_4
Download citation
DOI: https://doi.org/10.1007/978-981-13-7588-0_4
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-7587-3
Online ISBN: 978-981-13-7588-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


 , we can substitute
, we can substitute 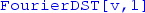 by
by 
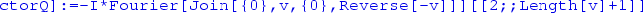 . In this sense it is the discrete Fourier transform of a list
. In this sense it is the discrete Fourier transform of a list  augmented with (i) zero boundary conditions and (ii) reflection anti-symmetry at the boundaries. Remember that the
augmented with (i) zero boundary conditions and (ii) reflection anti-symmetry at the boundaries. Remember that the 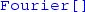 transform assumes periodic boundary conditions, which are incorrect in the present setup, and need to be modified into a DST-I.
transform assumes periodic boundary conditions, which are incorrect in the present setup, and need to be modified into a DST-I.