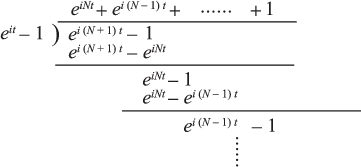Skip to main content
SpringerLink
Log in

Fourier Transforms of Measures

  • Chapter
  • First Online:
Fourier Analysis of Economic Phenomena

Part of the book series: Monographs in Mathematical Economics ((MOME,volume 2))

  • 1093 Accesses

Abstract

So far, we have studied Fourier transforms or Fourier coefficients of functions defined on \(\mathbb {R}\) or \(\mathbb {T}\). Inverse procedures to recover original functions from given Fourier transforms or Fourier coefficients were also discussed (spectral synthesis). However, there are many functions to which the methods of classical Fourier analysis can not be applied. In this chapter, we develop the theory of Fourier transforms of measures as a similar but new method to overcome such difficulties.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
eBook
USD 16.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 139.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    A function f is said to vanish at infinity if there exists, for each ε > 0, some compact set K ⊂ X such that |f(x)| < ε for all x ∈ K c.

  2. 2.

    Malliavin [7] pp. 96–97, Maruyama [9] pp. 300–315.

  3. 3.

    The interval of integration should be interpreted as [−π, π).

  4. 4.

    See p. 83 for dual operators.

  5. 5.

    For Sects. 6.3–6.8, we are very much indebted to Katznelson [5] Chap. I, §7 and Chap. VI, except for the distribution approach to the Herglotz–Bochner theorem.

  6. 6.

    The Fourier coefficients of P(x) are given by

    $$\displaystyle \begin{aligned} \frac{1}{\sqrt{2\pi}}\int_{-\pi}^\pi P(x)e^{-ijx}dx=\sqrt{2\pi}\alpha_j\end{aligned}$$

    for \(|j|\leqq n\), and 0 for \(|j|\geqq n+1\). Hence the Fourier series of P(x) is computed as

    $$\displaystyle \begin{aligned} P(x)=\sum_{j=-n}^n \sqrt{2\pi}\alpha_j \frac{1}{\sqrt{2\pi}}e^{ijx}=\sum_{j=-n}^n \alpha_j e^{ijx}. \end{aligned}$$
  7. 7.

    G may be, more generally, a commutative group.

  8. 8.

    See textbooks on linear algebra for Hermitian forms and their signs.

  9. 9.

    Herglotz [3]. Essentially the same result is obtained by Carathéodory [2] and Toeplitz [13]. The proof given here is due to Katznelson [5] Chap. 1, §7.

  10. 10.

    Due to Maruyama [9]. I acknowledge the priority of Lax [6], pp. 142–143 for the idea of proof.

  11. 11.

    See Theorem 2.5 (p. 37) and Remark 2.3 (p. 39).

  12. 12.

    See Appendix C, Sect. C.3, or Schwartz [12], Chap. 1, §4, Théorème 5. \(\mathfrak {M}_+(\mathbb {T})\) denotes the set of all the positive Radon measures on \(\mathbb {T}\).

  13. 13.

    See Sect. 6.7 in this chapter for the convolution of two measures.

  14. 14.

    “\(\hat {\mu }(\xi )=0\) for a.e. ξ” is sufficient to get μ = 0. However, \(\hat {\mu }(\xi )\) is eventually equal to 0 for every ξ, since we know that \(\hat {\mu }(\xi )\) is continuous.

  15. 15.

    cf. Lax [6] pp. 120–121, Maruyama [8] pp. 354–355.

  16. 16.

    \(g(\xi )\hat {\mu }(-\xi )\rightarrow g(\xi )\varphi (-\xi )\). And {μ n} is bounded (with respect to the operator norm), since μ n → μ in w ∗-topology. Furthermore, since ∥g∥∞ < ∞, there exists some \(F\in \mathfrak {L}^1\) such that

    $$\displaystyle \begin{aligned} |g(\xi)\hat{\mu}_n(-\xi)|\leqq |g(\xi)| \cdot C\leqq F(\xi). \end{aligned}$$

    Then apply the dominated convergence theorem.

  17. 17.

    Assume, on the contrary, that \(\hat {\mu }(-\bar {\xi })-\varphi (-\bar {\xi })\neq 0\) (say, > 0) for some \(\bar {\xi }\). Then there exists a neighborhood U of \(\bar {\xi }\) such that \(\hat {\mu }(-\xi )-\varphi (-\xi )>0\) on U. There exists some \(g\in \mathfrak {S}\) such that supp g ⊂ U and g(x) > 0 in the interior of its support. Then clearly

    $$\displaystyle \begin{aligned} \int_{-\infty}^\infty g(\xi)(\hat{\mu}(-\xi)-\varphi(-\xi))d\xi>0. \end{aligned}$$

    Contradiction.

  18. 18.

    For a 2π-periodic function f, we have

    $$\displaystyle \begin{aligned} \int_{-\infty}^\infty f(x)d\mu =\int_{-\pi}^\pi f(x)d\nu. \end{aligned}$$
  19. 19.

    Summing up the upper and lower ends of the integration (6.41) for all \(m\in \mathbb {Z}\), we get the integration over (−∞, ∞). See Fig. 6.1.

  20. 20.

    \(\displaystyle {\left ( \frac {x+2\pi m}{\lambda }\right )^2 \geqq \left (\frac {\pi -2\pi |m|}{\lambda }\right )^2 =\frac {\pi ^2}{\lambda ^2}(1-2|m|)^2 \geqq \frac {\pi ^2}{\lambda ^2}m^2, }\) where \(|m|\geqq 1.\)

  21. 21.

    For the Fejér kernel, see Chap. 5, Sect. 5.4 (pp. 111–115).

  22. 22.

    cf. Chap. 5, Sect. 5.5, p. 119.

  23. 23.

    We have already seen that K(λx) → 1∕2π (uniformly on any compact set) as λ → 0 (cf. p. 146). We can choose λ (independent of x ∈supp f) so that (6.59) holds good on supp f. The inequality (6.59) is satisfied, of course, outside supp f.

  24. 24.

    If \(f\in \mathfrak {A}\) and \(f\geqq 0\), there exists a sequence {g n} in \(\mathfrak {C}_0^\infty \) which converges to \(\hat {f}\) in \(\mathfrak {L}^1\). Let f n be the inverse Fourier transform of g n; i.e. \(\hat {f}_n=g_n\). Then {f n} is a sequence in \(\mathfrak {S}_c\). If

    $$\displaystyle \begin{aligned} \int_{-\infty}^\infty \hat{f}_n(\xi)\varphi(-\xi)d\xi =\int_{-\infty}^\infty g_n(\xi)\varphi(-\xi)d\xi \geqq 0 \end{aligned}$$

    for each n, we obtain, by passing to the limit,

    $$\displaystyle \begin{aligned} \int_{-\infty}^\infty \hat{f}(\xi)\varphi(-\xi)d\xi \geqq 0. \end{aligned}$$
  25. 25.

    Bochner [1]. μ, which satisfies (ii), is unique by Corollary 6.3.

  26. 26.

    By Lemma 6.4, a positive semi-definite function is uniformly continuous on \(\mathbb {R}\) if it is continuous at 0.

  27. 27.

    The basic ideas are given in Lax [6], pp. 144–146. See also Maruyama [10].

  28. 28.

    Here φ denotes the tempered distribution defined by the bounded function φ. Hence

    $$\displaystyle \begin{aligned} \varphi(s)=\int_{\mathbb{R}}\varphi(x)s(x)dx, \quad s \in \mathfrak{S}(\mathbb{R}). \end{aligned}$$
  29. 29.

    We note that there exists a unique function in \(\mathfrak {S}(\mathbb {R})\), the Fourier transform of which is just \(\sqrt {p}\).

  30. 30.

    I repeat again the exposition of the concept of the torus. A binary relation ∼ on \(\mathbb {R}\) is defined by

    $$\displaystyle \begin{aligned} x \sim y \Longleftrightarrow x-y\in 2\pi\mathbb{Z}. \end{aligned}$$

    ∼ is an equivalence relation, and any two numbers are equivalent if and only if the difference between them is a multiple of 2π. Any real number has its equivalent number in [−π, π).

    Given a function \(f:[-\pi , \pi ) \rightarrow \mathbb {C}\), we may not be able to define f(x + y), since x + y may not be in [−π, π). However, there exists some z ∈ [−π, π) which is equivalent to x + y. We understand f(x + y) as f(z). A similar convention applies to the Dirac measures on [−π, π). That is, we understand δ x+y as δ z. More generally, we can consider f(x 1 + x 2 + ⋯ + x n) or \(\delta _{x_1+x_2+\cdots +x_n}\) in the same way.

    When we consider a function on \(\mathbb {R}\) rather than [−π, π), such a convention is not necessary.

    Exactly speaking, we consider a function defined on the quotient group \(\mathbb {R}/2\pi \mathbb {Z}\) modulo \(2\pi \mathbb {Z}\). This is called torus and denoted by \(\mathbb {T}\). cf. Appendix A. We are indebted to Malliavin [7] Chap. III, §1 for the expositions in this section.

  31. 31.

    See Naimark [11], Lax [6] Chaps. 17–20 and Maruyama [8] Chap. 7 for normed algebras.

  32. 32.

    Any bounded Borel measure μ on G can be represented as μ = μ a + μ s + μ d, where μ a ≪ m (Lebesque measure) μ s is continuous and μ s ⊥ m, and μ d is discrete. Such a decomposition is uniquely determined. cf. Igari [4] p. 137.

  33. 33.

    \(\widehat {\mu ^\sharp }=\bar {\hat {\mu }}\).

  34. 34.

    We owe this to Katznelson [5] Chap. I, §7 and Chap. VI, §2.

  35. 35.
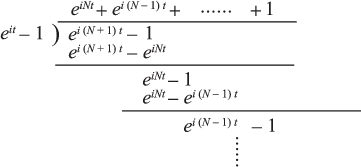
  36. 36.

    Assume t ≠ 0. Then

    $$\displaystyle \begin{aligned} \varphi_n(t)=\frac{1}{it}e^{i\xi t}\bigg|{}_{-n}^n =\frac{1}{it}(e^{int}-e^{-int}) =\frac{\, 2\,}{t} \sin nt.\end{aligned} $$

    Hence

    $$\displaystyle \begin{aligned} \frac{1}{2n}\varphi_n(t)=\frac{1}{nt}\sin t.\end{aligned} $$

    We obtain (6.88) as n →∞.

  37. 37.

    The upper and lower ends of the integration can be \(\displaystyle \int _{\theta _n}^{\theta _n+n}\) for any sequence {θ n}.

References

  1. Bochner, S.: Monotone Funktionen, Stieltjessche Integrale und harmonische Analyse. Math. Ann. 108, 378–410 (1933)

    MATH  Google Scholar 

  2. Carathéodory, C.: Über den Variabilitätsbereich der Koefficienten von Potenzreihen die gegebene Werte nicht annemen. Math. Ann. 54, 95–115 (1907)

    Article  Google Scholar 

  3. Herglotz, G.: Über Potenzreihen mit positiven reellen Teil in Einheitskreise. Berichte Verh Säcks. Akad. Wiss. Leipzig. Math.-phys. Kl. 63, 501–511 (1911)

    Google Scholar 

  4. Igari, S.: Jitsu-kaiseki Nyumon (Introduction to Real Analysis). Iwanami Shoten, Tokyo (1996) (Originally published in Japanese)

    Google Scholar 

  5. Katznelson, Y.: An Introduction to Harmonic Analysis, 3rd edn. Cambridge University Press, Cambridge (2004)

    Book  Google Scholar 

  6. Lax, P.D.: Functional Analysis. Wiley, New York (2002)

    MATH  Google Scholar 

  7. Malliavin, P.: Integration and Probability. Springer, New York (1995)

    Book  Google Scholar 

  8. Maruyama, T.: Kansu Kaisekigaku (Functional Analysis). Keio Tsushin, Tokyo (1980) (Originally published in Japanese)

    Google Scholar 

  9. Maruyama, T.: Sekibun to Kansu-kaiseki (Integration and Functional Analysis). Springer, Tokyo (2006) (Originally published in Japanese)

    Google Scholar 

  10. Maruyama, T.: Herglotz-Bochner representation theorem via theory of distributions. J. Oper. Res. Soc. Japan 60, 122–135 (2017)

    MathSciNet  MATH  Google Scholar 

  11. Naimark, M.A.: Normed Algebras. Wolters Noordhoff, Groningen (1972)

    Google Scholar 

  12. Schwartz, L.: Théorìe des distributions. Nouvelle édition, entièrement corrigée, refondue et augmentée, Hermann, Paris (1973)

    Google Scholar 

  13. Toeplitz, O.: Über die Fouriersche Entwickelung positive Funktionen. Rend. di Cinc. Mat. di Palermo 32, 191–192 (1911)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Professor Emeritus, Keio University, Tokyo, Japan

    Toru Maruyama

Authors
  1. Toru Maruyama
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer Nature Singapore Pte Ltd.

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Maruyama, T. (2018). Fourier Transforms of Measures. In: Fourier Analysis of Economic Phenomena. Monographs in Mathematical Economics, vol 2. Springer, Singapore. https://doi.org/10.1007/978-981-13-2730-8_6

Download citation

Publish with us

Policies and ethics

Search

Navigation