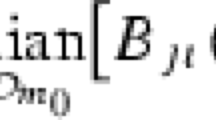Variant Maps of Elementary Equations

Abstract

Using four measures in Type B, there are 11 invariant expressions to form elementary equations of variant measurement. In this chapter, two invariant expressions are selected to illustrate sample procedures from elementary equations to relevant variant maps. Using various projections and multiple levels of representations, complicated binomial coefficients and their variations are illustrated under various conditions. Using multinomial coefficients, multiple viewpoints are used for references. Due to this type of variation framework contains rich structures, further explorations are required from multiple levels on both theoretical foundation and practical applications.

This work was supported by the Key Project on Electric Information and Next Generation IT Technology of Yunnan (2018ZI002), NSF of China (61362014), Yunnan Advanced Overseas Scholar Project.

1 Introduction

Variant construction starts from n 0–1 variables to form $2^n$ states and $2^{2^n}$ functions, via vector permutation and complement operations on state space to establish a variant logic framework to contain $2^n!\times 2^{2^n}$ configurations as a variation space. Variant measurement acts as a core of quantitative measurement, starting from m 0–1 variables to explore relevant clustering conditions on $2^m$ states. Since this type of variations has a close relationship to partition and recombination using binomial and multinomial coefficients under identically combinatorial expressions. Applying the results in Chapter “Elementary Equations of Variant Measurement”, Type B measures are composed of 11 nontrivial invariants. Two invariants are selected in this chapter, their different partition properties are illustrated to use coefficients on 2D and 3D distributions. Variant maps are generated from coefficient arrays as samples.

2 Measures and Maps

Two combinatorial invariants are selected: $\{m-p\}\{p\}$ and $\{2q\}\{m-2q\}$. Different distributions on their coefficients are explored.

2.1 Case 1. $\{m-p\}\{p\}$

For $\{m-p\}\{p\}$ formula, relevant equation is

$$\begin{aligned} {m \atopwithdelims ()p} = \sum _{k=0}^p {m-p \atopwithdelims ()k}{p \atopwithdelims ()k} \end{aligned}$$

(1)

A binomial coefficient is separated by sum of $(p+1)$ pairs of binomial coefficient products. For a selected value p, coefficients $\{{m-p \atopwithdelims ()k}{p \atopwithdelims ()k}\}, 0\le k \le p$ are arranged in a linear order.

This property is true for all p values. A special three tuple structure (m, p, k) has 1–1 correspondence with a coefficient $f(m,p, k)={m-p \atopwithdelims ()k}{p \atopwithdelims ()k}$. While m value increased, coefficient array will be increased as a 3D rectangular steps, each m value has a $(m+1)^2$ region.

The nontrivial coefficients are distributed as a triangle. Let$F(m,p) = \sum _{\forall k}f(m,p, k)$, $0\le p \le m$ and $G(m,k) = \sum _{\forall p}f(m,p, k), 0\le k \le m$, two projections $\{F(m,p), G(m, k)\}$ can be projected. Coefficients and relevant four maps are shown in Fig. 1.

Lemma 1

For $\{m-p\}\{p\}$ equation, coefficients are distributed in $(m+1)^2$ and all nontrivial coefficients are clustered in 1/4 region and 3/4 regions has coefficient 0.

Fig. 1

One set of coefficients and its two projections in four maps (a)–(d); a 3D f(10, p, k); b 2D f(10, p, k); c 1D F(10, p); d 1D G(10, k)

2.2 Case 2. $\{2q\}\{m-2q\}$

Briefly $\{m-p\}\{p\}$ and $\{2q\}\{m-2q\}$ are simple invariants. For $\{2q\}\{m-2q\}$ invariant, it has the following equation.

$$\begin{aligned} {m \atopwithdelims ()p} = \sum _{k=0}^p {2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k} \end{aligned}$$

(2)

where q is a free variable, $0\le q \le \lfloor m/2 \rfloor$. Different from Case 1, this equation can determine $lfloor m/2 \rfloor +1$ levels of coefficients according to different q values selected to form a 3D coefficient structure.

Let $f(m,q, p.k)={2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k}$ under $0\le q \le \lfloor m/2 \rfloor , 0 \le k, p \le m$ conditions, nontrivial coefficients are distributed in special shapes on multiple 2D regions.

Using color coding scheme, it is feasible to map coefficients into greyscale or color pixels as variant maps.

A binomial coefficient can be separated as sum of $(p+1)$ pairs of coefficient products $\{{2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k}\}, 0\le k \le p$ to be a linear order.

This type of property is true for all p values, a special tuple of four parameters (m, q, p, k) has 1–1 correspondence with coefficient ${2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k}$. Each selected m value is corresponding to $(m+1)^2\times (\lfloor m/2 \rfloor +1)$ region to locate all coefficients.

Lemma 2

For $\{2q\}\{m-2q\}$ combinatorial invariant, all coefficients are restricted in $(m+1)^2\times (\lfloor m/2 \rfloor +1)$ region.

3 Visual Results

It is convenient to use color coding to transfer each coefficient as a pixel in a variant map. Invariant coefficients provide ideal conditions for a practical measurement, it is feasible to check physical differences between an idea distribution and a practical measurement.

From a quantitative viewpoint, multinomial expressions provide proper basis on corresponding partitions to be a relative measurement in representation.

3.1 Case 1. Maps

Using ${m \atopwithdelims ()p} \rightarrow \{{m-p \atopwithdelims ()k}{p \atopwithdelims ()k}\}$, three maps are shown in Fig. 1 as 2D coefficients, 3D histograms, and 2D projections on four parameters $m=\{10,11,15,16\}$, respectively.

Fig. 2

$\{m-p\}\{p\}$ maps: $m=\{10,11,15,16\}$; $(a_1){-}(d_1)\; m=10$; $(a_2){-}(d_2)\; m=11$; $(a_3){-}(d_3)\; m=15$; $(a_4){-}(d_4)\; m=16$

3.2 Case 2. Maps

Different from Case 1, each m is associated with one 2D coefficient. In ${m \atopwithdelims ()p} \rightarrow \{{2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k}\}$ conditions, each q selection determines a 2D array of coefficients. Under $0\le q \le \lfloor m/2 \rfloor$ conditions, $\lfloor m/2 \rfloor +1$ levels are required. For $m=10$, it is necessary to have 6 levels.

To observe global properties, a 3D color map is shown in Fig. 3 to illustrate 3D coefficients under color coding.

4 Result Analysis

In maps of Figs. 1, 2, and 3, it is convenient to see variant maps transformed from elementary equations. From a certain viewpoint, $\{m-p\}\{p\}$ coefficients have symmetric properties on horizontal direction on $p:m-p$ with reflective properties. Nontrivial coefficients are located in 1/4 region of $(m+1)^2$ square. An isosceles triangle is composed of all nontrivial coefficients. Selecting any m, there is only one 2D coefficient associated with to be a unified distribution.

$\{2q\}\{m-2q\}$ coefficients are corresponding to multiple 2D distributions under various q values. While $q=0$, each nontrivial coefficient is located on diagonal position of $p=k$ and each coefficient is a ${2q \atopwithdelims ()k}{m-2q \atopwithdelims ()p-k}$ equation. In $0\le q \le 5$ conditions, 2D coefficient matrices are shown in six groups of $\{0:10, 2:8, 4:6, 6:4, 8:2, 10:0\}$, this can be described as $(x+y)^{n+l}=(x+y)^n(x+y)^l$ coefficient distributions that can be illustrated in Fig. 2 $\{\{(a_0){-}(c_0)\}-\{(a_5){-}(c_5)\}\}$ maps.

Fig. 3

$\{2q\}\{m-2q\}$ maps: $m=10$; $(a_0){-}(c_0) q=0$; $(a_1){-}(c_1) q=1$; $(a_2){-}(c_2) q=2$; $(a_3){-}(c_3) q=3$; $(a_4){-}(c_4) q=4$; $(a_5){-}(c_5) q=5$

Fig. 4

$\{2q\}\{m-2q\}$ map: $m=10$; 3D color map

5 Conclusion

It is a new exploration to use elementary equation to illustrate relevant variant maps. Based on the described model and calculation, it is convenient to do various analysis and visualization. It is an initial step to check two invariants from Type B for four variant measures. Further explorations are required on five levels of 11 nontrivial invariants in Type B. From results in this chapter, distinct distributions are observed on the two selected invariants. Other nine invariants in Type B will be discussed in future papers (Fig. 4).