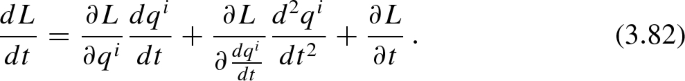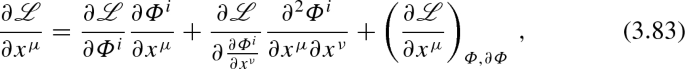Abstract
Relativistic mechanics is the mechanics based on the Einstein Principle of Relativity. It reduces to Newtonian mechanics in the limit \(c \rightarrow \infty \). We start from discussing the case of a free point-like particle and we then move to multi-body systems and fields.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The minus sign in front of \(ds^2\) is because we are using a metric with signature \((-+++)\) and therefore time-like trajectories have \(ds^2 < 0\). With a metric with signature \((+---)\), as is the common convention among the particle physics community, we could write Eq. (3.9) as
It is clear that the convention of the signature of the metric does not change the solution of the particle trajectory.
- 2.
Note that we are using Cartesian coordinates. In non-Cartesian coordinates, we have to be more careful. The conjugate momentum is
or, with the component notation,
The 3-momentum is \(p^i = g^{ij} p_j\). In Cartesian coordinates, \(g^{ij} = \delta ^{ij}\), and therefore \(\mathbf{p^*} = \mathbf{p}\).
- 3.
In a different coordinate system, the total 4-momentum may not be a conserved quantity. Remember, for instance, that \(p^\mu \)s and \(p_\mu \)s are not all constants of motion for a free particle in spherical coordinates.
- 4.
In Eq. (3.66) we assume that there are only two-body interactions, namely that interactions are only between two particles. In principle, there may exist even three-body and, more in general, multi-body interaction terms.
- 5.
The factor 1 / c in front of the integral is introduced because we define \(d^4\varOmega = c dt d^3V\), not \(d^4\varOmega = dt d^3V\).
- 6.
Note the confusion in the notation. In Sect. 1.6, the derivative of t was
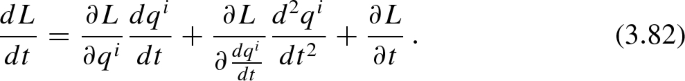
The counterpart here is
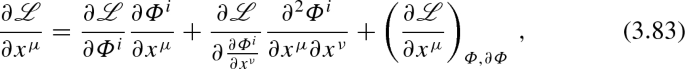
where the last term \(\left( \frac{\partial \mathscr {L}}{\partial x^\mu } \right) _{\varPhi , \partial \varPhi }\) is the possible contribution from an explicit dependence of \(\mathscr {L}\) on \(x^\mu \) (which we assume to vanish in Eq. (3.84)). In this section, we employ the partial derivatives because \(x = (x^0,x^1,x^2,x^3)\) and \(\frac{\partial \mathscr {L}}{\partial x^\mu }\) is not the counterpart of \(\partial L/\partial t\). The equivalent of \(\partial L/\partial t\) is now \(\left( \frac{\partial \mathscr {L}}{\partial x^\mu } \right) _{\varPhi , \partial \varPhi }\).
- 7.
Author information
Authors and Affiliations
Corresponding author
Problems
Problems
3.1
Write the 4-momentum \(p^\mu \) and \(p_\mu \) for a free point-like particle in spherical coordinates.
3.2
Find the constants of motion for a free point-like particles in spherical coordinates.
3.3
Repeat Problems 3.1 and 3.2 for cylindrical coordinates.
3.4
The counterpart of reaction (3.57) for cosmic ray photons is
namely a high-energy photon (\(\gamma \)) collides with a CMB photon (\(\gamma _{CMB}\)) and there is the production of a pair electron-positron (\(e^+ e^-\)). Calculate the threshold energy of the high-energy photon that permits the reaction. \(m_{e^+} c^2 = m_{e^-} c^2 = 0.5\) MeV.
3.5
Iron-56 is the most common isotope of iron. Its nucleus is made of 26 protons and 30 neutrons. Calculate the binding energy per nucleon, namely the binding energy divided the number of protons and neutrons. The mass of a nucleus of iron-56 is \(M c^2 = 52.103\) GeV. The masses of a proton and of a neutron are, respectively, \(m_p c^2 = 0.938\) GeV and \(m_n c^2 = 0.940\) GeV.
3.6
Write the field equations of the following Lagrangian density
3.7
Write the field equations in Problem 3.6 in Cartesian and spherical coordinates.
3.8
Let us consider a Cartesian coordinate system. Write the energy-momentum tensor associated with the Lagrangian in Problem 3.6.
3.9
Eqs. (3.103) and (3.104) are the expressions in Cartesian coordinates. Find their expressions in spherical coordinates and compare the result with that found in Problem 2.1.
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Bambi, C. (2018). Relativistic Mechanics. In: Introduction to General Relativity. Undergraduate Lecture Notes in Physics. Springer, Singapore. https://doi.org/10.1007/978-981-13-1090-4_3
Download citation
DOI: https://doi.org/10.1007/978-981-13-1090-4_3
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-1089-8
Online ISBN: 978-981-13-1090-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)