Abstract
In this chapter we develop a duality between a normed space X and the space \(X'\) consisting of all bounded linear functionals on X, known as the dual space of X. As a consequence of the Hahn–Banach extension theorem, we show that \(X'\ne \{0\}\) if \(X\ne \{0\}\). We also prove a companion result which is geometric in nature and is known as the Hahn–Banach separation theorem. We characterize duals of several well-known normed spaces. To a bounded linear map F from a normed space X to a normed space Y, we associate a bounded linear map \(F'\) from \(Y'\) to \(X'\), known as the transpose of F. To a bounded linear map A from a Hilbert space H to a Hilbert space G, we associate a bounded linear map \(A^*\) from G to H, known as the adjoint of A. We study maps that are ‘well behaved’ with respect to the adjoint operation. We also introduce the numerical range of a bounded linear map from a nonzero inner product space to itself. These considerations will be useful in studying the spectral theory in the next chapter.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Let \(r\in \{1,2,\infty \}\), and for \(x\in \ell ^\infty \), let \(F(x):=(f(x),0,0,\ldots )\in \ell ^r\). Then F is a nonzero continuous linear map from \(\ell ^\infty \) to \(\ell ^r\), but it is not a matrix transformation, since \(F(e_j)(i)=0\) for all \(i,j\in {\mathbb N}\).
Author information
Authors and Affiliations
Corresponding author
Exercises
Exercises
-
4.1.
Let \(X := {\mathbb K}^{2}\) with the norm \(\Vert \cdot \Vert _\infty .\)
-
(i)
Let \(Y := \{(x(1), x(2)) \in X : x(2) = 0\}\), and define \(g(y) := y(1) \) for \(y:=(y(1),y(2))\in Y\). The only Hahn–Banach extension of g to X is given by \(f(x) := x(1)\) for all \(x:=(x(1),x(2))\in X\).
-
(ii)
Let \(Z := \{(x(1), x(2)) \in X : x(1)=x(2)\}\), and define \(h(z) := z(1) \) for \(z:=(z(1),z(2))\in Z\). Then f is a Hahn–Banach extension of h to X if and only if there is \(t\in [0,1]\) such that \(f(x) := t\,x(1)+(1-t)x(2)\) for all \(x:=(x(1),x(2))\in X\).
-
(i)
-
4.2.
(Helly, 1912) Let X be a normed space. For each s in an index set S, let \(x_{s} \in X\) and \(k_{s} \in {\mathbb K}.\) There exists \(f\in X'\) such that \(f(x_{s}) = k_{s}\) for each \(s \in S\) if and only if there is \(\alpha >0\) such that \(\big |\sum _{s} c_{s} k_{s}\big | \le \alpha \big \Vert \sum _{s} c_{s} x_{s}\big \Vert ,\) where \(\sum _s\) is an arbitrary finite sum and \(c_s \in {\mathbb K}\) with \(s \in S\).
-
4.3.
Let Y be a subspace of a normed space X, and let \(g\in Y'\). Let E denote the set of all Hahn–Banach extensions of g to X. Then E is a nonempty, convex, closed and bounded subset of \(X'\), and E does not contain any open ball of \(X'\). However, E may not be a compact subset of \(X'\).
-
4.4.
(Taylor–Foguel, 1958) Let X be a normed space over \({\mathbb K}\). There is a unique Hahn–Banach extension to X of every continuous linear functional on every subspace of X if and only if the normed space \(X'\) is strictly convex. (Compare Exercise 2.10 and Theorem 4.17.)
-
4.5.
Let X and Y be normed spaces, and let \(X\ne \{0\}\). Then the following conditions are equivalent: (i) Y is a Banach space. (ii) BL(X, Y) is a Banach space. (iii) CL(X, Y) is a Banach space.
-
4.6.
Let X be a normed space, let Y be a subspace of X and let \(m\in {\mathbb N}\). Then every \(G\in BL(Y,{\mathbb K}^m)\) has an extension \(F\in BL(X,{\mathbb K}^m)\). If, in particular, the norm on \({\mathbb K}^m\) is the norm \(\Vert \cdot \Vert _\infty \), then every \(G\in BL(Y,{\mathbb K}^m)\) has a norm-preserving extension \(F\in BL(X,{\mathbb K}^m)\). Also, every \(G\in BL(Y,\ell ^\infty )\) has a norm-preserving extension \(F\in BL(X,\ell ^\infty )\).
-
4.7.
Let \(X:={\mathbb K}^3\) with \(\Vert \cdot \Vert _1\), and let \(Y:=\{x\in {\mathbb K}^3:x(1)+x(2)+x(3)=0\}\). If \(G:=I_Y\), the identity operator on Y, and if \(F:X\rightarrow Y\) is a linear extension of G, then \(\Vert F\Vert >\Vert G\Vert \). (This example is due to S.H. Kulkarni.)
-
4.8.
Let E be a convex subset of a normed space X, and let \(a \in X\). Then \(a \in \overline{E}\) if and only if (i) \(\mathrm{Re\, }f(a) \ge 1\) whenever \(f \in X'\) and \(\mathrm{Re\, }f (x)\ge 1\) for all \(x\in E\) and (ii) \(\mathrm{Re\, }f(a) \le 1\) whenever \(f \in X'\) and \(\mathrm{Re\, }f (x)\le 1\) for all \(x\in E\). (Compare Remark 4.7(ii).)
-
4.9.
Let X be a normed space over \({\mathbb K}\), and let Y be a subspace of X. Suppose E is a nonempty convex open subset of X such that \(Y\cap E=\emptyset \). Then there is a continuous linear functional f on X such that \(f(y)=0\) for all \(y\in Y\) and \(\mathrm{Re\, }f(x)>0\) for all \(x\in E\).
-
4.10.
Let \(E_1\) and \(E_2\) be nonempty disjoint convex subsets of a normed space X. Let \(E_1\) be compact, and let \(E_2\) be closed. Then there are \(f \in X'\), and \(t_1, t_2\) in \({\mathbb R}\) such that \(\mathrm{Re\, }f(x_1) \le t_1 < t_2 \le \mathrm{Re\, }f(x_2) \text{ for } \text{ all } x_1 \in E_1 \text{ and } x_2 \in E_2.\)
-
4.11.
-
(i)
For \(p\in \{1,2,\infty \}\), the dual space of \(({\mathbb K}^n,\Vert \cdot \Vert _p)\) is linearly isometric to \(({\mathbb K}^n,\Vert \cdot \Vert _q)\), where \((1/p)+(1/q)=1\).
-
(ii)
The dual space of \((c_0,\Vert \cdot \Vert _\infty )\) is linearly isometric to \(\ell ^1\).
-
(iii)
For \(p\in \{1,2,\infty \}\), the dual space of \((c_{00},\Vert \cdot \Vert _p)\) is linearly isometric to \(\ell ^q\), where \((1/p)+(1/q)=1\).
-
(i)
-
4.12.
-
(i)
For \(x'\in c'\), let \(\Psi (x')\) be the restriction of \(x'\) to \(c_0\). Then \(\Psi :c'\rightarrow (c_0)'\) is linear, and \(\Vert \Psi (x')\Vert \le \Vert x'\Vert \) for all \(x'\in c'\), but \(\Psi \) is not an isometry.
-
(ii)
Let \(y := (y(1), y(2), \ldots )\in \ell ^{1}\). For \(x\in c\), define \( f_y(x):=\ell _x\,y(1)\) + \(\sum ^{\infty }_{j=1} x(j)y(j+1)\), where \(\ell _x:=\lim _{j \rightarrow \infty } x(j)\). Then \(f_y\in c'\). If we let \(\Phi (y):=f_y\) for \(y\in \ell ^1\), then \(\Phi \) is a linear isometry from \(\ell ^1\) onto \(c'\).
-
(i)
-
4.13.
Let \(W^{1,2}:=W^{1,2}([a,b])\), as in Example 2.28(iv). For \(y\in W^{1,2}\), define
$$f_y(x)=\int _a^bx(t)y(t)dt+\int _a^b x'(t)y'(t)dm(t),\quad x\in W^{1,2}.$$Then \(f_y\in (W^{1,2})'\). If we let \(\Phi (y):=f_y\) for \(y\in W^{1,2}\), then \(\Phi \) is a linear isometry from \(W^{1,2}\) onto \((W^{1,2})'\).
-
4.14.
For \(p\in \{1,2\}\), the dual space of \((C([a,b]),\Vert \cdot \Vert _p)\) is linearly isometric to \(L^q([a,b])\), where \((1/p)+(1/q)=1\).
-
4.15.
Let X be a reflexive normed space. Then X is a Banach space. If, in addition, X is separable, then so is \(X'\). Not every Banach space is reflexive.
-
4.16.
Let X be a normed space, and let \((x_n)\) be a sequence in X. We say that \((x_n)\) converges weakly in X if there is \(x\in X\) such that \(x'(x_n)\rightarrow x'(x)\) for every \(x'\in X'\). In this case, we write \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X. If \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X, and \(x_n{\mathop {\rightarrow }\limits ^{w\;}} \tilde{x}\) in X, then \(\tilde{x}=x\), which is called the weak limit of \((x_n)\).
-
(i)
Let \(x\in X\). Then \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X if and only if \((x_n)\) bounded in X and \(x'(x_n)\rightarrow x'(x)\) for all \(x'\) in a subset of \(X'\) whose span is dense in \(X'\).
-
(ii)
If \(x_n\rightarrow x\) in X, then \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X. In case X is an inner product space, \(x_n\rightarrow x\) in X if and only if \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X and \(\Vert x_n\Vert \rightarrow \Vert x\Vert \).
-
(iii)
Let X be a Hilbert space. If \((x_n)\) is bounded, then a subsequence of \((x_n)\) converges weakly in X. If \((\langle {x_n},{\tilde{x}} \rangle )\) converges in \({\mathbb K}\) for every \(\tilde{x}\in X\), then \((x_n)\) is bounded and there is \(x\in X\) such that \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X
-
(iv)
Let \(x_n{\mathop {\rightarrow }\limits ^{w\;}} 0\) in X, and let Y be a normed space. If \(F\in BL(X,Y)\), then \(F(x_n){\mathop {\rightarrow }\limits ^{w\;}}0\) in Y. Further, if \(F\in CL(X,Y)\), then \(F(x_n)\rightarrow 0\) in Y.
-
(v)
If X is a Hilbert space, Y is a normed space, \(F\in CL(X,Y)\), and \((u_n)\) is an orthonormal sequence in X, then \(F(u_n)\rightarrow 0\). In particular, if \(M:=[k_{i,j}]\) defines a map \(F\in CL(\ell ^2),\) then \(\alpha _2(j)\rightarrow 0\) and \(\beta _2(i)\rightarrow 0\). (Compare Exercises 3.34 and 4.21.)
-
(i)
-
4.17.
Let X be a normed space, and let \((x_n)\) be a sequence in X.
-
(i)
Let \(X:=\ell ^1\). Define \(x'(x):=\sum _{j=1}^\infty x(j)\) for \(x\in X\). Then \(x'\in X'\), and \(x'(e_n)=1\) for all \(n\in {\mathbb N}\). In particular,
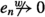 in X. with the projection
in X. with the projection -
(ii)
Let \(X:=\ell ^2\). Then \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X if and only if \((x_n)\) is bounded in X, and \(x_n(j)\rightarrow x(j)\) in \({\mathbb K}\) for every \(j\in {\mathbb N}\). In particular, \(e_n{\mathop {\rightarrow }\limits ^{w\;}} 0\) in \(\ell ^2\).
-
(iii)
Let \(X:=\ell ^\infty \). Suppose there are \(x\in X\) and \(\alpha >0\) such that for all \(j\in {\mathbb N}\), \(\sum _{n=1}^\infty |x_n (j)-x(j)|\le \alpha \). Then \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X. In particular, \(e_n{\mathop {\rightarrow }\limits ^{w\;}} 0\) in \(\ell ^\infty \).
-
(iv)
Let \(X:=c_0\), and \(x_n:=e_1+\cdots +e_n\) for \(n\in {\mathbb N}\). Then \((x'(x_n))\) is convergent in \({\mathbb K}\) for every \(x'\in X'\), but \((x_n)\) has no weak limit in X.
-
(v)
Let \(X:=C([a,b])\). Then \(x_n{\mathop {\rightarrow }\limits ^{w\;}} x\) in X if and only if \((x_n)\) is uniformly bounded on [a, b], and \(x_n(t)\rightarrow x(t)\) for every \(t\in [a,b]\).
-
(i)
-
4.18.
Let X be an inner product space. The following conditions are equivalent:
-
(i)
X is complete.
-
(ii)
\(X=Y\oplus Y^\perp \) for every closed subspace Y of X.
-
(iii)
\(Y=Y^{\perp \perp }\) for every closed subspace Y of X.
-
(iv)
\(Y^\perp \ne \{0\}\) for every proper closed subspace Y of X.
-
(v)
For every \(f\in X'\), there is \(y\in X\) such that \(f(x)=\langle {x},{y} \rangle \) for all \(x\in X\).
-
(i)
-
4.19.
Let X be an inner product space.
-
(i)
Let \(\{u_\alpha \}\) be an orthonormal subset of X. Then \(\mathrm{span\,}\{u_\alpha \}\) is dense in X if and only if \(x=\sum _n\langle {x},{u_n} \rangle u_n\) for every \(x\in X\), where \(\{u_1,u_2,\ldots \}:=\{u_\alpha :\langle {x},{u_\alpha } \rangle \ne 0\}\). (Compare Theorem 2.31.)
-
(ii)
Let Y be a closed subspace of X. Then there is an inner product \(\langle \langle \cdot , \cdot \rangle \rangle \) on X/Y such that \(\langle \langle x+Y, x+Y\rangle \rangle =\mathopen {|||} x+Y \mathclose {|||} ^2\) for all \(x\in X\). (Compare Exercise 2.40.)
-
(iii)
There is an inner product \(\langle \cdot , \cdot \rangle '\) on \(X'\) such that \(\langle f, f\rangle ' =\Vert f\Vert ^2\) for all \(f\in X'\). (Compare Corollary 4.16(i).)
-
(i)
-
4.20.
Let \(F \in BL(X,Y)\). Then F is of finite rank if and only if there are \(x'_1,\ldots ,x'_m\) in \(X'\) and \(y_1,\ldots ,y_m\) in Y such that \(F(x)=\sum _{i=1}^mx'_i(x)y_i\) for all \(x\in X\). Then \(F'\in BL(Y',X')\) is of finite rank, and \(F'(y')=\sum _{i=1}^my'(y_i)x'_i\) for all \(y'\in Y'\).
-
4.21.
Let \(p,r\in \{1,2\}\). If an infinite matrix M defines a map in \(CL(\ell ^p,\ell ^r)\), then the sequence of the rows of M tends to 0 in \(\ell ^q\), where \((1/p)+(1/q)=1\). This does not hold if \(p\in \{1,2,\infty \}\) and \(r:=\infty \). (Compare Exercise 3.34.)
-
4.22.
(Left shift operator on \(L^p\) ) Let \(p\in \{1,2,\infty \}\), and let \(L^p\) denote \(L^p([0,\infty ))\). For \(x\in L^p\), define \(A(x)(t):=x(t+1),\,t\in [0,\infty )\). Then \(A\in BL(L^p)\). If \(p\in \{1,2\}\), then \(A'\in BL((L^p)')\) can be identified with the right shift operator \(A^t\in BL(L^q)\), where \((1/p)+(1/q)=1\), and for \(y\in L^q\), \(A^t(y)(s):=0\) if \(s\in [0,1)\), while \(A^t(y)(s):=y(s-1)\) if \(s\in [1,\infty )\).
-
4.23.
Let \(p\in \{1,2\}\), and \(n\in {\mathbb N}\). For \(x:=(x(1),x(2),\ldots )\in \ell ^p\), define \(P_n(x):=(x(1),\ldots ,x(n),0,0,\ldots )\). Then \(P_n\in BL(\ell ^p)\) is a projection, and \(P_n'\) can be identified with the projection \(P_n^t\in BL(\ell ^q)\), where \((1/p)+(1/q)=1,\) and \(P_n^t(y):=(y(1),\ldots ,y(n),0,0,\ldots )\) for \(y:=(y(1),y(2),\ldots )\in \ell ^q\).
-
4.24.
Let X be a normed space, and let \(X = Y\oplus Z \), where Y and Z are closed subspaces of X. If \(P\in BL(X)\) is the projection operator onto Y along Z, then \(P'\in BL(X')\) is the projection operator onto \(Z^0:=\{x'\in X':x'(z)=0 \text{ for } \text{ all } z\in ~Z\}\) along \(Y^0:=\{x'\in X':x'(y)=0 \text{ for } \text{ all } y\in Y\}\).
-
4.25.
Let X and Y be normed spaces, let \(J_X\) and \(J_Y\) denote their canonical embeddings into \(X''\) and \(Y''\) respectively, and let \(F\in BL(X,Y)\). Define \(F'':=(F')'\in BL(X'',Y'')\). Then \(F''J_X=J_YF\) and \(\Vert F''\Vert =\Vert F\Vert \), and so \(F''\) yields a norm-preserving linear extension of F to \(X''\). Further, if \(X_c\) and \(Y_c\) denote the respective completions of X and Y, then there is a unique \(F_c\in BL(X_c,Y_c)\) such that \(F_cJ_X=J_YF\), and it satisfies \(\Vert F_c\Vert =\Vert F\Vert \).
-
4.26.
Let X be a normed space, Y be a Banach space, and let \(F\in BL(X,Y)\). If \(F'\in CL(Y',X')\), then \(F\in CL(X,Y)\). (Compare Theorem 4.21.)
-
4.27.
Let H and G be Hilbert spaces, and let \(A:H\rightarrow G\) and \(B:G\rightarrow H\) be linear maps such that \(\langle {A(x)},{y} \rangle _G=\langle {x},{B(y)} \rangle _H\) for all \(x\in H\) and all \(y\in G\). Then \(A\in BL(H,G),\, B\in BL(G,H)\), and \( B=A^*\).
-
4.28.
Let H and G be Hilbert spaces, and let \(A\in BL(H,G),\, B\in BL(G,H)\). Then \(AB = 0\) if and only if \(R(A^*)\perp R(B)\).
-
4.29.
Let H be a Hilbert space, G be a closed subspace of H, and let \(A\in BL(H)\). Then \(A(G)\subset G\) if and only if \(A^*(G^\perp )\subset G^\perp \).
-
4.30.
(Bounded inverse theorem) Let H and G be Hilbert spaces, and suppose \(A\in BL(H,G)\). If A is one-one and onto, then \(A^{-1}\in BL(G,H)\). (Note: This result can be proved without using the Baire theorem, the Zabreiko theorem and the closed graph theorem.) The open mapping theorem and the closed graph theorem can be deduced. (Compare Exercise 3.27.)
-
4.31.
Let H and G be Hilbert spaces.
-
(i)
Let \(A\in BL(H,G)\). Then \(A\in CL(H,G)\) if and only if \(A^*A\in CL(H)\).
-
(ii)
If \(A\in CL(H,G)\), then \(A^*\in CL(G,H)\). (Do not use Theorem 4.21.)
-
(iii)
Let H and G be separable. If \(A\in BL(H,G)\) is a Hilbert-Schmidt map, then \(A^*\) is a Hilbert–Schmidt map. In fact, if \(\{u_1,u_2,\ldots \}\) is a countable orthonormal basis for H, and \(\{v_1,v_2,\ldots \}\) is a countable orthonormal basis for G, then \(\sum _n\Vert A(u_n)\Vert ^2=\sum _m\Vert A^*(v_m)\Vert ^2\).
-
(i)
-
4.32.
A self-adjoint operator on a Hilbert space H is also known as a hermitian operator. Also, \(A \in BL(H)\) is called a skew-hermitian operator if \(A^* = -A .\) Let \(A\in BL(H).\) There are unique B and C in BL(H) such that B is hermitian, C is skew-hermitian, and \(A=B+C\). Further, A is normal if and only if \(BC = CB\), A is hermitian if and only if \(C = 0\), A is skew-hermitian if and only if \(B= 0\), and A is unitary if and only if \(BC = CB\) as well as \(B^2 - C^2 = I\). (Compare Proposition 4.29.)
-
4.33.
Let H be a Hilbert space, and let \(A \in BL(H)\). If \(A^*A - AA^*\ge 0\), then A is called hyponormal. A is hyponormal if and only if \(\Vert A(x)\Vert \ge \Vert A^*(x)\Vert \) for all \(x \in H\), and A is normal if and only if A and \(A^*\) are hyponormal. The right shift operator on \(\ell ^2\) is hyponormal, but not normal.
-
4.34.
Let H denote the Hilbert space of all ‘doubly infinite’ square-summable scalar sequences \(x:=(\ldots ,x(-2),x(-1),x(0),x(1),x(2),\ldots )\) with the inner product \(\langle {x},{y} \rangle :=\sum _{j=-\infty }^\infty x(j)\overline{y(j)},\,x,y\in H\). For x in H, let \(A(x)(j) := x(j-1)\) for all \(j\in {\mathbb Z}\). Then the right shift operator A is a unitary operator on H. (Compare the right shift operator on \(\ell ^2\).)
-
4.35.
(Fourier matrix) Let \(n\in {\mathbb N}\), and \(\omega _n:=e^{2\pi i/n}\). Let \(A\in BL({\mathbb C}^n)\) be defined by the matrix \(M_n:=[k_{p,j}]\), where \(k_{p,j}:=\omega _n^{(p-1)(j-1)}/\sqrt{n}\) for \(p,j=1,\ldots ,n\). Then A is unitary. Also, \(M_n\) is a symmetric matrix. (Note: This matrix is crucial in the development of the fast Fourier transform.)
-
4.36.
Let \((A_n)\) be a sequence of self-adjoint operators on a Hilbert space H.
-
(i)
Suppose there is \(\alpha \in {\mathbb R}\) such that \(A_n \le A_{n+1} \le \alpha I\) for all \(n\in {\mathbb N}\). Then there is a unique self-adjoint operator A on H such that \(A_n\le A\) for all \(n\in {\mathbb N}\), and \(A\le \widetilde{A}\) whenever \(\widetilde{A}\) is a self-adjoint operator on H satisfying \(A_n\le \widetilde{A}\) for all \(n\in {\mathbb N}\). In fact, \(A_n(x) \rightarrow A(x)\) for every \(x \in H.\)
-
(ii)
Suppose there is \(\beta \in {\mathbb R}\) such that \(\beta I \le A_{n+1}\le A_n \) for all \(n\in {\mathbb N}\). Then there is a unique self-adjoint operator A on H such that \( A\le A_n\) for all \(n\in {\mathbb N}\), and \(\widetilde{A}\le A\) whenever \(\widetilde{A}\) is a self-adjoint operator on H satisfying \(\widetilde{A}\le A_n\) for all \(n\in {\mathbb N}\). In fact, \(A_n(x) \rightarrow A(x)\) for every \(x \in H.\)
-
(i)
-
4.37.
Let A be a positive operator on a Hilbert space H, and let \(G:=\{x\in H:\langle {A(x)},{x} \rangle =0\}\). Then G is a closed subspace of H. For \( x+G,\,y+G\in H/G\), let \(\langle \langle x+G,y+G\rangle \rangle :=\langle {A(x)},{y} \rangle \). Then \(\langle \langle \cdot ,\cdot \rangle \rangle \) is an inner product on H/G. In particular, \(|\langle {A(x)},{y} \rangle |^2\le \langle {A(x)},{x} \rangle \langle {A(y)},{y} \rangle \) for all \(x,y\in H\). (Compare Exercise 2.13 and Proposition 4.31.)
-
4.38.
Let H be a Hilbert space, and let \((P_n)\) be a sequence of orthogonal projection operators on H such that \(P_nP_m=0\) if \(n\ne m\). Then \(\sum _nP_n(x)\) is summable in H for every \(x\in H\). For \(x\in H\), let P(x) denote this sum. Then P is an orthogonal projection operator on H, and R(P) is the closure of the linear span of \(\bigcup _{n=1}^\infty R(P_n)\), and \(Z(P)=\bigcap _{n=1}^\infty Z(P_n)\).
-
4.39.
Let \(X{\!}:=c_{00}\), or \(X{\!}:=\ell ^2\) with the usual inner product. For \(x{\!}:=(x(1), x(2),\ldots )\) in X, let \(A(x){\!}:=(0,x(1),x(2),\ldots )\). Then \(A\in BL(X)\), and \(\omega (A)=\{k\in {\mathbb K}:|k|<1\}\).
-
4.40.
(Generalized polarization identity) Let \((X,\langle {\cdot \,},{\cdot } \rangle )\) be an inner product space over \({\mathbb C}\), and let \(A : X \rightarrow X\) be a linear map. Then for \(x,y\in X\),
$$\begin{aligned} 4 \langle {A(x)},{y} \rangle&= \langle {A(x+y)},{x+y} \rangle - \langle {A(x-y)},{x-y} \rangle \\ {}&\qquad + i \langle {A(x+iy)},{x+iy} \rangle - i \langle {A(x-iy)},{x-iy} \rangle . \end{aligned}$$Consequently, if H is a nonzero Hilbert space over \({\mathbb C}\), and \(A\in BL(H)\) satisfies \(\omega (A)\subset {\mathbb R}\), then A is self-adjoint. (Compare Exercise 2.14.)
Rights and permissions
Copyright information
© 2016 Springer Science+Business Media Singapore
About this chapter
Cite this chapter
Limaye, B.V. (2016). Dual Spaces, Transposes and Adjoints. In: Linear Functional Analysis for Scientists and Engineers. Springer, Singapore. https://doi.org/10.1007/978-981-10-0972-3_4
Download citation
DOI: https://doi.org/10.1007/978-981-10-0972-3_4
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-0970-9
Online ISBN: 978-981-10-0972-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


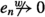 in X. with the projection
in X. with the projection