Abstract
The revisionary approach to semantic paradox is commonly thought to have a somewhat uncomfortable corollary, viz. that, on pain of triviality, we cannot affirm that all valid arguments preserve truth (Beall 2007, 2009; Field 2008, (2009b). We show that the standard arguments for this conclusion all break down once (i) the structural rule of contraction is restricted and (ii) how the premises can be aggregated—so that they can be said to jointly entail a given conclusion—is appropriately understood. In addition, we briefly rehearse some reasons for restricting structural contraction.
Thanks to Jc Beall, Colin Caret, Roy Cook, Charlie Donahue, Ole T. Hjortland, Jeff Ketland, Hannes Leitgeb, Francesco Paoli, Stephen Read, and Greg Restall for helpful discussion on some of the topics discussed herein, and to Dave Ripley and a referee for detailed comments on a previous draft. Julien Murzi warmly thanks the Alexander von Humboldt Foundation, the University of Padua, and the School of European Culture and Languages at the University of Kent for generous financial support. Lionel Shapiro is grateful to the Arché Research Centre at the University of St Andrews for making possible a productive visit.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Shapiro (2011) refers to the the claim that \(\mathsf{VTP}\) and the naïve view of truth we introduce in the next paragraph yield triviality as the ‘Field-Beall thesis’.
- 2.
- 3.
- 4.
Weir (2005) also addresses semantic paradox by restricting the transitivity of validity, though this shows up in his natural deduction system as a structure-based restriction on the use of operational rules.
- 5.
Both of these “substructural” approaches to semantic paradox have an advantage worth mentioning: they allow for a unified approach to the paradoxes of self-reference (Weir 2005; Zardini 2011; Ripley 2013), as opposed to the piecemeal approach proposed by current rcf theories, where similar paradoxes, e.g. the Liar and Curry, are treated in radically different ways. In recent unpublished work, Beall uses the desideratum of uniformity as one motivation for a new approach to paradox—one that retains the standardly accepted structural rules but gives up on a detaching conditional altogether. For a sketch of that approach, see Beall (2011).
- 6.
- 7.
It may help to make Field’s reasoning for the ‘only if’ direction explicit in natural deduction format, for the special case where we are considering an argument from the single premise α to the conclusion β. Complications raised by the multiple-premise case will be discussed in § 3.
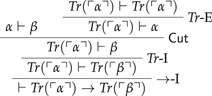
- 8.
In § 2.1, we will see that if our object-language contains a validity predicate, it is also possible to derive \(\mathsf{VTP}\) using an intuitively compelling elimination rule for that predicate. While we will discuss only a predicate that applies to single-premise arguments, a generalized version of that derivation would be subject to all our conclusions about the Validity Argument.
- 9.
This terminology was introduced in Beall and Murzi (2013).
- 10.
Let us briefly consider how the Validity Argument fares on the alternative substructural approach that restricts transitivity. In the version of c-Curry given above, in natural deduction format, \(\mathsf{SContr}\) is the only structural rule used. By contrast, the parallel Curry derivation in sequent calculus format will conclude with the following use of the structural rule of \(\mathsf{Cut}\)
$$\frac{\vdash_{\text{\emph{T}}} Tr(\ulcorner{\kappa}\urcorner) Tr(\ulcorner{\kappa}\urcorner) \vdash_{\text{\emph{T}}} \bot}{\vdash_{\text{\emph{T}}} \bot}$$Ripley (2013) proposes a semantic theory that blocks c-Curry reasoning by invalidating \(\mathsf{Cut}\). His theory adds rules for Tr to a sequent calculus with entirely classical operational rules and structural rules except for \(\mathsf{Cut}\), which is no longer admissible in the presence of the truth rules. We would like to make two observations about Ripley’s proposal. On the one hand, since it retains the rule →-I, it allows a defense of the Validity Argument’s “only if” direction (his truth rules replace \(\mathsf{Cut}\) in note 7 above), and thus of \(\mathsf{VTP}\). On the other hand, though Ripley’s theory also endorses the conclusion of every instance of the Validity Argument’s “if” direction, it won’t allow the above intuitive argument, since it renders the rule →-E inadmissible. See note 46 below.
- 11.
Strictly speaking, this should be expressed by a universal generalisation on codes of sentences, but, for the sake of simplicity, we won’t bother.
- 12.
- 13.
- 14.
For Field, who rejects excluded middle, rejecting an instance of \(\mathsf{VTP}\) doesn’t mean accepting its negation. Beall, by contrast, accepts that there are valid arguments, e.g. the argument from κ and \(\kappa \rightarrow \bot\) to ⊥, that fail to preserve truth. However, as Field and Beall both note, Beall’s position doesn’t require accepting that there are valid arguments whose premises are all true and whose conclusion is false. See Field (2006, p. 597) and Beall (2009, p. 36).
- 15.
For the record, we think that even if \(\mathsf{VTP}\) holds, an explanation of the role of the notion of validity will have to involve normative considerations such as those Field advances.
- 16.
To the best of our knowledge, these rules are first discussed in Priest (2010). For further discussion, see Beall and Murzi (2013) and Murzi (2014). Shapiro (2011) proposes introducing a validity predicate governed by the equivalences \(Val(\ulcorner{\alpha}\urcorner, \ulcorner{\beta}\urcorner) \dashv \vdash_{\text{\emph{T}}} \alpha \Rightarrow \beta\), where ⇒ is an entailment connective whose introduction and elimination rules in turn render \(\mathsf{VP}\) and \(\mathsf{VD}\) derivable. Such a connective is common in the tradition of relevant and paraconsistent logic: see e.g. Anderson and Belnap (1975, p. 7) and Priest and Routley (1982).
- 17.
We have written the rule \(\mathsf{VP}\) without side assumptions. That is because the acceptability of a version including side assumptions
$$(\mathsf{VP^*})\frac{\Upgamma, \alpha \vdash_{\text{\emph{T}}} \beta}{\Upgamma \vdash_{\text{\emph{T}}}Val(\ulcorner{\alpha}\urcorner, \ulcorner{\beta}\urcorner)}$$depends on the properties of the structural comma. For example, if the comma obeys weakening and we get \(\beta, \alpha \vdash_{\text{\emph{T}}} \beta\), then \(\mathsf{VP^*}\) allows us to derive \(\beta \vdash_{\text{\emph{T}}} Val(\ulcorner{\alpha}\urcorner, \ulcorner{\beta}\urcorner)\). But where β is contingent, it shouldn’t follow from β that it is entailed by any sentence. A similar problem arises if the comma obeys exchange. From \(\mathsf{VD}\) and \(\mathsf{Cut}\) we get \(Val(\ulcorner{\alpha}\urcorner, \ulcorner{\alpha}\urcorner), \alpha \vdash_{\text{\emph{T}}} \alpha\), whence exchange yields \(\alpha, Val(\ulcorner{\alpha}\urcorner, \ulcorner{\alpha}\urcorner) \vdash_{\text{\emph{T}}} \alpha\) and \(\mathsf{VP^*}\) allows us to derive \(\alpha \vdash_{\text{\emph{T}}} Val(\ulcorner{Val(\ulcorner{\alpha}\urcorner\urcorner, \ulcorner{\alpha}\urcorner)}, \ulcorner{\alpha}\urcorner)\). But if α is contingent, it shouldn’t follow from α that it is entailed by a logical truth. Zardini (2012), whose comma obeys both weakening and exchange, avoids these problems by restricting the side assumptions in \(\mathsf{VP^*}\) to logical compounds of validity claims. See also Priest and Routley (1982).
- 18.
Ripley (2013) offers a similar defense of \(\mathsf{VTP}\), using \(\mathsf{VP}\) and the sequent \(\alpha, Val(\ulcorner{\alpha}\urcorner,\ulcorner{\beta}\urcorner) \vdash_{\text{\emph{T}}} \beta\). Shapiro (2011) explains that on the version of the naïve view presented there (see note 17 above), \(Val(\ulcorner{\alpha}\urcorner, \ulcorner{\beta}\urcorner)\) implies \(Tr(\ulcorner{\alpha}\urcorner) \Rightarrow Tr(\ulcorner{\beta}\urcorner)\).
- 19.
Shapiro (2011) identifies two challenges to the naïve view: a “direct argument” that it leads straight to paradox, and an “indirect argument” that it entails a version of the paradox-producing \(\mathsf{VTP}\).
- 20.
To the best of our knowledge, the first known occurrence of the Validity Curry is in the 16thcentury author Jean de Celaya. See Read (2001, fn. 11–12) and references therein. Albert of Saxony includes a contrapositive version of the paradox among his “insolubles” (Read 2010, p. 165). A more recent version can be found in Priest and Routley (1982), and surfaces again in Whittle (2004, fn. 3), Clark (2007, pp. 234–235) and Shapiro (2011, fn. 29). For a first comprehensive discussion of the Validity Curry, see Beall and Murzi (2013). For a defence of the claim that Validity Curry is a genuine paradox of validity, see § 2.3 below and Murzi (2014).
- 21.
This terminology was first introduced in Beall and Murzi (2013). Ultimately, however, the distinction in terms of predicate versus connective may not be the essential one. Whittle (2004) and Shapiro (2011) discuss a version of Curry’s Paradox, involving a “consequence connective” or “entailment connective,” which poses much the same challenge to rcf theorists as does v-Curry. [See also Shapiro (2015, p. 82).]
- 22.
For an early anticipation of the argument from naïve validity to the rejection of \(\mathsf{SContr}\) (in the form of multiple discharge of assumptions), see Priest and Routley (1982). Priest and Routley, whose entailment connective obeys analogues of \(\mathsf{VP}\) and \(\mathsf{VD}\), discuss several resulting paradoxes which they blame on the “suppression of innocent premises.” By contrast, Ripley (2013) blocks v-Curry at the final step using \(\mathsf{VD}\), which is inadmissible in his nontransitive theory for the same reason that →-E is inadmissible. See note 46 below.
- 23.
Thanks to Roy Cook and Jeff Ketland for raising these potential concerns.
- 24.
Field (2008, § 20.4) himself advances versions of this line of argument, while discussing what is in effect a validity-involving version of the Knower Paradox resting on \(\mathsf{NEC^*}\) and \(\mathsf{T}^*\). See especially Field (2008, p. 304 and p. 306). On the question whether his conception of the extension of the validity predicate consistently allows him to do so, see note 27 below.
- 25.
Here we take the logical vocabulary to be the standard vocabulary of some first-order, perhaps non-classical, logic.
- 26.
Several semantic theorists, including rcf theorists such as Field and Priest, resort to notions of validity that are not purely logical. For instance, Field (2007, 2008) extensionally identifies validity with, essentially, preservation of truth in all \(\mathsf{ZFC}\) models of a certain kind, thus taking validity to (wildly) exceed purely logical validity. (Incidentally, it seems to us that this use of ‘valid’ is in tension with the purely logical sense Field (2008) appeals to at p. 304 and especially p. 306.) Likewise, McGee (1991, p. 43–49) takes logical necessity to extend to arithmetic and truth-theoretic principles.
- 27.
It might be objected that such a notion of validity presupposes \(\mathsf{VTP}\), and hence cannot be appealed to in the present context, where the question whether \(\mathsf{VTP}\) can be consistently upheld is the very point at issue. Our modest aim here, however, is simply to suggest that someone who already thinks, following perhaps logical orthodoxy, that valid arguments preserve truth and that, accordingly, consequence is to be explicated in terms of truth-preservation has a reason—the v-Curry Paradox—to reject \(\mathsf{SContr}\). Once \(\mathsf{SContr}\) is rejected, the standard challenges to \(\mathsf{VTP}\) no longer stand, as we’ll see in § 3 below. But, it seems to us, no illicit or question-begging appeal to \(\mathsf{VTP}\) has been made in the course of the foregoing reasoning. We thank an anonymous referee for raising this potential concern.
- 28.
In fact, Cook (2014) shows how this response can be strengthened: it is possible to formulate a modified Validity Curry paradox in such a way that the arithmetic necessary to prove the Diagonal Lemma need not be included in the scope of the validity relation.
- 29.
This view is implicitly assumed in the work of contemporary revisionary theorists—see e.g. Priest (2006b); Field (2007, 2008), Beall (2009), Beall and Murzi (2013). In particular, it is implicit in their assumption that the paradoxes of validity are (in an interesting sense) of the same kind as the Liar and c-Curry. One defence of that possibly controversial assumption would involve arguing that the Paradox of the Knower is nothing but a weakened Liar, and that, as we’ve observed in § 2.1, v-Curry is nothing but a generalised Knower, so that whatever the nature of the first paradox, it is inherited by the other two. See also Read (2001) and Beall and Murzi (2013). We should finally stress that in calling validity a semantic property, we merely intend to point to these parallels, without relying on any particular conception of what makes a property semantic.
- 30.
We don’t have space to expand on this point here. Priest (2006b, § 3.2) argues at length that the “naïve notion of proof” is recursive, whence naïve provability, a species of naïve validity, is recursively enumerable. Here we simply notice that his arguments are consistent with the view that naïve validity isn’t. Finally, we’d like to point out that some \(\mathsf{SContr}\)-free semantic theories extending contraction-free arithmetics may not be strong enough to satisfy Löb’s Theorem’s applicability conditions, in which case the objection from Löb’s Theorem we are considering would not apply in the first place.
- 31.
For arguments with an infinite number of premises, we will need universal quantification to express truth-preservation. None of the objections to \(\mathsf{VTP}\) we will consider, however, depend on consideration of infinite-premise arguments.
- 32.
- 33.
- 34.
In that case, however, the “if” direction of the Validity Argument will go through for & as premise-aggregating connective. Deriving \(Tr(\ulcorner{\alpha_1}\urcorner),...,Tr(\ulcorner{\alpha_n}\urcorner) \vdash Tr(\ulcorner{\beta}\urcorner)\) from \(Tr(\ulcorner{\alpha_1}\urcorner) \, \& \,... \, \& \, Tr(\ulcorner{\alpha_n}\urcorner) \vdash Tr(\ulcorner{\beta}\urcorner)\) requires the inverse of \(\mathsf{\&}\)-L, which obtains in the presence of \(\mathsf{SWeak}\).
- 35.
In single-conclusion sequent calculus formulations (which suffice for our purposes, as our derivations all involve the language’s negation-free fragment), the connective ⊗ is governed by the twin rules ⊗-I and ⊗-L.
- 36.
Field’s own reasoning, as sketched in §1.3, amounts to a special case of Zardini’s proof: the case in which we are considering the truth-preservingness of a single-conclusion argument and employ no side assumptions. Zardini’s proof does not depend on his acceptance of \(\mathsf{SWeak}\).
- 37.
For definitions, see Read (1988, § 4.1) and Restall (2000, pp. 19–20). In sequent calculus formulations, ⊗-E db is replaced by ⊗-L db below. Sequent calculi of this type were developed independently for fragments of relevant logics by Minc (1976) and by Dunn, whose version appears in Anderson and Belnap (1975, § 28.5). For natural deduction formulations, see Read (1988), Slaney (1990) and O’Hearn and Pym (1999), whose use of the comma we follow.
- 38.
Rather than rejecting the structural rule of associativity, we are avoiding the need for such a rule by allowing our comma to retain its variable polyadicity.
- 39.
Since assumptions can now be embedded in bunches specified using both comma and colon, we also need to generalize our statement of the cut rule:
$$(\mathsf{Cut}_{db})\frac{\Upgamma \vdash \alpha \Updelta(\alpha) \vdash \beta}{\Updelta(\Upgamma) \vdash \beta}$$ - 40.
But see (Paoli 2007, pp. 569–571) for opposition to the standard claim that the extensional conjunction of such logics is “truth functional.”
- 41.
The point extends naturally to cases in which the assumptions are aggregated using both kinds of structure. For instance, \(\alpha_1: (\alpha_2,\, \alpha_3) \vdash_{\text{\emph{T}}} \beta\) only if \(\vdash_{\text{\emph{T}}} Tr(\ulcorner{\alpha_1}\urcorner) \, \& \, (Tr(\ulcorner{\alpha_1}\urcorner) \otimes Tr(\ulcorner{\alpha_n}\urcorner)) \rightarrow Tr(\ulcorner{\beta}\urcorner)\).
- 42.
Most work on this issue has concerned the closely parallel case of a naïve set theory featuring an unrestricted axiom of comprehension. For proofs of the consistency or nontriviality of unrestricted comprehension in some “weak relevant logics” that can be specified via dual-bunching natural deduction, see Brady (1983, 1989, 2006). For applications of Brady’s techniques to naïve truth-theory, see Priest (1991) and Beall (2009), which do not however consider natural deduction systems. As for multiset-based logics, the consistency of unrestricted comprehension in an affine logic was shown by V. Grishin in 1974: see Došen (1993). For the consistency of a naïve truth theory based on an affine logic, see Zardini (2011).
- 43.
As Dave Ripley pointed out to us, a dual-bunching logic could also retain a connective \(\&_{A}\,\) that behaves like the “additive” conjunction and disjunction of a multiset-based logic, for instance in failing to validate Distribution over the corresponding \(\lor_{A}\). To achieve this, replace &-E1 and &-E2 with
$$(\&_{A}\!\!-\!\!E1)\frac{\Upgamma, \alpha \vdash \gamma \Updelta \vdash \alpha \, \&_{A}\, \beta}{\Upgamma,\Updelta \vdash \gamma} \hspace{0,2cm} (\&_{A}\!\!-\!\!E2)\frac{\Upgamma, \beta \vdash \gamma \Updelta \vdash \alpha \, \&_{A}\, \beta}{\Upgamma,\Updelta \vdash \gamma}$$By contrast, in the presence of \(\mathsf{Cut}_{db}\), our original &-E1 and &-E2 have the same “extensional” effect as the rules
$$(\mathsf{\&}\!\!-\!\!E1_{db})\frac{\Upgamma(\alpha) \vdash \gamma \Updelta \vdash \alpha \, \& \, \beta}{\Upgamma(\Updelta) \vdash \gamma} \hspace{0,2cm} (\mathsf{\&}\!\!-\!\!E2_{db})\frac{\Upgamma(\beta) \vdash \gamma\quad\Updelta \vdash \alpha \, \& \, \beta}{\Upgamma(\Updelta) \vdash \gamma}$$ - 44.
For relevant work on the interpretation of dual-bunching systems, see Read (1988) and Slaney (1990). For a recent and novel suggestion toward an interpretation of multiset-based systems, see Zardini (2011). For a sketch of a more deflationary approach to antecedent structure, see Shapiro (2011)[This sketch has since been elaborated in Shapiro (2015).
- 45.
According to the theory proposed by Ripley (2013) based on Cobreros et al. (2012), which is “substructural” only in rejecting \(\mathsf{Cut}\), the objection to \(\mathsf{VTP}\) we are considering in this section fails because \(\mathsf{MPA}\) fails to yield absurdity. This is because the argument’s final step from \(\vdash_{\text{\emph{T}}} \kappa \rightarrow \bot\) and \(\vdash_{\text{\emph{T}}} \kappa\) to \(\vdash_{\text{\emph{T}}} \bot\) fails. In Ripley’s sequent calculus, the rule →-E is inadmissible in the absence of \(\mathsf{Cut}\). Indeed, Ripley holds (p.c) that →-E shouldn’t be regarded as fundamental to the logic of a detaching conditional, as it covertly builds in extraneous transitivity in comparison with the sequent calculus rule
$$(\rightarrow\!\!-\!\!L)\frac{\Upgamma \vdash \alpha\quad\Updelta, \beta \vdash \gamma}{\Updelta, \alpha \rightarrow \beta, \Upgamma \vdash \gamma}$$To this, defenders of →-E may reply that each of ⊗-E and ⊗-L builds in transitivity in comparison with \(\alpha \to \beta, \alpha \vdash \beta\). It is true, as Ripley shows, that the transitivity built in by ⊗-E (which, given ⊗-I, yields \(\mathsf{Cut}\)) can be blamed for paradox. But in view of the option of blaming paradox on \(\mathsf{SContr}\) instead, this won’t suffice to show that ⊗-L is a more fundamental rule than ⊗-E.
- 46.
It makes no difference whether these connectives are those of a multiset-based or dual-branching logic. Nor, in the latter case, would it make a difference if we considered \(\&_{A}\) of note 44 in place of &.
- 47.
- 48.
Hjortland (2012) has recently proposed using an affine logic with additive conjunction and disjunction in a revisionary approach to semantic paradox. We take no position here on whether the consideration just rehearsed poses a serious problem for that approach.
- 49.
Restall (1994, Chap. 11) shows that an arithmetic based on the dual-bunching contraction-free logic \(\mathsf{RWK}\) (which he calls \(\mathsf{CK}\)) is classical Peano arithmetic, but it isn’t known whether \(\mathsf{RWK}\) supports a nontrivial naïve semantic theory in which \(Tr(\ulcorner{\alpha}\urcorner)\) is everywhere intersubstitutable with α (see Hjortland 2012).
- 50.
Here we are no longer thinking of natural deduction rules, but rather of the rules of a Hilbert system, rules for generating theorems.
- 51.
Here is a rough explanation. In the course of deriving \(\mathsf{TP}_R\) in our object-language, we will need to establish, under the assumption that three arbitrary sentences (denoted by a 1, a 2 and b) are the respective premises and conclusion of an instance of R, the claim \(\forall{x}(x=a_1 \lor x=a_2 \rightarrow Tr(x)) \vdash Tr(b)\). Assuming ∀ is lattice-theoretical, this claim will follow from \(Tr(a_1) \, \& \, Tr(a_2) \vdash Tr(b)\), whereas it won’t follow from \(Tr(a_1) \otimes Tr(a_2) \vdash Tr(b)\). For we have \(\forall{x}\phi(x) \vdash \phi(a_1) \, \& \, \phi(a_2)...\, \& \,...\phi(a_n)\), but not \(\forall{x}\phi(x) \vdash \phi(a_1) \otimes \phi(a_2)...\otimes...\phi(a_n)\). See Běhounek et al. (2007).
- 52.
Field himself claims that \(\mathsf{TP2}_R\) will “obviously” fail to establish \(\mathsf{TP}_R\) when the former is understood using what is, in effect, multiplicative conjunction. See Field (2006, p. 597) and Field (2008, p. 379). In his discussion, \(Tr(\ulcorner{\alpha \rightarrow \beta}\urcorner) \rightarrow (Tr(\ulcorner{\alpha}\urcorner) \rightarrow Tr(\ulcorner{\beta}\urcorner))\) takes the place of \(Tr(\ulcorner{\alpha \rightarrow \beta}\urcorner) \otimes Tr(\ulcorner{\alpha}\urcorner) \rightarrow Tr(\ulcorner{\beta}\urcorner)\), which is equivalent to the former in the logics we are considering. See also Priest (2010).
References
Anderson, A., & Belnap, N. (1975). Entailment: The logic of relevance and necessity (Vol. 1). Princeton: Princeton University Press.
Asenjo, F. G.. (1966). A calculus of antinomies. Notre Dame Journal of Formal Logic, 16, 103–105.
Asenjo, F., & Tamburino, J. (1975). Logic of antinomies. Notre Dame Journal of Formal Logic, 16, 17–44.
Avron, A. (1988). The semantics and proof theory of linear logic. Theoretical Computer Science, 57, 161–184.
Beall, J. (2007). Truth and paradox: A philosophical sketch. In D. Jacquette (ed.), Philosophy of logic (pp. 325–410). Amsterdam: Elsevier.
Beall, J. (2009) Spandrels of truth. Oxford: Oxford University Press.
Beall, J. (2011). Multiple-conclusion LP and default classicality. Review of Symbolic Logic, 4, 326–336.
Beall, J., & Murzi, J. (2013). Two flavors of Curry’s paradox. Journal of Philosophy, 110, 143–165.
Běhounek, L., Cintula, P., & Horčík, R. (2007). Multiplicative quantifiers in fuzzy and substructural logics. Presented at Logic Colloquium 2007, Wrocław.
Belnap, N. (1982) Display logic. Journal of Philosophical Logic, 11, 375–417.
Belnap, N. (1993). Life in the undistributed middle. In P. Schroeder-Heister & K. Došen (eds), Substructural logics (pp. 31–41). Oxford: Oxford University Press.
Brady, R. (1983). The simple consistency of set theory based on the logic CSQ. Notre Dame Journal of Formal Logic, 24, 431–39.
Brady, R. (1989). The non-triviality of dialectical set theory. In Priest, G., R. Routley & J. Norman (eds), Paraconsistent logic: Essays on the inconsistent (pp. 437–71). Munich: Philosophia.
Brady, R. (2006). Universal logic. Stanford: CSLI Publications.
Clark, M. (2007). Paradoxes from A to Z (2nd ed.). London: Routledge.
Cobreros, P., Egré, P., Ripley, D., van Rooij, R. (2012). Tolerant, classical, strict. Journal of Philosophical Logic, 41, pp. 347–385.
Cook, R. (2012). The T-schema is not a logical truth. Analysis, 72, pp. 231–239.
Cook, R. (2014). There is no paradox of logical validity! Logica Universalis, 8, pp. 447–467.
Došen, K. (1993). A historical introduction to substructural logics. In P. Schroeder-Heister & K. Došen (eds), Substructural logics (pp. 1–30). Oxford: Oxford University Press.
Etchemendy, J. (1990). The concept of logical consequence. Cambridge (Mass.): Harvard University Press.
Field, H. (2003). A revenge-immune solution to the semantic paradoxes. Journal of Philosophical Logic, 32, 139–177.
Field, H. (2006). Truth and the unprovability of consistency. Mind, 115, 567–606.
Field, H. (2007). Solving the paradoxes, escaping revenge. In J. Beall (ed.), Revenge of the liar (pp. 53–144). Oxford: Oxford University Press.
Field, H. (2008). Saving truth from paradox. Oxford: Oxford University Press.
Field, H. (2009a). Pluralism in logic. Review of Symbolic Logic, 2(2), 342–359.
Field, H. (2009b). What is the normative role of logic? Proceedings of the Aristotelian Society, 83, 251–268.
Field, H. (2015). Validity: Model-theoretic, proof-theoretic and genuine. Forthcoming in C. Caret & O. Hjortland (eds), Foundations of Logical Consequence. Oxford: Oxford University Press.
Girard, J. Y. (1987). Linear logic. Theoretical Computer Science, 50, 1–102.
Harman, G. (1986). Change in view: Principles of reasoning. Cambridge (Mass.): MIT Press.
Harman, G. (2009). Field on the normative role of logic. Proceedings of the Aristotelian Society, 109, 333–335.
Hjortland, O. T. (2012). Truth, paracompleteness and substructural logic. Unpublished manuscript.
Horsten, L. (2009). Levity. Mind, 118, 555–581.
Kaplan, D., & Montague, R. (1960). A paradox regained. Notre Dame Journal of Formal Logic, 1, 79–90.
Ketland, J. (2012). Validity as a primitive. Analysis, 72, 421–430.
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.
Mares, E., & Paoli, F. (2014). Logical consequence and the paradoxes. Journal of Philosophical Logic, 43, pp. 439–469.
Martin, R. L. (ed.) (1984). Recent essays on truth and the liar paradox. Oxford: Oxford University Press.
Martin, R. L., & Woodruff, P. W. (1975). On representing ‘true-in-L’ in L. Philosophia, 5, 217–221. Reprinted in Martin 1984.
McGee, V. (1991). Truth, vagueness, and paradox. Indianapolis: Hackett Publishing Company.
Meyer, R. K., & McRobbie, M. A. (1982a). Multisets and relevant implication I. Australasian Journal of Philosophy, 60, 107–139.
Meyer, R. K., & McRobbie, M. A. (1982b). Multisets and relevant implication II. Australasian Journal of Philosophy, 60, 265–181.
Meyer, R. K., Routley, R., & Dunn, J. M. (1979). Curry’s paradox. Analysis, 39, 124–128.
Minc, G. (1976). Cut-elimination theorem in relevant logics. Journal of Soviet Mathematics, 6, 422–428.
Murzi, J. (2014). The inexpressibility of validity. Analysis, 74, 65–81.
Myhill, J. (1960). Some remarks on the notion of proof. Journal of Philosophy, 57, 461–471.
O’Hearn, P., & Pym, D. (1999). The logic of bunched implications. Bulletin of Symbolic Logic, 5, 215–244.
Paoli, F. (2002). Substructural logics: A primer. Dordrecht: Kluwer.
Paoli, F. (2005). The ambiguity of quantifiers. Philosophical Studies, 124, 313–330.
Paoli, F. (2007). Implicational paradoxes and the meaning of logical constants. Australasian Journal of Philosophy, 85, 533–579.
Priest, G. (1979). The logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Priest, G. (1980). Sense, entailment, and modus ponens. Journal of Philosophical Logic, 9, 415–435.
Priest, G. (1991). Intensional paradoxes. Notre Dame Journal of Formal Logic, 32, 193–211.
Priest, G. (2006a). Doubt truth to be a liar. Oxford: Oxford University Press.
Priest, G. (2006b). In contradiction. Oxford: Oxford University Press. Expanded edition (first published 1987).
Priest, G. (2010). Hopes fade for saving truth. Philosophy, 85, 109–140. Critical notice of Field 2008.
Priest, G., & Routley, R. (1982). Lessons from Pseudo-Scotus. Philosophical Studies, 42, 189–199.
Read, S. (1988). Relevant logic: A philosophical examination of inference. London: Basil Blackwell.
Read, S. (2001). Self-reference and validity revisited. In M. Yrjönsuuri (ed.), Medieval formal logic (pp. 183–196). Dordrecht: Kluwer.
Read, S. (2010). Field’s paradox and its medieval solution. History and Philosophy of Logic, 31, 161–176.
Restall, G. (1993). How to be really contraction free. Studia Logica, 52, 381–391.
Restall, G. (1994). On logics without contraction. PhD thesis, The University of Queensland.
Restall, G. (2000). An introduction to substructural logics. London: Routledge.
Ripley, D. (2013). Paradoxes and failures of cut. Australasian Journal of Philosophy, 91, pp. 139–164.
Shapiro, L. (2011). Deflating logical consequence. The Philosophical Quarterly, 61, 320–342.
Shapiro, L. (2015). Naive structure, contraction and paradox. Topoi, 34, 75–87.
Slaney, J. (1990). A general logic. The Australasian Journal of Philosophy, 68, 74–88.
Troelstra, A. (1992). Lectures on linear logic. Stanford: CSLI.
Weir, A. (2005). Naïve truth and sophisticated logic. In J. Beall & B. Armour-Garb (eds), Deflationism and paradox (pp. 218–249). Oxford: Oxford University Press.
Whittle, B. (2004). Dialetheism, logical consequence and hierarchy. Analysis, 64, 318–326.
Zardini, E. (2011). Truth without contra(di)ction. Review of Symbolic Logic, 4, 498–535.
Zardini, E. (2013). Naive modus ponens. Journal of Philosophical Logic, 42, pp. 575–592.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Murzi, J., Shapiro, L. (2015). Validity and Truth-Preservation. In: Achourioti, T., Galinon, H., Martínez Fernández, J., Fujimoto, K. (eds) Unifying the Philosophy of Truth. Logic, Epistemology, and the Unity of Science, vol 36. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9673-6_22
Download citation
DOI: https://doi.org/10.1007/978-94-017-9673-6_22
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9672-9
Online ISBN: 978-94-017-9673-6
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)