Abstract
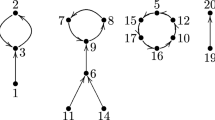
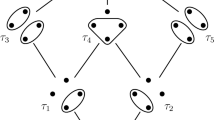
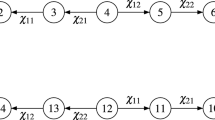
An inverse semigroup is said to be modular if its lattice LF (S) of full inverse subsemigroups is modular. We show that it is sufficient to study simple inverse semigroups which are not groups. Our main theorem states that such a semigroup S is modular if and only if (I) S is combinatorial, (II) its semilattice E of idempotents is “Archimedean” in S, (III) its maximum group homomorphic image G is locally cyclic and (IV) the poset of idempotents of each D-class of S is either a chain or contains exactly one pair of incomparable elements, each of which is maximal. It is shown that there is exactly one bisimple modular inverse semigroup which is not a group and that is nondistributive.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
T. Eršova. “Inverse semigroups with certain types of lattices of inverse subsemigroups”, Ural. Gos. Univ. Mat. Zap. 7 (1969/ 70), tetrad’ 1, 62–76, (Russian) (MR 43, 6348).
R. Freese and J.B. Nation, “Congruence lattices of semilattices”, Pacific J. Math. 49 (1973), 51–58.
L. Fuchs, “Infinite Abelian Groups, Vol.I”, Academic Press, New York, 1970.
J.M. Howie, “An Introduction to Semigroup Theory”, Academic Press, Londong, 1976.
K.G. Johnston, “Subalgebra lattices of completely simple semigroups”, Semigroup Forum 29 (1984), 109–121.
K.G. Johnston and P.R. Jones, “Modular inverse semigroups”, J. Austral. Math. Soc. (to appear).
P.R. Jones, “Semimodular inverse semigroups”, J. London Math. Soc. 17 (1978), 446–456.
P.R. Jones, “Distributive inverse semigroups”, J. London Math. Soc. 17 (1978), 457–466.
M. Petrich, “Inverse Semigroups”, Wiley, New York, 1984.
L.N. Ševrin and A.J. Ovsyannikov, “Semigroups and their subsemigroup lattices”, Semigroup Forum 27 (1983), 1–154.
M. Suzuki, “Structure of a Group and the Structure of its Lattice of Subgroups”, Springer, Berlin, 1956.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1987 D. Reidel Publishing Company
About this chapter
Cite this chapter
Johnston, K.G., Jones, P.R. (1987). Inverse Semigroups whose Lattices of Full Inverse Subsemigroups are Modular. In: Goberstein, S.M., Higgins, P.M. (eds) Semigroups and Their Applications. Springer, Dordrecht. https://doi.org/10.1007/978-94-009-3839-7_9
Download citation
DOI: https://doi.org/10.1007/978-94-009-3839-7_9
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-010-8209-9
Online ISBN: 978-94-009-3839-7
eBook Packages: Springer Book Archive