Abstract
In this chapter, we present the classical Hamilton-Jacobi theory. This theory has played an enormous role in the development of theoretical and mathematical physics. On the one hand, it builds a bridge between classical mechanics and other branches of physics, in particular, optics. On the other hand, it yields a link between classical and quantum theory. We start with deriving the Hamilton-Jacobi equation and proving the classical Jacobi Theorem. We interpret the Hamilton-Jacobi equation geometrically as an equation for a Lagrangian submanifold of phase space which is contained in the coisotropic submanifold given by a level set of the Hamiltonian. Using this geometric picture, we extract a general method for solving initial value problems for arbitrary first order partial differential equations of the Hamilton-Jacobi type, the method of characteristics. It turns out that one can go beyond the case where a solution is generated by a single function on configuration space. To do so, one must consider Morse families, that is, families of Morse functions depending on additional parameters. In this chapter, we develop the theory of Morse families in a systematic way. Subsequently, we present the theory of critical points of Lagrangian submanifolds in cotangent bundles. This includes a topological characterization in terms of the Maslov class and a description of the topological data in terms of generating Morse families. Finally, we discuss applications in the spirit of geometric asymptotics. First, we study the eikonal equation of geometric optics, including the formation of caustics. Second, we analyse the transport equation and present a detailed study of its geometry. On this basis, we derive first order short wave asymptotic solutions for a class of first-order partial differential equations. In this analysis a key role is played by a consistency condition of topological type, the Bohr-Sommerfeld quantization condition. We discuss applications to the Helmholtz and to the Schrödinger equations.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In this chapter, the phase space will always be the cotangent bundle of some configuration space.
- 2.
Points where the Lagrangian submanifold is not transversal to the fibres.
- 3.
The same statement holds true for a generating function \(S(\mathbf{q},\bar{\mathbf{p}},t)\) of the second kind with parameters \(\bar{p}_{i}\).
- 4.
For the case where
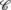 is an energy surface, this has already been discussed in Sect. 9.1.
is an energy surface, this has already been discussed in Sect. 9.1. - 5.
The notation \(\bar{q}^{i}\) for the parameters is a matter of convention, their physical meaning depends on the concrete context.
- 6.
Theorem 12.3.1 extends to this more general situation. For the proof one has to apply the Tubular Neighbourhood Theorem for embedded submanifolds to
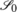 , see Remark 6.4.7.
, see Remark 6.4.7. - 7.
According to Example 1.6.6, Λ S (B S ) can nevertheless be equipped with a submanifold structure, though in two inequivalent ways. Both of them are Lagrangian.
- 8.
See Example 8.3.8/4.
- 9.
For an intrinsic definition, see [36, §4.3].
- 10.
We refer to Remark 12.6.16 for a comment on the notion of stability in this context.
- 11.
According to Remark 12.5.3/2, \(W = \mathrm{T}_{\xi}(\mathrm{T}^{\ast}_{x} Q) \cap\iota'(\mathrm{T}_{\xi}L)\).
- 12.
We may of course assume B S and hence \(\tilde{B}_{\tilde{S}}\) to be connected.
- 13.
This means, in particular, that F(L) does not intersect
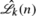 for \(n < \frac{k(k+1)}{2}\).
for \(n < \frac{k(k+1)}{2}\). - 14.
This is a consequence of the Sard Theorem 1.5.18, see Lemma 4.1.3 in [13].
- 15.
By an abuse of notation, via the diffeomorphism \(B_{S_{i}} \to U_{i}\) induced by \(\varLambda_{S_{i}}\), \(\mathrm{index} ((S_{i})''_{y_{i} y_{i}} )\) is viewed as a function on U i .
- 16.
For any two choices, the quadratic forms \(S''_{yy}(\xi )\) are similar and hence have the same index.
- 17.
If h is an even smooth function on ℝ, there exists a unique smooth function \(\tilde{h}\) on ℝ such that \(h(y) = \tilde{h}(y^{2})\). If h depends smoothly on parameters, then so does \(\tilde{h}\).
- 18.
A Morse family over Q is stable if it is an inner point of its stable equivalence class with respect to a certain C ∞-topology on the space of all Morse families over Q.
- 19.
- 20.
Thus, in particular, we ignore polarization phenomena.
- 21.
Built in analogy to the energy density and of the Poynting vector in Maxwell electrodynamics.
- 22.
More precisely, one may view light rays as wave packets, whose width in the direction transversal to the energy current vector is negligible. That such wave packets can be prepared follows from the uncertainty relation for the Fourier transform in the short wave approximation.
- 23.
This is the abstract counterpart of the condition \(|S_{0}^{\prime}(y)| < 1\) found in Example 12.7.10.
- 24.
For a quite exhaustive discussion of this equation in theoretical optics, we refer to the book of Römer [253].
- 25.
In brief, for s∈ℝ, an s-density on a real vector space W of dimension n is a mapping ν:W n→ℝ satisfying ν(Aw 1,…,Aw n )=|detA|s ν(w 1,…,w n ) for all endomorphisms A of W. The s-densities on W form a vector space of dimension 1. By taking the s-densities on the tangent spaces at every point of a manifold M one obtains the real line bundle |Λ|s M of pointwise s-densities on M. Sections in this bundle are called s-densities on M. Every n-form
 on M defines an s-density
on M defines an s-density 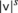 by
by 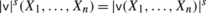 . In particular, if M is orientable, |Λ|s
M is trivial for every s. The product of an s
1-density ν
1 and an s
2-density ν
2 on M is defined by (ν
1
ν
2)(X
1,…,X
n
):=ν
1(X
1,…,X
n
)ν
2(X
1,…,X
n
). It yields an (s
1+s
2)-density. The calculus of differential forms, notably the pull-back and, based on that, the Lie derivative, extends in an obvious way to s-densities.
. In particular, if M is orientable, |Λ|s
M is trivial for every s. The product of an s
1-density ν
1 and an s
2-density ν
2 on M is defined by (ν
1
ν
2)(X
1,…,X
n
):=ν
1(X
1,…,X
n
)ν
2(X
1,…,X
n
). It yields an (s
1+s
2)-density. The calculus of differential forms, notably the pull-back and, based on that, the Lie derivative, extends in an obvious way to s-densities. - 26.
Because the analytic solutions are determined up to an additive constant.
- 27.
With respect to the Euclidean metric.
- 28.
For convenience, in the remainder, we stick to this simplified notation.
- 29.
Which can always be chosen to intersect the singular subset
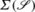 transversally.
transversally. - 30.
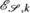 may be identified with the pull-back under ι of the so-called prequantum line bundle over (T∗
Q,dθ), see Sect. 4.1 and Appendix D of [36] for a detailed description.
may be identified with the pull-back under ι of the so-called prequantum line bundle over (T∗
Q,dθ), see Sect. 4.1 and Appendix D of [36] for a detailed description. - 31.
Named after Wentzel, Brillouin and Kramers.
- 32.
See e.g. [110, §IV.2].
- 33.
References
Agricola, I., Friedrich, T.: Globale Analysis. Vieweg, Wiesbaden (2001), in German
Anné, C.: A topological definition of the Maslov bundle. Math. J. Univ. Frontera 8, 1–15 (2006)
Arnold, V.I.: On a characteristic class entering in quantization conditions. Funct. Anal. Appl. 1, 1–13 (1967)
Arnold, V.I.: Singularities of smooth mappings. Russ. Math. Surv. 23, 1–43 (1968)
Arnold, V.I.: Normal forms of functions near degenerate critical points, Weyl groups A k , D k , E k , and Lagrangian singularities. Funct. Anal. Appl. 6, 254–272 (1972)
Arnold, V.I.: Critical points of smooth functions and their normal forms. Russ. Math. Surv. 30, 1–75 (1975)
Arnold, V.I.: Singularities of Caustics and Wave Fronts. Kluwer Academic, Norwell (1990)
Arnold, V.I.: Catastrophe Theory. Springer, Berlin (1992)
Arnold, V.I., Givental, A.B.: Symplectic geometry. In: Arnold, V.I., Novikov, S.P. (eds.) Dynamical Systems IV. Symplectic Geometry and Its Applications. Springer, Berlin (2001)
Arnold, V.I., Goryunov, V.V., Lyashko, O.V., Vasil’ev, V.A.: Singularity Theory, vol. I. Springer, Berlin (1998)
Bates, S., Weinstein, A.: Lectures on the Geometry of Quantization. Berkeley Mathematics Lecture Notes, vol. 8. AMS, Providence (1995)
Benenti, S.: Hamiltonian Optics and Generating Families. Napoli Series on Physics and Astrophysics, vol. 7. Bibliopolis, Naples (2003)
Benenti, S., Tulczyjew, W.M.: The geometrical meaning and globalization of the Hamilton-Jacobi method. In: Proc. Differential Geometrical Methods in Mathematical Physics, Aix-en-Provence, Salamanca, 1979. Lecture Notes in Mathematics, vol. 836. Springer, Berlin (1980)
Benenti, S., Tulczyjew, W.M.: Geometry of static mechanical systems with constraints. Ann. Mat. Pura Appl. 124, 139–160 (1980)
Boardman, J.M.: Singularities of differentiable maps. Publ. Math. Inst. Hautes Études Sci. 33, 21–57 (1967)
Byun, Y.: Maslov indices in practice. Trends Math. 5(1), 1–9 (2002). Information Center for Mathematical Sciences
Duistermaat, J.J.: Oscillatory integrals, Lagrange immersions and unfolding of singularities. Commun. Pure Appl. Math. 27, 207–281 (1974)
Erdélyi, A.: Asymptotic Expansions. Dover, New York (1956)
Galindo, A., Pascual, P.: Quantum Mechanics, vol. II. Springer, Berlin (1991)
Golubitski, M., Guillemin, V.: Stable Mappings and Their Singularities. Graduate Texts in Mathematics, vol. 14. Springer, Berlin (1974)
Guillemin, V., Sternberg, S.: Geometric Asymptotics. Math. Surveys Monogr., vol. 14. AMS, Providence (1977)
Guillemin, V., Sternberg, S.: Semi-classical analysis. Lecture Notes (2010). Available at Victor Guillemins homepage, http://math.mit.edu/~vwg
Hirzebruch, F.: Topological Methods in Algebraic Geometry. Springer, Berlin (1978)
Hörmander, L.: Fourier integral operators I. Acta Math. 127, 79–183 (1971)
Janeczko, S.: Singularities of Lagrangian varieties and related topics. Acta Appl. Math. 25, 21–57 (1991)
Keller, J.B.: A geometrical theory of diffraction. In: Calculus of Variations and Its Applications. Proc. Sympos. Appl. Math., vol. 8, pp. 27–52. McGraw-Hill, New York (1958)
Libermann, P., Marle, C.-M.: Symplectic Geometry and Analytical Mechanics. Reidel, Dordrecht (1987)
Ludwig, D.: Uniform asymptotic expansions at a caustic. Commun. Pure Appl. Math. 19, 215–250 (1966)
Maslov, V.P.: Théorie des Perturbations et Méthodes Asymptotiques. Gauthier-Villars, Paris (1971)
Maslov, V.P., Fedoryuk, M.V.: Quasi-Classical Approximation for the Equations of Quantum Mechanics. Reidel, Dordrecht (1981)
Mather, J.N.: Stability of C ∞-mappings: I. The division theorem. Ann. Math. 87, 89–104 (1968)
Mather, J.N.: Stability of C ∞-mappings: II. Infinitesimal stability implies stability. Ann. Math. 89, 254–291 (1969)
Mather, J.N.: Stability of C ∞-mappings: III. Finitely determined map-germs. Publ. Math. Inst. Hautes Études Sci. 35, 127–156 (1968)
Mather, J.N.: Stability of C ∞-mappings: IV. Classification of stable germs by R-relations. Publ. Math. Inst. Hautes Études Sci. 37, 223–248 (1969)
Mather, J.N.: Stability of C ∞-mappings: V. Transversality. Adv. Math. 4, 301–336 (1970)
Römer, H.: Theoretische Optik. VCH, Weinheim (1994)
Thom, R.: Les singularités des applications différentiables. Ann. Inst. Fourier (Grenoble) 6, 43–87 (1955)
Thom, R.: Structural Stability and Morphogenesis. An Outline of a General Theory of Models. Benjamin, Elmsford (1976)
Torrence, R.J., Tulczyjew, W.M.: Gauge invariant canonical mechanics for charged particles. J. Math. Phys. 14, 1725–1732 (1973)
Tulczyjew, W.M.: Gauge independent formulation of dynamics of charged particles. Ann. Inst. H. Poincaré Sect. A 34, 25–43 (1981)
Tulczyjew, W.M.: Lagrangian submanifolds, statics and dynamics of dynamical systems. In: Dynamical Systems and Microphysics, pp. 3–26. Academic Press, New York (1982)
Tulczyjew, W.M.: Control of static mechanical systems. In: Dynamical Systems and Microphysics, pp. 359–377. Academic Press, Orlando (1984)
Weinstein, A.: Lectures on Symplectic Manifolds. CBMS Regional Conference Series in Mathematics, vol. 29. AMS, Providence (1977)
Whitney, H.: On singularities of mappings of euclidean spaces: I. Mappings of the plane into the plane. Ann. Math. 62, 374–410 (1955)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Rudolph, G., Schmidt, M. (2013). Hamilton-Jacobi Theory. In: Differential Geometry and Mathematical Physics. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-5345-7_12
Download citation
DOI: https://doi.org/10.1007/978-94-007-5345-7_12
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-5344-0
Online ISBN: 978-94-007-5345-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


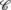 is an energy surface, this has already been discussed in Sect.
is an energy surface, this has already been discussed in Sect. 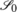 , see Remark 6.4.7.
, see Remark 6.4.7.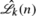 for
for  on M defines an s-density
on M defines an s-density 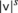 by
by 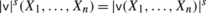 . In particular, if M is orientable, |Λ|s
M is trivial for every s. The product of an s
1-density ν
1 and an s
2-density ν
2 on M is defined by (ν
1
ν
2)(X
1,…,X
n
):=ν
1(X
1,…,X
n
)ν
2(X
1,…,X
n
). It yields an (s
1+s
2)-density. The calculus of differential forms, notably the pull-back and, based on that, the Lie derivative, extends in an obvious way to s-densities.
. In particular, if M is orientable, |Λ|s
M is trivial for every s. The product of an s
1-density ν
1 and an s
2-density ν
2 on M is defined by (ν
1
ν
2)(X
1,…,X
n
):=ν
1(X
1,…,X
n
)ν
2(X
1,…,X
n
). It yields an (s
1+s
2)-density. The calculus of differential forms, notably the pull-back and, based on that, the Lie derivative, extends in an obvious way to s-densities.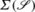 transversally.
transversally.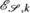 may be identified with the pull-back under ι of the so-called prequantum line bundle over (T∗
Q,dθ), see Sect. 4.1 and Appendix D of [
may be identified with the pull-back under ι of the so-called prequantum line bundle over (T∗
Q,dθ), see Sect. 4.1 and Appendix D of [