Abstract
We are interested in translating n-dimensional arrays of real numbers (images) into simpler structures that nevertheless capture the topological/geometrical essence of the objects in the images. In the case n=3 these structures may be used as descriptors of images in macromolecular databases. A foreground component tree structure (FCTS) contains all the information on the relationships between connected components when the image is thresholded at various levels. But unsimplified FCTSs are too sensitive to errors in the image to be good descriptors. This chapter presents a method of simplifying FCTSs which can be proved to be robust in the sense of producing essentially the same simplifications in the presence of small perturbations. We demonstrate the potential applicability of our methodology to macromolecular databases by showing that the simplified FCTSs can be used to distinguish between two slightly different versions of an adenovirus.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Note that no algorithm which actually creates the sequence σ that is defined by any such function f can run in
 time in all cases, because any comparison sort must perform Ω(nlogn) comparisons to sort a set of n items (here, leaves) in the worst case [3, Thm. 8.1].
time in all cases, because any comparison sort must perform Ω(nlogn) comparisons to sort a set of n items (here, leaves) in the worst case [3, Thm. 8.1]. - 2.
The tree defined here is the augmented contour tree of [1]. It may have many vertices s that have just two neighbors, of which one neighbor s′ satisfies I(s′)<I(s) while the other neighbor s″ satisfies I(s″)>I(s). Many authors define the contour tree to not include such vertices.
- 3.
Persistence diagrams are commonly defined (as in [4, pp. 150–152]) for a filter function
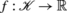 , where
, where 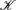 is a suitable simplicial complex. To define the 0th persistence diagram of −I based on the adjacency relation κ, we can take the simplicial complex
is a suitable simplicial complex. To define the 0th persistence diagram of −I based on the adjacency relation κ, we can take the simplicial complex  to be the simple graph whose vertex set is
to be the simple graph whose vertex set is 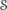 and whose edges join κ-adjacent elements of
and whose edges join κ-adjacent elements of  , and we can use the filter function
, and we can use the filter function  for which f(v)=−I(v) if v is a vertex of
for which f(v)=−I(v) if v is a vertex of  , and f(e)=−min(I(x),I(y)) if e is an edge of
, and f(e)=−min(I(x),I(y)) if e is an edge of 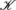 that joins the vertices x and y.
that joins the vertices x and y. - 4.
Let
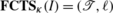 , and let leaf[1],…,leaf[n] be any ℓ-increasing enumeration of the leaves of
, and let leaf[1],…,leaf[n] be any ℓ-increasing enumeration of the leaves of  . For 1≤i<n, each leaf leaf[i] is represented in the persistence diagram by a point (−ℓ(leaf[i]),−ℓ(a)) where a is the closest ancestor of leaf[i] that is an ancestor of at least one of the leaves leaf[i+1],…,leaf[n]. The last leaf leaf[n] of the ℓ-increasing enumeration is represented in the persistence diagram by the point (−ℓ(leaf[n]),+∞). The diagram is defined to also contain, for each z∈ℝ, a point (z,z) with countably infinite multiplicity.
. For 1≤i<n, each leaf leaf[i] is represented in the persistence diagram by a point (−ℓ(leaf[i]),−ℓ(a)) where a is the closest ancestor of leaf[i] that is an ancestor of at least one of the leaves leaf[i+1],…,leaf[n]. The last leaf leaf[n] of the ℓ-increasing enumeration is represented in the persistence diagram by the point (−ℓ(leaf[n]),+∞). The diagram is defined to also contain, for each z∈ℝ, a point (z,z) with countably infinite multiplicity. - 5.
The bottleneck distance between two persistence diagrams D 1 and D 2 is the infimum of \(\sup_{d \in D_{1}} \|d - \eta(d)\|_{\infty}\) over all bijections η:D 1→D 2.
References
Carr, H., Snoeyink, J., Axen, U.: Computing contour trees in all dimensions. Comput. Geom. 24, 75–94 (2003)
Cohen-Steiner, D., Edelsbrunner, H., Harer, J.: Stability of persistence diagrams. Discrete Comput. Geom. 37, 103–120 (2007)
Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms, 2nd edn. MIT Press, Cambridge (2001)
Edelsbrunner, H., Harer, J.: Computational Topology: An Introduction. Am. Math. Soc., Providence (2010)
Herman, G.T.: Geometry of Digital Spaces. Birkhäuser Boston, Boston (1998)
Matas, J., Chum, O., Urban, M., Pajdla, T.: Robust wide baseline stereo from maximally stable extremal regions. In: Rosin, P.L., Marshall, D. (eds.) Proceedings of the British Machine Vision Conference, BMVC 2002, pp. 384–393. British Machine Vision Association, Malvern (2002).
Najman, L., Couprie, M.: Building the component tree in quasi-linear time. IEEE Trans. Image Process. 15, 3531–3539 (2006)
Russell, W.C.: Update on adenovirus and its vectors. J. Gen. Virol. 81, 2573–2604 (2000)
San Martín, C., Glasgow, J.N., Borovjagin, A., Beatty, M.S., Kashentseva, E.A., Curiel, D.T., Marabini, R., Dmitriev, I.P.: Localization of the N-terminus of minor coat protein IIIa in the adenovirus capsid. J. Mol. Biol. 383, 923–934 (2008)
Sarioz, D., Kong, T.Y., Herman, G.T.: History trees as descriptors of macromolecular structures. In: Bebis, G., et al. (eds.) Advances in Visual Computing: Second International Symposium, ISVC 2006, Proceedings, Part I, pp. 263–272. Springer, Berlin (2006)
Tarjan, R.E.: Efficiency of a good but not linear set union algorithm. J. Assoc. Comput. Mach. 22, 215–225 (1975)
Weber, G.H., Dillard, S.E., Carr, H., Pascucci, V., Hamann, B.: Topology controlled volume rendering. IEEE Trans. Vis. Comput. Graph. 13, 330–341 (2007)
Acknowledgements
We thank Edgar Garduño, Roberto Marabini, and Homeira Pajoohesh for discussions regarding this chapter. The work was supported by awards R01HL070472 from the National Heart, Lung, and Blood Institute and DMS-1114901 from the National Science Foundation. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung, and Blood Institute, the National Institutes of Health, or the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix A: Some Properties of Simplification Steps 2 and 3, and a Proof of the Correctness of Algorithm 1
1.1 A.1 Properties of Simplification Step 2
Here we prove the main result of Sect. 2.4.2, and establish other properties of simplification step 2 that are used in our proof of the Main Theorem.
Lemma A1
Let
 be any
κ-FCTS, let
λ>0, and let
s
and
s′ be any two distinct leaves of a
κ-FCTS
be any
κ-FCTS, let
λ>0, and let
s
and
s′ be any two distinct leaves of a
κ-FCTS
 that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ. Then (regardless of which
ℓ
in-increasing enumeration of
that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ. Then (regardless of which
ℓ
in-increasing enumeration of
 is used to perform the pruning):
is used to perform the pruning):
-
(i)
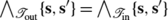
-
(ii)
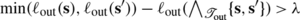
Proof
The hypotheses imply that properties P1–P4 hold with respect to some ℓ
in-increasing enumeration of  . It follows from P4 that, for all
. It follows from P4 that, for all  , every node in
, every node in  is also a node in
is also a node in  . Therefore
. Therefore  is the same set regardless of whether
is the same set regardless of whether  or
or  . So
. So  is the same node regardless of whether
is the same node regardless of whether  or
or  , since
, since  is just the element of
is just the element of  that is a descendant in
that is a descendant in  of every element of that set. Hence (i) holds.
of every element of that set. Hence (i) holds.
To prove (ii), we may assume without loss of generality that, in the ℓ
in-increasing leaf enumeration that is used for pruning, s occurs later than s′. (This assumption implies that min(ℓ
in(s),ℓ
in(s′))=ℓ
in(s′).) Then, since  , property P3 implies that
, property P3 implies that  , which is equivalent to:
, which is equivalent to:

But (A1) is equivalent to assertion (ii), because of assertion (i) and the fact that ℓ
out is just the restriction of ℓ
in to  . □
. □
Corollary A2
Let λ be any positive value, and \(\boldsymbol{\mathfrak{F}}_{\mathrm{out}}\) any κ-FCTS that results from pruning a κ-FCTS \(\boldsymbol {\mathfrak{F}}_{\mathrm{in}}\) by removing branches of length ≤λ. Then, for all \(\mathbf{v}\in\mathbf{Crit}(\boldsymbol{\mathfrak {F}}_{\mathrm{out}}) \setminus\mathbf{Leaves} (\boldsymbol{\mathfrak{F}}_{\mathrm{out}})\), we have that \(\mathbf{v}\in\mathbf{Crit}(\boldsymbol{\mathfrak {F}}_{\mathrm{in}}) \setminus\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}_{\mathrm{in}})\) and \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{out}}}(\mathbf {v}) > \lambda\).
Proof
Let  , and let \(\mathbf{v}\in\mathbf{Crit}(\boldsymbol{\mathfrak{F}}_{\mathrm {out}}) \setminus\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}_{\mathrm {out}})\). Then
, and let \(\mathbf{v}\in\mathbf{Crit}(\boldsymbol{\mathfrak{F}}_{\mathrm {out}}) \setminus\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}_{\mathrm {out}})\). Then  for some distinct leaves s and s′ of \(\boldsymbol{\mathfrak {F}}_{\mathrm{out}}\). Now
for some distinct leaves s and s′ of \(\boldsymbol{\mathfrak {F}}_{\mathrm{out}}\). Now  (by assertion (i) of Lemma A1), and so \(\mathbf{v}\in \mathbf{Crit}(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}) \setminus\mathbf{Leaves}(\boldsymbol{\mathfrak {F}}_{\mathrm{in}})\). Moreover, we have that
(by assertion (i) of Lemma A1), and so \(\mathbf{v}\in \mathbf{Crit}(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}) \setminus\mathbf{Leaves}(\boldsymbol{\mathfrak {F}}_{\mathrm{in}})\). Moreover, we have that  , where the second inequality follows from assertion (ii) of Lemma A1. □
, where the second inequality follows from assertion (ii) of Lemma A1. □
Lemma A3
Let
 be a
κ-FCTS, let
λ>0, and let
be a
κ-FCTS, let
λ>0, and let
 be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing leaf enumeration
σ=(leaf[1],…,leaf[n]) of
be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing leaf enumeration
σ=(leaf[1],…,leaf[n]) of
 . Then:
. Then:
-
(a)
For all
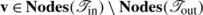 ,
, 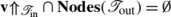 .
. -
(b)
For all
 ,
,  if and only if
if and only if
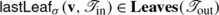 .
. -
(c)
For all
 , \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{out} }}(\mathbf{v}) = \mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm {in}}}(\mathbf{v})\).
, \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{out} }}(\mathbf{v}) = \mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm {in}}}(\mathbf{v})\).
Proof
For brevity, we write lastLeaf
σ
(v) for  . Evidently, (a) follows from P4, and the “if” part of (b) follows from (a). To establish the “only if” part of (b), let
. Evidently, (a) follows from P4, and the “if” part of (b) follows from (a). To establish the “only if” part of (b), let  , and let leaf[i]=lastLeaf
σ
(v). We need to show that
, and let leaf[i]=lastLeaf
σ
(v). We need to show that  . If i=n then this is true (by property P2), so let us assume i<n. Let j be any element of the set {i+1,…,n} (so that
. If i=n then this is true (by property P2), so let us assume i<n. Let j be any element of the set {i+1,…,n} (so that  ). Now we claim that leaf[j] must satisfy
). Now we claim that leaf[j] must satisfy  .
.
To see this, let leaf[k] be any leaf of  ; such a leaf must exist, by P4. As leaf[i]=lastLeaf
σ
(v), we have that i≥k and ℓ
in(leaf[i])≥ℓ
in(leaf[k]). As j∈{i+1,…,n}, we have that j∈{k+1,…,n}. Therefore, since
; such a leaf must exist, by P4. As leaf[i]=lastLeaf
σ
(v), we have that i≥k and ℓ
in(leaf[i])≥ℓ
in(leaf[k]). As j∈{i+1,…,n}, we have that j∈{k+1,…,n}. Therefore, since  , property P3 implies that:
, property P3 implies that:

But, since leaf[i] and leaf[k] are leaves of  but leaf[j] is not,
but leaf[j] is not,

and (since ℓ in(leaf[i])≥ℓ in(leaf[k])) this implies:

This and (A2) imply that our claim is valid (for any j in {i+1,…,n}). The “only if” part of (b) follows from this and property P3.
To prove (c), let  . Then
. Then  (by (b)), and every
(by (b)), and every  satisfies ℓ
out(w)=ℓ
in(w)≤ℓ
in(lastLeaf
σ
(v))=ℓ
out(lastLeaf
σ
(v)).
satisfies ℓ
out(w)=ℓ
in(w)≤ℓ
in(lastLeaf
σ
(v))=ℓ
out(lastLeaf
σ
(v)).
It follows that \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{out}}}(\mathbf {v}) = \ell_{\mathrm{out}}(\mathsf {lastLeaf}_{\sigma} (\mathbf{v})) - \ell_{\mathrm{out}}(\mathbf{v}) = \ell_{\mathrm{in}}(\mathsf {lastLeaf}_{\sigma}(\mathbf{v})) - \ell_{\mathrm{in} }(\mathbf{v}) = \mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{in} }}(\mathbf{v})\). □
Lemma A4
Let
 be a
κ-FCTS, let
λ>0, and let
be a
κ-FCTS, let
λ>0, and let
 be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing leaf enumeration
σ=(leaf[1],…,leaf[n]) of
be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing leaf enumeration
σ=(leaf[1],…,leaf[n]) of
 . Then:
. Then:
-
(a)
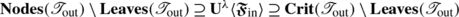
-
(b)
For all \(\mathbf{v}\in\mathbf{V}^{\lambda}\langle \boldsymbol{\mathfrak{F}}_{\mathrm{in}}\rangle \setminus\mathbf{V}_{1}^{\lambda}\langle\boldsymbol{\mathfrak {F}}_{\mathrm{in}}\rangle\),
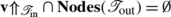 .
. -
(c)
For all \(\mathbf{v}\in\mathbf{V}_{1}^{\lambda}\langle \boldsymbol{\mathfrak{F}}_{\mathrm{in}}\rangle \),
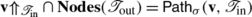 .
.
Proof
For brevity, we shall write U
λ, V
λ, \(\mathbf {V}_{1}^{\lambda}\), lastLeaf
σ
(v), and Path
σ
(v) for \(\mathbf{U}^{\lambda}\langle\boldsymbol{\mathfrak{F}}_{\mathrm {in}}\rangle\), \(\mathbf{V}^{\lambda}\langle\boldsymbol{\mathfrak{F}}_{\mathrm {in}}\rangle\), \(\mathbf{V}_{1}^{\lambda}\langle\boldsymbol{\mathfrak{F}}_{\mathrm {in}}\rangle\),  , and
, and  .
.
First, we prove (a). The inclusion  follows from Corollary A2 and Lemma A3(c). Moreover, since P4 implies that
follows from Corollary A2 and Lemma A3(c). Moreover, since P4 implies that  , we have that
, we have that  if u∈U
λ. So the other inclusion of (a) will follow if we can show that
if u∈U
λ. So the other inclusion of (a) will follow if we can show that  whenever u∈U
λ.
whenever u∈U
λ.
Let u be any element of U
λ, and let leaf[i]=lastLeaf
σ
(u). If i=n, then  (by property P2) and so
(by property P2) and so  (because of P4), as required. Now suppose i<n. Let j be any element of the set {i+1,…,n} (so
(because of P4), as required. Now suppose i<n. Let j be any element of the set {i+1,…,n} (so  ). Since leaf[i] is a leaf of
). Since leaf[i] is a leaf of  but leaf[j] is not, we have that
but leaf[j] is not, we have that  . Hence:
. Hence:

We see from this and property P3 that  , and hence (in view of P4) that
, and hence (in view of P4) that  , as required. This proves (a).
, as required. This proves (a).
Next, we prove (b). Let v be any node in \(\mathbf{V}^{\lambda}\setminus\mathbf {V}_{1}^{\lambda}\). Then it follows from the definitions of V
λ and \(\mathbf{V}_{1}^{\lambda}\) that  .
.
Let  . Then
. Then  , so we have that:
, so we have that:
Now \(\ell_{\mathrm{in}}(\mathbf{d}) - \ell_{\mathrm{in}}(\mathbf {v}) \leq\mathrm{depth}_{\boldsymbol{\mathfrak{F}} _{\mathrm{in}}}(\mathbf{v})\) for all  . Therefore:
. Therefore:

Here the second inequality follows from the definition of \(\mathbf {V}_{1}^{\lambda}\) and the facts that  and \(\mathbf{v}\in \mathbf{V}^{\lambda}\setminus\mathbf{V}_{1}^{\lambda}\). It follows from (A3) and (A4) that lastLeaf
σ
(p) is not a descendant of v in
and \(\mathbf{v}\in \mathbf{V}^{\lambda}\setminus\mathbf{V}_{1}^{\lambda}\). It follows from (A3) and (A4) that lastLeaf
σ
(p) is not a descendant of v in  , and so
, and so

Since  , we deduce from (A4) and (A5) that
, we deduce from (A4) and (A5) that

Since  and lastLeaf
σ
(p)≠lastLeaf
σ
(v) (e.g., by (A5)), the leaf lastLeaf
σ
(p) must occur later in the ℓ
in-increasing enumeration σ than the leaf lastLeaf
σ
(v). This, (A6), and P3 imply that
and lastLeaf
σ
(p)≠lastLeaf
σ
(v) (e.g., by (A5)), the leaf lastLeaf
σ
(p) must occur later in the ℓ
in-increasing enumeration σ than the leaf lastLeaf
σ
(v). This, (A6), and P3 imply that  . It now follows from assertion (b) of Lemma A3 that
. It now follows from assertion (b) of Lemma A3 that  . This and assertion (a) of Lemma A3 imply
. This and assertion (a) of Lemma A3 imply  , which proves (b).
, which proves (b).
Finally, we prove (c). Let v be any node in \(\mathbf{V}_{1}^{\lambda}\). We first make the claim that lastLeaf
σ
(v) is a leaf of  .
.
If  then the claim is certainly true (by property P2), so let us assume
then the claim is certainly true (by property P2), so let us assume  . Let
. Let  , and let s be any leaf of
, and let s be any leaf of  that occurs later in the ℓ
in-increasing enumeration σ than lastLeaf
σ
(v). Then
that occurs later in the ℓ
in-increasing enumeration σ than lastLeaf
σ
(v). Then  , and so
, and so  , which implies that:
, which implies that:

But, since \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm {in}}}(\mathbf{v}) = \ell_{\mathrm{in} }(\mathsf {lastLeaf}_{\sigma}(\mathbf{v})) - \ell_{\mathrm{in}}(\mathbf{v})\), we also have that
where the inequality follows from the definition of \(\mathbf {V}_{1}^{\lambda}\) and the facts that  and \(\mathbf{v}\in \mathbf{V}_{1}^{\lambda}\). Now it follows from (A7) and (A8) that:
and \(\mathbf{v}\in \mathbf{V}_{1}^{\lambda}\). Now it follows from (A7) and (A8) that:

Since this is true for every leaf s of  that occurs later in the ℓ
in-increasing enumeration σ than lastLeaf
σ
(v), our claim is justified (by property P3).
that occurs later in the ℓ
in-increasing enumeration σ than lastLeaf
σ
(v), our claim is justified (by property P3).
If w is any node in Path
σ
(v), then  and so it follows from our claim (and P4) that
and so it follows from our claim (and P4) that  . Thus every node in Path
σ
(v) lies in
. Thus every node in Path
σ
(v) lies in  .
.
It remains only to prove that  . To do this, we suppose there is a node
. To do this, we suppose there is a node  and deduce a contradiction. As
and deduce a contradiction. As  , we have that
, we have that  and so lastLeaf
σ
(v)≠lastLeaf
σ
(x). Moreover, each of the nodes lastLeaf
σ
(x) and lastLeaf
σ
(v) is a leaf of
and so lastLeaf
σ
(v)≠lastLeaf
σ
(x). Moreover, each of the nodes lastLeaf
σ
(x) and lastLeaf
σ
(v) is a leaf of  (by Lemma A3(b) and our claim).
(by Lemma A3(b) and our claim).
Let  . Then we have that
. Then we have that  ,
,  , and
, and  (by assertion (i) of Lemma A1). The latter implies
(by assertion (i) of Lemma A1). The latter implies  (as
(as  and
and  ); and
); and  implies \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{in}}} \mathbf {c}\leq\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{in}}} \mathbf {v}\leq\lambda\) (where the second inequality follows from the fact that \(\mathbf{v}\in\mathbf{V}_{1}^{\lambda}\subseteq \mathbf {V}^{\lambda}\)). Hence c∉U
λ. But this contradicts assertion (a) (since
implies \(\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{in}}} \mathbf {c}\leq\mathrm{depth}_{\boldsymbol{\mathfrak{F}}_{\mathrm{in}}} \mathbf {v}\leq\lambda\) (where the second inequality follows from the fact that \(\mathbf{v}\in\mathbf{V}_{1}^{\lambda}\subseteq \mathbf {V}^{\lambda}\)). Hence c∉U
λ. But this contradicts assertion (a) (since  ). It follows that x cannot exist, and so our proof of (c) is complete. □
). It follows that x cannot exist, and so our proof of (c) is complete. □
We can now prove the main result of Sect. 2.4.2:
Proposition
Let
 be a
κ-FCTS, let
λ>0, and let
be a
κ-FCTS, let
λ>0, and let
 be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing enumeration
σ
of
be the
κ-FCTS that results from pruning
\(\boldsymbol{\mathfrak{F}}_{\mathrm{in}}\)
by removing branches of length ≤λ
using an
ℓ
in-increasing enumeration
σ
of
 . Then the nodes of
\(\boldsymbol{\mathfrak{F}}_{\mathrm{out}}\)
consist just of:
. Then the nodes of
\(\boldsymbol{\mathfrak{F}}_{\mathrm{out}}\)
consist just of:
-
(i)
The nodes of \(\mathbf{U}^{\lambda}\langle \boldsymbol{\mathfrak{F}}_{\mathrm{in} }\rangle\).
-
(ii)
The nodes of
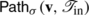 for each node
v
in
\(\mathbf{V}_{1}^{\lambda}\langle\boldsymbol {\mathfrak{F}}_{\mathrm{in} }\rangle\).
for each node
v
in
\(\mathbf{V}_{1}^{\lambda}\langle\boldsymbol {\mathfrak{F}}_{\mathrm{in} }\rangle\).
Proof
As  by Lemma A4(a), on putting
by Lemma A4(a), on putting  and \(\boldsymbol{\mathfrak {F}}= \boldsymbol{\mathfrak{F}}_{\mathrm{in}}\) in (2.1) and taking the intersection of each side with
and \(\boldsymbol{\mathfrak {F}}= \boldsymbol{\mathfrak{F}}_{\mathrm{in}}\) in (2.1) and taking the intersection of each side with  we see that:
we see that:

The proposition follows from this and assertions (b) and (c) of Lemma A4. □
1.2 A.2 Properties of Simplification Step 3
Here we establish some properties of simplification step 3 that are used in our proof of the Main Theorem and our justification of Algorithm 1.
For all \(j \in\{1, \dots, |D(\boldsymbol{\mathfrak{F}})|\}\), we see from E1–E5 that \(\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle \delta\rangle}) \subseteq\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle \delta' \rangle})\) whenever δ≥δ′. It follows that \(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\cdot\rangle}\) has the following monotonicity property:
In addition, \(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\cdot \rangle}\) has the following four properties for every λ>0 (as we will explain below):
-
E6:
For every \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol {\mathfrak{F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup \{\mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\})\) and every \(i \in\{0, \dots, |D(\boldsymbol{\mathfrak{F}})|-1\}\), \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle d^{\boldsymbol{\mathfrak{F}}}_{i+1} \rangle})\) if and only if, for every j∈{0,…,i}, \(\ell(\mathbf{c}) - \ell(\mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle d^{\boldsymbol{\mathfrak{F}} }_{j} \rangle}}(\mathbf{c})) > d^{\boldsymbol{\mathfrak{F}}}_{j+1}\).
-
E7:
For every \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol {\mathfrak{F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup \{\mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\})\), \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\) if and only if there is no critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\) such that ℓ(c)−ℓ(c′)≤λ and \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell (\mathbf{c}) - \ell(\mathbf{c}')) \rangle})\).
-
E8:
For every \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol {\mathfrak{F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup \{\mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\})\), \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\) if \(\ell(\mathbf{c}) - \ell(\mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}}(\mathbf {c})) > \lambda\).
-
E9:
For every \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol {\mathfrak{F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup \{\mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\})\), if \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\) then \(\ell(\mathbf{c}) - \ell(\mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle \lambda\rangle}}(\mathbf{c})) > \lambda\).
Our proof of the correctness of Algorithm 1 will be based on property E7. However, E1–E3, E8, and E9 are the only properties of simplification step 3 that will be used in our proof of the Main Theorem.
E6 is easily deduced from E5 by induction on i. Now we establish E7–E9. Let \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup\{\mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf{root}(\boldsymbol{\mathfrak{F}})\})\), and let λ be any positive value. We first claim that, for any critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\), the following four conditions are equivalent:
-
(a)
There is some \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak {F}})|-1\}\) such that \(\ell(\mathbf{c}) - \ell(\mathbf{c}') \leq d^{\boldsymbol {\mathfrak{F}}}_{j+1} \leq \lambda\) and \(\mathbf{c}' \in \mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle d^{\boldsymbol{\mathfrak{F}}}_{j} \rangle})\).
-
(b)
There is some \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak {F}})|-1\}\) such that \(\ell(\mathbf{c}) - \ell(\mathbf{c}') \leq d^{\boldsymbol {\mathfrak{F}}}_{j+1} \leq \lambda\) and \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol {\mathfrak{F}} }(\ell(\mathbf{c}) - \ell(\mathbf{c}')) \rangle})\).
-
(c)
ℓ(c)−ℓ(c′)≤λ and \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol{\mathfrak {F}}}(\ell(\mathbf{c}) - \ell(\mathbf {c}')) \rangle})\).
-
(d)
There is some \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak {F}})|-1\}\) such that \(\ell(\mathbf{c}) - \ell(\mathbf{c}') = d^{\boldsymbol{\mathfrak {F}}}_{j+1} \leq\lambda \) and \(\mathbf{c}' \in\mathbf{Nodes} (\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle d^{\boldsymbol {\mathfrak{F}}}_{j} \rangle})\).
Here (a) implies (b) because of the monotonicity property (A9) and the fact that if \(\ell(\mathbf{c}) - \ell(\mathbf{c}') \leq d^{\boldsymbol{\mathfrak{F}} }_{j+1}\) then \(\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell(\mathbf{c}) - \ell(\mathbf{c}')) \leq d^{\boldsymbol{\mathfrak{F}}}_{j}\). Evidently, (b) implies (c), and (d) implies (a). For any critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\), \(\ell(\mathbf{c}) - \ell(\mathbf{c}') = d^{\boldsymbol{\mathfrak {F}}}_{j+1}\) and \(\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell(\mathbf{c}) - \ell(\mathbf{c}')) = d^{\boldsymbol{\mathfrak{F}}}_{j}\) for some \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak{F}})|-1\}\), and so (c) implies (d). This justifies our claim that (a)–(d) are equivalent.
Next, we observe that \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\) holds if and only if c satisfies \(\ell(\mathbf{c}) - \ell(\mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle d^{\boldsymbol{\mathfrak{F}} }_{j} \rangle}}(\mathbf{c})) > d^{\boldsymbol{\mathfrak{F}}}_{j+1}\) for all \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak{F}})|-1\}\) such that \(d^{\boldsymbol{\mathfrak{F}}}_{j+1} \leq \lambda\). (This follows from E6 when \(\lambda\in D(\boldsymbol{\mathfrak {F}})\). It remains true if \(\lambda\notin D(\boldsymbol{\mathfrak{F}})\), because of E4.) So \(\mathbf{c}\notin\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle\lambda\rangle})\) just if there is some \(j \in\{0, \dots, |D(\boldsymbol{\mathfrak{F}})|-1\}\) such that \(\ell(\mathbf{c}) - \ell(\mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle d^{\boldsymbol{\mathfrak{F}} }_{j} \rangle}}(\mathbf{c})) \leq d^{\boldsymbol{\mathfrak{F}}}_{j+1} \leq\lambda\). Thus \(\mathbf{c}\notin\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle\lambda \rangle})\) just if (a) holds for some critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\). Equivalently, \(\mathbf{c}\notin\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle \lambda\rangle})\) just if (c) holds for some critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\). This proves E7. E8 follows from the “if” part of E7.
Suppose the node c violated E9. Then \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\). Moreover, when \(\mathbf{c}' = \mathbf{parent}_{\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle\lambda \rangle}}(\mathbf{c})\) we would have that ℓ(c)−ℓ(c′)≤λ and also that \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell (\mathbf{c}) - \ell(\mathbf{c}')) \rangle})\), where the latter follows from the former, the fact that \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\lambda\rangle})\), and the monotonicity property (A9). But this would contradict the “only if” part of E7. So E9 holds.
1.3 A.3 Justification of Algorithm 1
The correctness of Algorithm 1 will be deduced from Lemma A5 and Corollary A6 below.
Let  be any κ-FCTS, and let c be any node of \(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}\). Then we define \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak {F}}) = \infty\) if \(\mathbf{c}\in\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup\{ \mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\}\), and we define \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak {F}}) = \ell(\mathbf{c}) - \ell(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}))\) otherwise, where \(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol {\mathfrak{F}})\) is the closest critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\) such that
be any κ-FCTS, and let c be any node of \(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}\). Then we define \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak {F}}) = \infty\) if \(\mathbf{c}\in\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup\{ \mathbf{LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf {root}(\boldsymbol{\mathfrak{F}})\}\), and we define \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak {F}}) = \ell(\mathbf{c}) - \ell(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}))\) otherwise, where \(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol {\mathfrak{F}})\) is the closest critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\) such that

\(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}})\) exists for all \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}) \setminus (\mathbf{Leaves}(\boldsymbol{\mathfrak{F}}) \cup\{\mathbf {LCN}(\boldsymbol{\mathfrak{F}})\} \cup\{\mathbf{root}(\boldsymbol {\mathfrak{F}})\})\), because when \(\mathbf{c}' = \mathbf{LCN}(\boldsymbol{\mathfrak {F}})\) we see from E2 that \(\mathbf {c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\mu\rangle})\) for every μ≥0 and so c′ must satisfy the “either” or the “or” condition. Now \(\delta_{\lambda}(\cdot,\boldsymbol{\mathfrak{F}})\) satisfies the following condition:
Lemma A5
Let 0≤μ≤λ
and let
 be any
κ-FCTS. Then for all
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}})\)
we have that
\(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) > \mu\)
if and only if
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\mu\rangle})\).
be any
κ-FCTS. Then for all
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}})\)
we have that
\(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) > \mu\)
if and only if
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\mu\rangle})\).
Proof
Suppose \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves} (\boldsymbol{\mathfrak{F}}) \cup\{\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\} \cup\{\mathbf{root}(\boldsymbol{\mathfrak{F}})\})\). Then \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) > \mu\) holds just if \(\ell (\mathbf{c}) - \ell(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}})) > \mu\), and since μ≤λ we see from the definition of \(\mathbf{a}_{\lambda}(\mathbf {c},\boldsymbol{\mathfrak{F}})\) that this holds just if no critical proper ancestor c′ of c in \(\boldsymbol{\mathfrak{F}}\) satisfies ℓ(c)−ℓ(c′)≤μ and \(\mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell (\mathbf{c}) - \ell(\mathbf{c}')) \rangle})\). So in this case the lemma follows from E7.
The lemma also holds if \(\mathbf{c}\in\mathbf{Leaves}(\boldsymbol {\mathfrak{F}}) \cup\{\mathbf{LCN}(\boldsymbol{\mathfrak{F}} )\} \cup\{\mathbf{root} (\boldsymbol{\mathfrak{F}})\}\), because in that case \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) = \infty> \mu\) and E1–E3 imply \(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak{F}}^{\mathbf{crit}}{\langle\mu\rangle})\). □
Corollary A6
Let
λ
be any positive value, let
 be any
κ-FCTS, and let
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves} (\boldsymbol{\mathfrak{F}}) \cup\{\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\} \cup\{\mathbf{root}(\boldsymbol{\mathfrak{F}})\})\). Then
\(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) = \ell (\mathbf{c}) - \ell(\mathbf{a} )\), where
a
is the closest critical proper ancestor
c′ of
c
in
\(\boldsymbol{\mathfrak{F}}\)
such that
be any
κ-FCTS, and let
\(\mathbf{c}\in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}) \setminus(\mathbf{Leaves} (\boldsymbol{\mathfrak{F}}) \cup\{\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\} \cup\{\mathbf{root}(\boldsymbol{\mathfrak{F}})\})\). Then
\(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}}) = \ell (\mathbf{c}) - \ell(\mathbf{a} )\), where
a
is the closest critical proper ancestor
c′ of
c
in
\(\boldsymbol{\mathfrak{F}}\)
such that
Proof
We just have to show that \(\mathbf{a}= \mathbf{a}_{\lambda}(\mathbf {c},\boldsymbol{\mathfrak{F}})\). The definition of \(\mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol {\mathfrak{F}})\) differs from the definition of a only in the or condition “\(\ell(\mathbf{c}) - \ell(\mathbf{c}') \leq\lambda \mbox{ and } \mathbf{c}' \in\mathbf{Nodes}(\boldsymbol{\mathfrak {F}}^{\mathbf{crit}}{\langle\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell(\mathbf{c}) - \ell (\mathbf{c}')) \rangle})\)”.
On putting \(\mu= \operatorname{pred}_{\boldsymbol{\mathfrak {F}}}(\ell(\mathbf{c}) - \ell(\mathbf {c}'))\) in Lemma A5, we see that this condition holds if and only if ℓ(c)−ℓ(c′)≤λ and \(\operatorname{pred}_{\boldsymbol{\mathfrak{F}}}(\ell (\mathbf{c}) - \ell(\mathbf{c}')) < \delta_{\lambda}(\mathbf {c}',\boldsymbol{\mathfrak{F}})\), which is equivalent to the or condition in the definition of a (because either \(\delta_{\lambda}(\mathbf{c}',\boldsymbol{\mathfrak {F}}) = \ell(\mathbf {c}) - \ell(\mathbf{a}_{\lambda}(\mathbf{c}',\boldsymbol{\mathfrak{F}})) \in D(\boldsymbol{\mathfrak{F}})\) or \(\delta_{\lambda}(\mathbf{c}',\boldsymbol{\mathfrak{F}}) = \infty\)). So \(\mathbf{a}= \mathbf{a}_{\lambda}(\mathbf{c},\boldsymbol {\mathfrak{F}})\), as required. □
We can now explain why Algorithm 1 is correct. The algorithm sets  to a clone of
to a clone of  . Writing \(\boldsymbol{\mathfrak{F}}\) for
. Writing \(\boldsymbol{\mathfrak{F}}\) for  , we claim that the label c.label given by the algorithm to each node c of \(\boldsymbol{\mathfrak{F}}= \boldsymbol{\mathfrak{F}}^{\mathbf{crit}}\) is just the value \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}})\). Assuming this claim is valid, the correctness of the algorithm follows from Lemma A5. So it remains only to verify the claim.
, we claim that the label c.label given by the algorithm to each node c of \(\boldsymbol{\mathfrak{F}}= \boldsymbol{\mathfrak{F}}^{\mathbf{crit}}\) is just the value \(\delta_{\lambda}(\mathbf{c},\boldsymbol{\mathfrak{F}})\). Assuming this claim is valid, the correctness of the algorithm follows from Lemma A5. So it remains only to verify the claim.
The claim is certainly valid if c is \(\mathbf{root}(\boldsymbol{\mathfrak{F}})\) or \(\mathbf {LCN}(\boldsymbol{\mathfrak{F}})\), because those nodes are given the label ∞.
We see that the algorithm does a top-down traversal of  , during which the procedure labelDescendants is executed once for each proper descendant c of \(\mathbf {LCN}(\boldsymbol{\mathfrak{F}})\) in \(\boldsymbol{\mathfrak{F}}\). When labelDescendants is executed for such a node c that is a leaf, it gives c the label ∞. So the claim is valid for each proper descendant c of \(\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\) that is a leaf.
, during which the procedure labelDescendants is executed once for each proper descendant c of \(\mathbf {LCN}(\boldsymbol{\mathfrak{F}})\) in \(\boldsymbol{\mathfrak{F}}\). When labelDescendants is executed for such a node c that is a leaf, it gives c the label ∞. So the claim is valid for each proper descendant c of \(\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\) that is a leaf.
When labelDescendants is executed for a proper descendant c of \(\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\) that is not a leaf, the repeat loop in the procedure is executed. It follows from Corollary A6 that this loop labels c with the value \(\delta_{\lambda}(\mathbf {c},\boldsymbol{\mathfrak{F}})\). (Note that, when the loop is executed, \(\mathbf{c}'.\mathsf {label}= \delta_{\lambda}(\mathbf{c}',\boldsymbol {\mathfrak{F}})\) for each proper ancestor c′ of c in \(\boldsymbol {\mathfrak{F}}\).) Therefore the claim is also valid for each proper descendant c of \(\mathbf{LCN}(\boldsymbol {\mathfrak{F}})\) that is not a leaf.
Thus the claim is valid for all nodes c of \(\boldsymbol {\mathfrak{F}}= \boldsymbol{\mathfrak{F}}^{\mathbf{crit}}\), and Algorithm 1 is correct.
Appendix B: A Constructive Proof of Theorem 1
For any adjacency relation κ, any image I whose domain is finite and κ-connected, any λ>0, and any integer k≥0, let us say that the image I is (λ,k)-good with respect to κ if Λ κ (I)>λ and K κ (I)>k. Also, let us say that an image I′ is an ε-perturbation of an image I if I′ has the same domain as I and ∥I′−I∥∞≤ε. Then Theorem 1 can be deduced from the following lemma:
Fundamental Lemma
Let
κ
be any adjacency relation and
 an image whose domain
an image whose domain
 is finite and
κ-connected. Let
ε
be a positive value, let
k
be a nonnegative integer for which
I
good
is (4ε,k)-good with respect to
κ, and let
I′ be an
ε-perturbation of
I
good
. Then there is an essential isomorphism of
FCTS
κ
(I
good
) to the (2ε,k)-simplification of
FCTS
κ
(I′) that is level-preserving to within
ε.
is finite and
κ-connected. Let
ε
be a positive value, let
k
be a nonnegative integer for which
I
good
is (4ε,k)-good with respect to
κ, and let
I′ be an
ε-perturbation of
I
good
. Then there is an essential isomorphism of
FCTS
κ
(I
good
) to the (2ε,k)-simplification of
FCTS
κ
(I′) that is level-preserving to within
ε.
Proof of Theorem 1, assuming the Fundamental Lemma is valid
Suppose I, λ, and k satisfy the hypotheses of Theorem 1, so that 0<λ<Λ κ (I)/2 and 0≤k<K κ (I). Let I′ be any image that satisfies the conditions stated in the theorem (i.e., let I′ be any image whose domain is the same as that of I and which satisfies the condition ∥I′−I∥∞≤λ/2). Then we need to show that the conclusion of Theorem 1 holds—i.e., that there is an essential isomorphism of the (λ,k)-simplification of FCTS κ (I′) to FCTS κ (I) that is level-preserving to within λ/2. We now deduce this from the Fundamental Lemma.
Let I good =I, and let ε=λ/2. Then 4ε=2λ<Λ κ (I)=Λ κ (I good ) and k<K κ (I)=K κ (I good ), so that I good is (4ε,k)-good with respect to κ. We also have that ∥I′−I good ∥∞=∥I′−I∥∞≤λ/2=ε, so that I′ is a ε-perturbation of I good . Thus I good =I and I′ satisfy the hypotheses of the Fundamental Lemma, and must therefore satisfy the conclusion of the lemma, which implies the conclusion of Theorem 1 since 2ε=λ. □
We now prove the Fundamental Lemma by constructing an explicit essential isomorphism of FCTS κ (I good ) to the (2ε,k)-simplification of FCTS κ (I′) that is level-preserving to within ε.
Let  , and let
, and let  . Let
. Let  be the κ-FCTS that results from pruning \(\boldsymbol{\mathfrak{F}}'\) by removing nodes of size ≤k, and let I
1 be the image \(\mathit{I}_{\boldsymbol {\mathfrak{F}}_{1}}\), so that \(\boldsymbol{\mathfrak{F}}_{1} = \mathbf {FCTS}_{{\kappa}} (\mathit{I}_{1})\). Let
be the κ-FCTS that results from pruning \(\boldsymbol{\mathfrak{F}}'\) by removing nodes of size ≤k, and let I
1 be the image \(\mathit{I}_{\boldsymbol {\mathfrak{F}}_{1}}\), so that \(\boldsymbol{\mathfrak{F}}_{1} = \mathbf {FCTS}_{{\kappa}} (\mathit{I}_{1})\). Let  be the κ-FCTS that results from pruning \(\boldsymbol{\mathfrak{F}}_{1}\) by removing branches of length ≤2ε, and let
be the κ-FCTS that results from pruning \(\boldsymbol{\mathfrak{F}}_{1}\) by removing branches of length ≤2ε, and let  be the κ-FCTS that results from eliminating internal edges of length ≤2ε from \(\boldsymbol{\mathfrak{F}}_{2}^{\mathbf{crit}}\). Then
be the κ-FCTS that results from eliminating internal edges of length ≤2ε from \(\boldsymbol{\mathfrak{F}}_{2}^{\mathbf{crit}}\). Then  is the (2ε,k)-simplification of FCTS
κ
(I′), so what we want to do is to construct an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\) that is level-preserving to within ε. We will do this in three steps:
is the (2ε,k)-simplification of FCTS
κ
(I′), so what we want to do is to construct an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\) that is level-preserving to within ε. We will do this in three steps:
-
Step 1:
We define a suitable mapping
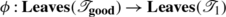 .
. -
Step 2:
We show that ϕ is 1-to-1, and that the range of the mapping ϕ is exactly the set of all the leaves of the subtree
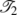 of
of  . Thereafter, we regard ϕ as a bijection
. Thereafter, we regard ϕ as a bijection  .
. -
Step 3:
We extend ϕ to a mapping
 by defining
by defining  . We then establish that, for all
. We then establish that, for all 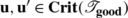 ,
,  if and only if
if and only if  , so that φ is 1-to-1 and order-preserving. We also show that the range of φ is the subset
, so that φ is 1-to-1 and order-preserving. We also show that the range of φ is the subset  of
of 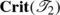 , and that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε for every
, and that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε for every  . Hence we can regard φ as a mapping
. Hence we can regard φ as a mapping  and, when so regarded, φ is an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\) that is level-preserving to within ε.
and, when so regarded, φ is an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\) that is level-preserving to within ε.
Note that the extension of ϕ to φ in step 3 is very natural because, if  is any rooted tree and
is any rooted tree and  , then
, then  . (In fact
. (In fact  if and only if
if and only if  and
and  .)
.)
2.1 B.1 Step 1 of the Proof of the Fundamental Lemma
We begin by defining a class of symmetric and transitive relations (on spels) that will be used in our definition of the mapping ϕ.
If  is an image and τ∈ℝ, then we write s ⇚I≥τ⇛ t to mean that
is an image and τ∈ℝ, then we write s ⇚I≥τ⇛ t to mean that  and
and  . It is readily confirmed that ⇚I≥τ⇛ is a symmetric and transitive relation (which depends on κ), and that s ⇚I≥τ⇛ s if and only if I(s)≥τ. Moreover, if s ⇚I≥τ
1⇛ t and t ⇚I≥τ
2⇛ u then s ⇚I≥min(τ
1,τ
2)⇛ u.
. It is readily confirmed that ⇚I≥τ⇛ is a symmetric and transitive relation (which depends on κ), and that s ⇚I≥τ⇛ s if and only if I(s)≥τ. Moreover, if s ⇚I≥τ
1⇛ t and t ⇚I≥τ
2⇛ u then s ⇚I≥min(τ
1,τ
2)⇛ u.
Now let  be any leaf of
be any leaf of  , and let z be any spel such that
, and let z be any spel such that
It follows from (B1) that:

Next, we define:

The set  is well defined by (B3) for the following reasons. First, if v′ is any spel such that
is well defined by (B3) for the following reasons. First, if v′ is any spel such that  (so that I
good
(v′)=I
good
(v)) then the condition obtained from (B1) when we replace v with v′ is equivalent to (B1). Second, if z′ is any spel that belongs to the set in (B1), then
(so that I
good
(v′)=I
good
(v)) then the condition obtained from (B1) when we replace v with v′ is equivalent to (B1). Second, if z′ is any spel that belongs to the set in (B1), then  (since I
1(z′)=I
1(z), and (B2) implies
(since I
1(z′)=I
1(z), and (B2) implies  ).
).
We can now define the mapping  by defining
by defining  to be the element of
to be the element of  that occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
that occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning  (to produce
(to produce  ) than all other elements of
) than all other elements of  . Note that if
. Note that if  has just one element, then
has just one element, then  is that element.
is that element.
This completes step 1 of the proof of the Fundamental Lemma.
2.2 B.2 Some Useful Observations
Steps 2 and 3 of the proof of the Fundamental Lemma will be based on the following observations:
-
A.
If
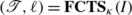 , where I is an arbitrary image whose domain is finite and κ-connected, and
, where I is an arbitrary image whose domain is finite and κ-connected, and  , then
, then 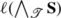 is the greatest real value τ such that s ⇚I≥τ⇛ t for all spels s,t∈⋃S.
is the greatest real value τ such that s ⇚I≥τ⇛ t for all spels s,t∈⋃S. -
B.
Whenever
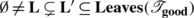 and
and  , we have that
, we have that  .
. -
C.
If
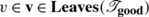 ,
,  , and
, and 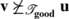 , then we have that
, then we have that  .
. -
D.
If
 and u ⇚I
good
≥I
good
(v)−4ε⇛ v, then we have that u ⇚I
good
≥I
good
(u)⇛ v or, equivalently,
and u ⇚I
good
≥I
good
(v)−4ε⇛ v, then we have that u ⇚I
good
≥I
good
(u)⇛ v or, equivalently,  .
. -
E.
If
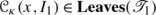 , then
, then  if and only if there is no node
if and only if there is no node  that satisfies both of the following conditions:
that satisfies both of the following conditions: -
(i)
x ⇚I 1≥I 1(x)−2ε⇛ y
-
(ii)
The leaf
 occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning  to produce
to produce  than the leaf
than the leaf  .
.
-
(i)
Here A is a consequence of the definitions of FCTS
κ
(I) and  . (The special case of A in which
. (The special case of A in which  is of particular interest; note that in this case s∈⋃S if and only if
is of particular interest; note that in this case s∈⋃S if and only if  .) B is a consequence of the fact that Λ
κ
(I
good
)>4ε, C can be deduced from B by putting L={v} and
.) B is a consequence of the fact that Λ
κ
(I
good
)>4ε, C can be deduced from B by putting L={v} and  , and D can be deduced from A and C.
, and D can be deduced from A and C.
Assertion E is a consequence of A and the fact that  is the result of pruning
is the result of pruning  by removing branches of length ≤2ε. In view of assertion (ii) of Lemma A1, we also have the following related fact:
by removing branches of length ≤2ε. In view of assertion (ii) of Lemma A1, we also have the following related fact:
- E′.:
-
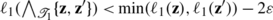 whenever z and z′ are distinct leaves of
whenever z and z′ are distinct leaves of  .
.
We could of course replace ℓ
1 with ℓ
2 in E′. Moreover, in view of assertion (i) of Lemma A1, we could also replace  with
with  .
.
Now let x be any spel in  . As \(\boldsymbol{\mathfrak {F}}_{1}\) is the result of pruning
. As \(\boldsymbol{\mathfrak {F}}_{1}\) is the result of pruning  by removing nodes of size ≤k, and \(\mathit{I}_{1} = \mathit {I}_{\boldsymbol{\mathfrak{F}}_{1}}\), we see from the definition of \(\mathit{I}_{\boldsymbol{\mathfrak {F}}_{1}}\) that
by removing nodes of size ≤k, and \(\mathit{I}_{1} = \mathit {I}_{\boldsymbol{\mathfrak{F}}_{1}}\), we see from the definition of \(\mathit{I}_{\boldsymbol{\mathfrak {F}}_{1}}\) that  . This is equivalent to
. This is equivalent to

since the nodes  for which x∈u are just the sets
for which x∈u are just the sets  for which
for which  . Now we claim that:
. Now we claim that:

To see this, we first observe that if y satisfies  then y also satisfies
then y also satisfies  . It follows from this observation that each element of the set
. It follows from this observation that each element of the set  in (B4) belongs to the set
in (B4) belongs to the set  and therefore belongs to the set
and therefore belongs to the set  in our claim (B5). So the right side of (B5) is no less than the right side of (B4); it remains to show that it is no greater.
in our claim (B5). So the right side of (B5) is no less than the right side of (B4); it remains to show that it is no greater.
For every τ≤I′(x), let y(τ,x) be any spel in  , so that I′(y(τ,x))≥τ, and it is easy to see that
, so that I′(y(τ,x))≥τ, and it is easy to see that

since I′≥I′(y(τ,x)) at every spel in  . Now if τ
0 is any element of the set
. Now if τ
0 is any element of the set  , then we have that I′(y(τ
0,x))≥τ
0 and we see from (B6) that
, then we have that I′(y(τ
0,x))≥τ
0 and we see from (B6) that  and
and  , so that I′(y(τ
0,x)) is an element of
, so that I′(y(τ
0,x)) is an element of  that is no less than τ
0. This shows that the right side of (B4) is no less than the right side of (B5). Hence the right sides of (B4) and (B5) are equal, and so our claim (B5) follows from (B4).
that is no less than τ
0. This shows that the right side of (B4) is no less than the right side of (B5). Hence the right sides of (B4) and (B5) are equal, and so our claim (B5) follows from (B4).
Next, we establish the following properties of I 1:
-
F.
I 1 is an ε-perturbation of I good , and if (I a,I b)=(I 1,I good ) or (I good ,I 1) then for any τ,δ∈ℝ and any spels
 we have that:
we have that: -
(i)
If s ⇚I a≥τ⇛ t then s ⇚I b≥τ−ε⇛ t.
-
(ii)
If s ⇚I a≥I a(u)−δ⇛ t then s ⇚I b≥I b(u)−δ−2ε⇛ t.
-
(i)
To see that I
1 has these properties, let x be any spel in  and note that
and note that  for every τ∈ℝ since ∥I′−I
good
∥∞≤ε. On putting τ=I
good
(x), we deduce that
for every τ∈ℝ since ∥I′−I
good
∥∞≤ε. On putting τ=I
good
(x), we deduce that  , whence
, whence  (as K
κ
(I
good
)>k). It follows from this and (B5) that I
1(x)≥I
good
(x)−ε. On the other hand, whenever τ>I
good
(x)+ε we have that I′(x)<τ (as ∥I′−I
good
∥∞≤ε), which implies that
(as K
κ
(I
good
)>k). It follows from this and (B5) that I
1(x)≥I
good
(x)−ε. On the other hand, whenever τ>I
good
(x)+ε we have that I′(x)<τ (as ∥I′−I
good
∥∞≤ε), which implies that  and hence (by (B5)) that I
1(x)<τ. From this it follows that I
1(x)≤I
good
(x)+ε. This shows that I
1 is an ε-perturbation of I
good
, as F asserts. Now (i) follows immediately, and (ii) can be deduced from (i) by putting τ=I
a(u)−δ, since the fact that I
a is an ε-perturbation of I
b implies that I
a(u)−δ≥I
b(u)−δ−ε for every
and hence (by (B5)) that I
1(x)<τ. From this it follows that I
1(x)≤I
good
(x)+ε. This shows that I
1 is an ε-perturbation of I
good
, as F asserts. Now (i) follows immediately, and (ii) can be deduced from (i) by putting τ=I
a(u)−δ, since the fact that I
a is an ε-perturbation of I
b implies that I
a(u)−δ≥I
b(u)−δ−ε for every  .
.
2.3 B.3 Step 2 of the Proof of the Fundamental Lemma
The main goals of this step are to show that the mapping ϕ defined in step 1 of the proof is 1-to-1 and that the range of ϕ is exactly the subset  of
of  . This will allow us to regard ϕ as a bijection
. This will allow us to regard ϕ as a bijection  .
.
We first state and prove the following easy lemma:
Lemma B1
Let
 be any leaf of
be any leaf of
 , let
x
be any spel in
, let
x
be any spel in
 that satisfies
x ⇚I
good
≥I
good
(v)−2ε⇛ v, and let
s
be any leaf of
that satisfies
x ⇚I
good
≥I
good
(v)−2ε⇛ v, and let
s
be any leaf of
 such that
such that
 . Then
. Then
 .
.
Proof
Let z be a spel that satisfies (B1) with respect to v. Then (B2) implies that  and hence that
and hence that  . This and (B3) imply
. This and (B3) imply  . □
. □
Next, we establish the following properties of  and the mapping ϕ:
and the mapping ϕ:
-
G.
The following are true for any leaf
 of
of 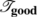 :
: -
(a)
If
 , then:
, then: -
(i)
y ⇚I good ≥I good (v)−4ε⇛ v
-
(ii)
y ⇚I good ≥I good (y)⇛ v
-
(iii)
y ⇚I 1≥I 1(y)−2ε⇛ v
-
(i)
-
(b)
If
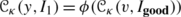 , then:
, then: -
(i)
I good (v)+ε≥I 1(y)≥I 1(v)≥I good (v)−ε
-
(ii)
y ⇚I good ≥I good (v)−2ε⇛ v
-
(iii)
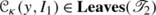
-
(i)
-
(a)
To establish (a), let  be any leaf of
be any leaf of  and let
and let  be an arbitrary element of
be an arbitrary element of  . Then it follows from the definition of the set
. Then it follows from the definition of the set  that
that  for some spel z that satisfies the condition v ⇚I
good
≥I
good
(v)−2ε⇛ z (which implies I
good
(z)≥I
good
(v)−2ε). Since
for some spel z that satisfies the condition v ⇚I
good
≥I
good
(v)−2ε⇛ z (which implies I
good
(z)≥I
good
(v)−2ε). Since  , we have that z ⇚I
1≥I
1(z)⇛ y. This implies z ⇚I
good
≥I
good
(z)−2ε⇛ y (in view of assertion (ii) of F), which implies z ⇚I
good
≥I
good
(v)−4ε⇛ y (as I
good
(z)≥I
good
(v)−2ε).
, we have that z ⇚I
1≥I
1(z)⇛ y. This implies z ⇚I
good
≥I
good
(z)−2ε⇛ y (in view of assertion (ii) of F), which implies z ⇚I
good
≥I
good
(v)−4ε⇛ y (as I
good
(z)≥I
good
(v)−2ε).
Combining z ⇚I
good
≥I
good
(v)−4ε⇛ y with v ⇚I
good
≥I
good
(v)−2ε⇛ z, we deduce assertion (i) of (a). Now (ii) follows from (i) and D because  , and (iii) follows from (ii) and F.
, and (iii) follows from (ii) and F.
Now we establish (b). Suppose  . Consider the node
. Consider the node  of
of  . Let s be a leaf of
. Let s be a leaf of  such that
such that  . Then we have that
. Then we have that  , by Lemma B1. Hence
, by Lemma B1. Hence  (as s cannot occur later in the ℓ
1-increasing leaf enumeration that is used in pruning
(as s cannot occur later in the ℓ
1-increasing leaf enumeration that is used in pruning  than
than  , by the definition of
, by the definition of  ). Therefore
). Therefore

which establishes the second inequality of assertion (i) of (b). The third inequality of (i) follows from F. Now I good (v)≥I good (y) (by assertion (ii) of (a)). This implies I good (v)≥I 1(y)−ε (by F), which is equivalent to the first inequality of assertion (i) of (b). This establishes assertion (i) of (b). It follows from F and assertion (i) of (b) that I good (y)≥I good (v)−2ε. Assertion (ii) of (b) follows from this and assertion (ii) of (a).
To see that assertion (iii) of (b) holds, let  be any leaf of
be any leaf of  that occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
that occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning  than
than  . Then it follows from the definitions of
. Then it follows from the definitions of  and of an ℓ
1-increasing leaf enumeration that:
and of an ℓ
1-increasing leaf enumeration that:
As I
1(w)≥I
1(y), (B7) implies that I
1(w)≥I
1(v), and now it follows from F that I
good
(w)≥I
good
(v)−2ε. So  ; otherwise the spel w would satisfy w ⇚I
good
≥I
good
(w)⇛ v, which would imply that w ⇚I
good
≥I
good
(v)−2ε⇛ v (since I
good
(w)≥I
good
(v)−2ε), which would in turn imply that
; otherwise the spel w would satisfy w ⇚I
good
≥I
good
(w)⇛ v, which would imply that w ⇚I
good
≥I
good
(v)−2ε⇛ v (since I
good
(w)≥I
good
(v)−2ε), which would in turn imply that  is an element of
is an element of  (by Lemma B1), which is false as we saw above.
(by Lemma B1), which is false as we saw above.
Since  , it follows from C and A that w does not satisfy w ⇚I
good
≥I
good
(v)−4ε⇛ v. This and assertion (ii) of F imply that w does not satisfy w ⇚I
1≥I
1(v)−2ε⇛ v, and so (since I
1(y)≥I
1(v), by (B7)) w does not satisfy w ⇚I
1≥I
1(y)−2ε⇛ v. But we know from assertion (iii) of (a) that y ⇚I
1≥I
1(y)−2ε⇛ v, so w also does not satisfy w ⇚I
1≥I
1(y)−2ε⇛ y. As
, it follows from C and A that w does not satisfy w ⇚I
good
≥I
good
(v)−4ε⇛ v. This and assertion (ii) of F imply that w does not satisfy w ⇚I
1≥I
1(v)−2ε⇛ v, and so (since I
1(y)≥I
1(v), by (B7)) w does not satisfy w ⇚I
1≥I
1(y)−2ε⇛ v. But we know from assertion (iii) of (a) that y ⇚I
1≥I
1(y)−2ε⇛ v, so w also does not satisfy w ⇚I
1≥I
1(y)−2ε⇛ y. As  is an arbitrary leaf of
is an arbitrary leaf of  that occurs later in the ℓ
1-increasing leaf enumeration used in pruning
that occurs later in the ℓ
1-increasing leaf enumeration used in pruning  than the leaf
than the leaf  , we see from E that
, we see from E that  —i.e., assertion (iii) of (b) holds.
—i.e., assertion (iii) of (b) holds.
Since  for every leaf
for every leaf  of
of  , we can regard ϕ as a mapping
, we can regard ϕ as a mapping  , and we will do this from now on.
, and we will do this from now on.
We next show that  is 1-to-1:
is 1-to-1:
-
H.
ϕ(v)≠ϕ(v′) whenever v and v′ are distinct leaves of
 .
.
Indeed, let  and
and  be any two distinct leaves of
be any two distinct leaves of  . To establish H, it is enough to show that
. To establish H, it is enough to show that  and
and  are disjoint. Suppose this is not the case. Then there is a leaf
are disjoint. Suppose this is not the case. Then there is a leaf  of
of  such that
such that  and
and  . Now assertion (i) of part (a) of G implies that v
a ⇚I
good
≥I
good
(v
a)−4ε⇛ x and that v
b ⇚I
good
≥I
good
(v
b)−4ε⇛ x.
. Now assertion (i) of part (a) of G implies that v
a ⇚I
good
≥I
good
(v
a)−4ε⇛ x and that v
b ⇚I
good
≥I
good
(v
b)−4ε⇛ x.
Assuming without loss of generality that I good (v a)≤I good (v b), these two properties imply that v a ⇚I good ≥I good (v a)−4ε⇛ v b, which is impossible in view of C and A. This contradiction establishes H and shows that ϕ is 1-to-1.
Next, we show that:
-
I.

To justify I, let  be any element of
be any element of  . Then what we need to show is that
. Then what we need to show is that  .
.
Let  be a leaf of
be a leaf of  such that
such that  . Then x ⇚I
good
≥I
good
(x)⇛ v and so it follows from F that x ⇚I
1≥I
1(x)−2ε⇛ v. Let
. Then x ⇚I
good
≥I
good
(x)⇛ v and so it follows from F that x ⇚I
1≥I
1(x)−2ε⇛ v. Let  . We now claim that:
. We now claim that:
-
 occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning 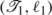 than
than  .
.
Now we justify this claim. Just one of the following is true:
-
(a)
I good (v)−2ε>I good (x)
-
(b)
I good (x)≥I good (v)−2ε
In case (a) it follows from F that I 1(v)>I 1(x), and so I 1(y)>I 1(x) (since I 1(y)≥I 1(v), by assertion (i) of part (b) of G); thus our claim is valid.
In case (b), we first observe that, since x ⇚I
good
≥I
good
(x)⇛ v, (b) implies that x ⇚I
good
≥I
good
(v)−2ε⇛ v, so that  (by Lemma B1). Therefore
(by Lemma B1). Therefore  , because
, because  is an element of
is an element of  . As
. As  and
and  , it follows from the definition of ϕ that our claim is again valid.
, it follows from the definition of ϕ that our claim is again valid.
In either case, we have that x ⇚I
1≥I
1(x)−2ε⇛ v (as we saw above), and the claim implies I
1(y)≥I
1(x). So, since we see from assertion (iii) of part (a) of G that v ⇚I
1≥I
1(y)−2ε⇛ y, we also have that x ⇚I
1≥I
1(x)−2ε⇛ y. From this, E, and the above claim, we deduce that  . This justifies I.
. This justifies I.
It follows from H and I that  is a bijection. This completes step 2 of the proof of the Fundamental Lemma.
is a bijection. This completes step 2 of the proof of the Fundamental Lemma.
2.4 B.4 Step 3 of the Proof of the Fundamental Lemma
We now extend ϕ to a mapping  by defining
by defining  . We will establish two properties of the mapping φ which together imply that φ is an essential isomorphism of \(\boldsymbol {\mathfrak{F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\). The first property is that, for all
. We will establish two properties of the mapping φ which together imply that φ is an essential isomorphism of \(\boldsymbol {\mathfrak{F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\). The first property is that, for all  ,
,  if and only if
if and only if  (so that φ is an order-preserving injection). The second property is that
(so that φ is an order-preserving injection). The second property is that  . To establish these two properties, we first show that:
. To establish these two properties, we first show that:
-
J.
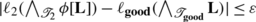 whenever
whenever  .
.
Indeed, suppose  . If |L|=1, then J is an immediate consequence of assertion (i) of part (b) of G, so we will assume |L|≥2.
. If |L|=1, then J is an immediate consequence of assertion (i) of part (b) of G, so we will assume |L|≥2.
For brevity, we will write τ
L
for  and τ
ϕ[L] for
and τ
ϕ[L] for  , so that J can be written as |τ
ϕ[L]−τ
L
|≤ε.
, so that J can be written as |τ
ϕ[L]−τ
L
|≤ε.
We first show that τ
ϕ[L]≥τ
L
−ε. For this purpose, let  and
and  be any two distinct elements of ϕ[L]. Then
be any two distinct elements of ϕ[L]. Then  and
and  , where
, where  and
and  are two distinct elements of L. From A and the definition of τ
L
we see that u ⇚I
good
≥τ
L
⇛ v. This and F imply that u ⇚I
1≥τ
L
−ε⇛ v. We see from the definition of ϕ and assertion (iii) of part (a) of G that x ⇚I
1≥I
1(x)−2ε⇛ u and y ⇚I
1≥I
1(y)−2ε⇛ v. Combining the last three observations, we deduce that:
are two distinct elements of L. From A and the definition of τ
L
we see that u ⇚I
good
≥τ
L
⇛ v. This and F imply that u ⇚I
1≥τ
L
−ε⇛ v. We see from the definition of ϕ and assertion (iii) of part (a) of G that x ⇚I
1≥I
1(x)−2ε⇛ u and y ⇚I
1≥I
1(y)−2ε⇛ v. Combining the last three observations, we deduce that:
However, it follows from C and the definition of τ L that

which implies that τ
L
−ε<min(I
good
(u)−5ε,I
good
(v)−5ε), which implies that τ
L
−ε<min(I
1(u)−4ε,I
1(v)−4ε) (in view of F), which in turn implies that τ
L
−ε<min(I
1(x)−4ε,I
1(y)−4ε) (by assertion (i) of part (b) of G). So (B8) can be simplified to x ⇚I
1≥τ
L
−ε⇛ y. It now follows from A that τ
ϕ[L]≥τ
L
−ε (since  and
and  are arbitrary distinct elements of ϕ[L]), as required.
are arbitrary distinct elements of ϕ[L]), as required.
To complete the proof of J, we show that τ
L
≥τ
ϕ[L]−ε. This time we let  and
and  be any two distinct elements of L, and then define
be any two distinct elements of L, and then define  and
and  , so that
, so that  ,
,  . From A and the definition of τ
ϕ[L] we see that x ⇚I
1≥τ
ϕ[L]⇛ y. This and F imply that x ⇚I
good
≥τ
ϕ[L]−ε⇛ y. We see from assertion (ii) of part (b) of G that u ⇚I
good
≥I
good
(u)−2ε⇛ x; we similarly have that v ⇚I
good
≥I
good
(v)−2ε⇛ y. Combining the last three observations, we see that:
. From A and the definition of τ
ϕ[L] we see that x ⇚I
1≥τ
ϕ[L]⇛ y. This and F imply that x ⇚I
good
≥τ
ϕ[L]−ε⇛ y. We see from assertion (ii) of part (b) of G that u ⇚I
good
≥I
good
(u)−2ε⇛ x; we similarly have that v ⇚I
good
≥I
good
(v)−2ε⇛ y. Combining the last three observations, we see that:
However, it follows from the definition of τ ϕ[L] and E′ that:

Hence τ
ϕ[L]−ε<min(I
1(x)−3ε,I
1(y)−3ε), which (by assertion (i) of part (b) of G) implies τ
ϕ[L]−ε<min(I
good
(u)−2ε,I
good
(v)−2ε). We now see from (B9) that u ⇚I
good
≥τ
ϕ[L]−ε⇛ v. It follows from this and A that τ
L
≥τ
ϕ[L]−ε (since  and
and  are arbitrary distinct elements of L), as required. Thus we have established J.
are arbitrary distinct elements of L), as required. Thus we have established J.
From B and J, we deduce:
-
K.
Whenever
 ,
, 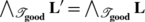 if and only if
if and only if  .
.
As we show in Appendix C, it is not difficult to deduce from K that:
-
L.
For all
 ,
, 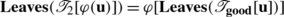 .
. -
M.
For all
 , there is no
, there is no  that satisfies the condition ℓ
2(x)−ℓ
2(y)≤2ε.
that satisfies the condition ℓ
2(x)−ℓ
2(y)≤2ε. -
N.
For all
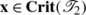 , some
, some  satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
We mention here that N is proved by showing that for every  the node
the node  has the stated property.
has the stated property.
Using L, it is quite easy to show that:
-
O.
For all
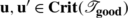 ,
, 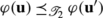 if and only if
if and only if 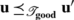 .
.
Details of the proof of O are given in Appendix C. It follows from O that φ is an order-preserving injection.
As  is the result of eliminating internal edges of length ≤2ε from \(\boldsymbol{\mathfrak{F}}_{2}^{\mathbf{crit}}\), it follows from M and property E8 of simplification step 3 that φ must satisfy
is the result of eliminating internal edges of length ≤2ε from \(\boldsymbol{\mathfrak{F}}_{2}^{\mathbf{crit}}\), it follows from M and property E8 of simplification step 3 that φ must satisfy  . Moreover, N implies that, for all
. Moreover, N implies that, for all  , some
, some  satisfies ℓ
2(x)−ℓ
2(z)≤2ε. We therefore have that:
satisfies ℓ
2(x)−ℓ
2(z)≤2ε. We therefore have that:
-
For all
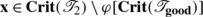 , some
, some  satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
From this and property E9 of simplification step 3 we deduce that φ satisfies  . Equivalently, φ satisfies the condition
. Equivalently, φ satisfies the condition  . Thus
. Thus  . So the order-preserving injection φ can be regarded as a bijection
. So the order-preserving injection φ can be regarded as a bijection  . When so regarded, φ is an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\). Finally, φ is level-preserving to within ε because, for any node
. When so regarded, φ is an essential isomorphism of \(\boldsymbol{\mathfrak {F}}_{\mathbf{good}}\) to \(\boldsymbol{\mathfrak{F}}_{3}\). Finally, φ is level-preserving to within ε because, for any node  , we deduce from J (on putting
, we deduce from J (on putting  , so that
, so that  ) that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε.
) that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε.
This completes the proof of the Fundamental Lemma.
Appendix C: Justification of Assertions L, M, N, and O in Step 3 of the Proof of the Fundamental Lemma
For any rooted tree  and any
and any  , we write
, we write  to denote the set
to denote the set  . It is readily confirmed that the following are true in any rooted tree
. It is readily confirmed that the following are true in any rooted tree  :
:






For all  and all
and all  , we write ϕ
L to mean ϕ[L] and we write ϕ
−1
L to mean ϕ
−1[L].
, we write ϕ
L to mean ϕ[L] and we write ϕ
−1
L to mean ϕ
−1[L].
If  or
or  , and λ is any positive value, then we write x≈
λ
y to mean that |ℓ
2(y)−ℓ
2(x)|≤λ, and write x≺
λ
y to mean that ℓ
2(y)−ℓ
2(x)>λ; in the latter case we must have that
, and λ is any positive value, then we write x≈
λ
y to mean that |ℓ
2(y)−ℓ
2(x)|≤λ, and write x≺
λ
y to mean that ℓ
2(y)−ℓ
2(x)>λ; in the latter case we must have that  . For brevity, we will write ⋀
good
and ⋀2 to mean
. For brevity, we will write ⋀
good
and ⋀2 to mean  and
and  , and write
, and write  and
and  to mean
to mean  and
and  . Note that the definition of the mapping φ can be rewritten in terms of ϕ and
. Note that the definition of the mapping φ can be rewritten in terms of ϕ and  as follows:
as follows:

If  , then
, then  and so
and so  (by (C1)). Hence assertion K can be restated as follows (for all nonempty sets
(by (C1)). Hence assertion K can be restated as follows (for all nonempty sets  ):
):
When  , the negations of ⋀2
ϕ
L≈2ε
⋀2
ϕ
L′ and ⋀
good
L′=⋀
good
L are ⋀2
ϕ
L′≺2ε
⋀2
ϕ
L and
, the negations of ⋀2
ϕ
L≈2ε
⋀2
ϕ
L′ and ⋀
good
L′=⋀
good
L are ⋀2
ϕ
L′≺2ε
⋀2
ϕ
L and  respectively (since
respectively (since  and
and  ), so (C8) can also be stated as follows (for all nonempty sets
), so (C8) can also be stated as follows (for all nonempty sets  ):
):

3.1 C.1 Proof of Assertion L
In view of (C7), L can be restated as follows:
-
For all
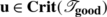 , we have that
, we have that 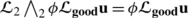 . Equivalently,
. Equivalently,  .
.
To prove this, let  . Then we successively deduce:
. Then we successively deduce:

The result will follow from (C10) if we can show that the following is not true:

To do this, we derive a contradiction from (C11) as follows:

3.2 C.2 Proof of Assertion M
In view of (C7), M is equivalent to:
-
If
 for some
for some 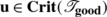 , and if
, and if 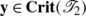 satisfies
satisfies  , then y≺2ε
x.
, then y≺2ε
x.
To prove this, suppose  for some
for some  , and
, and  satisfies
satisfies  . Then we can successively deduce:
. Then we can successively deduce:

This proves that y≺2ε x.
3.3 C.3 Proof of Assertion N
In view of (C7),  for every node x of
for every node x of  . So N can be proved by establishing that:
. So N can be proved by establishing that:
-
For all
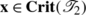 , the node
, the node  satisfies
satisfies  and x≈2ε
z.
and x≈2ε
z.
To prove this, let  and let
and let  . Then we successively deduce:
. Then we successively deduce:

This proves that  . We can also successively deduce:
. We can also successively deduce:

This proves that z≈2ε x.
3.4 C.4 Proof of Assertion O
Let  . Then:
. Then:

Rights and permissions
Copyright information
© 2012 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Herman, G.T., Kong, T.Y., Oliveira, L.M. (2012). Provably Robust Simplification of Component Trees of Multidimensional Images. In: Brimkov, V., Barneva, R. (eds) Digital Geometry Algorithms. Lecture Notes in Computational Vision and Biomechanics, vol 2. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-4174-4_2
Download citation
DOI: https://doi.org/10.1007/978-94-007-4174-4_2
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-4173-7
Online ISBN: 978-94-007-4174-4
eBook Packages: EngineeringEngineering (R0)


 time in all cases, because any comparison sort must perform Ω(nlogn) comparisons to sort a set of n items (here, leaves) in the worst case [
time in all cases, because any comparison sort must perform Ω(nlogn) comparisons to sort a set of n items (here, leaves) in the worst case [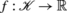 , where
, where  is a suitable simplicial complex. To define the 0th persistence diagram of −I based on the adjacency relation κ, we can take the simplicial complex
is a suitable simplicial complex. To define the 0th persistence diagram of −I based on the adjacency relation κ, we can take the simplicial complex  to be the simple graph whose vertex set is
to be the simple graph whose vertex set is 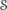 and whose edges join κ-adjacent elements of
and whose edges join κ-adjacent elements of  , and we can use the filter function
, and we can use the filter function  for which f(v)=−I(v) if v is a vertex of
for which f(v)=−I(v) if v is a vertex of  , and f(e)=−min(I(x),I(y)) if e is an edge of
, and f(e)=−min(I(x),I(y)) if e is an edge of 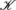 that joins the vertices x and y.
that joins the vertices x and y.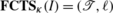 , and let
, and let  . For 1≤i<
. For 1≤i<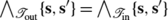
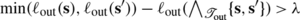
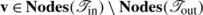 ,
, 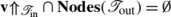 .
. ,
,  if and only if
if and only if
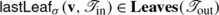 .
. ,
, 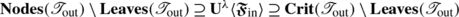
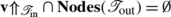 .
.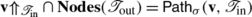 .
. for each node
v
in
for each node
v
in
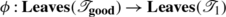 .
.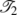 of
of  . Thereafter, we regard ϕ as a bijection
. Thereafter, we regard ϕ as a bijection  .
. by defining
by defining  . We then establish that, for all
. We then establish that, for all 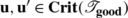 ,
,  if and only if
if and only if  , so that φ is 1-to-1 and order-preserving. We also show that the range of φ is the subset
, so that φ is 1-to-1 and order-preserving. We also show that the range of φ is the subset  of
of 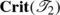 , and that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε for every
, and that |ℓ
3(φ(u))−ℓ
good
(u)|≤ε for every  . Hence we can regard φ as a mapping
. Hence we can regard φ as a mapping  and, when so regarded, φ is an essential isomorphism of
and, when so regarded, φ is an essential isomorphism of 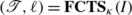 , where I is an arbitrary image whose domain is finite and κ-connected, and
, where I is an arbitrary image whose domain is finite and κ-connected, and  , then
, then 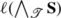 is the greatest real value τ such that s ⇚I≥τ⇛ t for all spels s,t∈⋃S.
is the greatest real value τ such that s ⇚I≥τ⇛ t for all spels s,t∈⋃S.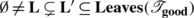 and
and  , we have that
, we have that  .
.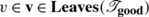 ,
,  , and
, and 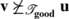 , then we have that
, then we have that  .
. and u ⇚I
good
≥I
good
(v)−4ε⇛ v, then we have that u ⇚I
good
≥I
good
(u)⇛ v or, equivalently,
and u ⇚I
good
≥I
good
(v)−4ε⇛ v, then we have that u ⇚I
good
≥I
good
(u)⇛ v or, equivalently,  .
.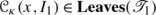 , then
, then  if and only if there is no node
if and only if there is no node  that satisfies both of the following conditions:
that satisfies both of the following conditions:  occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning  to produce
to produce  than the leaf
than the leaf  .
.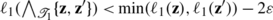 whenever z and z′ are distinct leaves of
whenever z and z′ are distinct leaves of  .
. we have that:
we have that:  of
of  :
:  , then:
, then: 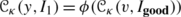 , then:
, then: 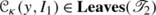


 .
.
 occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning
occurs later in the ℓ
1-increasing leaf enumeration that is used in pruning  than
than  .
.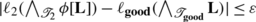 whenever
whenever  .
. ,
, 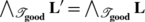 if and only if
if and only if  .
. ,
, 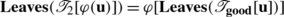 .
. , there is no
, there is no  that satisfies the condition ℓ
2(x)−ℓ
2(y)≤2ε.
that satisfies the condition ℓ
2(x)−ℓ
2(y)≤2ε.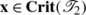 , some
, some  satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.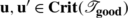 ,
, 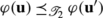 if and only if
if and only if 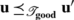 .
.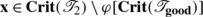 , some
, some  satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.
satisfies the condition ℓ
2(x)−ℓ
2(z)≤2ε.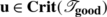 , we have that
, we have that 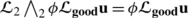 . Equivalently,
. Equivalently,  .
. for some
for some 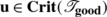 , and if
, and if 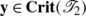 satisfies
satisfies  , then y≺2ε
x.
, then y≺2ε
x.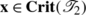 , the node
, the node  satisfies
satisfies  and x≈2ε
z.
and x≈2ε
z.