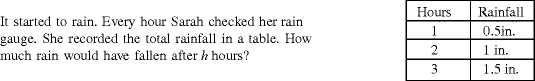Skip to main content
SpringerLink
Log in

Visuoalphanumeric Representations in Pattern Generalization Activity

  • Chapter
  • First Online:
Toward a Visually-Oriented School Mathematics Curriculum

Part of the book series: Mathematics Education Library ((MELI,volume 49))

Abstract

In Chapter 4, we drew on a few examples from my own classroom work in discussing a progressive account of symbol formation in school mathematics. A visually grounded approach provides an alternative and effective route that could assist students in understanding mathematics better. Otte (2007) notes how mathematical knowledge seems to be already “everything [that] just is and thus means itself” (p. 243). The more pressing issue appears to be “not that of rigor but the problem of the development of meaning” (Rene Thom quoted in Otte, 2007, pp. 244–245).

How general is general?

(Bastable & Schifter, 2008, p. 166).

The most important operation of the mind is that of generalization

(Peirce, 1960, p. 34).

(A)lgebra … not as symbol manipulation, not as arithmetic with letters, not even as the language of equations, but as a succinct and manipulable language in which to express generality and constraints on that generality

(Mason, 2008, p. 77).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    Parker and Baldridge (2004) emphasize the need for tables to have real (or experientially real) and predictable contexts with a sufficient number of particular instances in order to generate a reasonable algebraic expression (or formula). For example, the table below with the context about rainfall could not be assessed correctly, that is, even if the expression appears to take the algebraic form (1/2)h, “there is no reason why the rainfall will continue to be given by that expression, or any expression. This question cannot be answered” (p. 90). Other examples include stock market prices and gas prices, where tables could be generated but oftentimes do not lead to correct and justifiable algebraic expressions.

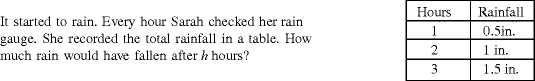
  2. 2.

    This notion conceptually shares Thagard’s (1978) interpretation of Peirce’s abduction as “cover[ing] both the act of arriving at plausible new hypotheses and the act of entertaining them for the sake of further investigation” (p. 166). The end result (i.e., at least in provisional terms) of progressive abduction is an inference to the best explanation (“IBE;” Hartman, 1965).

  3. 3.

    JRB stands for Joanne Rossi Becker, interviewer.

References

  • Abe, A. (2003). Abduction and analogy in chance discovery. In Y. Ohsawa & P. McBurney (Eds.), Chance discovery (pp. 231–248). New York: Springer.

    Google Scholar 

  • Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52, 215–241.

    Article  Google Scholar 

  • Arzarello, F., Micheletti, C., Olivero, F., & Robutti, O. (1998). A model for analyzing the transition to formal proofs in geometry. In A. Olivier & K. Newstead (Eds.), Proceedings of the 22nd annual conference of the international group for the psychology of mathematics education (Vol. 2, pp. 24–31). Stellenbosch, South Africa.

    Google Scholar 

  • Bastable, V., & Schifter, D. (2008). Classroom stories: Examples of elementary students engaged in early algebra. In J. Kaput, D. Carraher, & M. Blanton (Eds.), Algebra in the early grades (pp. 165–184). New York: Erlbaum.

    Google Scholar 

  • Boero, P., Garuti, R., & Mariotti, M. (1996). Some dynamical mental processes underlying producing and proving conjectures. In L. Puig & A. Gutierrez (Eds.), Proceedings of the 20th annual conference of the international group for the psychology of mathematics education (Vol. 2, pp. 121–128). Valencia, Spain.

    Google Scholar 

  • Cifarelli, V. (1999). Abductive inference: Connections between problem posing and solving. In O. Zaslavsky (Ed.), Proceedings of the 23rd annual conference of the international group for the psychology of mathematics education (Vol. 2, pp. 217–224). Haifa, Israel.

    Google Scholar 

  • Cifarelli, V., & Saenz-Ludlow, A. (1996). Abductive processes and mathematical learning. In E. Jakubowski, D. Watkins, & H. Biske (Eds.), Proceedings of the 18th annual meeting of the North American chapter of the international group for the psychology of mathematics education (Vol. 1, pp. 161–166). Columbus, Ohio.

    Google Scholar 

  • Clark, F., & Kamii, C. (1996). Identification of multiplicative thinking in children in grades 1–5. Journal for Research in Mathematics Education, 27(1), 41–51.

    Article  Google Scholar 

  • Curriculum Planning and Development Division. (2008). Primary mathematics textbooks. New Industrial Road, Singapore: Marshall Cavendish Education.

    Google Scholar 

  • Davis, P. (1993). Visual theorems. Educational Studies in Mathematics, 24, 333–344.

    Article  Google Scholar 

  • Dörfler, W. (2008). En route from patterns to algebra: Comments and reflections. ZDM, 40, 143–160.

    Article  Google Scholar 

  • Dretske, F. (1990). Seeing, believing, and knowing. In D. Osherson, S. Kosslyn, & J. Hollerback (Eds.), Visual cognition and action: An invitation to cognitive science (pp. 129–148). Cambridge, MA: MIT Press.

    Google Scholar 

  • Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1–2), 103–131.

    Article  Google Scholar 

  • Eco, U. (1983). Horns, hooves, insteps: Some hypotheses on three types of abduction. In U. Eco & T. Sebeok (Eds.), The sign of three: Dupin, Holmes, Peirce (pp. 198–220). Bloomington, IN: Indiana University Press.

    Google Scholar 

  • Filloy, E., & Rojano, T. (1989). Solving equations: The transition from arithmetic to algebra. For the Learning of Mathematics, 9(2), 19–25.

    Google Scholar 

  • Fischbein, E. (1993). The theory of figural concepts. Educational Studies in Mathematics, 24, 139–162.

    Article  Google Scholar 

  • Flach, P. (1996). Abduction and induction: Syllogistic and inferential perspectives. In P. Flach, & A. Kakas (Eds.), Contributing papers to the ECAI 96 workshop on abductive and inductive reasoning (pp. 31–35). Budapest, Hungary: ECAI.

    Google Scholar 

  • Freudenthal, H. (1981). Major problems of mathematics education. Educational Studies in Mathematics, 12, 133–150.

    Article  Google Scholar 

  • Gattis, M., & Holyoak, K. (1996). Mapping conceptual relations in visual reasoning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22(1), 231–239.

    Article  Google Scholar 

  • Giaquinto, M. (2007). Visual thinking in mathematics: An epistemological study. Oxford, UK: Oxford University Press.

    Book  Google Scholar 

  • Greenes, C., Cavanagh, M., Dacey, L., Findell, C., & Small, M. (2001). Navigating through algebra in prekindergarten – Grade 2. Reston, VA: National Council of Teachers of Mathematics.

    Google Scholar 

  • Hoffmann, M. (1999). Problems with Peirce’s concept of abduction. Foundations of Science, 4, 271–305.

    Article  Google Scholar 

  • Josephson, J. (1996). Inductive generalizations are abductions. In Flach, P. & Kakas, A. (Eds.), Contributing Paper to the ECAI ’96 Workshop on Abductive and Inductive Reasoning. Budapest, Hungary.

    Google Scholar 

  • Josephson, J. (2000). Smart inductive generalizations are abductions. In P. Flach & A. Kakas (Eds.), Abduction and induction: Essays on their relation and integration.

    Google Scholar 

  • Josephson, J., & Josephson, S. (1994). Abductive inference: Computation, philosophy, technology. New York: Cambridge University Press.

    Book  Google Scholar 

  • Kaput, J., Blanton, M., & Moreno, L. (2008). Algebra from a symbolization point of view. In J. Kaput, D. Carraher, & M. Blanton (Eds.), Algebra in the early grades (pp. 19–56). New York: Erlbaum.

    Google Scholar 

  • Lee, L. (1996). An initiation into algebraic culture through generalization activities. In N. Bednarz, C. Kieran, & Lee, L. (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 87–106). Dordrecht, Netherlands: Kluwer.

    Google Scholar 

  • Leslie, A., Xu, F., Tremoulet, P., & Scholl, B. (1998). Indexing and the object concept: Developing “what” and “where” systems. Trends in Cognitive Science, 2(1), 10–18.

    Article  Google Scholar 

  • Mason, J. (2008). Making use of children’s powers to produce algebraic thinking. In J. Kaput, D. Carraher, & M. Blanton (Eds.), Algebra in the early grades (pp. 57–94). New York: Erlbaum.

    Google Scholar 

  • Metzger, W. (2006). Laws of seeing. Cambridge, MA: The MIT Press.

    Google Scholar 

  • Moyer, P. (2001). Are we having fun yet? How teachers use manipulatives to teach mathematics. Educational Studies in Mathematics, 47, 175–197.

    Article  Google Scholar 

  • Neisser, U. (1976). Cognitive psychology. New York: Meredith Publishing Company.

    Google Scholar 

  • Otte, M. (2007). Mathematics history, philosophy, and education. Educational Studies in Mathematics, 66, 243–255.

    Article  Google Scholar 

  • Parker, T., & Baldridge, S. (2004). Elementary mathematics for teachers. Okemos, MI: Sefton-Ash Publishing.

    Google Scholar 

  • Pedemonte, B. (2007). How can the relationship between argumentation and proof be analyzed? Educational Studies in Mathematics, 66(1), 25–41.

    Article  Google Scholar 

  • Peirce, C. (1934). In C. Hartshorne & P. Weiss (Eds.), Collected papers of Charles Sanders Peirce: Volume V. Cambridge, MA: Harvard University Press.

    Google Scholar 

  • Peirce, C. (1957). In V. Tomas (Ed.), Essays in the philosophy of science. New York: The Bobbs-Merrill Company

    Google Scholar 

  • Peirce, C. (1958a). In A. Burks (Ed.), Collected papers of Charles Sanders Peirce: Volume VIII. Cambridge, MA: Harvard University Press.

    Google Scholar 

  • Peirce, C. (1960). In C. Hartshorne & P. Weiss (Eds.), Collected papers of Charles Sanders Peirce: Volume I and volume II. Cambridge, MA: The Belknap Press of Harvard University Press.

    Google Scholar 

  • Pylyshyn, Z. (2006). Seeing and visualizing: It’s not what you think. Cambridge, MA: MIT Press.

    Google Scholar 

  • Radford, L. (2008). Iconicity and contraction: A semiotic investigation of forms of algebraic generalizations of patterns in different context. ZDM: International Journal in Mathematics Education, 40(1), 83–96.

    Article  Google Scholar 

  • Resnik, M. (1997). Mathematics as a science of patterns. Oxford, UK: Oxford University Press.

    Google Scholar 

  • Rivera, F. (2007b). Visualizing as a mathematical way of knowing: Understanding figural generalization. Mathematics Teacher, 101(1), 69–75.

    Google Scholar 

  • Rivera, F. (2008). On the pitfalls of abduction: Complexities and complicities in patterning activity. For the Learning of Mathematics, 28(1), 17–25.

    Google Scholar 

  • Rivera, F. (2009). Visuoalphanumeric mechanisms that support pattern generalization. In I. Vale & A. Barbosa (Eds.), Patterns: Multiple perspectives and contexts in mathematics education (pp. 123–136). Portugal: Escola Superior de Educação do Instituto Politécnico de Viana de Coastelo.

    Google Scholar 

  • Rivera, F. (2010a). Visual templates in pattern generalization activity. Educational Studies in Mathematics, 73, 297–328.

    Article  Google Scholar 

  • Rivera, F. (2010b). There is more to mathematics than symbols. Mathematics Teaching, 218, 42–47.

    Google Scholar 

  • Rivera, F. (2010d). Spicing up counting through geometry. Mathematics Teacher.

    Google Scholar 

  • Rivera, F., & Becker, J. (2007a) Abductive–inductive (generalization) strategies of preservice elementary majors on patterns in algebra. Journal of Mathematical Behavior, 26(2), 140–155.

    Article  Google Scholar 

  • Rivera, F., & Becker, J. (2008). Middle school children’s cognitive perceptions of constructive and deconstructive generalizations involving linear figural patterns, ZDM, 40(1), 65–82.

    Article  Google Scholar 

  • Rivera, F., & Becker, J. (2010). Formation of linear pattern generalization in middle school children: Results of a three-year longitudinal study. In J. Cai & E. Knuth (Eds.), Early algebraization. Dordrecht, Netherlands: Springer.

    Google Scholar 

  • Rotman, B. (1995). Thinking diagrams: Mathematics, writing, and virtual reality. South Atlantic Quarterly, 94(2), 389–415.

    Google Scholar 

  • Sebeok, T. (1983). One, two, three spells U B E R T Y. In U. Eco & T. Sebeok (Eds.), The sign of three: Dupin, Holmes, Peirce (pp. 1–10). Bloomington, IN: Indiana University Press.

    Google Scholar 

  • Sophian, C. (2007). The origins of mathematical knowledge in childhood. Mahwah, NJ: Erlbaum.

    Google Scholar 

  • Thagard, P. (1978). Semiosis and hypothetic inference in C. S. Peirce. Versus Quaderni Di Studi Semiotici, 19/20, 163–172.

    Google Scholar 

  • Piaget, J. (1987). Possibility and necessity. Minneapolis, MN: University of Minnesota Press.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, San Jose State University, 1 Washington Square, San Jose California, 95192, USA

    Dr. Ferdinand D. Rivera

Authors
  1. Dr. Ferdinand D. Rivera
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ferdinand D. Rivera .

Rights and permissions

Reprints and permissions

Copyright information

© 2011 Springer Science+Business Media B.V.

About this chapter

Cite this chapter

Rivera, F.D. (2011). Visuoalphanumeric Representations in Pattern Generalization Activity. In: Toward a Visually-Oriented School Mathematics Curriculum. Mathematics Education Library, vol 49. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-0014-7_5

Download citation

Publish with us

Policies and ethics

Search

Navigation