Abstract
This chapter states peculiarities of investigation methods of magnetically coupled loops in A.C. machine with short-circuited rotor windings. Noted here are solutions of general problem on currents distribution in these windings: stated here is the solution algorithm for a system of equations, the concept is introduced on generalized characteristics of currents in rotor loops elements (for example, in elements of damper winding of salient pole machine). As practical usage an example of generalized characteristics of currents and MMF of short-circuited rotor loops is given with the calculation method of performance characteristics of high-power induction motors with nonlinear parameters (with account of skin effect in squirrel cage and magnetic circuit saturation). It is checked experimentally and is used in industry for calculation of machines with power up to 12–15 MW.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
I. Monographs, General Courses, Textbooks
Luriye A.I., The Theory of Elasticity. Moscow: Nauka. 1974. (in Russian).
Jeffris H., Swirles B., Methods of Mathematical Physics. Third Edition, Vol. 1–Vol. 3, Cambridge: Cambridge Univ. Press, 1966.
Korn G., Korn T., Mathematical Handbook, N.Y.: McGraw-Hill, 1961.
Mueller G., Ponick B., Elektrische Maschinen, N.Y., J. Wiley, 2009. (in German).
Schuisky W., Berechnung elektrischer Maschinen. Wien: Springer, 1960. (in German).
Richter R., Elektrische Maschinen. Berlin: Springer. Band I, 1924; Band II, 1930; Band III, 1932; Band IV, 1936; Band V, 1950. (in German).
Demirchyan K.S., Neyman L.R., Korovkin N.V., Theoretical Electrical Engineering. Moscow, St. Petersburg: Piter, 2009. Vols. 1, 2 (In Russian).
Kuepfmueller K., Kohn G., Theoretische Elektrotechnik und Elektronik. 15 Aufl. Berlin, New York: Springer, 2000. (in German).
Mueller G., Vogt K., Ponick B., Berechnung elektrischer Maschinen. Springer, 2007. (in German).
Electrical machines design. Edited by Kopylov O.P. Moscow: Energya. 1980. (in Russian).
ELCUT User Manual. Version 5.2. Private firm “TOR”. St.-Petersburg. 2005. (in Russian).
Binns K., Lawrenson P., Analysis and Computation of Electric and Magnetic Field Problems. Oxford: Pergamon Press, 1963.
Zienkiewicz O.C., Finite Element Method in Engineering Science. London; N.Y.: McGraw-Hill, 1971.
Gotter G., Erwaermumg und Kuehlung elektrischer Maschinen. Berlin, Goettingen, Heidelberg: Springer, 1954. (in German).
II. Induction Machines. Papers, Inventor’s Certificates, Patents
Demirchyan K.S., Boguslawsky I.Z., The calculation of the currents and the losses in the rotor short-circuited induction motor using the generalized characteristic of the rotor MMF. Electrichestvo, #5, 1980. (in Russian).
Antonov V.V., Boguslawsky I.Z., Savelyeva, M.G., Calculation of the characteristics of a powerful induction motor with non-linear parameters. In the book: Elektrosila, #35, 1984. (in Russian).
Antonov V.V., Boguslawsky I.Z., Kochetkova E.Yu., Rogachevskiy V.S., Method of steady state modes calculating of asynchronized synchronous generator. Elektrotechnika, #2, 1992. (in Russian).
Boguslawsky I.Z., Double power supplied asynchronous machine with converter in the rotor winding performance investigation method. Proceedings of the Int. Symp. UEES-01. Helsinki. 2001. (in Russian).
Korchagin N.V., Stepanov A.I., Boguslawsky I.Z., Veynger A.M., Ryabova T.S., Tsatskin A.Y., Problems of creating powerful four poles induction motors. Russian Engineering Research. 4. # 2008. (in Russian).
Antonov V.V., Boguslawsky I.Z., Lesokhin A.Z., Novik J.A., Semenov M.R. Asynchronous frequency controlled motor to drive the supercharger. In the book: Elektrosila, # 35, 1984. (in Russian).
Boguslawsky I.Z., Sikiryavy I.J., Method for solving nonlinear algebraic equations for the calculation of electric machines. In the book: Elektrosila, # 28, 1974.(In Russian).
III. Synchronous Machines. Papers, Inventor’s Certificates, Patents
Boguslawsky I.Z., Demirchyan K.S., Jigulin Yu.V., Lesokhin A.Z., The Pole of Synchronous Motor, Inventor’s certificate #817866, 1981. (in Russian).
Boguslawsky I.Z., Demirchyan K.S., Jigulin Yu.V., Lesokhin A.Z. The Armature of Synchronous Motor, Inventor’s certificate #915171, 1982. (in Russian).
Boguslawsky I.Z., The method of calculation of the screen on the pole shoe of low-frequency motor. Elektrotechnika, #8, 2004. (in Russian).
Boguslawsky I.Z., Generalized characteristics of currents and MMF of magnetically loops of rotor in A.C. machines. Proceedings of the Russian Academy of Sciences. Energetika, #5, 1995. (in Russian).
Boguslawsky I.Z., Magnetically coupled loops in A.C. machines under nonsinusoidal supply. Proceedings of the Russian Academy of Sciences. Energetika, #2, 1995. (in Russian).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 4.1: Screen Calculation Method of Large Low-Frequency Motor Pole Shoe
General The problem of field current distribution in a damper system of a powerful salient pole low-frequency motor (with shaft torque more than 50 T m) is of some interest in practical work. This system is designed as a screen (a rectangular conductive plate) and it is located at the rotor pole shoe [22–24]. Currents are induced by the mutual magnetic field in air gap. This design is effective for powerful low frequency machines. It is distinguished by its low level leakage flux between the poles [7–10] from the conventional design of damper system. The requirements to screen fields of higher order time harmonics generated by a stator circuit frequency inverter, as well as a field of negative phase-sequence in case of motor emergency modes (with its stator winding phase asymmetry, etc.) are only produced to the low-frequency motor damper system unlike the industrial frequency motor damper system. The synchronous starting is carried out for these motor types, so the damper winding is not used as a starting one.
Methods of calculating the screens at the poles, as set out in this appendix, can be used as a subroutine in the design of low speed high-power frequency-controlled motors with large values of the distortion factor of voltage and current waveforms.
Problem of determination. The screen dimensions are assumed to be specified parameters (Fig. 4.1): width FK = A = 2a; length FC = L = 2b; the screen thickness is assumed to be equal to h, where h << A; h << L. The origin of coordinates is located as follows: \( 0\le {\text{X}} \le 2{\text{a;}}\quad 0\le {\text{y}} \le 2 {\text{b}} . \) Note that the Y-axis direction coincides with the machine axis rotation direction. To simplify the design, no jumpers between the poles are installed. This screen is similar to incomplete damper winding of a salient-pole machine. The screen resistivity is equal to \( \uprho \), and the magnetic permeability—to \( \upmu_{ 0}. \) The ferromagnetic base (pole) resistivity is equal to \( \uprho_{{{\text{F{E}}}}} \) and its magnetic permeability—\( \upmu_{{{\text{F{E}}}}} \), while \( \uprho_{{{\text{F{E}}}}} \gg{ \rho } \). The mutual induction field lines in an air gap are taken as orthogonal to the screen surface and its ferromagnetic base. Stray fields of the screen laid on the ferromagnetic pole shoe surface are initially neglected unlike ordinary stray fields of a conventional damper winding, whose bars are laid in the semi-closed slots. Their accounting is described in Sect. 4.1.5.
The mutual flux coupled with a screen varies in an air gap sinusoidal. Now, the symbolic method [7, 8] is used. The flux density distribution in a gap of rotor coordinates can be presented as follows:
where \( \left| {{\text{B}}_{1} } \right| \) and \( {\text{B}}_{1} \)—amplitude and the corresponding complex flux density amplitude (phasor); \( \uptau \)—pole pitch, \( \upomega_{\text{ROT}} \)—screen current frequency; t—time; the flux density complex amplitude \( {\text{B}}_{1} \) is determined using the generalized MMF rotor characteristic from the magnetically coupled circuit theory [4–8, 15, 25, 26].
Now, the distributions of current I induced by the screen magnetic field (A.4.1.1): I = I(x, y) are found out. It is assumed in Sects. 4.6.1 and 4.6.2 that the screen element resistance does not depend on the temperature distribution in it. This dependence is taken into account in Sect. 4.6.4.
It is convenient to calculate the current distribution I using generalized characteristics, since the screen is a shorted circuit disposed on a rotor. Therefore, the currents I are determined with the help of the method outlined previously in this chapter with the accuracy up to the complex flux density value of the resulting field in an air gap. These currents I = I(x, y) are not enclosed in square brackets in order to make the notation simpler.
4.1.1 Simply Connected Domain
The method of solving this problem for a simply connected domain is considered: for the screen, made of a material with only one resistivity \( \uprho \), for example, without any- or additional soldered-in parts in it or structural openings; in this case:
The computational domain is subdivided into elements of the loop. Their number is chosen in such a way that it provides the practical calculation required accuracy of currents in a screen.
Regular grid
At first, the rectangular circuit elements with \( {\text{N}}_{\text{EQ}} = {\text{N}}_{\text{L}} {\text{N}}_{\text{W}} \) are chosen, where \( {\text{N}}_{\text{L}} ,{\text{N}}_{\text{W}} \)—number of elements along the screen length and width, correspondingly. It is expedient to subdivide the computational domain for this problem. Current components directed along the machine rotation axis (along the axis Y) are of the most practical interest. They form a flux in an air gap interacting with the stator winding flux.
The Maxwell equation [7, 8, 11, 12] is true for each element loop:

where e—electric field intensity; l—element part (the integration path); \( {\text{Q}} = \frac{{4{\text{AL}}}}{{{\text{N}}_{\text{EQ}} }} \)—rectangular element area.
If the mutual induction flow is changed according to (A.4.1.1), this equation is as follows:

(Hereinafter, the subscript “1 (one)” is omitted in the complex amplitude flux density \( \left. {{\text{B}}_{1} } \right) \).
Now the “mean value theorem (Lagrange)” [2, 3] is used. The right part of this equation can be presented for the arbitrary circuit TVWUT (Fig. 4.1) as follows:
where \( {\text{B}}^{ * } = {\text{Be}}^{{ - \frac{{{\text{j}}\uppi{\text{x}}_{\uppi}^{ * } }}{\uptau}}} \)—average value of flux density complex amplitude of arbitrary rectangular area element \( {\text{Q}}_{\Lambda } \), for example, TVWUT; \( {\text{x}}_{\Lambda }^{*} \)—abscissa of point “\( \Lambda \)”, where the flux density is equal to \( {\text{B}}^{ * } . \) This point is within the TVWUT circuit. Its position is determined according to the equation in Appendix 4.2. As it follows from the analysis, the point “\( \Lambda \)” can be combined with the gravity circuit center in practical calculations of the screen current field. Equation (A.4.1.2′) with (A.4.1.3) for TVWUT loop can be presented as:

Similar equations are true for other screen circuits.
Now, the concept of the current vector electric potential in the screen is used. The electric field intensity E in the element through the vector electric potential \( {\text{A}}^{\text{E}} \) [7, 8] can be presented as:
The ratio (A.4.1.5) is valid because the screen line currents are continuous and closed, so [7, 8]:
The vector components E in the chosen coordinate system are as follows:
Now, the difference approximation of Eqs. (A.4.1.4) and (A.4.1.7) is considered. The discrete vector values \( {\text{A}}^{\text{E}} \) are assigned to the screen element gravity centers (circuits), but not to the grid nodes, as it is sometimes taken in the numerical field calculations [13], for example in FEM (finite element method) [11–13].
One of the circuits, for example, the average TVWUT (Fig. 4.1) is chosen arbitrarily. The intensity vector components E along the axes X, Y are found for these circuit (mesh) portions TU, VW, VT, WU. They are required for making a line integral along these portions in accordance with (A.4.1.4). According to (A.4.1.7), the following is obtained:
For the portions TU: 
For the portions VW: 
For the portions TV:

For the portions WU: 
The parts along the axis are equal to: \( \Delta {\text{x}} = \frac{{2{\text{a}}}}{{{\text{N}}_{\text{W}} }};\quad \Delta {\text{y}} = \frac{{2{\text{b}}}}{{{\text{N}}_{\text{L}} }}. \)
Subject to the obtained Eq. (A.4.1.8) for tension components, Eq. (A.4.1.4) for an arbitrary circuit TVWUT is as follows:

After the conversing Eq. (A.4.1.9) for this arbitrary circuit TVWUT taking into account the tension component expressions presented in Eq. (A.4.1.8), the following equation is obtained:

The equations similar to (A.4.1.10) are written for other circuits belonging to the screen, for example, STURS, DEVTD,…. The number of such equations \( {\text{N}}_{\text{EQ}} \) is equal to that of circuits \( {\text{N}}_{\text{EQ}} = {\text{N}}_{\text{L}} {\text{N}}_{\text{W}} . \) They form a linear equation system with the imaginary right part, the unknown values of vector electric potentials, such as  are contained in the left part \( {\text{N}}_{\text{EQ}} . \) The methods for solving such systems are widely used in engineering practice [7, 8].
are contained in the left part \( {\text{N}}_{\text{EQ}} . \) The methods for solving such systems are widely used in engineering practice [7, 8].
Boundary conditions for the problem solution can be the electric potential vector invariant of the screen outer circuit CFKQC: \( {\text{A}}_{\text{CFKQC}}^{\text{E}} \) = const. Such a constant value can be “zero”.
Now, the physical interpretation of the obtained results can be considered in detail. The arbitrary portion (the rectangle side) of one of the circuits, for example, is the portion VW of circuit TVWUT. The first summand in Eq. (A.4.1.9) corresponds to this portion:

where \( \left( {\text{U}} \right)_{\text{VW}} \)—voltage between V and W nodes. Now, this expression is transformed as follows:

or

where  —circuit D.C. resistance limited by points 1234 in Fig. 4.1. This circuit has the length \( \Delta {\text{y}} \), width \( \Delta {\text{x}} \); its thickness is equal to h, and the resistivity—\( \uprho \). It must be assumed from the last expression analysis that both first cofactor terms in Eq. (A.4.1.11′)
—circuit D.C. resistance limited by points 1234 in Fig. 4.1. This circuit has the length \( \Delta {\text{y}} \), width \( \Delta {\text{x}} \); its thickness is equal to h, and the resistivity—\( \uprho \). It must be assumed from the last expression analysis that both first cofactor terms in Eq. (A.4.1.11′)

have the current dimension.
Now, dimension of the first summand in (A.4.1.12) is verified. It can be presented in the form of:

The second term dimension in (A.4.1.12) is similar. As a result, it is confirmed that the expression for \( {\text{I}}_{\text{VW}} \) in Eq. (A.4.1.12) also has the current dimension. Each of its terms is a vector. The first of them coincides in its direction with the vector  , the second—with the vector
, the second—with the vector  , correspondingly. The first summand is described as:
, correspondingly. The first summand is described as:

The vector of loop TVWUT as the mesh current. This vector has the current dimension. It characterizes physically the electric potential vector value  in the circuit (element) TVWUT. Similarly with (A.4.1.11′), the expression for the circuit VGHWV is valid as follows:
in the circuit (element) TVWUT. Similarly with (A.4.1.11′), the expression for the circuit VGHWV is valid as follows:

Thus, the branch current in the portion VW according to Eq. (A.4.1.12) is expressed in terms of the relations obtained for vectors (mesh currents) as follows:

The expressions for these mesh currents are used and the estimated equation for the selected circuit TVWUT is written down. Similar to (A.4.1.10), there is:

Here the D.C. resistance portion are calculated similarly (A.4.1.11′) for  . They are equal to:
. They are equal to:

Equations (A.4.1.15) and (A.4.1.16) are the formulation of the mesh current method [7, 8]. They can serve as a proof of its existence applied to this problem.
Two conditions are to be pointed out:
-
Equation (A.4.1.6) is carried out for an arbitrary grid point. It corresponds to the first Kirchhoff’s law at difference approximation of Eqs. (A.4.1.4) and (A.4.1.7). For example, there is an identity for the node T:
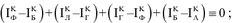 (A.4.1.6′)
(A.4.1.6′) -
for near-boundary areas (portions), for example, for the portion CD (Fig. 4.1), the D.C. resistance is calculated as follows: \( {\text{R}}_{\text{CD}} = \frac{{2\uprho\Delta {\text{x}}}}{{{\text{h}}\Delta {\text{y}}}}, \) and for the portion GH: \( {\text{R}}_{\text{GH}} = \frac{{2\uprho\Delta {\text{y}}}}{{\Delta {\text{xh}}}}. \)
Equations for other circuits, e.g., STURS, DEVTD, are similar (A.4.1.16). Their numbers are equal to the circuit numbers \( {\text{N}}_{\text{EQ}} \). They form a linear equation system with an imaginary right part containing in the left part some unknown mesh current values \( {\text{N}}_{\text{EQ}} \), as well as the equation system for vector electric potential. Branch currents in the screen portions are calculated using the expressions similar to (A.4.1.15).
The same mesh current value on the outer boundary of the screen CFKQC: \( {\text{I}}_{\text{CFKQCK}} \) = const can serve as a boundary condition for solving the current distribution problem. Such a constant value can be “zero”.
Note that in practice the mesh current method is generally set forth [7, 8] as a calculation sequence for a specific circuit selected as an example. At the same time we take all the assignments with regard to the circuit calculation method; pre-selection “direction of path tracing” and the assignment on dependence of sign of the “mutual impedance” (impedance of the branch between two adjacent meshes) of the circuits; use of Kirchhoff’s equations for mesh currents, instead for branch currents; sequence of calculations branch currents using mesh currents etc.). They are all derived from the Maxwell equations according (A.4.1.1)–(A.4.1.16).
Now, we will sum up the results obtained in this section:
-
the branch current distribution in the screen is set on the basis of equations linear system solutions with the imaginary right part either for the electric current vector potential of the type (A.4.1.10) or for mesh currents of the type (A.4.1.16);
-
the assumptions taken in the mesh current calculation sequence [7, 8] are confirmed for the problem under consideration by Eqs. (A.4.1.15), (A.4.1.16), (A.4.1.11′) and (A.4.1.16′).
Irregular triangular grid
Now, for the screen current distribution problem we use an irregular grid, e.g., consisting of triangular elements. The portions, bounding each triangle in the grid can be not only straight, but also curved. It is expedient in practice to use such grids instead of rectangular ones, when it is necessary to specify the current distribution in certain screen parts, or when some computational domain section forms are different from the square ones. The triangular grid consisting of \( {\text{N}}_{\text{EQ}} \) circuits (loops) is shown in Fig. 4.2. The circuits are limited by straight portions.
Now, one of its elements, such as BEDB is chosen. Equation (A.4.1.4) for this circuit have a form similar to (A.4.1.9)

where  —average value of flux density complex amplitude at the point “
—average value of flux density complex amplitude at the point “ “ of arbitrary triangular circuit BEDB of area
“ of arbitrary triangular circuit BEDB of area  according to Eq. (A.4.1.3).
according to Eq. (A.4.1.3).
It is easy to show in practical screen current field calculations that the point “ ” by \( {\text{N}}_{\text{EQ}} \to \infty \) can be combined with the triangular circuit gravity center, as well as the rectangular one discussed earlier. Equation (A.4.1.5) for the vector electric potential \( {\text{A}}^{\text{E}} \) applied to the triangular grid is written similar to Eq. (A.4.1.8) for the rectangular one:
” by \( {\text{N}}_{\text{EQ}} \to \infty \) can be combined with the triangular circuit gravity center, as well as the rectangular one discussed earlier. Equation (A.4.1.5) for the vector electric potential \( {\text{A}}^{\text{E}} \) applied to the triangular grid is written similar to Eq. (A.4.1.8) for the rectangular one:

Here  .
.
After conversing Eq. (A.4.1.17) with taking into account Eq. (A.4.1.18), the following is obtained:

The D.C. resistances of the triangular grid portion in Eq. (A.4.1.19) are equal to:

with ЛГ, ЛД, ЛM,ЛБ—according (A.4.1.18).
The number of these resistances is equal to that of triangle portions in the calculated area. Note that the resistance for the “border portion”, for example, the portion BC is calculated as follows:

Now, the vectors of electric potentials in Eq. (A.4.1.19) are called as mesh currents. This is similar to Eq. (A.4.1.14) for a rectangular grid:

After transforming Eq. (A.4.1.19) and considering (A.4.1.21), one of the equations of the mesh current calculation system is obtained:

The equations similar to (A.4.1.22) are also valid for the remaining triangular circuits, for example, BAEB, BFCB,…. The number of such equations \( {\text{N}}_{\text{EQ}} \) is equal to that of circuits (meshes). They form a linear equation system with the imaginary right part, containing \( {\text{N}}_{\text{EQ}} \) vectors of electric potential unknown values in the left part, such as  or the corresponding mesh currents
or the corresponding mesh currents  .
.
Equation (A.4.1.6) is valid for a grid arbitrary node, as well as the rectangular or triangular one. It corresponds to the first Kirchhoff’s law at difference approximation of Eqs. (A.4.1.4) and (A.4.1.7). For example, there is the following identity for the node F:

The use of a triangular mesh does not affect the boundary condition formulation for solving the current distribution problem, as it is the same used for a rectangular grid. For example, the conditions for the area shown in Fig. 4.2 are as follows: \( {\text{I}}_{\text{BLHCB}}^{\text{K}} = {\text{const}}. \) This constant value can be “zero”.
The branch currents are calculated after solving this linear equation system \( {\text{N}}_{\text{EQ}} \) in accordance with ratios arising from (A.4.1.19) and (A.4.1.21):

Thus, the following additional results are obtained using the triangular grid (as compared to rectangular grid):
-
the calculation expressions for estimating branch currents in screen grid portions through the electric circuits vector potential values or through the mesh current values remain unchanged;
-
also, the equations expressing mesh currents in grid elements through the vector electric potential values at their gravity centers also remain unchanged;
-
the assumptions usually made in the mesh current method are confirmed by Eqs. (A.4.1.21), (A.4.1.22) and (A.4.1.23).
Consequently, the use of vector electric potential and its value assignment (or the mesh current value) not to the nodes, but to the grid circuit mesh gravity centers allows reducing it to the electric circuit calculations for solving screen current problems numerically.
This requires solving the linear equation system. It helps prevent the variational problem implementation [11–13], as it is accepted in the FEM.
The electric circuit calculation methods are widely used in engineering practice. It allows us to use the experience gained in dealing with similar problems.
4.1.2 Multiply Connected Domain
Now, the method of solving this problem for multiply connected domains is considered: for the screen made of different resistivity materials, for example, with some additional soldered-in parts or structural holes. In this case,
The computational domain is subdivided into elements (circuits). Their number is determined in order to provide the necessary accuracy of screen current calculations.
Regular grid
The elements in the rectangular circuit forms similar to those described in Sect. 4.6.1.1 for a simply connected domain (A.4.1.1′) are chosen. The obtained results can be used in this section for multiply connected domains (A.4.1.24), provided that the equivalent resistive portions for the coefficients (resistivity) of the unknown mesh currents in the system consisting of Eq. (A.4.1.16) are calculated from the ratios of the type 

Similarly, the coefficients are calculated for the remaining resistivity equation system of the type (A.4.1.16). Note that the resistivities are calculated for near-boundary areas, for example, the segment CD, thus: \( \uprho_{\Phi }^{\text{EQ}} = 2\uprho_{\Phi } \) and for the segment GH: 
Irregular grid with triangular elements
The elements in the form of triangular circuits are similarly chosen to those described in Sect. 4.1.1 for a simply connected domain (A.4.1.1′). The results obtained therein may be used in this section provided that the coefficients (resistance) in the system consisting of Eq. (A.4.1.22) calculated taking into account the equivalent resistivity circuit domains are as follows 

Similarly, the coefficients are calculated for the remaining D.C. resistance equations system in (A.4.1.22).
Note that the D.C. resistance of these portions is calculated in the same way as in Sect. 4.1.1 for a simply connected domain (Eq. A.4.1.20′) for the near-border portions, for example, the portion BC, forming the simply connected circuit domain, for example, the circuit BFCB.
4.1.3 Irregular Grid with Arbitrary Configuration Elements
The results obtained in previous sections for the vector electric potential, mesh currents and circuit resistances can also be used to calculate the current distribution in a screen divided not only into rectangular or triangular elements, but also into other configuration elements. It is assumed that the part of these elements can be not only straight, but also curved, e.g., the parabolic portions.
The principal point of using these results is Eq. (A.4.1.3), which determines the flux density B* estimated value of each mesh with the help of the Lagrange’s mean value theorem [2, 3].
4.1.4 The Screen Element D.C. Resistance Depends on the Temperature Distributed in It (Nonlinear Problem); the Domain Is Simply—Or Multiply Connected
When the screen is flown around by the currents, induced by the mutual induction field in an air gap, the temperature \( \uptheta \) distribution in screen elements is not uniform. Accordingly, the resistivity of these elements is not the same even for a simply connected domain, so \( \uprho =\uprho\left( {{\text{x, y}}, \uptheta} \right), \) wherein the dependence of circuit resistivity \( \uprho \) on temperature is expressed by the ratio: \( \uprho_{\Theta } =\uprho_{0} \left( { 1+\uprho^{*}\uptheta} \right), \) where \( \uprho_{0} \)—circuit conductor resistivity at \( \uptheta = 0^{ \circ } {\text{C,}}\,\uprho^{ * } \)—high-resistivity temperature coefficient. Therefore, it is necessary to find simultaneously the temperature distribution in screen elements (circuits) in the steady state thermal mode in order to calculate the current distributions.
Practically, it is expedient to determine the steady state temperature and current elements as asymptotes to which they aspire in their transient thermal mode during the time \( \text{t} \to \infty \text{.} \) It is assumed that in initial state the screen is not flown by currents initially (no mutual induction field), the temperature of all the elements is equal to the ambient temperature \( \uptheta_{\text{AMB}} . \). Then the screen is exposed to the mutual induction field (A.4.1.1), and various resistivity and temperature value are fixed in all elements at \( \text{t} \to \infty \text{.} \)
The temperature rise process in the screen circuits (elements) can be presented as a differential equation system of the type [14] for each mesh, for example for mesh Л:

where
-
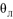 :
: -
element overheating
-
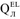 :
: -
losses evolved in time t
-
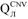 :
: -
losses allocated from the element by convection
-
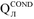 :
: -
losses allocated to the adjacent element (entering the element) by thermal conductivity
- c:
-
screen element specific heat
-
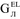 :
:
The initial conditions for this system from \( {\text{N}}_{\text{EQ}} \) first order differential equations are formulated as follows: the temperature of all screen elements is \( \uptheta =\uptheta_{\text{AMB}} \) at t = 0. Note that there are known solutions [24] of selecting the system integration step \( \Delta {\text{t}} \) from Eq. (A.4.1.27), its stability and convergence problems associated with choosing this step.
The determination of steady state screen temperature elements (circuits) as the transient thermal mode asymptotes assumes an alternate solution of two problems for each time t: the current distribution problem using the equation systems (A.4.1.16) or (A.4.1.22); the temperature distribution problems using the equation system of type (A.4.1.27).
4.1.5 Screen Element Reactance Accounting
The following should be noted formulating the current calculation problems. Unlike ordinary damper winding stray fields, whose bars are laid in the semi-closed slots, the stray fields of conductive screen laid on the pole shoe ferromagnetic surface are initially neglected.
The D.C. resistance is only taken into account, for example, the D.C. resistance \( {\text{R}}_{\text{BE}} \) of the triangular grid portion BE (Fig. 4.2).
However, it is expedient to consider these fields in general, for example, at high screen current frequency \( \upomega_{\text{ROT}} . \) Note that the symbolic method [7, 8] is used in Sects. 4.1.1 and 4.1.2 presenting the harmonic functions of mutual flux, electric field intensity, and screen currents. If necessary, these peculiarities allow taking into account the leakage field data and corresponding screen reactance circuits (elements).
If it is used, the equations for both Kirchhoff’s laws remain valid in general case, when each part of the chain domain contains not only the D.C. resistance, but also the complex one. For example, the triangular grid portion BE is complex and equal to the impedance \( {\text{Z}}_{\text{BE}} \) [7, 8].
Without any additional assumptions, these symbolic method features allow writing the linear equation system value \( {\text{N}}_{\text{EQ}} \) derived in Sects. 4.1.1 and 4.1.2 as follows:
Using a rectangular grid in the form of:

Using a triangular grid in the form of:

Appendix 4.2: Determination of Average Flux Density Point Location by “Mean Value Theorem (Lagrange)” [2, 3]
The original equation is:
where \( 1 < {\text{N}} \le {\text{N}}_{\text{W}}; 0 < {\alpha < 1}\text{.} \) The ratio for determining the number α is obtained from the equation:
The analyzed equation results are as follows: at the \( \frac{{\Delta \text{x}}}{\uptau} \le 0.01 \) value \( \upalpha \approx \text{0}\text{.5} \) is obtained. Thus, the point “Л” coincides with the rectangular circuit gravity center.
Appendix 4.3: Equivalent Circuit of Powerful Induction Motors Operating in Nonlinear Networks
Additional indications:
-
\( {\text{m}}_{\text{ST}} ,{\text{m}}_{\text{ROT}} \)—stator and rotor winding phase numbers, respectively;
-
\( {\text{P}}_{1} \)—network consumed power;
-
\( {\text{P}}_{2} \)—motor shaft power;
-
\( \sum {\text{Q}} \)—amount of losses for calculating magnetization current active component \( {\text{I}}_{\text{A}} \);
-
\( {\text{Q}}_{{1,{\text{OHM}}}} ,{\text{Q}}_{{2,{\text{OHM}}}} \)—stator and rotor winding D.C. losses;
-
\( {\text{R}}_{{1,{\text{OHM}}}} ,{\text{R}}_{{2,{\text{OHM}}}}^{\prime } \)—D.C. resistance of stator winding phase and rotor winding equivalent phase.
Problem statement A number of assumptions [4, 6–8] are used when calculating electromagnetic loads and performance of industrial frequency powerful motors operating in linear networks. In these assumptions we take into account neither mechanical losses (for ventilation, in bearings) very significant for powerful motors, nor consider them approximately.
The losses in stator winding A.C. resistance are taken approximately within the frameworks of these assumptions. It is approximately assumed in calculating the inductive current component \( {\text{I}}_{\upmu} \) of the magnetizing circuit and the secondary circuit current \( {\text{I}}_{2}^{\prime } \) that the EMF at its terminals is \( {\text{E}} \approx \left( {0.93 - 0.97} \right){\text{U}}_{\text{PH}} \) depending [9, 10] on pole numbers (2p = 4–10). The active magnetizing circuit component \( {\text{I}}_{\text{A}} \) is also calculated using approximate ratios derived on the basis of some assumptions.
All the assumptions are based on the experience of serial motor design and operation. However, these assumptions lead to errors in current calculation results loses and motor shaft power losses in circuits with increasing electromagnetic load levels of industrial motor use. For example, the power balance is disturbed when a rotor is locked \( \left( {{\text{S}}_{\text{SL}} = 1} \right) \): power consumption turns out to be not equal to the estimated amount of losses dissipated in its circuits [10]. This contradicts the problem physical conditions, etc. These assumptions lead to additional errors in calculation results of powerful frequency-controlled asynchronous motors and induction generators operating with frequency converters.
So, the practical task is to clarify the magnetizing circuit parameters, as well as parameters of stator and rotor circuits at powerful asynchronous machine with an increased level of electromagnetic load by accounting the distribution of main and additional losses in it.
4.3.1 Basic Equations of Powerful Asynchronous Machine Substitution Patterns \( \left( {{\varvec{Q}}_{{{\varvec{TIM}}}} \ge {\varvec{1}}} \right) \)
Note preliminarily that the procedure of EMF time harmonic and current order is denoted by the letter \( \text{Q}_{{\text{TIM}}} \) unlike other sections. This is due to the fact that the machine losses are marked here with the letter Q.
Now, we consider the equation system for calculating electromagnetic loads and performance characteristics of powerful frequency-controlled induction machines in motor mode for the harmonic order \( \text{Q}_{{\text{TIM}}} \ge 1 \) of the supply voltage. They correspond to the T-shape circuit for m = 1 [4–8] written for the effective current values, EMF and voltages.
The expression for network consumed total power is written additionally to the equation system (4.13)–(4.18) for magnetically coupled stator and rotor circuits. The following is obtained for the power \( {\text{P}}_{1}^{\prime } \) consumed by the primary winding (stator) phase and the secondary stator-reduced winding (rotor) phase at \( \text{Q}_{{\text{TIM}}} = 1: \)
where \( \left( {{\text{I}}_{1} } \right)^{ * } \)—complex conjugated with complex \( {\text{I}}_{1} \); the conjugated complexes \( \left( {{\text{I}}_{0} } \right)^{ * } ,\left( {{\text{I}}_{2}^{\prime } } \right)^{ * } \) are marked similarly.
Note that the real part of the component expression \( {\text{P}}_{1}^{\prime } \) is equal to the active component \( \left( {{\text{P}}_{1}^{\prime } } \right)_{\text{A}} \) of network power consumption and its imaginary part—to the reactive component \( \left( {{\text{P}}_{1}^{\prime } } \right)_{\text{R}} \) of this power:
Now, three summands in (A.4.3.1) of network totally-consumed power \( {\text{P}}_{1}^{\prime } \) are considered in detail.
The first of them corresponds to the total power consumed by the primary circuit phase (stator):
The second summand in (A.4.3.1) corresponds to the total power consumed by the magnetizing circuit. Considering Eq. (4.16), the following is obtained:
The third term in (A.4.3.1) corresponds to the total power consumed by the secondary circuit phase (rotor) reduced to a stator winding:
where \( \left| {{\text{Z}}_{2}^{\prime } } \right| = \sqrt {\left( {\frac{{{\text{R}}_{2}^{\prime } }}{{{\text{S}}_{\text{SL}} }}} \right) + \left( {{\text{X}}_{2}^{\prime } } \right)^{2} } . \)
Note that the total power \( {\text{P}}_{1,3} \) consumed by the \( {\text{m}}_{\text{ST}} \) phases of secondary circuit reduced to a stator winding can be presented as [4–6, 9]:
where
As a result, the expression for active power \( \left( {{\text{P}}_{1} } \right)_{\text{A}} \) consumed by the machine from network (with phase numbers of stator winding \( {\text{m}}_{\text{ROT}} \) and rotor winding \( \left. {{\text{m}}_{\text{ROT}} } \right) \) is obtained:
Accordingly, the expression for the reactive power \( \left( {{\text{P}}_{1} } \right)_{\text{R}} \) is as follows:
Note. According with (3.1) in the basic system (4.13)–(4.18) we have to, instead of the value \( {\text{U}} = {\text{U}}_{\text{PH}} = {\text{U}}_{1} \,\left( {{\text{Q}}_{\text{TIM}} = 1} \right), \) use the value \( {\text{U = U}}_{\text{Q}} \) for high time harmonics \( \left( {{\text{Q}}_{\text{TIM}} > 1} \right). \)
4.3.2 Machine Circuit Losses Components and Shaft Power
Now, the power balance is discussed. The condition is when the motor-consumed network power is equal to the sum of losses dissipated in its circuits and the developed motor shaft power should be found out analytically by \( {\text{Q}}_{\text{TIM}} = 1. \)
For the beginning, the first special case, namely the mode \( {\text{S}}_{\text{SL}} = 1 \) is considered. As it follows from the obtained Eq. (A.4.3.6), the calculated power value \( \left( {{\text{P}}_{{1,3{\text{SH}}}} } \right)_{\text{A}} \) is equal to “zero” at \( {\text{S}}_{\text{SL}} = 1. \) The expression for the machine network-consumed active power \( \left( {{\text{P}}_{1} } \right)_{\text{A}} \) at \( {\text{S}}_{\text{SL}} = 1, \) \( {\text{Q}}_{\text{TIM}} = 1 \) is as follows:
As it follows from a comparison of Eqs. (A.4.3.6) and (A.4.3.7):
-
(a)
The power balance is achieved at \( {\text{S}}_{\text{SL}} = 1 \) in (A.4.3.7): the calculated machine network-consumed active power \( \left( {{\text{P}}_{1} } \right)_{\text{A}} \) (at \( \left. {{\text{S}}_{\text{SL}} = 1} \right) \) is equal to the amount of losses \( \left( {{\text{P}}_{1,1} } \right)_{\text{A}} ;\left( {{\text{P}}_{1,2} } \right)_{\text{A}} ;\left( {{\text{P}}_{{1,3{\text{L}}}} } \right)_{\text{A}} \) scattered in its circuits only with a proviso that the component \( \left( {{\text{P}}_{1,2} } \right)_{\text{A}} \) is calculated from the ratio:
As it follows from (4.17), this component is equal to the sum of losses \( \sum {{\text{Q:}}\left( {{\text{P}}_{1,2} } \right)_{\text{A}} = \sum {{\text{Q}} .} } \) This amount includes the losses that are not proportional to the machine circuit currents square \( {\text{I}}_{1} \,{\text{and}}\,{\text{I}}_{2}^{\prime } \), for example, no-load losses in stator and rotor cores;
In practical calculations we usually accept in the basic system (4.13)–(4.18) for high time harmonics \( \left( {{\text{Q}}_{\text{TIM}} > 1} \right) \):
-
(b)
The regularities obtained in the equation analysis (A.4.3.7) for \( {\text{S}}_{\text{SL}} = 1 \) are preserved at \( {\text{S}}_{\text{SL}} \ne 1 \) in (A.4.3.6). The power balance takes place in this mode, when the following additional conditions are observed:
-
for \( {\text{Q}}_{\text{TIM}} = 1 \) the mechanical losses (for ventilation, in bearings), whose value is also not proportional to the machine circuit currents square \( {\text{I}}_{1} \,{\text{and}}\,{\text{I}}_{2}^{\prime } \), should be included in the amount of losses \( \sum {\text{Q}} \) in addition to the above-mentioned losses. These losses are dissipated as heat energy as well as the winding losses. It can be assumed conditionally that:
-
the component \( \left( {{\text{P}}_{{1,3{\text{SH}}}} } \right)_{\text{A}} = {\text{m}}_{\text{ROT}} \left| {{\text{I}}_{2} } \right|^{2} {\text{R}}_{2} \frac{{1 - {\text{S}}_{\text{SL}} }}{{{\text{S}}_{\text{SL}} }} \) corresponds to the power available at the machine shaft: \( \left( {{\text{P}}_{{1,3{\text{SH}}}} } \right)_{\text{A}} = {\text{P}}_{2} . \)
-
Thus, expanding the equation system (4.13)–(4.18) for magnetically coupled circuits with Eq. (A.4.3.6) for the network-consumed motor total power, the conditions are derived analytically, under which the arbitrary slip power balance \( {\text{S}}_{\text{SL}} \) is fulfilled: the active network-consumed power \( \left( {{\text{P}}_{1} } \right)_{\text{A}} \) is equal to the sum of losses dissipated in the motor circuits and the power \( \left( {{\text{P}}_{{1,3{\text{SH}}}} } \right)_{\text{A}} = {\text{P}}_{2} \) developed on the shaft.
The error arises in determining the magnetizing current effects on the calculation results of the currents distributions \( {\text{I}}_{1} \,{\text{and}}\,{\text{I}}_{2}^{\prime } \) and, consequently, on the calculated values of losses and on the motor efficiency, as well as the power \( {\text{P}}_{2} \). Besides, this error affects the estimated value of the magnetizing circuit reactance \( {\text{X}}_{\upmu} \) and, hence, the motor power factor \( { \cos }{\upvarphi } \).
4.3.3 Additional Losses and Equivalent Circuit Impedances
The following ratios for the equation system parameter calculations are obtained from Eqs. (A.4.3.6) and (A.4.3.7):
-
the methods of A.C. resistance calculation taking into account the skin effect [4–6, 9] (Field’s factor) are given for different constructions of stator windings in Chap. 23, for different constructions of rotor bars—in appendix of Chap. 23;
-
the active current magnetization value \( \left| {{\text{I}}_{\text{A}} } \right| \) is determined for \( {\text{Q}}_{\text{TIM}} { = 1} \) with the losses according to Eq. (4.17), for \( {\text{Q}}_{\text{TIM}} { > 1} \)—with the losses based on Eq. (A.4.3.8′).
At \( {\text{Q}}_{\text{TIM}} { > 1} \) the relationship between the magnetizing circuit EMF \( \left| {\text{E}} \right|_{{{\text{Q}}_{\text{TIM}} { = 1}}} \) and the magnetization current \( \left| {{\text{I}}_{\upmu} } \right|_{{{\text{Q}}_{\text{TIM}} { = 1}}} \) is convenient to present [3] in the form:
The asterisk (**) denotes the derivative at the main magnetization characteristics \( \left( {{\text{Q}}_{\text{TIM}}} = 1\right) \) corresponding to the EMF \( \left| {\text{E}} \right|_{{{\text{Q}}_{\text{TIM}} { = 1}}} \).
As for large asynchronous machines, their losses \( {\text{Q}}_{\text{AD}} \,{\text{at}}\,{\text{Q}}_{\text{TIM}} { = 1} \) are estimated by the method commonly used in practice [10]:
where \( {\text{P}}_{{2,{\text{RAT}}}} \)—rated motor power.
The test results of powerful serial asynchronous motors confirm that additional losses QAD are usually close in rated mode to the estimated values calculated from (A.4.3.9). The rated mode is understood as the mode with rated shaft power, rated network frequency and rated torque.
Note that the aforementioned condition is met in (A.4.3.9): the estimated losses QAD do not depend on the machine circuit currents squares \( {\text{I}}_{1} \,{\text{and}}\,{\text{I}}_{2}^{\prime } . \)
In recent years, it is required to clarify the calculated value QAD in (A.4.3.9) due to the increased level of electromagnetic load of modern machines including the frequency-controlled motors. This is especially applied to modern frequency-controlled motors: it is necessary to calculate the following operational modes for such motors:
-
with a rated torque supported throughout the control range. The machine power and frequency are not retained rated in this range;
-
with rated power maintained throughout the control range. The machine torque and frequency are not retained rated in this range.
Note that the losses QAD are not the same in these operating modes and they do not remain constant with frequency network changes, so it is impossible to use Eq. (A.4.3.9) for their calculations: it is not confirmed by the test results.
Researching the components included in the losses QAD, it is taken into account that they are actually determined by MMF and the magnetic flux in air gap [4–6].
These components are as follows:
-
no load losses determined by the harmonics of magnetic flux in air gap, for example, the rotor circuit losses caused by stator tooths;
-
load losses determined by MMF currents of stator and rotor circuit harmonics, for example, magnetic flux leakage losses in stator and rotor cores, in stator winding and in rotor bars.
It is necessary to separate the additional losses in this case:
-
no load losses QAD(NO LOAD). To determine the value \( \sum {\text{Q}} \) they are summed up to the main losses in stator and rotor cores, and at \( {\text{Q}}_{\text{TIM}} { = 1} \)—also with the mechanical losses (for ventilation, in bearings);
-
current dependent losses QAD(ST) and QAD(ROT) in stator and rotor windings (from the leakage field \( {\text{Q}}_{\text{TIM}} \ge 1 \) [4–6, 10]). These losses determine the operation mode overheating; they are considered during the calculation of the impedances of these windings. It should be noted that there are some additional losses in rotor bars under load (with account of the skew slots) comprising two components [10], one of which is dependent on the stator current square, and the second—on the rotor current square at the slot skewing of rotor short-circuited winding.
Brief Conclusions
-
1.
The equation system can be used for magnetically coupled circuits, whose solution is expedient to be performed by the iteration method for calculating the A.C. machine mode, and whose design foresees several short-circuited windings lumped on a rotor.
-
2.
The method feature is that the EMF currents, MMF rotor shorted circuits are calculated in the form of generalized characteristics, i.e., to the resultant field induction amplitude in air gap. The flux density itself is calculated by iteration on the basis of the stator winding specified voltage.
-
3.
These generalized characteristics of EMFs, currents, MMF of squirrel cage for a specific slip \( {\text{S}}_{\text{SL}} \) and the chosen rotor design can be regarded physically as the similarity criteria. They characterize the amplitudes of EMF, currents and MMF in the flux density scale amplitude \( {\text{B}}_{1} . \) They determine the rotor winding reaction, when it is subjected by the flux density amplitude equal to \( {\text{B}}_{1} \) in steady state mode.
-
4.
The current distribution calculation method in the screen on the low-frequency motor pole has the following features:
-
The current distribution is determined subject to its parameters (the screen conduction, its thickness, etc.) of the linear equation system solution either for the vector electric potential or mesh currents.
-
The method enables us to solve the current distribution problems in the screen, in which A.C. resistance depends on its temperature. It is convenient to obtain the solution as the thermal transient process asymptote.
-
The following is obtained with the help of the vector electric potential using electromagnetic field equations in the integral form. The assumptions accepted in the mesh current calculation method are valid for calculating the current screen for a computational grid of arbitrary shape. At the same time the relationship between the fictitious current circuit of arbitrary shape (mesh current) and the vector potential averaged within the same circuit is established.
-
-
5.
The conditions are found out analytically under which the power balance for the arbitrary slip \( {\text{S}}_{\text{SL}} \) is carried out for powerful asynchronous motors powered from the linear network or the frequency inverter. These conditions are obtained on the basis of the magnetically coupled circuit equations and the additional equation for the power, consumed by the motors from the power network.
List of Symbols
- AE :
-
Vector electric potential
- А:
-
Width of screen
- L:
-
Length of screen
- h:
-
Thickness of screen
- B1 :
-
Magnetic flux density amplitude of mutual flux in air gap
- E:
-
Electric field intensity
- \( {\text{E}}_{{{\text{N}} + 1,{\text{N}}}} \) :
-
EMF of loop
- F0 :
-
MMF magnetic circuit complex amplitude (phasor) corresponding to the flux \( \Phi _{0} \)
- F1, F2, F3 :
-
MMF of loops on the rotor according to the currents I1, I2, I3
- IA, Iμ :
-
Active and reactive components of magnetization current
- I0, I1, I ′2 :
-
Currents in the equivalent T-shape circuit
- I ′2 :
-
Reduced to stator winding
- JB, IR :
-
Currents in elements of short-circuits winding on the rotor
- k:
-
Number of iteration
- kCART, kSAT :
-
Carter’s factor and saturation factor accordingly
- L1,S, L2,S, L3,S :
-
Leakage inductance of rotor loops
- LCOR :
-
Core length
- m:
-
Number of spatial harmonic
- mPH,ST, mPH,ROT :
-
Stator an rotor winding phases number accordingly
- N0 :
-
Number of rotor meshes
- p:
-
Number of pole pairs
- Р1 :
-
Power consumed from network
- Р2 :
-
Power on the motor shaft
- PCOR, РMECH, РAD :
-
Losses in core, mechanical and additional losses accordingly
- Q:
-
Value of screen mesh square
- QTIM :
-
Number of time harmonic
- Q1,OHM, Q2,OHM :
-
D.C. losses in stator and rotor respectively
- ΣQ:
-
Summarized losses for the calculation value of IА
- R1, R2, R3 :
-
A.C. resistance of rotor circuits
- R1,OHM, R ′2,OHM :
-
D.C. resistances of stator and rotor phase windings
- Xμ :
-
Magnetizing circuit inductance
- SSL :
-
Slip
- TEL :
-
MMF expansion period
- UPH :
-
Phase circuit voltage
- W1, KW1; W2, KW2; W3, KW3 :
-
Number of circuit turns of three contours and their winding coefficients
- Z1, Z ′2 :
-
Primary and secondary circuit impedances
- ZB, ZR :
-
Impedances of bar and portion of short-circuited ring
- δ:
-
Equivalent air gap
- ε:
-
Accuracy of iteration method
- μ0 :
-
Air magnetic permeability
- ρ:
-
Specific resistivity of shield
- τ:
-
Pole pitch
- Ф0 :
-
Flux complex amplitude (phasor) in an air gap
- ψ2:
-
Angle between positive direction of vector I ′2 and real line
- ψE :
-
Angle between positive direction of vector E and real line
- ωREV :
-
Angular frequency of rotor rotation
- ω1 :
-
Circular frequency of network
Rights and permissions
Copyright information
© 2017 Springer Japan KK
About this chapter
Cite this chapter
Boguslawsky, I., Korovkin, N., Hayakawa, M. (2017). Peculiarities of Currents Investigation in Magnetically Coupled Circuits for A.C. Machines with Short-Circuited Rotor Windings. In: Large A.C. Machines. Springer, Tokyo. https://doi.org/10.1007/978-4-431-56475-1_4
Download citation
DOI: https://doi.org/10.1007/978-4-431-56475-1_4
Published:
Publisher Name: Springer, Tokyo
Print ISBN: 978-4-431-56473-7
Online ISBN: 978-4-431-56475-1
eBook Packages: EngineeringEngineering (R0)



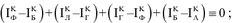

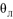 :
: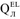 :
: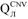 :
: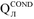 :
: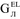 :
: