Keywords

1 Introduction

Molecular brain imaging with positron emission tomography (PET) using radiolabeled ligands (radioligands) that target neuroreceptors/transporters and neuropathological biomarker proteins such as amyloid β (Aβ) proteins and pathological tau proteins has many exciting clinical and research applications. The major advantage of PET imaging is that PET using suitable radioligands allows for the accurate quantification of the target binding site density. For accurate PET quantification, however, a good understanding of the in vivo pharmacokinetics of radioligands is important.

For many reversibly binding radioligands for which there exists a brain region devoid of molecular target binding sites called “reference tissue,” data analysis methods that do not require blood data including the standardized uptake value ratio (SUVR) method and reference tissue models to estimate binding potential (BP ND) are commonly used to quantify specific molecular target binding sites. The validity of these simple methods can be evaluated by detailed pharmacokinetic modeling of dynamically acquired PET data and radiometabolite corrected arterial plasma parent radioligand activity as an input function. In this respect, it is generally believed that radioligands should not ideally produce metabolites that can enter the brain because they might complicate accurate quantification of specific binding of the parent radioligand.

The purpose of this article is to show that PET quantification using the SUVR and reference tissue model methods can also be valid even when the metabolite contributes to the measured brain radioactivity. In the theory section, the concept of PET measured “brain tissue ratios” in the context of radiometabolites entering the brain will be explored first, and then our recent PET data analysis approach for a novel radioligand, 11C-PBB3 (2-((1E,3E)-4-(6-(11C-methylamino)pyridin-3-yl)buta-1,3-dienyl) benzo[d]thiazol-6-ol) [1], to quantify pathological tau accumulations in the brain of Alzheimer’s disease (AD) [2] will be highlighted as an example in which the SUVR and reference tissue model methods were validated by the dual-input graphical analysis model [3] that takes into account the contribution of the radiometabolite entering the brain.

2 Materials and Methods

2.1 Theory

PET data in molecular brain imaging are commonly analyzed by applying kinetic compartment models, which assume a compartmental system and derive the target binding parameters that reflect the densities of target binding sites in brain regions of interest (ROIs) [4]. Brain regions containing target binding sites (target tissue) have at least three compartments (or two-tissue (2T) compartments) (Fig. 17.1a top). The first compartment is the arterial plasma (C a), from which the unmetabolized parent radioligand passes into the second compartment or the first tissue compartment known as the nondisplaceable compartment (C ND). The third compartment or the second tissue compartment (C S) is the specific target binding sites. Reference tissue regions do not have the specific binding compartment (C S) (Fig. 17.1a bottom). In Fig. 17.1a, K 1 (mL⋅mL−1⋅min−1) is the delivery rate constant; k 2 (min−1), k 3 (min−1), and k 4 (min−1) are the first-order kinetic rate constants. Throughout the text, the prime sign is used to indicate the reference tissue. \( {C}_{\mathrm{B}}(t)={C}_{\mathrm{ND}}(t)+{C}_S(t) \) and \( {C}_{\mathrm{B}}^{\prime }(t)={C}_{\mathrm{ND}}^{\prime }(t) \) represent the target and reference tissue time activity, respectively, and C a (t) is the plasma parent radioligand activity at time t after the bolus radioligand administration.

Fig. 17.1
figure 1

Compartment configurations used to model in vivo radioligand kinetics when the parent only enters the brain (a) and both the parent and metabolite enter the brain (b). Terms are defined in the text

Full size image

Using C a (t) as an input function, compartment model approaches allow for the estimation of the distribution volume, V, which is the brain-to-plasma radioactivity ratio, C B(t)/C a (t), at equilibrium in which there is no net transfer of radioligand activity between all compartments. Of note is that this equilibrium condition cannot be achieved in the PET experimental paradigm with a bolus radioligand administration. However, the compartment model analysis allows for the estimation of parameters defined at equilibrium. By assuming that the nondisplaceable distribution volume in the target tissue (V ND) is the same as in the reference tissue (V ′ND ), the target binding parameter, binding potential (BP ND), is calculated as \( V-{V}^{\prime }/{V}^{\prime }={V}_{\mathrm{S}}/{V}_{\mathrm{ND}} \), which is directly proportional to the binding site density B avail, i.e., \( B{P}_{\mathrm{ND}}={f}_{\mathrm{ND}}\left({B}_{\mathrm{avail}}/{K}_{\mathrm{D}}\right) \), where f ND and K D represent the fraction of nondisplaceable compartment from which the radioligand can exchange with the specifically bound compartment (free tissue fraction) and the equilibrium dissociation constant for radioligand-binding site complex, respectively [5]. The above relationship between BP ND and B avail is derived from the principle used in in vitro binding assays, which is in turn based on the bimolecular enzymatic reaction described by Michaelis and Menten [6]. Of note is that BP ND can also be expressed as

$$ B{P}_{\mathrm{ND}}=\frac{V-{V}^{\prime }}{V^{\prime }}=\frac{\frac{C_{\mathrm{B}}(t)}{C_{\mathrm{a}}(t)}-\frac{C_{\mathrm{B}}^{\prime }(t)}{C_{\mathrm{a}}(t)}}{\frac{C_{\mathrm{B}}^{\prime }(t)}{C_{\mathrm{a}}(t)}}=\frac{C_{\mathrm{B}}(t)}{C_{\mathrm{B}}^{\prime }(t)}-1 $$
(17.1)

where t represents the time at which the compartment system is in equilibrium. BP ND is, therefore, equivalent to the tissue ratio minus 1 at equilibrium.

Reference tissue models derived from the above compartment model estimate BP ND by using C ′B (t) as an input function without requiring arterial plasma data (C a (t)) [4]. On the other hand, SUVR is the target-to-reference tissue ratio measured at a “fixed time point” after the bolus radioligand administration. The advantage of SUVR is that it can be calculated from static PET imaging data without the requirement of arterial data. \( \mathrm{SUVR}={C}_{\mathrm{B}}(t)/{C}_{\mathrm{B}}^{\prime }(t) \) is, therefore, closely related to BP ND (Eq. 17.1), the differences between the two being that BP ND is independent of radioligand delivery (blood flow) or its systemic clearance because it is defined at equilibrium,

On the other hand, in the situation where the metabolite enters the brain, the compartment system is more complex as shown in Fig. 17.1b in which superscripts P and M refer to “parent” and “metabolite,” respectively, and the metabolite is assumed not to bind specifically to targets (see the discussion about the situation where the metabolite also binds specifically) [3]. Here, let’s consider the tissue ratio minus 1 at equilibrium assuming that V ND is the same in the reference and target tissues, which is given by

$$ \begin{array}{ll}B{P}_{\mathrm{ND}}^{*}& =\frac{C_{\mathrm{B}}(t)}{C_{\mathrm{B}}^{\prime }(t)}-1=\frac{C_{\mathrm{B}}^{\mathrm{P}}(t)+{C}_{\mathrm{B}}^{\mathrm{M}}(t)}{{C^{\prime}}_{\mathrm{B}}^{\mathrm{P}}(t)+{C^{\prime}}_{\mathrm{B}}^{\mathrm{M}}(t)}-1=\frac{V^{\mathrm{P}}+\delta {V}^{\mathrm{M}}}{{V^{\prime}}^{\mathrm{P}}+\delta {V^{\prime}}^{\mathrm{M}}}-1\hfill \\ {}& =\frac{V_{\mathrm{S}}}{V_{\mathrm{ND}}^{\mathrm{P}}+\delta {V}_{\mathrm{ND}}^{\mathrm{M}}}\hfill \end{array} $$
(17.2)

where δ is the metabolite-to-parent activity ratio in plasma at equilibrium \( \left(\delta ={C}_a^{\mathrm{M}}(t)/{C}_a^{\mathrm{P}}(t)\right) \) and it is a constant value. This tissue ratio minus 1 at equilibrium has an additional term,\( \delta {V}_{\mathrm{ND}}^M \), the contribution of the metabolite nondisplaceable distribution volume in the denominator of Eq. 17.2, and it is here denoted by \( B{P}_{\mathrm{ND}}^{*} \) to distinguish it from BP ND, which is the tissue ratio minus 1 at equilibrium when only the parent enters the brain. To estimate this tissue ratio minus 1 by the reference tissue model, in fact, no knowledge of the metabolite status is needed because it uses \( {C}_{\mathrm{B}}(t) \) as an input function. The same argument applies to the SUVR. Importantly, \( B{P}_{\mathrm{ND}}^{*} \) like BP ND is directly proportional to the target binding site density, B avail, as shown below.

$$ B{P}_{\mathrm{ND}}^{*}=\frac{V_{\mathrm{S}}}{V_{\mathrm{ND}}^{\mathrm{P}}+\delta {V}_{\mathrm{ND}}^{\mathrm{M}}}=\frac{f_{\mathrm{P}}^{\mathrm{P}}}{\frac{f_{\mathrm{P}}^{\mathrm{P}}}{f_{\mathrm{ND}}^{\mathrm{P}}}+\delta \frac{f_{\mathrm{P}}^{\mathrm{M}}}{f_{\mathrm{ND}}^{\mathrm{M}}}}\times \frac{B_{\mathrm{avail}}}{K_{\mathrm{D}}} $$
(17.3)

where f PP or f MP the free fraction of parent (P) or metabolite (M) in plasma is a constant and so are f PND , f MND , and δ in the same individual. Note that \( {V}_{\mathrm{S}}={f}_{\mathrm{P}}^{\mathrm{P}}{B}_{\mathrm{avail}}/{K}_{\mathrm{D}} \) and V ND can be expressed as f P/f ND because the free radioligand or metabolite activity in the plasma and the tissue compartments are the same at equilibrium \( \left({f}_{\mathrm{P}}{C}_{\mathrm{a}}(t)={f}_{\mathrm{ND}}{C}_{\mathrm{ND}}(t)\right) \) [4, 5]. The validation of the reference tissue model BP *ND can be accomplished by the dual-input graphical analysis model derived from the model illustrated by Fig. 17.1b that takes into account the contribution of radiometabolites entering the brain using the combined plasma radioactivity \( \left({C}_{\mathrm{a}}^{\mathrm{P}}(t)+{C}_{\mathrm{a}}^{\mathrm{M}}(t)\right) \) as an input function [3]. The operational equation is given by

$$ \frac{{\displaystyle {\int}_0^t{C}_{\mathrm{B}}(t)dt}}{C_{\mathrm{B}}(t)}=\alpha (t)\frac{{\displaystyle {\int}_0^t\left({C}_{\mathrm{a}}^{\mathrm{P}}(t)+{C}_{\mathrm{a}}^{\mathrm{M}}(t)\right)\kern0.5em dt}}{C_{\mathrm{B}}(t)}+\beta (t) $$
(17.4)

Eq. 17.4 becomes linear when the system reaches transient equilibrium between the brain and plasma compartments at time t* and both the slope α and intercept β can be considered constant beyond t*. The tissue ratio minus 1 at equilibrium is calculated as

$$ B{P}_{\mathrm{ND}}^{*}=\frac{V_{\mathrm{S}}}{V_{\mathrm{ND}}^{\mathrm{P}}+\delta {V}_{\mathrm{ND}}^{\mathrm{M}}}=\frac{\alpha_{\mathrm{target}\ \mathrm{tissue}}}{\alpha_{reference\kern0.5em \mathrm{tissue}}}-1. $$

The tissue ratio minus 1 at equilibrium can also be estimated by the traditional compartment model (Fig. 17.1a) using the parent-only input function (C Pa (t)) if data fitting can be adequately accomplished. However, it may not match the tissue ratio minus 1 estimated by the reference tissue model or the dual-input model if a significant amount of the metabolite is entering the brain because the tissue radioactivity includes the metabolite contribution, which is not accounted for by the traditional compartment model (Fig. 17.1a).

2.2 Radioligand

11C-PBB3 is a novel radioligand developed at the National Institute of Radiological Sciences, Chiba, Japan, for PET imaging of pathological tau aggregates in the brain [1]. Neurofibrillary tau tangles are one of the two pathological hallmarks of AD, the other being the senile plaques containing Aβ deposition [7]. 11C-PBB3 binds reversibly to neurofibrillary tau tangles of a wide range of isoform compositions with high affinity (K D = 2.5 nM) and selectivity [1]. 11C-PBB3 upon intravenous administration is rapidly converted in plasma to one major radiometabolite identical chemically in both humans and mice, a significant amount of which enters the mouse brain (30% of radioactivity in brain 5 min after injection) [8]. 11C-PBB3 SUVR in AD patients has previously been shown to reflect the known pathological tau distribution at various stages of AD [9].

2.3 PET Data

The reader is referred to our recent 11C-PBB3 PET data analysis study [2] regarding the detail of PET data acquisition and full data analysis. Here, the description is limited to information relevant to illustrating the concept of tissue ratio estimation considering the contribution of radiometabolite to the brain activity.

11C-PBB3 PET data consisted of 70 min dynamic scans after a bolus injection of approximately 400 MBq of 11C-PBB3 in 7 AD patients (76 ± 7 y) and 7 elderly healthy control subjects (70 ± 6 y). Input functions (C Pa (t) and C Ma (t)) were obtained from multiple arterial samples by determining plasma fractions of the parent and its radiometabolites with high-performance liquid chromatography.

To improve the statistical quality of PET ROI data, we generated cerebral cortical ROIs pooling all voxels of high (>0.3, high), medium (0.15–0.3, middle), low (0–0.15, low), and non-binding (<0) \( {BP}_{\mathrm{ND}}^{*} \) values on preliminarily generated parametric images by the original multilinear reference tissue model (MRTMO)[10] using the cerebellar cortex as the reference tissue because tau accumulation is known to be histopathologically absent in the cerebellar cortex of either normal or AD brains [11].

2.4 Data Analysis

The tissue ratio minus 1 was estimated in four ways using cerebral cortical ROI data with the cerebellar cortex as the reference tissue:

  1. 1)

    BP *ND estimation by the dual-input graphical analysis using \( \left({C}_{\mathrm{a}}^{\mathrm{P}}(t)+{C}_{\mathrm{a}}^{\mathrm{M}}(t)\right) \) as an input function (Eq. 17.4)

  2. 2)

    BP ND estimation by 2T compartment kinetic analysis using C Pa (t) as an input function (Fig. 17.1a)

  3. 3)

    BP *ND estimation by the reference tissue model MRTMO using C ′B (t) as an input function

  4. 4)

    SUVR minus 1 at a fixed time point (50 min–70 min)

The tissue ratio minus 1 values obtained by the above 4 methods were then compared to validate the use of SUVR and the reference tissue model BP *ND . Additionally, parametric images of MRTMO and (SUVR-1) were generated and compared.

3 Results

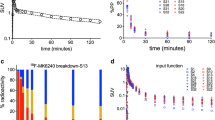
The brain 11C-PBB3 time activity curves (TACs) quickly peaked within a few minutes of intravenous injection of 11C-PBB3 with gradual decreases thereafter with a significantly slower washout for high binding cerebral cortex in ADs than in HCs (Fig. 17.2a). Plasma parent TACs peaked very quickly and decreased also quickly thereafter (Fig. 17.2b). One major radiometabolite of 11C-PBB3 appeared very quickly in the plasma and slowly decreased thereafter (Fig 17.2b). Both plasma parent and metabolite TACs in ADs and HCs were very similar (Fig. 17.2b)

Fig. 17.2
figure 2

Time activity curves (TACs) in the brain (a) and arterial plasma (b) after the injection of 11C-PBB3 in AD patients and healthy controls (HCs). (a) TACs are shown for the high tau binding (▲) cerebral cortical region and cerebellar cortex (◆) in ADs, and the cerebral cortical region (△) and the cerebellar cortex (◇) in HCs. (B) Plasma TACs are shown for the total radioactivity (thick (ADs) and thin (HCs) solid lines), metabolite (thick (ADs) and thin (HCs) dotted lines), and parent (thick (ADs) and thin (HCs) dashed lines). Data represent mean of all 7 ADs or 7 HCs

Full size image

Graphical plots (Eq. 17.4) with a combined \( {C}_{\mathrm{a}}^{\mathrm{P}}(t)+{C}_{\mathrm{a}}^{\mathrm{M}}(t) \) plasma input became linear beyond t* = 11 min when both α and β could be considered constant. BP *ND estimations were very stable for all regions. On the other hand, the 2T kinetic analysis to estimate BP ND was unstable in some regions with a large parameter estimation variability in the rest of the regions. The 2TC BP ND values were numerically quite different from the corresponding BP *ND values with a very poor correlation between the two-tissue ratio minus 1 estimations (\( B{P}_{\mathrm{ND}}=1.06\pm 0.66 \) vs. \( B{P}_{\mathrm{ND}}^{*}=0.36\pm 0.07 \) with r 2 = 0.04 in the high binding region, for example.

The reference tissue model MRTMO robustly estimated \( {BP}_{\mathrm{ND}}^{*} \) for the ROI data and enabled stable voxel-wise parametric imaging of \( {BP}_{\mathrm{ND}}^{*} \). The \( {BP}_{\mathrm{ND}}^{*} \) estimated by the ROI-based MRTMO analysis closely matched the corresponding BP *ND estimated by the dual-input graphical analysis with a perfect correlation between the two (r 2 = 1.00) (Fig. 17.3a). On the other hand, SUVR minus 1 values (calculated from the averaged 50 min to 70 min data) overestimated MRTMO BP *ND values by up to 38%. However, there was an excellent correlation between the two (r 2 = 0.97) (Fig. 17.3b). Both the MRTMO BP *ND parametric images and SUVR minus 1 images showed a clear delineation of tau pathology in the cerebral cortices including the hippocampal formation in AD (Fig. 17.4a, c) compared with HC (Fig. 17.4b, d).

Fig. 17.3
figure 3

(a) Correlation of ROI \( {BP}_{\mathrm{ND}}^{*} \) estimated by dual-input graphical model and reference tissue model MRTMO. (b) Correlation of ROI \( {BP}_{\mathrm{ND}}^{*} \) estimated by MRTMO and SUVR minus 1 (50 min–70 min)

Full size image
Fig. 17.4
figure 4

Coronal parametric images of AD and HC. The MRTMO \( {BP}_{\mathrm{ND}}^{*} \) images in ADs (a) and HCs (b). SUVR-1 images (50 min–70 min) in ADs (c) and HCs (d)

Full size image

4 Discussion

In the present article, we have shown that the reference tissue model-based binding potential (BP ND) that reflects the target binding site density (B avail) is theoretically equivalent to the tissue ratio minus 1 at equilibrium, whereas closely related SUVR minus 1 is the tissue ratio minus 1 at a fixed time point after the bolus radioligand administration. We have shown that the tissue ratio minus 1 at equilibrium (BP *ND ) also reflects B avail even in the situation where the radiometabolite enters the brain. The definition of binding potential, BP ND, therefore can be extended to this situation (expressed as BP *ND here). The validity of the reference tissue model BP *ND and SUVR, both of which do not require arterial plasma data, can be evaluated by the dual-input \( \left({C}_{\mathrm{a}}^{\mathrm{P}}(t)+{C}_{\mathrm{a}}^{\mathrm{M}}(t)\right) \) model but not by the conventional single input (C Pa (t)) model because the tissue ratio minus 1 at equilibrium includes the radiometabolite contribution to the tissue activity, which is not accounted for by the parent-only model. Of note is that the reference tissue \( {BP}_{\mathrm{ND}}^{*} \) or SUVR estimation does not require any assumption of metabolite, because the estimation is performed without blood data.

Although we assumed here that the radiometabolite does not bind to the target site, it can be shown that BP ND is also directly proportional to B avail when the metabolite binds specifically (17.2). BP *ND has additional term, δV MND , in the denominator (Eq. 17.2), which may increase the intersubject variability of BP *ND compared with BP ND. In our 11C-PBB3 analyses, there was no difference in the mean \( \left({V}_{\mathrm{ND}}^{\mathrm{P}}+\delta {V}_{\mathrm{ND}}^{\mathrm{M}}\right) \) values between ADs and HCs [2].

SUVR minus 1 at 50 min–70 min overestimated BP *ND . However, there was an excellent correlation between the two. SUVR is potentially affected by blood flow and systemic radioligand clearance, while BP *ND is independent of these factors because BP *ND represents the tissue ratio minus 1 at equilibrium. Therefore, a larger variability of cerebral blood flow in AD patents than in normal elderly subjects may result in a larger intersubject SUVR variability compared with BP *ND , although a longer dynamic imaging needed for BP *ND estimation might be less well tolerated for elderly patients than a shorter static imaging for SUVR measurements. The advantage of the reference tissue model-based estimation of the tissue ratio over the SUVR measurement has recently been shown for a long-term longitudinal Aβ PET imaging study [12].

5 Conclusions

The reference tissue-based binding potential (BP ND) that reflects the target binding site density (B avail) is equivalent to the tissue ratio minus 1 at equilibrium. The tissue ratio minus 1 at equilibrium (BP *ND ) also reflects B avail even in the situation where the radiometabolite enters the brain. The validity of the reference tissue model BP *ND and SUVR can be evaluated by the dual-input model not by the conventional single input model because the tissue ratio minus 1 at equilibrium includes the radiometabolite contribution to the tissue activity, which is not accounted for by the parent-only model.