Abstract
The neutron spectrum of a pulsed neutron reactor at subcritical state is different from that evaluated by k-eigenvalue mode, because of the time needed in the neutron slowing-down process from fast to thermal energy range. The time needed in slowing down does not depend on the degree of subcriticality, but the decreasing speed of neutron flux becomes fast as the subcriticality becomes deep. Therefore, the neutron spectrum becomes soft as the subcriticality becomes deep. This fact suggests to us that group constants to be used in the design study should change with the degree of subcriticality of the target system, even in the case of the same composition.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
The accelerator-driven subcritical reactor (ADSR) is considered as one of the best candidates to annihilate the radioactivity of nuclear waste and has been investigated in many institutes for many years. The ADSR is operated by the pulsed proton beam as an ignition of spallation reaction to produce many neutrons. Kyoto University Critical Assembly (KUCA) is one of the facilities to demonstrate the ADSR by using accelerated protons for the spallation reaction or deuterons for the deuterium-tritium (DT) reaction.
This study focused on the transient behavior of the neutron spectrum in a subcritical system after the injection of DT neutrons to know and discuss the physical behavior of the neutron spectrum in a subcritical system through the analysis of the experiments performed at KUCA. The subcritical system with pulsed neutrons has been widely analyzed in the steady state, although transient behavior of the neutron spectrum after the injection of DT neutrons can be analyzed in the transient state. This chapter focuses on the neutron spectrum evaluated in steady state, and two kinds of calculation modes in steady state are compared and discussed: the k-eigenvalue mode and the alpha-eigenvalue mode.
Chapter 2 shows a brief explanation of KUCA experiments and the major results. Analyses of the experiments and discussion are described in Chap. 3, and the conclusions are summarized in Chap. 4.
2 Experiment at KUCA and Measured Results
This chapter shows a brief explanation of experiments performed at KUCA for the convenience of easy understanding of the analysis described in the next chapter.
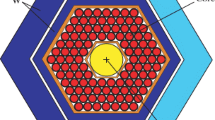
Experiments modeled on the ADSR were performed at the A-core with adjacent D+ accelerator. A typical core configuration is shown in Fig. 13.1 for the case of 13 fuel rods. Each square cell is 2 in. × 2 in. in size, with size in the horizontal direction about 1.5 m, composed of a central 40-cm-thick fuel region and upper and lower polyethylene reflector regions. All control rods are inserted through the experiment. Accelerated D+ ions are hit with tritium target, depicted as T-target in Fig. 13.1, and 14 MeV neutrons produced by D-T reaction at T-target are injected into the core region composed of the fuel rods, polyethylene reflector, etc. Neutrons are injected from outside the core region in this experiment.
The target subcriticality was widely changed by changing the number of fuel rods from 19 to 6 to check the validity of the fiber scintillation counter used in the measurement. The subcriticality of the system was evaluated by the so-called extrapolation area ratio method proposed by Gozani [1]. The counters used in the experiments were set at several positions inside the core, and the measured results summarized in Table 13.1 are the results obtained at the core central area, where the most reliable results are expected. Measured subcriticality is from 2.3 [$] (19 fuel rods case) to 49 [$] (6 fuel rods case).
3 Analysis and Discussion of Neutron Flux
The analysis results of neutron flux distribution and neutron spectrum are summarized in this chapter with some discussion. Neutron flux distribution and spectrum in the core are shown in Sects. 13.3.1 and 13.3.2, respectively. All analyses are done by a continuous energy Monte Carlo code named MVP-II [2] with JENDL-4.0 [3] library. The code has the function to simulate the experiment not only in eigenvalue mode but also in time-dependent mode, where the necessary time of neutron flight is used to account for the elapsed time after the injection of DT neutrons.
In this chapter, fast and thermal neutrons are in the energy range less than 4 eV and more than 100 keV, respectively.
3.1 Neutron Flux Distribution
Neutron flux distribution is drastically changed with the change in subcriticality of the system, because of the change in the number of fuel rods in the core. Figures 13.2, 13.3, and 13.4 show the neutron flux distribution along the central line from T-target to core for 13 fuel rods case in eigenvalue mode and time-dependent mode, respectively. Neutron flux distribution evaluated in time-dependent mode changes as a function of elapsed time after the injection of D-T neutrons, and the shape of neutron flux distribution is almost stable after 1e−4 s (Figs. 13.3 and 13.4). The comparison of neutron flux between two modes shows the discrepancy (Figs. 13.5 and 13.6). Thermal neutron flux distribution of the time-dependent mode is smaller at fuel region, but higher at the reflector region, than those of eigenvalue mode, although fast neutron flux distribution is almost the same between the two modes. Figures 13.5 and 13.6 also show that the neutron spectrum is different between two modes, and the details are discussed in the next section.
3.2 Neutron Spectrum
The neutron spectrum at the fuel region is shown in Figs. 13.7 and 13.8. The neutron spectrum in time-dependent mode changes as a function of elapsed time, although the neutron spectrum in eigenvalue mode is singular. In addition to this, the neutron spectrum at the fuel region evaluated in eigenvalue mode is almost the same among different subcritical states, because there is no change in fuel composition through the experiment. Neutron spectrum at the fuel region evaluated in time-dependent mode changes as a function of elapsed time after the injection of D-T neutrons, but the shape of the spectrum becomes stable after around 1e−4 s, although the magnitude of neutron flux decreases with elapsed time (Fig. 13.8). The neutron spectrum is compared between two modes, where the shape of the spectrum in time-dependent mode is almost stable (at 1e−3 s). The comparison of the neutron spectrum is shown in Fig. 13.9. The neutron spectrum in time-dependent mode depends on the subcriticality of the system, and the spectrum becomes soft as the subcriticality becomes deep. This tendency can be understood by considering the following facts. The magnitude of neutron flux decreases as a function of elapsed time in the subcritical system, and the decreasing speed of neutron flux becomes high for the deep subcritical system. Here the neutrons are slowed down by colliding with the medium in the thermal core, and the time needed in the slowing-down process does not depend on the subcriticality of the system. Therefore, the change in the neutron spectrum is caused by the time delay of decrease in thermal energy range where the neutrons are slowed down compared to that in the fast energy range.
The difference in neutron spectrum will cause the difference in collapsed cross sections widely used in design survey calculations, and the degree of the difference becomes remarkable as the subcriticality of the system becomes deep. It should be noted that collapsed cross sections depend on the subcriticality of target system because of the difference in neutron spectrum.
There is one recommendation to evaluate the proper neutron spectrum for collapsing. In eigenvalue mode, the k-eigenvalue mode expressed as Eq. (13.13.1) is usually used because the eigenvalue is an unbiased index to recognize the criticality, but there is another eigenvalue mode, named the alpha-eigenvalue mode, expressed as Eq. (13.13.2):
where L is the destruction operator including leakage and absorption reactions, M is the production operator including fission reactions, k is the k-eigenvalue called the effective multiplication factor, α is the alpha-eigenvalue, v is the neutron speed, and ϕ k , ϕ α are the neutron fluxes for each mode. Equation (13.1) is derived from a time-dependent equation by eliminating the term of time derivative, but Eq. (13.13.2) is derived by considering the exponential change of neutron flux in time. Usually a subcritical system such as the ADSR is operated not in stable but in transient conditions.
In the subcritical system, the alpha-eigenvalue is negative, and the impact of the negative alpha-eigenvalue on neutron flux is remarkable at thermal energy range where the neutron speed is small. Therefore, the neutron spectrum evaluated in alpha-eigenvalue mode is softer than that in k-eigenvalue mode. Similar to this consideration, the difference in neutron spectrum could be observed in the supercritical state. However, the difference is expected to be not remarkable compared to subcritical state, because excess reactivity is remarkably small compared to the subcriticality, as readily expected.
4 Conclusions
The neutron flux distribution evaluated in time-dependent mode changes with elapsed time after the ignition of neutrons into the subcritical system, and the neutron distribution in energy and space becomes almost stable in about 1 e−4 s after the ignition.
There is a remarkable difference in neutron spectrum between two results in k-eigenvalue and time-dependent modes. The neutron spectrum (at 1 μs after the ignition) evaluated in time-dependent mode is softer than that in k-eigenvalue mode, and the difference is more remarkable in a deep subcriticality system. This difference is caused by the fact that additional time is necessary to be moderated before decreasing neutron flux in the thermal energy range, and the time is independent of the subcriticality of the system, depending only on the material composition of the system.
The neutron spectrum of a pulsed neutron reactor is to be evaluated in alpha-eigenvalue mode instead of k-eigenvalue mode to match the neutron spectrum during the decrease with elapsed time after the ignition of pulsed neutrons into the subcritical system.
References
Gozani T (1962) Nukleonik 4:348
Nagaya Y, Okumura K, Mori T et al (2005) MVP/GMVP version 2: general purpose Monte Carlo codes for neutron and photon transport calculations based on continuous energy and multigroup methods. JAERI, p 1348
Shibata K, Iwamoto O, Nakagawa T, Iwamoto N, Ichihara A, Kunieda S, Chiba S, Furutaka K, Otuka N, Ohsawa T, Murata T, Matsunobu H, Zukeran A, Kamada S, Katakura J (2011) JENDL-4.0: a new library for nuclear science and engineering. J Nucl Sci Technol 48(1):1–30
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
This chapter is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
Copyright information
© 2015 The Author(s)
About this chapter
Cite this chapter
Kitada, T., Vu, T.M., Dobuchi, N. (2015). Study on Neutron Spectrum of Pulsed Neutron Reactor. In: Nakajima, K. (eds) Nuclear Back-end and Transmutation Technology for Waste Disposal. Springer, Tokyo. https://doi.org/10.1007/978-4-431-55111-9_13
Download citation
DOI: https://doi.org/10.1007/978-4-431-55111-9_13
Published:
Publisher Name: Springer, Tokyo
Print ISBN: 978-4-431-55110-2
Online ISBN: 978-4-431-55111-9
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)