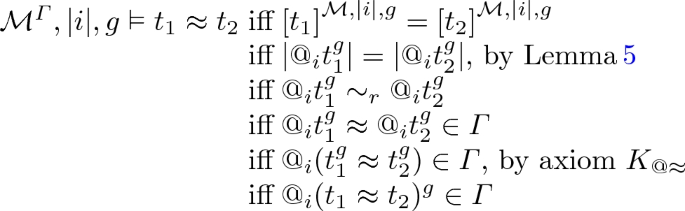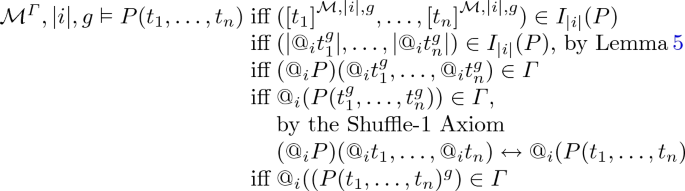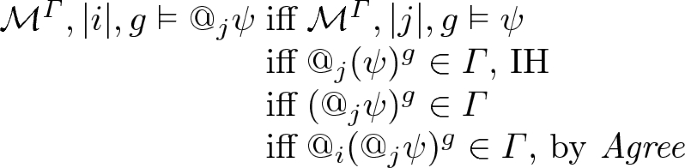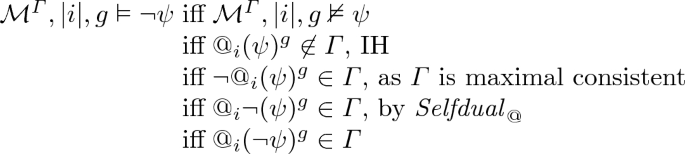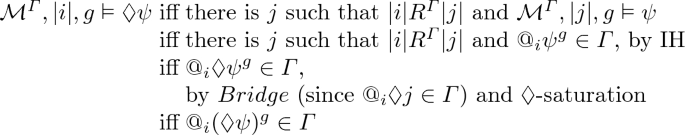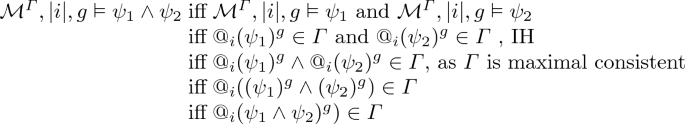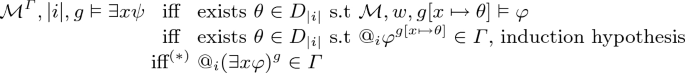Rigid First-Order Hybrid Logic

Abstract

Hybrid logic is usually viewed as a variant of modal logic in which it is possible to refer to worlds. But when one moves beyond propositional hybrid logic to first or higher-order hybrid logic, it becomes useful to view it as a systematic modal language of rigidification. The key point is this: @ can be used to rigidify not merely formulas, but other types of symbol as well. This idea was first explored in first-order hybrid logic (without function symbols) where @ was used to rigidify the first-order constants. It has since been used in hybrid type-theory: here one only has function symbols, but they are of every finite type, and @ can rigidify any of them. This paper fills the remaining gap: it introduces a first-order hybrid language which handles function symbols, and allows predicate symbols to be rigidified. The basic idea is straightforward, but there is a slight complication: transferring information about rigidity between the level of terms and formulas. We develop a syntax to deal with this, provide an axiomatization, and prove a strong completeness result for a varying domain (actualist) semantics.

Appendix

This appendix sketches the definitions and lemmas that lead to the Truth Lemma, and thus to the Completeness Theorem stated in the main text. As a first step, given an assignment function g on the Henkin structure $\mathcal {M}^\varGamma$ defined in Definition 12, we need an inductive definition of how to substitute a suitable rigid term for a variables inside terms and formulas; the substitution syntactically mirrors the assignment function.

We do so as follows. Given a variable assignment g into $\mathcal {M}^\varGamma$ (that is, $g:X\rightarrow \mathrm {Dom}^\varGamma$) we first define a substitution function $\hat{g}:X\rightarrow @{\mathrm {Term}}(\tau )$ in the following way: for any variable x, we define $x^ {\hat{g}} := t_k$, where $t_k$ is the first rigid ground term in $@{\mathrm {Term}}(\tau )$ with lowest k such that $g(x)= |t_k|$. Here we assume that $@{\mathrm {Term}}(\tau )$ is ordered. We extend ${\hat{g}}$ to arbitrary terms t by defining: if $t=f(t_1, \dots , t_n)$ then $t^ {\hat{g}}=f(t_1^ {\hat{g}}, \dots , t_n^ {\hat{g}})$.

We extend ${\hat{g}}$ to formulas in the following way:

• $i^ {\hat{g}}:=i$, $i\in {\mathrm {NOM}}$

• $(t_1\approx t_2)^ {\hat{g}}:=(t_1^ {\hat{g}}\approx t_2^ {\hat{g}})$, $t_1, t_2\in {\mathrm {Term}}(\tau )$

• $(P(t_1,\dots , t_n))^ {\hat{g}}:=P(t_1^ {\hat{g}},\dots , t_n^ {\hat{g}})$, $P\in {\mathrm {Rel}}_n \cup @{\mathrm {Rel}}_n$ and $t_1,\dots , t_n\in {\mathrm {Term}}(\tau )$

• $(@_i \varphi )^ {\hat{g}}:=@_i (\varphi ^ {\hat{g}})$, $\varphi \in \mathrm {Fm}(\tau )$ and $i\in {\mathrm {NOM}}$

• $(\lnot \varphi )^ {\hat{g}}:=\lnot (\varphi ^ {\hat{g}})$ and $(\Diamond \varphi )^ {\hat{g}}:=\Diamond (\varphi ^ {\hat{g}})$, $\varphi \in \mathrm {Fm}(\tau )$

• $(\varphi \wedge \psi )^ {\hat{g}}:=\varphi ^ {\hat{g}} \wedge \psi ^ {\hat{g}}$ and $(\varphi \vee \psi )^ {\hat{g}}:=\varphi ^ {\hat{g}} \vee \psi ^ {\hat{g}}$, for $\varphi \in \mathrm {Fm}(\tau )$ and $\psi \in \mathrm {Fm}(\tau )$

• $(\exists x\varphi )^ {\hat{g}}:=\exists x(\varphi ^{{\hat{g}_x^x}})$, $x\in X$ and $\varphi \in \mathrm {Fm}(\tau )$, where $\hat{g}^x_x=\hat{g}\setminus \{(x,\hat{g}(x))\})\cup \{(x,x)\}$)

For any $t\in {\mathrm {Term}}(\tau )$ and any assignment g on $\mathcal {M}^\varGamma$, in what follows we will simply write $t^g$ for $t^{\hat{g}}$. A similar simplification will be adopted for formulas.

Lemma 5

For any $t\in {\mathrm {Term}}(\tau )$ and any assignment g on $\mathcal {M}^\varGamma$ we have

$$[t]^{\mathcal {M}^{\varGamma },|i|,g} =|@_i t^g|$$

Proof

By induction on term structure.

Lemma 6

(Truth Lemma). For every nominal i, any assignment g on $\mathcal {M}^\varGamma$ and every formula $\varphi$

$${\mathcal {M}}^{\varGamma },|i|,g\vDash \varphi \; \; \mathbin {\Leftrightarrow }\; \; @_i\varphi ^g\in \varGamma $$

Proof

The proof proceeds by induction on the complexity of $\varphi$.

• $\varphi =j$

  We have that

  ${\mathcal {M}}^{\varGamma ^*},|i|,g\vDash j$ iff $|i|=|j|$ iff $@_i j\in \varGamma$ iff $@_i j^g\in \varGamma$.

• $\varphi = t_1\approx t_2$,

  

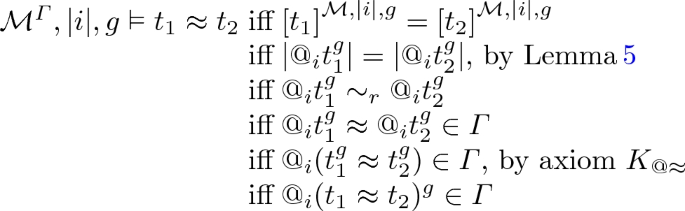
• $\varphi = P(t_1, \dots , t_n)$, with $P\in {\mathrm {Rel}}_n \cup @{\mathrm {Rel}}_n$ and $t_1,\dots , t_n\in {\mathrm {Term}}(\tau )$;

  If $P\in {\mathrm {Rel}}_n$:

  

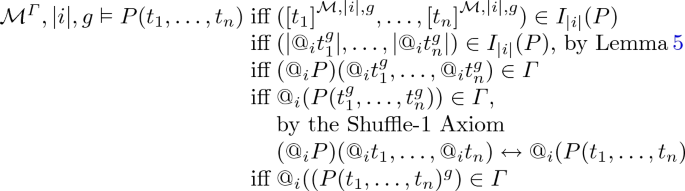
  If $P=(@_j S)$, with $S\in {\mathrm {Rel}}_n$:

  

• $\varphi =@_j\psi$.

  

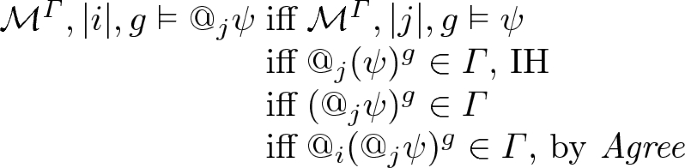
• $\varphi =\lnot \psi$.

  

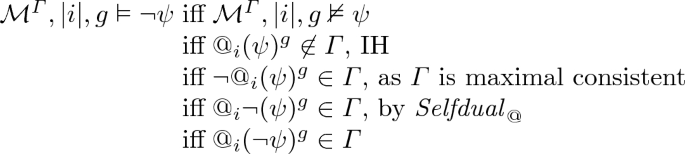
• $\varphi =\lozenge \psi$.

  

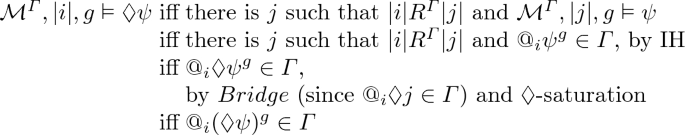
• $\varphi =\psi _1\wedge \psi _2$

  

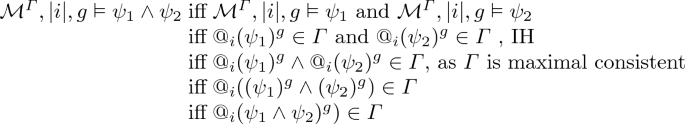
• $\varphi =\exists x\psi$.

  

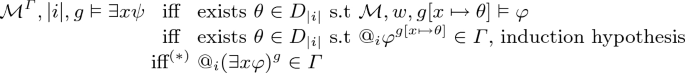
  Proof of $(*)$

  The implication “$\Rightarrow$” holds by the Corollary 1 clause 3.

  The implication “$\Leftarrow$” holds by $\exists$- saturation. $@_i (\exists x \varphi )^g\in \varGamma$ implies that there exists a constant c such that $@_i \mathsf {EXISTS}(c)\in \varGamma$ and $(\varphi )^{g^x_x}(x\mapsto @_i c)\in \varGamma$. So there is $\theta :=@_i c\in D_{|i|} (\text {because } @_i \mathsf {EXISTS}(c)\in \varGamma ) \text{ s.t } @_i \varphi ^{g[x\mapsto \theta ]}\in \varGamma$.

Lemma 7

Let $\varGamma$ be a consistent set of sentences. Then, there is a nominal k such that for every $\varphi \in \varGamma$,

$$\mathcal {M}^{\varGamma }, |k|\vDash \varphi $$

Theorem 3

(Completeness). Let $\tau$ be a first-order hybrid similarity type $\varphi$ be a sentence and $\varGamma$ a set of sentences. Then

$$ \varGamma \vdash \varphi \Rightarrow \varGamma \vDash \varphi . $$