Wechselnde Wirkung durch Wechselwirkung: Interferenz

Zusammenfassung

Auch die Begriffe Beugung und Interferenz spielen in der Wellenoptik eine große Rolle. In diesem Kapitel wird detailliert auf verschiedenste Interferenzeffekte eingegangen, einschließlich anschaulicher Skizzen und zugehöriger Formeln. Diese Effekte sind unter anderem Interferenz am Einfachspalt, am Doppelspalt, am Gitter, an dünnen Schichten, in Interferometern und an Antireflexschichten, genauso aber auch an der herkömmlichen CD, an Seifenblasen und am Ölfleck. Auch die Begriffe der Fresnel- und der Fraunhofer-Beugung und deren Unterschiede werden ausführlich beleuchtet. In den Aufgaben wird mit Hilfe der Interferenz unter anderem die Pixeldichte eines Smartphone-Displays vermessen.

Appendices

Aufgaben

6.1.1 6.1 Interferenz-Memory

Ordne die Interferenzmuster nachfolgender Tabelle zu.

Nr.	Bezeichnung	Spaltbreite ($\mathrm {nm}$)	Spaltabstand o. Gitterkonstante ($\upmu \mathrm {m}$)	Beleuchtete Spalte
1	Doppelspalt	$b\approx 0$	$d=1$	$N=2$
2	Doppelspalt	$b=150$	$d=1$	$N=2$
3	Doppelspalt	$b=150$	$d=2$	$N=2$
4	Doppelspalt	$b=400$	$d=2$	$N=2$
5	Einfachspalt	$b=400$	–	$N=1$
6	Gitter	$b\approx 0$	$d=1$	$N=4$
7	Gitter	$b\approx 0$	$d=1$	$N=6$
8	Gitter	$b=150$	$d=2$	$N=40$
9	Gitter	$b=400$	$d=2$	$N=4$

6.1.2 6.2 Pixeldichte

Lichtreflexionen an modernen Smartphonedisplays zeigen oft bunte Interferenzmuster. Die Ursache dafür liegt in den winzigen Pixeln und Subpixeln, die regelmäßig angeordnet sind (Gitterkonstanten $d_1$ und $d_2$) und als Reflexionsgitter wirken. Dadurch ergibt sich für das zweidimensionale, rote ($\lambda =620\,\mathrm {nm}$) Interferenzmuster ein Abstand der Maxima von $x_1=1\,\mathrm {cm}$ und $x_2=0{,}33\,\mathrm {cm}$, betrachtet aus einem Abstand von $a=40\,\mathrm {cm}$.

• a) Erstelle eine Skizze mit den relevanten Größen.

• b) Berechne die Pixeldichte des Smartphones, also die Anzahl der Pixel pro Zentimeter.

6.1.3 6.3 Bragg-Reflexion

Mithilfe der Bragg-Reflexion lässt sich die Struktur von Kristallen untersuchen. Hierbei kommt es zur Beugung von Röntgenstrahlung an den Gitterebenen des Kristalls. Dadurch entsteht ein gut detektierbares Interferenzmuster, aus dem sich die Dimensionen des winzig kleinen Kristallgitters berechnen lassen. Leite eine Formel für den Bragg-Winkel $\theta$ her, unter dem es zu konstruktiver Interferenz zwischen den in der Skizze eingezeichneten Strahlen kommt.

6.1.4 6.4 Mach-Zehnder-Interferometer

Der Brechungsindex von Luft unterscheidet sich geringfügig von 1. Mithilfe eines Mach-Zehnder-Interferometers ist es möglich, diesen Unterschied zu bestimmen. Dafür wird aus dem Messbehälter aus Abb. 6.27 zunächst Luft abgepumpt und anschließend langsam wieder vollständig eingelassen. Für monochromatisches Licht einer Wellenlänge $\lambda =632\,\mathrm {nm}$ beobachtet man an beiden Detektoren 20 Wechsel zwischen Minimum und Maximum. Der Messbehälter hat eine Länge von $5\,\mathrm {cm}$. Wie groß ist der Brechungsindex von Luft?

Lösungen

6.1.1 6.1 Interferenz-Memory

Um auf die richtigen Zuordnungen zu kommen, muss man sich Folgendes ins Gedächtnis rufen:

• Je größer die Spaltbreite b, desto schmäler ist die Einhüllende, die die Höhe der Maxima bestimmt.

• Je größer der Spaltabstand d, desto mehr Maxima treten pro Winkel auf.

• Je größer die Zahl der beleuchteten Spalte N, desto schärfer sind die einzelnen Maxima voneinander getrennt.

a) 1	b) 6	c) 7
d) 5	e) 9	f) 4
g) 2	h) 3	i) 8

Hierbei zeigt die komplette erste Reihe Interferenz bei ideal schmalen Spalten ($d\approx 0\,\mathrm {nm}$), in Reihe zwei sind die Spalte am breitesten (jeweils $d=2\,\upmu \mathrm {m}$). e) und i) zeigen je ein reales Gitter, also ein Gitter, bei dem die Breite der Spalte nicht als unendlich klein angenommen wird. Das Interferenzbild ergibt sich analog zum realen Doppelspalt (Abschn. 6.4.4) aus dem Produkt von Gitter und Einfachspalt.

6.1.2 6.2 Pixeldichte

• a)

  

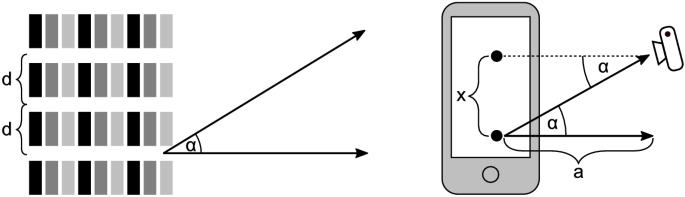
• b) Gegeben: $\lambda =620\,\mathrm {nm}$, $x_1=1\,\mathrm {cm}$, $x_2=0,33\,\mathrm {cm}$, $a=40\,\mathrm {cm}$

  Gesucht: Pixeldichte P

  Die Pixeldichte ergibt sich über den Abstand der Pixel $d_2$ zu

  $$ P_2=\frac{1}{d_2}. $$

  Außerdem kann man sie auch über den Abstand der Subpixel $d_1$ berechnen, denn drei Subpixel ergeben einen vollen Pixel:

  $$ P_1=\frac{1}{3d_1} $$

  Wir wollen nun beide Lösungswege verfolgen. Die Unbekannten der beiden Gleichungen lassen sich als Gitterkonstanten der Interferenz bestimmen. Für den Winkel $\sin {\alpha }$, unter dem zwei Maxima am Interferenzbild des Gitters abstrahlen, gilt gemäß Gl. 6.22:

  $$ \sin {\alpha } = \sin \alpha _{({\text {n}}+1).{\text {Max}}}- \sin \alpha _{{\text {n.Max}}} =(n+1)\frac{\lambda }{d}- n\frac{\lambda }{d} = \frac{\lambda }{d} $$

  Der Winkel $\alpha$ ist gemäß der Skizze aus (a) auch der Winkel, unter dem wir zwei benachbarte Maxima wahrnehmen. Aufgrund der Kleinwinkelnäherung gilt

  $$ \sin {\alpha }=\tan {\alpha }=\frac{x}{a}. $$

  Wir setzen die beiden Formeln ineinander ein und erhalten

  $$ \frac{\lambda }{d}=\frac{x}{a} $$

  und nach d aufgelöst

  $$ d_{1|2}=\lambda \frac{a}{x_{1|2}}. $$

  Darüber ergibt sich die Pixeldichte zu

  $$ P_2=\frac{x_2}{\lambda a} =13.306\frac{1}{\mathrm {m}}=133\frac{1}{\mathrm {cm}} \text { oder auch } P_1=\frac{x_1}{3\lambda a} =13.441\frac{1}{\mathrm {m}}=134\frac{1}{\mathrm {cm}}. $$

  Der Hersteller gibt die Pixeldichte mit $326\,\mathrm {dpi}$ (dots per inch) an, dies entspricht $128\frac{1}{\mathrm {cm}}$. Der Fehler unserer Messung liegt damit unter $5\%$.

  Mit dieser Methode lassen sich also durch leicht messbare große Interferenzbilder Rückschlüsse über sehr kleine, periodische Strukturen ziehen. Genauso funktioniert auch die Bragg-Reflexion an Kristallgittern in der nächsten Aufgabe.

6.1.3 6.3 Bragg-Reflexion

Wie immer bei Interferenz sind wir auf der Suche nach dem Gangunterschied $\Delta s$ zwischen den beteiligten Strahlen. Dafür erweitern wir die Skizze um ein paar Hilfsgrößen.

So lässt sich für $\Delta s$ ablesen:

$$ \frac{\Delta s}{2}=d\sin \theta $$

Konstruktive Interferenz erhalten wir für ganzzahlige Gangunterschiede $\Delta s= m\lambda , m \in \mathbb {Z}$:

$$ m\lambda =\Delta s=2d\sin \theta $$

Das ist die sogenannte Bragg-Gleichung oder Bragg-Bedingung.

6.1.4 6.4 Mach-Zehnder-Interferometer

Gegeben: $d=0{,}05\,\mathrm {m}$, $\lambda =632\,\mathrm {nm}$, $N=20$

Gesucht: $n_L$

Wir sehen uns, wie immer bei Interferenz, den Gangunterschied $\Delta s$ an. In diesem Fall genauer die Differenz zwischen der Lichtausbreitung mit und ohne Luft im Messbehälter. Diese ergibt sich zu

$$ \Delta s = n_{{\text {L}}}d-n_{{\text {Vakuum}}}d = (n_{\text {L}}-1)d. $$

Da sich beim Einlassen der Luft insgesamt $N=20$ Wechsel zwischen Minimum und Maximum ergeben, beinhaltet dieser Gangunterschied insgesamt $N=20$ ganze Wellenlängen, also

$$ \Delta s = N\lambda . $$

Gleichgesetzt ergibt sich

$$ (n_L-1)d = \Delta s = N\lambda $$

und

$$ n_L = \Delta s = \frac{N\lambda }{d}+1=1{,}00025. $$