Abstract
We consider average-energy games, where the goal is to minimize the long-run average of the accumulated energy. While several results have been obtained on these games recently, decidability of average-energy games with a lower-bound constraint on the energy level (but no upper bound) remained open; in particular, so far there was no known upper bound on the memory that is required for winning strategies.
By reducing average-energy games with lower-bounded energy to infinite-state mean-payoff games and analyzing the density of low-energy configurations, we show an almost tight doubly-exponential upper bound on the necessary memory, and prove that the winner of average-energy games with lower-bounded energy can be determined in doubly-exponential time. We also prove  -hardness of this problem.
-hardness of this problem.
Finally, we consider multi-dimensional extensions of all types of average-energy games: without bounds, with only a lower bound, and with both a lower and an upper bound on the energy. We show that the fully-bounded version is the only case to remain decidable in multiple dimensions.
A full version of this paper [4] is available online: https://arxiv.org/abs/1610.07858.
P. Bouyer and N. Markey—Supported by ERC project EQualIS (308087).
M. Randour—F.R.S.-FNRS postdoctoral researcher.
M. Zimmermann—Supported by the DFG project TriCS (ZI 1516/1-1).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Quantitative two-player games of infinite duration provide a natural framework for synthesizing controllers for reactive systems with resource restrictions in an antagonistic environment (see e.g., [1, 23]). In such games, player \(P_{0} \) (who represents the system to be synthesized) and player \(P_{1} \) (representing the antagonistic environment) construct an infinite path by moving a pebble through a graph, which describes the interaction between the system and its environment. The objective, a subset of the infinite paths that encodes the controller’s specification, determines the winner of such a play. Quantitative games extend this classical model by weights on edges for modeling costs, consumption, or rewards, and by a quantitative objective to encode the specification in terms of the weights.
As an example, consider the game in Fig. 1: we interpret negative weights as energy consumption and correspondingly positive weights as recharges. Then, \(P_{0} \) (who moves the pebble at the circular states) can always maintain an energy level (the sum of the weights seen along a play prefix starting with energy zero) between zero and six using the following strategy: when at state \(s_0\) with energy level at least two, go to state \(s_1\), otherwise go to state \(s_2\) in order to satisfy the lower bound. At state \(s_1\), always move to \(s_0\). It is straightforward to verify that the strategy has the desired property when starting at the initial state \(s_0\) with initial energy zero. Note that this strategy requires memory to be implemented, as its choices depend on the current energy level and not only on the state the pebble is currently at.
Formally, the energy objective requires \(P_{0} \) to maintain an energy level within some (lower and/or upper) bounds, which are either given as input or existentially quantified. In the example above, \(P_{0} \) has a strategy to win for the energy objective with lower bound zero and upper bound six. Energy objectives [3, 11, 18, 19] and their combinations with parity objectives [9, 11] have received significant attention in the literature.
However, a plain energy (parity) objective is sometimes not sufficient to adequately model real-life systems. For example, consider the following specification for the controller of an oil pump, based on a case study [7]: it has to keep the amount of oil in an accumulator within given bounds (an energy objective with given lower and upper bounds) while keeping the average amount of oil in the accumulator below a given threshold in the long run. The latter requirement reduces the wear and tear of the system, but cannot be expressed as an energy objective nor as a parity objective. Constraints on the long-run average energy level (which exactly represents the amount of oil in our example) can be specified using the average-energy objective [5]. As seen in this example, they are typically studied in conjunction with bounds on the energy level.
Recall the example in Fig. 1. The aforementioned strategy for \(P_{0} \) guarantees a long-run average energy level, i.e., average-energy, of at most 11/4 (recall we want to minimize it): the outcome with worst average-energy is \(\big (s_0 s_2 (s_0 s_1)^3\big )^\omega \), with energy levels \((4,6,4,4,2,2,0,0)^\omega \).
The average-energy objective was first introduced by Thuijsman and Vrieze under the name total-reward [24] (there is an unrelated, more standard, objective called total-reward, see [5] for a discussion). Recently, the average-energy objective was independently revisited by Boros et al. [2] and by Bouyer et al. [5]. The former work studies Markov decision processes and stochastic games with average-energy objectives. The latter studies non-stochastic games with average-energy objectives, with or without lower and upper bounds on the energy level; it determines the complexity of computing the winner and the memory requirements for winning strategies in such games. In particular, it solves games with average-energy objectives with both an upper and a lower bound on the energy level by a reduction to mean-payoff games: to this end, the graph is extended to track the energy level between these bounds (a losing sink for \(P_{0} \) is reached if these bounds are exceeded). Thus, the bounds on the energy level are already taken care of and the average-energy objective can now be expressed as a mean-payoff objective [13], as the new graph encodes the current energy level in its weights. This reduction yields an exponential-time decision algorithm. Moreover, it is shown in [5] that these games are indeed  -complete. Note that the algorithm crucially depends on the upper bound being given as part of the input, which implies that the graph of the extended game is still finite.
-complete. Note that the algorithm crucially depends on the upper bound being given as part of the input, which implies that the graph of the extended game is still finite.
One problem left open in [5] concerns average-energy games with only a lower bound on the energy level: computing the winner is shown to be  -hard, but it is not known whether this problem is decidable at all. Similarly, pseudo-polynomial lower bounds (i.e., lower bounds that are polynomial in the values of the weights, but possibly exponential in the size of their binary representations) on the necessary memory to implement a winning strategy for \(P_{0} \) are given, but no upper bound is known. The major obstacle toward solving these problems is that without an upper bound on the energy, a strategy might allow arbitrarily large energy levels while still maintaining a bounded average, by enforcing long stretches with a small energy level to offset the large levels.
-hard, but it is not known whether this problem is decidable at all. Similarly, pseudo-polynomial lower bounds (i.e., lower bounds that are polynomial in the values of the weights, but possibly exponential in the size of their binary representations) on the necessary memory to implement a winning strategy for \(P_{0} \) are given, but no upper bound is known. The major obstacle toward solving these problems is that without an upper bound on the energy, a strategy might allow arbitrarily large energy levels while still maintaining a bounded average, by enforcing long stretches with a small energy level to offset the large levels.
A step toward resolving these problems was taken by considering two variants of energy and average-energy objectives where (i) the upper bound on the energy level, or (ii) the threshold on the average energy level, is existentially quantified [21]. It turns out that these two variants are equivalent. One direction is trivial: if the energy is bounded, then the average-energy is bounded. On the other hand, if \(P_{0} \) can guarantee some upper bound on the average, then he can also guarantee an upper bound on the energy level, i.e., an (existential) average-energy objective can always be satisfied with bounded energy levels. This is shown by transforming a strategy satisfying a bound on the average (but possibly allowing arbitrarily high energy levels) into one that bounds the energy by skipping parts of plays where the energy level is much higher than the threshold on the average. However, the proof is not effective: it does not yield an upper bound on the necessary energy level, just a guarantee that some bound exists. Even more so, it is still possible that the average has to increase when keeping the energy bounded. Hence, it does not answer our problem: does achieving a given threshold on the average-energy require unbounded energy levels and infinite memory?
Another potential approach toward solving the problem is to extend the reduction presented in [5] (which goes from average-energy games with both lower and upper bound on the energy level to mean-payoff games) to games without such an upper bound, which results in an infinite graph. This graph can be seen as the configuration graph of a one-counter pushdown system, i.e., the stack height corresponds to the current energy level, and the average-energy objective is again transformed into a mean-payoff objective, where the weight of an edge is given by the stack height at the target of the edge. Hence, the weight function is unbounded. To the best of our knowledge, such mean-payoff games have not been studied before. However, mean-payoff games on pushdown systems with bounded weight functions are known to be undecidable [12].
Our Contribution. We develop the first algorithm for solving games with average-energy objectives and a lower bound on the energy level, and give an upper bound on the necessary memory to implement a winning strategy for \(P_{0} \) in such games.
First, we present an algorithm for solving such games in doubly-exponential time (for the case of a binary encoding of the weights). The algorithm is based on the characterization of an average-energy game as a mean-payoff game on an infinite graph described above. If the average-energy of a play is bounded by the threshold t, then configurations with energy level at most t have to be visited frequently. As there are only finitely many such configurations, we obtain cycles on this play. By a more fine-grained analysis, we obtain such a cycle with an average of at most t and whose length is bounded exponentially. Finally, by analyzing strategies for reachability objectives in pushdown games, we show that \(P_{0} \) can ensure that the distance between such cycles is bounded doubly-exponentially. From these properties, we obtain a doubly-exponential upper bound on the necessary energy level to ensure an average-energy of at most t. The resulting equivalent average-energy game with a lower and an upper bound can be solved in doubly-exponential time. Furthermore, if the weights and the threshold are encoded in unary (or are bounded polynomially in the number of states), then we obtain an exponential-time algorithm.
Second, from the reduction sketched above, we also obtain a doubly-exponential upper bound on the necessary memory for \(P_{0} \), the first such bound. In contrast, a certain succinct one-counter game due to Hunter [16], which can easily be expressed as an average-energy game with threshold zero, shows that our bound is almost tight: in the resulting game of size n, energy level \(2^{({2^{\sqrt{n}}}/{\sqrt{n}})-1}\) is necessary to win. Again, in the case of unary encodings, we obtain an (almost) tight exponential bound on the memory requirements.
Third, we improve the lower bound on the complexity of solving average-energy games with only a lower bound on the energy level from  to
to  by a reduction from succinct one-counter games [17].
by a reduction from succinct one-counter games [17].
Fourth, we show that multi-dimensional average-energy games are undecidable, both for the case without any bounds and for the case of only lower bounds. Only the case of games with both lower and upper bounds turns out to be decidable: it is shown to be both in  and in
and in  . This problem trivially inherits
. This problem trivially inherits  -hardness from the one-dimensional case.
-hardness from the one-dimensional case.
2 Preliminaries
Graph games. We consider finite turn-based weighted games played on graphs between two players, denoted by \(P_{0} \) and \(P_{1} \). Such a game is a tuple \( G = (S_0, S_1, E )\) where (i) \(S_0\) and \(S_1\) are disjoint sets of states belonging to \(P_{0} \) and \(P_{1} \), with \(S = S_0 \uplus S_1\), (ii) \( E \subseteq S \times [-W;W] \times S\), for some \(W\in \mathbb {N}\), is a set of integer-weighted edges. Given an edge \(e=(s, w, t) \in E \), we write \( src (e)\) for the source state s of e, \( tgt (e)\) for its target state t, and \( w (e)\) for its weight w. We assume that for every \(s \in S\), there is at least one outgoing edge \((s,w,s') \in E\).
Let \(s\in S\). A play from s is an infinite sequence of edges \(\pi = (e_i)_{1\le i}\) such that \( src (e_1) = s\) and \( tgt (e_i)= src (e_{i+1})\) for all \(i \ge 1\). A play induces a corresponding sequence of states, denoted \(\hat{\pi } = (s_j)_{0\le j}\), such that for any \(e_i\), \(i \ge 1\), in \(\pi \), \(s_{i-1} = src (e_i)\) and \(s_{i} = tgt (e_i)\). We write \( first (\pi )=s_0\) for its initial state (here, s). A play prefix from s is a finite sequence of edges \(\rho = (e_i)_{1\le i \le k}\) following the same rules and notations. We additionally write \( last (\rho )= s_k = tgt (e_k)\) for its last state. We let \(\epsilon _s\) (or \(\epsilon \) when s is clear from the context) denote the empty play prefix from s, with \( last (\epsilon _s) = first (\epsilon _s) = s\). A non-empty prefix \(\rho \) such that \( last (\rho ) = first (\rho )\) is called a cycle. The length of a prefix \(\rho = (e_i)_{1\le i \le k}\) is its number of edges, i.e., \(\ell (\rho ) = k\). For a play \(\pi \), \(\ell (\pi ) = \infty \). Given a prefix \(\rho \) and a play (or prefix) \(\pi \) with \( last (\rho )= first (\pi )\), the concatenation between \(\rho \) and \(\pi \) is denoted by \(\rho \cdot \pi \).
For a play \(\pi = (e_i)_{1\le i}\) and \(1 \le j \le k\), we write \(\pi _{[j,k]}\) to denote the finite sequence \((e_i)_{j\le i\le k}\), which is a prefix from \( src (e_j)\); we write \(\pi _{\le k}\) for \(\pi _{[1,k]}\). For any \(i \ge 1\) and \(j \ge 0\), we write \(\pi _i\) for edge \(e_i\) and \(\hat{\pi }_j\) for state \(s_j\). Similar notations are used for prefixes \(\rho \), with all indices bounded by \(\ell (\rho )\).
The set of all plays in \( G \) from a state s is denoted by \( Plays ( G ,s)\), and the set of all such prefixes is denoted by \( Prefs ( G ,s)\). We write \( Plays ( G )\) and \( Prefs ( G )\) for the unions of those sets over all states. We say that a prefix \(\rho \in Prefs ( G )\) belongs to \(P_{i} \), for \(i \in \{0,1\}\), if \( last (\rho ) \in S_i\). The set of prefixes that belong to \(P_{i} \) is denoted by \( Prefs _i ( G )\), and we define \( Prefs _i ( G ,s) = Prefs _i ( G ) \cap Prefs ( G ,s)\).
Payoffs. Given a non-empty prefix \(\rho = (e_i)_{1\le i\le n}\), we define the following payoffs:
-
its energy level as

-
its mean-payoff as
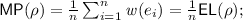
-
its average-energy as

These definitions are extended to plays by taking the upper limit of the respective functions applied to the sequence of prefixes of the plays, e.g.,

Example 1
We illustrate those definitions on a small example depicted in Fig. 2: it displays two small (1-player, deterministic) weighted games, together with the evolution of the energy level and average-energy along their unique play. As noted in [5], the average-energy can help in discriminating plays that have identical total-payoffs (i.e., the limits of high and low points in the sequence of energy levels), in the same way that total-payoff can discriminate between plays having the same mean-payoff. Indeed, in our example, both plays have mean-payoff equal to zero and supremum (resp. infimum) total-payoff equal to three (resp. \(-1\)), but they end up having different averages: the average-energy is 1 / 2 for the left play, while it is 3 / 2 for the right one.
Strategies. A strategy for \(P_{i} \), with \(i \in \{0,1\}\), from a state s is a function \(\sigma _i: Prefs _i( G , s) \rightarrow E \) satisfying \({ src (\sigma _i(\rho )) = last (\rho )}\) for all \(\rho \in Prefs _i( G , s)\). We denote by \( Strats _{i}( G , s)\), the set of strategies for \(P_{i} \) from state s. We drop \( G \) and s when they are clear from the context.
A play \(\pi = (e_j)_{1\le j}\) from s is called an outcome of strategy \(\sigma _i\) of \(P_{i} \) if, for all \(k \ge 0\) where \(\pi _{\le k} \in Prefs _i( G , s)\), we have \(\sigma _i(\pi _{\le k}) = e_{k+1}\). Given a state \(s \in S\) and strategies \(\sigma _0\) and \(\sigma _1\) from s for both players, we denote by \( Out (s, \sigma _0,\sigma _1)\) the unique play that starts in s and is an outcome of both \(\sigma _0\) and \(\sigma _1\). When fixing the strategy of only \(P_{i} \), we denote the set of outcomes by
Objectives. An objective in \( G \) is a set \(\mathcal {W} \subseteq Plays ( G )\). Given a game \( G \), an initial state \(s_{\mathsf{init}}\), and an objective \(\mathcal {W}\), a strategy \(\sigma _0 \in Strats _{0}\) is winning for \(P_{0} \) if \( Out (s_{\mathsf{init}}, \sigma _0) \subseteq \mathcal {W}\). We consider the following objectives for \(P_0\):
-
The lower-bounded energy objective
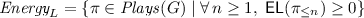 requires a non-negative energy level at all times.Footnote 1
requires a non-negative energy level at all times.Footnote 1
-
Given an upper bound \(U \in \mathbb {N}\), the lower- and upper-bounded energy objective
 requires that the energy always remains non-negative and below the upper bound U along a play.
requires that the energy always remains non-negative and below the upper bound U along a play. -
Given a threshold \(t \in \mathbb {Q}\), the mean-payoff objective \(\textit{MeanPayoff}(t) = \{ \pi \in Plays ( G ) \mid \mathsf {\overline{MP}}(\pi ) \le t \}\) requires that the mean-payoff is at most t.
-
Given a threshold \(t \in \mathbb {Q}\), the average-energy objective \(\textit{AvgEnergy}(t) = \{ \pi \in Plays ( G ) \mid \mathsf {\overline{AE}}(\pi ) \le t \}\) requires that the average-energy is at most t.
For the \(\textit{MeanPayoff}\) and \(\textit{AvgEnergy}\) objectives, \(P_{0} \) aims to minimize the payoff.
Decision problem. In this paper, we focus on weighted games with a combination of energy and average-energy objectives, by a detour via mean-payoff objectives. The exact problem we tackle is named the AEL threshold problem and is defined as follows: given a finite game \( G \), an initial state \(s_{\mathsf{init}}\in S\), and a threshold \(t \in \mathbb {Q}\) given as a fraction \(\frac{t_1}{t_2}\) with \(t_1\) and \(t_2\) two natural numbers given in binary, decide whether \(P_{0} \) has a winning strategy from \(s_{\mathsf{init}}\) for the objective \(\textit{AvgEnergy}_{L}(t) =\textit{Energy}_{L}\cap \textit{AvgEnergy}(t)\). As for the threshold, we consider a binary encoding of the weights in \( G \): we thus study the complexity of the problem with regard to the length of the input’s binary encoding (i.e., the number of bits used to represent the graph and the numbers involved).
Variants of this problem involving the above-mentioned payoff functions, and combinations thereof, had been previously investigated, see Table 1 for a summary of the results. In this paper, we focus on the remaining case, namely 2-player games with AEL objectives, for which decidability was not known, and proving the computational- and memory complexities given in the corresponding cells of the table.
3 Equivalence with an Infinite-State Mean-Payoff Game
Let \(G=(S_0,S_1,E)\) be a finite weighted game, \(s_{\mathsf{init}}\in S\) be an initial state, and \(t \in \mathbb {Q}\) be a threshold. We define its expanded infinite-state weighted game as \(G'=(\varGamma _0,\varGamma _1,\varDelta )\) defined by
-
\(\varGamma _0 = S_0 \times \mathbb {N}\), and \(\varGamma _1 = S_1 \times \mathbb {N}\uplus \{\bot \}\) (where \(\bot \) is a fresh sink state that does not belong to G); then \(\varGamma = \varGamma _0 \uplus \varGamma _1\) is the global set of states;
-
\(\varDelta \) is composed of the following edges:
-
a transition \(((s,c),c',(s',c')) \in \varDelta \) whenever there is \((s,w,s') \in E\) with \(c' = c+w \ge 0\);
-
a transition \(((s,c),\lceil t\rceil +1,\bot ) \in \varDelta \) whenever there is \((s,w,s') \in E\) such that \(c+w <0\);
-
finally, a transition \((\bot ,\lceil t\rceil +1, \bot ) \in \varDelta \).
-
In this expanded game, elements of \(\varGamma \) are called configurations, and the initial configuration is set to \((s_{\mathsf{init}},0)\).
Lemma 1
Player \(P_{0} \) has a winning strategy in G from state \(s_{\mathsf{init}}\) for the objective \(\textit{AvgEnergy}_{L}(t)\) if, and only if, he has a winning strategy in \(G'\) from configuration \((s_{\mathsf{init}},0)\) for the objective \(\textit{MeanPayoff}(t)\).
For the rest of this paper, we fix a weighted game \(G = (S_0,S_1,E)\) and a threshold \(t \in \mathbb {Q}\), and work on the corresponding expanded weighted game \(G' = (\varGamma _0,\varGamma _1,\varDelta )\). We write \(t = \frac{t_1}{t_2} = \lfloor t \rfloor + \frac{t'}{t_2}\), where \(t_1, t_2, t' \in \mathbb {N}\) (recall they are given in binary), and \(0 \le t' < t_2\), and \(\lfloor t \rfloor \) stands for the integral part of t. We also let \(\widetilde{t}= \lfloor t \rfloor +1-t = 1-\frac{t'}{t_2}\). Hence \(\widetilde{t}=1\) indicates that t is an integer. For a given threshold \(t\in \mathbb {Q}\), we consider \(\varGamma ^{\le t} = \{(s,c) \in \varGamma \mid c \le t\}\), i.e., the set of configurations below the threshold.
Note that \(G'\) can be interpreted as a one-counter pushdown mean-payoff game with an unbounded weight function. While it is well-known how to solve mean-payoff games over finite arenas, not much is known for infinite arenas (see Sect. 1). However, our game has a special structure that we will exploit to obtain an algorithm. Roughly, our approach consists in transforming the \(\textit{AvgEnergy}_{L}(t)\) objective into an equivalent \(\textit{AvgEnergy}_{LU}(t,U) = \textit{Energy}_{LU}(U) \cap \textit{AvgEnergy}(t)\) objective, where (the value of) U is doubly-exponential in the input by analyzing plays and strategies in \(G'\). In other terms, we show that any winning strategy for \(\textit{AvgEnergy}_{L}(t)\) can be transformed into another winning strategy along which the energy level remains upper-bounded by U.
The proof is two-fold: we first show (in Sect. 4) that we can bound the energy level for the special case where the objective consists in reaching a finite set of configurations of the game (with only a lower bound on the energy level). This is achieved by a detour to pushdown games: while there are known algorithms for solving reachability pushdown games, to the best of our knowledge, there are no (explicit) results bounding the maximal stack height.
As a second step (in Sect. 5), we identify good cycles in winning outcomes, and prove that they can be shown to have bounded length. The initial configurations of those cycles will then be the targets of the reachability games above. Combining these two results yields the desired upper bound on the energy levels.
4 Bounding One-Counter Reachability Games
We focus here on a reachability objective in \(G'\), where the target set is a subset \(\varGamma '\subseteq \varGamma ^{\le t}\): we aim at bounding the maximal energy level that needs to be visited with a winning strategy.
The game \(G'\) is a particular case of a pushdown game [26]. Hence we use results on pushdown games, and build a new winning strategy, in which we will be able to bound the energy level at every visited configuration. Note that the bound \(M'\) in the following lemma is doubly-exponential, as we encode W, the largest absolute weight in G, and the threshold t, in binary. The proof of the next lemma is based on the reformulation of the algorithm from [26] made in [15].
Lemma 2
Fix \(M \in \mathbb {N}\). There exists \(M' = 2^{\mathcal {O}(M + \left| S\right| + \left| E\right| \cdot W + \left| S\right| \cdot (\lceil t\rceil +1))}\) such that for every \(\gamma =(s,c)\) with \(c \le M\) and for every \(\varGamma ' \subseteq \varGamma ^{\le t}\), if there is a strategy for \(P_{0} \) to reach \(\varGamma '\) from \(\gamma \) in \(G'\), then there is also a strategy which ensures reaching \(\varGamma '\) from \(\gamma \) without exceeding energy level \(M'\).
5 A Doubly-Exponential Time Algorithm
Let  be a set of configurations of \({G'}\), and \({\rho }\) be a play prefix. We define
be a set of configurations of \({G'}\), and \({\rho }\) be a play prefix. We define

which denotes the proportion (or density) of configurations belonging to  along
along  . Observe that the initial configuration
. Observe that the initial configuration  is not taken into account: this is because
is not taken into account: this is because  will be strongly linked to the mean-payoff, as we now explain.
will be strongly linked to the mean-payoff, as we now explain.
5.1 Analyzing Winning Plays
In this section, we analyze winning plays in \(G'\), and prove that they must contain a cycle that is “short enough” and has mean-payoff less than or equal to t.
To achieve this, we observe that if the mean-payoff of a play \(\pi \) is less than t, then there must exist a configuration \(\gamma \in \varGamma ^{\le t}\) that appears frequently enough along \(\pi \). Applying a sequence of elementary arguments, we can even give a uniform lower bound on the density of \(\gamma \) along arbitrarily far and arbitrarily long segments of \(\pi \). More precisely, we show:
Lemma 3
Let \(\pi \) be a play in \(G'\) from \((s_{\mathsf{init}},0)\) with \(\mathsf {\overline{MP}}(\pi )\le t\). There exists \(\gamma \in \varGamma ^{\le t}\) such that for any \(n\in \mathbb {N}\), there are infinitely many positions \(n'\ge n\) for which
Next we say that a cycle of \(G'\) is good whenever it starts in \(\varGamma ^{\le t}\) and its mean-payoff is bounded by t. Since \(\gamma \) appears frequently along \(\pi \), we shall argue that it is not possible that all cycles along \(\pi \) delimited by \(\gamma \) are bad (i.e., not good), otherwise the global mean-payoff of \(\pi \) could not be bounded by t.
Hence we obtain that \(\pi \) contains a good cycle delimited by \(\gamma \). It remains to argue that such a minimal-length good cycle (i.e., with no good nested sub-cycle) cannot be too long. We write \(\mathcal {C}\) for a minimal-length good cycle delimited by \(\gamma \). This part of the proof appeals to a second density argument for \(\gamma \) along \(\mathcal {C}\): since \(\mathcal {C}\) does not contain good sub-cycles, it cannot contain too many sub-cycles at all. Letting \(N = 8 t_1 t_2 (t +1)^3|S|^2\), we prove:
Proposition 4
Let \(\pi \) be a play in \(G'\) from \((s_{\mathsf{init}},0)\) with \(\mathsf {\overline{MP}}(\pi )\le t\). Then there exist \(1 \le i \le j\) such that \(\pi _{[i,j]}\) is a good cycle of length at most N.
5.2 Strategies Described by Finite Trees
So far, we have proven that \(P_{0} \) should “target” short good cycles. However in a two-player context, \(P_{1} \) might prevent \(P_{0} \) from doing so. We therefore need to consider the branching behaviour of the game, and not only the linear point-of-view given by a play. Toward that aim, we represent strategies (of \(P_{0} \)) as strategy trees, and use them to bound the amount of memory and the counter values needed to win in \(G'\).
We consider labelled trees with backward edges \(\mathcal {T}= (\mathcal {N},\mathcal {E},\lambda ,\dashrightarrow )\), where \(\mathcal {N}\) is a finite set of nodes, \(\lambda :\mathcal {N}\rightarrow S \times \mathbb {N}\) (each node is labelled with a configuration of the game \(G'\)), and \(\mathord {\dashrightarrow } \subseteq \mathcal {N}\times \mathcal {N}\). We assume \(\mathcal {T}\) has at least two nodes. The relation \(\mathcal {E}\) is the successor relation between nodes. A node with no \(\mathcal {E}\)-successor is called a leaf; other nodes are called internal nodes. The root of \(\mathcal {T}\), denoted by \(\mathbf {n}_{\mathsf {root}}\), is the only node having no predecessor. The relation \(\dashrightarrow \) is an extra relation between nodes that will become clear later.
For such a tree to represent a strategy, we require that each internal node \(\mathbf {n}\) that is labelled by a \(P_{0} \)-configuration (s, c) has only one successor \(\mathbf {n'}\), with \(\lambda (\mathbf {n'})=(s',c')\) such that there is a transition \(((s,c),c',(s',c'))\) in the game \(G'\); we require that each internal node \(\mathbf {n}\) that is labelled with a \(P_{1} \)-state (s, c) has exactly one successor per transition \(((s,c),c',(s',c'))\) in \(G'\), each successor being labelled with its associated \((s',c')\). Finally, we require that each leaf \(\mathbf {n}\) of \(\mathcal {T}\) has a (strict) ancestor node \(\mathbf {n'}\) such that \(\lambda (\mathbf {n'}) = \lambda (\mathbf {n})\). The relation \(\dashrightarrow \) will serve witnessing that property. So we assume that for every leaf \(\mathbf n\), there is a unique ancestor node \(\mathbf n'\) such that  ; furthermore it should be the case that \(\lambda (\mathbf {n'}) = \lambda (\mathbf {n})\). Under all these constraints, \(\mathcal {T}\) is called a strategy tree. It basically represents a (finite) memory structure for a strategy, as we now explain.
; furthermore it should be the case that \(\lambda (\mathbf {n'}) = \lambda (\mathbf {n})\). Under all these constraints, \(\mathcal {T}\) is called a strategy tree. It basically represents a (finite) memory structure for a strategy, as we now explain.
Let \(\mathcal {T}= (\mathcal {N},\mathcal {E},\lambda ,\dashrightarrow )\) be strategy tree for \(G'\). We define \(\mathcal {G}_\mathcal {T}= (\mathcal {N},\mathcal {E}')\), a directed graph obtained from \(\mathcal {T}\) by adding extra edges \((\mathbf n, \mathbf {n''})\) for each leaf \(\mathbf n\) and node \(\mathbf {n''}\) for which there exists another node \(\mathbf {n'}\) satisfying \(\mathbf n\dashrightarrow \mathbf {n'}\) and \({(\mathbf {n'},\mathbf {n''})\in \mathcal {E}}\). We refer to these extra edges as back-edges. One may notice that for any \((\mathbf n,\mathbf {n'})\in \mathcal {E}'\) there is an edge from \(\lambda (\mathbf n)\) to \(\lambda (\mathbf {n'})\) in \(G'\). Given two nodes \(\mathbf n\) and \(\mathbf {n'}\) such that \(\mathbf {n'}\) is an ancestor of \(\mathbf n\) in \(\mathcal {T}\), we write \([\mathbf {n'} \leadsto \mathbf n]\) for the play prefix from \(\mathbf {n'}\) to \(\mathbf n\) (inclusive) using only transitions from \(\mathcal {E}\).
Now, we associate with any prefix \(\rho \) in \(\mathcal {G}_\mathcal {T}\) from \(\mathbf {n}_{\mathsf {root}}\) a prefix \(\overline{\rho }\) in \(G'\) from \(\lambda (\mathbf {n}_{\mathsf {root}})=(s_{\mathsf {root}}, c_{\mathsf {root}})\) such that \( last (\overline{\rho }) = \lambda ( last (\rho ))\). The construction is inductive:
-
with the empty prefix in \(\mathcal {G}_\mathcal {T}\) we associate the one in \(G'\): \(\overline{\epsilon _{\mathbf {n}_{\mathsf {root}}}} = \epsilon _{(s_{\mathsf {root}}, c_{\mathsf {root}})}\),
-
if \(\rho =\rho '\cdot (\mathbf {n'}, \mathbf n)\) with \((\mathbf {n'},\mathbf n)\in \mathcal {E}'\), writing \((s',c')=\lambda (\mathbf {n'})\) and \((s,c)=\lambda (\mathbf n)\), then \(\overline{\rho }= \overline{\rho '}\cdot ((s',c'),c,(s,c))\) (which by construction is indeed a prefix in \(G'\)).
We now explain how \(\mathcal {G}_\mathcal {T}\) corresponds to a strategy in \(G'\): for any prefix \(\rho \) in \(\mathcal {G}_\mathcal {T}\), if \(\lambda ( last (\rho ))=(s,c) \in \varGamma _0\), then \( last (\rho )\) has a unique successor \(\mathbf {n'}\) in \(\mathcal {G}_\mathcal {T}\), and, writing \((s',c')=\lambda (\mathbf {n'})\), we define \(\sigma _\mathcal {T}(\overline{\rho })=((s,c),c',(s',c'))\): \(\sigma _\mathcal {T}\) is a (partially defined) strategy in \(G'\). The following lemma states that \(\mathcal {G}_\mathcal {T}\) actually represents the outcomes of the well-defined strategy \(\sigma _\mathcal {T}\) from \(\lambda (\mathbf {n}_{\mathsf {root}})\) in \(G'\):
Lemma 5
Let \(\mu \) be a prefix in \(G'\) from \((s_{\mathsf {root}},c_{\mathsf {root}})\). Assume that for every \(i\le \ell (\mu )\) such that \( last (\mu _{\le i})\in \varGamma _0\), the function \(\sigma _\mathcal {T}\) is defined on \(\mu _{\le i}\) and \(\mu _{\le i+1}=\mu _{\le i}\cdot \sigma _{\mathcal {T}}(\mu _{\le i})\). Then there exists a unique prefix \(\rho \) in \(\mathcal {G}_\mathcal {T}\) such that \(\mu =\overline{\rho }\), Moreover, if \( last (\mu )\in \varGamma _0\), then \(\sigma _\mathcal {T}(\mu )\) is defined.
We now give conditions for \(\sigma _\mathcal {T}\) to be a winning strategy from \((s_{\mathsf {root}},c_{\mathsf {root}})\) in \(G'\). With a finite outcome \(\mu =\overline{\rho }\) of \(\sigma _\mathcal {T}\) from \((s_{\mathsf {root}},c_{\mathsf {root}})\), we associate a sequence \(\textit{decomp} _\mathcal {T}(\mu )\) of cycles in \(G'\), defined inductively as follows:
-
\(\textit{decomp} _\mathcal {T}(\epsilon _{(s_{\mathsf {root}}, c_{\mathsf {root}})})\) is empty;
-
if \(\rho =\rho '\cdot (\mathbf {n'},\mathbf n)\) and \(\mathbf n\) is not a leaf of \(\mathcal {T}\), then \(\textit{decomp} _{\mathcal {T}}(\overline{\rho })=\textit{decomp} _{\mathcal {T}}(\overline{\rho '})\);
-
if \(\rho =\rho '\cdot (\mathbf {n'},\mathbf n)\) and \(\mathbf n\) is a leaf of \(\mathcal {T}\), we let \(\mathbf {n''}\) be such that \(\mathbf n \dashrightarrow \mathbf {n''}\); the prefix \([\mathbf {n''}\leadsto \mathbf n]\) in \(\mathcal {T}\) corresponds to a cycle C in \(G'\), and we let \(\textit{decomp} _\mathcal {T}(\overline{\rho })=\textit{decomp} _\mathcal {T}(\overline{\rho '})\cdot C\).
The sequence \(\textit{decomp} _\mathcal {T}(\overline{\rho })\) hence contains all full cycles (closed at leaves) encountered while reading \(\rho \) in \(\mathcal {T}\): hence it comprises all edges of \(\rho \) except a prefix starting at \(\mathbf {n}_{\mathsf {root}}\) and a suffix since the last back-edge has been taken. It is not hard to see that those can actually be concatenated. By induction, we can easily show:
Proposition 6
Let \(\mu \) be a non-empty finite outcome of \(\sigma _{\mathcal {T}}\) from \((s_{\mathsf {root}},c_{\mathsf {root}})\) in \(G'\). Write \(\textit{decomp} _{\mathcal {T}}(\mu ) = C_0 \cdot C_1 \cdot \ldots \cdot C_h\) (where each \(C_i\) is a cycle). Let \(\rho \) be the prefix in \(\mathcal {G}_\mathcal {T}\) such that \(\mu =\overline{\rho }\), \(\mathbf n= last (\rho )\), and \(\nu =[\mathbf {n}_{\mathsf {root}}\leadsto \mathbf n]\). Write \((s_j,c_j)=\lambda (\hat{\nu }_j)\). Then:

We say that a tree is good if, for every \(\mathbf {n} \dashrightarrow \mathbf {n'}\) in \(\mathcal {T}\), writing \(\rho =[\mathbf {n'} \leadsto \mathbf n]\) and letting \(\lambda (\hat{\rho }_j)=(s_j,c_j)\), it holds \( \frac{\sum _{j=1}^{\ell (\rho )} c_j}{\ell (\rho )} \le t \).
Proposition 7
If \(\mathcal {T}\) is a finite good strategy tree, then \(\sigma _{\mathcal {T}}\) is a winning strategy from \((s_{\mathsf {root}},c_{\mathsf {root}})\) in \(G'\).
Note that \(\mathcal {T}\) can be interpreted as a finite memory structure for strategy \(\sigma _\mathcal {T}\): to know which move is given by \(\sigma _\mathcal {T}\), it is sufficient to move a token in tree \(\mathcal {T}\), going down in the tree, and following back-edges when stuck at leaves.
5.3 Analyzing Winning Strategies
We proved in the previous section that the finite-memory strategy associated with a finite good strategy tree is winning. In this section, we first show the converse direction, proving that from a winning strategy, we can obtain a finite good tree. In that tree, backward edges correspond to (short) good cycles. We then use the result of Sect. 4 for showing that those parts of the tree that do not belong to a segment \([\mathbf n \leadsto \mathbf {n'}]\) with  can be replaced with other substrategies in which the counter value is uniformly bounded. That way, we show that if there is a winning strategy for our games, then there is one where the counter value is uniformly bounded along all outcomes. This will allow to apply algorithms for solving games with average-energy payoff under lower- and upper-bound constraints [5].
can be replaced with other substrategies in which the counter value is uniformly bounded. That way, we show that if there is a winning strategy for our games, then there is one where the counter value is uniformly bounded along all outcomes. This will allow to apply algorithms for solving games with average-energy payoff under lower- and upper-bound constraints [5].
Fix a winning strategy \(\sigma \) for \(P_{0} \) from \((s_0,c_0)\) in \(G'\). We let

and for every \(\pi _{\le n} \in \textsf {goodpref}(\sigma )\), we define \( back (\pi _{\le n})\) as \(\pi _{\le m}\) such that \(\pi _{[m+1,n]}\) is a good cycle with no good strict sub-cycle.
We build a strategy tree \(\mathcal {T}_{\sigma }\) as follows:
-
the nodes of \(\mathcal {T}_\sigma \) are all the prefixes of the finite plays in \(\textsf {goodpref}(\sigma )\); the edges relate each prefix of length k to its extensions of length \(k+1\). For a node \(\mathbf n\) corresponding to prefix \(\rho _{\le k}\) (with \(\rho \in \textsf {goodpref}(\sigma )\)), we let \(\lambda (\mathbf n)= last (\rho _{\le k})\); we let \(\lambda (\mathbf {n}_{\mathsf {root}})=(s_0,c_0)\). The leaves of \(\mathcal {T}_\sigma \) then correspond to the play prefixes that are in \(\textsf {goodpref}(\sigma )\).
-
backward edges in \(\mathcal {T}_\sigma \) are defined by noticing that each leaf \(\mathbf n\) of \(\mathcal {T}_\sigma \) corresponds to a finite path \(\pi _{\le n}\) in \(\textsf {goodpref}(\sigma )\), so that the prefix \(\pi _{\le m}= back (\pi _{\le n})\) is associated with some node \(\mathbf m\) of \(\mathcal {T}_\sigma \) such that \(\pi _{[m+1,n]}\) is a good cycle. This implies \(\lambda (\pi _{\le n})=\lambda (\pi _{\le m})\), and we define
 . This way, \(\mathcal {T}_\sigma \) is a strategy tree as defined in Sect. 5.2.
. This way, \(\mathcal {T}_\sigma \) is a strategy tree as defined in Sect. 5.2.
Lemma 8
Tree \(\mathcal {T}_\sigma \) is a finite good strategy tree.
Applying Proposition 7, we immediately get:
Corollary 9
Strategy \(\sigma _{\mathcal {T}_{\sigma }}\) is a winning strategy from \((s_0,c_0)\).
Let  be two related nodes in \(\mathcal {T}_\sigma \). We say that a node \(\mathbf {n''}\) is just below \([\mathbf {n'} \leadsto \mathbf {n}]\) in \(\mathcal {T}_\sigma \) whenever its predecessor appears along \([\mathbf {n'} \leadsto \mathbf {n}]\), but node \(\mathbf {n''}\) itself does not appear along any path \([\mathbf {n_1} \leadsto \mathbf {n_2}]\) for which
be two related nodes in \(\mathcal {T}_\sigma \). We say that a node \(\mathbf {n''}\) is just below \([\mathbf {n'} \leadsto \mathbf {n}]\) in \(\mathcal {T}_\sigma \) whenever its predecessor appears along \([\mathbf {n'} \leadsto \mathbf {n}]\), but node \(\mathbf {n''}\) itself does not appear along any path \([\mathbf {n_1} \leadsto \mathbf {n_2}]\) for which  . Such nodes, together with the root of the tree, are called the critical nodes (see Fig. 3).
. Such nodes, together with the root of the tree, are called the critical nodes (see Fig. 3).
Lemma 10
If \(\mathbf {n}\) is a critical node in \(\mathcal {T}_\sigma \), then writing \(\lambda (\mathbf {n}) = (s,c)\), we have that \(c \le t + W \cdot (N+1)\).
Given a critical node \(\mathbf {n}\), we define

Looking again at Fig. 3, the targets of a critical node are the start nodes of the good cycles that are closest to that critical node. In particular, for the rightmost critical node on Fig. 3, there are two candidate target nodes (because there are two overlapping good cycles), but only the topmost one is a target.
For every critical node \(\mathbf {n}\), we apply Lemma 2 with \(\gamma = \lambda (\mathbf {n})\) and \(\varGamma '_\gamma = \{\gamma ' = \lambda (\mathbf {n'}) \mid \mathbf {n'} \in \textit{target}(\mathbf {n})\}\), setting \(M = t + W \cdot (N+1)\). We write \(\sigma _{\mathbf {n}}\) for the corresponding strategy: applying \(\sigma _{\mathbf {n}}\) from \(\lambda (\mathbf {n})\), player \(P_0\) will reach some configuration \((s',c')\) such that there is a node \(\mathbf {n'} \in \textit{target}(\mathbf {n})\) with \(\lambda (\mathbf {n'}) = (s',c')\).
Now, for any node \(\mathbf {n'}\) that is the target of a backward edge  , but whose immediate predecessor does not belong to any segment \([\mathbf {n_1} \leadsto \mathbf {n_2}]\) with
, but whose immediate predecessor does not belong to any segment \([\mathbf {n_1} \leadsto \mathbf {n_2}]\) with  , we define strategy \(\sigma _{[\mathbf {n'}]}\) which follows good cycles as much as possible; when a leaf \(\mathbf m\) is reached, the strategy replays similarly as from the equivalent node \(\mathbf {m'}\) for which
, we define strategy \(\sigma _{[\mathbf {n'}]}\) which follows good cycles as much as possible; when a leaf \(\mathbf m\) is reached, the strategy replays similarly as from the equivalent node \(\mathbf {m'}\) for which  . If, while playing that strategy, the play ever leaves a good cycle (due to a move of player \(P_1\)), then it reaches a critical node \(\mathbf {n''}\). From that node, we will apply strategy \(\sigma _{\mathbf {n''}}\) as defined above, and iterate like this.
. If, while playing that strategy, the play ever leaves a good cycle (due to a move of player \(P_1\)), then it reaches a critical node \(\mathbf {n''}\). From that node, we will apply strategy \(\sigma _{\mathbf {n''}}\) as defined above, and iterate like this.
This defines a strategy \(\sigma '\). Applying Lemma 2 to strategies \(\sigma _{\mathbf {n}}\) when \(\mathbf {n}\) is critical, and the previous analysis of good cycles, we get the following doubly-exponential bound on the counter value (which is only exponential in case constants W, \(t_1\), and \(t_2\) are encoded in unary):
Proposition 11
Strategy \(\sigma '\) is a winning strategy from \((s_0,c_0)\), and all visited configurations (s, c) when applying \(\sigma '\) are such that \(c \le M'\) with
5.4 Conclusion
Gathering everything we have done above, we get the following equivalence.
Proposition 12
Player \(P_{0} \) has a winning strategy in game G from \(s_{\mathsf{init}}\) for the objective \(\textit{AvgEnergy}_{L}(t)\) if, and only if, he has a wining strategy in G from \(s_{\mathsf{init}}\) for the objective \(\textit{AvgEnergy}_{LU}(t,U) =\textit{Energy}_{LU}(U) \cap \textit{AvgEnergy}(t)\), where \(U = M'\) is the bound from Proposition 11.
Hence we can use the algorithm for games with objectives \(\textit{AvgEnergy}_{LU}(t,U)\) in [5], which is polynomial in \(\left| S\right| \), \(\left| E\right| \), t, and U (hence pseudo-polynomial only). Having in mind that the upper bound U is doubly-exponential, we can deduce our main decidability result. The memory required is also a consequence of [5].
Theorem 13
The AEL threshold problem is in  . Furthermore doubly-exponential memory is sufficient to win (for player \(P_{0} \)).
. Furthermore doubly-exponential memory is sufficient to win (for player \(P_{0} \)).
We could not prove a matching lower-bound, but relying on [17], we can prove  -hardness:
-hardness:
Theorem 14
The AEL threshold problem is  -hard, even for the fixed threshold zero.
-hard, even for the fixed threshold zero.
In [16], a super-exponential lower bound is given for the required memory to win a succinct one-counter game. While the model of games is not exactly the same, the actual family of games witnessing that lower bound on the memory happens to be usable as well for the AEL threshold problem (with threshold zero). The reduction is similar to the one in the proof of Theorem 14. This yields a lower bound on the required memory to win games with \(\textit{AvgEnergy}_{L}(t)\) objectives which is \(2^{({2^{\sqrt{n}}}/{\sqrt{n}})-1}\).
For unary encodings or small weights we get better results from our technique:
Corollary 15
The AEL threshold problem is in  and exponential memory is sufficient to win (for player \(P_{0} \)), if the weights and the threshold are encoded in unary or polynomial in the size of the graph.
and exponential memory is sufficient to win (for player \(P_{0} \)), if the weights and the threshold are encoded in unary or polynomial in the size of the graph.
6 Multi-dimensional Average-Energy Games
We now turn to a more general class of games where integer weights on the edges are replaced by vectors of integer weights, representing changes in different quantitative aspects. That is, for a game \( G = (S_0, S_1, E )\) of dimension \(k \ge 1\), we now have \( E \subseteq S \times [-W,W]^k\times S\) for \(W \in \mathbb {N}\). Multi-dimensional games have recently gained interest as a powerful model to reason about interplays and trade-offs between different resources; and multi-dimensional versions of many classical objectives have been considered in the literature: e.g., mean-payoff [11, 25], energy [11, 19, 25], or total-payoff [10]. We consider the natural extensions of threshold problems in the multi-dimensional setting: we take the zero vector in \(\mathbb {N}^k\) as lower bound for the energy, a vector \(U \in \mathbb {N}^k\) as upper bound, a vector \(t \in \mathbb {Q}^k\) as threshold for the average-energy, and the payoff functions are defined using component-wise limits. That is, we essentially take the conjunction of our objectives for all dimensions. We quickly review the situation for the three types of average-energy objectives.
Average-energy games (without energy bounds). In the one-dimensional version of such games, memoryless strategies suffice for both players and the threshold problem is in  [5]. We prove here that already for games with three dimensions, the threshold problem is undecidable, based on a reduction from two-dimensional robot games [22]. Decidability for average-energy games with two dimensions remains open.
[5]. We prove here that already for games with three dimensions, the threshold problem is undecidable, based on a reduction from two-dimensional robot games [22]. Decidability for average-energy games with two dimensions remains open.
Theorem 16
The threshold problem for average-energy games with three or more dimensions is undecidable. That is, given a finite k-dimensional game \( G = (S_0, S_1, E)\), for \(k \ge 3\), an initial state \(s_{\mathsf{init}}\in S\), and a threshold \(t \in \mathbb {Q}^k\), determining whether \(P_{0} \) has a winning strategy from \(s_{\mathsf{init}}\) for objective \(\textit{AvgEnergy}(t)\) is undecidable.
Average-energy games with lower and upper bounds. One-dimensional versions of those games were proved to be  -complete in [5]. The algorithm consists in reducing (in two steps) the original game to a mean-payoff game on an expanded graph of pseudo-polynomial size (polynomial in the original game but also in the upper bound \(U \in \mathbb {N}\)) and applying a pseudo-polynomial time algorithm for mean-payoff games (e.g., [6]). Intuitively, the trick is that the bounds give strong constraints on the energy levels that can be visited along a play without losing and thus one can restrict the game to a particular graph where acceptable energy levels are encoded in the states and exceeding the bounds is explicitely represented by moving to “losing” states, just as we did in Sect. 3 for the lower bound. Carefully inspecting the construction of [5], we observe that the same construction can be generalized straightforwardly to the multi-dimensional setting. However, the overall complexity is higher: first, the expanded graph will be of exponential size in
k, the number of dimensions, while still polynomial in S and U. Second, multi-dimensional limsup mean-payoff games are in
-complete in [5]. The algorithm consists in reducing (in two steps) the original game to a mean-payoff game on an expanded graph of pseudo-polynomial size (polynomial in the original game but also in the upper bound \(U \in \mathbb {N}\)) and applying a pseudo-polynomial time algorithm for mean-payoff games (e.g., [6]). Intuitively, the trick is that the bounds give strong constraints on the energy levels that can be visited along a play without losing and thus one can restrict the game to a particular graph where acceptable energy levels are encoded in the states and exceeding the bounds is explicitely represented by moving to “losing” states, just as we did in Sect. 3 for the lower bound. Carefully inspecting the construction of [5], we observe that the same construction can be generalized straightforwardly to the multi-dimensional setting. However, the overall complexity is higher: first, the expanded graph will be of exponential size in
k, the number of dimensions, while still polynomial in S and U. Second, multi-dimensional limsup mean-payoff games are in  [25].
[25].
Theorem 17
The threshold problem for multi-dimensional average-energy games with lower and upper bounds is in  . That is, given a finite k-dimensional game \( G = (S_0, S_1, E)\), an initial state \(s_{\mathsf{init}}\in S\), an upper bound \(U \in \mathbb {N}^k\), and a threshold \(t \in \mathbb {Q}^k\), determining if \(P_{0} \) has a winning strategy from \(s_{\mathsf{init}}\) for objective \(\textit{Energy}_{LU}(U) \cap \textit{AvgEnergy}(t)\) is in
. That is, given a finite k-dimensional game \( G = (S_0, S_1, E)\), an initial state \(s_{\mathsf{init}}\in S\), an upper bound \(U \in \mathbb {N}^k\), and a threshold \(t \in \mathbb {Q}^k\), determining if \(P_{0} \) has a winning strategy from \(s_{\mathsf{init}}\) for objective \(\textit{Energy}_{LU}(U) \cap \textit{AvgEnergy}(t)\) is in  .
.
Whether the  -hardness that trivially follows from the one-dimensional case [5] can be enhanced to meet this upper bound (or conversely) is an open problem.
-hardness that trivially follows from the one-dimensional case [5] can be enhanced to meet this upper bound (or conversely) is an open problem.
Average-energy games with lower bound but no upper bound. Finally, we consider the core setting of this paper, which we just proved decidable in one-dimension, solving the open problem of [5]. Unfortunately, we show that those games are undecidable as soon as two-dimensional weights are allowed. To prove it, we reuse some ideas of the proof of undecidability for multi-dimensional total-payoff games presented in [10], but specific gadgets need to be adapted.
Theorem 18
The threshold problem for lower-bounded average-energy games with two or more dimensions is undecidable. That is, given a finite k-dimensional game \( G = (S_0, S_1, E)\), for \(k \ge 2\), an initial state \(s_{\mathsf{init}}\in S\), and a threshold \(t \in \mathbb {Q}^k\), determining whether \(P_{0} \) has a winning strategy from \(s_{\mathsf{init}}\) for objective \(\textit{AvgEnergy}_{L}(t)\) is undecidable.
Notes
- 1.
For the sake of readability, we assume the initial credit to be zero for energy objectives throughout this paper. Still, our techniques can easily be generalized to an arbitrary initial credit \(c_{\mathsf{init}}\in \mathbb {N}\).
References
Bloem, R., Chatterjee, K., Henzinger, T.A., Jobstmann, B.: Better quality in synthesis through quantitative objectives. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 140–156. Springer, Heidelberg (2009). doi:10.1007/978-3-642-02658-4_14
Boros, E., Elbassioni, K., Gurvich, V., Makino, K.: Markov decision processes and stochastic games with total effective payoff. In: Mayr , E.W., Ollinger, N. (eds.) STACS 2015, LIPics, vol. 30, pp. 103–115. Leibniz-Zentrum für Informatik (2015)
Bouyer, P., Fahrenberg, U., Larsen, K.G., Markey, N., Srba, J.: Infinite runs in weighted timed automata with energy constraints. In: Cassez, F., Jard, C. (eds.) FORMATS 2008. LNCS, vol. 5215, pp. 33–47. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85778-5_4
Bouyer, P., Hofman, P., Markey, N., Randour, M., Zimmermann, M.: Bounding average-energy games. arXiv:1610.07858 (2016)
Bouyer, P., Markey, N., Randour, M., Larsen, K.G., Laursen, S.: Average-energy games. Acta Informatica (2016, in press)
Brim, L., Chaloupka, J., Doyen, L., Gentilini, R., Raskin, J.-F.: Faster algorithms for mean-payoff games. Formal Methods Syst. Des. 38(2), 97–118 (2011)
Cassez, F., Jessen, J.J., Larsen, K.G., Raskin, J.-F., Reynier, P.-A.: Automatic synthesis of robust and optimal controllers – an industrial case study. In: Majumdar, R., Tabuada, P. (eds.) HSCC 2009. LNCS, vol. 5469, pp. 90–104. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00602-9_7
Chakrabarti, A., Alfaro, L., Henzinger, T.A., Stoelinga, M.: Resource interfaces. In: Alur, R., Lee, I. (eds.) EMSOFT 2003. LNCS, vol. 2855, pp. 117–133. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45212-6_9
Chatterjee, K., Doyen, L.: Energy parity games. Theor. Comput. Sci. 458, 49–60 (2012)
Chatterjee, K., Doyen, L., Randour, M., Raskin, J.-F.: Looking at mean-payoff and total-payoff through windows. Inf. Comput. 242, 25–52 (2015)
Chatterjee, K., Randour, M., Raskin, J.-F.: Strategy synthesis for multi-dimensional quantitative objectives. Acta Informatica 51(3–4), 129–163 (2014)
Chatterjee, K., Velner, Y.: Mean-payoff pushdown games. In: LICS 2012, pp. 195–204. IEEE Computer Society (2012)
Ehrenfeucht, A., Mycielski, J.: Positional strategies for mean payoff games. Int. J. Game Theor. 8(2), 109–113 (1979)
Fearnley, J., Jurdzinski, M.: Reachability in two-clock timed automata is PSPACE-complete. Inf. Comput. 243, 26–36 (2015)
Fridman, W., Zimmermann, M.: Playing pushdown parity games in a hurry. In: Faella, M., Murano, A. (eds.) GandALF 2012, EPTCS, vol. 96, pp. 183–196 (2012)
Hunter, P.: Reachability in succinct one-counter games. arXiv:1407.1996 (2014)
Hunter, P.: Reachability in succinct one-counter games. In: Bojańczyk, M., Lasota, S., Potapov, I. (eds.) RP 2015. LNCS, vol. 9328, pp. 37–49. Springer, Cham (2015). doi:10.1007/978-3-319-24537-9_5
Juhl, L., Larsen, K.G., Raskin, J.-F.: Optimal bounds for multiweighted and parametrised energy games. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Theories of Programming and Formal Methods. LNCS, vol. 8051, pp. 244–255. Springer, Heidelberg (2013)
Jurdziński, M., Lazić, R., Schmitz, S.: Fixed-dimensional energy games are in pseudo-polynomial time. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 260–272. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47666-6_21
Karp, R.M.: A characterization of the minimum cycle mean in a digraph. Discrete Math. 23(3), 309–3011 (1978)
Larsen, K.G., Laursen, S., Zimmermann, M.: Limit your consumption! Finding bounds in average-energy games. In: Tribastone, M., Wiklicky, B. (eds.), Proceedings 14th International Workshop Quantitative Aspects of Programming Languages and Systems, QAPL 2016, EPTCS, Eindhoven, The Netherlands, vol. 227, pp. 1–14, 2–3 April 2016
Niskanen, R., Potapov, I., Reichert, J.: Undecidability of two-dimensional robot games. In: Faliszewski, P., Muscholl, A., Niedermeier, R. (eds.) MFCS 2016, LIPIcs, vol. 58, pp. 73:1–73:13. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2016)
Randour, M.: Automated synthesis of reliable and efficient systems through game theory: a case study. In: Gilbert, T., Kirkilionis, M., Nicolis, G. (eds.) ECCS 2012, Springer Proceedings in Complexity, pp. 731–738. Springer, Heidelberg (2013)
Thuijsman, F., Vrieze, O.J.: The bad match; a total reward stochastic game. OR Spektrum 9(2), 93–99 (1987)
Velner, Y., Chatterjee, K., Doyen, L., Henzinger, T.A., Rabinovich, A., Raskin, J.-F.: The complexity of multi-mean-payoff and multi-energy games. Inf. Comput. 241, 177–196 (2015)
Walukiewicz, I.: Pushdown processes: games and model-checking. Inf. Comput. 164(2), 234–263 (2001)
Zwick, U., Paterson, M.: The complexity of mean payoff games on graphs. Theor. Comput. Sci. 158(1–2), 343–359 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Bouyer, P., Hofman, P., Markey, N., Randour, M., Zimmermann, M. (2017). Bounding Average-Energy Games. In: Esparza, J., Murawski, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2017. Lecture Notes in Computer Science(), vol 10203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54458-7_11
Download citation
DOI: https://doi.org/10.1007/978-3-662-54458-7_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54457-0
Online ISBN: 978-3-662-54458-7
eBook Packages: Computer ScienceComputer Science (R0)




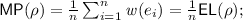


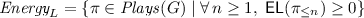 requires a non-negative energy level at all times.
requires a non-negative energy level at all times. requires that the energy always remains non-negative and below the upper bound U along a play.
requires that the energy always remains non-negative and below the upper bound U along a play. . This way,
. This way, 
