Abstract
Classical Linear Logic (CLL) has long inspired readings of its proofs as communicating processes. Wadler’s CP calculus is one of these readings. Wadler gave CP an operational semantics by selecting a subset of the cut-elimination rules of CLL to use as reduction rules. This semantics has an appealing close connection to the logic, but does not resolve the status of the other cut-elimination rules, and does not admit an obvious notion of observational equivalence. We propose a new operational semantics for CP based on the idea of observing communication. We use this semantics to define an intuitively reasonable notion of observational equivalence. To reason about observational equivalence, we use the standard relational denotational semantics of CLL. We show that this denotational semantics is adequate for our operational semantics. This allows us to deduce that, for instance, all the cut-elimination rules of CLL are observational equivalences.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Right from Girard’s introduction of Classical Linear Logic (CLL) [16], it has appeared to offer the tantalising hope of a “Curry-Howard for Concurrency”: a logical basis for concurrent computation, analogous to the standard Curry-Howard correspondence between intuitionistic logic and sequential computation in typed \(\lambda \)-calculi [10, 18]. To realise this hope, Abramsky proposed a programme of “Processes as Proofs” [2] in the early nineties. Abramsky [1] and Bellin and Scott [7] interpreted CLL proofs as terms in process calculi, matching  -reduction to process reduction. However, these correspondences interpret CLL proofs in an extremely restricted set of processes – those which never deadlock and never exhibit racy or nondeterministic behaviour – and so their correspondences could reasonably be criticised as not really capturing concurrency. Ehrhard and Laurent [14] attempted to remedy this problem by demonstrating a correspondence between a finitary \(\pi \)-calculus and Differential Linear Logic. However, their work was forcefully criticised by Mazza [23], who points out that there are crucial differences in how both systems model nondeterminism, and further states:
-reduction to process reduction. However, these correspondences interpret CLL proofs in an extremely restricted set of processes – those which never deadlock and never exhibit racy or nondeterministic behaviour – and so their correspondences could reasonably be criticised as not really capturing concurrency. Ehrhard and Laurent [14] attempted to remedy this problem by demonstrating a correspondence between a finitary \(\pi \)-calculus and Differential Linear Logic. However, their work was forcefully criticised by Mazza [23], who points out that there are crucial differences in how both systems model nondeterminism, and further states:
[...] all further investigations have failed to bring any deep logical insight into concurrency theory, in the sense that no concurrent primitive has found a convincing counterpart in linear logic, or anything even remotely resembling the perfect correspondence between functional languages and intuitionistic logic. In our opinion, we must simply accept that linear logic is not the right framework for carrying out Abramsky’s “proofs as processes” program (which, in fact, more than 20 years after its inception has yet to see a satisfactory completion).
Despite the apparent failure of Abramsky’s programme for concurrency, there has recently been interest in using Linear Logic as a basis for calculi of structured communication, also known as session types. Session types were originally proposed by Honda [17] in the context of the \(\pi \)-calculus as a way to ensure that processes conform to a protocol. The linear logic-based study of session types was initiated by Caires and Pfenning [9], who presented an assignment of \(\pi \)-calculus terms to sequent calculus proofs of Intuitionistic Linear Logic (ILL) that interprets the connectives of ILL as session types in the sense of Honda. The fundamental ideas of Caires and Pfenning were later adapted by Wadler to CLL [35, 36], yielding a more symmetric system of “Classical Processes” (CP).
Wadler presents CP as a calculus with an associated reduction relation, and shows that there is a type preserving translation into Gay and Vasconcelos’ functional language with session-typed communication [15]. This translation was later shown to also preserve reduction semantics, and to be reversible, by Lindley and Morris [20], establishing that CP can be seen as a foundational calculus for session-typed communication.
In this paper, we take a more direct approach to CP. We treat CP as a programming language in its own right by endowing it with an operational semantics, a notion of observational equivalence, and a denotational semantics. We do this for several reasons: (i) if CLL is intended as a logical foundation for programming with structured communication, there ought to be a way of interpreting CP processes as executable artefacts with observable outputs, which, as we argue below, Wadler’s reduction semantics does not; (ii) establishing a theory of observational equivalence for CP resolves the status of the ( )-elimination rules on non-principal cuts by reading them as observational equivalences; and (iii) we can use the rich theory of denotational semantics for CLL (see, e.g., Melliès [25]) to reason about observational equivalence in CP. We further envisage that the introduction of denotational semantics into the theory of CP and session types will lead to further development of CP as a foundational calculus for session-typed communication.
)-elimination rules on non-principal cuts by reading them as observational equivalences; and (iii) we can use the rich theory of denotational semantics for CLL (see, e.g., Melliès [25]) to reason about observational equivalence in CP. We further envisage that the introduction of denotational semantics into the theory of CP and session types will lead to further development of CP as a foundational calculus for session-typed communication.
1.1 Problems with Wadler’s Reduction Semantics for CP
Our starting point is in asking the following question:
What is the observable output of a CP process?
The semantics proposed by Wadler [36] defines a reduction relation between CP processes, derived from the  -elimination rules for principal cuts. For example, processes that transmit and receive a choice interact via the following rule:
-elimination rules for principal cuts. For example, processes that transmit and receive a choice interact via the following rule:
Here, a shared communication channel is established by the \(\nu x.(- \mid -)\) construct, which is the syntax for the ( ) rule. The x[i].P emits a bit i along channel x and continues as P, while \(x.\mathrm {case}(Q_0,Q_1)\) receives a bit along x and proceeds as \(Q_0\) or \(Q_1\) according to the value of that bit.
) rule. The x[i].P emits a bit i along channel x and continues as P, while \(x.\mathrm {case}(Q_0,Q_1)\) receives a bit along x and proceeds as \(Q_0\) or \(Q_1\) according to the value of that bit.
A problem arises with CP processes that have free channels that are not connected to any other process. Since CP uses \(\pi \)-calculus notation, there is a relatively rigid left-to-right sequentialisation of actions. This means that the presence of attempts to communicate along unconnected channels can block other communication. An example is the following process, where communication along the unconnected \(x'\) channel blocks the communication across x:
This arrangement corresponds to ( )-elimination for a “non-principal” cut, i.e. the formula being cut in is not the last one introduced on both sides. In these cases, (
)-elimination for a “non-principal” cut, i.e. the formula being cut in is not the last one introduced on both sides. In these cases, ( )-elimination commutes the offending rule past the (
)-elimination commutes the offending rule past the ( ) rule:
) rule:
The rules that perform these rearrangements that do not correspond to any actual communication are referred to as “commuting conversions”. They serve to bubble “stuck” communication to the outermost part of a process term.
With the reduction rules as proposed, we have two answers to our question. If a CP process P has no free channels, then we can always apply reduction rules corresponding to actual interaction, but we will never see the results of any of these interactions. Since CP is strongly normalising (a property it inherits from CLL [3]), all closed processes have the same termination behaviour, so this does not distinguish them. (CP, as presented by Wadler, does not admit completely closed processes unless we also include the (Mix\(_0\)) rule, as we do here.)
Alternatively, if a CP process P has free channels, then we can use the commuting conversion rules to move the stuck prefixes to the outermost layer. We could then either proceed to eliminate all ( )s deeper in the process term, or we could halt immediately, in the style of weak reduction in the \(\lambda \)-calculus.
)s deeper in the process term, or we could halt immediately, in the style of weak reduction in the \(\lambda \)-calculus.
This approach is appealing because it corresponds to the similar approach to defining the result of \(\lambda \)-calculus/proof-term reduction in sequential programming. We could also define a natural equivalence between CP processes in terms of barbed bisimulations [26], using the topmost action as the barb. However, in a multi-output calculus like CP, we run into ambiguity. The process:
can be converted in two steps to:
Intuitively, these processes are equivalent. Processes connected to distinct channels in CP are always independent so it is not possible for any observer to correlate communication over the channels y and z and to determine the difference between these processes. We could treat all CP processes quotiented by these permutations, but that would presuppose these equivalences, rather than having them induced by the actual behaviour of CP processes. (Bellin and Scott do such an identification in [7], pg. 14, rule (1).) If we were to define observational equivalence of CP processes via barbed bisimulation of CP processes up to permutations, then we would be effectively building the consequences of linearity into the definition of equivalence, rather than deducing them.
Another approach to resolving the non-determinism problem is to restrict processes to having one free channel that is designated as “the” output channel. With only one channel there can be no ambiguity over the results of the ordering of commuting conversions. This is the path taken in Caires and Pfenning’s [9] ILL-based formalism. Pérez et al. [27] define a notion of observational equivalence for Caires and Pfenning’s system based on a Labelled Transition System (LTS) over processes with one free channel. CLL, and hence CP, do not have a notion of distinguished output channel. Indeed, it is not immediately obvious why a process dealing with multiple communication partners ought to designate a particular partner as “the one” as Caires and Pfenning’s system does.
1.2 A Solution: Observed Communication Semantics
We appear to have a tension between two problems. CP processes need partners to communicate with, but if we connect two CP processes with the ( ) rule we cannot observe what they communicate! If we leave a CP process’s channels free, then we need reduction rules that do not correspond to operationally justified communication steps, and we admit spurious non-determinism unless we make ad-hoc restrictions on the number of free channels.
) rule we cannot observe what they communicate! If we leave a CP process’s channels free, then we need reduction rules that do not correspond to operationally justified communication steps, and we admit spurious non-determinism unless we make ad-hoc restrictions on the number of free channels.
Our solution is based on the idea that the observed behaviour of a collection of processes is the data exchanged between them, not their stuck states. In sequential calculi, stuck computations are interpreted as values, but this viewpoint does not remain valid in the world of message-passing communicating processes.
We propose a new operational semantics for CP on the idea of “visible” applications of the ( ) rule that allow an external observer to see the data transferred. We define a big-step evaluation semantics that assigns observations to “configurations” of CP processes. For example, the configuration:
) rule that allow an external observer to see the data transferred. We define a big-step evaluation semantics that assigns observations to “configurations” of CP processes. For example, the configuration:
consists of a pair of CP processes x[1].x[] and \(x.\mathrm {case}(x().0, x().0)\) that will communicate over the public channel x, indicated by the \(\mid _x\) notation. The split typing context on the right hand side indicates that there are no unconnected channels, \(\cdot \), and one observable channel \(x : 1 \oplus 1\).
Our semantics assigns the observation to \((1,*)\) to this configuration:
This observation indicates that “1” was transferred, followed by “end-of-session”.
Observations in our operational semantics are only defined for configurations with no free channels. Hence we do not have the problem of processes getting stuck for lack of communication partners, and the rules of our operational semantics (Fig. 3) are only concerned with interactions and duplication and discarding of servers. There is no need for non-operational steps.
Our operational semantics enables us to define observational equivalence between CP processes in the standard way: if two processes yield the same observed communications in all contexts, then they are observationally equivalent (Definition 1). We will see that the ( )-elimination rules of CLL, seen as equations between CP terms are observational equivalences in our sense (Sect. 5).
)-elimination rules of CLL, seen as equations between CP terms are observational equivalences in our sense (Sect. 5).
Proving observational equivalences using our definition directly is difficult, for the usual reason that the definition quantifies over all possible contexts. Therefore, we define a denotational semantics for CP processes and configurations, based on the standard relational semantics for CLL (Sect. 3). This denotational semantics affords us a compositional method for assigning sets of potential observable communication behaviours to CP processes and configurations. In Sect. 4 we show that, on closed configurations, the operational and denotational semantics agree, using a proof based on \(\perp \perp \)-closed Kripke logical relations. Coupled with the compositionality of the denotational semantics, adequacy yields a sound technique for proving observational equivalences.
1.3 Contributions
This paper makes three contributions to logically-based session types:
-
1.
In Sect. 2, we define a communication observing semantics for Wadler’s CP calculus. This semantics assigns observations to “configurations” of processes that are communicating over channels. The data communicated over these channels constitutes the observations an external observer can make on a network of processes. Our semantics enables a definition of observational equivalence for CP processes that takes into account the restrictions imposed by CP’s typing discipline.
-
2.
In Sect. 4, we show that the standard “folklore” relational semantics of CLL proofs (spelt out in Sect. 3) is adequate for the operational semantics via a logical relations argument. Adequacy means that we can use the relational semantics, which is relatively straightforward to calculate with, to reason about observational equivalence. An additional conceptual contribution is the reading of the relational semantics of CLL in terms of observed communication between concurrent processes.
-
3.
We use the denotational semantics to show that all of the standard
 -elimination rules of CLL are observational equivalences in our operational semantics, in Sect. 5. This means that the
-elimination rules of CLL are observational equivalences in our operational semantics, in Sect. 5. This means that the  -elimination rules can be seen as a sound equational theory for reasoning about observational equivalence. We also show that permutations of communications along independent channels are observational equivalences.
-elimination rules can be seen as a sound equational theory for reasoning about observational equivalence. We also show that permutations of communications along independent channels are observational equivalences.
In Sect. 7, we assess the progress made in this paper and point to areas for future work.
2 Observed Communication Semantics for CP
2.1 Classical Processes
Wadler’s CP is a term language for sequent calculus proofs in Girard’s Classical Linear Logic (CLL), with a syntax inspired by the \(\pi \)-calculus [31].
Formulas. The formulas of CLL are built by the following grammar:

The connectives of CLL are collected into several groupings, depending on their proof-theoretic behaviour. As we shall see, these groupings will also have relevance in terms of their observed communication behaviour.
The connectives  are referred as the multiplicatives, and \(\oplus \) and
are referred as the multiplicatives, and \(\oplus \) and  are the additives. Multiplicatives correspond to matters of communication topology, while the additives will correspond to actual data transfer. The
are the additives. Multiplicatives correspond to matters of communication topology, while the additives will correspond to actual data transfer. The  and
and  connectives are referred to as the exponential connectives, because they allow for unrestricted duplication of the multiplicative structure. Another grouping of the connectives distinguishes between the positive connectives 1, \(\otimes \), \(\oplus \), and
connectives are referred to as the exponential connectives, because they allow for unrestricted duplication of the multiplicative structure. Another grouping of the connectives distinguishes between the positive connectives 1, \(\otimes \), \(\oplus \), and  that describe output, and the negative connectives
that describe output, and the negative connectives  ,
,  and
and  that describe input. Positive and negative are linked via duality: each A has a dual \(A^\perp \):
that describe input. Positive and negative are linked via duality: each A has a dual \(A^\perp \):

The key to the structure of the CP calculus is that CLL formulas are types assigned to communication channels. Duality is how we transform the type of one end of a channel to the type of the other end. Hence the swapping of positive and negative connectives: we are swapping descriptions of input and output.
Example. The additive connective \(\oplus \) indicates the transmission of a choice between two alternative sessions. Using the multiplicative unit 1 to represent the empty session, we can build a session type/formula representing transmission of a single bit, and its dual representing the receiving of a single bit:

With these, we can build the type of a server that accept arbitrarily many requests to receive two bits and return a single bit:

We read this type as making the following requirements on a process: the outer  indicates that it must allow for arbitrarily many uses; it then must receive two bits, transmit a bit, and then signal the end of the session. We obtain the type of a compatible client by taking the dual of this type:
indicates that it must allow for arbitrarily many uses; it then must receive two bits, transmit a bit, and then signal the end of the session. We obtain the type of a compatible client by taking the dual of this type:

We read this as requirements that are dual to those on the server: the  indicates that it can use the server as many times as necessary, whereupon it must transmit two bits, receive a bit and receive an end of session signal.
indicates that it can use the server as many times as necessary, whereupon it must transmit two bits, receive a bit and receive an end of session signal.
Processes. Processes in CP communicate along multiple named and typed channels, which we gather into contexts \(\varGamma = x_1 : A_1, \dots , x_n : A_n\) where the channel names \(x_i\) are all distinct, and we do not care about order.
The syntax of processes in CP is given by the grammar:

The rules defining CP are given in Fig. 1. They define a judgement \(\vdash P \,{:}{:}\, \varGamma \), indicating that P is well-typed with respect to type assignment \(\varGamma \). We differ from Wadler by writing P to the right of the \(\vdash \); it is not an assumption.
The rules are divided into four groups. The first group are the structural rules: ( ) introduces a process linking two channels, note the use of duality to type the two ends of the link; (
) introduces a process linking two channels, note the use of duality to type the two ends of the link; ( ) establishes communication between two processes via a hidden channel x, again note the use of duality; and (Mix\(_0\)) is the nil process which performs no communication over no channels.
) establishes communication between two processes via a hidden channel x, again note the use of duality; and (Mix\(_0\)) is the nil process which performs no communication over no channels.
The second group contains the multiplicative rules. Following Wadler’s notation, square brackets \([\cdots ]\) indicate output and round brackets \((\cdots )\) indicate input. Thus ( ) introduces a process that outputs an end-of-session signal and dually (\(\bot \)) introduces a process that inputs such. Likewise, (\(\otimes \)) introduces a process that outputs a fresh channel name for a forked-off process P to communicate on, and
) introduces a process that outputs an end-of-session signal and dually (\(\bot \)) introduces a process that inputs such. Likewise, (\(\otimes \)) introduces a process that outputs a fresh channel name for a forked-off process P to communicate on, and  inputs a channel name for it to communicate on in the future. Neither of these pairs communicates any unexpected information. By duality, if a \(\otimes \) process is going to send a channel and fork a process, then it is communicating with
inputs a channel name for it to communicate on in the future. Neither of these pairs communicates any unexpected information. By duality, if a \(\otimes \) process is going to send a channel and fork a process, then it is communicating with  process that is ready to receive a channel and communicate with that process. In our semantics in Sect. 2.3, multiplicative connectives affect the structure of observations, but not their information content.
process that is ready to receive a channel and communicate with that process. In our semantics in Sect. 2.3, multiplicative connectives affect the structure of observations, but not their information content.
Processes that communicate information are introduced by the additive rules in the third group. The process introduced by (\(\oplus _{\textsc {i}}\)) transmits a bit i along the channel x, and continues using x according to the type \(A_i\). Dually, ( ) introduces processes that receive a bit, and proceed with either P or Q given its value.
) introduces processes that receive a bit, and proceed with either P or Q given its value.
The final group covers the exponential rules. The rule ( ) introduces an infinitely replicable server process that can communicate according to the type A on demand. To ensure that this process is infinitely replicable, all of the channels it uses must also be connected to infinitely replicable servers, i.e., channels of type
) introduces an infinitely replicable server process that can communicate according to the type A on demand. To ensure that this process is infinitely replicable, all of the channels it uses must also be connected to infinitely replicable servers, i.e., channels of type  . We indicate the requirement that all the channels in \(\varGamma \) be of
. We indicate the requirement that all the channels in \(\varGamma \) be of  ’d typed by the notation
’d typed by the notation  . Processes introduced by the (
. Processes introduced by the ( ) rule query a server process to obtain a new channel for communication. The exponentials are given their power by the structural rules (C) and (W). Contraction, by rule (C) allows a process to use the same server twice. Weakening, by the rule (W) allows a process to discard a channel connected to a server.
) rule query a server process to obtain a new channel for communication. The exponentials are given their power by the structural rules (C) and (W). Contraction, by rule (C) allows a process to use the same server twice. Weakening, by the rule (W) allows a process to discard a channel connected to a server.
Example. As a programming language, CP is very low-level. We make use of the following syntactic sugar (from [4]) for transmitting and receiving bits along channels of type \( Bit \) and \( Bit ^\perp \):
Using these abbreviations, we can write an implementation of our \( Server \) type that computes the logical AND of a pair of bits:

This process creates an infinitely replicable server via ( ), receives two channels
), receives two channels  , receives two bits along them, and in each case transmits the appropriate returned value and signals end of session. A dual client process is written so:
, receives two bits along them, and in each case transmits the appropriate returned value and signals end of session. A dual client process is written so:

This process contacts a server, sends the bit \(\mathbf {1}\) twice, and then, no matter the outcome, receives the end of session signal and halts.
2.2 Configurations
The well-typed process judgement \(\vdash P \,{:}{:}\, \varGamma \) relates processes P to unconnected channels \(\varGamma \). When processes communicate via the (Cut) rule, that communication is invisible to external observers: the common channel x is removed from the context. In order to make communication visible, we introduce configurations of processes. A configuration \(\vdash _c C \, {:}{:}\, \varGamma \mid \varTheta \) has unconnected channels \(\varGamma \) and connected but observable channels \(\varTheta \). Observable channel contexts \(\varTheta = x_1 : A_1, \dots , x_n : A_n\) are similar to normal channel contexts \(\varGamma \), except that we identify contexts whose type assignments are the same up to duality. Thus, as observable channel contexts, \(x : A \otimes B, y : C \oplus D\) is equivalent to  . We make this identification because the CLL connectives encode two things: (i) the form of the communication and (ii) its direction (i.e., whether it is positive or negative). When observing communication, we are not interested in the direction, only the content. Hence identification up to duality.
. We make this identification because the CLL connectives encode two things: (i) the form of the communication and (ii) its direction (i.e., whether it is positive or negative). When observing communication, we are not interested in the direction, only the content. Hence identification up to duality.
Configurations are defined using the rules in Fig. 2. The rule ( ) treats processes as configurations with unconnected channels and no publicly observable channels. The (
) treats processes as configurations with unconnected channels and no publicly observable channels. The ( ) rule is similar to the (
) rule is similar to the ( ) rule in that it puts two configurations together to communicate, but here the common channel is moved to the observable channel context instead of being hidden. The remainder of the rules, (cfg0), (
) rule in that it puts two configurations together to communicate, but here the common channel is moved to the observable channel context instead of being hidden. The remainder of the rules, (cfg0), ( ), and (
), and ( ) are the analogues of the structural rules of CP, lifted to configurations. The rule (
) are the analogues of the structural rules of CP, lifted to configurations. The rule ( ) is required to contract channel names appearing in two separate processes in a configuration, and (
) is required to contract channel names appearing in two separate processes in a configuration, and ( ) is required for weakening even when there are no processes in a configuration. There are no contraction or weakening rules for observable contexts \(\varTheta \). Such contexts record connected channels, which cannot be discarded or duplicated.
) is required for weakening even when there are no processes in a configuration. There are no contraction or weakening rules for observable contexts \(\varTheta \). Such contexts record connected channels, which cannot be discarded or duplicated.
We define a structural congruence \(C_1 \equiv C_2\) on configurations, generated by commutativity and associativity (where permitted by the typing) for \(\mid _x\), with \(\underline{0}\) as the unit. Structural congruence preserves typing.
A configuration with no unconnected channels, \(\vdash _c C \, {:}{:}\, \cdot \mid \varTheta \), is called a closed configuration of type \(\varTheta \). Closed configurations will be our notion of complete systems: the observed communication semantics we define below in Sect. 2.4 is only defined for closed configurations.
Example. Continuing our example from above, we can connect the server process \( ServerP \) to the client process \( ClientP \) in a configuration with a visible communication channel x, using the ( ) rule:
) rule:
Note that this configuration also has typing \(\vdash _c ServerP \mid _x ClientP \,{:}{:}\, \cdot \mid x : Client \) due to the conflation of dual types in observation contexts.
2.3 Observations
Our observed communication semantics assigns observations to closed configurations. The range of possible observations is defined in terms of the types of the channels named in \(\varTheta \). As stated above, observations only track the data flowing across a communication channel, not the direction. Therefore, the positive and negative connective pairs each have the same sets of possible observations:

where \(\mathcal {M}_{ f }(X)\) denotes finite multisets with elements from X. We will use the \(\emptyset \) for empty multiset, \(\uplus \) for multiset union, and  for multiset literals.
for multiset literals.
The sets of possible observations for a given observation context \(\varTheta = x_1 : A_1, \dots , x_n : A_n\) are defined as the cartesian product of the possible observations for each channel: \(\llbracket \varTheta \rrbracket = \llbracket x_1 : A_1, \dots , x_n : A_n \rrbracket = \llbracket A_1 \rrbracket \times \dots \times \llbracket A_n \rrbracket \).
2.4 Observed Communication Semantics
Observable evaluation is defined by the rules in Fig. 3. These rules relate closed configurations \(\vdash _c C \, {:}{:}\, \cdot \mid \varTheta \) with observations \(\theta \in \llbracket \varTheta \rrbracket \). To derive \(C \Downarrow \theta \) is to say that execution of C completes with observed communication \(\theta \). For convenience, in Fig. 3, even though observations \(\theta \) are tuples with “anonymous” fields, we refer to the individual fields by the corresponding channel name. The rules in Fig. 3 makes use of the shorthand notation \(C[-]\) to indicate that the matched processes involved in each rule may appear anywhere in a configuration.
The first rule, ( ), is the base case of evaluation, yielding the trivial observation () for the empty configuration. The next three rules, (
), is the base case of evaluation, yielding the trivial observation () for the empty configuration. The next three rules, ( ), (
), ( ), and (0) describe the behaviour of the processes introduced by the (
), and (0) describe the behaviour of the processes introduced by the ( ), (
), ( ) and (Mix\(_0\)) rules respectively. (
) and (Mix\(_0\)) rules respectively. ( ) evaluates links via substitution of channel names; and the observed communication across the link is shared between the two channels. (
) evaluates links via substitution of channel names; and the observed communication across the link is shared between the two channels. ( ) evaluates two processes communicating over a private channel by evaluating them over a public channel and then hiding it. (0) evaluates the empty process 0 by turning it into the empty configuration \(\underline{0}\).
) evaluates two processes communicating over a private channel by evaluating them over a public channel and then hiding it. (0) evaluates the empty process 0 by turning it into the empty configuration \(\underline{0}\).
The rules (\(\textsc {1}\bot \)), ( ), (
), ( ) and (
) and ( ) describe how processes introduced by dual pairs of rules interact across public channels, and the observed communication that results. For (\(\textsc {1}\bot \)), the trivial message \(*\) is sent. For (
) describe how processes introduced by dual pairs of rules interact across public channels, and the observed communication that results. For (\(\textsc {1}\bot \)), the trivial message \(*\) is sent. For ( ), communication that occured across two independent channels is grouped into one channel. For (
), communication that occured across two independent channels is grouped into one channel. For ( ), a single bit, i is transmitted, which is paired with the rest of the communication. For (
), a single bit, i is transmitted, which is paired with the rest of the communication. For ( ), an observation arising from a single use of a server is turned into a multiset observation with a single element.
), an observation arising from a single use of a server is turned into a multiset observation with a single element.
The rules ( W) and (
W) and ( C) describe how server processes are discarded or duplicated when they have no clients or multiple clients respectively. In terms of observed communication, these correspond to multiset union (\(\uplus \)) and the empty multiset (\(\emptyset \)), respectively. Finally, the (\(\equiv \)) rule states that configuration semantics is unaffected by permutation of processes (we have elided the matching reordering within \(\theta \), following our convention of using channel names to identify parts of an observation).
C) describe how server processes are discarded or duplicated when they have no clients or multiple clients respectively. In terms of observed communication, these correspond to multiset union (\(\uplus \)) and the empty multiset (\(\emptyset \)), respectively. Finally, the (\(\equiv \)) rule states that configuration semantics is unaffected by permutation of processes (we have elided the matching reordering within \(\theta \), following our convention of using channel names to identify parts of an observation).
Example. Our operational semantics assigns the following observation to the configuration we built at the end of Sect. 2.2:

We observe the two 1-bits sent by the client, the 1-bit returned by the server, and the final \(*\) indicating end of session. The additional \(*\)s accompanying each bit are an artifact of our encoding of bits as the formula \(1 \oplus 1\).
2.5 Observational Equivalence
Observational equivalence between a pair of processes is defined as having the same set of observations in all typed contexts. By its definition in terms of typed contexts \(CP[-]\), our definition of observational equivalence takes into account the (in)abilities of typed processes to interact with each other. In particular, the inability of CP processes to distinguish permutations of actions on distinct channels yields a family of observational equivalences (Fig. 8).
Our definition of observational equivalence is defined in terms of typed contexts \( CP [-]\), which consist of configurations and processes with a single (typed) hole. Compared to the configuration contexts \(C[-]\) in Fig. 3, configuration-process contexts allow the hole to appear within a process.
Definition 1
Two processes \(\vdash P_1, P_2 \,{:}{:}\, \varGamma \) are observationally equivalent, written \(P_1 \simeq P_2\), if for all configuration-process contexts \( CP [-]\) where \(\vdash _c CP [P_1] \, {:}{:}\, \cdot \mid \varTheta \) and \(\vdash _c CP [P_2] \, {:}{:}\, \cdot \mid \varTheta \), and all \(\theta \in \llbracket \varTheta \rrbracket \), \( CP [P_1] \Downarrow \theta \Leftrightarrow CP [P_2] \Downarrow \theta \).
Reasoning about observational equivalence is difficult, due to the quantification over all contexts. In the next two sections, we present a denotational semantics of CP which is sound for reasoning about observational equivalence.
3 Denotational Semantics of CP
The observed communication semantics of the previous section assigns observations to closed configurations. To reason about open configurations and processes, and hence observational equivalence, we require a semantics that assigns observations to processes and open configurations. We do this via a denotational semantics that interprets processes and open configurations as relations between the possible observations on each of their channels. Since CP processes are a syntax for CLL proofs, our denotations of processes will be identical to the relational semantics of proofs in CLL (see, for example, Barr [6]). We extend this semantics to configurations by interpreting them as relations between observations on their unconnected channels and observations on their connected channels. Compared to other denotational semantics for process calculi (e.g. [30, 32]), this semantics is notable in its non-use of traces, synchronisation trees, or other temporally ordered formalism to record the I/O behaviour of processes. This is due to the linearity constraints imposed by the typing rules inherited from CLL, which enforce the invariant that distinct channels are completely independent. A trace-based semantics would impose an ordering on actions performed by processes which is not observable by a CP context. This “temporal-obliviousness” speaks to the point that CP is about structured communication determined by types, not about concurrency. We return to this in Sect. 5 when we discuss the observational equivalences between processes that permute independent actions.
In Sect. 4, we will see that on closed configurations the operational semantics and the denotational semantics agree.
3.1 Semantics of Formulas
The semantics of formulas does not take into account whether data is being transmitted or received; the relational semantics of CLL is sometimes referred to as “degenerate” in this sense. We discuss this further in Sect. 3.4. For now, we use the same interpretation of formulas as we did for observation contexts in Sect. 2.3:

The sets of possible observations for a given context \(\varGamma = x_1 : A_1, \dots , x_n : A_n\) are again defined as the cartesian product of the sets for each of the \(A_i\):
3.2 Semantics of Processes
The basic idea of the semantics of processes is that if \((a_1, \dots , a_n) \in \llbracket \vdash P \, {:}{:}\, \varGamma \rrbracket \), then \((a_1, \dots , a_n)\) is a possible observed behaviour of P along its unconnected channels. So, to every \(\vdash P \, {:}{:}\, \varGamma \), we assign a subset of the interpretation of \(\varGamma \):
by induction on the derivation of \(\vdash P \,{:}{:}\, \varGamma \). The ( ) rule is interpreted by the diagonal relation, indicating that whatever is observed at one end of the linked channels is observed at the other:
) rule is interpreted by the diagonal relation, indicating that whatever is observed at one end of the linked channels is observed at the other:
The ( ) rule is interpreted by taking observations from both processes that share a common observation along the shared channel:
) rule is interpreted by taking observations from both processes that share a common observation along the shared channel:
The (Mix\(_0\)) rule is interpreted as the only possible observation in an empty context:
The multiplicative units observe trivial data:
For the multiplicative binary connectives, the (\(\otimes \)) rule is interpreted by combining the interpretations of its two subprocesses into a single observation; while  rule is interpreted by pairing the observations on two channels into one.
rule is interpreted by pairing the observations on two channels into one.

For the additive connectives, sending bits via the (\(\oplus _{{i}}\)) rules is interpreted by prepending that bit on to the observation on that channel; and receiving a bit via ( ) is interpreted by taking the union of possible observations:
) is interpreted by taking the union of possible observations:

For the exponential connectives, a “server” process introduced by the ( ) rule is interpreted as the multiset of k-many observations of its underlying process, taking the union of their auxillary observations on the context
) rule is interpreted as the multiset of k-many observations of its underlying process, taking the union of their auxillary observations on the context  . A “client” process introduced by (
. A “client” process introduced by ( ) makes a singleton multiset’s worth of observations:
) makes a singleton multiset’s worth of observations:

The exponential structural rules dictate how singleton observations from client processes are combined, or channels are discarded. Contraction (C) is interpreted via multiset union, and weakening (W) is interpreted by the empty multiset:

When these rules are put into communication with servers generated by ( ) they will dictate the multiplicity of uses of the server process.
) they will dictate the multiplicity of uses of the server process.
Example. We compute the denotation of the process \( ServerP \) from our running example to be the set of arbitrarily sized multisets of possible interactions with the underlying process:

where the underlying process’s denotation includes all possible \(2^2\) possibilities for inputs and relates them to the corresponding output (their logical AND):
The client’s denotation is a singleton multiset (recording the fact that it uses the server only once). Dually to the server’s denotation, the first two bits are determined but the last one is completely undetermined because we cannot know what the response from the server will be.

3.3 Semantics of Configurations
The denotational semantics of configurations extends the semantics of processes to include the connected channels. Configurations \(\vdash _c C \,{:}{:}\, \varGamma \mid \varTheta \) are assigned subsets of \(\llbracket \varGamma \rrbracket \times \llbracket \varTheta \rrbracket \). The idea is that, if \(((a_1, \dots , a_n), (b_1, \dots , b_n)) \in \llbracket \vdash _c C \,{:}{:}\, \varGamma \mid \varTheta \rrbracket \), then \((a_1, \dots , a_n)\) and \((b_1, \dots , b_n)\) are a possible observed behaviour of C along its unconnected and connected channels respectively. We assign denotations to each configuration by structural recursion on their derivations:

The interpretation of (cfg0), ( ), and (
), and ( ) are similar to the analogous rules for processes. The interpretation of (
) are similar to the analogous rules for processes. The interpretation of ( ) is also similar, except that the observation on the shared channel is retained. The interpretation of (
) is also similar, except that the observation on the shared channel is retained. The interpretation of ( ) lifts interpretations of processes up to configurations with no connected channels.
) lifts interpretations of processes up to configurations with no connected channels.
Example. Using the above rules, we compute the denotation of our example configuration linking our server to its client:

The denotation is the set with the single observation we computed in Sect. 2.4 for this configuration. In Sect. 4, we will see that this is no accident.
3.4 More Precise Semantics?
As we noted in Sect. 3.1, the relational semantics of CLL assigns the same interpretation to the positive and negative variants of each connective. Thus, the semantics of formulas do not model the direction of data flow for inputs and outputs. The logical relations we will define in Sect. 4 will refine the semantics of formulas to identify subsets of the observations possible for each formula that are actually feasible in terms of the input/output behaviour of connectives, but it is also possible to perform such a refinement purely at the level of the denotational semantics. Girard’s motivating semantics for CLL was coherence spaces [16], which can be seen as a refined version of the relational semantics where particular distinguished subsets, cliques, are identified as the possible denotations of processes. The defining property of coherence spaces is that for every clique \(\alpha \) in a coherence space and every clique \(\beta \) in its dual, the intersection \(\alpha \cap \beta \) has at most one element. The coherence space semantics can be extended to configurations by stipulating that subsets X assigned to configurations must satisfy the property that if \((\gamma _1, \theta _1)\) and \((\gamma _2, \theta _2)\) are both in X, then whenever \(\gamma _1\) and \(\gamma _2\) are coherent (i.e., \(\{\gamma _1, \gamma _2\}\) is a clique), then \(\theta _1 = \theta _2\). The semantics for configurations in Sect. 3.3 satisfies this property, and the adequacy proof in the next section goes through unchanged.
Operationally, this means that CP processes can only interact in at most one way. Therefore, using a coherence space semantics would consistute a semantic proof of determinacy for CP with our semantics. It might be possible to go further and use Loader’s totality spaces [22], which stipulate that cliques in dual spaces have exactly one element in their intersection, to also prove termination. However, the construction of exponentials in totality spaces is not clear.
4 Adequacy
We now present our main result: on closed configurations, the operational and denotational semantics agree. Consequently, we can use the denotational semantics to reason about observational equivalences between CP processes (Sect. 5).
Theorem 1
If \(\vdash _c C \,{:}{:}\, \cdot \mid \varTheta \), then \(C \Downarrow \theta \) iff \(\theta \in \llbracket \vdash _c C \,{:}{:}\, \cdot \mid \varTheta \rrbracket \).
The forwards direction of this theorem states that if an observation can be generated by the evaluation rules, then it is also within the set of possible observations predicted by the denotational semantics. This is straightfoward to prove by induction on the derivation of \(C \Downarrow \theta \). The backwards direction, which states that the denotational semantics predicts evaluation, is more complex and occupies the rest of this section.
4.1 Agreeability via \(\perp \perp \)-Closed Logical Relations
We adapt the standard technique for proving adequacy for sequential languages [28] and use a logical relation to relate open configurations with denotations. For each channel name x and CLL formula A, we use ternary relations that relate observable contexts, denotations, and configurations, which we call agreeability relations:
where \(\mathsf {ObsCtxt}\) is the set of observable contexts, \(\mathcal {P}\) is the power set, and \(\mathrm {Cfg}(x : A \mid \varTheta )\) is the set of well-typed configurations \(\vdash _c C \,{:}{:}\, x : A \mid \varTheta \). We are interested in special agreeability relations: those that are closed under double negation.
Negation. Given an agreeability relation X for a channel x : A, its negation \(X^\perp \) is an agreeability relation for \(x : A^\perp \). Intuitively, if X identifies a set of configurations and denotations with some property, then \(X^\perp \) is the set of configurations and denotations that “interact well” with the ones in X. For our purposes, “interact well” means that the communication we observe when the two configurations interact is predicted by their associated denotations.
Definition 2
(Negation). Let X be a relation for x : A as in (1). Its negation \(X^\perp \) is a relation for \(x : A^\perp \), defined as:
We are interested in agreeability relations that are \(\perp \perp \)-closed: \(X^{\perp \perp } = X\). These are related denotations and configurations that “interact well with anything that interacts well with them”. This kind of double-negation closure was used by Girard [16] to construct the Phase Space semantics of CLL and to show weak normalisation. Ehrhard notes that double-negation closure is a common feature of many models of CLL [13]. Double-negation, \((\cdot )^{\perp \perp }\), has the following properties, which mean that it is a closure operator [12]:
Lemma 1
-
1.
\(X \subseteq X^{\perp \perp }\);
-
2.
If \(X \subseteq Y\), then \(Y^\perp \subseteq X^\perp \);
-
3.
\(X^{\perp \perp \perp } = X^{\perp }\).
By (3), \(X^{\perp \perp }\) is automatically \(\perp \perp \)-closed for any agreeability relation X.
Duplicable and Discardable. We generalise the duplicable and discardable capability of  ’d processes (the (
’d processes (the ( C) and (
C) and ( W) rules) to arbitrary configurations with one free channel of
W) rules) to arbitrary configurations with one free channel of  ’d type:
’d type:
Definition 3
(Duplicable and Discardable). A configuration  is
is
-
1.
duplicable if, for all
 , $$\begin{aligned} \begin{array}{l} D[(C' \mid _x C) \mid _{x'} C\{x'/x,z'_1/z_1,\dots ,z'_n/z_n\}] \Downarrow \\ \quad \quad \quad \quad \quad \theta \left[ \begin{array}{@{}l@{}l@{}l@{}l@{}} x \mapsto \alpha , &{} z_1 \mapsto \alpha _1, &{} \dots , &{} z_n \mapsto \alpha _n, \\ x' \mapsto \alpha ', &{} z'_1 \mapsto \alpha '_1, &{} \dots , &{} z'_n \mapsto \alpha '_n \end{array} \right] \end{array} \end{aligned}$$
, $$\begin{aligned} \begin{array}{l} D[(C' \mid _x C) \mid _{x'} C\{x'/x,z'_1/z_1,\dots ,z'_n/z_n\}] \Downarrow \\ \quad \quad \quad \quad \quad \theta \left[ \begin{array}{@{}l@{}l@{}l@{}l@{}} x \mapsto \alpha , &{} z_1 \mapsto \alpha _1, &{} \dots , &{} z_n \mapsto \alpha _n, \\ x' \mapsto \alpha ', &{} z'_1 \mapsto \alpha '_1, &{} \dots , &{} z'_n \mapsto \alpha '_n \end{array} \right] \end{array} \end{aligned}$$implies
$$\begin{aligned} \begin{array}{l} D[C'\{x/x'\} \mid _x C] \Downarrow \theta [x \mapsto \alpha \uplus \alpha ', z_1 \mapsto \alpha _1 \uplus \alpha '_1, \dots , z_n \mapsto \alpha _n \uplus \alpha '_n] \end{array} \end{aligned}$$ -
2.
discardable if, for all \(\vdash _c C' \,{:}{:}\, \varGamma \mid \varTheta \), \(D[C'] \Downarrow \theta \) implies that \(D[C' \mid _x C] \Downarrow \theta [x \mapsto \emptyset , z_1 \mapsto \emptyset , \dots , z_n \mapsto \emptyset ]\).
The definition of duplicability uses the ( ) rule to ensure that the second configuration is well-typed. Likewise, discardability uses the (
) rule to ensure that the second configuration is well-typed. Likewise, discardability uses the ( ) rule. The next lemma states that configurations built from duplicable and discardable parts are themselves duplicable and discardable. We will use this in the proof of Lemma 4, below, when showing that processes of the form
) rule. The next lemma states that configurations built from duplicable and discardable parts are themselves duplicable and discardable. We will use this in the proof of Lemma 4, below, when showing that processes of the form  agree with their denotations after they have been closed by connecting their free channels to duplicable and discardable configurations.
agree with their denotations after they have been closed by connecting their free channels to duplicable and discardable configurations.
Lemma 2
Let  be a process, and let
be a process, and let  be duplicable and discardable configurations. Then the configuration
be duplicable and discardable configurations. Then the configuration

is duplicable and discardable.
Interpretation of Process Types. Figure 4 defines a \(\perp \perp \)-closed agreeability relation on x : A for each CLL proposition A by structural recursion. We only need definitions for the positive cases, relying on negation for the negative cases. We ensure that all the positive cases are \(\perp \perp \)-closed by explicitly doing so. The negative cases are the negations of the positive cases, and hence are automatically \(\perp \perp \)-closed by Lemma 1.
The general method for each definition in Fig. 4 is to define what the “ideal” configuration inhabitant and denotation of each type looks like, and then use \(\perp \perp \)-closure to close that relation under all possible interactions. In the case of x : 1, there is one possible process, x[], and denotation, \(*\). For the \(x : A \otimes B\) case, ideal inhabitants are composed of two inhabitants of the types A and B (processes P, \(P'\) plus their associated support processes \(D_i\) and \(D'_i\)). In the \(x : A_0 \oplus A_1\) case, ideal inhabitants are processes that are inhabitants of \(A_i\) after outputing some i. For the exponentials,  , the ideal inhabitant is one whose auxillary resources are all duplicable and discardable (indicated by the
, the ideal inhabitant is one whose auxillary resources are all duplicable and discardable (indicated by the  ). In each case, the associated denotations are determined by the denotational semantics defined in Sect. 3.
). In each case, the associated denotations are determined by the denotational semantics defined in Sect. 3.
Agreeable Processes. The definition of \(\llbracket x : A \rrbracket \) defines what it means for configurations with one free channel to agree with a denotation. We use this definition to define what it means for a process to agree with its denotation by connecting it to configurations and denotations that are related and stating that the communications predicted by the denotations is matched by evaluation:
Definition 4
A process \(\vdash P \,{:}{:}\, x_1 : A_1, \dots , x_n : A_n\) is agreeable if for all
if \((a_1, \dots , a_n) \in \llbracket \vdash P \,{:}{:}\, x_1 : A_1, \dots , x_n : A_n \rrbracket \) and \((a_1,\theta _1) \in \alpha _1, \dots , (a_n,\theta _n) \in \alpha _n\), then
Closing an agreeable process so that it has one free channel yields an inhabitant of the semantic type of the free channel:
Lemma 3
If the process \(\vdash P \,{:}{:}\, x_1 : A_1, \dots , x_n : A_n, x : A\) is agreeable, then for all \((\varTheta _1, \beta _1, C_1) \in \llbracket x_1 : A_1 \rrbracket ^\perp , \dots , (\varTheta _n, \beta _n, C_n) \in \llbracket x_n : A_n \rrbracket ^\perp \), it is the case that
where
\(\alpha = \{ (a, \theta _1, a_1, \dots , \theta _n, a_n) | (a_1, \dots , a_n, a) \in \llbracket P \rrbracket , (a_1, \theta _1) \in \beta _1, \dots , (a_n, \theta _n) \in \beta _n \}\)
For all processes, when connected to well-typed configurations, their denotational semantics predicts their behaviour:
Lemma 4
All processes \(\vdash P \,{:}{:}\, \varGamma \) are agreeable.
Proof
(Sketch) By induction on the derivation of \(\vdash P \,{:}{:}\, \varGamma \). The structural rules (( ), (
), ( ), (Mix\(_0\))) all involve relatively straightforward unfoldings of the definitions. The rest of the rules follow one of two patterns, depending on whether they are introducing a negative or positive connective. For the negative connectives,
), (Mix\(_0\))) all involve relatively straightforward unfoldings of the definitions. The rest of the rules follow one of two patterns, depending on whether they are introducing a negative or positive connective. For the negative connectives,  , and for the contraction and weakening rules, we are using (
, and for the contraction and weakening rules, we are using ( ) to connect the configuration composed of P and configurations for the other free channels with a triple \((\varTheta , \alpha , C)\) that is a semantic inhabitant of the negation of a negative type. To proceed, we use the fact that the positive types are all defined via double-negation closure to deduce the following:
) to connect the configuration composed of P and configurations for the other free channels with a triple \((\varTheta , \alpha , C)\) that is a semantic inhabitant of the negation of a negative type. To proceed, we use the fact that the positive types are all defined via double-negation closure to deduce the following:
where “ideal” indicates the defining property of the negation of the formula being introduce, as defined in Fig. 4, and \(-\mathord \perp -\) indicates the property that the denotational semantics correctly predicts the operational semantics when  -ing two configurations. Thus we can reason as if the triple \((\varTheta , \alpha , C)\) is an “ideal” inhabitant of the negation of the introduced type.
-ing two configurations. Thus we can reason as if the triple \((\varTheta , \alpha , C)\) is an “ideal” inhabitant of the negation of the introduced type.
For the positive connectives,  , the situation is slightly simpler. By point (3) of Lemma 1, we deduce that, if \((\varTheta , \alpha , C)\) is the interacting process of the negation of the introduced type, then:
, the situation is slightly simpler. By point (3) of Lemma 1, we deduce that, if \((\varTheta , \alpha , C)\) is the interacting process of the negation of the introduced type, then:
Therefore, our job is to prove that the newly introduced process conforms to the “ideal” specification introduced in Fig. 4. This is mostly straightforward, save for the ( ) case, where we need an auxillary induction over the context
) case, where we need an auxillary induction over the context  to deduce that all the configurations connected to these channels are themselves duplicable and discardable.
to deduce that all the configurations connected to these channels are themselves duplicable and discardable.
Agreeable Configurations. We now extend the definition of agreeability from processes to configurations. After we show that all configurations are agreeable, the special case of this definition for closed processes will give us the backwards direction of Theorem 1 (Corollary 1).
Definition 5
A configuration \(\vdash _c C \,{:}{:}\, x_1 : A_1, \dots , x_n : A_n \mid \varTheta \) is agreeable if for all \((\varTheta _1, \alpha _1, C_1) \in \llbracket x_1 : A_1 \rrbracket ^\perp , \dots , (\varTheta _n, \alpha _n, C_n) \in \llbracket x_n : A_n \rrbracket ^\perp \), and \((a_1, \dots , a_n, \theta ) \in \llbracket \vdash _c C \,{:}{:}\, x_1 : A_1, \dots , x_n : A_n \mid \varTheta \rrbracket \) and \((a_1,\theta _1) \in \alpha _1\), \(\dots \), and \((a_n,\theta _n) \in \alpha _n\), then \((\cdots (C \mid _{x_1} C_1) \cdots \mid _{x_n} C_n) \Downarrow (\theta , \theta _1, a_1, \dots , \theta _n, a_n)\).
Lemma 5
All configurations \(\vdash _c C \,{:}{:}\, \varGamma \mid \varTheta \) are agreeable.
Proof
By induction on the derivation of \(\vdash _c C \,{:}{:}\, \varGamma \mid \varTheta \). Lemma 4 is used to handle the ( ) case, and all the other cases are similar to the corresponding case in the proof of Lemma 4.
) case, and all the other cases are similar to the corresponding case in the proof of Lemma 4.
When \(\varGamma \) is empty, Lemma 5 yields the backwards direction of Theorem 1:
Corollary 1
If \(\vdash _c C \,{:}{:}\, \cdot \mid \varTheta \) and \(\theta \in \llbracket \vdash _c C \,{:}{:}\, \cdot \mid \varTheta \rrbracket \), then \(C \Downarrow \theta \).
5 Observational Equivalences
Theorem 1 enables us to predict the behaviour of processes without having to first embed them in a closing configuration. In particular, we can use it as a method for proving observational equivalences:
Corollary 2
If \(\vdash P_1, P_2 \,{:}{:}\, \varGamma \) and \(\llbracket P_1 \rrbracket = \llbracket P_2 \rrbracket \), then \(P_1 \simeq P_2\).
Proof
For any closing configuration context \( CP [-]\) and observation \(\theta \), we have:
We now use this corollary to show that the cut elimination rules of CLL and permutation rules yield observational equivalences for our operational semantics. Since we have used the standard relational semantics of CLL, which is known to be equationally sound for cut-elimination [25], all these statements are immediate. The force of Corollary 2 is that these rules also translate to observational equivalences for our independently defined operational semantics.
 -Elimination Rules. Figure 5 shows the rules arising from the interaction of (
-Elimination Rules. Figure 5 shows the rules arising from the interaction of ( ) with itself and the (
) with itself and the ( ) rule: (
) rule: ( ) is associative and commutative, and has (
) is associative and commutative, and has ( ) as an identity element. These rules amount to the observation that one can construct a category from CLL proofs (see Melliès [25], Sect. 2).
) as an identity element. These rules amount to the observation that one can construct a category from CLL proofs (see Melliès [25], Sect. 2).
Figure 6 shows the rules arising from elimination of “principal cuts”: ( ) rule applications that are on a formula and its dual that are introduced by the two immediate premises. Oriented left-to-right, and restricted to top-level (i.e., not under a prefix), these are the rules that are taken as the reduction rules of CP by Wadler. They are also the inspiration for our evaluation rules in Fig. 3. However, here these rules are observational equivalences, so we can use them anywhere in process to replace two communicating processes with the result of their communication. Figure 7 presents the rules for eliminiating non-principal cuts: (
) rule applications that are on a formula and its dual that are introduced by the two immediate premises. Oriented left-to-right, and restricted to top-level (i.e., not under a prefix), these are the rules that are taken as the reduction rules of CP by Wadler. They are also the inspiration for our evaluation rules in Fig. 3. However, here these rules are observational equivalences, so we can use them anywhere in process to replace two communicating processes with the result of their communication. Figure 7 presents the rules for eliminiating non-principal cuts: ( ) rule applications where the cut formula is not the most recently introduced one. These rules are also called “commuting conversion” rules because they commute input/output prefixes with applications of the (
) rule applications where the cut formula is not the most recently introduced one. These rules are also called “commuting conversion” rules because they commute input/output prefixes with applications of the ( ) rule in order to expose potential interactions. The fact that these are now observational equivalences formalises the informal statement given by Wadler in Sect. 3.6 of [36] that these rules are justified for CP. Note that the semantics we presented in Sect. 2.4 does not make use of commuting conversions. It only requires immediate interactions between process. Since there are no channels left unconnected, there is no way for a process to get stuck.
) rule in order to expose potential interactions. The fact that these are now observational equivalences formalises the informal statement given by Wadler in Sect. 3.6 of [36] that these rules are justified for CP. Note that the semantics we presented in Sect. 2.4 does not make use of commuting conversions. It only requires immediate interactions between process. Since there are no channels left unconnected, there is no way for a process to get stuck.
Permutation of Independent Channels. Figure 8 presents a set of observational equivalence rules arising from permutation of communication along independent channels. We have omitted the type information to save space. The admissibility of these rules is an indication of the relative weakness of CP contexts to make observations on a process. If a process has a access to a pair of channels, the processes connected to the other ends of those channels must be independent, and so cannot communicate between themselves to discover which one was communicated with first. This is why the denotational semantics of CP that we defined in Sect. 3 does not explain processes’ behaviour in terms of traces as is more common when giving denotation semantics to process calculi [30]. The typing constraints of CP mean that there is no global notion of time: the only way that a CP process can “know” the past from the future is by receiving a bit of information via the ( ) rule. Everything else that a CP process does is pre-ordained by its type.
) rule. Everything else that a CP process does is pre-ordained by its type.
There are a large number of equations in Fig. 8 due to the need to account for the permutation of each kind of prefix with itself and with every other prefix. The (\(\otimes \)) rule is particularly bad due to the presence of two sub-processes, either of which may do perform the permuted action.
6 Related Work
Wadler’s papers introducing CP, [35, 36], contain discussions of work related to the formulation of CP as a session-typed language derived from CLL, and how this relates to session types. Here, we discuss work related to logical relations and observational equivalences for session-typed calculi, and the use of denotational semantics for analysing the proofs of CLL.
Just as the Iron Curtain during the Cold War lead to the same work being done twice, once in the East and once in the West, the existence of two logically-based session-typed concurrency formalisms, one based on Intuitionistic Linear Logic (ILL) [9], and one based on Classical Linear Logic, means that analogous work is performed on both sides. (Indeed, ILL has both left and right rules for each connective, meaning that working with ILL-based formalisms already doubles the amount of work one needs to do.) Notions of observational equivalence and logical relations for \(\pi \)DILL have already been studied by Pérez et al. [27]. Pérez et al. use logical relations to prove strong normalisation and confluence for their session-typed calculus based on ILL, and define a notion of observational equivalence between session-typed processes, based on bisimulation. They prove observational equivalences based on the ( )-elimination rules of their calculus, analogous to ones we proved in the previous section.
)-elimination rules of their calculus, analogous to ones we proved in the previous section.
As we noted in the introduction Pérez et al. define an LTS over stuck processes with one free output channel. They use this to coinductively define their notion of observational equivalence. This means that to prove individual equivalences requires the construction of the appropriate bisimulation relation. In contrast, our denotational technique for proving equivalences is much more elementary, involving only simple set theoretic reasoning. Moreover, their technique requires additional proofs that their definition of observational equivalence is a congruence, a fact that is immediate in our definition.
Pérez et al. go further than we have done in also proving that their calculus is strongly normalising and confluent, using a logical relations based proof. As we discussed in Sect. 3.4, it is possible to use a coherence space semantics to prove determinacy, and we conjecture that totality spaces can prove termination.
\(\bot \bot \)-closed relations are a standard feature of proofs in the meta-theory of Linear Logic: for example weak normalisation proofs by Girard [16] and Baelde [5] and strong normalisation proofs by Accattoli [3]. They have also been used for parametricity results in polymorphically typed \(\pi \)-calculi [8]. An innovation in this paper is the use of Kripke \(\bot \bot \)-closed relations to account for the contexts \(\varTheta \) describing the possible observations on configurations.
7 Conclusions and Future Work
We have introduced an operational semantics for Wadler’s CP calculus that agrees with the standard relational semantics of CLL proofs. We have been able to show that the ( )-elimination rules of CLL are precisely observational equivalences with respect to our operational semantics. We view this work as a crucial step in treating CP as a foundational language of structured communication. We now highlight some areas of research that we have opened up.
)-elimination rules of CLL are precisely observational equivalences with respect to our operational semantics. We view this work as a crucial step in treating CP as a foundational language of structured communication. We now highlight some areas of research that we have opened up.
Refined Denotational Semantics for CP. As we discussed in Sect. 3.4, there is a close connection between semantics of CLL that assign cliques to proofs and the operational properties of the corresponding processes. Further refinements of the relational semantics, beyond coherence spaces, such as Loader’s totality spaces [22] and Ehrhard’s Finiteness spaces [13], should yield insights into the operational behaviour of CP and its extensions with features such as non-determinism. Laird et al. [19]’s weighted relational semantics interprets processes as semiring-valued matrices. This could be used to model a variant of CP with complexity measures. Probabilistic Coherence Spaces, introduced by Danos and Ehrhard [11], are another refinement that model probabilistic computation.
Recursive Types for CP. In this paper, we have only investigated the basic features of CP. Extensions of CP with recursive types, based on the work in CLL by Baelde [5], have been carried out by Lindley and Morris [21]. Extension of our operational semantics and the denotational semantics with recursive types is an essential step in turning CP into a more realistic language for structured communication. Constructing concurrency features on CP may be possible by allowing racy interleaving of clients and servers expressive via recursive types.
Dependent Types for CP. More ambitiously, we intend to extend CP with dependent types. Dependent types for logically-based session-typed calculi have already been investigated by Toninho et al. [33] and Toninho and Yoshida [34]. However, these calculi enforce a strict separation between data and communication: there are session types \(\Pi x \mathord : \tau .A(x)\) and \(\varSigma x \mathord : \tau .A(x)\) which correspond to receiving or transmitting a value of value type \(\tau \). Taking inspiration from McBride’s investigation of the combination of linear and dependent types [24], we envisage a more general notion of session-dependent session type \((x : A) \rhd B\), where the value of x in B is determined by the actual observed data transferred in the session described by A. This type is a dependent generalisation of Retoré’s “before” connective [29]. To make this idea work, we need a notion of observed communication in CP, which the observed communication semantics proposed in this paper provides.
References
Abramsky, S.: Computational interpretations of linear logic. Theor. Comput. Sci. 111, 3–57 (1993)
Abramsky, S.: Proofs as processes. Theor. Comput. Sci. 135(1), 5–9 (1992)
Accattoli, B.: Linear logic and strong normalization. In: 24th International Conference on Rewriting Techniques and Applications, RTA 2013, 24–26 June 2013, Eindhoven, The Netherlands, pp. 39–54 (2013)
Atkey, R., Lindley, S., Morris, J.G.: Conflation confers concurrency. In: Lindley, S., McBride, C., Trinder, P., Sannella, D. (eds.) A List of Successes That Can Change the World. LNCS, vol. 9600, pp. 32–55. Springer, Heidelberg (2016). doi:10.1007/978-3-319-30936-1_2
Baelde, D.: Least, greatest fixed points in linear logic. ACM Trans. Comput. Logic 13(1), 2:1–2:44 (2012)
Barr, M.: *-Autonomous categories and linear logic. Math. Struct. Comput. Sci. 1(2), 159–178 (1991)
Bellin, G., Scott, P.J.: On the \(\uppi \)-calculus and linear logic. Theoret. Comput. Sci. 135(1), 11–65 (1994)
Berger, M., Honda, K., Yoshida, N.: Genericity and the \(\uppi \)-calculus. In: Gordon, A.D. (ed.) FoSSaCS 2003. LNCS, vol. 2620, pp. 103–119. Springer, Heidelberg (2003). doi:10.1007/3-540-36576-1_7
Caires, L., Pfenning, F.: Session types as intuitionistic linear propositions. In: Gastin, P., Laroussinie, F. (eds.) CONCUR 2010. LNCS, vol. 6269, pp. 222–236. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15375-4_16
Curry, H.B.: Functionality in combinatory logic. Proc. Natl. Acad. Sci. 20, 584–590 (1934)
Danos, V., Ehrhard, T.: Probabilistic coherence spaces as a model of higher-order probabilistic computation. Inf. Comput. 209(6), 966–991 (2011)
Davey, B.A., Priestley, H.A.: Introduction to Lattices and Order, 2nd edn. Cambridge University Press, Cambridge (2002)
Ehrhard, T.: Finiteness spaces. Math. Struct. Comput. Sci. 15(4), 615–646 (2005)
Ehrhard, T., Laurent, O.: Interpreting a finitary \(\uppi \)-calculus in differential interaction nets. Inf. Comput. 208(6), 606–633 (2010)
Gay, S.J., Vasconcelos, V.T.: Linear type theory for asynchronous session types. J. Funct. Program. 20(01), 19–50 (2010)
Girard, J.-Y.: Linear logic. Theor. Comput. Sci. 50, 1–101 (1987)
Honda, K.: Types for dyadic interaction. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 509–523. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_35
Howard, W.A.: The formulae-as-types notion of construction. In: Seldin, J.P., Hindley, J.R. (eds.) To H.B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism. Academic Press, Boston (1980)
Laird, J., Manzonetto, G., McCusker, G., Pagani, M.: Weighted relational models of typed \(\lambda \)-calculi. In: 28th Annual ACM/IEEE Symposium on Logic in Computer Science, LICS 2013, 25–28 June 2013, New Orleans, LA, USA, pp. 301–310 (2013)
Lindley, S., Morris, J.G.: A semantics for propositions as sessions. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 560–584. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46669-8_23
Lindley, S., Morris, J.G.: Talking bananas: structural recursion for session types. In: ICFP (2016, to appear)
Loader, R.: Linear logic, totality and full completeness. In: Proceedings of the Ninth Annual Symposium on Logic in Computer Science (LICS 1994), 4–7 July 1994, Paris, France, pp. 292–298 (1994)
Mazza, D.: The true concurrency of differential interaction nets. Math. Struct. Comput. Sci. (2015, to appear)
McBride, C.: I got plenty o’ nuttin’. In: Lindley, S., McBride, C., Trinder, P., Sannella, D. (eds.) A List of Successes That Can Change the World. LNCS, vol. 9600, pp. 207–233. Springer, Heidelberg (2016). doi:10.1007/978-3-319-30936-1_12
Melliès, P.-A.: Categorical semantics of linear logic. In: Curien, P.-L., Herbelin, H., Krivine, J.-L., Melliès, P.-A. (eds.) Interactive Models of Computation and Program Behavior, Number 27 in Panoramas et Synthèses. Société Mathématique de France (2009)
Milner, R., Sangiorgi, D.: Barbed bisimulation. In: Kuich, W. (ed.) ICALP 1992. LNCS, vol. 623, pp. 685–695. Springer, Heidelberg (1992). doi:10.1007/3-540-55719-9_114
Pérez, J.A., Caires, L., Pfenning, F., Toninho, B.: Linear logical relations and observational equivalences for session-based concurrency. Inf. Comput. 239, 254–302 (2014)
Plotkin, G.D.: LCF considered as a programming language. Theor. Comput. Sci. 5(3), 223–255 (1977)
Retoré, C.: Pomset logic: a non-commutative extension of classical linear logic. In: Groote, P., Roger Hindley, J. (eds.) TLCA 1997. LNCS, vol. 1210, pp. 300–318. Springer, Heidelberg (1997). doi:10.1007/3-540-62688-3_43
Roscoe, A.W.: The Theory and Practice of Concurrency. Prentice Hall, Upper Saddle River (1998)
Sangiorgi, D., Walker, D.: The \(\uppi \)-Calculus - A Theory of Mobile Processes. Cambridge University Press, Cambridge (2001)
Stark, I.: A fully abstract domain model for the \(\uppi \)-calculus. In: Proceedings of the 11th Annual IEEE Symposium on Logic in Computer Science, 27–30 July 1996, New Brunswick, New Jersey, USA, pp. 36–42 (1996)
Toninho, B., Caires, L., Pfenning, F.: Dependent session types via intuitionistic linear type theory. In: Proceedings of the 13th International ACM SIGPLAN Conference on Principles and Practice of Declarative Programming, 20–22 July 2011, Odense, Denmark, pp. 161–172 (2011)
Toninho, B., Yoshida, N.: Certifying data in multiparty session types. In: A List of Successes That Can Change the World - Essays Dedicated to Philip Wadler on the Occasion of His 60th Birthday, pp. 433–458 (2016)
Wadler, P.: Propositions as sessions. In: Proceedings of the 17th ACM SIGPLAN International Conference on Functional Programming, ICFP 2012. ACM (2012)
Wadler, P.: Propositions as sessions. J. Funct. Program. 24(2–3), 384–418 (2014)
Acknowledgements
Thanks to Sam Lindley, J. Garrett Morris, Conor McBride and Phil Wadler for helpful discussions and comments on this paper. This work was partly funded by a Science Faculty Starter Grant from the University of Strathclyde.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Atkey, R. (2017). Observed Communication Semantics for Classical Processes. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)



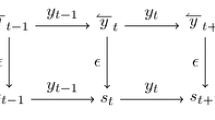

 -elimination rules of CLL are observational equivalences in our operational semantics, in Sect.
-elimination rules of CLL are observational equivalences in our operational semantics, in Sect.  -elimination rules can be seen as a sound equational theory for reasoning about observational equivalence. We also show that permutations of communications along independent channels are observational equivalences.
-elimination rules can be seen as a sound equational theory for reasoning about observational equivalence. We also show that permutations of communications along independent channels are observational equivalences.


 ,
, 




