The Power of Non-determinism in Higher-Order Implicit Complexity

Abstract

We investigate the power of non-determinism in purely functional programming languages with higher-order types. Specifically, we consider cons-free programs of varying data orders, equipped with explicit non-deterministic choice. Cons-freeness roughly means that data constructors cannot occur in function bodies and all manipulation of storage space thus has to happen indirectly using the call stack.

While cons-free programs have previously been used by several authors to characterise complexity classes, the work on non-deterministic programs has almost exclusively considered programs of data order 0. Previous work has shown that adding explicit non-determinism to cons-free programs taking data of order 0 does not increase expressivity; we prove that this—dramatically—is not the case for higher data orders: adding non-determinism to programs with data order at least 1 allows for a characterisation of the entire class of elementary-time decidable sets.

Finally we show how, even with non-deterministic choice, the original hierarchy of characterisations is restored by imposing different restrictions.

The authors are supported by the Marie Skłodowska-Curie action “HORIP”, program H2020-MSCA-IF-2014, 658162 and by the Danish Council for Independent Research Sapere Aude grant “Complexity via Logic and Algebra” (COLA).

1 Introduction

Implicit complexity is, roughly, the study of how to create bespoke programming languages that allow the programmer to write programs which are guaranteed to (a) only solve problems within a certain complexity class (e.g., the class of polynomial-time decidable sets of binary strings), and (b) to be able to solve all problems in this class. When equipped with an efficient execution engine, the programs of such a language may themselves be guaranteed to run within the complexity bounds of the class (e.g., run in polynomial time), and the plethora of means available for analysing programs devised by the programming language community means that methods from outside traditional complexity theory can conceivably be brought to bear on open problems in computational complexity.

One successful approach to implicit complexity is to syntactically constrain the programmer’s ability to create new data structures. In the seminal paper [12], Jones introduces cons-free programming. Working with a small functional programming language, cons-free programs are read-only: recursive data cannot be created or altered (beyond taking sub-expressions), only read from input. By imposing further restrictions on data order (i.e., order 0 = integers, strings; order 1 = functions on data of order 0; etc.) and recursion scheme (e.g., full/tail/primitive recursion), classes of cons-free programs turn out to characterise various deterministic classes in the time and space hierarchies of computational complexity.

However, Jones’ language is deterministic and, perhaps as a result, his characterisations concern only deterministic complexity classes. It is tantalising to consider the method in a non-deterministic setting: could adding non-deterministic choice to Jones’ language increase its expressivity; for example, from $\mathsf {P}$ to $\mathsf {NP}$?

The immediate answer is no: following Bonfante [4], adding a non-deterministic choice operator to cons-free programs with data order 0 makes no difference in expressivity—deterministic or not, they characterise $\mathsf {P}$. However, the details are subtle and depend heavily on other features of the language; when only primitive recursion is allowed, non-determinism does increase expressivity from $\mathsf {L}$ to $\mathsf {NL}$ [4].

While many authors consider the expressivity of higher types, the interplay of higher types and non-determinism is not fully understood. Jones obtains several hierarchies of deterministic complexity classes by increasing data orders [12], but these hierarchies have at most an exponential increase between levels. Given the expressivity added by non-determinism, it is a priori not evident that similarly “tame” hierarchies would arise in the non-deterministic setting.

The purpose of the present paper is to investigate the power of higher-order (cons-free) programming to characterise complexity classes. The main surprise is that while non-determinism does not add expressivity for first-order programs, the combination of second-order (or higher) programs and non-determinism characterises the full class of elementary-time decidable sets—and increasing the order beyond second-order programs does not further increase expressivity. However, we will also show that there are simple changes to the restrictions that allow us to obtain a hierarchy of characterisations as in the deterministic setting.

An extended version of this paper with full proofs is available online [15].

1.1 Overview and Contributions

We define a purely functional programming language with non-deterministic choice and, following Jones [12], consider the restriction to cons-free programs.

Fig. 1.

Overview of the results discussed or obtained in this paper.

Our results are summarised in Fig. 1. For completeness, we have also included the results from [12]; although the language used there is slightly more syntactically restrictive than ours, the results easily generalise provided we limit interest to deterministic programs, where the $\mathtt {choose}$ operator is not used. As the technical machinations involved to procure the results for a language with full recursion are already intricate and lengthy, we have not yet considered the restriction to tail- or primitive recursion in the non-deterministic setting.

Essentially, our paper has two major contributions: (a) we show that previous observations about the increase in expressiveness when adding non-determinism change dramatically at higher types, and (b) we provide two characterisations of the $\mathsf {EXP}^{}\mathsf {TIME}$ hierarchy using a non-deterministic language—which may provide a basis for future characterisation of common non-deterministic classes as well.

Note that (a) is highly surprising: As evidenced by early work of Cook [6] merely adding full non-determinism to a restricted (i.e., non-Turing complete) computation model may result in it still characterising a deterministic class of problems. This also holds true for cons-free programs with non-determinism, as shown in different settings by Bonfante [4], by de Carvalho and Simonsen [7], and by Kop and Simonsen [14], all resulting only in characterisations of deterministic classes such as $\mathsf {P}$. With the exception of [14], all of the above attempts at adding non-determinism consider data order at most 0, and one would expect few changes when passing to higher data orders. This turns out to be patently false as simply increasing to data order 1 already results in an explosion of expressive power.

1.2 Overview of the Ideas in the Paper

Cons-free programs (Definition 5) are, roughly, functional programs where function bodies are allowed to contain constant data and substructures of the function arguments, but no data constructors—e.g., clauses $\mathtt {tl}\ (x\mathtt {{:}{:}}xs) = xs$ and $\mathtt {tl}\ \mathtt {[]}= \mathtt {[]}$ are both allowed, but $\mathtt {append}\ (x\mathtt {{:}{:}}xs)\ ys = x\mathtt {{:}{:}}(\mathtt {append}\ xs\ ys)$ is not.¹ This restriction severely limits expressivity, as it means no new data can be created.

A key idea in Jones’ original work on cons-free programming is counting: expressions which represent numbers and functions to calculate with them. It is not in general possible to represent numbers in the usual unary way as $\mathtt {0}$, $\mathtt {s}\ \mathtt {0}$, $\mathtt {s}\ (\mathtt {s}\ \mathtt {0})$, etc., or as lists of bits—since in a cons-free program these expressions cannot be built unless they already occur in the input—but counting up to limited bounds can be achieved by other tricks. By repeatedly simulating a single step of a Turing Machine up to such bounds, Jones shows that any decision problem in $\mathsf {EXP}^{K}\mathsf {TIME}$ can be decided using a cons-free program ([12] and Lemma 6).

The core insight in the present paper is that in the presence of non-determinism, an expression of type $\sigma \Rightarrow \tau$ represents a relation between expressions of type $\sigma$ and expressions of type $\tau$ rather than a function. While the number of functions for a given type is exponential in the order of that type, the number of relations is exponential in the depth of arrows occurring in it. We exploit this (in Lemma 11) by counting up to arbitrarily high numbers using only first-order data. This observation also suggest that by limiting the arrow depth rather than the order of types, the increase in expressive power disappears (Theorem 3).

Conversely, we also provide an algorithm to compute the output of cons-free programs potentially much faster than the program’s own running time, by using a tableaux to store results. Although similar to Jones’ ideas, our proof style deviates to easily support both non-deterministic and deterministic programs.

1.3 Related Work

The creation of programming languages that characterise complexity classes has been a research area since Cobham’s work in the 1960ies, but saw rapid development only after similar advances in the related area of descriptive complexity (see, e.g., [10]) in the 1980ies and Bellantoni and Cook’s work on characterisations of $\mathsf {P}$ [2] using constraints on recursion in a purely functional language with programs reminiscent of classic recursion theoretic functions. Following Bellantoni and Cook, a number of authors obtained programming languages by constraints on recursion, and under a plethora of names (e.g., safe, tiered or ramified recursion, see [5, 19] for overviews), and this area continues to be active. The main difference with our work is that we consider full recursion in all variables, but place syntactic constraints on the function bodies (both cons-freeness and unitary variables). Also, as in traditional complexity theory we consider decision problems (i.e., what sets can be decided by programs), whereas much research in implicit complexity considers functional complexity (i.e., what functions can be computed).

Cons-free programs, combined with various limitations on recursion, were introduced by Jones [12], building on ground-breaking work by Goerdt [8, 9], and have been studied by a number of authors (see, e.g., [3, 4, 17, 18]). The main difference with our work is that we consider full recursion with full non-determinism, but impose constraints not present in the previous literature.

Characterisation of non-deterministic complexity classes via programming languages remains a largely unexplored area. Bellantoni obtained a characterisation of $\mathsf {NP}$ in his dissertation [1] using similar approaches as [2], but at the cost of having a minimisation operator (as in recursion theory), a restriction later removed by Oitavem [20]. A general framework for implicitly characterising a larger hierarchy of non-deterministic classes remains an open problem.

2 A Purely Functional, Non-deterministic, Call-by-Value Programming Language

We define a simple call-by-value programming language with explicit non-deterministic choice. This generalises Jones’ toy language in [12] by supporting different types and pattern-matching as well as non-determinism. The more permissive language actually simplifies proofs and examples, since we do not need to encode all data as boolean lists, and have fewer special cases.

2.1 Syntax

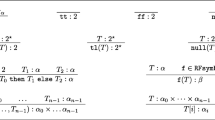
We consider programs defined by the syntax in Fig. 2

Fig. 2.

Syntax

We call elements of $\mathcal {V}$ variables, elements of $\mathcal {C}$ data constructors and elements of $\mathcal {D}$ defined symbols. The root of a clause $\mathtt {f}\ \ell _1 \cdots \ell _k = s$ is the defined symbol $\mathtt {f}$. The main function $\mathtt {f}_1$ of the program is the root of $\rho _1$. We denote $Var (s)$ for the set of variables occurring in an expression s. An expression s is ground if $Var (s) = \emptyset$. Application is left-associative, i.e., $s\ t\ u$ should be read $(s\ t)\ u$.

Definition 1

For expressions s, t, we say that t is a sub-expression of s, notation $s \unrhd t$, if this can be derived using the clauses:

$$\begin{aligned} \begin{array}{rclclrclcl} s &{} \unrhd &{} t &{} \text {if} &{} s = t\ \text {or}\ s \rhd t \\ (s_1,s_2) &{} \rhd &{} t &{} \text {if} &{} s_1 \unrhd t\ \text {or}\ s_2 \unrhd t\quad &{} \ \mathtt {if} \, s_1 \, \mathtt {then} \, s_2 \, \mathtt {else} \, s_3 &{} \rhd &{} t &{} \text {if} &{} s_i \unrhd t\ \text {for some}\ i \\ s_1\ s_2 &{} \rhd &{} t &{} \text {if} &{} s_1 \rhd t\ \text {or}\ s_2 \unrhd t &{} \mathtt {choose}\ s_1 \cdots s_n&{} \rhd &{} t &{} \text {if} &{} s_i \unrhd t \ \text {for some}\ i \\ \end{array} \end{aligned}$$

Note: the head s of an application $s\ t$ is not considered a sub-expression of $s\ t$.

Note that the programs we consider have no pre-defined data structures like integers: these may be encoded using inductive data structures in the usual way.

Example 1

Integers can be encoded as bitstrings of unbounded length: $\mathcal {C}\supseteq \{ \mathtt {false},\mathtt {true},\mathtt {{:}{:}},\mathtt {[]}\}$. Here, $\mathtt {{:}{:}}$ is considered infix and right-associative, and $\mathtt {[]}$ denotes the end of the string. Using little endian, 6 is encoded by $\mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {[]}$ as well as $\mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {[]}$. We for instance have $\mathtt {true}\mathtt {{:}{:}}(\mathtt {succ}\ xs) \unrhd xs$ (for $xs \in \mathcal {V}$). The program below imposes $\mathcal {D}= \{\mathtt {succ}\}$:

$$\begin{aligned} \begin{array}{lcl} \mathtt {succ}\ \mathtt {[]}= \mathtt {true}\mathtt {{:}{:}}\mathtt {[]}&{} \quad \quad &{} \mathtt {succ}\ (\mathtt {false}\mathtt {{:}{:}}xs) = \mathtt {true}\mathtt {{:}{:}}xs \\ &{} &{} \mathtt {succ}\ (\mathtt {true}\mathtt {{:}{:}}xs) = \mathtt {false}\mathtt {{:}{:}}(\mathtt {succ}\ xs) \\ \end{array} \end{aligned}$$

2.2 Typing

Programs have explicit simple types without polymorphism, with the usual definition of type order $ord \!\left( \sigma \right)$; this is formally given in Fig. 3.

Fig. 3.

Types and type orders

The (finite) set $\mathcal {S}$ of sorts is used to type atomic data such as bits; we assume $\mathtt {bool}\in \mathcal {S}$. The function arrow $\Rightarrow$ is considered right-associative. Writing $\kappa$ for a sort or a pair type $\sigma \times \tau$, any type can be uniquely presented in the form $\sigma _1 \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa$. We will limit interest to well-typed, well-formed programs:

Definition 2

A program $\mathsf {p}$ is well-typed if there is an assignment $\mathcal {F}$ from $\mathcal {C}\cup \mathcal {D}$ to the set of simple types such that:

• the main function $\mathtt {f}_1$ is assigned a type $\kappa _1 \Rightarrow \dots \Rightarrow \kappa _M \Rightarrow \kappa$, with $ord \!\left( \kappa _i\right) = 0$ for $1 \le i \le M$ and also $ord \!\left( \kappa \right) = 0$

• data constructors $\mathtt {c} \in \mathcal {C}$ are assigned a type $\kappa _1 \Rightarrow \dots \Rightarrow \kappa _m \Rightarrow \iota$ with $\iota \in \mathcal {S}$ and $ord \!\left( \kappa _i\right) = 0$ for $1 \le i \le m$

• for all clauses $\mathtt {f}\ \ell _1 \cdots \ell _k = s \in \mathsf {p}$, the following hold:

  • $Var (s) \subseteq Var (\mathtt {f}\ \ell _1 \cdots \ell _k)$ and each variable occurs only once in $\mathtt {f}\ \ell _1 \cdots \ell _k$;

  • there exist a type environment $\varGamma$ mapping $Var (\mathtt {f}\ \ell _1 \cdots \ell _k)$ to simple types, and a simple type $\sigma$, such that both $\mathtt {f}\ \ell _1 \cdots \ell _k : \sigma$ and $s : \sigma$ using the rules in Fig. 4; we call $\sigma$ the type of the clause.

Fig. 4.

Typing (for fixed $\mathcal {F}$ and $\varGamma$, see Definition 2)

Note that this definition does not allow for polymorphism: there is a single type assignment $\mathcal {F}$ for the full program. The assignment $\mathcal {F}$ also forces a unique choice for the type environment $\varGamma$ of variables in each clause. Thus, we may speak of the type of an expression in a clause without risk of confusion.

Example 2

The program of Example 1 is typed using $\mathcal {F}= \{ \mathtt {false}: \mathtt {bool}, \mathtt {true}: \mathtt {bool}, \mathtt {[]}: \mathtt {list}, \mathtt {{:}{:}}: \mathtt {bool}\Rightarrow \mathtt {list}\Rightarrow \mathtt {list}, \mathtt {succ} : \mathtt {list}\Rightarrow \mathtt {list}\}$. As all argument and output types have order 0, the variable restrictions are satisfied and all clauses can be typed using $\varGamma = \{ xs : \mathtt {list}\}$, the program is well-typed.

Definition 3

A program $\mathsf {p}$ is well-formed if it is well-typed, and moreover:

• data constructors are always fully applied: for all $\mathtt {c} \in \mathcal {C}$ with $\mathtt {c} : \kappa _1 \Rightarrow \dots \Rightarrow \kappa _m \Rightarrow \iota \in \mathcal {F}$: if a sub-expression $\mathtt {c}\ t_1 \cdots t_n$ occurs in any clause, then $n = m$;

• the number of arguments to a given defined symbol is fixed: if $\mathtt {f}\ \ell _1 \cdots \ell _k = s$ and $\mathtt {f}\ \ell _1' \cdots \ell _n' = t$ are both in $\mathsf {p}$, then $k = n$; we let $\mathtt {arity}_\mathsf {p}(\mathtt {f})$ denote k.

Example 3

The program of Example 1 is well-formed, and $\mathtt {arity}_\mathsf {p}(\mathtt {succ}) = 1$.

However, the program would not be well-formed if the clauses below were added, as here the defined symbol $\mathtt {or}$ does not have a consistent arity.

$$\begin{aligned} \begin{array}{rclcrclcrcl} \mathtt {id}\ x &{} = &{} x &{} \quad \quad &{} \mathtt {or}\ \mathtt {true}\ x &{} = &{} \mathtt {true}&{} \quad \quad &{} \mathtt {or}\ \mathtt {false}&{} = &{} \mathtt {id} \\ \end{array} \end{aligned}$$

Remark 1

Data constructors must (a) have a sort as output type (not a pair), and (b) occur only fully applied. This is consistent with typical functional programming languages, where sorts and constructors are declared with a grammar such as:

In addition, we require that the arguments to data constructors have type order 0. This is not standard in functional programming, but is the case in [12]. We limit interest to such constructors because, practically, these are the only ones which can be used in a cons-free program (as we will discuss in Sect. 3).

Definition 4

A program has data order K if all clauses can be typed using type environments $\varGamma$ such that, for all $x : \sigma \in \varGamma$: $ord \!\left( \sigma \right) \le K$.

Example 4

We consider a higher-order program, operating on the same data constructors as Example 1; however, now we encode numbers using functions:

$$\begin{aligned} \begin{array}{l} \mathtt {fsucc}\ F\ \mathtt {[]}= \mathtt {if} \, \,F\ \mathtt {[]}\, \, \mathtt {then} \, \,\mathtt {set}\ F\ []\ \mathtt {false}\, \, \mathtt {else} \, \,\mathtt {set}\ F\ \mathtt {[]}\ \mathtt {true}\, \\ \mathtt {fsucc}\ F\ xs = \mathtt {if} \, \,F\ xs\, \, \mathtt {then} \, \,\mathtt {fsucc}\ (\mathtt {set}\ F\ xs\ \mathtt {false})\ (\mathtt {tl}\ xs)\\ \qquad \qquad {\mathtt {fsucc}\ F\ xs = } \, \mathtt {else} \, \,\mathtt {set}\ F\ xs\ \mathtt {true}\, \\ \mathtt {set}\ F\ val \ xs\ ys = \mathtt {if} \, \,\mathtt {eqlen}\ xs\ ys\, \, \mathtt {then} \, \,val\, \, \mathtt {else} \, \,F\ ys \\ \mathtt {tl}\ (x\mathtt {{:}{:}}xs) = xs {ABEfg} \mathtt {eqlen}\ (x\mathtt {{:}{:}}xs)\ (y\mathtt {{:}{:}}ys) = \mathtt {eqlen}\ xs\ ys \\ \mathtt {eqlen}\ \mathtt {[]}\ \mathtt {[]}= \mathtt {true} {ABE} \mathtt {eqlen}\ xs\ ys = \mathtt {false}\\ \end{array} \end{aligned}$$

Only one typing is possible, with $\mathtt {fsucc}: (\mathtt {list}\Rightarrow \mathtt {bool}) \Rightarrow \mathtt {list}\Rightarrow \mathtt {list}\Rightarrow \mathtt {bool}$; therefore, F is always typed $\mathtt {list}\Rightarrow \mathtt {bool}$—which has type order 1—and all other variables with a type of order 0. Thus, this program has data order 1.

To explain the program: we use boolean lists as unary numbers of a limited size; assuming that (a) F represents a bitstring of length $N+1$, and (b) $lst$ has length N, the successor of F (modulo wrapping) is obtained by $\mathtt {fsucc}\ F\ lst$.

2.3 Semantics

Like Jones, our language has a closure-based call-by-value semantics. We let data expressions, values and environments be defined by the grammar in Fig. 5.

Fig. 5.

Data expressions, values and environments

Let $\mathtt {dom}(\gamma )$ denote the domain of an environment (partial function) $\gamma$. Note that values are ground expressions, and we only use well-typed values with fully applied data constructors. To every pattern $\ell$ and environment $\gamma$ with $\mathtt {dom}(\gamma ) \supseteq Var (\ell )$, we associate a value $\ell \gamma$ by instantiation in the obvious way, see Fig. 5.

Note that, for every value v and pattern $\ell$, there is at most one environment $\gamma$ with $\ell \gamma = v$. We say that an expression $\mathtt {f}\ s_1 \cdots s_n$ instantiates the left-hand side of a clause $\mathtt {f}\ \ell _1 \cdots \ell _k$ if $n = k$ and there is an environment $\gamma$ with each $s_i = \ell _i\gamma$.

Both input and output to the program are data expressions. If $\mathtt {f}_1$ has type $\kappa _1 \Rightarrow \dots \Rightarrow \kappa _M \Rightarrow \kappa$, we can think of the program as calculating a function $[\![\mathsf {p}]\!](d_1,\dots ,d_M)$ from M input data arguments to an output data expression.

Expression and program evaluation are given by the rules in Fig. 6. Since, in [Call], there is at most one suitable $\gamma$, the only source of non-determinism is the $\mathtt {choose}$ operator. Programs without this operator are called deterministic. By contrast, we may refer to a non-deterministic program as one which is not explicitly required to be deterministic, so which may or may not contain $\mathtt {choose}$.

Fig. 6.

Call-by-value semantics

Example 5

For the program from Example 1, $[\![\mathsf {p} ]\!](\mathtt {true}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {[]}) \mapsto \mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {[]}$, giving $5+1 = 6$. In the program $\mathtt {f}_1\ x\ y = \mathtt {choose}\ x\ y$, we can both derive $[\![\mathsf {p} ]\!](\mathtt {true},\mathtt {false}) \mapsto \mathtt {true}$ and $[\![\mathsf {p} ]\!](\mathtt {true},\mathtt {false}) \mapsto \mathtt {false}$.

The language is easily seen to be Turing-complete unless further restrictions are imposed. In order to assuage any fears on whether the complexity-theoretic characterisations we obtain are due to brittle design choices, we add some remarks.

Remark 2

We have omitted some constructs common to even some toy pure functional languages, but these are in general simple syntactic sugar that can be readily expressed by the existing constructs in the language, even in the presence of non-determinism. For instance, a let-binding $\texttt {let} \, x = s_1 \, \texttt {in} \, s_2$ can be straightforwardly encoded by a function call in a pure call-by-value setting (replacing $\texttt {let} \, x = s_1 \, \texttt {in} \, s_2$ by $\mathtt {helper}\ s_1$ and adding a clause $\mathtt {helper}\ x = s_2$).

Remark 3

We do not require the clauses of a function definition to exhaust all possible patterns. For instance, it is possible to have a clause $\mathtt {f} \, \mathtt {true}= \cdots$ without a clause for $\mathtt {f} \, \mathtt {false}$. Thus, a program has zero or more values.

Data Order Versus Program Order. We have followed Jones in considering data order as the variable for increasing complexity. However, an alternative choice—which turns out to streamline our proofs—is program order, which considers the type order of the function symbols. Fortunately, these notions are closely related; barring unused symbols, $\langle$program order$\rangle$ = $\langle$data order$\rangle$ + 1.

More specifically, we have the following result:

Lemma 1

For every well-formed program $\mathsf {p}$ with data order K, there is a well-formed program $\mathsf {p}'$ such that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ iff $[\![\mathsf {p}' ]\!](d_1,\dots ,d_M) \mapsto b$ for any $b_1,\dots ,b_M,d$ and: (a) all defined symbols in $\mathsf {p}'$ have a type $\sigma _1 \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa$ such that both $ord \!\left( \sigma _i\right) \le K$ for all i and $ord \!\left( \kappa \right) \le K$, and (b) in all clauses, all sub-expressions of the right-hand side have a type of order $\le K$ as well.

Proof

(Sketch). $\mathsf {p}'$ is obtained from $\mathsf {p}$ through the following successive changes:

• 1. Replace any clause $\mathtt {f}\ \ell _1 \cdots \ell _k = s$ where $s : \sigma \Rightarrow \tau$ with $ord \!\left( \sigma \Rightarrow \tau \right) = K+1$, by $\mathtt {f}\ \ell _1 \cdots \ell _k\ x = s\ x$ for a fresh x. Repeat until no such clauses remain.

• 2. In any clause $\mathtt {f}\ \ell _1 \cdots \ell _k = s$, replace all sub-expressions $(\mathtt {choose}\ s_1 \cdots s_m)\ t_1 \cdots {t_n}$ or $(\mathtt {if} \, s_1 \, \mathtt {then} \, s_2 \, \mathtt {else} \, s_3)\ t_1 \cdots t_n$ of s with $n > 0$ by $\mathtt {choose}\ (s_1\ t_1 \cdots t_n) \cdots {(s_m\ t_1 \cdots t_n)}$ or $\mathtt {if} \, s_1 \, \mathtt {then} \, (s_2\ t_1 \cdots t_n) \, \mathtt {else} \, (s_3\ t_1 \cdots t_n)$ respectively.

• 3. In any clause $\mathtt {f}\ \ell _1 \cdots \ell _k = s$, if s has a sub-expression $t = \mathtt {g}\ s_1 \cdots s_n$ with $\mathtt {g} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _n \Rightarrow \tau$ such that $ord \!\left( \tau \right) \le K$ but $ord \!\left( \sigma _i\right) > K$ for some i, then replace t by a fresh symbol $\bot _\tau$. Repeat until no such sub-expressions remain, then add clauses $\bot _\tau = \bot _\tau$ for the new symbols.

• 4. If there exists $\mathtt {f} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa \in \mathcal {F}$ with $ord \!\left( \kappa \right) > K$ or $ord \!\left( \sigma _i\right) > K$ for some i, then remove the symbol $\mathtt {f}$ and all clauses with root $\mathtt {f}$.

The key observation is that if the derivation for $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ uses some $\mathtt {f}\ s_1 \cdots s_n : \sigma$ with $ord \!\left( \sigma \right) \le K$ but $s_i : \tau$ with $ord \!\left( \tau \right) > K$, then there is a variable with type order $> K$. Thus, if a clause introduces such an expression, either the clause is never used, or the expression occurs beneath an $\mathtt {if}$ or $\mathtt {choose}$ and is never selected; it may be replaced with a symbol whose only rule is unusable. This also justifies step 1; for step 4, only unusable clauses are removed.

   $\square$

Example 6

The following program has data order 0, but clauses of functional type; $\mathtt {fst}$ and $\mathtt {snd}$ have output type $\mathtt {nat}\Rightarrow \mathtt {nat}$ of order 1. The program is changed by replacing the last two clauses by $\mathtt {fst}\ x\ y = \mathtt {const}\ x\ y$ and $\mathtt {snd}\ x\ y = \mathtt {id}\ y$.

3 Cons-Free Programs

Jones defines a cons-free program as one where the list constructor $\mathtt {{:}{:}}$ does not occur in any clause. In our setting (where more constructors are in principle admitted), this translates to disallowing non-constant data constructors from being introduced in the right-hand side of a clause. We define:

Definition 5

A program $\mathsf {p}$ is cons-free if all clauses in $\mathsf {p}$ are cons-free. A clause $\mathtt {f}\ \ell _1 \cdots \ell _k = s$ is cons-free if for all $s \unrhd t$: if $t = \mathtt {c}\ s_1 \cdots s_m$ with $\mathtt {c} \in \mathcal {C}$, then t is a data expression or $\ell _i \unrhd t$ for some i.

Example 7

Example 1 is not cons-free, due to the second and third clause (the first clause is cons-free). Examples 4 and 6 are both cons-free.

The key property of cons-free programming is that no new data structures can be created during program execution. Formally, in a derivation tree with root $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$, all data values (including b) are in the set $\mathcal {B}_{d_1,\dots , d_M}^\mathsf {p}$:

Definition 6

Let .

$\mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$ is a set of data expressions closed under $\rhd$, with a linear number of elements in the size of $d_1, \dots ,d_M$ (for fixed $\mathsf {p}$). The property that no new data is created during execution is formally expressed by the following lemma.

Lemma 2

Let $\mathsf {p}$ be a cons-free program, and suppose that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ is obtained by a derivation tree T. Then for all statements $\mathsf {p}, \gamma \vdash s \rightarrow w$ or $\mathsf {p},\gamma \vdash ^{\mathtt {if}}b',s_1,s_2 \rightarrow w$ or $\mathsf {p}\vdash ^{\mathtt {call}}\mathtt {f}\ v_1 \cdots v_n \rightarrow w$ in T, and all expressions t such that (a) $w \unrhd t$, (b) $b' \unrhd t$, (c) $\gamma (x) \unrhd t$ for some x or (d) $v_i \unrhd t$ for some i: if t has the form $\mathtt {c}\ b_1 \cdots b_m$ with $\mathtt {c} \in \mathcal {C}$, then $t \in \mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$.

That is, any data expression in the derivation tree of $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ (including occurrences as a sub-expression of other values) is also in $\mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$.

Proof

(Sketch). Induction on the form of T, assuming that for a statement under consideration, (1) the requirements on $\gamma$ and the $v_i$ are satisfied, and (2) $\gamma$ maps expressions $t \unlhd s,s_1,s_2$ to elements of $\mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$ if $t = \mathtt {c}\ t_1 \cdots t_m$ with $\mathtt {c} \in \mathcal {C}$.    $\square$

Note that Lemma 2 implies that the program result b is in $\mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$. Recall also Remark 1: if we had admitted constructors with higher-order argument types, then Lemma 2 shows that they are never used, since any constructor appearing in a derivation for $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ must already occur in the (data!) input.

4 Turing Machines, Decision Problems and Complexity

We assume familiarity with the standard notions of Turing Machines and complexity classes (see, e.g., [11, 21, 22]); in this section, we fix the notation we use.

4.1 (Deterministic) Turing Machines

Turing Machines (TMs) are triples (A, S, T) where A is a finite set of tape symbols such that $A \supseteq \{0,1,\mathbf \textvisiblespace \}$, $S \supseteq \{ \mathtt {start}, \mathtt {accept}, \mathtt {reject} \}$ is a finite set of states, and T is a finite set of transitions (i, r, w, d, j) with $i \in S \setminus \{\mathtt {accept},\mathtt {reject}\}$ (the original state), $r \in A$ (the read symbol), $w \in A$ (the written symbol), $d \in \{ \mathtt {L},\mathtt {R} \}$ (the direction), and $j \in S$ (the result state). We sometimes denote this transition as $i~\displaystyle {\mathop {=\!\!=\!\!\! \Longrightarrow }^{r/w\ d}}~j$. A deterministic TM is a TM such that every pair (i, r) with $i \in S \setminus \{\mathtt {accept},\mathtt {reject}\}$ and $r \in A$ is associated with exactly one transition (i, r, w, d, j). Every TM in this paper has a single, right-infinite tape.

A valid tape is an element t of $A^\mathbb {N}$ with $t(p) \ne \mathbf \textvisiblespace$ for only finitely many p. A configuration is a triple (t, p, s) with t a valid tape, $p \in \mathbb {N}$ and $s \in S$. The transitions T induce a relation $\Rightarrow$ between configurations in the obvious way.

4.2 Decision Problems

A decision problem is a set $X \subseteq \{0,1\}^+$. A deterministic TM decides X if for any $x \in \{0,1\}^+$: $x \in X$ iff $\mathbf \textvisiblespace x_1\dots x_n \mathbf \textvisiblespace \mathbf \textvisiblespace \dots ,0,\mathtt {start}) \Rightarrow ^* (t,i,\mathtt {accept})$ for some t, i, and $(\mathbf \textvisiblespace x_1\dots x_n\mathbf \textvisiblespace \mathbf \textvisiblespace \dots ,0,\mathtt {start}) \Rightarrow ^* (t,i,\mathtt {reject})$ iff $x \notin X$. Thus, the TM halts on all inputs, ending in $\mathtt {accept}$ or $\mathtt {reject}$ depending on whether $x \in X$.

If $h: \mathbb {N}\longrightarrow \mathbb {N}$ is a function, a deterministic TM runs in time $\lambda n.h(n)$ if for all $n \in \mathbb {N}\setminus \{0\}$ and $x \in \{0,1\}^n$: any evaluation starting in $(\mathbf \textvisiblespace x_1\dots x_n\mathbf \textvisiblespace \mathbf \textvisiblespace \dots ,0, \mathtt {start})$ ends in the $\mathtt {accept}$ or $\mathtt {reject}$ state in at most h(n) transitions.

4.3 Complexity and the $\mathsf {EXP}^{}\mathsf {TIME}$ Hierarchy

We define classes of decision problem based on the time needed to accept them.

Definition 7

Let $h: \mathbb {N}\rightarrow \mathbb {N}$ be a function. Then, $\text {TIME}\left( h(n)\right)$ is the set of all $X \subseteq \{0,1\}^+$ such that there exist $a > 0$ and a deterministic TM running in time $\lambda n.a \cdot h(n)$ that decides X.

By design, $\text {TIME}\left( h(n)\right)$ is closed under $\mathcal {O}$: $\text {TIME}\left( h(n)\right) = \text {TIME}\left( \mathcal {O}(h(n))\right)$.

Definition 8

For $K,n \ge 0$, let $\exp _2^0(n) = n$ and $\exp _2^{K+1}(n) = \exp _2^K(2^n) = 2^{\exp _2^K(n)}$. For $K \ge 0$, define $\mathsf {EXP}^{K}\mathsf {TIME} \triangleq \bigcup _{a,b \in \mathbb {N}} \text {TIME}\left( \text {exp}_2^{K}(an^b)\right)$.

Since for every polynomial $h$, there are $a,b \in \mathbb {N}$ such that $h(n) \le a \cdot n^b$ for all $n > 0$, we have $\mathsf {EXP}^{0}\mathsf {TIME} = \mathsf {P}$ and $\mathsf {EXP}^{1}\mathsf {TIME} = \mathsf {EXP}$ (where $\mathsf {EXP}$ is the usual complexity class of this name, see e.g., [21, Ch. 20]). In the literature, $\mathsf {EXP}$ is sometimes called $\mathsf {EXPTIME}$ or $\mathsf {DEXPTIME}$ (e.g., in the celebrated proof that ML typability is complete for $\mathsf {DEXPTIME}$ [13]). Using the Time Hierarchy Theorem [22], it is easy to see that $\mathsf {P}= \mathsf {EXP}^{0}\mathsf {TIME} \subsetneq \mathsf {EXP}^{1}\mathsf {TIME} \subsetneq \mathsf {EXP}^{2}\mathsf {TIME} \subsetneq \cdots$.

Definition 9

The set $\mathsf {ELEMENTARY}$ of elementary-time computable languages is $\bigcup _{K \in \mathbb {N}} \mathsf {EXP}^{K}\mathsf {TIME}$.

4.4 Decision Problems and Programs

To solve decision problems by (cons-free) programs, we will consider programs with constructors $\mathtt {true},\mathtt {false}$ of type $\mathtt {bool}$, $\mathtt {[]}$ of type $\mathtt {list}$ and $\mathtt {{:}{:}}$ of type $\mathtt {bool}\Rightarrow \mathtt {list}\Rightarrow \mathtt {list}$, and whose main function $\mathtt {f}_1$ has type $\mathtt {list}\Rightarrow \mathtt {bool}$.

Definition 10

We define:

• A program $\mathsf {p}$ accepts $\mathtt {a}_1\mathtt {a}_2\dots \mathtt {a}_n \in \{0,1\}^*$ if $[\![\mathsf {p} ]\!](\overline{\mathtt {a}_1 }\mathtt {{:}{:}}\dots \mathtt {{:}{:}}\overline{\mathtt {a}_n}) \mapsto \mathtt {true}$, where $\overline{\mathtt {a}_i} = \mathtt {true}$ if $\mathtt {a}_i = 1$ and $\overline{\mathtt {a}_i} = \mathtt {false}$ otherwise.

• The set accepted by program $\mathsf {p}$ is $\{ \mathtt {a} \in \{0,1\}^* \mid \mathsf {p}$ accepts $\mathtt {a} \}$.

Although we focus on programs of this form, our proofs will allow for arbitrary input and output—with the limitation (as guaranteed by the rule for program execution) that both are data. This makes it possible to for instance consider decision problems on a larger input alphabet without needing encodings.

Example 8

The two-line program with clauses $\mathtt {even}\ \mathtt {[]}= \mathtt {true}$ and $\mathtt {even}\ (x\mathtt {{:}{:}}xs) = \mathtt {if} \, \,x\, \, \mathtt {then} \, \,\mathtt {false}\, \, \mathtt {else} \, \,\mathtt {true}\,$ accepts the problem $\{ x \in \{0,1\}^* \mid x$ is a bitstring representing an even number (following Example 1)$\}$.

We will sometimes speak of the input size, defined by:

Definition 11

The size of a list of data expressions $d_1,\dots ,d_M$ is $\sum _{i = 1}^M size (d_i)$, where $size (\mathtt {c}\ b_1 \cdots b_m)$ is defined as $1 + \sum _{i = 1}^m size (b_i)$.

5 Deterministic Characterisations

As a basis, we transfer Jones’ basic result on time classes to our more general language. That is, we obtain the first line of the first table in Fig. 1.

	data order 0	data order 1	data order 2	data order 3	...
cons-free deterministic	$\mathsf {P}=$ $\mathsf {EXP}^{0}\mathsf {TIME}$	$\mathsf {EXP}=$ $\mathsf {EXP}^{1}\mathsf {TIME}$	$\mathsf {EXP}^{2}\mathsf {TIME}$	$\mathsf {EXP}^{3}\mathsf {TIME}$	...

To show that deterministic cons-free programs of data order K characterise $\mathsf {EXP}^{K}\mathsf {TIME}$ it is necessary to prove two things:

• 1. if $h(n) \le \exp _2^K(a \cdot n^b)$ for all n, then for every deterministic Turing Machine M running in $\text {TIME}\left( h(n)\right)$, there is a deterministic, cons-free program with data order at most K, which accepts $x \in \{0,1\}^+$ if and only if M does;

• 2. for every deterministic cons-free program $\mathsf {p}$ with data order K, there is a deterministic algorithm operating in $\text {TIME}\left( \exp _2^K(a \cdot n^b)\right)$ for some a, b which, given input expressions $d_1,\dots ,d_M$, determines b such that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ (if such b exists). Like Jones [12], we assume our algorithms are implemented on a sufficiently expressive Turing-equivalent machine like the RAM.

We will show part (1) in Sect. 5.1, and part (2) in Sect. 5.2.

5.1 Simulating TMs Using Deterministic Cons-Free Programs

Let $M := (A,S,T)$ be a deterministic Turing Machine running in time $\lambda n.h(n)$. Like Jones, we start by assuming that we have a way to represent the numbers $0,\dots ,h(n)$ as expressions, along with successor and predecessor operators and checks for equality. Our simulation uses the data constructors $\mathtt {true}: \mathtt {bool},\ \mathtt {false}: \mathtt {bool},\ \mathtt {[]}: \mathtt {list}$ and $\mathtt {{:}{:}}: \mathtt {bool}\Rightarrow \mathtt {list}\Rightarrow \mathtt {list}$ as discussed in Sect. 4.4; $\mathtt {a} : \mathtt {symbol}$ for $a \in A$ (writing $\mathtt {B}$ for the blank symbol), $\mathtt {L},\mathtt {R} : \mathtt {direc}$ and $\mathtt {s} : \mathtt {state}$ for $s \in S$; $\mathtt {action} : \mathtt {symbol}\Rightarrow \mathtt {direc}\Rightarrow \mathtt {state}\Rightarrow \mathtt {trans}$; and $\mathtt {end} : \mathtt {state} \Rightarrow \mathtt {trans}$. The rules to simulate the machine are given in Fig. 7.

Fig. 7.

Simulating a deterministic Turing Machine (A, S, T)

Types of defined symbols are easily derived. The intended meaning is that $\mathtt {state}\ cs\ [n]$, for cs the input list and $[n]$ a number in $\{0, \dots ,h(|cs|)\}$, returns the state of the machine at time $[n]$; $\mathtt {pos}\ cs\ [n]$ returns the position of the reader at time $[n]$, and $\mathtt {tape}\ cs [n]\ [p]$ the symbol at time $[n]$ and position $[p]$.

Clearly, the program is highly exponential, even when $h(|cs|)$ is polynomial, since the same expressions are repeatedly evaluated. This apparent contradiction is not problematic: we do not claim that all cons-free programs with data order 0 (say) have a derivation tree of at most polynomial size. Rather, as we will see in Sect. 5.2, we can find their result in polynomial time by essentially using a caching mechanism to avoid reevaluating the same expression.

What remains is to simulate numbers and counting. For a machine running in $\text {TIME}\left( h(n)\right)$, it suffices to find a value $[i]$ representing i for all $i \in \{0,\dots ,h(n)\}$ and cons-free clauses to calculate predecessor and successor functions and to perform zero and equality checks. This is given by a $(\lambda n.h(n)+1)$-counting module. This defines, for a given input list cs of length n, a set of values $\mathcal {A}_\pi ^n$ to represent numbers and functions $\mathtt {seed}_{\pi },\ \mathtt {pred}_{\pi }$ and $\mathtt {zero}_{\pi }$ such that (a) $\mathtt {seed}_{\pi }\ cs$ evaluates to a value which represents $h(n)$, (b) if v represents a number k, then $\mathtt {pred}_{\pi }\ cs\ v$ evaluates to a value which represents $k-1$, and (c) $\mathtt {zero}_{\pi }\ cs\ v$ evaluates to $\mathtt {true}$ or $\mathtt {false}$ depending on whether v represents 0. Formally:

Definition 12

(Adapted from [12]). For $P : \mathbb {N}\rightarrow \mathbb {N}\setminus \{0\}$, a P-counting module is a tuple $C_\pi = (\alpha _{\pi },\mathcal {D}_\pi ,\mathcal {A}_\pi , \langle \cdot \rangle _\pi ,\mathsf {p}_\pi )$ such that:

• $\alpha _{\pi }$ is a type (this will be the type of numbers);

• $\mathcal {D}_\pi$ is a set of defined symbols disjoint from $\mathcal {C},\mathcal {D},\mathcal {V}$, containing symbols $\mathtt {seed}_{\pi },\ \mathtt {pred}_{\pi }$ and $\mathtt {zero}_{\pi }$, with types $\mathtt {seed}_{\pi }: \mathtt {list}\Rightarrow \alpha _{\pi },\ \mathtt {pred}_{\pi }: \mathtt {list}\Rightarrow \alpha _{\pi }\Rightarrow \alpha _{\pi }$ and $\mathtt {zero}_{\pi }: \mathtt {list}\Rightarrow \alpha _{\pi }\Rightarrow \mathtt {bool}$;

• for $n \in \mathbb {N}$, $\mathcal {A}_\pi ^n$ is a set of values of type $\alpha _{\pi }$, all built over $\mathcal {C}\cup \mathcal {D}_\pi$ (this is the set of values used to represent numbers);

• for $n \in \mathbb {N}$, $\langle \cdot \rangle _\pi ^n$ is a total function from $A_{\pi }^n$ to $\mathbb {N}$;

• $\mathsf {p}_\pi$ is a list of cons-free clauses on the symbols in $\mathcal {D}_\pi$, such that, for all lists $cs : \mathtt {list}\in \texttt {Data}$ with length n:

  • there is a unique value v such that $\mathsf {p}_\pi \vdash ^{\mathtt {call}}\mathtt {seed}_{\pi }\ cs \rightarrow v$;

  • if $\mathsf {p}_\pi \vdash ^{\mathtt {call}}\mathtt {seed}_{\pi }\ cs \rightarrow v$, then $v \in \mathcal {A}_{\pi }^n$ and $\langle v \rangle _\pi ^n = P(n)-1$;

  • if $v \in \mathcal {A}_\pi$ and $\langle v \rangle _\pi ^n = i > 0$, then there is a unique value w such that $\mathsf {p}_\pi \vdash ^{\mathtt {call}}\mathtt {pred}_{\pi }\ cs\ v \rightarrow w$; we have $w \in \mathcal {A}_\pi ^n$ and $\langle w \rangle _\pi ^n = i-1$;

  • for $v \in \mathcal {A}_\pi ^n$ with $\langle v \rangle _\pi ^n = i$: $\mathsf {p}_\pi \vdash ^{\mathtt {call}}\mathtt {zero}_{\pi }\ cs\ v \rightarrow \mathtt {true}$ if and only if $i = 0$, and $\mathsf {p}_\pi \vdash ^{\mathtt {call}}\mathtt {zero}_{\pi }\ cs\ v \rightarrow \mathtt {false}$ if and only if $i > 0$.

It is easy to see how a P-counting module can be plugged into the program of Fig. 7. We only lack successor and equality functions, which are easily defined:

Since the clauses in Fig. 7 are cons-free and have data order 0, we obtain:

Lemma 3

Let x be a decision problem which can be decided by a deterministic TM running in $\text {TIME}\left( h(n)\right)$. If there is a cons-free $(\lambda n.h(n)+1)$-counting module $C_\pi$ with data order K, then x is accepted by a cons-free program with data order K; the program is deterministic if the counting module is.

Proof

By the argument given above.    $\square$

The obvious difficulty is the restriction to cons-free clauses: we cannot simply construct a new number type, but will have to represent numbers using only sub-expressions of the input list cs, and constant data expressions.

Example 9

We consider a P-counting module $C_\mathtt {x}$ where $P(n) = 3 \cdot (n+1)^2$. Let $\alpha _{\mathtt {x}} := \mathtt {list}\times \mathtt {list}\times \mathtt {list}$ and for given n, let $\mathcal {A}_\pi ^n := \{ (d_0,d_1,d_2) \mid d_0$ is a list of length $\le 2$ and $d_1,d_2$ are lists of length $\le n \}$. Writing $|\ x_1\mathtt {{:}{:}}\dots \mathtt {{:}{:}}x_k \mathtt {{:}{:}}\mathtt {[]}\ | = k$, let $\langle (d_0,d_1,d_2) \rangle _\mathtt {x}^n := |d_0| \cdot (n+1)^2 + |d_1| \cdot (n+1) + |d_2|$. Essentially, we consider 3-digit numbers $i_0 i_1 i_2$ in base $n+1$, with each $i_j$ represented by a list. $\mathsf {p}_\mathtt {x}$ is:

$$\begin{aligned} \begin{array}{ll} \mathtt {seed}_{\mathtt {x}}\ cs = (\mathtt {false}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {[]},\ cs,\ cs)\ \ \\ \mathtt {pred}_{\mathtt {x}}\ cs\ (x_0,x_1,y\mathtt {{:}{:}}ys) = (x_0,x_1,ys) &{} \mathtt {zero}_{\mathtt {x}}\ cs\ (x_0,x_1,y\mathtt {{:}{:}}ys) = \mathtt {false}\\ \mathtt {pred}_{\mathtt {x}}\ cs\ (x_0,y\mathtt {{:}{:}}ys,\mathtt {[]}) = (x_0,ys,cs) &{} \mathtt {zero}_{\mathtt {x}}\ cs\ (x_0,y\mathtt {{:}{:}}ys,\mathtt {[]}) = \mathtt {false}\\ \mathtt {pred}_{\mathtt {x}}\ cs\ (y\mathtt {{:}{:}}ys,\mathtt {[]},\mathtt {[]}) = (ys,cs,cs) &{} \mathtt {zero}_{\mathtt {x}}\ cs\ (y\mathtt {{:}{:}}ys,\mathtt {[]},\mathtt {[]}) = \mathtt {false}\\ \mathtt {pred}_{\mathtt {x}}\ cs\ (\mathtt {[]},\mathtt {[]},\mathtt {[]}) = (\mathtt {[]},\mathtt {[]},\mathtt {[]}) &{} \mathtt {zero}_{\mathtt {x}}\ cs\ (\mathtt {[]},\mathtt {[]},\mathtt {[]}) = \mathtt {true}\end{array} \end{aligned}$$

If $cs = \mathtt {true}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {[]}$, one value in $\mathcal {A}_\mathtt {x}^3$ is $v = (\mathtt {false}\mathtt {{:}{:}}\mathtt {[]},\ \mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}} \mathtt {[]},\ \mathtt {[]})$, which is mapped to the number $1 \cdot 4^2 + 2 \cdot 4 + 0 = 24$. Then $\mathsf {p}_\mathtt {x}\vdash ^{\mathtt {call}}\mathtt {pred}_{\mathtt {x}}\ cs\ v \rightarrow w := (\mathtt {false}\mathtt {{:}{:}}\mathtt {[]},\ \mathtt {true}\mathtt {{:}{:}}\mathtt {[]},\ cs)$, which is mapped to $1 \cdot 4^2 + 1 \cdot 4 + 3 = 23$ as desired.

Example 9 suggests a systematic way to create polynomial counting modules.

Lemma 4

For any $a,b \in \mathbb {N}\setminus \{0\}$, there is a $(\lambda n.a \cdot (n+1)^b)$-counting module $C_{\langle a,b\rangle }$ with data order 0.

Proof

(Sketch). A straightforward generalisation of Example 9.    $\square$

By increasing type orders, we can obtain an exponential increase of magnitude.

Fig. 8.

The clauses used in $\mathsf {p}_{\mathtt {e}[\pi ]}$, extending $\mathsf {p}_\pi$ with an exponential step.

Lemma 5

If there is a P-counting module $C_\pi$ of data order K, then there is a $(\lambda n.2^{P(n)})$-counting module $C_{\mathtt {e}[\pi ]}$ of data order $K+1$.

Proof

(Sketch). Let $\alpha _{{\mathtt {e}[\pi ]}} := \alpha _{\pi }\Rightarrow \mathtt {bool}$; then $ord \!\left( \alpha _{{\mathtt {e}[\pi ]}}\right) \le K+1$. A number i with bit representation $b_0 \dots b_{P(n)-1}$ (with $b_0$ the most significant digit) is represented by a value v such that, for w with $\langle w \rangle _\pi = i$: $\mathsf {p}_{{\mathtt {e}[\pi ]}} \vdash ^{\mathtt {call}}v\ w \rightarrow \mathtt {true}$ iff $b_i = 1$, and $\mathsf {p}_{{\mathtt {e}[\pi ]}} \vdash ^{\mathtt {call}}v\ w \rightarrow \mathtt {false}$ iff $b_i = 0$. We use the clauses of Fig. 8.

We also include all clauses in $\mathsf {p}_\pi$. Here, note that a bitstring $b_0 \dots b_m$ represents 0 if each $b_i = 0$, and that the predecessor of $b_0\dots b_i 1 0 \dots 0$ is $b_0 \dots b_i 0 1 \dots 1$.

   $\square$

Combining these results, we obtain:

Lemma 6

Every decision problem in $\mathsf {EXP}^{K}\mathsf {TIME}$ is accepted by a deterministic cons-free program with data order K.

Proof

A decision problem is in $\mathsf {EXP}^{K}\mathsf {TIME}$ if it is decided by a deterministic TM operating in time $\exp _2^K(a \cdot n^b))$ for some a, b. By Lemma 3, it therefore suffices if there is a Q-counting module for some $Q \ge \lambda n.\exp _2^K(a \cdot n^b)+1$, with data order K. Certainly $Q(n) := \exp _2^K(a \cdot (n+1)^b)$ is large enough. By Lemma 4, there is a $(\lambda n.a \cdot (n+1)^b)$-counting module $C_{\langle a,b\rangle }$ with data order 0. Applying Lemma 5 K times, we obtain the required Q-counting module $C_{\mathtt {e}[\dots [\mathtt {e}[{\langle a,b\rangle }]]]}$.    $\square$

Remark 4

Our definition of a counting module significantly differs from the one in [12], for example by representing numbers as values rather than expressions, introducing the sets $\mathcal {A}_\pi ^n$ and imposing evaluation restrictions. The changes enable an easy formulation of the non-deterministic counting module in Sect. 6.

5.2 Simulating Deterministic Cons-Free Programs Using an Algorithm

We now turn to the second part of characterisation: that every decision problem solved by a deterministic cons-free program of data order K is in $\mathsf {EXP}^{K}\mathsf {TIME}$. We give an algorithm which determines the result of a fixed program (if any) on a given input in $\text {TIME}\left( \exp _2^K(a \cdot n^b)\right)$ for some a, b. The algorithm is designed to extend easily to the non-deterministic characterisations in subsequent settings.

Key Idea. The principle of our algorithm is easy to explain when variables have data order 0. Using Lemma 2, all such variables must be instantiated by (tuples of) elements of $\mathcal {B}_{d_1, \dots ,d_M}^\mathsf {p}$, of which there are only polynomially many in the input size. Thus, we can make a comprehensive list of all expressions that might occur as the left-hand side of a [Call] in the derivation tree. Now we can go over the list repeatedly, filling in reductions to trace a top-down derivation of the tree.

In the higher-order setting, there are infinitely many possible values; for example, if $\mathtt {id} : \mathtt {bool}\Rightarrow \mathtt {bool}$ has arity 1 and $\mathtt {g} : (\mathtt {bool}\Rightarrow \mathtt {bool}) \Rightarrow \mathtt {bool}\Rightarrow \mathtt {bool}$ has arity 2, then $\mathtt {id},\ \mathtt {g}\ \mathtt {id}, \ \mathtt {g}\ (\mathtt {g}\ \mathtt {id})$ and so on are all values. Therefore, instead of looking directly at values we consider an extensional replacement.

Definition 13

Let $\mathcal {B}$ be a set of data expressions closed under $\rhd$. For $\iota \in \mathcal {S}$, let $\langle \!\left| \iota \right| \!\rangle _\mathcal {B} = \{ d \in \mathcal {B}\mid \ \vdash d : \iota \}$. Inductively, let $\langle \!\left| \sigma \times \tau \right| \!\rangle _\mathcal {B} = \langle \!\left| \sigma \right| \!\rangle _\mathcal {B} \times \langle \!\left| \tau \right| \!\rangle _\mathcal {B}$ and $\langle \!\left| \sigma \Rightarrow \tau \right| \!\rangle _\mathcal {B} = \{ A_{\sigma \Rightarrow \tau } \mid A \subseteq \langle \!\left| \sigma \right| \!\rangle _\mathcal {B} \times \langle \!\left| \tau \right| \!\rangle _\mathcal {B} \wedge \forall e \in \langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$ there is at most one u with $(e,u) \in A_{\sigma \Rightarrow \tau } \}_{\sigma \Rightarrow \tau }$. We call the elements of any $\langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$ deterministic extensional values.

Note that deterministic extensional values are data expressions in $\mathcal {B}$ if $\sigma$ is a sort, pairs if $\sigma$ is a pair type, and sets of pairs labelled with a type otherwise; these sets are exactly partial functions, and can be used as such:

Definition 14

For $e \in \langle \!\left| \sigma _1 \Rightarrow \dots \Rightarrow \sigma _n \Rightarrow \tau \right| \!\rangle _\mathcal {B}$ and $u_1 \in \langle \!\left| \sigma _1 \right| \!\rangle _\mathcal {B},\dots , u_n \in \langle \!\left| \sigma _n \right| \!\rangle _\mathcal {B}$, let $e(u_1,\dots ,u_n)$ be $\{ e \}$ if $n = 0$ and $\bigcup _{A_{\sigma _n \Rightarrow \tau } \in e(u_1,\dots ,u_{n-1})} \{ o \in \langle \!\left| \tau \right| \!\rangle _\mathcal {B} \mid (u_n,o) \in A \}$ if $n > 0$.

By induction on n, each $e(u_1,\dots ,u_n)$ has at most one element as would be expected of a partial function. We also consider a form of matching.

Definition 15

Fix a set $\mathcal {B}$ of data expressions. An extensional expression has the form $\mathtt {f}\ e_1 \cdots e_n$ where $\mathtt {f} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _n \Rightarrow \tau \in \mathcal {D}$ and each $e_i \in \langle \!\left| \sigma _i \right| \!\rangle _\mathcal {B}$. Given a clause $\rho :\mathtt {f}\ \ell _1 \cdots \ell _k = r$ with $\mathtt {f} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _k \Rightarrow \tau \in \mathcal {F}$ and variable environment $\varGamma$, an ext-environment for $\rho$ is a partial function $\eta$ mapping each $x : \tau \in \varGamma$ to an element of $\langle \!\left| \tau \right| \!\rangle _\mathcal {B}$, such that $\ell _j\eta \in \langle \!\left| \sigma _j \right| \!\rangle _\mathcal {B}$ for $1 \le j \le n$. Here,

• $\ell \eta = \eta (\ell )$ if $\ell$ is a variable and $\ell \eta = (\ell ^{(1)}\eta ,\ell ^{(2)}\eta )$ if $\ell = (\ell ^{(1)},\ell ^{(2)})$;

• $\ell \eta = \ell [x:=\eta (x) \mid x \in Var (\ell )]$ otherwise (in this case, $\ell$ is a pattern with data order 0, so all its variables have data order 0, so each $\eta (x) \in \texttt {Data}$).

Then $\ell \eta$ is a deterministic extensional value for $\ell$ a pattern. We say $\rho$ matches an extensional expression $\mathtt {f}\ e_1 \cdots e_k$ if there is an ext-environment $\eta$ for $\rho$ such that $\ell _i\eta = e_i$ for all $1 \le i \le k$. We call $\eta$ the matching ext-environment.

Finally, for technical reasons we will need an ordering on extensional values:

Definition 16

We define a relation $\sqsupseteq$ on extensional values of the same type:

• For $d,b \in \langle \!\left| \iota \right| \!\rangle _\mathcal {B}$ with $\iota \in \mathcal {S}$: $d \sqsupseteq b$ if $d = b$.

• For $(e_1,e_2),(u_1,u_2) \in \langle \!\left| \sigma \times \tau \right| \!\rangle _\mathcal {B}$: $(e_1,e_2) \sqsupseteq (u_1,u_2)$ if each $e_i \sqsupseteq u_i$.

• For $A_\sigma ,B_\sigma \in \langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$ with $\sigma$ functional: $A_\sigma \sqsupseteq B_\sigma$ if for all $(e,u) \in B$ there is $u' \sqsupseteq u$ such that $(e,u') \in A$.

The Algorithm. Let us now define our algorithm. We will present it in a general form—including a case 2d which does not apply to deterministic programs—so we can reuse the algorithm in the non-deterministic settings to follow.

Algorithm 7

Let $\mathsf {p}$ be a fixed, deterministic cons-free program, and suppose $\mathtt {f}_1$ has a type $\kappa _1 \Rightarrow \dots \Rightarrow \kappa _M \Rightarrow \kappa \in \mathcal {F}$.

Input: data expressions $d_1 : \kappa _1,\dots ,d_M : \kappa _M$.

Output: The set of values b with $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$.

• 1. Preparation.

  • (a) Let $\mathsf {p}'$ be obtained from $\mathsf {p}$ by the transformations of Lemma 1, and by adding a clause $\mathtt {start}\ x_1 \cdots x_M = \mathtt {f}_1\ x_1 \cdots x_M$ for a fresh symbol $\mathtt {start}$ (so that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ iff $\mathsf {p}'\vdash ^{\mathtt {call}}\mathtt {start}\ d_1 \cdots d_M \rightarrow b$).

  • (b) Denote $\mathcal {B}:= \mathcal {B}_{d_1,\dots ,d_M}^\mathsf {p}$ and let $\mathcal {X}$ be the set of all “statements”:

    • i. $\vdash \mathtt {f}\ e_1 \cdots e_n \leadsto o$ for (a) $\mathtt {f} \in \mathcal {D}$ with $\mathtt {f} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa ' \in \mathcal {F}$, (b) $0 \le n \le \mathtt {arity}_\mathsf {p}(\mathtt {f})$ such that $ord \!\left( \sigma _{n+1} \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa '\right) \le K$, (c) $e_i \in \langle \!\left| \sigma _i \right| \!\rangle _\mathcal {B}$ for $1 \le i \le n$ and (d) $o \in \langle \!\left| \sigma _{n+1} \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa ' \right| \!\rangle _\mathcal {B}$;

    • ii. $\eta \vdash t \leadsto o$ for (a) $\rho :\mathtt {f}\ \ell _1 \cdots \ell _k = s$ a clause in $\mathsf {p}'$, (b) $s \unrhd t : \tau$, (c) $o \in \langle \!\left| \tau \right| \!\rangle _\mathcal {B}$ and (d) $\eta$ an ext-environment for $\rho$.

  • (c) Mark statements of the form $\eta \vdash t \leadsto o$ in $\mathcal {X}$ as confirmed if either $t \in \mathcal {V}$ and $\eta (t) \sqsupseteq o$, or if $t = \mathtt {c}\ t_1 \cdots t_m$ with $\mathtt {c} \in \mathcal {C}$ and $t\eta = o$. All statements not of either form are marked unconfirmed.

• 2. Iteration: repeat the following steps, until no further changes are made.

  • (a) For all unconfirmed statements $\vdash \mathtt {f}\ e_1 \cdots e_n \leadsto o$ in $\mathcal {X}$ with $n < \mathtt {arity}_\mathsf {p}(\mathtt {f})$: write $o = O_\sigma$ and mark the statement as confirmed if for all $(e_{n+1},u) \in O$ there exists $u' \sqsupseteq u$ such that $\vdash \mathtt {f}\ e_1 \cdots e_{n+1} \leadsto u'$ is marked confirmed.

  • (b) For all unconfirmed statements $\vdash \mathtt {f}\ e_1 \cdots e_k \leadsto o$ in $\mathcal {X}$ with $k = \mathtt {arity}_\mathsf {p}(\mathtt {f})$:

    • i. find the first clause $\rho :\mathtt {f}\ \ell _1 \cdots \ell _k = s$ in $\mathsf {p}'$ that matches $\mathtt {f}\ e_1 \cdots e_k$ and let $\eta$ be the matching ext-environment (if any);

    • ii. determine whether $\eta \vdash s \leadsto o$ is confirmed and if so, mark the statement $\mathtt {f}\ e_1 \cdots e_k \leadsto o$ as confirmed.

  • (c) For all unconfirmed statements of the form $\eta \vdash \mathtt {if} \, s_1 \, \mathtt {then} \, s_2 \, \mathtt {else} \, s_3 \leadsto o$ in $\mathcal {X}$, mark the statement confirmed if both $\eta \vdash s_1 \leadsto \mathtt {true}$ and $\eta \vdash s_2 \leadsto o$ are confirmed, or both $\eta \vdash s_1 \leadsto \mathtt {false}$ and $\eta \vdash s_3 \leadsto o$ are confirmed.

  • (d) For all unconfirmed statements $\eta \vdash \mathtt {choose}\ s_1 \cdots s_n \leadsto o$ in $\mathcal {X}$, mark the statement as confirmed if $\eta \vdash s_i \leadsto o$ for any $i \in \{1, \dots ,n\}$.

  • (e) For all unconfirmed statements $\eta \vdash (s_1,s_2) \leadsto (o_1,o_2)$ in $\mathcal {X}$, mark the statement confirmed if both $\eta \vdash s_1 \leadsto o_1$ and $\eta \vdash s_2 \leadsto o_2$ are confirmed.

  • (f) For all unconfirmed statements $\eta \vdash x\ s_1 \cdots s_n \leadsto o$ in $\mathcal {X}$ with $x \in \mathcal {V}$, mark the statement as confirmed if there are $e_1 \in \langle \!\left| \sigma _1 \right| \!\rangle _\mathcal {B},\dots ,e_n \in \langle \!\left| \sigma _n \right| \!\rangle _\mathcal {B}$ such that each $\eta \vdash s_i \leadsto e_i$ is marked confirmed, and there exists $o' \in \eta (x)(e_1, \dots ,e_n)$ such that $o' \sqsupseteq o$.

  • (g) For all unconfirmed statements $\eta \vdash \mathtt {f}\ s_1 \cdots s_n \leadsto o$ in $\mathcal {X}$ with $\mathtt {f} \in \mathcal {D}$, mark the statement as confirmed if there are $e_1 \in \langle \!\left| \sigma _1 \right| \!\rangle _\mathcal {B},\dots ,e_n \in \langle \!\left| \sigma _n \right| \!\rangle _\mathcal {B}$ such that each $\eta \vdash s_i \leadsto e_i$ is marked confirmed, and:

    • i. $n \le \mathtt {arity}_\mathsf {p}(\mathtt {f})$ and $\vdash \mathtt {f}\ e_1 \cdots e_n \leadsto o$ is marked confirmed, or

    • ii. $n > k := \mathtt {arity}_\mathsf {p}(\mathtt {f})$ and there are $u,o'$ such that $\vdash \mathtt {f}\ e_1 \cdots e_k \leadsto u$ is marked confirmed and $u(e_{k+1},\dots ,e_n) \ni o' \sqsupseteq o$.

• 3. Completion: return $\{ b \mid b \in \mathcal {B}\wedge \vdash \mathtt {start}\ d_1 \cdots d_M \leadsto b$ is marked confirmed$\}$.

Note that, for programs of data order 0, this algorithm closely follows the earlier sketch. Values of a higher type are abstracted to deterministic extensional values. The use of $\sqsupseteq$ is needed because a value of higher type is associated to many extensional values; e.g., to confirm a statement $\vdash \mathtt {plus}\ \mathtt {3} \leadsto \{ (\mathtt {1}, \mathtt {4}), (\mathtt {0},\mathtt {3}) \}_{\mathtt {nat}\Rightarrow \mathtt {nat}}$ in some program, it may be necessary to first confirm $\vdash \mathtt {plus}\ \mathtt {3} \leadsto \{ (\mathtt {0},\mathtt {3}) \}_{\mathtt {nat}\Rightarrow \mathtt {nat}}$.

The complexity of the algorithm relies on the following key observation:

Lemma 8

Let $\mathsf {p}$ be a cons-free program of data order K. Let $\varSigma$ be the set of all types $\sigma$ with $ord \!\left( \sigma \right) \le K$ which occur as part of an argument type, or as an output type of some $\mathtt {f} \in \mathcal {D}$. Suppose that, given input of total size n, $\langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$ has cardinality at most F(n) for all $\sigma \in \varSigma$, and testing whether $e_1 \sqsupseteq e_2$ for $e_1,e_2 \in [\![\sigma ]\!]_\mathcal {B}$ takes at most F(n) steps. Then Algorithm 7 runs in $\text {TIME}\left( a \cdot F(n)^b\right)$ for some a, b.

Here, the cardinality $\mathsf {Card}(A)$ of a set A is just the number of elements of A.

Proof

(Sketch). Due to the use of $\mathsf {p}'$, all intensional values occurring in Algorithm 7 are in $\bigcup _{\sigma \in \varSigma } \langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$. Writing a for the greatest number of arguments any defined symbol $\mathtt {f}$ or variable x in $\mathsf {p}'$ may take and r for the greatest number of sub-expressions of any right-hand side in $\mathsf {p}'$ (which is independent of the input!), $\mathcal {X}$ contains at most $\textsf {a} \cdot |\mathcal {D}| \cdot F(n)^{\textsf {a}+1} + |\mathsf {p}'| \cdot \textsf {r} \cdot F(n)^{\textsf {a}+1}$ statements. Since in all but the last step of the iteration at least one statement is flipped from unconfirmed to confirmed, there are at most $|\mathcal {X}|+1$ iterations, each considering $|\mathcal {X}|$ statements. It is easy to see that the individual steps in both the preparation and iteration are all polynomial in $|\mathcal {X}|$ and F(n), resulting in a polynomial overall complexity.    $\square$

The result follows as $\mathsf {Card}(\langle \!\left| \sigma \right| \!\rangle _\mathcal {B})$ is given by a tower of exponentials in $ord \!\left( \sigma \right)$:

Lemma 9

If $1 \le \mathsf {Card}(\mathcal {B}) < N$, then for each $\sigma$ of length L (where the length of a type is the number of sorts occurring in it, including repetitions), with $ord \!\left( \sigma \right) \le K$: $\mathsf {Card}(\langle \!\left| \sigma \right| \!\rangle _\mathcal {B}) < \exp _2^K(N^L)$. Testing $e \sqsupseteq u$ for $e,u \in \langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$ takes at most $\exp _2^K(N^{(L+1)^3})$ comparisons between elements of $\mathcal {B}$.

Proof

(Sketch). An easy induction on the form of $\sigma$, using that $\exp _2^K(X) \cdot \exp _2^K(Y) \le \exp _2^K(X \cdot Y)$ for $X \ge 2$, and that for $A_{\sigma _1 \Rightarrow \sigma _2}$, each key $e \in \langle \!\left| \sigma _1 \right| \!\rangle _\mathcal {B}$ is assigned one of $\mathsf {Card}(\langle \!\left| \sigma _2 \right| \!\rangle _\mathcal {B})+1$ choices: an element u of $\langle \!\left| \sigma _2 \right| \!\rangle _\mathcal {B}$ such that $(e,u) \in A$, or non-membership. The second part (regarding $\sqsupseteq$) uses the first.    $\square$

We will postpone showing correctness of the algorithm until Sect. 6.3, where we can show the result together with the one for non-deterministic programs. Assuming correctness for now, we may conclude:

Lemma 10

Every decision problem accepted by a deterministic cons-free program $\mathsf {p}$ with data order K is in $\mathsf {EXP}^{K}\mathsf {TIME}$.

Proof

We will see in Lemma 20 in Sect. 6.3 that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ if and only if Algorithm 7 returns the set $\{b\}$. For a program of data order K, Lemmas 8 and 9 together give that Algorithm 7 operates in $\text {TIME}\left( \exp _2^K(n)\right)$.    $\square$

Theorem 1

The class of deterministic cons-free programs with data order K characterises $\mathsf {EXP}^{K}\mathsf {TIME}$ for all $K \in \mathbb {N}$.

Proof

A combination of Lemmas 6 and 10.    $\square$

6 Non-deterministic Characterisations

A natural question is what happens if we do not limit interest to deterministic programs. For data order 0, Bonfante [4] shows that adding the choice operator to Jones’ language does not increase expressivity. We will recover this result for our generalised language in Sect. 7. However, in the higher-order setting, non-deterministic choice does increase expressivity—dramatically so. We have:

	data order 0	data order 1	data order 2	data order 3	...
cons-free	$\mathsf {P}$	$\mathsf {ELEMENTARY}$	$\mathsf {ELEMENTARY}$	$\mathsf {ELEMENTARY}$	...

As before, we will show the result—for data orders 1 and above—in two parts: in Sect. 6.1 we see that cons-free programs of data order 1 suffice to accept all problems in $\mathsf {ELEMENTARY}$; in Sect. 6.2 we see that they cannot go beyond.

6.1 Simulating TMs Using (Non-deterministic) Cons-Free Programs

We start by showing how Turing Machines in $\mathsf {ELEMENTARY}$ can be simulated by non-deterministic cons-free programs. For this, we reuse the core simulation from Fig. 7. The reason for the jump in expressivity lies in Lemma 3: by taking advantage of non-determinism, we can count up to arbitrarily high numbers.

Lemma 11

If there is a P-counting module $C_\pi$ with data order $K \le 1$, there is a (non-deterministic) $(\lambda n.2^{P(n)-1})$-counting module $C_{\psi [{\pi }]}$ with data order 1.

Proof

We let $\alpha _{\psi [{\pi }]} := \mathtt {bool}\Rightarrow \alpha _{\pi }$ (which has type order $\max (1, ord \!\left( \alpha _{\pi }\right) )$), and:

• $\mathcal {A}_{\psi [{\pi }]}^n :=$ the set of those values $v : \alpha _{\psi [{\pi }]}$ such that:

  • there is $w \in \mathcal {A}_\pi$ with $\langle w \rangle _\pi ^n = 0$ such that $\mathsf {p}_{\psi [{\pi }]} \vdash ^{\mathtt {call}}v\ \mathtt {true} \rightarrow w$;

  • there is $w \in \mathcal {A}_\pi$ with $\langle w \rangle _\pi ^n = 0$ such that $\mathsf {p}_{\psi [{\pi }]} \vdash ^{\mathtt {call}}v\ \mathtt {false} \rightarrow w$;

  and for all $1 \le i < P(n)$ exactly one of the following holds:

  • there is $w \in \mathcal {A}_\pi ^n$ with $\langle w \rangle _\pi ^n = i$ such that $\mathsf {p}_{\psi [{\pi }]} \vdash ^{\mathtt {call}}v\ \mathtt {true} \rightarrow w$;

  • there is $w \in \mathcal {A}_\pi ^n$ with $\langle w \rangle _\pi ^n = i$ such that $\mathsf {p}_{\psi [{\pi }]} \vdash ^{\mathtt {call}}v\ \mathtt {false} \rightarrow w$;

  We will say that $v\ \mathtt {true} \mapsto i$ or $v\ \mathtt {false} \mapsto i$ respectively.

• $\langle v \rangle _{\psi [{\pi }]}^n := \sum _{i=1}^{P(n)-1} \{ 2^{P(n)-1-i} \mid v\ \mathtt {true} \mapsto i \}$;

• $\mathsf {p}_{\psi [{\pi }]}$ be given by Fig. 9 appended to $\mathsf {p}_\pi$, and $\mathcal {D}_{\psi [{\pi }]}$ by the symbols in $\mathsf {p}_{\psi [{\pi }]}$.

So, we interpret a value v as the number given by the bitstring $b_1 \dots b_{P(n)-1}$ (most significant digit first), where $b_i$ is 1 if $v\ \mathtt {true}$ evaluates to a value representing i in $C_\pi$, and $b_i$ is 0 otherwise—so exactly if $v\ \mathtt {false}$ evaluates to such a value.    $\square$

Fig. 9.

Clauses for the counting module $C_{\psi [{\pi }]}$.

To understand the counting program, consider 4, with bit representation 100. If 0, 1, 2, 3 are represented in $C_\pi$ by values $O,w_1,w_2,w_3$ respectively, then in $C_{\psi [{\pi }]}$, the number 4 corresponds to $Q := \mathtt {st1}\ w_1\ (\mathtt {st0}\ w_2\ (\mathtt {st0}\ w_3\ (\mathtt {base}_{\psi [{\pi }]}\ O)))$. The null-value O functions as a default, and is a possible value of both $Q\ \mathtt {true}$ and $Q\ \mathtt {false}$ for any function Q representing a bitstring.

The non-determinism comes into play when determining whether $Q\ \mathtt {true} \mapsto i$ or not: we can evaluate $F\ \mathtt {true}$ to some value, but this may not be the value we need. Therefore, we find some value of both $F\ \mathtt {true}$ and $F\ \mathtt {false}$; if either represents i in $C_\pi$, then we have confirmed or rejected that $b_i = 1$. If both evaluations give a different value, we repeat the test. This gives a non-terminating program, but there is always exactly one value b such that $\mathsf {p}_{\psi [{\pi }]} \vdash ^{\mathtt {call}}\mathtt {bitset}_{\psi [{\pi }]}\ cs\ F\ i \rightarrow b$.

The $\mathtt {seed}_{\psi [{\pi }]}$ function generates the bit string $1\dots 1$, so the function F with $F\ \mathtt {true} \mapsto i$ for all $i \in \{0, \dots ,P(n)-1\}$ and $F\ \mathtt {false} \mapsto i$ for only $i = 0$. The $\mathtt {zero}_{\psi [{\pi }]}$ function iterates through $b_{P(n)-1},b_{P(n)-2}, \dots ,b_1$ and tests whether all bits are set to 0. The clauses for $\mathtt {pred}_{\psi [{\pi }]}$ assume given a bitstring $b_1\dots b_{i-1}10\dots 0$, and recursively build $b_1 \dots b_{i-1}01\cdots 1$ in the parameter G.

Example 10

Consider an input string of length 3, say $\mathtt {false}\mathtt {{:}{:}}\mathtt {false}\mathtt {{:}{:}}\mathtt {true}\mathtt {{:}{:}}\mathtt {[]}$. Recall from Lemma 4 that there is a $(\lambda n.n+1)$-counting module $C_{\langle 1,1\rangle }$ representing $i \in \{0,\dots ,3\}$ as suffixes of length i from the input string. Therefore, there is also a second-order $(\lambda n.2^n)$-counting module $C_{\psi [{\langle 1,1\rangle }]}$ representing $i \in \{0,\dots , 7\}$. The number 6—with bitstring 110—is represented by the value $w_6$:

But then there is also a $(\lambda n.2^{2^n-1})$-counting module $C_{\psi [\psi [\langle 1,1\rangle ]]}$, representing $i \in \{0,\dots ,2^7-1\}$. For example 97—with bit vector 1100001—is represented by:

$$\begin{aligned} \begin{array}{c} S = \mathtt {st1}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_1\ (\ \mathtt {st1}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_2\ (\ \mathtt {st0}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_3\ (\\ {S =}\ \mathtt {st0}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_4\ (\ \mathtt {st0}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_5\ (\ \mathtt {st0}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_6\ (\\ \mathtt {st1}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_7\ (\ \mathtt {cons}_{\psi [\psi [\langle 1,1\rangle ]]}\ w_7\ )\ )\ )\ )\ )\ )\ ) \end{array} \end{aligned}$$

Here $\mathtt {st1}_{\psi [\psi [\langle 1,1\rangle ]]}$ and $\mathtt {st0}_{\psi [\psi [\langle 1,1\rangle ]]}$ have the type $(\mathtt {bool}\Rightarrow \mathtt {list}) \Rightarrow (\mathtt {bool}\Rightarrow \mathtt {bool}\Rightarrow \mathtt {list}) \Rightarrow \mathtt {bool}\Rightarrow \mathtt {bool}\Rightarrow \mathtt {list}$ and each $w_i$ represents i in $C_{\psi [{\langle 1,1\rangle }]}$, as shown for $w_6$ above. Note: $S\ \mathtt {true}\mapsto w_1,w_2,w_7$ and $S\ \mathtt {false}\mapsto w_3,w_4,w_5,w_6$.

Since $2^{2^m-1}-1 \ge 2^m$ for all $m \ge 2$, we can count up to arbitrarily high bounds using this module. Thus, already with data order 1, we can simulate Turing Machines operating in $\text {TIME}\left( \exp _2^K(n)\right)$ for any K.

Lemma 12

Every decision problem in $\mathsf {ELEMENTARY}$ is accepted by a non-deterministic cons-free program with data order 1.

Proof

A decision problem is in $\mathsf {ELEMENTARY}$ if it is in some $\mathsf {EXP}^{K}\mathsf {TIME}$ which, by Lemma 3, is certainly the case if for any a, b there is a Q-counting module with $Q \ge \lambda n.\exp _2^K( a \cdot n^b)$. Such a module exists for data order 1 by Lemma 11.    $\square$

6.2 Simulating Cons-Free Programs Using an Algorithm

Towards a characterisation, we must also see that every decision problem accepted by a cons-free program is in $\mathsf {ELEMENTARY}$—so that the result of every such program can be found by an algorithm operating in $\text {TIME}\left( \exp _2^K(a \cdot n^b)\right)$ for some a, b, K. We can reuse Algorithm 7 by altering the definition of $\langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$.

Definition 17

Let $\mathcal {B}$ be a set of data expressions closed under $\rhd$. For $\iota \in \mathcal {S}$, let $[\![\iota ]\!]_\mathcal {B} = \{ d \in \mathcal {B}\mid \ \vdash d : \iota \}$. Inductively, define $[\![\sigma \times \tau ]\!]_\mathcal {B} = [\![\sigma ]\!]_\mathcal {B} \times [\![\tau ]\!]_\mathcal {B}$ and $[\![\sigma \Rightarrow \tau ]\!]_\mathcal {B} = \{ A_{\sigma \Rightarrow \tau } \mid A \subseteq [\![\sigma ]\!]_\mathcal {B} \times [\![\tau ]\!]_\mathcal {B} \}$. We call the elements of any $[\![\sigma ]\!]_\mathcal {B}$ non-deterministic extensional values.

Where the elements of $\langle \!\left| \sigma \Rightarrow \tau \right| \!\rangle _\mathcal {B}$ are partial functions, $[\![\sigma \Rightarrow \tau ]\!]_\mathcal {B}$ contains arbitrary relations: a value v is associated to a set of pairs (e, u) such that $v\ e$ might evaluate to u. The notions of extensional expression, $e(u_1,\dots ,u_n)$ and $\sqsupseteq$ immediately extend to non-deterministic extensional values. Thus we can define:

Algorithm 13

Let $\mathsf {p}$ be a fixed, non-deterministic cons-free program, with $\mathtt {f}_1 : \kappa _1 \Rightarrow \dots \Rightarrow \kappa _M \Rightarrow \kappa \in \mathcal {F}$.

Input: data expressions $d_1 : \kappa _1,\dots ,d_M : \kappa _M$.

Output: The set of values b with $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$.

Execute Algorithm 7, but using $[\![ \sigma ]\!]_\mathcal {B}$ in place of $\langle \!\left| \sigma \right| \!\rangle _\mathcal {B}$.

In Sect. 6.3, we will see that indeed $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ if and only if Algorithm 13 returns a set containing b. But as before, we first consider complexity. To properly analyse this, we introduce the new notion of arrow depth.

Definition 18

A type’s arrow depth is given by: $depth (\iota ) = 0,\ depth (\sigma \times \tau ) = \max ( depth (\sigma ), depth (\tau ))$ and $depth (\sigma \Rightarrow \tau ) = 1 + \max ( depth (\sigma ), depth (\tau ))$.

Now the cardinality of each $[\![\sigma ]\!]_\mathcal {B}$ can be expressed using its arrow depth:

Lemma 14

If $1 \le \mathsf {Card}(\mathcal {B}) < N$, then for each $\sigma$ of length L, with $depth (\sigma ) \le K$: $\mathsf {Card}([\![\sigma ]\!]_\mathcal {B}) < \exp _2^K(N^L)$. Testing $e \sqsupseteq u$ for $e,u \in [\![\sigma ]\!]_\mathcal {B}$ takes at most $\exp _2^K(N^{(L+1)^3})$ comparisons.

Proof

(Sketch). A straightforward induction on the form of $\sigma$, like Lemma 9.    $\square$

Thus, once more assuming correctness for now, we may conclude:

Lemma 15

Every decision problem accepted by a non-deterministic cons-free program $\mathsf {p}$ is in $\mathsf {ELEMENTARY}$.

Proof

We will see in Lemma 18 in Sect. 6.3 that $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ if and only if Algorithm 13 returns a set containing b. Since all types have an arrow depth and the set $\varSigma$ in Lemma 8 is finite, Algorithm 13 operates in some $\text {TIME}\left( \exp _2^K(n)\right)$. Thus, the problem is in $\mathsf {EXP}^{K}\mathsf {TIME} \subseteq \mathsf {ELEMENTARY}$.    $\square$

Theorem 2

The class of non-deterministic cons-free programs with data order K characterises $\mathsf {ELEMENTARY}$ for all $K \in \mathbb {N}\setminus \{0\}$.

Proof

A combination of Lemmas 12 and 15.    $\square$

6.3 Correctness proofs of Algorithms 7 and 13

Algorithms 7 and 13 are the same—merely parametrised with a different set of extensional values to be used in step 1b. Due to this similarity, and because $\langle \!\left| \sigma \right| \!\rangle _\mathcal {B} \subseteq [\![ \sigma ]\!]_\mathcal {B}$, we can largely combine their correctness proofs. The proofs are somewhat intricate, however; details are provided in [15, Appendix E].

We begin with soundness:

Lemma 16

If Algorithm 7 or 13 returns a set $A \cup \{b\}$, then $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$.

Proof

(Sketch). We define for every value $v : \sigma$ and $e \in [\![\sigma ]\!]_\mathcal {B}$: $v\!\Downarrow \!e$ iff: (a) $\sigma \in \mathcal {S}$ and $v = e$; or (b) $\sigma = \sigma _1 \times \sigma _2$ and $v = (v_1,v_2)$ and $e = (e_1,e_2)$ with $v_1\!\Downarrow \!e_1$ and $v_2\!\Downarrow \!e_2$; or (c) $\sigma = \sigma _1 \Rightarrow \sigma _2$ and $e = A_\sigma$ with $A \subseteq \{ (u_1,u_2) \mid u_1 \in [\![\sigma _1 ]\!]_\mathcal {B} \wedge u_2 \in [\![\sigma _2 ]\!]_\mathcal {B} \wedge$ for all values $w_1 : \sigma _1$ with $w_1\!\Downarrow \!u_1$ there is some value $w_2 : \sigma _2$ with $w_2\!\Downarrow \!u_2$ such that $\mathsf {p}'\vdash ^{\mathtt {call}}v\ w_1 \rightarrow w_2 \}$.

We now prove two statements together by induction on the confirmation time in Algorithm 7, which we consider equipped with unspecified subsets $[\sigma ]$ of $[\![\sigma ]\!]_\mathcal {B}$:

• 1. Let: (a) $\mathtt {f} : \sigma _1 \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa \in \mathcal {F}$ be a defined symbol; (b) $v_1 : \sigma _1,\dots ,v_n : \sigma _n$ be values, for $1 \le n \le \mathtt {arity}_\mathsf {p}(\mathtt {f})$; (c) $e_1 \in [\![\sigma _1 ]\!]_\mathcal {B},\dots ,e_n \in [\![\sigma _n ]\!]_\mathcal {B}$ be such that each $v_i\!\Downarrow \!e_i$; (d) $o \in [\![\sigma _{n+1} \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa ]\!]_\mathcal {B}$. If $\vdash \mathtt {f}\ e_1 \cdots e_n \leadsto o$ is eventually confirmed, then $\mathsf {p}'\vdash ^{\mathtt {call}}\mathtt {f}\ v_1 \cdots v_n \rightarrow w$ for some w with $w\!\Downarrow \!o$.

• 2. Let: (a) $\rho :\mathtt {f}\ \mathbf {\ell } = s$ be a clause in $\mathsf {p}'$; (b) $t : \tau$ be a sub-expression of s; (c) $\eta$ be an ext-environment for $\rho$; (d) $\gamma$ be an environment such that $\gamma (x)\!\Downarrow \!\eta (x)$ for all $x \in Var (\mathtt {f}\ \mathbf {\ell })$; (e) $o \in [\![\tau ]\!]_\mathcal {B}$. If the statement $\eta \vdash t \leadsto o$ is eventually confirmed, then $\mathsf {p}',\gamma \vdash t \rightarrow w$ for some w with $w\!\Downarrow \!o$.

Given the way $\mathsf {p}'$ is defined from $\mathsf {p}$, the lemma follows from the first statement. The induction is easy, but requires minor sub-steps such as transitivity of $\sqsupseteq$.    $\square$

The harder part, where the algorithms diverge, is completeness:

Lemma 17

If $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$, then Algorithm 13 returns a set $A \cup \{b\}$.

Proof

(Sketch). If $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$, then $\mathsf {p}'\vdash ^{\mathtt {call}}\mathtt {start}\ d_1 \cdots d_M \rightarrow b$. We label the nodes in the derivation trees with strings of numbers (a node with label $l$ has immediate subtrees of the form $l\cdot i$), and let > denote lexicographic comparison of these strings, and $\succ$ lexicographic comparison without prefixes (e.g., $1 \cdot 2 > 1$ but not $1 \cdot 2 \succ 1$). We define the following function:

• $\psi (v,l) = v$ if $v \in \mathcal {B}$, and $\psi ((v_1,v_2),l) = (\psi (v_1,l),\psi (v_2,l))$;

• for $\mathtt {f}\ v_1 \cdots v_n : \tau = \sigma _{n+1} \Rightarrow \dots \Rightarrow \sigma _m \Rightarrow \kappa$ with $m > n$, let $\psi (\mathtt {f}\ v_1 \cdots v_n,l) = \{ (e_{n+1},u) \mid \exists q\succ p> l$ [the subtree with index $p$ has a root $\mathsf {p}'\vdash ^{\mathtt {call}}\mathtt {f}\ v_1 \cdots v_{n+1} \rightarrow w$ with $\psi (w,q) = u$ and $e_{n+1} \sqsupseteq '\psi (v_{n+1}, p)] \}_\tau$.

Here, $\sqsupseteq '$ is defined the same as $\sqsupseteq$, except that $A_\sigma \sqsupseteq 'B_\sigma$ iff $A \supseteq B$. Note that clearly $A \sqsupseteq 'B$ implies $A \sqsupseteq B$, and that $\sqsupseteq '$ is transitive by transitivity of $\supseteq$. Then, using induction on the labels of the tree in reverse lexicographical order (so going through the tree right-to-left, top-to-bottom), we can prove:

• 1. If the subtree labelled $l$ has root $\mathsf {p}'\vdash ^{\mathtt {call}}\mathtt {f}\ v_1 \cdots v_n \rightarrow w$, then for all $e_1,\dots , e_n$ such that each $e_i \sqsupseteq '\psi (v_i,l)$, and for all $p\succ l$ there exists $o \sqsupseteq '\psi (w,p)$ such that $\vdash \mathtt {f}\ e_1 \cdots e_n \leadsto o$ is eventually confirmed.

• 2. If the subtree labelled $l$ has root $\mathsf {p}',\gamma \vdash t \rightarrow w$ and $\eta (x) \sqsupseteq '\psi (\gamma (x), l)$ for all $x \in Var (t)$, then for all $p\succ l$ there exists $o \sqsupseteq '\psi (w,p)$ such that $\eta \Vdash t \leadsto o$ is eventually confirmed.

Assigning the main tree a label 0 (to secure that $p \succ 0$ exists), we obtain that $\vdash \mathtt {start}\ d_1 \cdots d_M \leadsto b$ is eventually confirmed, so b is indeed returned.    $\square$

By Lemmas 16 and 17 together we may immediately conclude:

Lemma 18

$[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ iff Algorithm 13 returns a set containing b.

The proof of the general case provides a basis for the deterministic case:

Lemma 19

If $[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ and $\mathsf {p}$ is deterministic, then Algorithm 13 returns a set $A \cup \{b\}$.

Proof

(Sketch). We define a consistency measure $\wr$ on non-deterministic extensional values: $e\wr u$ iff $e = u \in \mathcal {B}$, or $e = (e_1,e_2),\ u = (u_1,u_2),\ e_1\wr u_1$ and $e_2\wr u_2$, or $e = A_\sigma ,\ u = B_\sigma$ and for all $(e_1,u_1) \in A$ and $(e_2,u_2) \in B$: $e_1\wr e_2$ implies $u_1\wr u_2$.

In the proof of Lemma 17, we trace a derivation in the algorithm. In a deterministic program, we can see that if both $\vdash \mathtt {f}\ e_1 \cdots e_n \rightarrow o$ and $\vdash \mathtt {f}\ e_1' \cdots e_n' \rightarrow o'$ are confirmed, and each $e_i\wr e_n'$, then $o\wr o'$—and similar for statements $\eta \vdash s \Rightarrow o$. We use this to remove statements which are not necessary, ultimately leaving only those which use deterministic extensional values as used in Algorithm 7.    $\square$

Lemma 20

$[\![\mathsf {p}]\!](d_1,\dots ,d_M) \mapsto b$ iff Algorithm 7 returns a set containing b.

Proof

This is a combination of Lemmas 16 and 19.    $\square$

Note that it is a priori not clear that Algorithm 7 returns only one value; however, this is obtained as a consequence of Lemma 20.

7 Recovering the $\mathsf {EXP}^{}\mathsf {TIME}$ hierarchy

While interesting, Lemma 12 exposes a problem: non-determinism is unexpectedly powerful in the higher-order setting. If we still want to use non-deterministic programs towards characterising non-deterministic complexity classes, we must surely start by considering restrictions which avoid this explosion of expressivity.

One direction is to consider arrow depth instead of data order. Using Lemma 14, we easily recover the original hierarchy—and obtain the last line of Fig. 1.

	arrow depth 0	arrow depth 1	arrow depth 2	...
cons-free	$\mathsf {P}= \mathsf {EXP}^{0}\mathsf {TIME}$	$\mathsf {EXP}= \mathsf {EXP}^{1}\mathsf {TIME}$	$\mathsf {EXP}^{2}\mathsf {TIME}$	...

Theorem 3

The class of non-deterministic cons-free programs where all variables are typed with a type of arrow depth K characterises $\mathsf {EXP}^{K}\mathsf {TIME}$.

Proof

(Sketch). Both in the base program in Fig. 7, and in the counting modules of Lemmas 4 and 5, type order and arrow depth coincide. Thus every decision problem in $\mathsf {EXP}^{K}\mathsf {TIME}$ is accepted by a cons-free program with “data arrow depth” K. For the other direction, the proof of Lemma 1 is trivially adapted to use arrow depth rather than type order. Thus, altering the preparation step in Algorithm 13 gives an algorithm which determines the possible outputs of a program with data arrow depth K, with the desired complexity by Lemma 14.

   $\square$

A downside is that, by moving away from data order, this result is hard to compare with other characterisations using cons-free programs. An alternative is to impose a restriction alongside cons-freeness: unitary variables. This gives no restrictions in the setting with data order 0—thus providing the first column in the table from Sect. 6—and brings us the second-last line in Fig. 1:

	data order 0	data order 1	data order 2	data order 3
cons-free unitary variables	$\mathsf {P}=$ $\mathsf {EXP}^{0}\mathsf {TIME}$	$\mathsf {EXP}=$ $\mathsf {EXP}^{1}\mathsf {TIME}$	$\mathsf {EXP}^{2}\mathsf {TIME}$	$\mathsf {EXP}^{3}\mathsf {TIME}$

Definition 19

A program $\mathsf {p}$ has unitary variables if clauses are typed with an assignment mapping each variable x to a type $\kappa$ or $\sigma \Rightarrow \kappa$, with $ord \!\left( \kappa \right) = 0$.

Thus, in a program with unitary variables, a variable of a type $(\mathtt {list}\times \mathtt {list}\times \mathtt {list}) \Rightarrow \mathtt {list}$ is admitted, but $\mathtt {list}\Rightarrow \mathtt {list}\Rightarrow \mathtt {list}\Rightarrow \mathtt {list}$ is not. The crucial difference is that the former must be applied to all its arguments at the same time, while the latter may be partially applied. This avoids the problem of Lemma 11.

Theorem 4

The class of (deterministic or non-deterministic) cons-free programs with unitary variables of data order K characterises $\mathsf {EXP}^{K}\mathsf {TIME}$.

Proof

(Sketch). Both the base program in Fig. 7 and the counting modules of Lemmas 4 and 5 have unitary variables, and are deterministic—this gives one direction. For the other, let a recursively unitary type be $\kappa$ or $\sigma \Rightarrow \kappa$ with $ord \!\left( \kappa \right) = 0$ and $\sigma$ recursively unitary. The transformations of Lemma 1 are easily extended to transform a program with unitary variables of type order ${\le K}$ to one where all sub-expressions have a recursively unitary type. Since here data order and arrow depth are the same in this case, we complete with Theorem 3.    $\square$

8 Conclusion and Future Work

We have studied the effect of combining higher types and non-determinism for cons-free programs. This has resulted in the—highly surprising—conclusion that naively adding non-deterministic choice to a language that characterises the $\mathsf {EXP}^{K}\mathsf {TIME}$ hierarchy for increasing data orders immediately increases the expressivity of the language to $\mathsf {ELEMENTARY}$. Recovering a more fine-grained complexity hierarchy can be done, but at the cost of further syntactical restrictions.

The primary goal that we will pursue in future work is to use non-deterministic cons-free programs to characterise hierarchies of non-deterministic complexity classes such as $\mathsf {NEXP}^{K}\mathsf {TIME}$ for $K \in \mathbb {N}$. In addition, it would be worthwhile to make a full study of the ramifications of imposing restrictions on recursion, such as tail-recursion or primitive recursion, in combination with non-determinism and higher types (akin to the study of primitive recursion in a successor-free language done in [16]). We also intend to study characterisations of classes more restrictive than $\mathsf {P}$, such as $\mathsf {LOGTIME}$ and $\mathsf {LOGSPACE}$.

Finally, given the surprising nature of our results, we urge readers to investigate the effect of adding non-determinism to other programming languages used in implicit complexity that manipulate higher-order data. We conjecture that the effect on expressivity there will essentially be the same as what we have observed.