Structure-Preserving Chosen-Ciphertext Security with Shorter Verifiable Ciphertexts

Abstract

Structure-preserving cryptography is a world where messages, signatures, ciphertexts and public keys are entirely made of elements of a group over which a bilinear map is efficiently computable. While structure-preserving signatures have received much attention the last 6 years, structure-preserving encryption schemes have undergone slower development. In particular, the best known structure-preserving cryptosystems with chosen-ciphertext (IND-CCA2) security either rely on symmetric pairings or require long ciphertexts comprised of hundreds of group elements or do not provide publicly verifiable ciphertexts. We provide a publicly verifiable construction based on the SXDH assumption in asymmetric bilinear groups $e : \mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$, which features relatively short ciphertexts. For typical parameters, our ciphertext size amounts to less than 40 elements of $\mathbb {G}$. As a second contribution, we provide a structure-preserving encryption scheme with perfectly randomizable ciphertexts and replayable chosen-ciphertext security. Our new RCCA-secure system significantly improves upon the best known system featuring similar properties in terms of ciphertext size.

1 Introduction

Structure-preserving cryptography is a paradigm where handled objects all live in discrete-log-hard abelian groups over which a bilinear map is efficiently computable. The structure-preserving property allows for a smooth interaction of the considered primitives with Groth-Sahai (GS) proof systems [36], making them very powerful tools for the modular design of privacy-preserving cryptographic protocols [3, 8, 16, 17, 19, 27, 32, 37, 44, 51].

In structure-preserving signatures (SPS) [6, 8], messages, signatures, public keys all live in the source groups $(\mathbb {G},{\hat{\mathbb {G}}})$ of a bilinear map $e: \mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$. The roots of SPS schemes can be traced back to the work of Groth [34], which initiated a line of work seeking to obtain short signatures [4,5,6, 23, 40, 45], security under standard assumptions [4, 18, 24, 37, 40, 45], tight security proofs [5, 37] or lower bounds [1, 7]. Beyond signatures, structure-preserving cryptography was also developed in the context of commitment schemes [6, 9, 10, 35, 42], public-key [5, 16] and identity-based encryption [41, 52] as well as in deterministic primitives [2].

Structure-preserving encryption. Camenisch et al. [16] came up with the first chosen-ciphertext-secure (IND-CCA2) structure-preserving public-key encryption scheme. Structure-preserving CCA2 security is motivated by applications in the realization of oblivious third parties protocols [20] or proofs of knowledge of leakage-resilient signatures [28]. Among the use cases of structure-preserving CCA-secure encryption, [16] mentions various settings where a user, who has a ciphertext and a Groth-Sahai proof of its well-formedness, wants to convince a third party that it is in possession of such a ciphertext without revealing it. Structure-preserving encryption also allows two users to jointly compute an encryption (of a function) of two plaintexts such that neither player learns the plaintext of the other player and only one of them obtains the ciphertext.

As pointed out in [16], structure-preserving encryption should make it possible to efficiently and non-interactively prove possession of a valid ciphertext, which rules out the use of standard techniques – like hash functions [26] or ordinary (i.e., non-structure-preserving) one-time signatures [21, 29, 50] – that are typically used to achieve chosen-ciphertext security [49] in the standard model. In particular, the original Cramer-Shoup cryptosystem [26] does not provide the sought-after structure-preserving property and neither do direct applications of the Canetti-Halevi-Katz paradigm [21]: for example, merely combining Kiltz’s tag-based encryption [39] with a one-time SPS does not work as the security proof of [39] requires (hashed) verification keys to be encoded as exponents. Nevertheless, Camenisch et al. [16] managed to twist the design principle of Cramer-Shoup [26] so as to obtain a variant of the scheme that only resorts to algebraic operations when it comes to tying all ciphertexts components altogether in a non-malleable manner.

While efficient and based on the standard Decision Linear assumption [14], the initial construction of [16] still suffers from certain disadvantages. In the first variant of their scheme, for example, one of the ciphertext components lives in the target group $\mathbb {G}_T$ of a bilinear map $e: \mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$ which complicates its use in applications requiring to prove knowledge of a ciphertext: recall that Groth-Sahai proofs require witnesses to live in the source group of a bilinear (i.e., they need strictly structure-preserving components in the sense of [9]). While Camenisch et al. [16] suggested a technique of moving all ciphertext components to the source groups in their scheme, this is only known to be possible using symmetric bilinear groups (where $\mathbb {G}={\hat{\mathbb {G}}}$) as it relies on the one-sided pairing randomization technique of [8]. Another limitation of [16] is that, analogously to the original Cramer-Shoup system [26], valid ciphertexts (i.e., which lie in the range of the legitimate encryption algorithm) are not publicly recognizable. As a result, only the sender of a ciphertext (who knows the random encryption coins) can generate a proof that this particular ciphertext is indeed a valid ciphertext without revealing it. Ideally, any ciphertext observer should be able to commit to that ciphertext and prove statements about it without any interaction with the sender, which would be possible with publicly verifiable ciphertexts.

Abe et al. [5] provided several constructions of structure-preserving CCA2-secure encryption with publicly verifiable ciphertexts. On the downside, their solutions incur substantially longer ciphertexts than [16]: under the Decision Linear assumption, the most efficient solution of [5] entails 321 group elements per ciphertext. Moreover, it was only described in terms of symmetric pairings.

In addition, symmetric pairings have become significantly less efficient (see, e.g., [31]) as the use of small-characteristic fields is now considered insecure [11]. This motivates the search for efficient structure-preserving CCA2-secure systems which provide shorter ciphertexts and can operate in asymmetric pairings.

Our Contributions. We provide a new CCA2-secure structure-preserving encryption scheme wherein the validity of ciphertexts is publicly verifiable and ciphertexts only consist of 16 elements of $\mathbb {G}$ and 11 elements of ${\hat{\mathbb {G}}}$. By “public verifiability”, we mean that ciphertexts which are rejected by the decryption algorithm should be recognizable given the public key. While stronger definitions of verifiability could be used¹, this notions suffices to ensure confidentiality in settings – like threshold decryption [13, 46, 54] – where potentially harmful decryption queries should be publicly detectable. In particular, our first scheme readily implies a CCA2-secure structure-preserving cryptosystem that enables threshold decryption in the adaptive corruption setting.

In our first scheme, the ciphertext size amounts to 38 elements of $\mathbb {G}$ assuming that each element of ${\hat{\mathbb {G}}}$ has a representation which is twice as large as the representation of $\mathbb {G}$ elements. The security is proved under the standard symmetric eXternal Diffie-Hellman (SXDH) assumption [53] in asymmetric bilinear maps.

As a second contribution, we provide a different structure-preserving cryptosystem which features perfectly re-randomizable ciphertexts and replayable chosen-ciphertext (RCCA) security. As defined by Canetti, Krawczyk and Nielsen [22], RCCA security is a meaningful relaxation of CCA2 security that tolerates a “benign” form of malleability: namely, anyone should be able to randomize a given ciphertext into another encryption of the same plaintext. Under the SXDH assumption, our construction features statistically randomizable ciphertexts which only consist of 34 elements of $\mathbb {G}$ and 18 elements of ${\hat{\mathbb {G}}}$. Under the same² assumption, the best known RCCA-secure realization thus far was the scheme of Chase et al. [25] which costs 49 elements of $\mathbb {G}$ and 20 elements of ${\hat{\mathbb {G}}}$.

Our techniques. Our structure-preserving CCA2 secure cryptosystem builds on a public-key encryption scheme suggested by Libert and Yung [46], which is not structure-preserving in its original form. Our starting observation is that, unlike Kiltz’s tag-based encryption scheme [39], the security proof of [46] does not require to interpret one-time signature verification keys as exponents. The construction of [46] is obtained by tweaking the Cramer-Shoup paradigm [26] and replacing the designated verifier NIZK proofs of ciphertext validity by a universally verifiable Groth-Sahai proof. In order to obtain publicly verifiable proofs with the desired security property called simulation-soundness [50], the authors of [46] used Groth-Sahai common reference strings (CRSes) which depend on the verification key of a one-time signature. In the security proof, the key idea was to enable the simulation of fake NIZK proofs of ciphertext validity while making it impossible for the adversary to create such a fake proof himself. In Groth-Sahai proofs, this can be achieved by programming the Groth-Sahai CRSes in such a way that they form a linear subspace of dimension 1 in the challenge ciphertext whereas adversarially-generated ciphertexts involve CRSes of dimension 2 (which are perfectly sound CRSes).

We build on the observation that the approach of [46] still works if one-time verification keys consist of group elements instead of exponents. One difficulty is that we need one-time signature verification keys comprised of a single group element while the best known one-time SPS [6] have longer verification keys. Our solution is to “hash” the one-time verification keys of [6] in a structure-preserving manner. For this purpose, we apply a strictly structure-preserving commitment scheme proposed by Abe et al. [10] as if it was a chameleon hash function: namely, we replace the hash value by a commitment to the one-time verification key while the corresponding de-commitment information is included in the ciphertext. One caveat is that [10] considers a relaxed security notion for strictly structure-preserving commitments, called chosen-message target collision-resistance, which appears insufficient for our purposes. We actually need a stronger notion, called enhanced chosen-message target collision-resistance (ECM-TCR), where the adversary should also be able to come up with a different opening to the same message for a given commitment. Fortunately, we can prove that the strictly structure-preserving commitment of [10] does provide ECM-TCR security under the SXDH assumption.

The security proof of our construction addresses another technical hurdle which arises from the fact that ciphertexts contain elements from both sources groups $\mathbb {G}$ and ${\hat{\mathbb {G}}}$. Directly adapting the security proof of [46] would require to sign all elements of $\mathbb {G}$ and ${\hat{\mathbb {G}}}$ that are contained in the ciphertext, which would require a one-time SPS where messages contain elements of both groups $(\mathbb {G},{\hat{\mathbb {G}}})$. While such schemes exist [4], they are less efficient than one-time SPS schemes for unilateral messages. Our solution to this problem is to modify the security proof of Libert and Yung [46] in such a way that not all ciphertexts components have to be signed using the one-time signature. In short, we leverage the fact that only Groth-Sahai commitments have to live in the group ${\hat{\mathbb {G}}}$: proof elements and other components of the ciphertext can indeed dwell in $\mathbb {G}$. In GS commitments for linear multi-exponentiation equations, we notice that Groth-Sahai commitments are uniquely determined by the proof elements and the statement. For this reason, even if the adversary tampers with the GS commitments of the challenge ciphertext, it will be unable to create another ciphertext that will be accepted by the decryption oracle. This saves us from having to one-time-sign the Groth-Sahai commitments in the encryption algorithm, which is the reason why we only need such a system for unilateral messages.

Our construction of RCCA-secure encryption extends the ideas of Chase et al. [25]. In a nutshell, the RCCA-secure scheme of [25] combines a semantically secure encryption scheme and a randomizable witness indistinguishable proof of a statement of the form “Either I know the plaintext OR a signature of a ciphertext that this ciphertext is a randomization of”. Our construction proceeds in an analogous way by demonstrating a statement of the form “Either I know the plaintext OR this ciphertext is a randomization of the challenge ciphertext”.

In a high level, for the two branches of the statement we rely on proofs which nicely share a common structure to optimize our OR-proof. On the one hand, for the knowledge of the plaintext we use a quasi-adaptive NIZK (QA-NIZK) proof, which are NIZK proofs introduced by [38] where the CRS may depend on the specific language for which proofs have to be generated. Our QA-NIZK is built from the one-time structure-preserving linearly homomorphic signature (LHSPS) of Libert, Peters, Joye and Yung [42]. On the other hand, for the one-time signature we use the strongly unforgeable one-time SPS of Abe et al. [5] that we make re-randomizable thanks to LHSPS. These tools allows to combine some of the verification equations for which Groth-Sahai proofs of satisfiability are included in ciphertexts.

Related Work. Several different approaches [15, 30, 47, 48] were taken to reconcile chosen-ciphertext-security and homomorphism. Relaxed flavors of chosen-ciphertext security [22] opened the way to perfectly randomizable encryption schemes offering stronger guarantees than just semantic security. Groth described [33] a weakly RCCA secure variant of Cramer-Shoup which only encrypts messages in a bit-by-bit manner. Prabhakaran and Rosulek [47] showed how to more efficiently encrypt many bits at once in a RCCA-secure realization from the DDH assumption. While their solution features shorter ciphertexts than our RCCA-secure scheme, it is not structure-preserving as it cannot be readily instantiated in groups with a bilinear maps. On the other hand, unlike our scheme and the one of [25], it allows re-randomizing ciphertexts without knowing under which public key they were encrypted.

Prabhakaran and Rosulek subsequently generalized the RCCA security notion [22] into a model [48] of homomorphic encryption that only supports a limited form of malleability. Boneh, Segev and Waters [15] took a different approach aiming for restricted malleability properties. Chase et al. [25] considered a modular design of HCCA-secure encryption [48] based on malleable proof systems. Their proposals turn out to be the only known HCCA/RCCA-secure structure-preserving candidates thus far.

2 Background and Definitions

2.1 Hardness Assumptions

We consider groups $(\mathbb {G},{\hat{\mathbb {G}}},\mathbb {G}_T)$ of prime-order p endowed with a bilinear map $e:\mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$.

Definition 1

The Diffie-Hellman problem (DDH) in $\mathbb {G}$, is to distinguish the distributions $(g, g^a, g^b, g^{ab})$ and $(g, g^a, g^b, g^c)$ with $a, b, c \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. The Diffie-Hellman assumption asserts the intractability of DDH for any PPT distinguisher.

In the asymmetric setting $(\mathbb {G},{\hat{\mathbb {G}}}, \mathbb {G}_T)$, we consider the SXDH assumption, which posits that the DDH assumption holds in both $\mathbb {G}$ and ${\hat{\mathbb {G}}}$.

Definition 2

The Double Pairing problem (DP) in $(\mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T)$ is, given a pair of group elements $({\hat{g}}_z, {\hat{g_r}}) \in {\hat{\mathbb {G}}}^2$, to find a non-trivial triple $(z, r) \in \mathbb {G}^2\backslash \{(1_{\mathbb {G}}, 1_{\mathbb {G}})\}$ such that $e(z, {\hat{g}}_z) \cdot e(r, {\hat{g}}_r) = 1_{\mathbb {G}_T}$.

It is known [8] that the DP assumption is implied by the DDH assumption in $\mathbb {G}$. By exchanging the roles of $\mathbb {G}$ and ${\hat{\mathbb {G}}}$ in the definition of DP, we obtain a variant of the assumption which implies the hardness of DDH in ${\hat{\mathbb {G}}}$.

2.2 One-Time Structure-Preserving Signatures

Structure-preserving signatures (SPS) [6, 8] are signature schemes where messages and public keys all consist of elements of a group over which a bilinear map $e: \mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$ is efficiently computable. Constructions based on simple assumptions were put forth in [4, 5].

In the forthcoming sections, we will rely on one-time SPS schemes.

Definition 3

A one-time signature scheme is a tuple of efficient algorithms $\mathcal {OTS}= ({\mathsf {Setup}}, {\mathsf {KeyGen}}, {\mathsf {Sign}}, {\mathsf {Verify}})$ where:

• Setup $({\lambda })$ : This algorithm takes as input a security parameter $\lambda$ and generates the public parameters $\mathsf {PP}$ for the scheme.

• KeyGen $(\mathsf {PP})$ : This algorithm takes as input $\mathsf {PP}$ and generates a one-time secret key $\mathsf {osk}$ and a one-time verification key $\mathsf {ovk}$.

• Sign $(\mathsf {PP}, \mathsf {osk}, \varvec{M})$ : Given as input $(\mathsf {PP}, \mathsf {osk})$ and a message $\varvec{M}$, this algorithm produces a signature $\sigma$ for $\varvec{M}$.

• Verify $(\mathsf {PP}, \mathsf {ovk}, \varvec{M}, \sigma )$ : The verification algorithm takes $(\mathsf {PP}, \mathsf {ovk}, \varvec{M}, \sigma )$ and returns 1 or 0.

Correctness mandates that, for any $\lambda \in \mathbb {N}$, any $\mathsf {PP}\leftarrow \mathsf {Setup}(\lambda )$, any pair $(\mathsf {osk},\mathsf {ovk}) \leftarrow \mathsf {KeyGen}(\mathsf {PP})$, we have ${\mathsf {Verify}}(\mathsf {PP}, \mathsf {ovk}, \varvec{M}, {\mathsf {Sign}}(\mathsf {PP}, \mathsf {osk}, \varvec{M})) =1$ for any message $\varvec{M}$.

In addition, a one-time signature is said structure-preserving if the components of $\mathsf {ovk}$, $\varvec{M}$ and $\sigma$ all live in the source groups $(\mathbb {G},{\hat{\mathbb {G}}})$ of a configuration $(\mathbb {G},{\hat{\mathbb {G}}},\mathbb {G}_T)$ of bilinear groups.

Definition 4

A one-time signature scheme $\mathcal {OTS}= ({\mathsf {Setup}}, {\mathsf {KeyGen}}, {\mathsf {Sign}}, {\mathsf {Verify}})$ is strongly unforgeable against chosen message attack $(SUF\text {-}CMA)$ if

is negligible against any PPT adversary $\mathcal {A}$. Here, ${\mathsf {Sign}}^{OT}_{\mathsf {osk}}(\cdot )$ is a signing oracle which allows the adversary to obtain a signature $\sigma _m$ of only one message m for which $(m, \sigma _m)$ is stored in $Q_{{\mathsf {Sign}}^{OT}}$.

We recall a construction of the one-time Structure-Preserving Signature scheme which was proposed in [5].

• Setup $(\lambda )$ : Choose asymmetric bilinear groups $(\mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T)$ of prime order $p>2^\lambda$ and output $\mathsf {PP}=(\mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T)$.

• KeyGen $(\mathsf {PP})$ : Generates the signing key $\mathsf {osk}$ and the verification key $\mathsf {ovk}$ using the security parameter $\lambda$ and the number n of messages to be signed.

  • 1. Choose ${\hat{g}}_z, {\hat{g}}_r, g \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}{\hat{\mathbb {G}}}$.

  • 2. For $i = 1$ to n, pick $(\chi _i, \gamma _i) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^2$ and compute ${\hat{g}}_i={\hat{g}}_z^{\chi _i}{\hat{g}}_r^{\gamma _i}$.

  • 3. Pick $(\zeta , \rho ) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^2$ and compute ${\hat{A}} = g_z^{\zeta } \cdot g_r^{\rho }$.

  • 4. Set $\mathsf {osk}= (\{(\chi _i, \gamma _i)\}_{i = 1}^n, \zeta , \rho ) \in \mathbb {G}^{2n+2}$ and

    $$\mathsf {ovk}= ({\hat{g}}_z, {\hat{g}}_r, \{\hat{g}_i\}_{i=1}^n, {\hat{A}}) \in {\hat{\mathbb {G}}}^{n+3}.$$

• Sign $(\mathsf {osk}, \varvec{M} = (M_1, \dots , M_n))$ : In order to sign $\varvec{M} = (M_1, \dots , M_n) \in \mathbb {G}^n$, compute $z = g^{\zeta }\prod _{i = 1}^n M_i^{\chi _i}$ and $r = g^{\rho }\prod _{i=1}^n M_i^{\gamma _i}$. Output $\sigma = (z,r)$.

• Verify $(\mathsf {ovk}, \varvec{M} = (M_1, \dots , M_n), \sigma = (z, r))$ : Return 1 if and only if the following equations are satisfied: $e(z, {\hat{g}}_z) \cdot e(r, {\hat{g}}_r) = e(g, {\hat{A}}) \cdot \prod _{i=1}^ne(M_i, {\hat{g}}_i).$

2.3 Partial One-Time Signature

A special case of the one-time signature presented in Sect. 2.2 is called Partial One-Time Signature (POTS) [12]. In a such scheme, part of the verification key can be re-used in multiple signatures and the remaining part must be refreshed at every signature generation.

Definition 5

A partial one-time signature (POTS) scheme is a tuple of algorithms $POTS = (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {OKeyGen}, \mathsf {Sign}, \mathsf {Verify})$.

• $\varvec{\mathsf {Setup}(\lambda )}$ : The setup algorithm takes as input a security parameter $\lambda$ and generates the public parameters $\mathsf {PP}$ for the scheme.

• $\varvec{\mathsf {KeyGen}(\mathsf {PP})}$ : The key generation algorithm takes as input the public parameters $\mathsf {PP}$ and generates the long-term signing key $\mathsf {sk}$ and long-term verification key $\mathsf {vk}$.

• $\varvec{\mathsf {OKeyGen}(\mathsf {PP})}$ : The key generation algorithm takes $\mathsf {PP}$ and generates the one-time signing key $\mathsf {osk}$ and the one-time verification key $\mathsf {ovk}$.

• $\varvec{\mathsf {Sign}(\mathsf {PP}, \mathsf {sk}, \mathsf {osk}, \varvec{M})}$ : The signature algorithm uses the $(\mathsf {PP}, \mathsf {osk})$ to produce a valid signature $\sigma$ for the message vector $\varvec{M}$.

• $\varvec{\mathsf {Verify}(\mathsf {PP}, \mathsf {vk}, \mathsf {ovk}, \varvec{M}, \sigma )}$ : The verification algorithm takes $(\mathsf {PP}, \mathsf {vk}, \mathsf {ovk}, \varvec{M}, \sigma )$ and returns 1 or 0.

Correctness requires that, for any $\mathsf {PP}\leftarrow \mathsf {Setup}(\lambda )$, $(\mathsf {sk}, \mathsf {vk}) \leftarrow \mathsf {KeyGen}(\mathsf {PP})$ and $(\mathsf {osk}, \mathsf {ovk}) \leftarrow \mathsf {OKeyGen}(\mathsf {PP})$, the partial one-time signature scheme is correct if and only if ${\mathsf {Verify}}(\mathsf {PP}, \mathsf {vk}, \mathsf {ovk}, \varvec{M}, \mathsf {Sign}(\mathsf {PP}, \mathsf {sk}, \mathsf {osk}, \varvec{M})) = 1$.

We focus on the strong unforgeability against one-time chosen-message attack of our POTS.

Definition 6

A POTS scheme $POTS = (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {OKeyGen}, \mathsf {Sign}, \mathsf {Verify})$ is strongly unforgeable against one-time chosen-message attack (or OT-CMA secure) if:

is negligible for any PPT adversary $\mathcal {A}$. Here, the signing oracle takes as input a message m, generates $(\mathsf {ovk}, \mathsf {osk}) \leftarrow \mathsf {OKeyGen}(\mathsf {PP})$, $\sigma \leftarrow \mathsf {Sign}(\mathsf {sk}, \mathsf {osk}, m)$. Then, it records $(\mathsf {ovk}, m)$ to Q and returns $(\sigma , \mathsf {ovk})$.

Here, we recall an instantiation of the POTS scheme [4], which is strongly unforgeable against the one-time chosen-message attack (SU-OTCMA) under the DP assumption.

• $\varvec{{\mathsf {Setup}}(\lambda , \ell )}$ : On input of a security parameter $\lambda$ and an integer $\ell \in poly(\lambda )$, the setup algorithm chooses a large prime $p > 2^\lambda$, asymmetric groups $(\mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T)$ of prime order p, with a bilinear map $e: \mathbb {G}\times {\hat{\mathbb {G}}} \rightarrow \mathbb {G}_T$ and the corresponding generators $(g, {\hat{g}} ) \in \mathbb {G}\times {\hat{\mathbb {G}}}$. The algorithm outputs

  $$\begin{aligned} \mathsf {PP}&= (p, \mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T, e, g, {\hat{g}}, \ell ). \end{aligned}$$

• $\varvec{{\mathsf {KeyGen}}(\mathsf {PP})}$ : Parse $\mathsf {PP}$ as $(p, \mathbb {G}, {\hat{\mathbb {G}}}, \mathbb {G}_T, e, g, {\hat{g}}, \ell )$. Choose $w_z \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^*$ and compute $g_z \leftarrow g^{w_z}$. For $i \in \{1, \dots , \ell \}$, choose $\chi _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute $g_i \leftarrow g^{\chi _i}$. Return

  $$\begin{aligned} \mathsf {vk}&= (g_z, g_1, \dots , g_\ell ) \in \mathbb {G}^{\ell +1}&\qquad \mathsf {sk}&= (w_z, \chi _1, \dots , \chi _\ell ) \in \mathbb {Z}_p^{\ell +1} \end{aligned}$$

• $\varvec{{\mathsf {OKeyGen}}(\mathsf {PP})}$ : Parse $\mathsf {PP}$, choose $a \leftarrow \mathbb {Z}_p$, compute $A \leftarrow g^a$ and output

  $$\begin{aligned} \mathsf {ovk}&= A&\qquad \mathsf {osk}&= a \end{aligned}$$

• $\varvec{\mathsf {Sign}(\mathsf {sk}, \mathsf {osk}, \varvec{\hat{M}})}$ : Parse $\varvec{\hat{M}}$ as $({\hat{M}}_1, \dots , {\hat{M}}_{\ell }) \in {\hat{\mathbb {G}}}^{\ell }$. Parse $\mathsf {sk}$ and $\mathsf {osk}$, choose $\zeta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^*$, then compute and output

  $$\begin{aligned} {\hat{Z}}&= {\hat{g}}^\zeta&\qquad {\hat{R}}&= {\hat{g}}^{a - \zeta w_z} \prod \nolimits _{i=1}^\ell \hat{M_i}^{-\chi _i}. \end{aligned}$$

• $\varvec{\mathsf {Verify}(\mathsf {vk}, \mathsf {ovk}, \varvec{\hat{M}}, \sigma )}$ : Parse $\sigma$ as $({\hat{Z}}, \hat{R}) \in {\hat{\mathbb {G}}}^2$, $\varvec{\hat{M}}$ as $({\hat{M}}_1, \dots , {\hat{M}}_\ell ) \in {\hat{\mathbb {G}}}^\ell$ and $\mathsf {ovk}$ as $A \in \mathbb {G}$. The algorithm returns 1 if the following equation holds:

  $$\begin{aligned} e(A, {\hat{g}})&= e(g_z, {\hat{Z}}) \cdot e(g, {\hat{R}}) \cdot \prod _{i = 1}^{\ell } e(g_i, {\hat{M}}_i) \end{aligned}$$

  otherwise the algorithm returns 0.

2.4 One-Time Linearly Homomorphic Structure-Preserving Signatures

Libert et al. [42] considered structure-preserving with linear homomorphic properties (see the full version of the paper for formal definitions). This section recalls the one-time linearly homomorphic structure-preserving signature (LHSPS) of [42].

• $\varvec{\mathsf {Keygen}(\lambda ,n)}{} \mathbf :$ Given a security parameter $\lambda$ and the dimension $n \in \mathbb {N}$ of the subspace to be signed, choose bilinear group $(\mathbb {G},{\hat{\mathbb {G}}},\mathbb {G}_T)$ of prime order p. Then, choose $\hat{g_z},\hat{g_r} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\hat{\mathbb {G}}$. For $i=1$ to n, pick $\chi _i,\gamma _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute $\hat{g}_i=\hat{g_z}^{\chi _i} \hat{g_r}^{\gamma _i}$. The private key is defined to be $\mathsf {sk}= \{ (\chi _i, \gamma _i ) \}_{i=1}^n$ while the public key is $\mathsf {pk}=\big ( \hat{g_z},~\hat{g_r}, ~\{ \hat{g}_i \}_{i=1}^n \big ) \in \hat{\mathbb {G}}^{ n+2}$.

• $\varvec{\mathsf {Sign}(\mathsf {sk}, (M_1,\ldots ,M_n))}{} \mathbf :$ To sign a $(M_1,\ldots ,M_n) \in \mathbb {G}^n$ using $\mathsf {sk}= \{ (\chi _i, \gamma _i ) \}_{i=1}^n$, output $\sigma =(z,r ) \in \mathbb {G}^2$, where $z = \prod _{i=1}^n M_i^{\chi _i}$, $r = \prod _{i=1}^n, M_i^{\gamma _i}$.

• $\varvec{\mathsf {SignDerive}(\mathsf {pk}, \{(\omega _i, \sigma ^{(i)})\}_{i=1}^\ell )}{} \mathbf :$ given $\mathsf {pk}$ as well as $\ell$ tuples $(\omega _i,\sigma ^{(i)})$, parse $\sigma ^{(i)}$ as $\sigma ^{(i)}=\big ( z_i,r_i \big )$ for $i=1$ to $\ell$. Compute and return $\sigma =(z,r )$, where $z = \prod _{i=1}^\ell z_{i}^{\omega _i}$, $r=\prod _{i=1}^{\ell } r_i^{\omega _i}$.

• $\varvec{\mathsf {Verify}(\mathsf {pk},\sigma , (M_1,\ldots ,M_n))}{} \mathbf :$ Given a signature $\sigma =(z,r ) \in \mathbb {G}^2$ and a vector $(M_1,\ldots ,M_n)$, return 1 iff $(M_1,\ldots ,M_n)\ne (1_{\mathbb {G}},\ldots ,1_{\mathbb {G}})$ and (z, r) satisfy

  $$\begin{aligned} e(z,\hat{g_z}) \cdot e(r,\hat{g_r})&= \prod _{i=1}^n e(M_i,\hat{g}_i) . \end{aligned}$$

The one-time security of the scheme (of which the definition is recalled in the full version of the paper) was proved [42] under the DP assumption. In short, the security notion implies the infeasibility of deriving a signature on a vector outside the subspace spanned by the vectors authenticated by the signer. Here, “one-time” security means that a given public key allows signing only one subspace.

We remark that the one-time structure-preserving signature of Sect. 2.2 can be seen as a special case of the above LHSPS scheme, in which we fix the first element of the vector to be signed. The one-time security of this signature scheme can be directly deduced from the security of the LHSPS scheme.

2.5 Strictly Structure-Preserving (Trapdoor) Commitments

In this section, we recall the notion of Chosen-Message Target Collision Trapdoor Commitment as it was defined by Abe et al. [10].

Definition 7

A non-interactive commitment scheme is a tuple of polynomial-time algorithms $\{{\mathsf {Setup}}, {\mathsf {KeyGen}}, {\mathsf {Commit}}, {\mathsf {Verify}}\}$ that:

• Setup $({\lambda })$ : The parameter generation algorithm takes the security parameter $\lambda$ and outputs a public parameter $\mathsf {PP}$.

• KeyGen $(\mathsf {PP})$ : The key generation algorithm takes $\mathsf {PP}$ and outputs the commitment key $\mathsf {ck}$.

• Com $(\mathsf {PP}, \mathsf {ck}, m)$ : The commitment algorithm takes $(\mathsf {PP}, \mathsf {ck})$ and a message m, then it outputs a commitment $\mathsf {com}$ and an opening information $\mathsf {open}$.

• Verify $(\mathsf {PP}, \mathsf {com}, m, \mathsf {open})$ : The verification algorithm takes $(\mathsf {PP}, \mathsf {com}, m, \mathsf {open})$ and outputs 1 or 0.

In trapdoor commitment schemes, the $\mathsf {Setup}$ algorithm additionally outputs a trapdoor tk which, on input of a message m and random coins r such that $c=\mathsf {Com}(\mathsf {PP},\mathsf {ck},m;r)$, allows opening the commitment c to any message $m'$. In our construction, we need a length-reducing commitment scheme which satisfies a stronger notion of Chosen-Message Target Collision Resistance (CM-TCR) than the one considered in [10, Definition 10].

Definition 8

A Commitment Scheme provides enhanced chosen-message target collision-resistance (ECM-TCR) if the advantage

is negligible for any PPT adversary $\mathcal {A}$. Here, $\mathcal {O}_{\mathsf {ck}}$ is an oracle that, given a message m, executes $(\mathsf {com}, \mathsf {open}) \leftarrow \mathsf {Com}(\mathsf {PP},\mathsf {ck}, m)$, records $(\mathsf {com}, m, \mathsf {open})$ in Q and returns $(\mathsf {com}, \mathsf {open})$.

We note that Definition 8 captures a stronger requirement than the original definition [10, Definition 10] in that the latter only requires that the adversary be unable to open a target commitment $\mathsf {com}^\star$ to a different message than the one queried to the oracle $\mathcal {O}_{\mathsf {ck}}$. Here, the adversary is also considered successful if it provides a different opening $\mathsf {open}^\star \ne \mathsf {open}'$ of $\mathsf {com}^\star$ to the same message $m^\star =m^\dagger$ as the one queried to $\mathcal {O}_{\mathsf {ck}}$.

We now recall the Strictly Structure-Preserving Trapdoor Commitment of Abe et al. [10] and show that it actually satisfies our stronger notion of ECM-TCR security.

• $\varvec{TC.{\mathsf {Setup}}({\lambda },\ell )}$ : On input of a security parameter $\lambda$ and an integer $\ell \in \mathsf {poly}(\lambda )$, the public parameters are generated by choosing a large prime $p> 2^{\lambda }$, asymmetric groups $(\mathbb {G}, \hat{\mathbb {G}}, \mathbb {G}_T)$ of prime order p, with a bilinear map $e : \mathbb {G}\times \hat{\mathbb {G}} \rightarrow \mathbb {G}_T$ and group generators $(g, \hat{g}) \in \mathbb {G}\times \hat{\mathbb {G}}$. The algorithm outputs

  $$\mathsf {PP}= (p, \mathbb {G}, \hat{\mathbb {G}}, \mathbb {G}_T, e, g, \hat{g},\ell ).$$

• $\varvec{TC.{\mathsf {KeyGen}}(\mathsf {PP})}$ : For $i = 1, \ldots , \ell +2$, choose $\rho _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^*$ and compute

  $$\hat{X}_i \leftarrow \hat{g}^{\rho _i} \qquad \forall i \in \{1,\ldots ,\ell +2 \}.$$

  Output the commitment key $\mathsf {ck}:= \{\hat{X}_i\}_{i = 1}^{\ell +2}$. Optionally, the algorithm may output the trapdoor $tk := \{\rho _i\}_i^{\ell +2}$.

• $\varvec{TC.{\mathsf {Commit}}(\mathsf {PP}, \mathsf {ck}, \varvec{M})}$ : To commit to $\varvec{\hat{M}} = (\hat{M}_1, \dots , \hat{M}_\ell ) \in \hat{\mathbb {G}}^\ell$, conduct the following step.

  • 1. Generate a key pair $(\mathsf {vk}_{pots},\mathsf {sk}_{pots})$ for the partial one-time signature of Sect. 2.3. Namely, choose $\mathsf {sk}_{pots} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}(w_z,\chi _1, \dots , \chi _\ell ) \in \mathbb {Z}_p^{\ell +1}$ and set

    $$\mathsf {vk}_{pots} = (g_z, g_1, \dots , g_\ell ) =( g^{w_z},g^{\chi _1},\ldots , g^{\chi _{\ell }} ) \in \mathbb {G}^{\ell +1}.$$

  • 2. Choose $a \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute $\mathsf {ovk}_{pots} =A = g^{a}$ and $\mathsf {osk}_{pots} = a$.

  • 3. Using $\mathsf {sk}_{pots}$, generate a partial one-time signature on the message $\varvec{\hat{M}}$ w.r.t. to the one-time secret key $\mathsf {osk}_{pots}$. To this end,

    • a. Pick $\zeta _1 \in \mathbb {Z}_p$.

    • b. Compute $(\hat{Z}, \hat{R}) \in \hat{\mathbb {G}}^2$ as a partial one-time signature of $\varvec{\hat{M}}$ as

      $$\begin{aligned} \hat{Z}&= \hat{g}^{\zeta _1}&\quad \hat{R} = \hat{g}^{a-\zeta _1 w_z}\prod _{i=1}^{\ell } \hat{M}_i^{\chi _i} \end{aligned}$$

  • 4. Generate a commitment to the message.

    • a. Set $(m_1, \dots , m_{\ell +2}) \leftarrow (\chi _1, \dots , \chi _\ell , w_z, a)$

    • b. Parse $\varvec{\mathsf {ck}}$ as $(\hat{X}_1, \dots , \hat{X}_{\ell +2})$.

    • c. Choose a random value $\zeta _2 \leftarrow \mathbb {Z}_p^*$ and compute:

      $$\begin{aligned} \hat{C}&= \hat{g}^{\zeta _2} \cdot \prod _{i = 1}^{\ell +2}\hat{X}_i^{m_i}&\qquad D&= g^{\zeta _2} \end{aligned}$$

  • 5. Output the commitment $\hat{\mathsf {com}}= \hat{C}$ as well as the opening information

    $$\begin{aligned} \mathsf {open}= \big ( D, g_z, g_1, \dots , g_\ell , A = g^a, \hat{Z}, \hat{R} \big ) \in \mathbb {G}^{\ell +3} \times \hat{\mathbb {G}}^{2}. \end{aligned}$$

    (1)

• $\varvec{TC.{\mathsf {Verify}}(\mathsf {ck}, \hat{\mathsf {com}}, \varvec{\hat{M}}, \mathsf {open})}$ : Given $\hat{\mathsf {com}}= \hat{C} \in \hat{\mathbb {G}}$, parse $\varvec{\hat{M}}$ as $(\hat{M}_1, \dots , \hat{M}_\ell )$ and $\mathsf {open}$ as in (1).

  • 1. Set $\varvec{N} = (N_1, \dots , N_{\ell +2}) = (g_1, \dots , g_\ell , g_z, A )$

  • 2. Using $\mathsf {ovk}_{pots} = A \in \mathbb {G}$, return 1 if the following equalities hold:

    $$\begin{aligned} e(g, \hat{C})&= e(D, \hat{g}) \cdot \prod _{i = 1}^{\ell +2} e(N_i, \hat{X}_i) \\ \nonumber e(A, \hat{g})&= e(g_z, \hat{Z}) \cdot e(g, \hat{R}) \cdot \prod _{i = 1}^\ell e(g_i, \hat{M}_i) . \end{aligned}$$

    (2)

    Otherwise, return 0.

Using $tk := \{\rho _i\}_i^{\ell +2}$, it is possible to trapdoor-open a commitment $\hat{\mathsf {com}}=\hat{C}$ in the same way as a Pedersen commitment since $\hat{C}$ is nothing but a Pedersen commitment to $(\mathsf {sk}_{pots},\mathsf {osk}_{pots})$.

We now prove that the above commitment does not only provide CM-TCR security as defined in [10], but also ECM-TCR security. The proof builds on the same ideas as that of [10] but also takes advantage of the strong unforgeability³ of the underlying partial one-time signature.

Theorem 1

The scheme provides ECM-CTR security under the SXDH assumption.

Proof

For the sake of contradiction, let us assume that a PPT adversary $\mathcal {A}$ can win the game of Definition 8 with noticeable probability. We observe that the adversary can only win in two mutually exclusive cases.

• I. $\mathcal {A}$ outputs a commitment $\hat{C}^\star \in \hat{\mathbb {G}}$ for which it provides an opening

  $$\begin{aligned} \varvec{M}^\star= & {} (M_1^\star , \ldots , M_n^\star ) \\ \mathsf {open}^\star= & {} \big ( D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star , \hat{Z}^\star , \hat{R}^\star \big ) , \end{aligned}$$

  where $(D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star )$ differs from the tuple $(D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger )$ returned by $\mathcal {O}_{\mathsf {ck}}$ as part of the opening

  $$\begin{aligned} \mathsf {open}^\dagger= & {} \big ( D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger , \hat{Z}^\dagger , \hat{R}^\dagger \big ) , \end{aligned}$$

  of $\hat{C}^\star$ when $\mathcal {A}$ queried $\mathcal {O}_{\mathsf {ck}}$ to obtain a commitment to $\hat{\varvec{M}}^\dagger =(\hat{M}_1^\dagger ,\ldots ,\hat{M}_{\ell }^\dagger )$.

• II. $\mathcal {A}$ outputs a commitment $\hat{C}^\star \in \hat{\mathbb {G}}$ which it opens by revealing a pair

  $$\begin{aligned} \varvec{M}^\star= & {} (M_1^\star , \ldots , M_n^\star ) \\ \mathsf {open}^\star= & {} \big ( D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star , \hat{Z}^\star , \hat{R}^\star \big ) , \end{aligned}$$

  such that $(D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger )= (D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star )$. In this case, we must have either $\varvec{M}^\star \ne \varvec{M}^\dagger$ or $(\hat{Z}^\star ,\hat{R}^\star ) \ne (\hat{Z}^\dagger ,\hat{R}^\dagger )$.

Let us first assume that situation I occurs with noticeable probability. We show that $\mathcal {A}$ can be turned into an algorithm $\mathcal {B}_I$ that breaks the DDH assumption in $\hat{G}$ by finding a pair (Z, R) such that $e(Z,\hat{g}) \cdot e(R,\hat{h}) = 1_{\mathbb {G}_T}$ for a given pair $(\hat{g},\hat{h}) \in \hat{\mathbb {G}}^2$. This algorithm $\mathcal {B}_I$ proceeds in the same way as in [10]. Namely, it creates the commitment key $\mathsf {ck}$ by choosing $\rho _i,\theta _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and setting $\hat{X}_i=\hat{g}^{\rho _i} \cdot \hat{h}^{\theta _i}$ for each $i \in \{1,\ldots , \ell +2 \}$. It faithfully answers all queries made by $\mathcal {A}$ to $\mathcal {O}_{\mathsf {ck}}$. By hypothesis, $\mathcal {A}$ outputs a commitment $\hat{C}^\star \in \hat{\mathbb {G}}$ as well as an opening $(\varvec{M}^\star ,\mathsf {open}^\star )$ which satisfy the conditions of situation I. In particular, $\mathsf {open}^\star = \big ( D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star , \hat{Z}^\star , \hat{R}^\star \big )$ satisfies

$$\begin{aligned} e(g, \hat{C}^\star ) = e(D^\star , \hat{g}) \cdot \prod _{i = 1}^{\ell } e(g_i^\star , \hat{X}_i) \cdot e(g_z^\star , \hat{X}_{\ell +1}) \cdot e(A^\star ,\hat{X}_{\ell +2}) \end{aligned}$$

(3)

and the set Q must contain $\mathsf {open}^\dagger = \big ( D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger , \hat{Z}^\dagger , \hat{R}^\dagger \big )$ such that

$$\begin{aligned} e(g, \hat{C}^\star ) = e(D^\dagger , \hat{g}) \cdot \prod _{i = 1}^{\ell } e(g_i^\dagger , \hat{X}_i) \cdot e(g_z^\dagger , \hat{X}_{\ell +1}) \cdot e(A^\dagger ,\hat{X}_{\ell +2}) . \end{aligned}$$

(4)

Dividing (4) out of (3), we find that the pair

$$\begin{aligned} Z= & {} \Bigl ( \frac{D^\star }{D^\dagger } \Bigr ) \cdot \Bigl ( \frac{g_{z}^\star }{g_{z}^\dagger } \Bigr )^{ \rho _{\ell +1}} \cdot \Bigl ( \frac{A^\star }{A^\dagger } \Bigr )^{ \rho _{\ell +2}} \cdot \prod _{i=1}^\ell \Bigl ( \frac{g_i^\star }{g_i^\dagger } \Bigr )^{ \rho _i} \\ R= & {} \Bigl ( \frac{D^\star }{D^\dagger } \Bigr ) \cdot \Bigl ( \frac{g_{z}^\star }{g_{z}^\dagger } \Bigr )^{ \theta _{\ell +1}} \cdot \Bigl ( \frac{A^\star }{A^\dagger } \Bigr )^{ \theta _{\ell +2}} \cdot \prod _{i=1}^\ell \Bigl ( \frac{g_i^\star }{g_i^\dagger } \Bigr )^{ \theta _i} \\ \end{aligned}$$

satisfies $e(Z,\hat{g}) \cdot e(R,\hat{h}) = 1_{\mathbb {G}_T}$. Moreover, we have $Z \ne 1_\mathbb {G}$ with all but negligible probability since $\{\rho _i\}_{i=1}^\ell$ are completely independent of $\mathcal {A}$’s view.

We now turn to situation II and show that it implies an algorithm $\mathcal {B}_{II}$ that defeats the strong unforgeability of the partial one-time signature scheme. Algorithm $\mathcal {B}_{II}$ takes as input a POTS verification key $\mathsf {vk}_{pots}=(g_z^\dagger ,g_1^\dagger ,\ldots ,g_{\ell }^\dagger )$ supplied by its own challenger in the POTS security game. It generates $\mathsf {ck}= \{ \hat{X}_i \}_{i=1}^{\ell +2}$ by picking $\rho _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and defining $\hat{X}_i=\hat{g}^{\rho _i}$ for each $i \in \{1,\ldots , \ell +2\}$. Letting $Q_c \in \mathsf {poly}(\lambda )$ denote the number of queries made by $\mathcal {A}$ to $\mathcal {O}_{\mathsf {ck}}$, $\mathcal {B}_{II}$ draws a random index $k^\star \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\{1,\ldots , Q_c \}$ as a guess that $\mathcal {A}$ will choose to equivocate the commitment $\hat{C}^\dagger$ returned as the output of the $k^\star$-th query. It answers all queries to $\mathcal {O}_\mathsf {ck}$ as follows. For each $k \in \{1,\ldots ,Q_c \} \backslash \{k^\star \}$, the k-th query is answered by faithfully running the commitment algorithm. When the $k^\star$-th query occurs, $\mathcal {B}_{II}$ embeds $\mathsf {vk}_{pots}=(g_z^\dagger ,g_1^\dagger ,\ldots ,g_{\ell }^\dagger )$ into the opening of the $k^\star$-th commitment. To this end, it chooses $\zeta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^*$ and computes $\hat{C}^\dagger = \hat{g}^{\zeta }$.

Next, $\mathcal {B}_{II}$ queries its own POTS challenger to obtain a signature $(A^\dagger ,(\hat{Z},\hat{R}))$ on the message $\hat{\varvec{M}}=(\hat{M}_1,\ldots ,\hat{M}_{\ell }) \in \hat{\mathbb {G}}^{\ell }$ queried by $\mathcal {A}$ at this $k^\star$-th query. Upon receiving a partial one-time signature $(A^\dagger ,(\hat{Z}^\dagger ,\hat{R}^\dagger ))$ from its POTS challenger, $\mathcal {B}_{II}$ defines $(N_1,\ldots ,N_{\ell },N_{\ell +1},N_{\ell +2})=(g_1^\dagger ,\ldots , g_{\ell }^\dagger ,g_z^\dagger , A^\dagger )$ and computes

$$\begin{aligned} D^\dagger = g^\zeta \cdot \prod _{i=1}^{\ell +2} N_i^{-\rho _i} \in \mathbb {G}, \end{aligned}$$

which satisfies $e(g,\hat{C}^\dagger ) = e(D^\dagger ,\hat{g}) \cdot \prod _{i=1}^{\ell +2} e(N_i,\hat{X}_i)$. Given that $(A^\dagger ,(\hat{Z}^\dagger ,\hat{R}^\dagger ))$ satisfies the second verification equation of (2) by construction, we observe that

$$ \mathsf {open}^\dagger = \big ( D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger , \hat{Z}^\dagger , \hat{R}^\dagger \big ) $$

forms a valid opening of $\hat{C}^\dagger$. When $\mathcal {A}$ halts, we know that, with probability $1/Q_c$, it chooses to output a pair $(\varvec{M}^\star ,\mathsf {open}^\star )$ which opens $\hat{C}^\star = \hat{C}^\dagger$. Given that $(D^\star , g_z^\star , g_1^\star , \ldots , g_\ell ^\star , A^\star )=(D^\dagger , g_z^\dagger , g_1^\dagger , \ldots , g_\ell ^\dagger , A^\dagger )$ and since we must have $(\varvec{M}^\star ,\mathsf {open}^\star ) \ne (\varvec{M}^\dagger , \mathsf {open}^\dagger )$ by the definition of ECM-TCR security, we know that $(\varvec{M}^\star ,(\hat{Z}^\star ,\hat{R}^\star )) \ne (\varvec{M}^\dagger ,(\hat{Z}^\dagger ,\hat{R}^\dagger ))$. This means that $\mathcal {B}_{II}$ can win the game against its POTS challenger by outputting $(\varvec{M}^\star ,(A^\star ,\hat{Z}^\star ,\hat{R}^\star ))$. In turn, the result of [4] implies that $\mathcal {B}_{II}$ would contradict the DDH assumption in $\mathbb {G}$.    $\square$

3 A Structure-Preserving CCA2-Secure Public-Key Cryptosystem with Shorter Publicly Verifiable Ciphertexts

In this section, we use the all-but-one hash proof systems of [46] and combine them with the structure-preserving commitment scheme of Sect. 2.5 and a strongly unforgeable signature scheme. We show that the ECMTCR property of the commitment scheme suffices to construct the sought-after CCA2-secure structure preserving encryption scheme with publicly verifiable ciphertexts.

In the notations hereafter, for any vector $\varvec{\hat{h}}=(\hat{h}_1,\hat{h}_2) \in \hat{\mathbb {G}}^2$ and any $g \in \mathbb {G}$, we denote by $E(g,\varvec{\hat{h}})$ the vector $(e(g,\hat{h}_1),e(g,\hat{h}_2))$. For any vectors $\hat{\varvec{u}}_1,\hat{\varvec{u}}_2 \in \hat{\mathbb {G}}^2$, the product $\hat{\varvec{u}}_1 \cdot \hat{\varvec{u}}_2 \in \hat{\mathbb {G}}^2$ refers to the component-wise multiplication in $\hat{\mathbb {G}}$.

• $\varvec{{\mathsf {KeyGen}}(\lambda )}{} \mathbf :$

  • 1. Run the setup algorithm of the commitment scheme in Sect. 2.5 to obtain $\mathsf {PP}= (p, \mathbb {G}, \hat{\mathbb {G}}, \mathbb {G}_T, e, g, \hat{g},\ell =6) \leftarrow TC.{\mathsf {Setup}}({\lambda },6)$, which will be used to commit to messages in $\hat{\mathbb {G}}^6$.

  • 2. Generate $(\mathsf {ck},\mathsf {tk})\leftarrow TC.{\mathsf {KeyGen}}(\mathsf {PP})$, where ${\mathsf {ck}} \in \hat{\mathbb {G}}^8$ is the commitment key and ${\mathsf {tk}} \in \mathbb {Z}_p^8$ is the trapdoor key which can be erased.

  • 3. Choose also group generators $g_1, g_2 \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}$ and random values $x_1, x_2 \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and set $X = g_1^{x_1}g_2^{x_2}$.

  • 4. Choose $\rho _u \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and $\hat{h} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\hat{\mathbb {G}}^2$ at random.

  • 5. Define $(\hat{\varvec{u}}_1, \hat{\varvec{u}}_2)$ with $\hat{\varvec{u}}_1 = (\hat{g}, \hat{h}) \in \hat{\mathbb {G}}^2$ and $\hat{\varvec{u}}_2 = (\hat{g}^{\rho _u}, \hat{h}^{\rho _u }) \in \hat{\mathbb {G}}^2$. Note that $\hat{\varvec{u}}_1$ and $\hat{\varvec{u}}_2$ are linearly dependent.

  • 6. Define $\mathsf {SK}= (x_1, x_2)$ and

    $$\mathsf {PK}= (g_1, g_2, \hat{\varvec{u}}_1, \hat{\varvec{u}}_2, X, \mathsf {PP}, {\mathsf {ck}}).$$

• $\varvec{{\mathsf {Encrypt}}(M,\mathsf {PK})}{} \mathbf :$ To encrypt $M \in \mathbb {G}$, conduct the following steps.

  • 1. Generate a key pair $(\mathsf {SSK}, \mathsf {SVK}) \leftarrow OT1.{\mathsf {KeyGen}}(\mathsf {PP},5)$ for the one-time SPS of Sect. 2.2 so as to sign messages in $\mathbb {G}^5$. Let the resulting key pair consist of $\mathsf {SSK}= \big ( \{\chi _i, \gamma _i\}_{i=1}^5, \zeta , \rho \big ) \in \mathbb {Z}_p^{14}$ and $\mathsf {SVK}= \big ( \{\hat{g}_i\}_{i =1}^5, \hat{A} \big ) \in \hat{\mathbb {G}}^6,$ where $\hat{g}_i=\hat{g}_z^{\chi _i} \cdot \hat{g}_r^{\delta _i}$ and $\hat{A}=\hat{g}_z^{\zeta } \cdot \hat{g}_r^{\rho }$.

  • 2. Choose $\theta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute

    $$\begin{aligned} C_0&= M\cdot X^{\theta },&\quad C_1&= g_1^{\theta },\quad&C_2&= g_2^{\theta }. \end{aligned}$$

  • 3. Generate a commitment to $\mathsf {SVK}= (\{\hat{g}_i\}_{i =1}^5, \hat{A})$ and let

    $$(\hat{\mathsf {com}}, \mathsf {open}) \leftarrow TC.{\mathsf {Commit}}(\mathsf {PP}, {ck}, \mathsf {SVK}) \in \hat{\mathbb {G}} \times (\mathbb {G}^9 \times \hat{\mathbb {G}}^2)$$

    be the resulting commitment/opening pair.

  • 4. Define vector $\hat{\varvec{u}}_{\hat{\mathsf {com}}} = \hat{\varvec{u}}_2\cdot (1, \hat{\mathsf {com}}) \in \hat{\mathbb {G}}^2$ as well as the Groth-Sahai CRS $\hat{\mathbf {u}}_{\hat{\mathsf {com}}} =(\hat{\varvec{u}}_{\hat{\mathsf {com}}},\hat{\varvec{u}}_1) \in \hat{\mathbb {G}}^2$.

  • 5. Pick $r \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. Compute $\hat{\varvec{C}}_{\theta } = \hat{\varvec{u}}_{\hat{\mathsf {com}}}^{\theta } \cdot \hat{\varvec{u}}_1^r$.

  • 6. Using the randomness of the commitment $\varvec{C}_{\theta }$, generate proof elements $\varvec{\pi }=(\pi _1,\pi _2)=(g_1^r,g_2^r) \in \mathbb {G}^2$ showing that the committed $\theta \in \mathbb {Z}_p$ satisfies the multi-exponentiation equations

    $$\begin{aligned} C_1&= g_1^{\theta }&\qquad C_2&= g_2^{\theta } \end{aligned}$$

  • 7. Output the ciphertext

    $$\begin{aligned} \varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma }) \in \mathbb {G}^{16} \times \hat{\mathbb {G}}^{11} \end{aligned}$$

    (5)

    where $\varvec{\sigma } \leftarrow OT1.{\mathsf {Sign}}(\mathsf {SSK}, (C_0, C_1, C_2, {\pi }_1,\pi _2)) \in \mathbb {G}^2$.

• $\varvec{{\mathsf {Decrypt}}(\mathsf {PK}, \varvec{C}, \mathsf {SK})}{} \mathbf :$ Parse the ciphertext $\varvec{C}$ as in (5). Then, conduct the following steps.

  • 1. Parse $\mathsf {PK}$ as $({g}_1, {g}_2, X, \mathsf {PP}, \mathsf {ck})$ and $\mathsf {SK}$ as $(x_1, x_2)$.

  • 2. Return $\perp$ if $OT1.{\mathsf {Verify}}(\mathsf {SVK}, (C_0, C_1, C_2, \pi _1,\pi _2), \sigma ) = 0$.

  • 3. Return $\perp$ if $\hat{\mathsf {com}}=1_{\hat{\mathbb {G}}}$ or $TC.{\mathsf {Verify}}(\mathsf {ck}, \hat{\mathsf {com}}, \mathsf {SVK}, \mathsf {open}) = 0$.

  • 4. Verify that $\varvec{\pi }=(\pi _1,\pi _2)$ is a valid Groth-Sahai proof w.r.t. $(C_1, C_2, \varvec{C}_{\theta }, \hat{\mathsf {com}})$. Namely, it should satisfy

    $$\begin{aligned} E(g_1,\hat{\varvec{C}}_{\theta })= & {} E(C_1 , \hat{\varvec{u}}_{\hat{\mathsf {com}}}) \cdot E(\pi _1,\hat{\varvec{u}}_1) \\ \nonumber E(g_2,\hat{\varvec{C}}_{\theta })= & {} E(C_2 , \hat{\varvec{u}}_{\hat{\mathsf {com}}}) \cdot E(\pi _2,\hat{\varvec{u}}_1) \end{aligned}$$

    (6)

  • 5. If the above verifications all succeed, output $M=C_0/(C_1^{x_1}\cdot C_2^{x_2})$.

Note that, in step 3 of the decryption algorithm, the condition $\hat{\mathsf {com}}\ne 1_{\hat{\mathbb {G}}}$ ensures that vectors $(\hat{\varvec{u}}_{\hat{\mathsf {com}}}, \hat{\varvec{u}}_1)$ form a perfectly sound Groth-Sahai CRS, so that ciphertexts such that $\log _{g_1}(C_1) \ne \log _{g_2}(C_2)$ are always rejected.

The proof of the following theorem follows the strategy of [46] with additional arguments showing that omitting to sign the Groth-Sahai commitments does not affect the security of the scheme.

Theorem 2

The scheme provides IND-CCA2 security under the SXDH assumption. More precisely, $\mathbf {Adv}^{\mathsf {CCA}}(\lambda )\le 5 \times \mathbf {Adv}^{\mathsf {SXDH}}(\lambda ) + q_d \times 2^{-\lambda }$.

Proof

The proof proceeds with a sequence of games that begins with the real game and ends with a game where no advantage is left to the adversary whatsoever. In each game, we call $W_i$ the event that the experiment outputs 1. The security parameter $\lambda$ is implicitly given in all the games. Let $q_d$ denote the number of decryption queries made by the adversary.

 

Game 0: :

This is the real game. The adversary is given the public key $\mathsf {PK}$ which contains vectors $(\hat{\varvec{u}}_1, \hat{\varvec{u}}_2)$ such that

$$\begin{aligned} \hat{\varvec{u}}_1&= (\hat{g}, \hat{h}) \in \hat{\mathbb {G}}^2&\quad \hat{\varvec{u}}_2&= (\hat{g}^{\rho _u}, \hat{h}^{\rho _u }) \in \hat{\mathbb {G}}^2, \end{aligned}$$

(7)

where $\hat{g},\hat{h} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\hat{\mathbb {G}}$, $\rho _u \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. In the challenge phase, it chooses two messages $M_0,M_1 \in \mathbb {G}$ and obtains a challenge ciphertext

$$ \varvec{C}^\star = (\mathsf {SVK}^\star , \hat{\mathsf {com}}^\star , \mathsf {open}^\star , C_0^\star , C_1^\star , C_2^\star , \hat{\varvec{C}}_{\theta }^\star , \varvec{\pi }^\star , \varvec{\sigma }^\star ) $$

where, for some random bit $\beta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\{0,1\}$,

$$\begin{aligned} C_0^\star&= M_{\beta } \cdot X^{\theta ^\star },&\quad C_1^\star&= g_1^{\theta ^\star },&\quad C_2^\star&= g_2^{\theta ^\star }, \end{aligned}$$

as well as $(\hat{\mathsf {com}}, \mathsf {open}) \leftarrow TC.{\mathsf {Commit}}(\mathsf {PP}_{TC}, {ck}, \mathsf {SVK})$, $\hat{\varvec{C}}_{\theta }^\star =\hat{\varvec{u}}_{\hat{\mathsf {com}}^\star }^{\theta ^\star } \cdot \hat{\varvec{u}}_1^{r^\star }$ and $\varvec{\pi }^\star =(\pi _1^\star ,\pi _2^\star ) =(g_1^{r^\star },g_2^{r^\star })$, where $\hat{\varvec{u}}_{\hat{\mathsf {com}}^\star } = \hat{\varvec{u}}_2\cdot (1, \hat{\mathsf {com}}^\star )$. We assume w.l.o.g. that $\mathsf {SVK}^\star$ and $\hat{\mathsf {com}}^\star =\hat{C}^\star$ are generated at the outset of the game.

The adversary’s decryption queries are always faithfully answered by the challenger. When the adversary halts, it outputs $\beta ' \in \{0,1\}$ and wins if $\beta ' =\beta$. In this case, the experiment outputs 1. Otherwise, it outputs 0. The adversary’s advantage is thus $|\Pr [W_0]-1/2|$.

Game 1: :

This game is like Game 0 except that, if the adversary makes a pre-challenge decryption query $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that $\hat{\mathsf {com}}=\hat{\mathsf {com}}^\star$, the experiment halts and outputs a random bit. Since Game 1 is identical to Game 0 until this event $F_1$ occurs, we have the inequality $|\Pr [W_1]-\Pr [W_0]| \le \Pr [F_1]$. Moreover, since $\hat{\mathsf {com}}^\star$ was chosen uniformly in $\hat{\mathbb {G}}$ and remains independent of $\mathcal {A}$’s view until the challenge phase, we have $|\Pr [W_1]-\Pr [W_0]| \le \Pr [F_1] \le q_d/p$.

Game 2: :

In this game, we modify the generation of the public key and define

$$\begin{aligned} \hat{\varvec{u}}_1= & {} (\hat{g}, \hat{h}) \in \hat{\mathbb {G}}^2 \\ \nonumber \hat{\varvec{u}}_2= & {} (\hat{g}^{\rho _u}, \hat{h}^{\rho _u }) \cdot (1, \hat{\mathsf {com}}^\star )^{-1} \in \hat{\mathbb {G}}^2, \end{aligned}$$

(8)

for a random $\rho _u \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$, instead of computing $(\hat{\varvec{u}}_1,\hat{\varvec{u}}_2)$ as in (7). Note that $(\hat{\varvec{u}}_1,\hat{\varvec{u}}_2)$ are now linearly independent and $\hat{\mathsf {com}}^\star$ is no longer statistically hidden before the challenge phase. However, a straightforward argument based on the semantic security of ElGamal (and thus the DDH assumption in $\hat{\mathbb {G}}$) shows that this modification does not affect the adversary’s view. We have $|\Pr [W_2]-\Pr [W_1]| \le 2 \times \mathbf {Adv}_{\hat{\mathbb {G}},\mathcal {B}}^{\mathrm {DDH}}(\lambda )$.

Game 3: :

This game is like Game 2 but we modify the decryption oracle. Namely, if the adversary makes a post-challenge decryption query for a valid ciphertext $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that $\hat{\mathsf {com}}=\hat{\mathsf {com}}^\star$ but $(\mathsf {SVK},\mathsf {open}) \ne (\mathsf {SVK}^\star ,\mathsf {open}^\star )$, the experiment halts and outputs a random bit. If we call $F_3$ the latter event, we have $|\Pr [W_3]-\Pr [W_2]| \le \Pr [F_3]$. As shown by Lemma 1, event $F_3$ implies an adversary $\mathcal {B}_3$ against the ECM-TCR property (as formalized by Definition 8) of the trapdoor commitment in Sect. 2.5, which contradicts the SXDH assumption. We thus have $|\Pr [W_3]-\Pr [W_2]| \le \mathbf {Adv}_{TC,\mathcal {B}_3}^{\mathsf {ECM}\textsf {-}\mathsf {TCR}}(\lambda ) \le \mathbf {Adv}_{\mathcal {B}_3}^{\mathrm {SXDH}}(\lambda )$.

Game 4: :

We modify again the decryption oracle in post-challenge decryption queries. After the challenge phase, if the adversary $\mathcal {A}$ queries the decryption of a ciphertext $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that we have $(\hat{\mathsf {com}},\mathsf {open})=(\hat{\mathsf {com}}^\star ,\mathsf {open}^\star )$ but $(C_0,C_1,C_2,\pi _1,\pi _2) \ne (C_0^\star ,C_1^\star ,C_2^\star ,\pi _1^\star ,\pi _2^\star )$, the experiment halts and outputs a random bit. If we call $F_4$ this event, we have the inequality $|\Pr [W_4]-\Pr [W_3]| \le \Pr [F_4]$ since Game 4 is identical to Game 3 until $F_4$ occurs. Moreover, $F_4$ would contradict the strong unforgeability of the one-time structure-preserving signature and thus the DP assumption. This implies $|\Pr [W_4]-\Pr [W_3]| \le \mathbf {Adv}_\mathcal {B}^{\mathsf {SUF}\textsf {-}\mathsf {OTS}}(\lambda ) \le \mathbf {Adv}_\mathcal {B}^{\mathrm {DP}}(\lambda )$.

Game 5: :

We introduce another modification in the decryption oracle. We reject all ciphertexts $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that

$$\begin{aligned}&(\hat{\mathsf {com}},\mathsf {open})=(\hat{\mathsf {com}}^\star ,\mathsf {open}^\star ) \quad \wedge \quad \nonumber \\&\qquad \qquad \! (C_0,C_1,C_2,\pi _1,\pi _2) = (C_0^\star ,C_1^\star ,C_2^\star ,\pi _1^\star ,\pi _2^\star ) \quad \wedge \quad \hat{\varvec{C}}_{\theta } \ne \hat{\varvec{C}}_{\theta }^\star . \end{aligned}$$

(9)

Let $F_5$ be the event that the decryption oracle rejects a ciphertext that would not have been rejected in Game 4. We argue that $\Pr [W_5] = \Pr [W_4]$ since Game 5 is identical to Game 4 until event $F_5$ occurs and we have $\Pr [F_5]=0$. Indeed, for a given $(C_1^\star ,C_2^\star ,\pi _1^\star ,\pi _2^\star ) \in \mathbb {G}^4$, there exists only one commitment $\hat{\varvec{C}}_{\theta }^\star \in \hat{\mathbb {G}}^2$ that satisfies the equalities (6). This follows from the fact that, since $(C_1^\star ,C_2^\star ,\pi _1^\star ,\pi _2^\star )=(g_1^{\theta ^\star },g_2^{\theta ^\star },g_1^{r^\star },g_2^{r^\star })$, relations (6) can be written

$$\begin{aligned} E(g_1,\hat{\varvec{C}}_{\theta }^\star )= & {} E(g_1^{\theta ^\star } , \hat{\varvec{u}}_{\hat{\mathsf {com}}}) \cdot E(g_1^{r^\star },\hat{\varvec{u}}_1) = E(g_1 , \hat{\varvec{u}}_{\hat{\mathsf {com}}}^{\theta ^\star }) \cdot E(g_1,\hat{\varvec{u}}_1^{r^\star }) \\ \nonumber E(g_2,\hat{\varvec{C}}_{\theta }^\star )= & {} E(g_2^{\theta ^\star } , \hat{\varvec{u}}_{\hat{\mathsf {com}}}) \cdot E(g_2^{r^\star },\hat{\varvec{u}}_1) =E(g_2 , \hat{\varvec{u}}_{\hat{\mathsf {com}}}^{\theta ^\star }) \cdot E(g_2, \hat{\varvec{u}}_1^{r^\star }) \end{aligned}$$

which uniquely determines the only commitment $\hat{\varvec{C}}_{\theta }^\star = \hat{\varvec{u}}_{\hat{\mathsf {com}}}^{\theta ^\star } \cdot \hat{\varvec{u}}_1^{r^\star } \in \hat{\mathbb {G}}^2$ that satisfies (6). This shows that $\Pr [F_5] = 0$, as claimed.

Game 6: :

In this game, we modify the distribution of the public key. Namely, instead of generating the vectors $(\hat{\varvec{u}}_1, \hat{\varvec{u}}_2)$ as in (8), we set

$$\begin{aligned} \hat{\varvec{u}}_1&= (\hat{g}, \hat{h}) \in \hat{\mathbb {G}}^2&\qquad \hat{\varvec{u}}_2&= (\hat{g}^{\rho _u}, \hat{h}^{\rho _u}) \cdot (1,{\hat{C}^{\star {-1}}}) \in \hat{\mathbb {G}}^2. \end{aligned}$$

(10)

Said otherwise, $\hat{\varvec{u}}_2$ is now the product of two terms, the first one of which lives in the one-dimensional subspace spanned by $\hat{\varvec{u}}_1$. Under the DDH assumption in $\hat{\mathbb {G}}$, this modified distribution of $\mathsf {PK}$ should have not noticeable impact on the adversary’s behavior. A straightforward reduction shows that $|\Pr [W_6]-\Pr [W_5] | \le \mathbf {Adv}^{\mathrm {DDH}}_\mathcal {B}(\lambda )$. Note that, although the vectors $(\hat{\varvec{u}}_{\hat{\mathsf {com}}^\star },\hat{\varvec{u}}_1) \in \hat{\mathbb {G}}^2$ are no longer linearly independent, $\hat{\varvec{C}}_{\theta }^\star = \hat{\varvec{u}}_1^{\rho _u \cdot \theta ^\star +r^\star }$ remains the only commitment that satisfies the verification equations for a given tuple $(C_1^\star ,C_2^\star ,\pi _1^\star ,\pi _2^\star )$.

Game 7: :

In this game, we modify the challenge ciphertext and replace the NIZK proof $\varvec{\pi }^\star =(\pi _1^\star ,\pi _2^\star ) \in \mathbb {G}^2$ by a simulated proof which is produced using $\rho _u \in \mathbb {Z}_p$ as a simulation trapdoor. Namely, $(\hat{\varvec{C}}_\theta ^\star ,\varvec{\pi }^\star )$ is obtained by picking $r \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and computing

$$\begin{aligned} \hat{\varvec{C}}_{\theta }^\star= & {} \varvec{u}_1^{r}, \qquad \qquad \quad \pi _1^\star = g_1^{r} \cdot {C_1^\star }^{-\rho _u} , \qquad \qquad \quad \pi _2^\star = g_2^{r} \cdot {C_2^\star }^{-\rho _u} \end{aligned}$$

Observe that, although $(\hat{\varvec{C}}_\theta ^\star ,\pi _1^\star ,\pi _2^\star )$ are generated without using the witness $\theta ^\star = \log _{g_1}(C_1^\star ) = \log _{g_2}(C_2^\star )$, the NIZK property of GS proofs ensures that their distribution remains exactly as in Game 6: indeed, if we define ${\tilde{r}} =r -\rho _u \cdot \theta ^\star$, we have

$$\begin{aligned} \hat{\varvec{C}}_{\theta }^\star= & {} \hat{\varvec{u}}_{\hat{\mathsf {com}}^\star }^{\theta ^\star } \cdot \hat{\varvec{u}}_1^{\tilde{r}}, \qquad \qquad \quad \pi _1^\star = g_1^{\tilde{r}} , \qquad \qquad \quad \pi _2^\star = g_2^{\tilde{r}} , \end{aligned}$$

which implies $\Pr [W_7]=\Pr [W_6]$.

Game 8: :

We modify the generation of the challenge ciphertext, which is generated using the private key $\mathsf {SK}=(x_1,x_2)$ instead of the public key: Namely, the challenger computes

$$\begin{aligned} C_1^\star&= g_1^{\theta ^\star },&C_2^\star&= g_2^{\theta ^\star },&C_0^\star&= M_{\beta } \cdot {C_1^\star }^{x_1} \cdot {C_2^\star }^{x_2} , \end{aligned}$$

while $(\hat{\varvec{C}}_\theta ^\star ,\pi _1^\star ,\pi _2^\star )$ are computed using the NIZK simulation trapdoor $\rho _u \in \mathbb {Z}_p$ as in Game 7. This change does not affect the adversary’s view since the ciphertext retains the same distribution. We have $\Pr [W_8]=\Pr [W_7]$.

Game 9: :

We modify again the distribution of the challenge ciphertext which is obtained as

$$\begin{aligned} C_1^\star&= g_1^{\theta _1^\star },&C_2^\star&= g_2^{\theta _2^\star },&C_0^\star&= M_{\beta } \cdot {C_1^\star }^{x_1} \cdot {C_2^\star }^{x_2} , \end{aligned}$$

for random and independent $\theta _1^\star ,\theta _2^\star \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$, while the NIZK proof $(\hat{\varvec{C}}_\theta ^\star ,\pi _1^\star ,\pi _2^\star )$ is simulated using $\rho _u \in \mathbb {Z}_p$ as in Game 8. Since the witness $\theta ^\star \in \mathbb {Z}_p$ was not used anymore in Game 8, a straightforward reduction shows that any noticeable change in $\mathcal {A}$’s output distribution implies a DDH distinguisher in $\mathbb {G}$. We have $|\Pr [W_9]-\Pr [W_8]| \le \mathbf {Adv}_{\mathcal {B},\mathbb {G}}^{\mathrm {DDH}}(\lambda )$.

 

In the final game, it is easy to see that $\Pr [W_9]=1/2$ since the challenge ciphertext does not carry any information about $\beta \in \{0,1\}$. Indeed, we have

$$\begin{aligned} C_1^\star&= g_1^{\theta _1^\star },&C_2^\star&= g_2^{\theta _1^\star + \theta _1'},&C_0^\star&= M_{\beta } \cdot X^{\theta _1^\star } \cdot {g_2}^{\theta _1' \cdot x_2} , \end{aligned}$$

for some random $\theta _1' \in _R \mathbb {Z}_p$, which implies that the term ${g_2}^{\theta _1' \cdot x_2}$ perfectly hides $M_\beta$ in the expression of $C_0^\star$. This follows from the fact that $x_2 \in \mathbb {Z}_p$ is perfectly independent of the adversary’s view. Indeed, the public key leaves $x_2 \in \mathbb {Z}_p$ completely undetermined as it only reveals $X=g_1^{x_1} g_2^{x_2}$. During the game, decryption queries are guaranteed not to reveal anything about $x_2$ since all NIZK proofs $(\hat{\varvec{C}}_{\theta },\pi _1,\pi _2)$ take place on Groth-Sahai CRSes $(\hat{\varvec{u}}_{\hat{\mathsf {com}}},\hat{\varvec{u}}_1)$ which are perfectly sound (as they span the entire vector space $\hat{\mathbb {G}}^2$) whenever $\hat{\mathsf {com}}\ne \hat{\mathsf {com}}^\star$. This implies that, although the adversary can see a simulated NIZK proof $(\hat{\varvec{C}}_\theta ^\star ,\pi _1^\star ,\pi _2^\star )$ for a false statement in the challenge phase, it remains unable to trick the decryption oracle into accepting a ciphertext $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that $\log _{g_1}(C_1) \ne \log _{g_2}(C_2)$. As a consequence, the adversary does not learn anything about $x_2$ from responses of the decryption oracle.    $\square$

Lemma 1

In Game 3, there exists an ECM-TCR adversary with advantage $\epsilon \ge \Pr [F_3]$ against the trapdoor commitment scheme of Sect. 2.5 and which runs in about the same time as $\mathcal {A}$.

Proof

Let $\mathcal {A}$ be an adversary against the SP-CCA encryption scheme as in the proof of Theorem 2 and let the event $F_3$ be defined as in Game 3. Then, we build an adversary $\mathcal {B}_3$ against the ECM-CTR security of the structure-preserving trapdoor commitment defined in Sect. 2.5 which efficiently runs $\mathcal {A}$.

The challenger $\mathcal {B}_3$ is given the public parameter $\mathsf {PP}_{TC}$ and a commitment key $\mathsf {ck}$ generated as in the trapdoor commitment scheme as well as an access to a commit-open oracle $\mathcal {O}_{\mathsf {ck}}$ as defined in Definition 8. Then, $\mathcal {B}_3$ runs step 3 to step 6 of the key generation algorithm of the encryption scheme to get $\mathsf {PK}$ and $\mathsf {SK}=(x_1,x_2)$ as specified in Game 2 and Game 3.

The adversary $\mathcal {A}$ is given $\mathsf {PK}$ and $\mathcal {B}_3$ is easily able to answer to $\mathcal {A}$’s decryption queries as described in Game 2 and Game 3 thanks to $\mathsf {SK}$. In order to compute the challenge ciphertext given $\{m_0,m_1\}$, $\mathcal {B}_3$ picks $\beta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\{0,1\}$, runs all the steps of the encryption algorithm with $m_\beta$ except for step 3 for which $\mathcal {B}_3$ queries $\mathcal {O}_{\mathsf {ck}}$ on $\mathsf {SVK}^\star$ to get $(\hat{\mathsf {com}}^\star , \mathsf {open}^\star )$. The computed ciphertext $\varvec{C}^\star$ is then given to $\mathcal {A}$.

Assuming that $F_3$ occurs, which means that $\mathcal {A}$ makes a post-challenge decryption query for a valid ciphertext $\varvec{C} = (\mathsf {SVK}, \hat{\mathsf {com}}, \mathsf {open}, C_0, C_1, C_2, \hat{\varvec{C}}_{\theta }, \varvec{\pi }, \varvec{\sigma })$ such that $\hat{\mathsf {com}}=\hat{\mathsf {com}}^\star$ but $(\mathsf {SVK},\mathsf {open}) \ne (\mathsf {SVK}^\star ,\mathsf {open}^\star )$, the challenger simply outputs $(\hat{\mathsf {com}}^\star ,\mathsf {SVK},\mathsf {open})$.

Obviously, we have $TC.{\mathsf {Verify}}(\mathsf {ck}, \hat{\mathsf {com}}^\star , \mathsf {SVK}, \mathsf {open}) = 1$ since $\varvec{C}$ is valid. However, during the ECM-TR experiment $\mathcal {B}_3$ only chose a single message $\mathsf {SVK}^\star$ so that there is only one target in $Q=\{(\hat{\mathsf {com}}^\star ,\mathsf {SVK}^\star ,\mathsf {open}^\star )\}$. Moreover, since we also have $(\hat{\mathsf {com}}^\star ,\mathsf {SVK},\mathsf {open})\not \in Q$, we find $\Pr [F_3]=\mathbf {Adv}_{TC,\mathcal {B}_3}^{ECM\text {-}TCR}(\lambda )$.    $\square$

While we do not explicit provide a threshold decryption mechanism in the paper, this can be easily achieved in the same way as in the SXDH-based threshold cryptosystem described in [46]. As a result, we readily obtain a robust and non-interactive structure-preserving threshold cryptosystem with CCA2-security in the adaptive corruption setting.

It would be interesting to improve the efficiency of the scheme using quasi-adaptive NIZK arguments [38] in the same way as in [43]. Unfortunately, we did not manage to obtain the required simulation-soundness property while keeping the QA-NIZK arguments structure-preserving.

4 A Randomizable RCCA-Secure Construction

Given a message M over $\mathbb {G}$, the encryption algorithm computes an ElGamal-like encryption of the form $(c_0,c_1,c_2)=(f^\theta ,g^\theta ,M \cdot h^\theta )$. In order to have an alternative decryption in the reduction as well as publicly verifiable ciphertexts, the algorithm then derives an LHSP signature (Sect. 2.4) on the vector $\varvec{v} = (c_0^b,c_1^b,g^{1-b},c_1^{1-b},c_2^{1-b})$, where $b=1$ is a hidden bit. This is made possible by giving an LHSP signature on $\varvec{v}_1=(f,g,1,1,1)$ and $\varvec{v}_2=(1,1,1,g,h)$ in the public key since $\varvec{v}=\varvec{v}_1^\theta$. Note that, if $b=0$, the encryption algorithm cannot derive a signature on $\varvec{v}$ since $(1,1,g,c_1,c_2)$ is outside the linear span of $\varvec{v}_1$ and $\varvec{v}_2$. The goal of the security reduction is to compute the challenge ciphertext with $b=0$ (using the signing key) and force the adversary to keep this $b=0$ in any re-randomization of the challenge. This allows detecting when the adversary attempts to obtain the decryption of a replayed ciphertext.

In order to make freshly generated ciphertexts indistinguishable from (re-randomizations of) the challenge ciphertext, we use Groth-Sahai commitments and NIWI proofs to hide b. The encryption algorithm computes a commitment to $g^b$ and $\varvec{v}$ and proves that $b \in \{0,1\}$ and that $\varvec{v}$ is well-formed with respect to $(c_0,c_1,c_2)$. Then, it proves that the LHSP signature on $\varvec{v}$ is valid.

This proof can be seen as a quasi-adaptive NIZK proof [38] that either $(c_0,c_1,c_2)$ is well-formed or that I know a one-time signature on $(c_1,c_2)$ (of Sect. 2.2) which corresponds to an LHSP signature on $(g,c_1,c_2)$, where g is the fixed element of the verification-key.

In order to statistically re-randomize ciphertext, the OR-proof should be efficiently and publicly adaptable and at the same time it should not support any other kind of malleability. Even though in the NIWI setting the Groth-Sahai proofs are perfectly re-randomizable the constants of the proofs are modified when we compute $(c_0',c_1',c_2')=(c_0,c_1,c_2)\cdot (f,g,h)^{\theta '}$ as well as the variables $\varvec{v}'=\varvec{v}\cdot (\varvec{v}_1^{b} \cdot \varvec{v}_2^{1-b})^{\theta '}$. Since proving that $\varvec{v}'$ has the correct form requires the same random coins as those used in the commitment of $g^b$, the encryption algorithm simply adds in the ciphertext a commitment to $\varvec{v}_1^b \cdot \varvec{v}_2^{1-b}$, a proof of well-formedness and a Groth-Sahai NIWI proof of an LHSP signature that can be derived from the public key.

At a first glance, ciphertexts may appear not to prevent malleability of the encrypted message M since nothing seems to “freeze” $c_2$ in the ciphertext when $c_2^{1-b}=1$ in honest execution. However, the ciphertext actually binds $c_2$ in the proof elements which depend on the random coins of the commitments.

• $\varvec{\mathsf {Keygen}(\lambda )}{} \mathbf :$ Choose bilinear groups $(\mathbb {G},\hat{\mathbb {G}},\mathbb {G}_T)$ of prime order $p>2^{\lambda }$ with generators $f,g\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}$, $\hat{g},\hat{h}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\hat{\mathbb {G}}$ and do the following.

  • 1. Choose a random exponent $\alpha \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and set $h=g^\alpha$.

  • 2. Choose random $\varvec{u}_1,\varvec{u}_2\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}^2$ and $\varvec{\hat{u}}_1,\varvec{\hat{u}}_2\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\hat{\mathbb {G}}^2$.

  • 3. Define $\varvec{v}_1=(f,g,1,1,1)$ and $\varvec{v}_2=(1,1,1,g,h)$, then generate a $\mathsf {crs}$ for a QA-NIZK proof system for the language of vectors in $\mathsf {span}\langle \varvec{v}_1,\varvec{v}_2\rangle$: pick $\mathsf {tk}=(\chi _j,\gamma _j)_{j=1}^{5}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p^{2\times 5}$ and compute $\hat{g}_j=\hat{g}^{\chi _j}\hat{h}^{\gamma _j}$, for each $1\le j \le 5$, as well as the language dependent parameters $(z_1,r_1)=(f^{\chi _1}g^{\chi _2},f^{\gamma _1}g^{\gamma _2})$ and $(z_2,r_2)=(g^{\chi _4}h^{\chi _5},g^{\gamma _4}h^{\gamma _5})$. Then, we have

    $$\begin{aligned} e(z_1,\hat{g})\cdot e(r_1,\hat{h})&=(f,\hat{g}_{1}) \cdot (g,\hat{g}_{2}),\\ e(z_2,\hat{g})\cdot e(r_2,\hat{h})&=(g,\hat{g}_{4}) \cdot (h,\hat{g}_{5}). \end{aligned}$$

  • 4. Define the private key as $\mathsf {SK}=\alpha \in \mathbb {Z}_p$ and erase $\mathsf {tk}$. The public key $\mathsf {PK}\in \mathbb {G}^{11} \times \hat{\mathbb {G}}^{16}$ is defined to be

    $$\begin{aligned} \mathsf {PK}&= \bigl ( f, ~g, ~ h, ~\varvec{{u}}_1, ~\varvec{{u}}_2, ~z_1,~r_1,~r_2, ~z_2 , ~\hat{g}, ~\hat{h}, ~\varvec{\hat{u}}_1, ~\varvec{\hat{u}}_2, ~\{\hat{g}_j \}_{j=1}^5 \bigr ) . \end{aligned}$$

• $\varvec{\mathsf {Encrypt}(\mathsf {PK},M)}{} \mathbf :$ To encrypt $M \in \mathbb {G}$, conduct the following steps:

  • 1. Pick $\theta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute $(c_0,c_1,c_2)=(f^\theta ,g^\theta ,M\!\cdot \! h^\theta )$.

  • 2. Define the bit $b=1$ and set $G=g^b\in \mathbb {G}$ and $\hat{g}^b\in \hat{\mathbb {G}}$. Prove that

    $$\begin{aligned} e(\boxed {G},\hat{g})&= e(g,\boxed {\hat{g}^b})&e(\boxed {G},\hat{g}/ \boxed {\hat{g}^b})&= 1_{\mathbb {G}_T}. \end{aligned}$$

    (11)

    Namely, compute commitments to $G=g^b$ (resp. $\hat{g}^b$), which are obtained as $C_G=(1,G) \cdot \varvec{u}_1^{r_g} \cdot \varvec{u}_2^{s_g}$ (resp. $\hat{C}_b= (1,\hat{g}^{b}) \cdot \varvec{\hat{u}}_1^{ r_b} \cdot \varvec{\hat{u}}_2^{ s_b}$), for random $r_g,s_g,r_b,s_b\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. Let $\pi _G\in \mathbb {G}^2\times \hat{\mathbb {G}}^2$ and $\pi _{bit}\in \mathbb {G}^4\times \hat{\mathbb {G}}^4$ be the proof elements for relations (11).

  • 3. Define $(\varTheta _0,\varTheta _1,\varTheta _2)=(c_0^b,c_1^b,c_2^b)$ and prove that⁴

    $$\begin{aligned} e(\boxed {\varTheta _1},\hat{g})&= e(c_1,\boxed {\hat{g}^b})&e(\boxed {\varTheta _2},\hat{g})&= e(c_2,\boxed {\hat{g}^b}) . \end{aligned}$$

    (12)

    More precisely, compute commitments to $\varTheta _i$ as $C_i=(1,\varTheta _i) \cdot \varvec{u}_1^{\bar{r}_{i}} \cdot \varvec{u}_2^{\bar{s}_{i}}$, for each $i \in \{0,1,2\}$, and for random $\bar{r}_{i},\bar{s}_{i}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. The corresponding proof elements $\pi _1,\pi _2$ both live in $\mathbb {G}^2\times \hat{\mathbb {G}}^2$.

  • 4. Derive a QA-NIZK proof $(z,r)=(z_1^{\theta },r_1^\theta )$ that $\varvec{v}:=\varvec{v}_1^\theta \in \mathbb {G}^5$ belongs to $\mathsf {span}\langle \varvec{v}_1,\varvec{v}_2\rangle$. Since $b=1$, we have

    $$\varvec{v}=(\varvec{v}_1^\theta )^b \cdot (\varvec{v}_2^\theta )^{1-b}=(c_0^b,c_1^b,1,1,1)=(c_0^b,c_1^b,g^{1-b},c_1^{1-b},c_2^{1-b}),$$

    which allows generating a NIWI proof $\pi _{enc}\in \hat{\mathbb {G}}^2$ that $(z,r,\varTheta _0,\varTheta _1,\varTheta _2,g^b)$ satisfy

    $$\begin{aligned} \begin{aligned} e(\boxed {z},\hat{g}) \cdot e(\boxed {r},\hat{h})&= e(\boxed {\varTheta _0},\hat{g}_1) \cdot e(\boxed {\varTheta _1},\hat{g}_2) \cdot e(g/\boxed {g^b},\hat{g}_3) \\&\cdot e(c_1/\boxed {\varTheta _1},\hat{g}_4) \cdot e(c_2/\boxed {\varTheta _2},\hat{g}_5). \end{aligned} \end{aligned}$$

    (13)

    together with the Groth-Sahai commitments $C_{z},C_{r}\in \mathbb {G}^2$ of $z,r\in \mathbb {G}$.

  • 5. To enable re-randomization, define $H=h^b$ and $F=f^b$ and compute Groth-Sahai commitments to H and F as $C_H=(1,h^b) \cdot \varvec{u_1}^{r_h} \cdot \varvec{u_2}^{s_h}\in \mathbb {G}^2$ and $C_F=(1,f^b) \cdot \varvec{u_1}^{r_f} \cdot \varvec{u_2}^{s_f}\in \mathbb {G}^2$ for random $r_h,r_f,s_h,s_f\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. Then, generate a NIWI proof $\pi _H\in \mathbb {G}^2\times \hat{\mathbb {G}}^2$ that

    $$ e(\boxed {H},\hat{g}) = e(h,\boxed {\hat{g}^b}).$$

  • 6. Derive a QA-NIZK argument $(z_{rand},r_{rand})=(z_1^b \cdot z_2^{1-b},r_1^b \cdot r_2^{1-b})$ that $\varvec{w}:=v_1^b \cdot v_2^{1-b}$ belongs to . Since $\varvec{w}=(f^b,g^b,1,g^{1-b},h^{1-b})$, generate a proof $\pi _{rand}\in \hat{\mathbb {G}}^2$ that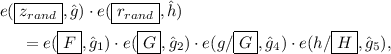

    

    together with the commitments $C_{z_{rand}},C_{r_{rand}}\in \mathbb {G}^2$.

  Return the ciphertext $\varvec{c}=(c_1,c_2,\pi _\mathsf {Enc},\pi _\mathsf {Rand})$ of $\mathbb {G}^{34}\times \hat{\mathbb {G}}^{18}$ where,

  $$\begin{aligned} \pi _\mathsf {Enc}= & {} (C_G,\hat{C}_b,\pi _G,\pi _{bit}, C_0,C_1,C_2,\pi _1,\pi _2,C_z,C_r,\pi _{enc}) ,\\ \pi _\mathsf {Rand}= & {} (C_H,\pi _H,C_F, C_{z_{rand}},C_{r_{rand}}, \pi _{rand}) . \end{aligned}$$

• $\varvec{\mathsf {ReRand}(\mathsf {PK},c)}{} \mathbf :$ Parse $\varvec{c}=(c_1,c_2,\pi _\mathsf {Enc},\pi _\mathsf {Rand})$ as above and do the following:

  • 1. Pick $\theta '\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$ and compute $(c_1',c_2')=(c_1\!\cdot \! g^{\theta '},c_2\!\cdot \! h^{\theta '})$.

  • 2. Update⁵ the commitments $C_0,C_1,C_2$ and the proofs $\pi _1,\pi _2$ of relations (12) according to the update of the constants $c_1,c_2$ into $c_1',c_2'$. Namely, compute $(C_0',C_1',C_2')= (C_0\cdot C_F^{\theta '},C_1\cdot C_G^{\theta '},C_2\cdot C_H^{\theta '})$ as well as $\pi _1'=\pi _1 \cdot \pi _G^{\theta '}$ and $\pi _2'=\pi _2 \cdot \pi _H^{\theta '}$.

  • 2. Update⁶ $C_z,C_r$ and the NIWI proof $\pi _{enc}$ for relation (13). Namely, compute $C_z'=C_z\cdot C_{z_{rand}}^{\theta '}$ and $C_r'=C_r\cdot C_{r_{rand}}^{\theta '}$ as well as $\pi _{enc}'=\pi _{enc}\cdot \pi _{rand}^{\theta '}$. We should have

    $$\begin{aligned} \varTheta _0'=f^{b \cdot (\theta +\theta ')}, \qquad \varTheta _1'=g^{b \cdot (\theta +\theta ')}, \qquad \varTheta _2'=M^b\cdot h^{b \cdot (\theta +\theta ')}, \end{aligned}$$

    while $C_z'$ and $C_r'$ are now commitments to

    $$\begin{aligned} z'= & {} z\cdot z_{rand}^{\theta '}=(z_1^b \cdot z_2^{1-b})^{\theta +\theta '} \\ r'= & {} r\cdot r_{rand}^{\theta '}=(r_1^b \cdot r_2^{1-b})^{\theta +\theta '}. \end{aligned}$$

  • 3. Re-randomize $C_G,\hat{C}_b,C_0',C_1',C_2', C_z',C_r',C_H$, $C_F$, $C_{z_{rand}},C_{r_{rand}}$ and the proofs $\pi _G,\pi _{bit},\pi _1',\pi _2',\pi _{enc}',\pi _H,\pi _{rand}$ so as to get $C_G'',\hat{C}_b'',C_0'',C_1'',C_2'',C_z''$, $C_r'',C_H'',C_F'', C_{z_{rand}}'',C_{r_{rand}}''$ and $\pi _G'',\pi _{bit}''$, $\pi _1'',\pi _2''$, $\pi _{enc}'',\pi _H'',\pi _{rand}''$.

  Return the ciphertext $\varvec{c'}=(c_1',c_2',\pi _\mathsf {Enc}',\pi _\mathsf {Rand}')$ where,

  $$\begin{aligned} \pi _\mathsf {Enc}'= & {} (C_G'',\hat{C}_b'',\pi _G'',\pi _{bit}'', C_0'',C_1'',C_2'',\pi _1'',\pi _2'',C_z'',C_r'',\pi _{enc}'') ,\\ \pi _\mathsf {Rand}'= & {} (C_H'',\pi _H'',C_F'',C_{z_{rand}}'', C_{r_{rand}}'', \pi _{rand}'') . \end{aligned}$$

• $\varvec{\mathsf {Decrypt}(\mathsf {SK},c)}{} \mathbf :$ Parse $\varvec{c}=(c_1,c_2,\pi _\mathsf {Enc},\pi _\mathsf {Rand})$ as above and check whether all the proofs are valid. If not, output $\bot$, and otherwise return $M=c_1/c_2^{\alpha }$.

As far as efficiency goes, ciphertexts consist of 34 elements of $\mathbb {G}$ and 18 elements of $\hat{\mathbb {G}}$. Correctness follows from the correctness of the Groth-Sahai proofs and the correctness of the underlying LHSP signatures.

We show that the above scheme, denoted by $\mathcal {E}$, is statistically re-randomizable even for adversarially chosen ciphertexts, as defined in  [47] (with the difference that the randomization algorithm uses the public key).

Theorem 3

The above scheme $\mathcal {E}$ provides statistical unlinkability.

Proof

We only consider valid adversarially-generated ciphertext $\varvec{c}$ since the validity of ciphertext is efficiently recognizable. Given $\varvec{c}\leftarrow \mathcal {A}(\mathsf {PK})$, we define two distributions on ciphertexts as in the definition of unlikability. The first distribution generates $\varvec{c}'\leftarrow \mathsf {Encrypt}(\mathsf {PK},\mathsf {Decrypt}(\mathsf {SK},\varvec{c}))$ while the second distribution generates $\varvec{c}'\leftarrow \mathsf {ReRand}(\mathsf {PK},\varvec{c})$. Clearly if we write $\varvec{c'}=(c_1',c_2',\pi _\mathsf {Enc}',\pi _\mathsf {Rand}')$, the first distribution generates $(c_1,c_2)$ as a fresh ElGamal ciphertext and the perfectly NIWI proofs $(\pi _\mathsf {Enc}',\pi _\mathsf {Rand}')$ are completely random subject to the verification of all the pairing product equations detailed in the encryption algorithm of $\mathcal {E}$. Indeed, the key generation algorithm sets the CRSes $(\varvec{u}_1,\varvec{u}_2)$ and $(\varvec{\hat{u}}_1,\varvec{\hat{u}}_2)$ as random elements as in the perfect NIWI setting of the Groth-Sahai proof system [36]. For the same reason, $\mathsf {ReRand}$ transforms $\varvec{c}$ into a perfectly re-randomized ciphertext $\varvec{c}'$. Indeed, step 1 leads to a perfectly re-randomized ElGamal ciphertext $(c_1',c_2')=(c_1,c_2)\cdot (g,h)^{\theta '}$. Steps 2 and 3 adapt the Groth-Sahai commitments and proofs with respect to the constant $(c_1',c_2')$ to keep the validity of the ciphertext. Finally, step 4 completely re-randomizes these commitments and proofs and the NIWI setting ensures that the resulting $(\pi _\mathsf {Enc}',\pi _\mathsf {Rand}')$ are uniformly re-distributed among all the valid proofs satisfying the same pairing product equations with the constant $(c_1',c_2')$. Consequently, $\varvec{c'}$ is distributed as a fresh ciphertext of $\mathsf {Decrypt}(\mathsf {SK},\varvec{c})$ even if the adversary tried to put some subliminal information in $\varvec{c}$.    $\square$

Next, we show that $\mathcal {E}$ is secure against a Replayable Chosen-Ciphertext Attack (RCCA) in the sense of [22].

Theorem 4

The above scheme $\mathcal {E}$ provides RCCA security under the SXDH assumption. More precisely, we have $\mathbf {Adv}_{\mathcal {A}, \mathcal {E}}^{\mathrm {RCCA}} (\lambda ) \le 4 \times \mathbf {Adv}^{\mathrm {SXDH}}(\lambda ) + q_d \times 2^{-\lambda }$.

Proof

The proof uses a sequence of games starting with the real game and ending with a game where even an unbounded adversary has no advantage. For each i, $S_i$ is the event that the challenger outputs 1 in Game i meaning that the adversary rightly guesses which message is encrypted in the challenge ciphertext. We assume that security parameter $\lambda$ is given in each game.

• Game 1: This is the real attack game where the adversary chooses $M_0$ and $M_1$ and obtains a challenge ciphertext $\varvec{c}^\star$ as a real encryption of $M_\beta$, for some $\beta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\{0,1\}$ chosen by the challenger, in the challenge phase. We recall that the adversary may query the decryption of any ciphertext. In the post-challenge phase, when the challenger uses $\mathsf {SK}$ to faithfully reply to the decryption queries it runs the decryption algorithm and returns $\bot$ if the (public) verification fails. If the decryption returns M, the challenger sends back M except if $M\in \{M_0,M_1\}$, in which case “replay” is returned. We denote by $S_1$ the event that the adversary outputs $\beta '=\beta$, which causes the challenger to output 1.

• Game 2: This game is like Game 1 except that, in the challenge phase, the challenge ciphertext $\varvec{c}^\star =(c_1^\star ,c_2^\star ,\pi _{\mathsf {Enc}}^\star , \pi _{\mathsf {Rand}}^\star )$, the proofs

  $$\begin{aligned} \pi _\mathsf {Enc}^\star= & {} (C_G^\star ,\hat{C}_b^\star ,\pi _G^\star , \pi _{bit}^\star ,C_0^\star ,C_1^\star ,C_2^\star , \pi _1^\star ,\pi _2^\star ,C_z^\star ,C_r^\star ,\pi _{enc}^\star ) ,\\ \pi _\mathsf {Rand}^\star= & {} (C_H^\star ,\pi _H^\star ,C_F^\star , C_{z_{rand}}^\star ,C_{r_{rand}}^\star , \pi _{rand}^\star ) . \end{aligned}$$

  are obtained by computing $\pi _{\mathsf {Enc}}^\star ,\pi _{\mathsf {Rand}}^\star$ as simulated proofs using the trapdoor $\mathsf {tk}=\{(\chi _{i},\gamma _{i})\}_{i=1}^5$. This is achieved by computing $({\tilde{z}},{\tilde{r}}) \in \mathbb {G}^2$ as a linearly homomoprhic signature on the vector $\varvec{v}^\star =(1_\mathbb {G},1_\mathbb {G},g,c_1^\star ,c_2^\star )$. In step 2 of the encryption algorithm, the challenger thus sets $b=0$, and conducts the remaining steps of the encryption algorithm except for $({\tilde{z}},{\tilde{r}})$ at step 4. Thanks to the perfect witness indistinguishability of Groth-Sahai proofs (recall that $(\varvec{u}_1,\varvec{u}_2)$ and $(\hat{\varvec{u}}_1,\hat{\varvec{u}}_2)$ form CRSes for the perfect NIWI setting in the real game), the NIWI proofs $\pi _{\mathsf {Enc}}^\star ,\pi _{\mathsf {Rand}}^\star$ have exactly the same distribution as in Game 1 and $\mathcal {A}$’s view remains unchanged. We have ${\text {Pr}}[S_2]={\text {Pr}}[S_1]$. Note that $\mathsf {tk}$ is also used to generate the LHSP signatures on the vectors $\varvec{v}_1,\varvec{v}_2$ of the public key.

• Game 3: In this game, we modify the distribution of the public key. In step 2 of the key generation algorithm, we choose $\varvec{u}_2=\varvec{u}_1^{\xi }$ and $\varvec{\hat{u}}_2=\varvec{\hat{u}}_1^{\zeta }$, with $\xi ,\zeta \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$, instead of choosing $\varvec{u}_2\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}^2$ and $\varvec{\hat{u}}_2\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}^2$ uniformly. Under the SXDH assumption, this change should not significantly affect $\mathcal {A}$’s behavior and we have $|{\text {Pr}}[S_3]-{\text {Pr}}[S_2]| \le 2 \times \mathbf {Adv}^{\mathrm {SXDH}}(\lambda )$. Note that $\big ( \varvec{u}_1,\varvec{u}_2)$ and $(\varvec{\hat{u}}_1, \varvec{\hat{u}}_2 \big )$ now form perfectly sound CRSes.

• Game 4: We modify the decryption oracle. When the adversary $\mathcal {A}$ queries the decryption of $\varvec{c}=(c_1,c_2,\pi _{\mathsf {Enc}},\pi _{\mathsf {Rand}})$, the challenger parses the proofs as

  $$\begin{aligned} \pi _\mathsf {Enc}= & {} (C_G,\hat{C}_b,\pi _G,\pi _{bit}, C_0,C_1,C_2,\pi _1,\pi _2,C_z,C_r,\pi _{enc}) ,\\ \pi _\mathsf {Rand}= & {} (C_H,\pi _H,C_F, C_{z_{rand}},C_{r_{rand}}, \pi _{rand}) \end{aligned}$$

  and rejects $\varvec{c}$ if the proofs do not properly verify. Otherwise, instead of merely using the private key $\mathsf {SK}=\alpha$ to compute $M =c_1 / c_2^{\alpha }$ as in the real decryption algorithm, the challenger $\mathcal {B}$ uses the extraction trapdoor $\beta =\log _{u_{1,1}}(u_{1,2})$ of the Groth-Sahai CRS $(\varvec{u}_1,\varvec{u}_2)$, where $\varvec{u}_1=(u_{1,1},u_{1,2})$, to extract the witnesses $g^b$, (z, r) and $\varvec{v}=(\varTheta _0, \varTheta _1,g/g^b,c_1/\varTheta _1,c_2/\varTheta _2)$ from their commitments $C_G$, $C_{z },C_{r }$ and $\{C_i\}_{i=0}^2$ which are contained in $\pi _{\mathsf {Enc}}$. Then, the challenger uses $\mathsf {tk}=\{(\chi _i,\gamma _i)\}_{i=1}^5$ to compute an LHSP signatures on $\varvec{v}=(v_1,v_2,v_3,v_4,v_5)$

  $$\begin{aligned} z^\dagger&= \prod \nolimits _{i=1}^5 v_i^{\chi _i} ,&\qquad r^\dagger&= \prod \nolimits _{i=1}^5 v_i^{\gamma _i} , \end{aligned}$$

  and rejects the ciphertext in the event that $z^\dagger \ne z$. If $\varvec{c}$ is not rejected, $\mathcal {B}$ computes $M=c_1 / c_2^{\alpha }$. If $M \in \{M_0,M_1\}$ in the post-challenge phase, $\mathcal {B}$ returns “replay” as in the actual RCCA game. Otherwise, it returns M to $\mathcal {A}$. It is easy to see that, if $\mathcal {B}$ rejects a ciphertext that would not have been rejected in Game 3, then $\mathcal {B}$ is able to solve the DP problem. This is because $(\varvec{u}_1,\varvec{u}_2)$ and $(\varvec{\hat{u}}_1,\varvec{\hat{u}}_2)$ are perfectly sound Groth-Sahai CRSes and the validity of the proof $\pi _{enc}$ implies that (z, r) would be another valid homomorphic signature on $\varvec{v} \in \mathbb {G}^5$ than the one that $\mathcal {B}$ can compute. Therefore, this would provide $\mathcal {B}$ with two distinct linearly homomorphic signatures on the same vector and allow $\mathcal {B}$ to solve an instance of the DP problem as done in the proof of [42, Theorem 1]. We thus have $|{\text {Pr}}[S_4]-{\text {Pr}}[S_3]| \le \mathbf {Adv}_{\mathcal {B}}^{\mathrm {DP}}(\lambda )$.

• Game 5: We modify the decryption oracle in all pre-challenge and post-challenge decryption queries $\varvec{c}=(c_1,c_2,\pi _{\mathsf {Enc}},\pi _{\mathsf {Rand}})$ to avoid the use of the secret key $\mathsf {SK}=\alpha =\log _g h$. This change allows modifying the generation of the public element $h=g^xf^y$ with uniformly sampled $x,y\mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$.

  In the case of pre-challenge queries, if the commitment $C_G$ contained in $\pi _{\mathsf {Enc}}$ opens to $g^b=1$ (meaning that $b=0$), $\mathcal {B}$ rejects the ciphertext. In the case of post-challenge queries $\varvec{c}$, if $g^b=1$ (i.e., $b=0$) and the ciphertext is not rejected by the rules of Game 4, the challenger $\mathcal {B}$ returns “replay” without extracting the encrypted message. Additionally, in all decryption queries, if $g^b=g$ (namely, $b=1$), $\mathcal {B}$ computes $M:=c_2 \cdot c_1^{-x}\cdot \varTheta _0^{-y}$. Before the challenge phase, it always outputs M. In the case of post-challenge queries, $\mathcal {B}$ returns “replay” if $M \in \{M_0,M_1\}$ and M otherwise. We now analyze the adversary’s view in this game under the light of the unforgeability of LHSP signatures:

  Before the challenge: It is easy to see that the probability to reject a ciphertext that would not have been rejected in Game 4 is statistically negligible. This follows from the fact that, from the public key, $\mathcal {A}$ has only obtained linearly homomorphic signatures on $(\varvec{v}_1,\varvec{v}_2)$, the span of which clearly does not contain $\varvec{v}=(\varTheta _0,\varTheta _1,g/g^b,C_1/\varTheta _1,C_2/\varTheta _2)$ when $g/g^b\ne 1_\mathbb {G}$. Therefore, pre-challenge decryption queries for which $g^b=1$ are rejected in Game 4 except in the event that $z^\dagger =z$. This event only occurs with probability at most 1 / p at each such query since $z^\dagger$ (as computed from $\varvec{v}$ using $\mathsf {tk}$) is completely unpredictable from the public key. This follows from the fact that honestly-generated LHSP signatures are deterministic functions of $\mathsf {tk}$ while there exist exponentially many valid signatures on each vector of messages. The signing key $\mathsf {tk}$ retains sufficient entropy to make it statistically impossible to predict the honestly-generated signature on a vector outside the span of $(\varvec{v}_1,\varvec{v}_2)$, which are given in $\mathsf {PK}$.

  After the challenge: First, the perfect soundness of the Groth-Sahai proofs $\{\varvec{\pi }_{i}\}_{i=1}^2$ for relation (12) allows extracting witnesses that satisfy $\varTheta _i=c_i^b$, for each $i \in \{1,2 \}$, and then $\varvec{v}=(\varTheta _0,c_1^{b},g^{1-b},c_1^{1-b},c_2^{1-b})$. The difference with pre-challenge queries is that the adversary is also given information on the signature on $\varvec{v}^\star$ from the challenge ciphertext $\varvec{c}^\star$. Hence, in post-challenge queries, LHSP signatures must be in $\mathsf {span}\langle \varvec{v}_1,\varvec{v}_2,\varvec{v}^\star \rangle$. Secondly, we consider the two cases $b \in \{0,1 \}$:

  • If $g^b=1_\mathbb {G}$ (i.e., $b=0$), we have $\varvec{v}=(\varTheta _0,1_\mathbb {G},g,c_1,c_2)$. Since $\varvec{c}$ was not rejected, the vector $\varvec{v}$ must be in $\mathsf {span}\langle \varvec{v}_2 , (1_\mathbb {G},1_\mathbb {G},g,c_1^\star ,c_2^\star ) \rangle$ (i.e. without $\varvec{v}_1$ because the second component of $\varvec{v}$ is $1_\mathbb {G}$) except with probability 1 / p. Indeed, otherwise, the same argument as in Game 4 shows that $\varvec{c}$ can only avoid rejection if it contains a commitment $C_z$ to $z^\dagger =z$ and we argued that it is statistically independent of $\mathcal {A}$’s view for vectors outside $\mathsf {span}\langle \varvec{v}_1,\varvec{v}_2, (1_\mathbb {G},1_\mathbb {G},g,c_1^\star ,c_2^\star ) \rangle$. This means that $\varvec{v}=\varvec{v}_0 \cdot \varvec{v}_2^{\theta }$, for some $\theta$, where $\varvec{v}_0:=(1_\mathbb {G},1_\mathbb {G},g,1_\mathbb {G},M_\beta )$. Said otherwise, the queried ciphertext is a randomization of the challenge ciphertext, so that $\mathcal {B}$ can rightfully return “replay” without changing the view of $\mathcal {A}$.

  • If $g^b=g$ (i.e., $b=1$), we have $\varvec{v}=(\varTheta _0,c_1,1_\mathbb {G}, 1_\mathbb {G},1_\mathbb {G})$. Since $\varvec{c}$ was not rejected, $\varvec{v}$ must be in the span of $\varvec{v}_1$ except with probability 1 / p (via the same argument on the event $z^\dagger =z$ as above). With overwhelming probability $(p-1)/p$, we thus have $\varTheta _0=f^{\log _g c_1}$, which implies that

    $$\begin{aligned} c_1^x \cdot \varTheta _0^{y}=h^{\log _g c_1} = c_1^\alpha \end{aligned}$$

    if $\mathsf {SK} :=\alpha = x + \log _g(f) \cdot y$ is the secret key that underlies $h=g^x f^y$. It follows that $\mathcal {A}$ obtains the same response as in Game 4.

  At each decryption query, $\mathcal {B}$’s response deviates from its response in Game 4 with probability at most 1 / p. A union bound over all decryption queries leads to $|{\text {Pr}}[S_5]-{\text {Pr}}[S_4]| \le q_d/p$ if $q_d$ is the number of decryption queries.

• Game 6: We modify the distribution of the challenge ciphertext. Namely, we choose $(c_0^\star ,c_1^\star ,c_2^\star )$ as a completely random triple $(c_0^\star ,c_1^\star ,c_2^\star ) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {G}^3$ instead of a well-formed tuple $(1_\mathbb {G},1_\mathbb {G},M_\beta )\cdot (f,g,h)^{\theta ^\star }$, for a random $\theta ^\star \mathop {\leftarrow }\limits ^{{\scriptscriptstyle R}}\mathbb {Z}_p$. Under the SXDH assumption, this modification has no noticeable impact on $\mathcal {A}$’s output distribution since, given a DDH$_1$ instance $(g,f,g^a,f^{a+c})$ (where either $c=0$ or $c \in _R \mathbb {Z}_p$), it is sufficient to define $h=g^x \cdot f^y$, as previously, and set $c_0^\star =f^{a+c}$, $c_1^\star =g^a$ and $c_2^\star = M_\beta \cdot (g^a)^x \cdot (f^{a+c})^y$ during the challenge phase. At this point, $(g^a)^x \cdot (f^{a+c})^y=h^a \cdot f^{ cy}$ and we obtain the inequality $|{\text {Pr}}[S_6]-{\text {Pr}}[S_5]|\le \mathbf {Adv}^{\mathrm {SXDH}}(\lambda ) .$

In Game 6, no information about $\beta \in \{0,1\}$ is leaked anywhere, so that we get $\Pr [S_6]=1/2$. Since the SXDH assumption implies the DP assumption, we thus find the following advantage

$$\begin{aligned} \vert \Pr [S_1]-1/2&\vert \le 4 \times \mathbf {Adv}^{\mathrm {SXDH}}(\lambda ) + q_d \times 2^{-\lambda } , \end{aligned}$$

which concludes the proof.    $\square$