On the Security of Supersingular Isogeny Cryptosystems

Abstract

We study cryptosystems based on supersingular isogenies. This is an active area of research in post-quantum cryptography. Our first contribution is to give a very powerful active attack on the supersingular isogeny encryption scheme. This attack can only be prevented by using a (relatively expensive) countermeasure. Our second contribution is to show that the security of all schemes of this type depends on the difficulty of computing the endomorphism ring of a supersingular elliptic curve. This result gives significant insight into the difficulty of the isogeny problem that underlies the security of these schemes. Our third contribution is to give a reduction that uses partial knowledge of shared keys to determine an entire shared key. This can be used to retrieve the secret key, given information leaked from a side-channel attack on the key exchange protocol. A corollary of this work is the first bit security result for the supersingular isogeny key exchange: Computing any component of the j-invariant is as hard as computing the whole j-invariant.

Our paper therefore provides an improved understanding of the security of these cryptosystems. We stress that our work does not imply that these systems are insecure, or that they should not be used. However, it highlights that implementations of these schemes will need to take account of the risks associated with various active and side-channel attacks.

Keywords

1 Introduction

In 2011, Jao and De Feo [17] introduced the supersingular isogeny Diffie–Hellman key exchange protocol as a candidate for a post-quantum key exchange. The security of this scheme is based on so-called supersingular isogeny problems. Similar problems had appeared in a previous hash function construction by Charles–Lauter–Goren [6], and were subsequently used to build other cryptographic functions such as public-key encryption, undeniable signatures and designated verifier signatures [13, 18, 34]. As with classical Diffie–Hellman, the basic version of the key exchange protocol uses ephemeral elements, but the encryption scheme and some of the more sophisticated applications use static values for at least one element.

The idea behind the supersingular isogeny key exchange protocol is largely based on the isogeny protocol for ordinary elliptic curves proposed in [29]. However, there is a (subexponential) quantum algorithm [7] to break the system in the ordinary case (in part since the ordinary case is based on commutative ring theory). In contrast, the case of supersingular curves is non-commutative and seems to be a promising candidate for a post-quantum-secure system [2].

One particular feature of Jao and De Feo’s protocols compared to other schemes based on isogeny problems is the publication of auxiliary points, which are used to get around the difficulties of non-commutativity. These auxiliary points open the door to active attacks on the encryption scheme (or key exchange where one party uses a static key). To be precise, one could try to perform some kind of “small subgroup” or “invalid curve” attacks such as have been proposed for DLP cryptosystems in the past [8, 23]. The possibility of active attacks has been mentioned by Kirkwood, Lackey, McVey, Motley, Solinas and Tuller [20] and Costello, Longa and Naehrig [9]. Both papers discuss “validation” techniques that are designed to prevent such attacks, but neither paper demonstrates all the details of the attacks. Some of the validation methods discussed in [9] use pairings, but we observe a stronger property of pairings that makes detecting such attacks easier. Note that [9] is only concerned with ephemeral Diffie–Hellman key exchange, and so their scheme is not subject to attacks on static keys.

The first contribution of our paper (Sect. 3) is to describe a general active attack against the static-key variant of the protocol. Our attack allows to recover the whole static key with the minimum number of queries and negligible computation. Our attack is not prevented by any of the validation techniques introduced in [9], nor by our stronger validation technique using pairings. Our attack is prevented by the method in [20] (see Sect. 2.5), but this adds significant cost to the running time of the system.

The second contribution of our paper (Sect. 4) is to explore the security of the schemes assuming there is an efficient algorithm to compute the endomorphism ring of a supersingular elliptic curve. It is known that computing endomorphism rings of supersingular curves is equivalent to computing isogenies between supersingular elliptic curves, and it is believed that both these problems are hard [6, 17]. But previous techniques were not sufficient to break the Jao–De Feo cryptosystems if the endomorphism ring was known (the resulting isogeny would have too high degree). We present a new method to find an isogeny of the correct degree in the special case of the isogeny problem arising in these cryptosystems. This shows that the hardness of computing endomorphism rings is necessary for the security of any cryptosystem based on the Jao and De Feo concept (it is not restricted to ElGamal or key exchange, and requires no interaction with a user). We give heuristic and experimental evidence that our algorithm is practical.

Our third contribution (Sect. 5) is to define and analyse an isogeny analogue of the hidden number problem. Our main result is an algorithm to compute the j-invariant of a “hidden” elliptic curve given partial information of the j-invariants of “nearby” curves. We believe that, as with the original hidden number problem in finite fields, this result will have applications of two flavours. On the one hand, our theorem shows how to mount a type of side-channel attack on the key exchange protocol: An attacker can compute the shared secret with high probability if they can get partial information of the shared key during “correlated” executions of the key exchange protocol. On the other hand, the result gives the first bit security result for the supersingular isogeny key exchange: Computing one component of the finite field representation of the j-invariant is as hard as computing the whole j-invariant. A consequence of this result is that it is secure for an implementation to use only one component of the j-invariant of the shared key.

The paper is organised as follows. Section 2 quickly reviews the Jao–De Feo cryptosystem and other preliminaries. Our results and discussions are given in Sects. 3, 4 and 5. In Sect. 6 we present our conclusions.

2 Preliminaries

2.1 Supersingular Elliptic Curves and Isogenies

Fix a prime p and a prime power $q=p^k$ and let $E_1$ and $E_2$ be elliptic curves defined over $\mathbb {F}_q$. An isogeny between $E_1$ and $E_2$ is a non-constant morphism defined over $\mathbb {F}_q$ that sends the identity in $E_1$ to the identity in $E_2$. Then $\phi$ is a group homomorphism from $E_1(\overline{\mathbb {F}}_q)$ to $E_2(\overline{\mathbb {F}}_q)$ [30, III.4.8]. The degree of $\phi$ as an isogeny is equal to the degree of $\phi$ as a morphism. In addition, if $\phi$ is separable, then $\deg \phi =\#\ker \phi$ [30, III.4.10]. In this case, we say that $E_1$ and $E_2$ are isogeneous.

The isogeny is defined by its kernel in the sense that for every finite subgroup $G\subset E_1$, there is a unique $E_2$ (up to isomorphism) and a separable isogeny $\phi :E_1\rightarrow E_2$ such that $\ker \phi =G$ [30, III.4.12]. We sometimes write $E_1 / G$ for $E_2$. Vélu [32] gave an algorithm to construct an isogeny given a finite subgroup. Notice that the total number of distinct isogenies with degree $\ell$, which we now call $\ell$-isogenies, is equal to the number of distinct subgroups of $E_1$ of order $\ell$. For every prime $\ell$ not dividing p, there are $\ell +1$ isogenies of degree $\ell$ since the group of $\ell$-torsion points form a subgroup $E[\ell ]=\mathbb {Z}/\ell \mathbb {Z}\oplus \mathbb {Z}/\ell \mathbb {Z}$ [30, III.6.4].

If $G = \langle P \rangle \subset E_1$ is a cyclic group of order $\ell ^n$ then the isogeny with kernel G factors as a chain of isogenies

$$ E_1 \rightarrow E_2 \rightarrow \cdots \rightarrow E_{\ell + 1} $$

such that each $\phi _i : E_i \rightarrow E_{i+1}$ is an isogeny of degree $\ell$ with kernel in $E_i[ \ell ]$. We will use the following notation

$$\begin{aligned} G_1&=G,\quad G_{i+1}=\phi _i(G_i),\\ P_1&=P,\quad P_{i+1}=\phi _i(P_i). \end{aligned}$$

Now, note that $\phi _i( G_i ) = \langle \phi _i(P_i) \rangle \subseteq E_{i+1}[ \ell ^{n-i} ]$. The kernel of $\phi _1$ is $\langle [\ell ^{n-1}] P \rangle$ and for $i > 1$ the kernel of $\phi _i$ is $\langle [\ell ^{n-i} ]\phi _{i-1}(P_{i-1}) \rangle$.

For every $\phi : E_1\rightarrow E_2$, there exists an isogeny $\hat{\phi }:E_2\rightarrow E_1$ such that

$$\begin{aligned} \phi \circ \hat{\phi }=[\deg \phi ]=\hat{\phi }\circ \phi . \end{aligned}$$

We call $\hat{\phi }$ the dual isogeny of $\phi$. This allows us to define an equivalence relation on elliptic curves that are isogenous.

If we have a pair of isogenies $\phi :E_1\rightarrow E_2$ and $\psi :E_2\rightarrow E_1$ such that $\phi \circ \psi$ and $\psi \circ \phi$ are the identity, then we say that $\phi$ and $\psi$ are isomorphisms. We also then say that $E_1$ and $E_2$ are isomorphic curves. This naturally defines an equivalence relation and the isomorphism classes can be represented by the j-invariants [30, III.1.4(b)].

Isogenies that have the same domain and range are known as endomorphisms. For an elliptic curve E, we write ${{\mathrm{End}}}(E)$ for the set of all endomorphisms $\phi :E\rightarrow E$ together with the zero morphism. In fact, we can define addition and multiplication on endomorphisms by setting $(\phi +\psi )(P)=\phi (P)+\psi (P)$ and $(\phi \cdot \psi )(P)=\phi (\psi (P))$ for all $\phi ,\psi \in {{\mathrm{End}}}(E)$ and $P\in E$. This gives it a ring structure. The multiplication-by-n maps are examples of endomorphisms and so $\mathbb {Z}\hookrightarrow {{\mathrm{End}}}(E)$. In fact, over a finite field, ${{\mathrm{End}}}(E)$ is isomorphic to either a maximal order in a quaternion algebra or to an order in an imaginary quadratic field [30, III.9.3]. In the former case, we say that E is supersingular, otherwise, we say that it is ordinary.

An elliptic curve $E / \mathbb {F}_{p^k}$ is supersingular if and only if $|E( \mathbb {F}_{p^k} )| \equiv 1 \pmod {p}$. It is known that there are approximately p / 12 isomorphism classes of supersingular elliptic curves E over $\overline{\mathbb {F}}_p$ [30, V.4.1]. It is also known that every supersingular curve is isomorphic to one defined over $\mathbb {F}_{p^2}$ [30, V.3.1(a)(iii)]. A theorem of Tate states that $E_1$ and $E_2$ are isogenous over $\mathbb {F}_{p^k}$ if and only if $|E_1(\mathbb {F}_{p^k})|=|E_2(\mathbb {F}_{p^k})|$ [31, Sect. 3].

2.2 Hard Problem Candidates Related to Isogenies

Starting from the work of Charles–Lauter–Goren [6] and later Jao–De Feo [17], several recent cryptosystems have been based on the computational hardness of computing isogenies between supersingular elliptic curves. The main problem in this area can be described as follows:

Definition 1 (Supersingular Isogeny Problem)

Given a finite field K and two supersingular elliptic curves $E_1,E_2$ defined over K such that $|E_1|=|E_2|$, compute an isogeny $\varphi :E_1\rightarrow E_2$.

We stress that this isogeny is not unique (in fact there are infinitely many of them without additional restrictions). Further, the most natural representations of an isogeny are either as a pair of rational maps or as a kernel, and both these representations generally require exponential space. However, one can also represent an isogeny of smooth degree as a composition of low degree isogenies, and this can be done in polynomial space. Hence the computational problem makes sense.

This problem has been studied in a number of previous works. The cryptanalysis of Charles–Lauter–Goren’s hash function requires to compute isogenies of degree $\ell ^e$ for some small, fixed prime $\ell$. Similarly, the Jao–De Feo schemes involve isogenies of the same form with an additional condition on e.

Another important problem in this area is the problem of computing the endomorphism ring of a given elliptic curve.

Definition 2 (Endomorphism Ring Computation)

Given an elliptic curve E defined over a finite field K, compute its endomorphism ring.

This problem was studied by Kohel [21]. In the supersingular case Kohel described a probabilistic algorithm running in time $\tilde{O}(p)$, where p is the characteristic of the field. This was later improved to $\tilde{O}(\sqrt{p})$ by Galbraith [15] using birthday paradox arguments. We remark that for some supersingular elliptic curves the problem is easy (for example when $j=0$), but the problem is believed to be hard on average.

Heuristically, one can turn an algorithm that computes isogenies into an algorithm that computes the full endomorphism ring of an elliptic curve; the reduction actually underlies Kohel’s algorithm.

It turns out that the converse is also true, at least heuristically. There is an equivalence of categories between the set of supersingular curves and the set of maximal orders of a quaternion algebra (see [12, 21, 22]). Given the endomorphism rings of the two elliptic curves, one can identify the corresponding maximal orders in the quaternion algebra, and then use techniques developed in [22] to compute paths between them in the quaternion algebra and translate these paths into isogeny paths.

The algorithm in [22] solves the quaternion algebra analog of the supersingular isogeny problem, which requires to compute an ideal with a smooth norm connecting two given maximal orders. However, the degree of the ideal returned by this algorithm is about $p^{7}$ in general and $p^{7/2}$ if one of the orders is special (a p-extremal order, as defined in [22]), whereas a degree about p is expected to suffice in general, and a degree about $p^{1/2}$ would be needed to break the Jao–De Feo cryptosystems. Here p is the characteristic of the field.

2.3 Jao–De Feo scheme

Key Exchange Protocol. There are three steps in the key exchange protocol: The set-up, the key exchange and the key derivation.

In the set-up, a prime of the form $p=2^{n}\cdot 3^{m}\cdot f-1$ is generated where f is small and $2^n\approx 3^m$ (more generally $p = \ell _A^n \ell _B^m f \pm 1$ where $\ell _A, \ell _B$ are small primes). A supersingular elliptic curve E over $\mathbb {F}_{p^2}$ is constructed, and linearly independent points $P_A,Q_A\in E[2^n]$ and $P_B,Q_B\in E[3^{m}]$ are chosen. Here “linearly independent” means that the group $\langle P_A, Q_A \rangle$ generated by $P_A$ and $Q_A$ has order $2^{2n}$, and similarly, $| \langle P_B, Q_B \rangle | = 3^{2m}$.

In the key exchange, Alice picks random integers $0 \le a_1, a_2 < 2^n$ (not both divisible by 2) and Bob picks random integers $0 \le b_1, b_2 < 3^m$ (not both divisible by 3). Alice and Bob compute

$$ G_A=\langle [a_1]P_A+[a_2]Q_A\rangle , \quad G_B=\langle [b_1]P_B+[b_2]Q_B\rangle $$

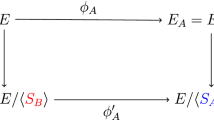
respectively. Using Vélu’s formulas [32], they will then be able to compute the isogenies $\phi _A$ and $\phi _B$ with respective kernels $G_A$ and $G_B$. They then compute $E_A=\phi _A(E) = E/G_A$, $\phi _A(P_B)$, $\phi _A(Q_B)$ and $E_B=\phi _B(E)= E/G_B$, $\phi _B(P_A)$, $\phi _B(Q_A)$ respectively. Their respective messages in the protocol will be

$$ (E_A,\phi _A(P_B),\phi _A(Q_B)), \quad (E_B,\phi _B(P_A),\phi _B(Q_A)). $$

Upon receipt of Bob’s message, to derive the shared key, Alice would compute

$$\begin{aligned} \langle [a_1]\phi _B(P_A)+[a_2]\phi _B(Q_A)\rangle =\langle \phi _B([a_1]P_A+[a_2]Q_A)\rangle =\phi _B(G_A). \end{aligned}$$

Alice then computes the isogeny from $E_B$, with kernel equal to this subgroup. Bob will perform a similar computation and the resulting isogeny will be generated by $G_A$ and $G_B$ (since the subgroups have a trivial intersection). The shared secret will be

$$\begin{aligned} E_{AB}:=E / \langle G_A, G_B \rangle = E_A / \langle \phi _A( G_B ) \rangle = E_B / \langle \phi _B( G_A ) \rangle . \end{aligned}$$

This can be summarised in the following diagram, where we use the notation from above.

The Jao–De Feo key exchange scheme originates from a similar scheme for ordinary elliptic curves proposed by Rostovtsev and Stolbunov [29]. The ordinary case is based on a commutative mathematical structure, however this structure enables a subexponential-time quantum algorithm [7] to break the system. On the other hand, the supersingular curves variant is based on a non-commutative structure and so it seems to be a promising candidate for a post-quantum-secure system. The auxiliary points included in the protocol messages allow Jao and De Feo to get around the difficulties of non-commutativity.

We stress that the isogeny problem involved here differs from a general one in several ways. On the one hand, the special primes used and the auxiliary points given to an attacker may make the supersingular isogeny problem easier than the general isogeny problem. On the other hand there is a very strong constraint imposed on the degree of the isogeny, and this might a priori make the problem harder; we discuss this issue in more detail in Sect. 4. We remark that our first and third results use the auxiliary points in essential ways. However the result of Sect. 4 does not use the auxiliary points and only uses the fact that the required isogeny has a strongly constrained degree.

Encryption Protocol. The public-key encryption scheme is constructed from the key exchange scheme with a few adaptations [13]. Namely, the shared secret would be used as a key for a symmetric encryption scheme (below we use the one-time pad) to encrypt the message. We will use the same notation as above and assume that Bob wants to send a message to Alice. There are four steps to the encryption protocol: The set-up, key generation, encryption and decryption.

The set-up is almost identical to the key exchange protocol, where the two parties Alice and Bob agree on a prime of the form $p=2^{n}\cdot 3^{m}\cdot f-1$, a supersingular elliptic curve over $\mathbb {F}_{p^2}$, and linearly independent points $P_A,Q_A\in E[2^n]$ and $P_B,Q_B\in E[3^{m}]$. In addition, they agree on a keyed hash function $H_k$ that sends $\mathbb {F}_{p^2}$ to the set $\{0,1\}^w$ of w-bit strings.

In the key generation phase, Alice picks random integers $0 \le a_1, a_2 < 2^n$ (not both divisible by 2) and computes

$$\begin{aligned} E_A,\phi _A(P_B),\phi _A(Q_B) \end{aligned}$$

as above. She also chooses a random ephemeral key, k, for the hash and publishes the tuple

$$\begin{aligned} \left( E_A,\phi _A(P_B),\phi _A(P_B),k\right) \end{aligned}$$

as her public key. She retains $\left( a_1,a_2\right)$ as her private key.

Upon the receipt of Alice’s public keys, Bob selects a w-bit message $m\in \{0,1\}^w$ and chooses random integers $0 \le b_1, b_2 < 3^m$ (not both divisible by 3) and computes

$$\begin{aligned} E_B,\phi _B(P_A),\phi _B(Q_A). \end{aligned}$$

Using his randomly generated keys $b_1$ and $b_2$, he can also compute $E_{AB}$ as in the key-exchange protocol. He then computes

$$\begin{aligned} c=m\oplus H_k(j(E_{AB})) \end{aligned}$$

and sends the tuple

$$\begin{aligned} \left( E_B,\phi _B(P_A),\phi _B(Q_A),c\right) \end{aligned}$$

to Alice.

To decrypt Bob’s message, Alice computes $E_{AB}$ using $E_B,\phi _B(P_A),\phi _B(Q_A)$ and $a_1,a_2$ and recovers the message m by computing

$$\begin{aligned} m=c\oplus H_k(j(E_{AB})). \end{aligned}$$

We stress that encryption is just one possible application where a static key may be used for at least one element in the protocol. We anticipate that as the subject develops further there will be more protocols of this type.

Equivalent Keys and Normalisation. The Vélu formulas tell us that the isogeny is determined solely by its kernel. In Alice’s case, there are $3\cdot 2^{n-1}$ choices of kernels, and the total number of choices for $(a_1,a_2)$ is about $2^{2n}$, so there will be private keys that correspond to the same public keys.

We define an equivalence relation on the private keys, by saying $(a_1, a_2) \sim (a_1', a_2')$ if the two keys lead to the same subgroup for all possible input points. The relation is satisfied by $(a_1', a_2') = (\theta a_1, \theta a_2)$ for any $\theta \in \mathbb {Z}_{2^n}^*$, and so the equivalence class is a point in projective space over a ring. We may define a unique equivalence class representative by “normalising” as explained in the following lemma (this fact is also used by [9]).

Lemma 1

Let $P,Q\in E[2^n]$ be linearly independent generators of $E[2^n]$. Then for some $(a_1,a_2)\in \mathbb {Z}^2$ (not simultaneously even), we have that $(a_1,a_2)\sim (1,\alpha )$ or $(a_1,a_2)\sim (\alpha ,1)$ for some $\alpha \in \mathbb {Z}$ (using the equivalence relation defined above).

Proof

If $a_1$ is odd, then it is invertible modulo the order of the group, so let $\theta \equiv a_1^{-1}\pmod {2^n}$, then $\theta$ must be odd, hence

$$\begin{aligned} \langle [a_1]P_A+[a_2]Q_A\rangle =\langle [\theta a_1]P_A+[\theta a_2]Q_A\rangle =\langle P_A+[\alpha ]Q_A\rangle , \end{aligned}$$

where the first equality stems from the fact that $\theta$ is co-prime to the order of the generator, and the last equality is obtained by setting $\alpha =\theta a_2$.

If $a_1$ is even, then $a_2$ must be odd, and repeating the procedure gives $(\alpha ,1)$.    $\square$

This result tells us that there is no loss of generality for Alice to restrict her secret key to be $(1,\alpha )$ or $(\alpha , 1 )$. This was noted by [9]. However, even if Alice does not employ such a simplification, the result also tells us that there is no loss of generality for an attacker to assume the secret key is of one of these two forms. This observation is used repeatedly in the adaptive attack presented in Sect. 3.

2.4 Active Attacks and Validation Methods

Active attacks are a standard type of attack on cryptosystems that use a static private key. These first arose in the setting of protocols based on the discrete logarithm problem, where a user can be treated as an oracle that takes as input a group element g and returns $g^a$ for some long-term secret value a. A first kind of attack is the “small subgroup” attack of Lim and Lee [23]. Here a group element g of small order $\ell$ is sent, so that on receipt of the value $g^a$ one can do a search and learn $a \pmod {\ell }$. Similar ideas have been used based on “invalid curve” attacks, which involve providing a point that lies in a different group altogether (see Ciet and Joye [8]).

In the context of the isogeny cryptosystem, if Alice has a fixed key $(a_1, a_2)$ then a dishonest Bob can send her (E, P, Q) and then Alice will compute an isogeny $\phi : E \rightarrow E'$ with kernel $\langle [a_1] P + [a_2] Q \rangle$. The idea is to try to learn something about Alice’s secret key $(a_1, a_2)$ using knowledge of $E'$. The possibility of such attacks is mentioned in [9, 20], but neither paper presented full details of them.

The concept of “validation” is intended to prevent active attacks. In the case of protocols based on the DLP, the typical countermeasures check that g does lie in the correct group, and that the order of g is the correct value. In the context of supersingular isogeny cryptosystems the validation of (E, P, Q) should test that E really is a supersingular elliptic curve, that P and Q lie on the curve and have the correct order, and that P and Q are independent. Methods to do this are given in [9].

In particular, Sect. 9 of [9] presented some explicit validation steps. Their two requirements are: The points in the public key have full order and they are independent. They use the Weil pairing of the two points to check independence. We remark that it is not necessary to use the Weil pairing: Since the DLP is easy in a group of order $2^n$ one can just try to solve the DLP of Q to the base P, and if the algorithm fails then the points are independent. In particular, to show that $\langle P, Q \rangle = E[ 2^n ]$ it suffices to compute $[2^{n-1}]P$ and $[2^{n-1}]Q$ and verify that these points are both different, and neither is the identity.

Remark 1

We now observe that the Weil pairing can be used to check a lot more than just independence. A standard fact is that if $\phi : E \rightarrow E'$ is an isogeny and if $P, Q \in E[ N ]$ then

$$ e_N( \phi (P), \phi (Q)) \ = \ e_N( P, Q )^{\deg (\phi )} $$

where the first Weil pairing is computed on $E'$ and the second on E (for details see [30, III.8.2] or [4, IX.9]). This allows to validate not only that the points are independent but also that they are consistent with being the image of the correct points under an isogeny of the correct degree. Hence, a natural validation step for Alice to run in the Jao–De Feo scheme is to check

$$ e_{2^n}( \phi _B( P_A), \phi _B( Q_A) ) = e_{2^n}( P_A, Q_A )^{3^m}. $$

This will give her some assurance that the points $\phi _B( P_A), \phi _B( Q_A)$ provided by Bob are consistent with being the images of the correct points under an isogeny of the correct degree. However, as we will show, this validation step is not sufficient to prevent all adaptive attacks. It will be necessary to use a much stronger protection, which we describe in the next section.

2.5 The Kirkwood et al. Validation Method

The Fujisaki-Okamoto transform [14] leads to a general method to secure any key exchange protocol of a certain type. This is explained in Sect. 5.2 of Peikert [28] and, in the context of the isogeny cryptosystem, it is discussed by Kirkwood et al. [20].

The idea is to complete the key exchange protocol and then for each party to encrypt to the other party the randomness used in the protocol so that they can check that the protocol has been performed correctly. Note that [20] does not contain a formal analysis of the security of the resulting protocol.

We now briefly describe the key exchange protocol that arises when this transform is applied to the Jao–De Feo protocol. In the following description, we show what Bob should do and how Alice can verify that Bob has followed the protocol correctly (this is suited for the case where Alice is using a static key and where Bob is a potential adversary).

• (1) Bob obtains Alice’s static public key $(E_A,\phi _A(P_B),\phi _A(Q_B))$.

• (2) Bob chooses a random seed $r_B$ and derives his private key using a pseudo-random function PRF (Kirkwood et al. call this a key derivation function).

  $$\begin{aligned} (b_1,b_2)={\text {PRF}}(r_B). \end{aligned}$$

  He then computes his message $(E_B,\phi _B(P_A),\phi _B(Q_A))$ where $\phi _B$ is defined to have kernel $\langle [b_1]P_B + [b_2] Q_B \rangle$.

• (3) Bob derives the shared secret value $E_{AB}$ from $(E_A,\phi _A(P_B),\phi _A(Q_B))$ and $(b_1,b_2)$ and computes a session key (SK) and validation key ($V\!K$) via a key derivation function (KDF)

  $$\begin{aligned} SK\mid V\!K={\text {KDF}}(j(E_{AB})). \end{aligned}$$

• (4) Bob then sends $(E_B,\phi _B(P_A),\phi _B(Q_A))$ and $c_B={\text {Enc}}_{V\!K}(r_B\oplus SK)$ to Alice.

• (5) From $(a_1,a_2)$ and $(E_B,\phi _B(P_A),\phi _B(Q_A))$, Alice derives $E_{AB}'$, then $SK'$ and $V\!K'$.

• (6) Alice computes

  $$\begin{aligned} r_B'={\text {Dec}}_{V\!K'}(c_B)\oplus SK'. \end{aligned}$$

  She then computes ${\text {PKDF}}(r_B')$ and recomputes Bob’s operations. If the resulting message is equal to the value $(E_B,\phi _B(P_A),\phi _B(Q_A))$ originally sent by Bob then Alice terminates the protocol correctly and uses $SK'=SK$ for future communicate with Bob. If not, the protocol terminates in a non-accepting state.

Notice that this protocol requires that Bob reveals his secret key to Alice, so it compels him to change his secret key after each verification. This validation method can be used for both the key-exchange and the encryption protocols.

3 Adaptive Attack

In this section, we will assume that Alice is using a static key $(a_1,a_2)$, and that a dishonest user is playing the role of Bob and trying to learn her key. Our discussion is entirely about Alice’s key and points in $E[ 2^n ]$, but it should be clear that the same methods would work for points in $E[ \ell ^m ]$ for any small prime $\ell$ (see Remark 2 for further discussion).

There are two attack models that can be defined in terms of access to an oracle O:

• 1. $O( E, R, S ) = E/\langle [a_1] R + [a_2] S \rangle$. This corresponds to Alice taking Bob’s protocol message, completing her side of the protocol, and outputting the shared key.

• 2. $O( E, R, S, E' )$ which returns 1 if $j(E') = j( E/\langle [a_1] R + [a_2] S \rangle )$ and 0 otherwise. This corresponds to Alice taking Bob’s protocol message, completing her side of the protocol, and then performing some operations using the shared key that return an error message if the shared key is not the same as the j-invariant provided (e.g., the protocol involves verifying a MAC corresponding to a key derived from the session key).

Our attacks can be mounted in both models. To emphasise their power we explain them in the context of the second, weaker, model.

3.1 First Step of the Attack

From Lemma 1, we may assume that the private key is normalised. In the following exposition, we will assume that the normalisation is $(1,\alpha )$. The case where we have $(\alpha ',1)$ where $\alpha '$ is even is performed in exactly the same way with some tweaks. Note that if $\alpha '$ is odd then it can be converted to the $(1,\alpha )$ case, so we may assume $\alpha '$ is even in the second case.

To differentiate between $(1,\alpha )$ and $(\alpha ',1)$ an attacker honestly generates Bob’s ephemeral values $(E_B, R = \phi _B(P_A), S = \phi _B(Q_A))$ and follows the protocol to compute the resulting key $E_{AB}$. Then the attacker sends $(E_B, R, S + [2^{n-1}]R)$ to Alice and tests the resulting j-invariant. Expressing this in terms of the oracle access: The attacker queries an oracle of the second type on $( E_B, R, S + [2^{n-1}]R, E_{AB} )$. If the oracle returns 1 then the curve $E_B/ \langle [a_1]R + [a_2](S + [2^{n-1}]R) \rangle$ is isomorphic to $E_{AB}$ and so $\langle [a_1]R + [a_2](S + [2^{n-1}]R) \rangle = \langle [a_1]R + [a_2]S \rangle$. Hence, by the following Lemma, $a_2$ is even and we are in the first case. If the oracle returns 0 then $a_2$ is odd.

Lemma 2

Let $R, S \in E[ 2^n]$ be linearly independent points of order $2^n$ and let $a_1, a_2 \in \mathbb {Z}$. Then

$$ \langle [a_1]R + [a_2](S + [2^{n-1}]R) \rangle = \langle [a_1]R + [a_2]S \rangle $$

if and only if $a_2$ is even.

Proof

If $a_2$ is even then $[a_2][2^{n-1}]R = 0$ and so the result follows. Conversely, if the two groups are equal then there is some $\lambda \in \mathbb {Z}_{2^n}^*$ such that

$$ \lambda ( [a_1]R + [a_2](S + [2^{n-1}]R) ) = [a_1]R + [a_2]S. $$

Since the points are independent we have $\lambda a_2 = a_2$ and so $\lambda = 1$. Hence, since S has order $2^n$, we have $a_2 2^{n-1} \equiv 0 \pmod {2^n}$ and $a_2$ is even.    $\square$

Note that the Weil pairing

$$\begin{aligned} e_{2^n}( R, S + [2^{n-1}]R ) = e_{2^n}( R, S ) = e_{2^n}( P_A, Q_A )^{3^m} \end{aligned}$$

and so the attack is not detectable using pairings.

Similarly one can call the oracle on $( E_B, R + [2^{n-1}]S, S , E_{AB} )$. The oracle returns 1 if and only if $a_1$ is even. Hence, we can determine which of the two cases we are in and determine if $\alpha$ is even or odd. Having recovered a single bit of $\alpha$, we will now explain how to use similar ideas to recover the rest of the bits of $\alpha$.

3.2 Continuing the Attack

We now assume that Alice’s static key is of the form $(1, \alpha )$ and we write

$$\begin{aligned} \alpha =\alpha _0+2^1\alpha _1+2^2\alpha _2+\dots +2^{n-1}\alpha _{n-1}. \end{aligned}$$

The attacker will learn one bit of $\alpha$ for each query of the oracle. Algorithm 1 gives pseudo-code for the attack.

We now give some explanation and present the derivation of the algorithm. Suppose an attacker has recovered the first i bits of $\alpha$, so that

$$\begin{aligned} \alpha =K_i+2^{i}\alpha _{i}+2^{i+1}\alpha ', \end{aligned}$$

where $K_i$ is known but $\alpha _i \in \{ 0,1 \}$ and $\alpha '\in \mathbb {Z}$ are not known.

The attacker generates $E_B, R = \phi _B(P_A), S = \phi _B(Q_A)$ and $E_{AB}$ as in the protocol. To recover $\alpha _i$, the attacker will choose suitable integers a, b, c, d and query the oracle on

$$\begin{aligned} (E_B,[a]R+[b]S,\ [c]R+[d]S, E_{AB}). \end{aligned}$$

The integers a, b, c, and d will be chosen to satisfy the following conditions:

• 1. If $\alpha _{i}=0$, then $\langle [a+\alpha c]R+[b+\alpha d]S\rangle =\langle R+[\alpha ]S\rangle$.

• 2. If $\alpha _{i}=1$, then $\langle [a+\alpha c]R+[b+\alpha d]S\rangle \ne \langle R+[\alpha ]S\rangle$.

• 3. $[a]R+[b]S$ and $[c]R+[d]S$ both have order $2^n$.

• 4. The Weil pairing $e_{2^n}([a]R+[b]S,[c]R+[d]S)$ must be equal to

  $$\begin{aligned} e_{2^n}(\phi _B(P_A),\phi _B(Q_A))=e_{2^n}(P_A,Q_A)^{\deg \phi _B}=e_{2^n}(P_A,Q_A)^{3^{m}}. \end{aligned}$$

The first two conditions help us distinguish the bit $\alpha _{i}$ and the latter two prevent the attack from being detected via order checking and Weil pairing validation checks respectively.

Consider the following integers:

$$\begin{aligned} a_i&=1,\quad b_i=-2^{n-i-1}K_i,\\ c_i&=0,\quad d_i=1+2^{n-i-1}. \end{aligned}$$

One can verify that they satisfy the third condition. To satisfy the fourth condition we need to use a scaling by $\theta$ that we will discuss later.

To show that the first two conditions are satisfied, note that $\langle [a]R+[b]S + [\alpha ]( [c]R+[d]S) \rangle$ is equal to

$$\begin{aligned}&\quad \,\,\langle R-[2^{n-i-1}K_i]S+[\alpha ][1+2^{n-i-1}]S\rangle \\&=\langle R+[\alpha ]S +[-2^{n-i-1}K_i+2^{n-i-1}(K_i+2^{i}\alpha _{i}+2^{i+1}\alpha ')]S\rangle \\&= \langle R+[\alpha ]S +[\alpha _{i}2^{n-1}]S\rangle \\&= {\left\{ \begin{array}{ll} \langle R+[\alpha ]S \rangle &{} \text {if }\alpha _{i}=0,\\ \langle R+[\alpha ]S +[2^{n-1}]S\rangle &{} \text {if }\alpha _{i}=1. \end{array}\right. } \end{aligned}$$

By the following Lemma, these two subgroups are different. Hence the response of the oracle tells us $\alpha _i$.

Lemma 3

Let R and S be linearly independent elements of the group $E[2^n]$ with full order, then the subgroups

$$\begin{aligned} \langle R+[\alpha ]S +[2^{n-1}]S\rangle \quad \text {and}\quad \langle R+[\alpha ]S\rangle \end{aligned}$$

are different.

Proof

The proof is very similar to the proof of Lemma 2. The subgroups have order $2^n$, since R has order $2^n$, and R and S are linearly independent. Then if the subgroups are the same, we must have some $\lambda$ such that

$$\begin{aligned}{}[\lambda ]R+[\lambda \alpha ]S=R+[\alpha ]S +[2^{n-1}]S. \end{aligned}$$

By the linear independence of R and S, we can compare coefficients and conclude that $\lambda =1$, and that $[2^{n-1}]S=\mathcal {O}$, which implies that S has order a factor of $2^{n-1}$, which is a contradiction.    $\square$

Finally, we address the fourth condition. We need that

$$\begin{aligned} e_{2^n}([a]R+[b]S,[c]R+[d]S)=e_{2^n}(R,S)^{ad-bc}=e_{2^n}(P_A,Q_A)^{3^{m}}. \end{aligned}$$

The idea is that we can mask the points chosen from the attack above to satisfy the fourth condition. Recall that the points we wish to send to Alice are

$$\begin{aligned} (R', S') = (R-[2^{n-i-1}K_i]S, [1+2^{n-i-1}]S). \end{aligned}$$

Computing the Weil pairing of the two points, we have

$$\begin{aligned}&e_{2^n}( R', S' ) \\ =&e_{2^n}(R-[K_i2^{n-i-1}]S, [1+2^{n-i-1}]S)\\ =&e_{2^n}(R,[1+2^{n-i-1}]S)\cdot e_{2^n}(-[K_i2^{n-i-1}]S,[1+2^{n-i-1}]S)\\ =&e_{2^n}(R,S)^{1+2^{n-i-1}}, \end{aligned}$$

which is not the correct value. So we choose $\theta$ such that

$$\begin{aligned} e_{2^n}( \theta R', \theta S' ) = e_{2^n}(R,S)^{\theta ^2(1+2^{n-i-1})}=e_{2^n}(P_A,Q_A)^{3^{m}}=e_{2^n}(R,S). \end{aligned}$$

Note that $\langle [\theta ]R' + [\alpha ][\theta ]S' \rangle = \langle [\theta ] ( R' + [\alpha ]S') \rangle = \langle R' + [\alpha ]S'\rangle$ as long as $\theta$ is coprime to the order $2^n$. Hence we need $\theta$ to be the square root of $1+2^{n-i-1}$ modulo $2^n$. The following lemma shows that such a square root exists as long as $n-i-1\ge 3$. Note that $\theta$ will be odd, as required.

Lemma 4

If a is an odd number and $m=8$, 16, or some higher power of 2, then a is a quadratic residue modulo m if and only if $a\equiv 1\pmod {8}$.

The condition $n-i-1\ge 3$ means we may not be able to launch the attack in an undetected way for the last two bits. This is why we use a brute force method to determine these bits.

The attack in the case $(\alpha ', 1 )$ follows by swapping the roles of R and S.

3.3 Analysis and Complexity of the Attack

The attack requires fewer than $n\approx \frac{1}{2}\log _2(p)$ interactions with Alice. This seems close to optimal for attack model 2, where the attacker only gets one bit of information at each query. We can reduce the number of queries by doing more computation (increasing the range of the brute-force search).

We now consider the attack in the context of [9, 20]. Due to our third and fourth conditions, the attack passes the validation steps in [9], and even the stronger check of taking the degree of the isogeny into account as mentioned in Remark 1.

The approach in [20] would be able to detect the attack. This is because the auxiliary points sent to Alice in the attack are not the correct values generated in an honest protocol run.

Remark 2

We now say a few words about attacking odd prime power isogenies. Let $\ell$ be an odd prime such that $\ell ^n \mid (p+1)$ and $E[ \ell ^n ] \subset E( \mathbb {F}_{p^2} )$. Let $P_A$, $Q_A$ be generators of $E[\ell ^n]$. Alice would compute an $\ell ^n$-isogeny with kernel $\langle [a_1] P_A + [a_2] Q_A \rangle$ and a dishonest user Bob is trying to learn her key $a_1$, $a_2$, where $a_1$ and $a_2$ are not simultaneously divisible by $\ell$. As above, we take Alice’s secret key to be $(1,\alpha )$.

The obvious generalisation for this attack is to set $R=\phi _B(P_A)$ and $S=\phi _B(Q_A)$ and to send Alice points

$$\begin{aligned} (R-[x\ell ^{n-i-1}]S, [1+\ell ^{n-i-1}]S). \end{aligned}$$

In her computation for the subgroup, Alice would compute

$$\begin{aligned} \langle R+[\alpha ]S+[\ell ^{n-i-1}][\alpha -x]S\rangle . \end{aligned}$$

Since we want to compare this subgroup against $\langle R+[\alpha ]S\rangle$, we need

$$\begin{aligned} (\ell ^{n-i-1})(\alpha -x)\equiv 0\pmod {\ell ^n} \end{aligned}$$

to ensure the subgroups computed are the same. Hence for each coefficient of a power of $\ell$ in the $\ell$-expansion of $\alpha$, we will need at most $\ell -1$ queries to recover it.

For $\ell = 3$ this is as good as one would expect (at most two queries), but for primes $\ell \ge 5$ this seems not optimal since one would hope that given an oracle that returns one bit of information one could learn the value with only $\lceil \log _2( \ell ) \rceil$ queries. In Appendix B we specify a simple attack, that is easily detectable and uses a stronger oracle, but can be used to efficiently handle the case $\ell > 3$.

4 Solving the Isogeny Problem When the Endomorphism Ring Is Known

Let $p=\ell _A^n\ell _B^mf - 1$ as in the Jao–De Feo cryptosystems, and let E and $E_A$ be two supersingular elliptic curves such that there exists an isogeny $\phi _A : E \rightarrow E_A$ of degree $\ell _A^n$ between them. In this section we additionally suppose that we know (or can compute) the endomorphism rings ${{\mathrm{End}}}(E)$ and ${{\mathrm{End}}}( E_A )$, and we provide an efficient algorithm to recover $\phi _A$ assuming a certain natural heuristic holds. A formal statement of our reduction is below and we will prove this in Sect. 4.2.

Theorem 1

Let E and $E_A$ be supersingular elliptic curves over $\mathbb {F}_{p^2}$ such that $E[ \ell _A^n ] \subseteq E( \mathbb {F}_{p^2} )$ and there is an isogeny $\phi _A : E \rightarrow E_A$ of degree $\ell _A^n$ from E to $E_A$. Suppose there is no isogeny $\phi : E \rightarrow E_A$ of degree $< \ell _A^n$. Then, given an explicit description of ${{\mathrm{End}}}(E)$ and ${{\mathrm{End}}}( E_A )$, there is an efficient algorithm to compute $\phi _A$.

As recalled in Sect. 2.2, computing the endomorphism ring of a supersingular elliptic curve is a problem essentially equivalent to computing an arbitrary isogeny between two supersingular elliptic curves. However, the the algorithm of [22] does not produce an isogeny that satisfies the additional constraint that it must be of small degree, as is required in the Jao–De Feo cryptosystems ($\ell _A^n\approx p^{1/2}$). Hence the current state of knowledge does not give a reduction of the form we require. The aim of this section is to present an alternative method to [22] in this context. We use the notation of [22].

4.1 The Importance of the Correct Isogeny

We first explain that to break the Jao–De Feo protocol it is not sufficient to compute any isogeny from E to $E_A$. There are infinitely many such isogenies, but to break the Jao and De Feo cryptosystems it is necessary to find the right sort of isogeny, as we now explain.

Suppose there are curves E and isogenies $\phi _A : E \rightarrow E_A$, $\phi _B : E \rightarrow E_B$ with $\ker (\phi _A) = G_A, \ker ( \phi _B ) = G_B$ satisfying the usual isogeny diagram from Sect. 2.3:

The correctness of the protocol follows from the fact that $E / \langle G_A, G_B \rangle = E_A / \langle \phi _A( G_B ) \rangle = E_B / \langle \phi _B( G_A ) \rangle$ and that $\phi _A( G_B )$ and $\phi _B( G_A )$ can be computed by the honest parties.

Suppose an attacker given $E, E_A, E_B$ can compute an isogeny $\phi ':E\rightarrow E_A$. So the picture now looks like:

The natural approach for an attacker to try to compute $E_{AB}$ is to compute $\phi _B( \ker ( \phi ' ))$ and hence an isogeny from $E_B$ with this kernel. However, the attacker only has the points $\phi _B( P_A), \phi _B( Q_A)$ to work with, and so can only compute $\phi _B( \ker ( \phi ' ))$ if $\ker ( \phi ' ) \subseteq \langle P_A, Q_A \rangle$ (in which case $\phi '$ is an isogeny of degree dividing $2^n$). A random isogeny $\phi '$ is unlikely to have this property. Indeed, $\phi _A$ is likely to be the only isogeny from E to $E_A$ with kernel in $\langle P_A, Q_A \rangle$ (apart from composing with an automorphism, which is of no consequence).

This is the crux of the difficulty in giving a reduction from computing endomorphism rings to computing the secret key in the Jao–De Feo cryptosystem: Known algorithms to compute an isogeny from E to $E_A$, given ${{\mathrm{End}}}(E)$ and ${{\mathrm{End}}}( E_A )$, are not likely to give an isogeny of the correct degree. However, as we now explain, the particularly small degree of the secret key gives the reduction an advantage that does not arise in the general case.

4.2 Reduction of Problem to Computation of Endomorphism Ring

We show how the existence of a small degree isogeny actually helps the cryptanalysis of Jao–De Feo’s cryptosystems, assuming we know (or we are able to compute) the endomorphism rings of the curves in play.

We write $B_{p,\infty }$ for the quaternion algebra ramified at p and $\infty$ and use the standard notions of reduced trace and reduced norm (see Vigneras [33] for background). One extends the reduced norm to ideals in $B_{p,\infty }$.

Given two maximal orders $\mathcal {O}$ and $\mathcal {O}_A$, one can compute in polynomial time an ideal I that connects them (see [22, Lemma 8]). Computing an isogeny of the correct degree corresponds to computing an equivalent ideal of the correct norm. In order to find such an equivalent ideal we use the following lemma.

Lemma 5

[22, Lemma 5] Let I be a left $\mathcal {O}$-ideal of reduced norm N and $\alpha$ an element in I. Then $I\gamma$, where $\gamma =\bar{\alpha }/N$, is a left $\mathcal {O}$-ideal of norm $n(\alpha )$.

We observe that in the context of Jao–De Feo cryptosystems, there exists by construction an element $\alpha$ of small norm $N\ell _A^n$ in I, corresponding via this lemma to an ideal of norm $\ell _A^n$. Moreover as Minkowski bases can be computed in polynomial time for lattices of dimension up to 4 [27], this element $\alpha$ can be efficiently recovered as long as it is in fact the smallest element in I. These observations lead to the following first simple algorithm:

All the steps in this algorithm can be performed in polynomial time. The above discussion forms the proof of Theorem 1.

Proof

(Theorem 1). Given an explicit representation of the endomorphism rings, we can translate the endomorphism rings into maximal orders of quaternion algebras. One can then find, in polynomial time, an ideal I connecting them by [22, Lemma 8].

By Lemma 5, it is sufficient to find an element of I of the correct norm. But given that the norm we seek is the smallest norm in the ideal, we can use lattice reduction methods to recover the smallest norm in polynomial time. Then using methods in [22], we can recover the isogeny we seek.    $\square$

In the remainder of this section, we study the success probability of this algorithm on average, and show how to use it to achieve a very large success probability.

Heuristically, we can approximate the probability that E and $E_A$ are connected by an isogeny of degree $\ell$ by estimating the probability that two randomly chosen supersingular elliptic curves are connected by an isogeny of the same degree.¹

Random pairs of elliptic curves over $\mathbb {F}_{p^2}$ are unlikely to be connected by isogenies of degrees significantly smaller than $\sqrt{p}$. Indeed, when $\ell =\prod _ip_i^{e_i}$, there are exactly

$$\begin{aligned} a(\ell ):=\prod _i(p_i+1)p_i^{e_i-1} \end{aligned}$$

isogenies of degree $\ell$ from any curve E, hence any curve E is connected to at most $\sum _{\ell \le D}a(\ell )$ curves $E_A$ by an isogeny of degree at most D. A calculation given in Appendix A shows that this sum converges to

$$\begin{aligned} \frac{15}{2\pi ^2} D^2 \end{aligned}$$

as D tends to infinity. As there are roughly p / 12 supersingular invariants over $\mathbb {F}_{p^2}$ we can evaluate the success probability of the above algorithm as

$$\begin{aligned} SR\approx \max \left( 0, \ 1-\frac{90}{\pi ^2}\frac{\ell _A^{2n}}{p}\right) . \end{aligned}$$

For the parameters used in Jao–De Feo’s cryptosystems we expect this basic attack to succeed with a probability larger than 50 % as soon as $f>\frac{180}{\pi ^2}\approx 18.23$, where f is the cofactor in $p=\ell _A^n\ell _B^m f \pm 1$.

The success rate of our attack can be easily improved in two ways. First, we can apply the algorithm separately on all curves that are at distance $\ell _A^e$ of $E_A$ for some small constant e, until it succeeds for one of them. Clearly one of these curves will be connected to E by an isogeny of degree $\ell _A^{n-e}$, and as a result the success rate will increase to

$$\begin{aligned} SR\approx \max \left( 0, \ 1-\frac{90}{\pi ^2}\frac{\ell _A^{2(n-e)}}{p}\right) . \end{aligned}$$

With $\ell _A=2$ and $e=10$ this method will lead to a success rate above 99 %, even when $f=1$. Second, we can try to use the Minkowski-reduced basis computed in Step 3 of the algorithm to find an element $\alpha$ of the appropriate norm, even when it is not the smallest element. We explore two heuristic methods in that direction in our experiments below.

4.3 Experimental Results

We tested our algorithm in Magma with $\ell _A=2$ and with a $\lambda$-bit prime p, a randomly selected maximal order, another random maximal order connected to the first by a path of length $\lceil \log _{\ell _A}(p)/2 \rceil +\delta$, with $\delta \in \{-5,\ldots ,5\}$. One can traverse from the first order to the second via $\lceil \log _{\ell _A}(p)/2 \rceil +\delta$ steps in the $\ell _A$-isogeny tree.

The first three columns of Table 1 (“First basis element”) correspond to the attack described in the previous section. The next three columns (“All basis elements”) correspond to a variant where instead of considering only the smallest element in Step 4 of the algorithm, we try all elements in the Minkowski-reduced basis. Finally, the last three columns (“Linear combinations”) correspond to a variant where we search for $\alpha$ of the right norm amongst all elements of the form $\sum _{i=1}^4 c_i\beta _i$, where $c_i\in \{-4,\ldots ,4\}$ and $\beta _i$ are the Minkowski-reduced basis elements. Each percentage in the table corresponds to a success rate over 100 experiments.

Table 1. Experimental results for $\delta$ values. $\ell =2$.

The experimental results are entirely convincing, so we leave better strategies to identify $\alpha$ from the Minkowski-reduced basis to further work.

5 Isogeny Hidden Number Problem

In this section we present an algorithm that takes partial information about the shared j-invariant $j(E_{AB})$ of Alice and Bob, and recovers the entire j-invariant, i.e. their shared key. This algorithm can therefore be used as a tool to obtain the shared key from a side-channel attack and to prove a bit security result.

Influenced by work on Diffie–Hellman key exchange in $\mathbb {Z}_p^*$, we propose the isogeny hidden number problem as a useful abstraction for analysing different cases where partial information is provided.

Hidden number problems have been used in other research. For example, [5] proved that some bits are hardcore for Diffie–Hellman shared keys in $\mathbb {Z}_p^*$, [16, 25, 26] studied partial leakage of nonces in DSA and EC-DSA signatures, and [1, 24] discussed side-channel attacks in the context of signatures.

Definition 3 (Isogeny hidden number problem)

Let $E_s$ be an unknown supersingular elliptic curve over $\mathbb {F}_{p^2}$. The isogeny hidden number problem is to compute the j-invariant $j(E_s)$ given an oracle O such that O(r) outputs partial information on $j(E')$ for some curve $E'$ which is r-isogenous to $E_s$.

We now explain how the oracle O in this problem can be realized in the context of the supersingular isogeny Diffie–Hellman key exchange. We use the same notation as earlier in the paper, so that $P_A,Q_A,P_B,Q_B \in E$ are known, and so are Alice and Bob’s session values: $E_A,E_B,\phi _A(P_B),\phi _A(Q_B),\phi _B(P_A),\phi _B(Q_A)$. We set $E_s:=E_{AB}$ to be the unknown elliptic curve. We suppose we have another oracle $O'$ that takes these values and produces some partial information on $j(E_{AB})$, which we interpret as the oracle query O(1).

As a second stage, the adversary chooses a small integer r (coprime to Alice’s prime $\ell$) and a point $R \in E_B[r]$ of full order. Let $\phi _{BC} : E_B \rightarrow E_C$ be an isogeny of degree r with kernel $\langle R \rangle$, that is $E_C = E_B/\langle R \rangle$. Note that there is a curve $E':=E_{AC}$ and an r-isogeny $E_{AB} \rightarrow E_{AC}$ corresponding to the image of R under the isogeny from $E_B$ to $E_{AB}$. We also have that $E_{AC} = E_C / \phi _C( G_A )$ where $G_A$ is the kernel of $\phi _A$ and $\phi _C = \phi _{BC} \circ \phi _B$. This situation is pictured below.

The curves $E_A$, $E_C$ and the corresponding values $\phi _A(P_B)$, $\phi _A(Q_B)$, $\phi _C(P_A) = \phi _{BC}( \phi _B(P_A) )$, $\phi _C(Q_A) = \phi _{BC}(\phi _B(Q_A))$ can be used to perform a key exchange, which will constitute the curve $E_{AC}$ (this is the dotted arrow in the figure).

Querying the oracle $O'$ on these values results in some partial information on $j(E_{AC})$. We interpret this as the oracle query O(r).

We give a full solution to the isogeny hidden number problem in the case where the oracle outputs an entire component of the j-invariant, and propose an attack where the oracle outputs some most significant bits of both components. This leads to a bit security result and to an active attack, which can be realized by a side-channel attack, when Alice uses a static key.

5.1 Algorithms for the Isogeny Hidden Number Problem

We recall that each j-invariant is an element in $\mathbb {F}_{p^2}$. Let $\mathbb {F}_{p^2} = \mathbb {F}_p(\theta )$, where $\theta ^2 + A\theta + B = 0$, with $A,B \in \mathbb {F}_p$. We write $j = j_1 + j_2\theta$. For simplicity we only consider two cases of partial knowledge:

• 1. Oracle returns an entire component $j_i$ of each j-invariant.

• 2. Oracle returns the most significant bits of both components.

Other models of partial information could be considered as well.

We first remark that, since there are only around p / 12 supersingular j-invariants, one might expect that knowledge of one component $j_i$ uniquely determines the entire j-invariant. This is not true in general, and it seems to be the case that there is no bound independent of p on the number of supersingular j-invariants in $\mathbb {F}_{p^2}$ with a fixed value for $j_i$ (one exception is the rare class of j-invariants that actually lie in $\mathbb {F}_p$ and so are uniquely determined by their first component; the number of such j-invariants grows proportional to $\sqrt{p}$). Furthermore, there seems to be no known efficient algorithm that computes the other component $j_{3-i}$ given the value $j_i$ together with the fact that the curve is supersingular. Hence, even the first case is not trivial.

Our result is based on the modular polynomials $\varPhi _r(x,y)$, which have the property that there is an isogeny $\phi : E \rightarrow E'$ of degree r with cyclic kernel if and only if $\varPhi _r( j(E), j(E')) = 0$. We refer to [10, Sect.  11.C], [3, Sect.  3.8] for background. These polynomials give a way to relate the known information on the different j-invariants. The degree of $\varPhi _r(x,y)$, as well as their number of monomials, grow with r. Since the degree of these polynomials influences the complexity of the computation, it is desirable to work with the smallest possible r (in practice we can take either $r=2$ or $r=3$). For $r=2$ we have

$$\begin{aligned} \begin{aligned} \varPhi _2(x,y)&= x^3 + y^3 - x^2y^2 + 1488x^2y + 1488xy^2\\&- 162000x^2 - 162000y^2 + 40773375xy \\&+ 8748000000x + 8748000000y - 157464000000000. \end{aligned} \end{aligned}$$

The framework is the following. Let $x=x_1+x_2\theta , y=y_1+y_2\theta$. We call $x_1$ a “coefficient of 1” and $x_2$ a “coefficient of $\theta$”. Then $\varPhi _2(x,y)=F_1(x_1,x_2,y_1,y_2) + F_2(x_1,x_2,y_1,y_2)\theta$ for $F_1,F_2 \in \mathbb {F}_p[x_1,x_2,y_1,y_2]$, of total degree 4. Let $j=j(E)=j_1+j_2\theta$ and $j'=j(E')=j'_1+j'_2\theta$, then if $\varPhi _2(j,j') \equiv 0$ (mod p) it holds that $F_1(j_1,j_2,j'_1,j'_2) = F_2(j_1,j_2,j'_1,j'_2) \equiv 0$ (mod p).

Given some most significant bits of x, a common approach is to write

$$\begin{aligned} h := {\text {MSB}}_k(x) = x - e,\quad \text {for }|e|<\frac{p}{2^{k+1}}, \end{aligned}$$

so e is a relatively small integer. If all the bits are given, then $e=0$. Substituting the known values that the oracle provides into each $F_i$, one constructs new polynomials $G_i$ whose roots can be used to fully recover the j-invariant j(E). The problem reduces to the problem of recovering desired roots of $G_i$.

Complete Component. In this case we assume the attacker has a whole component for each j-invariant. We show that two samples are sufficient to recover the secret j-invariant $j(E_{s})$. That is, we need one component of $j(E_{s})$ and one component of another $j(E')$. Moreover, we can work with any pair of components (the components do not have to be in the same position).

Theorem 2

Let the oracle O in the isogeny hidden number problem output one component of the finite field representation of $j(E') \in \mathbb {F}_{p^2}$. Then there is an algorithm to solve the isogeny hidden number problem that makes two queries to O and succeeds with probability at least 1 / 18 if both components are coefficients of 1, with probability at least 1 / 12 if both components are coefficients of $\theta$, and with probability at least 1 / 15 otherwise.

Proof

Let $E_s$ be the desired elliptic curve. The query O(1) gives one component of $j(E_s)$ and the query O(2) gives one component of $j(E')$ where $\varPhi _2( j(E_s), j(E') ) = 0$.

Writing $j(E_s) = j_1+j_2\theta$ and $j(E') = j'_1+j'_2\theta$ then, as explained, $\varPhi _2(j,j') = 0$ can be expressed as $F_1(j_1,j_2,j'_1,j'_2) = F_2(j_1,j_2,j'_1,j'_2) = 0$ for two polynomials $F_1, F_2$.

The oracle queries provide values $x_{3-k}=j_{3-k},y_{3-l}=j'_{3-l}$ for $k,l \in \{1,2\}$. Plugging these values into the polynomials $F_i$, we construct two bivariate polynomials $G_i$ in variables $x_k,y_l$ where the highest degree of each variable is at most 3. By taking the resultant of these polynomials with respect to $y_l$ we get a univariate polynomial in $x_k$ of degree at most 18. We show in Appendix C that the resultant is not the constant zero. One can then factor this polynomial to get at most 18 roots over $\mathbb {F}_p$, where one of the roots is $j_k$. As we have $j_k$ and $j_{3-k}$, we can construct $j(E_s)$. Hence, taking one of these solutions at random, we have determined the unknown j-invariant of $E_s$ with probability at least 1 / 18.

Note that if the oracle queries yield $j_2,j'_2$, then $G_2$ is of degree 2, and so the resultant is of degree at most 12 (see Appendix C). Therefore, there are at most 12 possibilities of $\mathbb {F}_p$-solutions to the remaining unknown, which bound the success probability by 1 / 12. Similarly, if only one of the components is a coefficient of $\theta$, then the degree of the variable associated to this component in $G_2$ is 2, and so the resultant is of degree at most 15.    $\square$

Remark 3

The solution given in Theorem 2 applies directly to any degree r. Note that the degree of $\varPhi _r(x,y)$ increases with r, so we get more candidates for $j_k$. The proof holds with non-negligible probability for any low degree r. Notice that one can run the algorithm for several different degrees r and test if there is only one root which is common to all lists of candidates, this will be $j_k$.

This solution assumes the oracle always gives the correct answer. An oracle that gives correct answers with some probability can be treated using the ideas in the next partial information model.

Theorem 2 provides the following bit security result for the supersingular isogeny key-exchange in a manner analogous to how the hidden number problem is used to give bit security results for Diffie–Hellman key exchange in $\mathbb {Z}_p^*$ [5].

Theorem 3

Computing any component of the shared j-invariant $j(E_{AB})$ in the supersingular isogeny key exchange is as hard as computing the entire j-invariant $j(E_{AB})$.

Indeed, the isogeny hidden number problem in this case can be derived from the oracle $O'$ described above, that takes the public parameters as well as the values $E_A$, $E_C$, $\phi _A(P_B)$, $\phi _A(Q_B)$, $\phi _C(P_A)$, $\phi _C(Q_A)$ and outputs a component of $j(E_{AC})$ (if Alice’s prime $\ell$ is 2, one can take $r=3$ or work with Bob’s values and $E_{BC}$). We have just shown that, given an algorithm that computes a component of the shared j-invariant from the public keys, there is an algorithm that computes the entire j-invariant.

Partial Components. In this case we assume the attacker has most significant bits of both component for each j-invariant. Therefore, we write $j_i = h_i + e_i$ and $j'_i = h'_i + e'_i$ for $i=1,2$ and for a pair of j-invariants $j,j'$. Substituting these values to the equations of $F_i$, we construct two new polynomials $G_1,G_2 \in \mathbb {F}_p[u_1,u_2,v_1,v_2]$ of degree 4, such that

$$\begin{aligned} G_1(e_1,e_2,e'_1,e'_2) = G_2(e_1,e_2,e'_1,e'_2) \equiv 0\pmod {p}. \end{aligned}$$

The problem of computing the hidden j-invariant can therefore be expressed in terms of finding a small solution to a system of multivariate polynomial equations modulo p. One can then solve the problem by applying the well-known lattice-based techniques due to Coppersmith and Howgrave-Graham. We refer to [19] for a survey of these methods, where multivariate polynomials are considered.

These lattice methods require several relations, so we expect to need more than the six relations that are coming from the three 2-isogenous curves to $E_s$. To get more relations one can take isogenies of higher degrees, but we suggest working with degree 2 to get a stronger attack. That is, instead of fixing $E_s$ and taking several r-isogenous curves $E'$ for increasing r, we suggest following a (short) path in the 2-isogeny graph rooted at $E_s$. This ensures that the only polynomial being used is $\varPhi _2$, which has minimal degree and the minimal number of monomials.

The main idea is to consider a part of the 2-isogeny graph close to $E_s$ (typically it will be a tree rooted at $E_s$). For every edge in the graph we obtain partial information on a j-invariant, which gives rise to two polynomials, namely $G_1,G_2$, which are satisfied by a simultaneous “small” solution.

Once enough polynomials are gathered, one can apply the techniques mentioned above to get a solution to the entire system where some of the roots are small (coming from the coordinates of a short vector in a corresponding lattice). Given these roots, one can recover the j-invariant for a curve $E_d$ in this path. Using the modular polynomials, we can “travel back” to find the j-invariant of the root $E_s$. Indeed, suppose our path is $E_0 = E_s, E_1,\ldots ,E_k$. Then as we know $j(E_d)$ for some $d \le k$, we can use $\varPhi _2$ to compute $j(E_{d-1})$ by solving $\varPhi _2(j(E_d),y) \equiv 0 \pmod {p}$. We get at most 3 candidates for $j(E_{d-1})$, and we proceed recursively to find candidates for $j(E_{d-2}),\ldots ,j(E_0)$. Since the distance from $E_d$ to the root $E_s$ is short, this results in a small list of candidates for $j(E_s)$.

We remark that in practice the polynomials $G_1,G_2$ consist of many monomials, and therefore this approach would require knowledge of many bits. However, Coopersmith’s method shows how to generate more relations, which help to reduce the number of bits, and as an attack one can also rely on lattice algorithms working better in practice than theoretically guaranteed.

5.2 Active Attack When Alice Uses a Static Key

We assume that Alice uses a static key for encryption or key exchange. A legitimate key exchange protocol takes place between Alice and Bob, and an adversary Eve who sees the protocol messages wishes to obtain the resulting shared j-invariant $j_{AB}$. Hence Eve knows $(E, E_A, E_B )$ and the corresponding points.

We further assume that Eve can (adaptively) engage in protocol sessions with Alice (who always uses the same static secret key) and that, through some side-channel or other means, Eve is able to obtain partial information on the shared key computed by Alice on each protocol session.

Here, Alice acts as the oracle O that provides the partial information. Eve first observes a protocol exchange between Alice and Bob, and so sees $(E_B, \phi _B( P_A), \phi _B(Q_A))$. She learns some partial information on $j(E_{AB})$.

Eve then chooses a small integer r coprime to Alice’s prime $\ell$, and as described above computes an isogeny $\phi _C$, the curve $E_C$ and the corresponding points $\phi _C(P_A)$, $\phi _C(Q_A)$. She sends $(E_C, \phi _C(P_A), \phi _C(Q_A))$ to Alice as part of a key exchange session. Alice then computes $E_{AC} = E_C/\phi _C(G_A)$ and some partial information about this j-invariant $j( E_{AC} )$ is leaked. This leads to the scenario described in the isogeny hidden number problem, and using one of the solutions to this problem yields the desired j-invariant $j(E_{AB})$.

Note that this attack can be detected by the countermeasure of Kirkwood et al. [20], since the query on $E_C$ is not on a correct execution of the protocol. However, the protocol still requires Alice to compute $E_{AC}$ and so in the context of a side-channel attack, an attacker might already have received enough information to determine the desired secret key $j(E_{AB})$.

6 Conclusion

We have given several results on the security of cryptosystems based on the Jao–De Feo concept. Our main conclusion is that it seems very hard to prevent all active attacks using simple methods. Our first active attack seems to be undetectable using pairings or any other tools, as the curves and points appear to be indistinguishable from correct executions of the protocol. Similarly, our side-channel attack based on leakage of partial knowledge of the key seems to be hard to detect (without storing all previous sessions and each user checking that all curves $E_C$ sent to her are not related to previous curves $E_B$ by an isogeny of small degree). However, both these active attacks are detected by the heavy-duty countermeasure of Kirkwood et al. [20]. The latter attack comes from a reduction that gives the first bit security result for the supersingular isogeny key exchange.

Our paper therefore suggests that there is no way to avoid the use of such general countermeasures. It also shows that there is a risk of side-channel and fault attacks on these protocols, and these topics will no doubt generate a small following of literature in the coming years.

We have also discussed the connection between the problem of computing endomorphism rings and computing isogenies. In general, knowledge of ${{\mathrm{End}}}(E_A)$ does not immediately lead to a 2-power isogeny of low degree from E to $E_A$. But in the setting of the Jao and De Feo scheme such an isogeny can be efficiently computed when ${{\mathrm{End}}}( E)$ and ${{\mathrm{End}}}(E_A)$ are known. This demonstrates that the isogenies considered in these cryptosystems are special, which is natural to suspect since they are too short to provide good mixing in the expander graph.

Appendices

A Number of Isogenies of Degree Smaller Than D

To the sum $\sum _{n=2}^Da(n)$ with $a(n)=\prod _{p^e|n}(p+1)p^{e-1}$ we can associate a Dirichlet series $d(s)=\sum _{n\ge 1}\frac{a(n)}{n^s}$. This Dirichlet series is in fact equal to $d(s)=\frac{\zeta (s)\zeta (s-1)}{\zeta (2s)}$ by applying Euler’s product formula. The function has a pole at $s=2$ with residue equal to $\zeta (2)/\zeta (4)$. Using Perron’s formula and Cauchy’s Residue theorem, we arrive at

$$\sum _{n\le D}a(n) \sim c\cdot D^2$$

where

$$c={\text {Res}}(s=2)=\frac{1}{2}\frac{\zeta (2)}{\zeta (4)}=\frac{15}{2\pi ^2}.$$

B Low Order Adaptive Attack

In this appendix, we will discuss an adaptive attack that is easily detected but can be more powerful than the attack in Sect. 3. This adaptive attack uses points of small order; in particular, the attacker uses points $\left( R,[\ell ^{k}]S\right)$, where $R,S\in E[\ell ^n]$. We will illustrate the attack using the first oracle model and when $\ell >3$.

As with the attack presented in Sect. 3, we will assume that Alice is using a static key $(1,\alpha )$, and that a dishonest user is playing the role of Bob to learn her key. It will be immediately clear that the attack will not stand up to the validations proposed by [9].

Let Alice be working in $E[\ell ^n]\subset E(\mathbb {F}_{p^2})$, where $\ell ^n \mid (p+1)$ and $\ell >3$. Suppose that an attacker has recovered the first i bits of $\alpha$, so that

$$\begin{aligned} \alpha =K_i+\ell ^i\alpha _i+\ell ^{i+1}\alpha ' \end{aligned}$$

where $K_i$ is known but $\alpha _i\in \{0,1,\dots ,\ell -1\}$ and $\alpha '$ are not known.

The attacker computes $E_B$, $R=\phi _B(P_A)$, $S=\phi _B(Q_A)$ and queries the oracle on $(E_B,R,[\ell ^{n-i-1}]S)$. The resulting elliptic curve that the oracle computes is

$$\begin{aligned} E_B/\langle R+[\alpha ][\ell ^{n-i-1}]S\rangle&=E_B/\langle R+[\ell ^{n-i-1}][K_i+\ell ^i\alpha _i+\ell ^{i+1}\alpha ']S\rangle \\&=E_B/\langle R+[\ell ^{n-i-1}][K_i]S+[\ell ^{n-1}\alpha _i]S\rangle . \end{aligned}$$

Since the component $R+[\ell ^{n-i-1}][K_i]S$ is known, the attacker can recover $\alpha _i$ if he knows the j-invariant by trying all of the $\ell$ different values of $\alpha _i$. For each $\ell$-ary bit, we only need one oracle interaction. This therefore solves the problem mentioned in Remark 2. The pseudo-code for this attack is presented in Algorithm 3.

Notice that with the second oracle model the attacker would need to make at most $\ell$ queries to the $O(E,R,S,E')$ oracle to recover $\alpha _i$.

C The Resultant of $G_1(x_k,y_l)$ and $G_2(x_k,y_l)$

Let $p,q \in k[x,y]$ be two polynomials, and k some field. The resultant of p and q with respect to y, denoted ${{\mathrm{Res}}}(p,q,y)$, is given by the determinant of the Sylvester matrix of p and q as univariate polynomials in y, that is, we consider $p,q \in k(x)[y]$. The resultant ${{\mathrm{Res}}}(p,q,y)$ is a univariate polynomial in x, so belongs to k[x]. For background on the resultant we refer to Sects. 5 and 6 of Chap. 3 in [11].

We show that the resultant ${{\mathrm{Res}}}(G_1,G_2,y_l)$, considered in Sect. 5.1, is not identically zero. We will use the fact that the modular polynomial $\varPhi _r( X, Y ) \in \mathbb {F}_p[X, Y]$ is absolutely irreducible (irreducible over the algebraic closure). We therefore consider $\varPhi _r$, as well as $G_1,G_2$, in $\overline{\mathbb {F}}_p[ X , Y ]$. Recall that there are four cases depending on the values of (k, l). For example when $(k,l) = (1,2)$ we have $G_1( x_1, y_2 ) + G_2( x_1, y_2 )\theta = \varPhi _2( x_1 + j_2\theta , j'_1 + y_2 \theta )$.

Assume for contradiction that ${\text {Res}}(G_1,G_2,y_l)\equiv 0$. By Proposition 1(ii) in [11, Chap.3, $\S 6$], ${{\mathrm{Res}}}(G_1,G_2,y_l)\equiv 0$ if and only if there exists a polynomial $h \in \overline{\mathbb {F}}_p[ x_k, y_l ]$ with positive degree in $y_l$ such that $h \mid G_1$ and $h \mid G_2$.

Consider the following linear substitution of variables:

• If $k=1$ then set $x_1 = X - j_2\theta$ and if $k=2$ then set $x_2 = (X - j_1)\theta ^{-1}$.

• If $l=1$ then set $y_1 = Y - j_2'\theta$ and if $l=2$ then set $y_2 = (Y - j_1')\theta ^{-1}$.

One can check that these substitutions give

$$ G_1( x_k , y_l ) + G_2( x_k , y_l )\theta = \varPhi _r( X, Y ). $$

Hence, letting $\bar{h}( X, Y )$ be the polynomial obtained by evaluating $h( x_k, y_l )$ with these substitutions we have

$$ \bar{h}( X, Y ) \mid \varPhi _r( X, Y ). $$

From the facts that the degree of $\bar{h}$ is equal to the degree of h, and that $\varPhi _r$ is irreducible, it follows that (since we assumed h is non-constant) that h is a constant multiple of both $G_1$ and $G_2$. But by comparing the monomials in $G_1,G_2$, it is easy to see that they are not constant multiples of each other. Hence we have a contradiction and the resultant is non-zero.

We now explain the degrees arising in the proof of Theorem 2. Given the components $j_{3-k},j'_{3-l}$, consider $\varPhi _2(x,y)$ and the corresponding polynomials $G_1(x_k,y_l)$, $G_2(x_k,y_l)$. We have

$$ \deg _{x_k} {{\mathrm{Res}}}(G_1,G_2,y_l) = \left\{ \begin{array}{ll} 12 &{} \text { if } k=l=1 , \\ 18 &{} \text { if } k=l=2 , \\ 15 &{} \text { otherwise}. \end{array} \right. $$

It follows from the following lemma, since $\deg _{x_1} F_1 = \deg _{y_1} F_1 = 3$, $\deg _{x_2} F_1 = \deg _{y_2} F_1 \le 3$, $\deg _{x_1} F_2 = \deg _{y_1} F_2 \le 2$ and $\deg _{x_2} F_2 = \deg _{y_2} F_2 \le 3$.

Lemma 6

Let $p,q \in k[x,y]$ be two polynomials with

$$\begin{aligned} \deg _x p = n_x,&\ \deg _y p = n_y, \\ \deg _x q = m_x,&\ \deg _y q = m_y. \end{aligned}$$

Then $\deg _x {{\mathrm{Res}}}(p,q,y) \le m_y n_x + n_y m_x$.

Proof

The Sylvester matrix of p and q with respect to y is a $(m_y+n_y) \times (m_y+n_y)$ matrix. The first $m_y$ rows, coming from the coefficients of p, contain polynomials in x of degree at most $n_x$. Similarly, the last $n_y$ rows contain polynomials in x of degree at most $m_x$. The resultant ${{\mathrm{Res}}}(p,q,y)$ is given by the determinant of this matrix, which is formed by summing products of an entry from each row. The first $m_y$ rows contribute at most $m_y n_x$ to the degree of x, and the last $n_y$ rows contribute at most $n_y m_x$.    $\square$