Abstract
In a selective opening attack (SOA) on an encryption scheme, the adversary is given a collection of ciphertexts and she selectively chooses to see some subset of them “opened”, meaning that the messages and the encryption randomness are revealed to her. A scheme is SOA secure if the data contained in the unopened ciphertexts remains hidden. A fundamental question is whether every CPA secure scheme is necessarily also SOA secure. The work of Bellare et al. (EUROCRYPT’12) gives a partial negative answer by showing that some CPA secure schemes do not satisfy a simulation-based definition of SOA security called SIM-SOA. However, until now, it remained possible that every CPA-secure scheme satisfies an indistinguishability-based definition of SOA security called IND-SOA.
In this work, we resolve the above question in the negative and construct a highly contrived encryption scheme which is CPA (and even CCA) secure but is not IND-SOA secure. In fact, it is broken in a very obvious sense by a selective opening attack as follows. A random value is secret-shared via Shamir’s scheme so that any t out of n shares reveal no information about the shared value. The n shares are individually encrypted under a common public key and the n resulting ciphertexts are given to the adversary who selectively chooses to see t of the ciphertexts opened. Counter-intuitively, by the specific properties of our encryption scheme, this suffices for the adversary to completely recover the shared value. Our contrived scheme relies on strong assumptions: public-coin differing inputs obfuscation and a certain type of correlation intractable hash functions.
We also extend our negative result to the setting of SOA attacks with key opening (IND-SOA-K) where the adversary is given a collection of ciphertexts under different public keys and selectively chooses to see some subset of the secret keys.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
When it comes to defining the security of encryption schemes, the standard definitions of chosen-plaintext attack (CPA) and chosen-ciphertext attack (CCA) security are generally thought of as the gold standard. Nevertheless, there are scenarios in which these notions do not appear to provide sufficient guarantees. One such scenario is that of selective opening attacks (SOA) [4, 11].
Selective Opening Attacks. In a selective opening attack, the adversary gets a collection of n ciphertexts \((c_i = \mathsf {Enc} _{ pk }(m_i; r_i))_{i \in [n]}\) encrypting messages \(m_i\) with randomness \(r_i\) under a common public key \( pk \). The adversary can adaptively choose to see some subset \(\mathcal {I} \subseteq [n]\) of the ciphertexts “opened”, meaning that she gets \((m_i,r_i)_{ i \in \mathcal {I}}\). For example, this could model a scenario where these ciphertexts are created by different senders and the adversary adaptively corrupts some subset of them. Intuitively, a scheme is SOA secure if the data contained in the unopened ciphertexts remains hidden. Formalizing this notion requires great care, and several definitions have been proposed.
Simulation-Based SOA Security. Perhaps the strongest notion of SOA security is a simulation-based definition, which we denote SIM-SOA. It was originally proposed for commitments by Dwork et al. [11] and later adapted to encryption by Bellare et al. [4]. This definition requires that for any n-tuple of messages \(\mathbf {m} = (m_1,\ldots ,m_n)\) the view of the adversary in the above SOA scenario is indistinguishable from a simulated view created as follows: the simulator selects a message subset \(I\), obtains \((m_i)_{i\in I}\), and is then supposed to output a view of a selective opening attack with ciphertexts, random coins, and an adversary as above. At when constructing the simulator in a black-box fashion out of a given adversary, this means that the simulator must initially creates a collection of simulated ciphertexts \(\mathbf {c} = (c_1,\ldots ,c_n)\) without knowing anything about the messages. The adversary then gets \(\mathbf {c} \) and specifies a subset \(\mathcal {I} \subseteq [n]\) of the ciphertexts to be opened. At this point, the simulator learns the messages \((m_i)_{i \in \mathcal {I}}\) and has to produce simulated openings \((m_i,r_i)_{ i \in \mathcal {I}}\) to give to the adversary.
On the positive side, this definition is easy to use in applications and clearly captures the intuitive goal of SOA security, since the adversary’s view can be simulated without using any knowledge of the unopened messages. Moreover, we have constructions that achieve SIM-SOA security from a wide variety of number theoretic assumptions [4, 12, 14, 18, 19, 21].
On the negative side, this definition might be overkill in many applications and therefore also unnecessarily hard to achieve. The work of Bellare et al. [3] shows that many natural encryption schemes are not SIM-SOA secure, in the sense that there is no efficient simulator that would satisfy the given definition. The lack of a simulator already constitutes an attack on SIM-SOA security in the formal sense. However, these schemes are also not “obviously broken” by a selective opening attack in the intuitive sense. In particular, it is not clear how to, e.g., extract an unopened plaintext in a selective opening attack. At the very least, it remains unclear what exactly can go wrong when using such schemes in the context of the SOA scenario described above.
Indistinguishability-Based SOA Security. The work of Bellare et al. [4] also proposes an indistinguishability-based security definition, which we denote IND-SOA. The definition requires that we have an “efficiently re-samplable” distribution on n-tuples of messages \(\mathbf {m} = (m_1,\ldots ,m_n)\) such that for any set \(\mathcal {I} \subseteq [n]\) we can efficiently sample from the correct conditional distribution with a fixed choice of \((m_i)_{i \in \mathcal {I}}\). For any such distribution we consider the SOA scenario where the adversary initially gets encryptions of the messages \(\mathbf {m} = (m_1,\ldots ,m_n)\) chosen from the distribution, and selectively gets to see an opening of a subset \(\mathcal {I} \) of the ciphertext. At the end of the game the adversary either gets the initially encrypted message vector \(\mathbf {m} \) or a freshly re-sampled message vector \(\mathbf {m} ' = (m_1',\ldots ,m_n')\) conditioned on \(m'_i =m_i\) matching in the opened positions \(i \in \mathcal {I} \). The adversary should not be able to distinguish these two cases.
On the negative side, the definition of IND-SOA security is more complex and its implications are harder to interpret. However, it can already provide sufficient security guarantees in many interesting applications and might be significantly easier to achieve than SIM-SOA security. Prior to this work, we did not know whether it is the case that every CPA secure encryption scheme is also IND-SOA secure. The work of Hofheinz and Rupp [20] shows that, if one considers a definition that combines IND-SOA security with CCA security, denoted by IND-SO-CCA, then there are schemes that are CCA secure but are not IND-SO-CCA secure. However, this result crucially relies on the embedding of an attack in the decryption oracle, and does not appear to extend to the standard IND-SOA. In fact, the same work of [20] gave a partial positive result showing that CPA security implies IND-SOA security for a large class of encryption schemes in a generic group model, but it was unclear what the situation is in the standard model.
More Related Work. The relations between different definitions of SOA security have also been investigated by Böhl et al. [6]. It turns out that the notion of IND-SOA security we consider is the weakest known notion of SOA security among the ones studied (and that the “efficient resamplability” condition is essential for this property). Hazay et al. [17] recently studied SOA for keys (where the adversary receives secret keys of corresponding chosen subset of ciphertexts) and showed that the indistinguishability-based security is strictly weaker than the simulation-based counterpart. Furthermore, there exist several efficient constructions of IND-SOA secure encryption schemes that are not known to be SIM-SOA secure. Most prominently, every lossy encryption scheme is IND-SOA secure [4], which opens the door for efficient IND-SOA secure schemes from various computational assumptions [26–28]. In that sense, the notion of IND-SOA we consider is very attractive from a practical point of view. In an orthogonal direction, Fuchsbauer et al. [13], recently showed that standard security implies IND-SOA for certain specific graph-induced distributions; it is interesting to note that, while we used dependencies of messages to show our negative result, [13] used the lack of dependencies to show a positive result.
Secret Sharing: A Concrete SOA Scenario. At this point, an intuitive definition of SOA security might appear elusive, with strong definitions like SIM-SOA that could be overkill and weaker definitions like IND-SOA that are hard to interpret. Instead of trying to pin down a general notion of SOA security, we will focus on defining a concrete and easy to understand security goal, which any reasonable definition of SOA security should satisfy. We call this goal secret-sharing selective-opening attack (SecShare-SOA) security, and define it via the following game.
The challenger chooses a random polynomial F of degree \(\le t\) and sets \(m_i = F(i)\) for \(i \in [n]\). We can think of this as a Shamir secret sharing of a random value F(0) where any t of the n shares preserve privacy. The adversary is given encryptions of the shares \(( c_i = \mathsf {Enc} _{ pk }(m_i;r_i) )_{i \in [n]}\) and can selectively choose to get openings \((m_i,r_i)_{i \in \mathcal {I}}\) for a subset \(\mathcal {I} \) of the ciphertexts where \(|\mathcal {I} | =t\). The adversary should not be able to predict F(0).
It is easy to show that SecShare-SOA security is implied by IND-SOA (and therefore also SIM-SOA) security. At first thought, it may seem that SecShare-SOA security should also follow from standard CPA security. However, upon some reflection, it becomes clear that natural reductions fail. In particular, there is no easy way to embed the challenge ciphertext \(c^*\) into a correctly distributed vector \((c_i)_{i \in [n]}\) while maintaining the ability to provide openings for a large subset of the ciphertexts.
Our Results. In this work, we construct a contrived encryption scheme which is CPA (and even CCA) secure, but is not SecShare-SOA secure (and therefore also not IND-SOA secure). In particular, we have an attack against the SecShare-SOA security of the scheme where the attacker always recovers the shared secret with probability 1. This is the first example of a CPA secure scheme which is obviously broken in the SOA setting. As a corollary, this shows that not every CPA secure scheme is IND-SOA secure.
We also extend our results to selective opening attacks on receiver keys (IND-SOA-K), also known as selective opening under receiver corruption. In this setting, the adversary is given a collection of ciphertexts under different public keys and he can selectively chose to see some subset of the secret keys. We give an analogous example of a scheme which is CCA secure but is not IND-SOA-K secure.
Our results rely on strong assumptions: public-coin differing inputs obfuscation [23] and a certain type of correlation-intractable hash functions [8].
1.1 Our Techniques
We construct a scheme which is CCA secure but for which there is an attack on the SecShare-SOA security. For concreteness, we will show an attack on the SecShare-SOA game using a secret sharing scheme with parameters \(t=k\) (degree of polynomial) and \(n = 3k\) (number of shares) where k is the security parameter.
An SOA Helper Oracle. As our starting point, we consider the construction of Hofheinz and Rupp [20] which gives a CCA secure scheme that is not IND-SO-CCA secure. Their construction starts with any CCA secure scheme and, as an implicit first step, defines a (stateful and interactive) “SOA helper oracle” that has knowledge of the secret key \( sk \) of the scheme. The way that the oracle is defined ensures that the scheme remains CCA secure but is not SecShare-SOA secure relative to this oracle. They then show how to embed this oracle into the decryption procedure of the scheme to get a scheme which is not IND-SO-CCA secure.
The SOA helper oracle gets as input ciphertexts \((c_i)_{i \in [3k]}\) and it randomly chooses a subset \(\mathcal {I} \subset [3k]\) of size \(|\mathcal {I} | = k\) of them to open. It then receives the openings \((m_i,r_i)_{i \in \mathcal {I}}\) and decrypts the remaining ciphertexts using knowledge of \( sk \). It checks that there is a (unique) degree \(\le k\) polynomial F such that \(F(i) = m_i\) for \(>2k\) of the indices \(i \in [3k]\) and that this polynomial also satisfies \(F(i) = m_i\) for all of the indices \(i \in \mathcal {I} \). If so, it outputs F(0) and else \(\bot \).
It is easy to see that this oracle breaks SecShare-SOA security. The harder part is showing that the scheme remains CPA/CCA secure relative to the oracle. In particular, we want to show that this oracle will not help the adversary decrypt some challenge ciphertext \(c^*\). We do so by defining an “innocuous SOA helper oracle” that functions the same way as the real SOA helper oracle but it never decrypts \(c^*\). Instead, it just pretends that the decryption of \(c^*\) is \(\bot \). The only time that innocuous SOA helper and the real SOA helper give a different answer is when the ciphertexts \((c_i)_{ i \in [3k]}\) encrypt messages \((m_i)\) such that there is a unique degree \(\le k\) polynomial F with \(F(i) = m_i\) for exactly \(2k+1\) of the indices \(i \in [3k]\), and this polynomial satisfies \(F(i) = m_i\) for all \(i \in \mathcal {I} \). Only in this case, there is a possibility that the SOA helper correctly outputs F while the innocuous SOA helper outputs \(\bot \) when the decryption of \(c^*\) is replaced by \(\bot \). However, since the set \(\mathcal {I} \subseteq [3k]\) of size \(|\mathcal {I} |= k\) is chosen randomly and independently of \((c_i)\), the probability that it is fully contained in the set of \(2k+1\) indices for which \(F(i) = m_i\) is negligible. Therefore, the SOA helper and the innocuous SOA helper give the same answer with all but negligible probability, meaning that the former cannot break CCA security.
Obfuscating the SOA Helper. Our main idea is that, instead of embedding the SOA helper in the secret-key decryption procedure, we obfuscate the SOA helper and include the obfuscated code in the public key of the scheme. (We note that a similar technique of “obfuscating a helper oracle that aids an attacker” has been used in the key-dependent message setting [24, 25].) There are two main difficulties that we must take care of.
The first difficulty is that the SOA helper is stateful/interactive whereas we can only obfuscate a stateless program. We squash the interactive helper into a non-interactive one by choosing the set of indices \(\mathcal {I} \subseteq [3k], |\mathcal {I} | = k\) via a hash function h applied to the ciphertexts \((c_i)_{ i \in [3k]}\). One can think of this as an analogue of the Fiat-Shamir heuristic which is used to squash a 3 move \(\varSigma \)-protocol into a non-interactive argument. (We stress, however, that we do not rely on random oracles, as in the Fiat-Shamir heuristic. Instead, we use a suitable standard-model hash function.) The squashed SOA helper now expects to get the ciphertexts \((c_i)_{i \in [3k]}\) and the opening \((m_i, r_i)_{i \in \mathcal {I}}\) where \(\mathcal {I} = h( (c_i)_{i \in [3k]})\) in one shot. Previously, we used the fact that the set \(\mathcal {I} \) is random to argue that the SOA helper and the innocuous SOA helper are indistinguishable. We now instead rely on correlation intractability [8] of the hash function h to argue that it is hard to find an input on which the two oracles would give a different answer (even given the entire code and secrets of the oracles).
The second difficulty is how to use reasonable notions of obfuscation to argue that the obfuscated SOA helper, which contains the decryption key inside it, does not break CPA/CCA security. We rely on public-coin differing inputs obfuscation (PdiO) [23]. This security notion says that, given two programs represented as circuits \(C,C'\), together with all the random coins used to sample them, if it is hard to find an input x such that \(C(x) \ne C'(x)\) then the obfuscations of C and \(C'\) are indistinguishable. We can rely on public-coin differing-inputs obfuscation and the correlation intractability of h to replace the obfuscated SOA oracle with an obfuscated “innocuous SOA oracle” that never decrypts the challenge ciphertext \(c^*\). However, even the latter oracle still has the secret key \( sk \) hard-coded and therefore it is not clear if an obfuscated version of the innocuous oracle remains innocuous. To solve this problem, we will need the underlying CCA encryption scheme to be “puncturable” meaning that we can create a punctured secret key \( sk [c^*]\) which correctly decrypts all ciphertexts other than \(c^*\) but preserves the semantic security of \(c^*\). Such encryption schemes were constructed in the work of [9] from indistinguishability obfuscation. With this approach we can argue that security of the challenge ciphertext \(c^*\) is preserved.
Discussion on our Assumptions. We recall that two of the main assumptions behind our results are public-coin differing inputs obfuscation and correlation-intractable hash functions.
The notion of public-coin differing inputs obfuscation (PdiO) is stronger than indistinguishability obfuscation (iO) but weaker than differing-inputs obfuscation (diO) [1]. There is some evidence that diO is unachievable in its full generality [5, 16], but no such evidence exists for PdiO. Indeed, at present we do not have much more evidence for the existence of iO than we do for PdiO. We note that if PdiO exists, then by the “best-possible” nature of iO, any iO obfuscator (with sufficient padding) is already also a PdiO obfuscator as well. All that said, we view it as an intriguing open problem to base our results on iO rather than PdiO.
The correlation intractability assumption that we need is in a parameter regime with no known counter-examples and has been conjectured to be achievable. As evidence, a recent work [7] constructs such correlation-intractable hash functions under obfuscation-based assumptions. However, the description of the hash functions is not public-coin samplable, whereas we need a hash function that is. We simply conjecture that standard hash function constructions such as SHA-3 achieve this property. We note that the notion of correlation intractability that we need is also a special case of entropy-preserving hashing [2, 10] which is sufficient to guarantee the soundness of the Fiat-Shamir heuristic for all proof (but not argument) systems and has been conjectured to exist.
On this note, an interesting direction for future work is to re-establish the results based on weaker assumptions.
2 Preliminaries
General Notation. For \(n \in \mathbb {N} \) we define \([n] := \{1,\ldots ,n\}\). Throughout the paper, \(k\in \mathbb {N} \) denotes the security parameter. For any function \(g(\cdot )\), we let \(g(k) = \mathsf{{negl}}(k)\) denote that \(g(\cdot )\) is a negligible function. For any two distributions \(\mathcal {D} _0, \mathcal {D} _1\) parameterized by k, we denote that they are computationally (resp., statistically) indistinguishable by \(\mathcal {D} _0 \approx _{\mathsf {c}}\mathcal {D} _1\) (resp., \(\mathcal {D} _0 \approx _{\mathsf {s}}\mathcal {D} _1\)); we denote that they are identical by \(\mathcal {D} _0 \equiv \mathcal {D} _1\).
Interpolation, Error Decoding. Let \(\mathbb {F} \) be the finite field. For pairwise different \(X_i \in \mathbb {F} \) we let \(\mathsf {ipol} ((X_i,Y_i)_{i \in [k+1]})\) denote the unique degree \(\le k\) polynomial \(F\in \mathbb {F} [X]\) with \(F(X_i)=Y_i\) for all \(i \in [k+1]\). We note that \(\mathsf {ipol}\) can be efficiently computed, e.g., via Lagrange interpolation. Also, let \(\mathsf {decc} _k((X_i,Y_i)_{i \in [n]})\) denote the the unique degree \(\le k\) polynomial \(F \in \mathbb {F} [X]\) such that \(F(X_i) = Y_i\) for \(> n-(n-k)/2\) of the indices \(i \in [n]\), or \(\bot \) if no such polynomial exists. Evaluating \(\mathsf {decc}\) amounts to performing error correction for the Reed-Solomon code with distance \(d = (n-k)\) when there are \(< d/2\) errors, which can be done efficiently. Let \(\mathcal {S} _\ell ^S\) denote the set of all \(\ell \)-sized subsets of \(S\).
PKE Schemes. A public-key encryption (PKE) scheme \(\mathsf {PKE}\) with message space \(\mathcal {M}\) (parameterized by the security parameter k) consists of three PPT algorithms \(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec} \). Key generation \(\mathsf {Gen} (1^k)\) outputs a public key \( pk \) and a secret key \( sk \). Encryption \(\mathsf {Enc} ( pk ,m)\) takes \( pk \) and a message \(m \in \mathcal {M} \), and outputs a ciphertext \(c\). Decryption \(\mathsf {Dec} ( sk ,c)\) takes \( sk \) and a ciphertext \(c\), and outputs a message \(m\). For correctness, we want \(\mathsf {Dec} ( sk ,c)=m \) for all \(m \in \mathcal {M} \), all \(( pk , sk )\leftarrow \mathsf {Gen} (1^k)\), and all \(c \leftarrow \mathsf {Enc} ( pk ,m)\).
CCA Security. We recall the standard definition of IND-CCA security from the literature.
Definition 1 (IND-CCA security.)
We say that a scheme \(\mathsf {PKE}\) is IND-CCA secure if for all PPT attackers \(A\) the advantage
is negligible in the security parameter k, where the experiment \(\mathsf {Exp}^{\mathsf {ind\text {-}cca}}_{\mathsf {PKE},A}\) is defined in Fig. 1, and \({\mathsf {Dec} _{c ^*}( sk ,\cdot )}\) is an oracle that outputs \({\mathsf {Dec} ( sk ,c)}\) for every input \(c \ne c ^*\) and \(\perp \) for input \(c ^*\).
IND-SOA Security. We now recall the definition of indistinguishability-based SOA security from [4]. By default, we will consider the weakest variant where the adversary specifies an efficiently re-samplable distribution.
Definition 2 (Efficiently re-samplable)
Let \(n=n(k)>0\), and let \(\mathcal {D}\) be a joint distribution over \(\mathcal {M} ^n\). We say that \(\mathcal {D}\) is efficiently re-samplable if there is a PPT algorithm \(\mathsf {msamp} _\mathcal {D} \) such that for any \(\mathcal {I} \subseteq [n]\) and any partial vector \(\mathbf {m} _\mathcal {I} ':=(m '_{i})_{i\in \mathcal {I}}\in \mathcal {M} ^{|\mathcal {I} |}\), \(\mathsf {msamp} _\mathcal {D} (\mathbf {m} _\mathcal {I} ')\) samples from \(\mathcal {D} \mid \mathbf {m} '_\mathcal {I} \), i.e., from the distribution \(\mathbf {m} \leftarrow \mathcal {D} \), conditioned on \(m _{i}=m '_{i}\) for all \(i\in \mathcal {I} \). Note that in particular, \(\mathsf {msamp} _{\mathcal {D}}()\) samples from \(\mathcal {D}\).
Definition 3 (IND-SOA Security)
For a PKE scheme \(\mathsf {PKE} =(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\), a polynomially bounded function \(n=n(k)>0\), and a stateful PPT adversary \(A\), consider the experiment in Fig. 1. We only allow \(A\) that always output re-sampling algorithms as in Definition 2. We call \(\mathsf {PKE}\) IND-SOA secure if for all polynomials \(n\) and all PPT \(A\), we have
Public-Coin Differing-Inputs Obfuscation. In this paper, we require a strengthening [22, 23] of the notion of indistinguishability obfuscation [1, 15].
We shall first define the notion of a public-coin differing-inputs sampler.
Definition 4 (Public-Coin Differing-Inputs Sampler)
A (circuit) sampling algorithm \(\mathsf {csamp} \) is an algorithm that takes as input random coins \(r\in \{0,1\}^{\ell (k)}\) for a suitable polynomial \(\ell =\ell (k)\), and outputs the description of two circuits \(C_0\) and \(C_1\). We call \(\mathsf {csamp} \) a public-coin differing-inputs sampler for the parameterized collection of circuits \(\mathcal {C}= \{\mathcal {C}_k\}\) if the output of \(\mathsf {csamp} \) is distributed over \(\mathcal {C}_k \times \mathcal {C}_k\), and for every PPT adversary \(A\), we have

Observe that the sampler and the attacker both receive the same random coins as input. Therefore, \(\mathsf {csamp} \) cannot keep any “secret” from \(A\). We now define the notion of a public-coin differing-inputs obfuscator.
Definition 5 (Public-Coin Differing-Inputs Obfuscator)
A uniform PPT algorithm \(\mathsf {PdiO}\) is a public-coin differing-inputs obfuscator for the parameterized collection of circuits \(\mathcal {C}= \{\mathcal {C}_k\}\) if the following requirements hold:
- Correctness: :
-
\(\forall k\), \(\forall C \in \mathcal {C}_k\), \(\forall x\), it is \(\Pr [C'(x) = C(x) : C' \leftarrow \mathsf {PdiO}(1^k, C)] =1\).
- Security: :
-
for every public-coin differing-inputs sampler \(\mathsf {csamp} \) for the collection \(\mathcal {C}\), every PPT (distinguishing) algorithm \(D\), we have
$$\begin{aligned}&\mathsf {Adv}^{\mathsf {pdio}}_{\mathsf {PdiO},D} :=\\&\quad \big |\Pr [D(1^k, r, C') = 1 : (C_0, C_1) \leftarrow \mathsf {csamp} (1^k; r), C' \leftarrow \mathsf {PdiO}(1^k, C_0)] - \\&\quad \; \Pr [D(1^k, r, C') = 1 : (C_0, C_1) \leftarrow \mathsf {csamp} (1^k;r), C' \leftarrow \mathsf {PdiO}(1^k, C_1)] \big | = \mathsf{{negl}}(k) \end{aligned}$$
Correlation-intractable Hash Functions. We begin by reviewing the definition of correlation-intractable hash function from [8].
Definition 6 (Hash Function Ensembles)
A family of functions \(\mathcal {H}= \{h_{s} : {D}_k \rightarrow {R}_k\}_{k \in \mathbb {N}, s\in \{0,1\}^{\ell (k)}}\) with domain \({D}_k\), range \({R}_k\), and seed length \(\ell (k)\) is said to be an efficient hash function ensemble, if there exists a PPT algorithm that given \(x \in {D}_k\) and \(s\), outputs \(h_{s}(x)\).
In the sequel, we shall simply denote this computation by \(h_{s}(x)\). Furthermore, we shall often call \(s\) the description or the seed of the function \(h_{s}\).
Definition 7 (Binary Relations)
A class of efficient binary relations consists of \(\mathcal {REL}= \{\mathrm {Rel}_{r} \subseteq ({D}_k,{R}_k)\}_{k \in \mathbb {N}, r \in \{0,1\}^{\ell '(k)}}\), where membership in \(\mathrm {Rel}_r\) is testable in polynomial time given r.
The relation \(\mathcal {REL}\) is said to be evasive if for any \(r \in \{0,1\}^{\ell '(k)}, x \in {D}_k\) we have:

Definition 8 (Correlation Intractability)
Assume an efficient hash function ensemble \(\mathcal {H}= \{h_{s} : {D}_k \rightarrow {R}_k \}_{k \in \mathbb {N}, s\in \{0,1\}^{\ell (k)}}\). Furthermore, let \(\mathcal {REL}= \{\mathrm {Rel}_{r} \subseteq ({D}_k,{R}_k)\}_{k \in \mathbb {N}, r \in \{0,1\}^{\ell '(k)}}\) be a class of efficient binary relations. We say that \(\mathcal {H}\) is correlation intractable with respect to \(\mathcal {REL}\) if for every PPT \(A \),

The work of [8] showed that no hash function ensemble is correlation-intracta- ble with respect to all evasive binary relations \(\mathcal {REL}\). However, for any fixed domains/ranges \({D}_k,{R}_k\) it is plausible that there is a correlation-intractable hash function \(\mathcal {H}\) for all evasive relations over \({D}_k,{R}_k\) as long as the seed length \(\ell (k)\) of the hash function is made sufficiently large relative to \({D}_k,{R}_k\). This would be sufficient for our needs. For concreteness, we define a specific class of relations \(\mathcal {REL}\) for which we need correlation intractability.
Definition 9 (Special Class of Evasive Binary Relations)
Let \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme with plaintext space \(\mathbb {F} \) (a field), ciphertext space \(\mathcal {C}\) (parametrized by the security parameter k), and which uses \(\ell '(k)\) bits of randomness in key-generation. We define a special class of binary relations \(\mathcal {REL}^{\mathsf {PKE}} = \{\mathrm {Rel}_{r} \subseteq (\mathcal {C}^{3k},\mathcal {S} _k^{[3k]})\}_{k \in \mathbb {N}, r \in \{0,1\}^{\ell '(k)}}\), as follows.
-
To determine if \(((c _{i})_{i\in [3k]}, \mathcal {I}) \in \mathrm {Rel}_{r}\): Let \((pk,sk) = \mathsf {Gen} (1^k;r)\), \(m_i = \mathsf {Dec} ( sk ,c_i)\), \(F = \mathsf {decc} _k((i,m _{i})_{i \in [3k]})\) and \(Q = \{ i \in [3k] : F(i) = m_i\}\). The tuple is in the relation if \(F \ne \bot \), \(|Q| = 2k+1\) and \(\mathcal {I} \subseteq Q\).
Intuitively, the above says that a tuple \(((c _{i})_{i\in [3k]}, \mathcal {I}) \in \mathrm {Rel}_{r}\) if the decrypted messages \((m_i)_{i \in [3k]}\) agree with the evaluations of a degree \(\le k\) polynomial F in exactly \(2k+1\) positions and the set \(\mathcal {I} \) only contains these positions. It is easy to see that this is an evasive relation as shown below (following [20, Lemma 3.3]).
Lemma 1
The relation \(\mathcal {REL}^{\mathsf {PKE}}\) is evasive. In particular, for any \(r \in \{0,1\}^{\ell '(k)}\) any \((c _{i})_{i\in [3k]} \in \mathcal {C}^{3k}\) we have \(\Pr _{\mathcal {I} \leftarrow \mathcal {S} _k^{[3k]}}\left[ ((c _{i})_{i\in [3k]}, \mathcal {I}) \in \mathrm {Rel}_{r} \right] = \mathsf{{negl}}(k).\)
Proof
Let \((pk,sk) = \mathsf {Gen} (1^k;r)\), \(m_i = \mathsf {Dec} ( sk ,c_i)\), \(F = \mathsf {decc} _k((i,m _{i})_{i \in [3k]})\) and \(Q = \{ i \in [3k] : F(i) = m_i\}\). If \(F = \bot \) or \(|Q| \ne 2k+1\) then the probability in the lemma is 0. Otherwise

for all \(k \ge 2\), which proves the lemma.
Special Correlation-intractable Hash Functions. Let \(\mathcal {REL}^{\mathsf {PKE}}\) be a special class of binary relations for PKE scheme \(\mathsf {PKE} \), like in Definition 9. We define special correlation-intractable hash functions \(\mathcal {H}= \{h_{s}: \mathcal {C}^{3k} \rightarrow \mathcal {S} _k^{[3k]} \}_{k \in \mathbb {N}, s\in \{0,1\}^{\ell (k)}}\) as a function ensemble that is correlation intractable with respect to the relation \(\mathcal {REL}^{\mathsf {PKE}}\). We reiterate that this is a special case of correlation intractability with respect to all evasive relations, which is conjectured to be possible as long as the seed length \(\ell (k)\) of the hash function is made sufficiently large relative to the domain/range. In our case, we allow \(\ell (k)\) to be an arbitrarily large polynomial.
2.1 Puncturable Encryption Schemes
We will rely on the notion of puncturable encryption from [9]. Let \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec},\mathsf {Puncture})\) be a tuple of PPT algorithms. \(\mathsf {PKE} \) is said to be a puncturable encryption scheme, if the following holds.
- Syntax. :
-
\((\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) is a PKE scheme with message space \(\mathcal {M} = \{\mathcal {M} _k\}_{k \in \mathbb {N}}\) and ciphertext space \(\mathcal {C} = \{\mathcal {C} _k\}\) which are efficiently sampleable.
- Correctness. :
-
For all \(m \in \mathcal {M} \) it holds that \(\Pr [ \mathsf {Dec} ( sk ,c) = m~:~ ( pk , sk ) \leftarrow \mathsf {Gen} (1^k), c \leftarrow \mathsf {Enc} ( pk ,m)] = 1\).
- Puncturability. :
-
\(\forall ( pk , sk )\) in the support of \(\mathsf {Gen} (1^k)\), \(\forall c_0,c_1\in \mathcal {C} \), \(\forall sk [\{c_0,c_1\}]\) in the support of \(\mathsf {Puncture} ( sk ,\{c_0,c_1\})\), and \(\forall c \notin \{c_0,c_1\}\), it holds that: \(\mathsf {Dec} ( sk [\{c_0,c_1\}], c) = \mathsf {Dec} ( sk ,c)\).
- Security. :
-
For every PPT adversary \(A\),
$$\begin{aligned} \mathsf {Adv}^{\mathsf {\mathsf {punc\text {-}ind\text {-}cca}}}_{\mathsf {PKE},A}(k) := \left| \Pr \left[ {\mathsf {Exp}^{\mathsf {punc\text {-}ind\text {-}cca}}_{\mathsf {PKE},A}(k)=1}\right] - \frac{1}{2}\right| = \mathsf{{negl}}(k) \end{aligned}$$where the experiment \(\mathsf {Exp}^{\mathsf {punc\text {-}ind\text {-}cca}}_{\mathsf {PKE},A}(k)\) is defined in Fig. 2.
- Ciphertext sparseness. :
-
\(\forall ( pk , sk )\) we have
$$\begin{aligned} \Pr \left[ {\mathsf {Dec} ( sk ,c)\ne \bot }\right] = \mathsf{{negl}}(k), \end{aligned}$$where the probability is over \(c \leftarrow \mathcal {C} _ pk \).
Note that the puncturing algorithm \(\mathsf {Puncture}\) takes as input a set of two ciphertexts, so that the distribution of \(\mathsf {Puncture} ( sk ,\{c _0,c _1\})\) is identical to that of \(\mathsf {Puncture} ( sk ,\{c _1,c _0\})\).
3 Secret-Sharing Selective Opening Attack (SecShare-SOA)
We now define a special case of IND-SOA security that we call SecShare-SOA. It corresponds to the case where the encrypted values are shares in a t-out-of-n secret sharing scheme.
Secret-sharing Message Distribution. Let \(\mathbb {F} \) be a field of cardinality p. We consider a distribution \(\mathcal {D} \) which chooses a polynomial in \(F \in \mathbb {F} [X]\) of degree at most \(t\) and sets the messages to be \(m_i = F(i)\) for \(i \in [n]\). We let \(t\) and \(n\) be two polynomials in the security parameter, such that \(t< n\le p\). More formally,

Note that there exists an efficient re-sampling algorithm \(\mathsf {msamp} \) for the above distribution. In particular, for any \(\mathcal {I} \), \(\mathsf {msamp}\) can randomly extend its input \((F(i))_{i\in \mathcal {I}}\) to \(t+1\) evaluation points as necessary and then use polynomial interpolation to retrieve \(F\) and thus all \(F(i)\).
Note that, conditioned on any choice of F(i) for \(i \in \mathcal {I} \) where \(|\mathcal {I} | \le t\), the value F(0) is uniformly random.
Definition 10 (SecShare-SOA Security)
Let \(\mathbb {F} \) be a field of size determined by the security parameter and let \(\mathsf {PKE} =(\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme, with message space \(\mathcal {M} = \mathbb {F} \). For any polynomials parameters \(t= t(k), n= n(k)\) such that \(t< n\le |\mathbb {F} |\), consider the experiment in Fig. 2 with a stateful PPT adversary \(A\). We say that \(\mathsf {PKE}\) secret-sharing selective opening attack secure if
is negligible for all PPT \(A\).
3.1 IND-SOA Implies SecShare-SOA
Theorem 1
If a PKE scheme \(\mathsf {PKE}\) is IND-SOA secure, then it is SecShare-SOA secure.
Proof
Let \(\mathsf {PKE}\) be a PKE scheme with message space \(\mathcal {M} = \mathbb {F} \) which is a field. Suppose there exists an adversary \(A\) that breaks the SecShare-SOA security of \(\mathsf {PKE}\) with probability \(\varepsilon =\mathsf {Adv}^{\mathsf {secsh\text {-}soa}}_{\mathsf {PKE},A}(k)\). Then we construct an adversary \(B \) that, given access to \(A\), breaks the IND-SOA security of \(\mathsf {PKE}\). We describe the adversary below.
Adversary \(B \). By using \(A\), \(B \) interacts with its challenger in the IND-SOA game as follows. Upon receiving a public key \( pk \), \(B \) presents the secret-sharing message distribution \(\mathcal {D} \) to its challenger. To recall,

for some \(t< n\). Upon receiving a tuple of ciphertexts \(\mathbf {c}:=(c _{i})_{i\in [n]}\), \(B \) forwards \(( pk , \mathbf {c})\) to \(A\). Upon receiving \(\mathcal {I} \) from \(A\), \(B \) forwards it to the challenger. Recall that \(\mathcal {I} \in [n]\) and \(|\mathcal {I} | = t\). Upon receiving a message vector \(\mathbf {m} \) and the openings \((R _{i})_{i\in \mathcal {I}}\) of \((c _{i})_{i\in \mathcal {I}}\) to \((m _{i})_{i\in \mathcal {I}}\), \(B \) proceeds as follows. It computes \(F = \mathsf {ipol} ((i,m _{i})_{i\in [n]})\). Thereafter, it forwards the messages and openings just for \(i \in \mathcal {I} \); namely, \((m _{i},R _{i})_{i\in \mathcal {I}}\). Let \( out _{A} \) be the value output by \(A\). \(B \) compares whether \( out _{A} = F(0)\). If so, then it outputs 0, else it outputs 1.
Analysis. We shall now analyze the success probability of \(B \) in the IND-SOA game. Intuitively, \(B \) succeeds in the IND-SOA game whenever the \(A\) succeeds in the SSSOA game except when the resampling results in the same message vector as the original plaintext message. More formally, we have:
Thus,
which is non-negligible by assumption.
4 CCA Secure, SOA Insecure Encryption
In this section, we describe a PKE scheme that is IND-CCA secure, but not IND-SOA secure.
4.1 The Scheme
Let \(\mathsf {PKE} ' = (\mathsf {Gen} ',\mathsf {Enc} ',\mathsf {Dec} ',\mathsf {Puncture} ')\) be a puncturable encryption scheme with message space \(\mathbb {F} \) for some field of size \(|\mathbb {F} | \ge 3k\) and \(|\mathbb {F} | = O(k)\) and with ciphertext space \(\mathcal {C}\). Let \(\mathcal {H}= \{h_{s} : \mathcal {C}^{3k} \rightarrow \mathcal {S} _k^{[3k]} \}_{k \in \mathbb {N}, s\in \{0,1\}^{\ell (k)}}\) be a special correlation-intractable hash function ensemble with respect to \(\mathcal {REL}^{\mathsf {PKE} '}\) and with seed length \(\ell (k)\). Let \(\mathsf {PdiO}\) be a public-coin differing-inputs obfuscator.
We construct a scheme \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) as follows.
-
\(\mathsf {Gen} (1^k):\) Run \(( pk ', sk ')\leftarrow \mathsf {Gen} '(1^k)\). Sample \(s\leftarrow \{0,1\}^{\ell (k)}\) as a seed of the hash function \(h_s \in \mathcal {H}\). Then construct the program \(\mathsf {SOA\text {-}Helper}\) in Fig. 3. Set secret key \( sk = sk '\) and public key \( pk = ( pk ',s,\mathsf {PdiO}(\mathsf {SOA\text {-}Helper}))\).
-
\(\mathsf {Enc} ( pk ,m):\) Parse \( pk = ( pk ',s,\mathsf {PdiO}(\mathsf {SOA\text {-}Helper}))\). Output \(\mathsf {Enc} '( pk ',m)\).
-
\(\mathsf {Dec} ( sk ,c):\) Output \(\mathsf {Dec} '( sk ',c)\).
4.2 \(\mathsf {PKE}\) is Not SecShare-SOA Secure
We now formally show that \(\mathsf {PKE}\) allows for a simple SecShare-SOA attack.
Theorem 2
The PKE scheme \(\mathsf {PKE}\) from Sect. 4.1 is not SecShare-SOA secure.
Proof
We construct a PPT algorithm \(A\) that breaks the SecShare-SOA security of \(\mathsf {PKE}\) with non-negligible probability.
Adversary \(A\): Upon receiving a public key \( pk = ( pk ',s,\mathsf {PdiO}(\mathsf {SOA\text {-}Helper}))\) and a tuple of ciphertexts \(\mathbf {c}:=(c _{i})_{i\in [3k]}\), \(A\) computes \( \mathcal {I} = h_s((c _{i})_{i\in [3k]})\). This \(\mathcal {I}\) is the subset that \(A\) submits to its SecShare-SOA experiment. By the security of \(\mathsf {PKE} '\), we may assume that \(c '_{i}\ne c '_{j}\) for all \(i\ne j\), except with some negligible probability \(\nu (k)\) (otherwise, an adversary on \(\mathsf {PKE} '\) could simply encrypt a challenge message and hope for a collision).
Upon receiving openings \((m _{i},R _{i})_{i\in \mathcal {I}}\), \(A\) runs the program \(\mathsf {PdiO}(\mathsf {SOA\text {-}Helper})\) on input \(((c _{i})_{i\in [3k]},(m _{i},R _{i})_{i\in \mathcal {I}})\). By construction of the program, the output is a polynomial \(F\) with \(m _{i}=F(i)\) for all \(i\in [3k]\). Thus, the adversary can finally compute F(0) and give it to the challenger.
Analysis: The analysis is pretty straight-forward, as, by design, the output of the program is exactly what the adversary needs to break the SecShare-SOA security. Thus, we have that,
which is non-negligible by assumption about \(\nu (k)\).
4.3 \(\mathsf {PKE}\) is Still IND-CCA Secure
We show that \(\mathsf {PKE}\) inherits \(\mathsf {PKE} '\)’s IND-CCA security.
Theorem 3
Suppose that \(\mathsf {PKE} '\) is puncturably IND-CCA secure, \(\mathcal {H}\) is a special correlation-intractable hash function ensemble with respect to \(\mathcal {REL}^{\mathsf {PKE} '}\), and \(\mathsf {PdiO}\) be a secure public-coin differing-inputs obfuscator. Then, the PKE scheme \(\mathsf {PKE}\) from Sect. 4.1 is IND-CCA secure.
Proof
Recall that our scheme has polynomial-size message space. We consider a variation to the IND-CCA game where the challenger himself chooses the pair of challenge messages. We call this modified game the \(\$\)-IND-CCA game (defined formally in Definition 13). The IND-CCA game and the \(\$\)-IND-CCA game are polynomially equivalent (as proved in Theorem 7) for polynomially-sized message spaces. Thus, it suffices to show here that our \(\mathsf {PKE}\) scheme is \(\$\)-IND-CCA secure.
Assume for contradiction that there exists an adversary \(A\) that breaks the \(\$\)-IND-CCA security of \(\mathsf {PKE}\) with some non-negligible advantage \(\varepsilon \). We shall arrive at a contradiction through a sequence of hybrid arguments defined below. Let us denote the event that a hybrid \(\mathsf {Hyb}_i\) outputs 1 by \(\mathsf {Hyb}_i \rightarrow 1\). The first hybrid corresponds to the original \(\$\)-IND-CCA security game.
-
\({\mathsf {Hyb}_0}{:}\) In the first hybrid the following game is played.
-
Sample \(b \leftarrow \{0,1\}\).
-
Sample \(m _0,m _1 \leftarrow \mathcal {M} \)
-
Sample \(s\leftarrow \{0,1\}^{\ell (k)}\).
-
Run \(( pk ', sk ')\leftarrow \mathsf {Gen} '(1^k)\). Let \( sk = sk '\).
-
\(c ^*\leftarrow \mathsf {Enc} ( pk ,m _b)\)
-
Construct the program \(\mathsf {SOA\text {-}Helper}\) in Fig. 3 and obfuscate it to get \(\mathsf {PdiO}(\mathsf {SOA\text {-}Helper})\).
-
Let \( pk =( pk ',s,\mathsf {PdiO}(\mathsf {SOA\text {-}Helper}))\).
-
Give \( pk , m _0,m _1, c^*\) to the adversary, and offer the adversary access to a decryption oracle \(\mathsf {Dec} _{c ^*}( sk ,\cdot )\).
-
Finally, let \(b'\) be the output of \(A\). Output 1 if \(b' = b\) and 0 otherwise.
-
We note here that \(\mathsf {Exp}^{\$\text {-}\mathsf {ind\text {-}cca}}_{\mathsf {PKE},A}(k) \equiv \mathsf {Hyb}_0\).
-
\({\mathsf {Hyb}_1}{:}\) This hybrid is the same as \(\mathsf {Hyb}_0\) with the exception of the following modifications. Just before generating the program \(\mathsf {SOA\text {-}Helper}\), sample \(c _r\leftarrow \mathcal {C} \). Compute \( sk [\{c ^*,c _r\}] \leftarrow \mathsf {Puncture} ( sk ,\{c ^*,c _r\})\). We then make the following modifications in Step 3 of the program obfuscated, and denote the resulting program by \(\mathsf {SOA\text {-}Helper}_2\):
-
3.
Decrypt
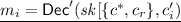 for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\).
for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\).
Furthermore, we now use the punctured key \( sk [\{c ^*,c _r\}]\) to answer \(A \)’s decryption queries, and we output \(\bot \) on inputs \(c ^*,c _r\).
-
3.
Claim
\(\mathsf {Hyb}_1 \approx _{\mathsf {c}}\mathsf {Hyb}_0\).
Proof
We observe that the input/output functionality of the program has not changed with overwhelming probability (over the choice of \(c _r\)), thanks to the puncturability and ciphertext sparseness properties of \(\mathsf {PKE} '\). Furthermore, there is also no change in the functionality of the decryption oracle. Thus, by relying on the indistinguishability obfuscation security (which follows from public-coin differing inputs security) of \(\mathsf {PdiO}\), we have \(\mathsf {Hyb}_1 \approx _{\mathsf {c}}\mathsf {Hyb}_0\).
-
\({\mathsf {Hyb}_2}{:}\) This hybrid is the same as \(\mathsf {Hyb}_1\) with the exception of the following modifications in Step 3 of the program obfuscated. Denote the resulting program by Program \(\mathsf {SOA\text {-}Helper}_2\).
-
3.
Decrypt
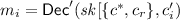 for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\). Use \({{{\underline{\perp }}}}\) and \(\perp \) as the plaintext values when \(c '_{i} = c ^*\) and \(c '_{i} = c _r\), respectively.
for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\). Use \({{{\underline{\perp }}}}\) and \(\perp \) as the plaintext values when \(c '_{i} = c ^*\) and \(c '_{i} = c _r\), respectively.
-
3.
Claim
\(\mathsf {Hyb}_2 \approx _{\mathsf {c}}\mathsf {Hyb}_1\).
Proof
We employ the public-coins differing-inputs obfuscation security of \(\mathsf {PdiO}\) and the special correlation intractability of \(\mathcal {H}\) to prove this claim. More specifically, consider an algorithm \(\mathsf {csamp} (1^k)\) that generates two circuits \(\mathsf {SOA\text {-}Helper}_1\) and \(\mathsf {SOA\text {-}Helper}_2\).
We first show that \(\mathsf {csamp} \) is a public-coin differing-inputs sampler, by employing the special correlation intractability of \(\mathcal {H}\). Recall the special class of binary relations \(\mathcal {REL}^{\mathsf {PKE} '} = \{\mathrm {Rel}_{r}\}_{k \in \mathbb {N}, r \in \{0,1\}^{\ell '(k)}}\) from Definition 9.
Let \(Z = ((c'_i)_{i \in [3k]}, (m_i, R_I)_{i \in \mathcal {I}})\) be an input to the two programs. We will now argue that the only time that \(\mathsf {SOA\text {-}Helper}_1(Z) \ne \mathsf {SOA\text {-}Helper}_2(Z)\) is if \(((c'_i)_{i \in [3k]}, \mathcal {I}) \in \mathrm {Rel}_r\) where r is the randomness of the key-generation procedure used to create \(( pk ', sk ')\) and \(\mathcal {I} =h_{s}((c '_{i})_{i\in [3k]})\).
In order to do so, let \(m'_i = \mathsf {Dec} _{ sk '}(c'_i)\) for \(i \in [3k] \setminus \mathcal {I} \). Now if \(m'_i \ne m_i\) for some \(i \in \mathcal {I} \) then both programs output \(\bot \) since the check in line 2 will fail (by correctness of decryption). Let \(F_1 = \mathsf {decc} _k( (i,m'_i)_{i \in [3k]})\) and let \(F_2 = \mathsf {decc} _k( (i,m''_i)_{i \in [3k]})\) where \(m''_i = m'_i\) unless \(c'_i = c^*\) and \(i \not \in \mathcal {I} \) in which case \(m''_i = \bot \). These are the two polynomials that are used in line 3 of the execution of \(\mathsf {SOA\text {-}Helper}_1(Z), \mathsf {SOA\text {-}Helper}_2(Z)\) respectively. Let \(Q = \{ i~:~ F_1(i) = m'_i\}\). If \(F_1 = F_2\) then both programs have the same output. The only case where this does not happen is if \(F_1 \ne \bot \), \(|Q| = 2k+1\) and \(F_2 = \bot \). Moreover, even in this case both programs output \(\bot \) unless it is the case that \(\mathcal {I} \subseteq Q\). Therefore, the only case where the two programs might produce differing outputs is if \(F_1 \ne \bot \), \(|Q| = 2k+1\) and \(\mathcal {I} \subseteq Q\). This means that \(((c_i)_{i \in [3k]}, \mathcal {I}) \in \mathrm {Rel}_{r}\) where \(\mathcal {I} = h_s((c_i)_{i \in [3k]})\).
By the special correlation intractability property of \(\mathcal {H}\) such inputs Z such that \(\mathsf {SOA\text {-}Helper}_1(Z) \ne \mathsf {SOA\text {-}Helper}_2(Z)\) are computationally hard to find, even given all of the random coins used to generate the two programs, including the hash-seed s and the randomness r used to generate \(( pk ', sk ')\). In other words this shows that algorithm \(\mathsf {csamp} \) that generates two circuits \(\mathsf {SOA\text {-}Helper}_1\) and \(\mathsf {SOA\text {-}Helper}_2\) defines a public-coin differing-inputs family. We can therefore rely on the public-coin differing-input security of \(\mathsf {PdiO}\) to see that \(\mathsf {Hyb}_2\) and \(\mathsf {Hyb}_1\) are indistinguishable.
-
\({\mathsf {Hyb}_3}{:}\) This hybrid is the same as \(\mathsf {Hyb}_2\) with the following exception. Instead of giving \(c ^*\) to the adversary, give \(c _r\) to the adversary as a challenge.
Claim
\(\mathsf {Hyb}_3 \approx _{\mathsf {c}}\mathsf {Hyb}_2\).
Proof
Assume that for an adversary \(A\), \(\Pr [\mathsf {Hyb}_2 \rightarrow 1]\) and \(\Pr [\mathsf {Hyb}_3 \rightarrow 1]\) differ by a non-negligible amount \(\varepsilon \). Then we shall construct an adversary \(B \) that breaks the puncturability of \(\mathsf {PKE} '\) with probability \(\varepsilon \). \(B \) behaves the same as the challenger in \(\mathsf {Hyb}_2\) and interacts with \(A\) except for the following modifications. It first samples \(b,m _0,m _1\), and gives \(m _b\) to its challenger. Upon receiving two ciphertexts \(c_{\hat{b}},c_{1-\hat{b}}\), proceed by giving \(c_{\hat{b}}\) to \(A\) as the challenge ciphertext. Finally, output the output of the experiment.
Observe that if \(\hat{b} = 0\), then we are in \(\mathsf {Hyb}_2\). Else, we are in \(\mathsf {Hyb}_3\). Thus,
-
\({\mathsf {Hyb}_4}{:}\) This hybrid is the same as \(\mathsf {Hyb}_3\) with the exception of the following modifications in Step 3 of the program obfuscated. Denote the resulting program by Program \(\mathsf {SOA\text {-}Helper}_4\).
-
3.
Decrypt
 for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\).
for \(i\in [3k]\setminus \mathcal {I} \) and for \(c '_{i} \not \in \{c ^*,c _r\}\).Use
 and \(\perp \) as the plaintext values when \(c '_{i} = c ^*\) and \(c '_{i} = c _r\), respectively.
and \(\perp \) as the plaintext values when \(c '_{i} = c ^*\) and \(c '_{i} = c _r\), respectively.
-
3.
Claim
\(\mathsf {Hyb}_4 \approx _{\mathsf {c}}\mathsf {Hyb}_3\).
Proof
The modification introduced in \(\mathsf {Hyb}_4 \) is similar to the modification introduced in \(\mathsf {Hyb}_2\) earlier. Hence, the proof here follows on the same lines as the proof of Claim 4.3.
-
\({\mathsf {Hyb}_5}{:}\) This hybrid is the same as \(\mathsf {Hyb}_4\) with the following exception. In the obfuscated program, instead of hardcoding the punctured secret key, we shall hardcode again the original secret key.
Claim
\(\mathsf {Hyb}_5 \approx _{\mathsf {c}}\mathsf {Hyb}_4\).
Proof
Note that the input/output functionalities of the programs have not changed as we moved from \(\mathsf {Hyb}_4\) to \(\mathsf {Hyb}_5\). By applying the indistinguishability obfuscation security of \(\mathsf {PdiO}\), we have that \(\mathsf {Hyb}_5 \approx _{\mathsf {c}}\mathsf {Hyb}_4\).
Finally, note that in \(\mathsf {Hyb}_5\), the adversary’s view does not depend on the challenge bit \(b\) anymore: neither the obfuscated circuit \(\mathsf {SOA\text {-}Helper}\) nor the challenge ciphertext \(c _r\) depend on \(b\). We get that \(\mathsf {Hyb}_5\) outputs \(1\) with probability exactly \(1/2\). The theorem follows.
5 Extension to Selective Opening of Keys (SOA-K)
We now show how to extend our main result to selective opening of keys (SOA-K), where the adversary gets ciphertexts under many different public keys and can selectively request to see some of the secret keys. This corresponds to a setting where there are multiple receivers and the adversary can corrupt some subset of them and get their keys (rather than the previous setting where there were multiple senders and the adversary could corrupt some subset of them and get their encryption randomness).
For this notion, we will consider PKE schemes where the public/secret key pairs are generated dependent on some common public parameters. More specifically, in addition to the triple of algorithms \((\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\), we introduce an algorithm \(\mathsf {PGen}\) that takes the security parameter and outputs some public parameters \(\mathsf {params}\leftarrow \mathsf {PGen}(1^k)\). All the other algorithms take \(\mathsf {params}\) as an additional input. We show how to construct such PKE schemes which are CCA secure but are IND-SOA-K insecure. We leave it as an open problem to construct such examples in the setting without public parameters.
SOA-K has been considered before [3, 17]; while [3] only treated the the simulation-based definition, [17] treated the indistinguishability-based definition that we will also consider in this work.
Definition 11 (IND-SOA-K Security)
For a PKE scheme \(\mathsf {PKE} =(\mathsf {PGen}, \mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\), a polynomially bounded function \(n=n(k)>0\), and a stateful PPT adversary \(A\), consider the experiment in Fig. 4. We only allow \(A\) that always output re-sampling algorithms as in Definition 2. We call \(\mathsf {PKE}\) IND-SOA-K (for “indistinguishable under selective-opening key attacks”) secure if for all PPT \(A\), we have
Secret Sharing SOA-K Security. We now define the dual of SecShare-SOA-K security for key corruption. The only difference from the SecShare-SOA-K security security is that each secret share is encrypted with an independently sampled public key (instead of one public key being used to encrypt all shares), and corruption would reveal the corresponding secret keys (instead of the random coins used to generate the ciphertexts). Details follow.
Definition 12 (SecShare-SOA-K Security)
Let \(\mathbb {F} \) be a field of size determined by the security parameter and let \(\mathsf {PKE} =(\mathsf {PGen},\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme, with message space \(\mathcal {M} = ([n] \times \mathbb {F})\). For any parameters \(t,n\) that are polynomial in the security parameter, consider the experiment in Fig. 4 with a stateful PPT adversary \(A\). We say that \(\mathsf {PKE}\) receiver-corruption secret-sharing selective opening attack secure if
is negligible for all PPT \(A\).
Theorem 4
If a PKE scheme \(\mathsf {PKE}\) is IND-SOA-K secure, then it is SecShare-SOA-K secure.
The proof of Theorem 4 follows with the same argument as Theorem 1.
In this section, we describe a PKE scheme \(\mathsf {PKE} ^*\) that is IND-CCA secure, but not IND-SOA-K secure.
5.1 A CCA Secure, SecShare-SOA-K Insecure Encryption
Let \(\mathsf {PKE'} = (\mathsf {Gen'},\mathsf {Enc'},\mathsf {Dec'})\) be any encryption scheme that is IND-CPA secure but is not SecShare-SOA secure (with sender-randomness corruption), and whose message space is a field \(\mathbb {F} \) and randomness space is \(\mathcal {R} _{\mathsf {Enc'}}\). In particular, this can be the scheme that we constructed in Sect. 4. Let \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be an IND-CCA secure encryption scheme with message space \(\mathbb {F} \times \mathcal {R} _{\mathsf {Enc'}}\). We construct a PKE scheme \(\mathsf {PKE} ^*= (\mathsf {PGen}^*,\mathsf {Gen} ^*,\mathsf {Enc} ^*,\mathsf {Dec} ^*)\) as follows.
-
\({\mathsf {PGen}^*(1^k)}{:}\) Sample \(( pk ', sk ')\leftarrow \mathsf {Gen'} (1^k)\) and set public parameters \(\mathsf {params}= pk '\).
-
\({\mathsf {Gen} ^*(1^k,\mathsf {params})}{:}\) Run \(( pk , sk )\leftarrow \mathsf {Gen} (1^k)\). Output \(( pk , sk )\) as the public-key secret-key pair.
-
\({\mathsf {Enc} ^*(\mathsf {params}, pk ,m)}{:}\) Parse \(\mathsf {params}= pk '\). Sample \(r\leftarrow \mathcal {R} _{\mathsf {Enc'}}\) and compute \(c'\leftarrow \mathsf {Enc'} ( pk ',m;r)\). Compute \(c\leftarrow \mathsf {Enc} ( pk ,(m,r))\). Output the ciphertext \(c^*= (c',c)\).
-
\({\mathsf {Dec} ^*(\mathsf {params}, sk ,c^*)}{:}\) Parse \(\mathsf {params}= pk '\) and \(c^*= (c',c)\). Compute \((m,r) = \mathsf {Dec} ( sk ,c)\). Verify if \(c'\leftarrow \mathsf {Enc'} ( pk ',m;r)\). If so, then output m, else output \(\perp \).
\(\mathsf {PKE} ^*\) is not SecShare-SOA-K secure. We now formally show that \(\mathsf {PKE} ^*\) allows for a simple SecShare-SOA-K attack. The idea is straight-forward. An SecShare-SOA-K adversary, upon learning secret keys can decrypt the ciphertexts and learn the random coins used to compute the \(\mathsf {PKE'} \) part of ciphertexts. This amounts to an SecShare-SOA attack on \(\mathsf {PKE'} \), which is SecShare-SOA insecure.
Theorem 5
If \(\mathsf {PKE'} \) is not SecShare-SOA secure then \(\mathsf {PKE} ^*\) is not SecShare-SOA-K secure. In particular, if there is a polynomial-time attack with advantage \(\varepsilon \) against the SecShare-SOA security of \(\mathsf {PKE'} \) then there is also a polynomial time attack with the same advantage \(\varepsilon \) against the SecShare-SOA-K security of \(\mathsf {PKE} ^*\).
Proof
Assume that there exists a PPT adversary \(A\) with non-negligible advantage \(\varepsilon \) against SecShare-SOA security of \(\mathsf {PKE'} \). We construct a PPT algorithm \(B \) that breaks the SecShare-SOA-K security of \(\mathsf {PKE} ^*\) also with probability \(\varepsilon \).
Adversary \({B}{: }\) Upon receiving \(\mathsf {params}= pk '\), \(B \) gives \( pk '\) to \(A\). Upon receiving a tuple of public keys \(\mathbf {pk}:= ( pk _1,\ldots , pk _n)\) and a tuple of ciphertexts \(\mathbf {c} ^*:=(c^*_{i})_{i\in [n]}\), where \(c^*_i = (c'_i,c_i)\), give \((c'_1,\ldots ,c'_n)\) to \(A\). When \(A\) responds with a subset \(\mathcal {I} \in [n]\), give \(\mathcal {I} \) to the challenger. Then, upon receiving \((m_i, sk _i)_{i \in \mathcal {I}}\), compute \((m_i,r_i) = \mathsf {Dec} ( sk _i,c_i)\) for every \(i \in \mathcal {I} \). Then, give \((m_i,r_i)_{i \in \mathcal {I}}\) to \(A\). Since this emulates the SecShare-SOA attack on \(\mathsf {PKE'} \) to \(A\), \(A\)’s output is such that it breaks SecShare-SOA security of \(\mathsf {PKE'} \) with probability \(\varepsilon \). In turn, by outputting \(A\)’s output, \(B \) also breaks SecShare-SOA-K security of \(\mathsf {PKE} ^*\) with probability \(\varepsilon \).
\(\mathsf {PKE} ^*\) is IND-CCA secure. We now show that \(\mathsf {PKE} ^*\) inherits \(\mathsf {PKE} \)’s IND-CCA security.
Theorem 6
Suppose that \(\mathsf {PKE} \) is an IND-CCA-secure encryption scheme, \(\mathsf {PKE'} \) is an IND-CPA secure encryption scheme. Then, \(\mathsf {PKE} ^*\) is IND-CCA secure.
Proof
Assume for contradiction that there exists an adversary \(A\) that breaks the IND-CCA security of \(\mathsf {PKE} ^*\) with some advantage \(\varepsilon \). We shall show that \(\varepsilon \) is negligible through a hybrid argument as follows. Let us denote the event that a hybrid \(\mathsf {Hyb}_i\) outputs 1 by \(\mathsf {Hyb}_i = 1\). The first hybrid corresponds to the original IND-CCA security game.
-
\({\mathsf {Hyb}_0}{:}\) In the first hybrid the following game is played.
-
1.
Sample \(b\leftarrow \{0,1\}\).
-
2.
Sample \(( pk ', sk ')\leftarrow \mathsf {Gen'} (1^k)\) and set \(\mathsf {params}= pk '\).
-
3.
Sample \(( pk , sk )\leftarrow \mathsf {Gen} (1^k)\).
-
4.
Give \((\mathsf {params}, pk )\) to \(A\) and answer its decryption queries using \( sk \).
-
5.
Upon receiving \(m _0,m _1\), proceed as follows.
-
6.
Sample \(r\leftarrow \mathcal {R} _{\mathsf {Enc'}}\) and compute \(\tilde{c}'\leftarrow \mathsf {Enc'} ( pk ',m_b;r)\).
-
7.
Compute \(\tilde{c}\leftarrow \mathsf {Enc} ( pk ,(m_b,r))\).
-
8.
Give \((\tilde{c}',\tilde{c})\) to \(A\) and continue to answer \(A\)’s decryption queries using \( sk \).
-
9.
Finally, let \(b'\) be the output of \(A\). Output 1 if \(b' = b\) and 0 otherwise.
-
1.
-
\({\mathsf {Hyb}_1}{:}\) This hybrid is the same as \(\mathsf {Hyb}_0\), except that all of \(A \)’s decryption queries \(c^*=(c',c)\) with \(c=\tilde{c}\) are automatically rejected.
We note that this change is purely conceptual: any such query would have been rejected already in \(\mathsf {Hyb}_0\) (by the decryption check for \(c'=\mathsf {Enc} ( pk ',m;r)\), where \((m,r)\leftarrow \mathsf {Dec} ( sk ,c)\)).
-
\({\mathsf {Hyb}_2}{:}\) This hybrid is the same as \(\mathsf {Hyb}_1\) except for the following modification. In constructing \(\tilde{c}\), instead of using \((m_b,r)\) as the plaintext, we use \((m_{\tilde{b}},\tilde{r})\) for an indendently sampled random bit \(\tilde{b}\), and a freshly uniformly sampled random string \(\tilde{r}\).
-
7.
Sample \(\tilde{b}\leftarrow \{0,1\}\) and \(\tilde{r}\leftarrow \mathcal {R} _{\mathsf {Enc'}}\). Compute \(\tilde{c}\leftarrow \mathsf {Enc} ( pk ,({{{\underline{m_{\tilde{b}},\tilde{r}}}}}))\).
-
7.
Claim
\(\mathsf {Hyb}_2 \approx _{\mathsf {c}}\mathsf {Hyb}_1\).
Proof
We shall establish this claim by relying on the CCA security of \(\mathsf {PKE} \). Assume for contradiction that \(|\Pr [\mathsf {Hyb}_2 = 1] - \Pr [\mathsf {Hyb}_1 = 1]| = \varepsilon \) is non-negligible. Then we construct an adversary \(B \) that breaks CCA security of \(\mathsf {PKE} \) with advantage \(\varepsilon \).
Adversary \(B \). \(B \) simultaneously interacts with its CCA challenger for \(\mathsf {PKE} \) and \(A\) as follows. Upon receiving \( pk \) from the challenger, sample \(( pk ', sk ')\leftarrow \mathsf {Gen'} (1^k)\), set \(\mathsf {params}= pk '\), and give \(\mathsf {params}, pk \) to \(A\). Answer A’s decryption queries by using its own decryption oracle as follows. Upon given a query \(c^*= (c',c)\) by \(A\), decrypt \(c\) using its own oracle to get (m, r); verify whether \(c'\leftarrow \mathsf {Enc'} ( pk ',m;r)\). If so, then give m to \(A\) and give \(\perp \) otherwise. Next, upon receiving \((m_0,m_1)\) from \(A\), sample \(r\leftarrow \mathcal {R} _{\mathsf {Enc'}}\) and compute \(\tilde{c}'\leftarrow \mathsf {Enc'} ( pk ',m_b;r)\). Also sample \(\tilde{b}\leftarrow \{0,1\}\) and \(\tilde{r}\leftarrow \mathcal {R} _{\mathsf {Enc'}}\). Give \((m_b,r),(m_{\tilde{b}},\tilde{r})\) to the challenger. Upon receiving \(\tilde{c}\), give \(\tilde{c}^*= (\tilde{c}',\tilde{c})\) to the \(A\). Continue to answer decryption queries in the same manner, except that all of \(A\)’s decryption queries with \(c=\tilde{c}\) are automatically rejected. (Note that \(B \) cannot decrypt the corresponding \(c\) on its own; however, by our change from \(\mathsf {Hyb}_1\), this is not necessary.)
Analysis. Observe that \(A\) perfectly simulates \(\mathsf {Hyb}_2\) or \(\mathsf {Hyb}_1\), depending on \(\tilde{c}\).
-
\({\mathsf {Hyb}_3}{:}\) This hybrid is the same as \(\mathsf {Hyb}_2\) except for the following modification. In constructing \(\tilde{c}'\), instead of encrypting \(m_b\) as the plaintext, we encrypt \(m_{\tilde{b}}\).
-
6.
Sample \(r\leftarrow \mathcal {R} _{\mathsf {Enc'}}\) and compute \(\tilde{c}'\leftarrow \mathsf {Enc'} ( pk ',{{{\underline{m_{\tilde{b}}}}}};r)\).
-
6.
Claim
\(\mathsf {Hyb}_3 \approx _{\mathsf {c}}\mathsf {Hyb}_2\).
Proof
We shall establish this claim by relying on the CPA security of \(\mathsf {PKE'} \). Assume for contradiction that \(|\Pr [\mathsf {Hyb}_3 = 1] - \Pr [\mathsf {Hyb}_2 = 1]| = \varepsilon \) is non-negligible. Then we construct an adversary \(B \) that breaks CPA security of \(\mathsf {PKE'} \) with advantage \(\varepsilon \).
Adversary \(B \). \(B \) simultaneously interacts with its CPA challenger for \(\mathsf {PKE'} \) and \(A\) as follows. \(B \) behaves the same way as the \(\mathsf {Hyb}_2\) challenger, except for the following modification. Instead of generating \( pk '\) and \(\tilde{c}'\) by himself, he uses \( pk '\) from the challenger and generates \(\tilde{c}'\) as follows. Upon \(A\) giving \((m_0,m_1)\), send \((m_b,m_{\tilde{b}})\) to the challenger and use the response as \(\tilde{c}'\) in the interaction with \(A\). Finally, output the output of \(A\).
Analysis. Firstly, we argue that the above description of \(B \) is sound: note that the random coins used in computing \(\tilde{c}'\) is not used in any part of \(B \)’s interaction with \(A\). Next, we observe that when \(\tilde{c}'\) encrypts 0 then the view of \(A\) is identical to that in \(\mathsf {Hyb}_2\); when \(\tilde{c}'\) encrypts 1 then the view of \(A\) is identical to that in \(\mathsf {Hyb}_3\). Thus, \(\mathsf {Adv}^{\mathsf {ind\text{- }cpa}}_{\mathsf {PKE'},B} (k) = \varepsilon \), a contradiction.
We note here that in \(\mathsf {Hyb}_3\), A’s view is independent of the challenge bit \(b\), and thus the theorem follows.
6 Conclusions
In this paper, we show that there are schemes which are CPA and even CCA secure, but which are clearly insecure in the selective opening scenario. Several open questions remain. Most importantly, it would be interesting to get such examples under weaker assumptions. As a first step, one could hope for an example that only relies on indistinguihsability obfuscation rather than public-coin differing-inputs obfuscation and correlation-intractable hash functions. Ideally, one would get rid of obfuscation altogether. Alternatively, it would be interesting if such examples can lead to surprising positive results or perhaps can imply (some variant of) obfuscation. Another open question is to construct a counterexample for SOA-K security without relying on a scheme with common public parameters.
References
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Barak, B., Lindell, Y., Vadhan, S.P.: Lower bounds for non-black-box zero knowledge. In: Proceedings of 44th Symposium on Foundations of Computer Science, FOCS 2003, 11–14 October 2003, Cambridge, MA, USA, pp. 384–393. IEEE Computer Society (2003). http://dx.doi.org/10.1109/SFCS.2003.1238212
Bellare, M., Dowsley, R., Waters, B., Yilek, S.: Standard security does not imply security against selective-opening. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 645–662. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_38
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01001-9_1
Bellare, M., Stepanovs, I., Waters, B.: New negative results on differing-inputs obfuscation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 792–821. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_28
Böhl, F., Hofheinz, D., Kraschewski, D.: On definitions of selective opening security. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 522–539. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_31
Canetti, R., Chen, Y., Reyzin, L.: On the correlation intractability of obfuscated pseudorandom functions. IACR ePrint Archive, report 2015/334 (2015). http://eprint.iacr.org/2015/334
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: Proceedings of STOC 1998, pp. 209–218. ACM (1998)
Cohen, A., Holmgren, J., Vaikuntanathan, V.: Publicly verifiable software watermarking. IACR ePrint Archive, report 2015/373 (2015). http://eprint.iacr.org/2015/373
Dodis, Y., Ristenpart, T., Vadhan, S.: Randomness condensers for efficiently samplable, seed-dependent sources. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 618–635. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28914-9_35
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. In: Proceedings of FOCS 1999, pp. 523–534. IEEE Computer Society (1999)
Fehr, S., Hofheinz, D., Kiltz, E., Wee, H.: Encryption schemes secure against chosen-ciphertext selective opening attacks. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 381–402. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_20
Fuchsbauer, G., Heuer, F., Kiltz, E., Pietrzak, K.: Standard security does imply security against selective opening for markov distributions. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 282–305. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_12
Fujisaki, E.: All-but-many encryption - a new framework for fully-equipped uc commitments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 426–447. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45608-8_23
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, 26–29 October 2013, Berkeley, CA, USA, pp. 40–49. IEEE Computer Society (2013). http://dx.doi.org/10.1109/FOCS.2013.13
Garg, S., Gentry, C., Halevi, S., Wichs, D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 518–535. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_29
Hazay, C., Patra, A., Warinschi, B.: Selective opening security for receivers. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 443–469. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_19
Hemenway, B., Libert, B., Ostrovsky, R., Vergnaud, D.: Lossy encryption: constructions from general assumptions and efficient selective opening chosen ciphertext security. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 70–88. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_4
Hofheinz, D.: All-but-many lossy trapdoor functions. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 209–227. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_14
Hofheinz, D., Rupp, A.: Standard versus selective opening security: separation and equivalence results. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 591–615. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_25
Huang, Z., Liu, S., Qin, B.: Sender-equivocable encryption schemes secure against chosen-ciphertext attacks revisited. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 369–385. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_23
Ishai, Y., Pandey, O., Sahai, A.: Public-coin differing-inputs obfuscation and its applications. IACR ePrint Archive, report 2014/942 (2014). http://eprint.iacr.org/2014/942
Ishai, Y., Pandey, O., Sahai, A.: Public-coin differing-inputs obfuscation and its applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 668–697. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_26
Koppula, V., Ramchen, K., Waters, B.: Separations in circular security for arbitrary length key cycles. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 378–400. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_15
Marcedone, A., Orlandi, C.: Obfuscation \(\Rightarrow \) (IND-CPA security \(\nRightarrow \) circular security). In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 77–90. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_5
Naor, M., Pinkas, B.: Efficient oblivious transfer protocols. In: Proceedings of SODA 2001, pp. 448–457. ACM/SIAM (2001)
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_31
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: Proceedings of STOC 2008, pp. 187–196. ACM (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A IND-CCA Game with Random Challenge Messages
A IND-CCA Game with Random Challenge Messages
We shall now define a variation of the IND-CCA game. The modification at a high level is that, in the new game, the challenger himself samples the challenge message pair uniformly at random.
Definition 13
( \(\$\) -IND-CCA Secure PKE). Let \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) be a tuple of PPT algorithms. \(\mathsf {PKE} \) is said to be a \(\$\)-IND-CCA-secure encryption, if it for every PPT adversary \(A\),
is negligible.
Theorem 7
Let \(\mathsf {PKE} = (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) is a PKE scheme with polynomial-size message ciphertext. If \(\mathsf {PKE}\) is \(\$\)-IND-CCA secure as per Definition 13, then \(\mathsf {PKE}\) is IND-CCA secure.
Proof
Let the message space of \(\mathsf {PKE}\) be \(\mathcal {M} \), with \(|\mathcal {M} | = \ell (k)\), for a polynomial \(\ell \). Assume for contradiction that there exists an adversary \(A\) that breaks the IND-CCA security of \(\mathsf {PKE}\) with advantage \(\varepsilon \). Then we shall show an adversary \(B \) that breaks the \(\$\)-IND-CCA security of \(\mathsf {PKE}\) with advantage \(\varepsilon /\ell (k)^2\). With the help of \(A\), \(B \) interacts with its \(\$\)-IND-CCA challenger as follows (Fig. 5).
Adversary \({B}{: }\) Upon receiving \( pk ,(m _0,m _1),c ^*\), give \( pk \) to \(A\). Let \((m '_0,m '_1)\) be the pair of message given in response by \(A\). Check if \((m '_0,m '_1) = (m _0,m _1)\). If not, sample \(b' \leftarrow \{0,1\}\) and respond to the challenger with \(b'\). Otherwise, give \(c ^*\) to \(A\). Output whatever \(A\) outputs.
Analysis: Let \(\mathsf {E_{SameChal}}\) denote the event that \((m '_0,m '_1) = (m _0,m _1)\). Note that, since \(m _0,m _1\) are chosen uniformly at random, we have that \(\Pr [\mathsf {E_{SameChal}}] = \frac{1}{\ell (k)^2}\). Furthermore,
On the other hand,
Putting them together, we have that, Thus,
leading to a contradiction.
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Hofheinz, D., Rao, V., Wichs, D. (2016). Standard Security Does Not Imply Indistinguishability Under Selective Opening. In: Hirt, M., Smith, A. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9986. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53644-5_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-53644-5_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53643-8
Online ISBN: 978-3-662-53644-5
eBook Packages: Computer ScienceComputer Science (R0)








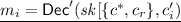 for
for 
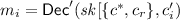 for
for  for
for  and
and 

