Single-Key to Multi-Key Functional Encryption with Polynomial Loss

Abstract

Functional encryption (FE) enables fine-grained access to encrypted data. In a FE scheme, the holder of a secret key $\mathsf {FSK}_f$ (associated with a function f) and a ciphertext c (encrypting plaintext x) can learn f(x) but nothing more.

An important parameter in the security model for FE is the number of secret keys that adversary has access to. In this work, we give a transformation from a FE scheme for which the adversary gets access to a single secret key (with ciphertext size sub-linear in the circuit for which this secret key is issued) to one that is secure even if adversary gets access to an unbounded number of secret keys. A novel feature of our transformation is that its security proof incurs only a polynomial loss.

This paper was jointly presented with the paper titled “Compactness vs Collusion Resistance in Functional Encryption” by Baiyu Li and Daniele Micciancio. Research supported in part from a DARPA/ARL SAFEWARE Award, AFOSR Award FA9550-15-1-0274, NSF CRII Award 1464397 and a research grant from the Okawa Foundation. The views expressed are those of the author and do not reflect the official policy or position of the funding agencies.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Functional encryption [SW05, BSW11, O’N10] generalizes the traditional notion of encryption by providing recipients fine-grained access to data. In a functional encryption ($\mathsf {FE}$) system, holder of the master secret key $\mathsf {MSK}$ can derive secret key $\mathsf {FSK}_f$ for a circuit f. Given a ciphertext c (encrypting x) and the secret key $\mathsf {FSK}_f$, one can learn f(x) but nothing else about x is leaked. Functional encryption emerged as a generalization of several other cryptographic primitives like identity based encryption [Sha84, BF01, Coc01], attribute-based encryption [GPSW06, GVW13] and predicate encryption [KSW08, GVW15].

Single-Key vs Multi-Key. Results by Sahai and Seyalioglu [SS10] and Goldwasser, Kalai, Popa, Vaikuntanathan, and Zeldovich [GKP+13] provided $\mathsf {FE}$ scheme supporting all of ${\mathsf {P}}/{\mathsf {poly}}$ circuits (based on standard assumptions). However, these constructions provide security only when the adversary is limited to obtaining a single functional secret key.¹ We call such a scheme as a single-key $\mathsf {FE}$ scheme. On the other hand, Garg, Gentry, Halevi, Raykova, Sahai and Waters [GGH+13] construct an $\mathsf {FE}$ scheme for ${\mathsf {P}}/{\mathsf {poly}}$ circuits and supporting security even when the adversary has access to an unbounded (polynomial) number of functional secret keys. We call such as scheme as a multi-key $\mathsf {FE}$ scheme. However, the work of Garg et al. assumes indistinguishability obfuscation ($i\mathcal {O}$) [GGH+13].

A single-key $\mathsf {FE}$ scheme is said to have weakly compact ciphertexts if the size of the encryption circuit grows sub-linearly with the circuit for which secret key is given out. Ananth and Jain [AJ15] and Bitansky and Vaikuntanathan [BV15] showed that using single-key $\mathsf {FE}$ with weakly compact ciphertexts one can construct $i\mathcal {O}$ which can then be used to construct multi-key $\mathsf {FE}$ [GGH+13, Wat15]. However, this transformation incurs an exponential loss in security reduction. We ask:

1.1 Our Results

In this work, we answer the above question positively. More specifically, we give a generic transformation from single-key, compact $\mathsf {FE}$ to multi-key $\mathsf {FE}$. Below, we highlight two additional features of our transformation:

• 1. Our transformation works even if the single key scheme we start with is weakly selective secure. The selective notion of security considered in literature restricts the adversary to commit to the challenge messages before seeing the public parameters but still allows functional secret key queries to be adaptively made (after seeing the challenge ciphertext and the public parameters). The weakly selective security (denoted by ${\mathsf {Sel}}^*$) restricts the adversary to commit to her challenge messages as well as make all the functional secret key queries before seeing the public parameters. Nonetheless, the multi-key scheme that we obtain is selectively secure.

• 2. For our transformation to work it is sufficient if the single-key scheme has weakly compact ciphertexts. However, the multi-key scheme resulting from our transformation has fully compact ciphertexts (independent of the circuit size).

Comparison with Concurrent and Independent Work. In a concurrent and independent work, Li and Micciancio [LM16] obtain a result similar to our, but using very different techniques. Their construction is based on two building blocks: SUM and PRODUCT constructions. The SUM and PRODUCT constructions take two $\mathsf {FE}$ schemes as input with security when $q_1$ and $q_2$ secret keys are given to the adversary, respectively. These constructions output a $\mathsf {FE}$ scheme with security when $q_1 + q_2$ and $q_1\cdot q_2$ secret keys are provided to the adversary, respectively. Using these two building blocks, they present two constructions of multi-key $\mathsf {FE}$ with different security and efficiency tradeoffs. A nice feature of their result is that their construction just uses length doubling pseudorandom generator in addition to $\mathsf {FE}$. However, their resultant multi-key $\mathsf {FE}$ scheme inherits the security and compactness property of the single-key scheme they start with. In particular, if the starting scheme in their transformation is weakly selectively secure (resp., weakly compact) then the resulting multi-key scheme is also weakly selectively secure (resp., weakly compact). On the other hand, our transformation always yields a selectively secure and fully compact scheme.

Fig. 1.

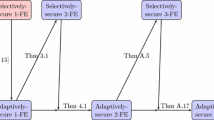
Relationships between different notions of $\mathsf {IND}$-$\mathsf {FE}$ parameterized by (xx, yy, zz). $xx \in \{1,\mathsf {Unb}\}$ denotes the number of functional secret keys. $yy \in \{{\mathsf {Sel}}^*,{\mathsf {Sel}},\mathsf {Adp}\}$ denotes weakly selective, selective or adaptive security. $zz \in \{{\mathsf {NC}},\mathsf {WC},\mathsf {FC},\mathsf {WidC}\}$ denotes the efficiency of the system: ${\mathsf {NC}}$ denotes non-compact ciphertexts, $\mathsf {WC}$ denotes weakly compact ciphertexts, $\mathsf {FC}$ denotes fully-compact ciphertexts and $\mathsf {WidC}$ denotes width-compact ciphertexts. Non-trivial relationships are given by solid arrows, and trivial relationships are given by dashed arrows.

1.2 Obtaining Compactness and Adaptivity in $\mathsf {FE}$

Using the transformation of Ananth, Brakerski, Segev and Vaikuntanathan [ABSV15] we can boost the security of our transformation from selectively to adaptive (while maintaining a polynomial loss). However, we note this transformation does not preserve compactness. In particular, even if the input to this transformation is a fully compact scheme, the resulting $\mathsf {FE}$ scheme is non-compact (where the ciphertext size can depend arbitrarily on the circuit size). In contrast, note that Ananth and Sahai [AS16] do provide an adaptively secure fully compact $\mathsf {FE}$ scheme based on $i\mathcal {O}$. Whether adaptive security with full compactness can be obtained from poly-hard $\mathsf {FE}$ is an interesting open problem. Partial progress on this question can be obtained using Hemenway et al. [HJO+15] who note that using the transformation of Ananth and Sahai [AS16] (starting with a fully compact selective $\mathsf {FE}$, something that our transformation provides) along with adaptively secure garbled circuits [BHR12, HJO+15] yields an adaptively secure $\mathsf {FE}$ scheme whose ciphertext size grows with the on-line complexity of garbled circuits. The state of the art construction of adaptively secure garbled circuits [HJO+15] achieves an online-complexity that grows with the width of the circuit to be garbled. Hence, this yields a $\mathsf {FE}$ scheme with width compact ciphertexts ($\mathsf {WidC}$); for which the size of the ciphertext grows with the width of circuits for which secret-keys are given out. We note that Ananth, Jain and Sahai [AJS15] and Bitansky and Vaikuntanthan [BV15] provide techniques for obtaining compactness in $\mathsf {FE}$ schemes. However, these results are limited to the selective security setting. Figure 1 shows known relationship between various notions of $\mathsf {FE}$ and the new relationships resulting from this work.

2 Our Techniques

We now give an overview of the techniques used in constructing multi-key, selective $\mathsf {FE}$ from single-key, weakly selective $\mathsf {FE}$. We first give a description of a multi-key, selective $\mathsf {FE}$ scheme based on indistinguishability obfuscation ($i\mathcal {O}$). Though this result is not new, our construction is arguably different than the schemes of Garg et al. [GGH+13] and Waters [Wat15] and makes use of garbled circuits [Yao86]. Later, using techniques from works of Garg et al. [GPS15, GPSZ16] we obtain a $\mathsf {FE}$ scheme whose security can be based on polynomially hard single-key, weakly selective $\mathsf {FE}$. The main novelty lies in designing a $\mathsf {FE}$ scheme from $i\mathcal {O}$ that is “amenable” to the techniques of Garg et al. [GPS15, GPSZ16] to avoid exponential loss in security.

$i\mathcal {O}$ Based Construction. Recall that a circuit garbling scheme (or randomized encoding in general) allows to encode an input x and a circuit C to obtain garbled input labels $\widetilde{x}$ and garbled circuit $\widetilde{C}$ respectively. Informally, the security of garbled circuits ensures that given $\widetilde{x}$ and $\widetilde{C}$, it is possible to learn C(x) but nothing else. An additional feature of Yao’s garbled circuits is that it is possible to encode the input x and the circuit C separately as long as the two encoding schemes share the same random tape.

At a high level, the ciphertext of our $\mathsf {FE}$ scheme corresponds to garbled input labels and the functional secret key corresponds to the garbled circuit. Intuitively, from the security of garbled circuits we can deduce that given the $\mathsf {FE}$ ciphertext c (encrypting x) and the functional secret key $\mathsf {FSK}_f$ it is possible to learn f(x) but nothing else. But as mentioned before, to enable encoding the input x and the circuit C separately, the random coins used must be correlated in a certain way. The main crux of the construction is in achieving this correlation using indistinguishability obfuscation ($i\mathcal {O}$).

The correlation between the randomness used for garbling the input labels and the circuit is achieved by deriving the coins pseudorandomly using a $\mathsf {PRF}$ key S. This $\mathsf {PRF}$ key S also serves as the master secret key of our $\mathsf {FE}$ scheme. We now give the details of how the public key and the functional secret keys are derived from the master secret key S.

The public key of our $\mathsf {FE}$ scheme is an obfuscation of a program that takes as input some randomness r and outputs a “token” $t = \mathsf {PRG}(r)$ where $\mathsf {PRG}$ is a length doubling pseudorandom generator and a key $K = \mathsf {PRF}(S,t)$. The key K is used for deriving the input labels for the garbled circuit scheme say, that the two labels of the i-th input wire are given by $\{\mathsf {PRF}(K,i\Vert b)\}_{b \in \{0,1\}}$. The $\mathsf {FE}$ ciphertext encrypting a message m is given by the token t and the input labels corresponding to m i.e. $(t,\{\mathsf {PRF}(K,i\Vert m_i)\}_{i \in [n]})$. The description of the program implementing the public key is given in Fig. 2.

Fig. 2.

Program implementing the public key

The functional secret key for a circuit $C_f$ is an obfuscation of another program that takes as input the token t and first derives the key $K = \mathsf {PRF}(S,t)$. It then outputs a garbled circuit $\widetilde{C}_f$ where the garbled input labels are derived using key K. In particular, the input labels “encrypted” in the garbled evaluation table of $\widetilde{C}_f$ are given by $\{\mathsf {PRF}(K,i\Vert b)\}_{i \in [n],b \in \{0,1\}}$. The description of the program implementing the functional secret key is given in Fig. 3. The $\mathsf {FE}$ decryption corresponds to evaluation of this garbled circuit using the input labels given in the ciphertext. We now argue correctness and security.

Fig. 3.

Program implementing the functional secret key for a circuit $C_f$

The correctness of the above construction follows from having the “correct” input labels encrypted in the garbled evaluation tables in $\widetilde{C}_f$. It remains to show that the security holds when the obfuscation is instantiated with $i\mathcal {O}$. To achieve this, we use the punctured programming approach of Sahai and Waters [SW14].

We now give a high level overview of the security argument. The goal is to change from a hybrid where the adversary is given a challenge ciphertext encrypting message $m_b$ for some $b \in \{0,1\}$ to a hybrid where she is given a challenge ciphertext independent of the bit b. This is accomplished via a hybrid argument. In the first hybrid, we change the token t in the challenge ciphertext to an uniformly chosen random string $t^*$ relying on the pseudorandomness property of the $\mathsf {PRG}$. Next, we change the public key to be an obfuscation of a program that has the $\mathsf {PRF}$ key S punctured at $t^*$ hardwired instead of S. The rest of the program is same as described in Fig. 2. Intuitively, the indistinguishability follows from $i\mathcal {O}$ security as the $\mathsf {PRG}$ has sparse images. In the next hybrid, the functional secret keys are generated as described in Fig. 4 where $\widetilde{C}^*_f$ hardwired in the program is exactly equal to garbled circuit $\widetilde{C}_f$ with $\{\mathsf {PRF}(K,i\Vert b_i)\}_{i \in [n],b_i\in \{0,1\}}$ (where $K = \mathsf {PRF}(S,t^*)$) as the input labels and generated using $\mathsf {PRF}(S_f,t^*)$ as the random coins. The indistinguishability of the two hybrids follows from $i\mathcal {O}$ security as the two programs described in Figs. 3 and 4 are functionally equivalent. Now, relying on the pseudorandomness at punctured point property of the $\mathsf {PRF}$ we change the input labels in the challenge ciphertext as well as the random coins used for generating $\widetilde{C}^*_f$ to uniformly chosen random strings. We can now change the challenge ciphertext to be independent of the bit b by relying on the security of garbled circuit. To be more precise, we change the input labels in the challenge ciphertext and $\widetilde{C}^*_f$ to be output of the garbled circuit simulator. Notice that we can still use the security of garbled circuits even if several garbled circuits share the same input labels. Thus, the above construction achieves security against unbounded collusions.

Fig. 4.

Program implementing the functional secret key for a circuit $C_f$ in the security proof

Construction from Poly Hard $\mathsf {FE}.$ The main idea behind our construction from polynomially hard, single-key, selectively secure $\mathsf {FE}$ is to simulate the effect of the obfuscation in the above construction using $\mathsf {FE}$. To give a better insight into our construction we would first recall the $\mathsf {FE}$ to $i\mathcal {O}$ transformation of Ananth and Jain [AJ15] and Bitansky and Vaikuntanathan [BV15]. We note that this reduction suffers an exponential loss in security and we will be modifying this construction to achieve our goal of relying only on polynomially hard $\mathsf {FE}$ scheme. For this step, we rely on the techniques built by Garg et al. in [GPS15, GPSZ16] to avoid the exponential loss in security reduction. Parts of this section are adapted from [GPS15, GPSZ16].

$\mathsf {FE}$ to $i\mathcal {O}$ Transformation. We describe a modification of $i\mathcal {O}$ construction from $\mathsf {FE}$ of Bitansky and Vaikuntanathan [BV15] (Ananth and Jain [AJ15] take a slightly different route to achieve the same result). We note that the modified construction is not sufficient to obtain $i\mathcal {O}$ security but is “good enough” for our purposes.

The “obfuscation” of a circuit $C:\{0,1\}^{\kappa } \rightarrow \{0,1\}^{\kappa }$ consists of the following components: a $\mathsf {FE}$ ciphertext $\mathsf {CT}_{\phi }$ and $\kappa +1$ functional secret keys $\mathsf {FSK}_1,\cdots ,\mathsf {FSK}_{\kappa +1}$ generated using independently sampled master secret keys $\mathsf {MSK}_1,\cdots ,\mathsf {MSK}_{\kappa +1}$. $\mathsf {CT}_{\phi }$ encrypts the empty string $\phi$ under the public key $\mathsf {PK}_1$. The first $\kappa$ functional secret keys $\mathsf {FSK}_1,\cdots ,\mathsf {FSK}_{\kappa }$ implement the bit-extension functionality. To be more precise, $\mathsf {FSK}_i$ implements the function $F_{i}$ that takes as input an $(i-1)$-bit string x and outputs two ciphertexts $\mathsf {CT}_{x \Vert 0}$ and $\mathsf {CT}_{x \Vert 1}$ encrypting $x \Vert 0$ and $x \Vert 1$ respectively under $\mathsf {PK}_{i+1}$. The final function secret key $\mathsf {FSK}_{\kappa +1}$ implements the circuit C.

Let us discuss how to evaluate the “obfuscated” circuit on an input $x = x_1\cdots x_{\kappa }$ where $x_i \in \{0,1\}$. The first step is to decrypt $\mathsf {CT}_{\phi }$ using $\mathsf {FSK}_1$ to obtain $\mathsf {CT}_0,\mathsf {CT}_1$. Depending on $x_1$ we choose either the left encryption ($\mathsf {CT}_0$) or the right encryption ($\mathsf {CT}_1$) and recursively decrypt the chosen ciphertext under $\mathsf {FSK}_2$ and so on. After $\kappa +1$ $\mathsf {FE}$ decryptions, we obtain the output of the circuit on input $x_1\cdots x_{\kappa }$.

An alternate way to view this evaluation (which would be useful for this work) is as a traversal along a path from the root to a leaf node of a complete binary tree. The binary tree has the empty string at the root and traversal chooses either the left or the right child depending on the bits $x_1,x_2,\cdots ,x_{\kappa }$ i.e. at level i, bit $x_i$ is used to determine whether to go left or right. We would refer to this binary tree as the evaluation binary tree.

Our Construction. Recall that our main idea is to simulate the effect of obfuscation by appropriately modifying the above $\mathsf {FE}$ to $i\mathcal {O}$ transformation. We first explain the modifications to the “obfuscation” computing the master public key.

Let $C_{pk}[S]$ (having S hardwired) be the circuit that implements the public key of our $i\mathcal {O}$-based construction. Recall that this circuit takes as input some randomness r, expands it using the $\mathsf {PRG}$ to obtain the token t and outputs $(t,\mathsf {PRF}(S,t))$. The goal is to produce an “obfuscation” of this circuit using $\mathsf {FE}$ to $i\mathcal {O}$ transformation explained above. Recall that the $\mathsf {FE}$ to $i\mathcal {O}$ transformation has $\kappa +1$ functional secret keys $\mathsf {FSK}_1,\cdots ,\mathsf {FSK}_{\kappa +1}$ and an initial ciphertext $\mathsf {CT}_{\phi }$ encrypting the empty string. The final functional secret key $\mathsf {FSK}_{\kappa +1}$ implements the circuit $C_{pk}[S]$. The first observation is that we cannot naively hardwire the $\mathsf {PRF}$ key in the circuit $C_{pk}$. This is because to achieve some “meaningful” mechanisms of hiding the $\mathsf {PRF}$ key (via puncturing) we need to go via the $i\mathcal {O}$ route that incurs an exponential loss in security. Therefore, the first modification is to change $C_{pk}$ such that it takes the $\mathsf {PRF}$ key S as input instead of having it hardwired. We now include the $\mathsf {PRF}$ key S in the initial ciphertext $\mathsf {CT}_{\phi }$ i.e. $\mathsf {CT}_{\phi }$ is now an encryption of $(\phi ,S)$. We run into the following problem: the initial ciphertext now contains the $\mathsf {PRF}$ key S whereas we actually need S to be given as input to the final circuit $C_{pk}$ that is implemented in $\mathsf {FSK}_{\kappa +1}$. Therefore, we need a mechanism to make the $\mathsf {PRF}$ key S “available” to the final functional secret key $\mathsf {FSK}_{\kappa +1}$ so that it can compute $\mathsf {PRF}$ evaluation on the token. In other words, we need to “propagate” the PRF key S from the root to every leaf.

To propagate the $\mathsf {PRF}$ key, we make use of the “puncturing along the path” idea of Garg, Pandey and Srinivasan [GPS15]. This idea uses a primitive called as prefix puncturable $\mathsf {PRF}$ introduced in [GPS15]. Informally, prefix puncturable $\mathsf {PRF}$ allows to puncture the $\mathsf {PRF}$ key S at a specific prefix z to obtain $S_z$. The correctness guarantee is that given $S_z$, one can evaluate the $\mathsf {PRF}$ on any input x such that z is a prefix of x. The security guarantee is that as long as any adversary does not get access to $S_z$ where z is a prefix of x, $\mathsf {PRF}(S,x)$ is indistinguishable from random string. An additional feature is that prefix puncturing can be done recursively i.e. given $S_z$ one can obtain $S_{z \Vert 0}$ and $S_{z \Vert 1}$. Additionally, if we need to puncture the $\mathsf {PRF}$ key at an input x it is sufficient to change the distribution of $\mathsf {FE}$ ciphertexts only along the root to the leaf x in the evaluation binary tree. This gives us hope of basing security on polynomially hard $\mathsf {FE}$. As a result, if we were to use this primitive, the problem reduces to the following: design a mechanism wherein the $\mathsf {PRF}$ key S prefix punctured at token t is available at the final functional secret key $\mathsf {FSK}_{\kappa +1}$ as this can then be used to derive $\mathsf {PRF}(S,t)$.

Recall that the circuit $C_{pk}$ generates the token t as $\mathsf {PRG}(r)$ by taking r as input. If we naively try to combine this circuit with the “puncturing along the way” trick of Garg et al., we obtain $S_r$ at the final functional secret key. It is not clear if there is a way of obtaining $S_{\mathsf {PRG}(r)}$ from $S_{r}$. Garg et al. [GPSZ16] faced a similar challenge in designing the sampler for trapdoor permutation and fortunately the solution they provide is applicable to our setting. The solution given in their work is to consider a different token generation mechanism. To be more precise, instead of generating the token as an output of a $\mathsf {PRG}$ on the input randomness r, the token now corresponds to a public key of a semantically secure encryption scheme. To give more details, the circuit $C_{pk}$ now takes as input P which is a public key that also functions as the token. The circuit now computes $\mathsf {PRF}(S,P)$ and outputs a public key encryption of $\mathsf {PRF}(S,P)$ using P as the public key.² We combine this circuit with the “puncturing along the way” technique of Garg et al. to obtain the “obfuscation” of our public key.

The functional secret key for a function $C_f$ (denoted by $\mathsf {FSK}_f$) is constructed similarly to that of the public key. Recall that the functional secret key takes as input the token t (which is now given by the public key P) and computes $K = \mathsf {PRF}(S,t)$. It then uses the key K to derive the input garbled labels and outputs a garbled circuit $\widetilde{C}_f$. $\mathsf {FSK}_f$ also implements the “puncturing along the way” trick of Garg et al. to obtain $S_P$ (which is the PRF key prefix punctured at P) which is used by the final circuit to derive the garbled input labels.

Proof Technique: “Tunneling.” We now briefly explain the main proof technique called as the “tunneling” technique which is adapted from Garg et al.’s works [GPS15, GPSZ16]. Recall that the proof of our $i\mathcal {O}$ based construction relies on the punctured programming approach of Sahai and Waters [SW14]. We also follow a similar proof strategy. Let us explain how to “puncture” the master public key on the token P. At a high level, if we have punctured the $\mathsf {PRF}$ key at P then relying on the security guarantee of prefix punctured $\mathsf {PRF}$ to replace $\mathsf {PRF}(S,P)$ with a random string.

Recall that puncturing the $\mathsf {PRF}$ key S at a string P involves “removing” $S_z$ for every z such that z is a strict prefix of P from the “obfuscation.” To get better intuition on how the puncturing works it would be helpful to view the “obfuscation” in terms of the evaluation binary tree. As mentioned before, the crucial observation that helps us to base security on polynomially hard $\mathsf {FE}$ is that $S_z$ where z is a prefix of P occurs only along the path from the root to the leaf node P in this tree. Hence, it is sufficient to change the distribution of the $\mathsf {FE}$ ciphertexts only along this path in such a manner that they don’t contain $S_z$. To implement this change, we rely on the “Hidden trapdoor mechanism” (also called as the Trojan method) of Ananth et al. in [ABSV15]. To give more details, every functional secret key $\mathsf {FSK}_i$ implements a function $F_i$ that has two “threads” of operation. In thread-1 or the normal mode of operation, it performs the bit-extension on input x and the prefix puncturing on input $S_x$. In thread-2 or the trapdoor mode, it does not perform any computation on the input $(x,S_x)$ and instead outputs some fixed value that is hardwired. We change the $\mathsf {FE}$ ciphertexts in such a way that the trapdoor thread is invoked in every functional secret key when the “obfuscation” is run on input P. Metaphorically, we create a “tunnel” (i.e. a path from the root to a leaf where the trapdoor mode of operation is invoked in every intermediate node) from the root to the leaf labeled P in the complete binary tree corresponding to the obfuscation. Additionally, we change the $\mathsf {FE}$ ciphertexts along the path from root to leaf P such that they do not contain any prefix punctured keys. A consequence of our “tunneling” is that along the way we would have removed $S_z$ for every z which is a strict prefix of P from the “obfuscation.”

3 Preliminaries

$\lambda$ denotes the security parameter. A function $\mu (\cdot ) : \mathbb {N} \rightarrow \mathbb {R}^+$ is said to be negligible if for all polynomials ${\mathsf {poly}}(\cdot )$, $\mu (\lambda ) < \frac{1}{{\mathsf {poly}}(\lambda )}$ for large enough $\lambda$. For a probabilistic algorithm $\mathcal {A}$, we denote $\mathcal {A}(x;r)$ to be the output of $\mathcal {A}$ on input x with the content of the random tape being r. We will omit r when it is implicit from the context. We denote $y \leftarrow \mathcal {A}(x)$ as the process of sampling y from the output distribution of $\mathcal {A}(x)$ with a uniform random tape. For a finite set S, we denote $x \leftarrow S$ as the process of sampling x uniformly from the set S. We model non-uniform adversaries $\mathcal {A}= \{\mathcal {A}_{\lambda }\}$ as circuits such that for all $\lambda$, $\mathcal {A}_{\lambda }$ is of size $p(\lambda )$ where $p(\cdot )$ is a polynomial. We will drop the subscript $\lambda$ from the adversary’s description when it is clear from the context. We will also assume that all algorithms are given the unary representation of security parameter $1^{\lambda }$ as input and will not mention this explicitly when it is clear from the context. We will use PPT to denote Probabilistic Polynomial Time algorithm. We denote $[\lambda ]$ to be the set $\{1,\cdots ,\lambda \}$. We will use $\mathsf {negl}(\cdot )$ to denote an unspecified negligible function and ${\mathsf {poly}}(\cdot )$ to denote an unspecified polynomial. We assume without loss of generality that all cryptographic randomized algorithms use $\lambda$-bits of randomness. If the algorithm needs more than $\lambda$-bit of randomness it can extend to arbitrary polynomial stretch using a pseudorandom generator ($\mathsf {PRG}$).

A binary string $x \in \{0,1\}^{\lambda }$ is represented as $x_1 \cdots x_{\lambda }$. $x_1$ is the most significant (or the highest order bit) and $x_{\lambda }$ is the least significant (or the lowest order bit). The i-bit prefix $x_1 \cdots x_i$ of the binary string x is denoted by $x_{[i]}$. We use $x \Vert y$ to denote concatenation of binary strings x and y. We say that a binary string y is a prefix of x if and only if there exists a string $z \in \{0,1\}^{*}$ such that $x = y \Vert z$.

Puncturable Pseudorandom Function. We recall the notion of puncturable pseudorandom function from [SW14]. The construction of pseudorandom function given in [GGM86] satisfies the following definition [BW13, KPTZ13, BGI14].

Definition 1

A puncturable pseudorandom function $\mathsf {PRF}$ is a tuple of PPT algorithms $(\mathsf {KeyGen}_{\mathsf {PRF}},\mathsf {PRF},\mathsf {Punc})$ with the following properties:

• Efficiently Computable: For all $\lambda$ and for all $S \leftarrow \mathsf {KeyGen}_{\mathsf {PRF}}(1^{\lambda })$, $\mathsf {PRF}_S : \{0,1\}^{{\mathsf {poly}}(\lambda )} \rightarrow \{0,1\}^{\lambda }$ is polynomial time computable.

• Functionality is preserved under puncturing: For all $\lambda$, for all $y \in \{0,1\}^{\lambda }$ and $\forall x \ne y$,

  $$ \Pr [\mathsf {PRF}_{S\{y\}}(x) = \mathsf {PRF}_{S}(x)] = 1 $$

  where $S \leftarrow \mathsf {KeyGen}_{\mathsf {PRF}}(1^{\lambda })$ and $S\{y\} \leftarrow \mathsf {Punc}(S,y)$.

• Pseudorandomness at punctured points: For all ${\lambda }$, for all $y \in \{0,1\}^{{\lambda }}$, and for all poly sized adversaries $\mathcal {A}$

  $$ |\Pr [\mathcal {A}(\mathsf {PRF}_S(y),S\{y\}) = 1] - \Pr [\mathcal {A}(U_{{\lambda }},S\{y\}) = 1]| \le \mathsf {negl}({\lambda }) $$

  where $S \leftarrow \mathsf {KeyGen}_{\mathsf {PRF}}(1^{\lambda })$, $S\{y\} \leftarrow \mathsf {Punc}(S,y)$ and $U_{{\lambda }}$ denotes the uniform distribution over $\{0,1\}^{\lambda }$.

Symmetric Key Encryption. A Symmetric-Key Encryption scheme $\mathsf {SKE}$ is a tuple of algorithms $(\mathsf {SK.KeyGen},\mathsf {SK.Enc},\mathsf {SK.Dec})$ with the following syntax:

• $\mathsf {SK.KeyGen}(1^{\lambda })$: Takes as input an unary encoding of the security parameter $\lambda$ and outputs a symmetric key SK.

• $\mathsf {SK.Enc}_{SK}(m)$: Takes as input a message $m \in \{0,1\}^*$ and outputs an encryption C of the message m under the symmetric key SK.

• $\mathsf {SK.Dec}_{SK}(C)$: Takes as input a ciphertext C and outputs a message $m'$.

We say that $\mathsf {SKE}$ is correct if for all $\lambda$ and for all messages $m \in \{0,1\}^*$, $\Pr [\mathsf {SK.Dec}_{SK}(C) = m] = 1$ where $SK \leftarrow \mathsf {SK.KeyGen}(1^{\lambda })$ and $C \leftarrow \mathsf {SK.Enc}_{SK}(m)$.

Definition 2

For all $\lambda$ and for all polysized adversaries $\mathcal {A}$,

$$ \left| \Pr [\mathsf {Expt}_{1^{\lambda },0,\mathcal {A}} = 1] - \Pr [\mathsf {Expt}_{1^{\lambda },1,\mathcal {A}} = 1] \right| \le \mathsf {negl}(\lambda ) $$

where $\mathsf {Expt}_{1^{\lambda },b,\mathcal {A}}$ is defined below:

• Challenge Message Queries: The adversary $\mathcal {A}$ outputs two messages $m_0$ and $m_1$ such that $|m_{0}| = |m_{1}|$ for all $i \in [n]$.

• The challenger samples $SK \leftarrow \mathsf {SK.KeyGen}(1^{\lambda })$ and generates the challenge ciphertext C where $C \leftarrow \mathsf {SK.Enc}_{SK}(m_{b})$. It then sends C to $\mathcal {A}$.

• Output is $b'$ which is the output of $\mathcal {A}$.

Remark 1

We will denote range of a secret key $\mathsf {FSK}$ (denoted by $\mathsf {Range}_n(SK)$) to be $\{\mathsf {SK.Enc}(SK,x)\}_{x \in \{0,1\}^{n}}$ for a specific n. We will require that for any two secret keys $SK_1,SK_2$ where $SK_1 \ne SK_2$ we have $\mathsf {Range}_n(SK_1) \cap \mathsf {Range}_n(SK_2) = \phi$ with overwhelming probability. We will also require that the existence of an efficient procedure that checks if a given ciphertext c belongs to $\mathsf {Range}_n(SK)$ for a particular secret key SK. We call such a scheme to be symmetric key encryption with disjoint range. We note that symmetric key encryption with disjoint ranges can be obtained from one-way functions [LP09].

Public Key Encryption. A public-key Encryption scheme $\mathsf {PKE}$ is a tuple of algorithms $(\mathsf {PK.KeyGen},\mathsf {PK.Enc},\mathsf {PK.Dec})$ with the following syntax:

• $\mathsf {PK.KeyGen}(1^{\lambda })$: Takes as input an unary encoding of the security parameter $\lambda$ and outputs a public key, secret key pair (pk, sk).

• $\mathsf {PK.Enc}_{pk}(m)$: Takes as input a message $m \in \{0,1\}^*$ and outputs an encryption C of the message m under the public key pk.

• $\mathsf {PK.Dec}_{sk}(C)$: Takes as input a ciphertext C and outputs a message $m'$.

We say that $\mathsf {PKE}$ is correct if for all $\lambda$ and for all messages $m \in \{0,1\}^*$, $\Pr [\mathsf {PK.Dec}_{sk}(C) = m] = 1$ where $(pk,sk) \leftarrow \mathsf {PK.KeyGen}(1^{\lambda })$ and $C \leftarrow \mathsf {PK.Enc}_{pk}(m)$.

Definition 3

For all $\lambda$ and for all polysized adversaries $\mathcal {A}$ and for all messages $m_0,m_1 \in \{0,1\}^{*}$ such that $|m_0| = |m_1|$,

$$ \left| \Pr [\mathcal {A}(pk,\mathsf {PK.Enc}_{pk}(m_0)) = 1] - \Pr [\mathcal {A}(pk,\mathsf {PK.Enc}_{pk}(m_1)) = 1] \right| \le \mathsf {negl}(\lambda ) $$

where $(pk,sk) \leftarrow \mathsf {PK.KeyGen}(1^{\lambda })$.

Prefix Puncturable Pseudorandom Functions. We now define the notion of prefix puncturable pseudorandom function $\mathsf {PPRF}$. We note that the construction of the pseudorandom function in [GGM86] is prefix puncturable according to the following definition.

Definition 4

A prefix puncturable pseudorandom function $\mathsf {PPRF}$ is a tuple of PPT algorithms $(\mathsf {KeyGen}_{\mathsf {PPRF}},\mathsf {PrefixPunc})$ satisfying the following properties:

• Functionality is preserved under repeated puncturing: For all $\lambda$, for all $y \in \cup _{k=0}^{{\mathsf {poly}}(\lambda )}{\{0,1\}^{k}}$ and for all $x \in \{0,1\}^{{\mathsf {poly}}(\lambda )}$ such that there exists a $z \in \{0,1\}^{*}$ s.t. $x = y \Vert z$,

  $$ \Pr [\mathsf {PrefixPunc}(\mathsf {PrefixPunc}(S,y),z) = \mathsf {PrefixPunc}(S,x)] = 1 $$

  where $S \leftarrow \mathsf {KeyGen}_{\mathsf {PPRF}}$.

• Pseudorandomness at punctured prefix: For all ${\lambda }$, for all $x \in \{0,1\}^{{\mathsf {poly}}({\lambda })}$, and for all poly sized adversaries $\mathcal {A}$

  $$ |\Pr [\mathcal {A}(\mathsf {PrefixPunc}(S,x),\mathsf {Keys}) = 1] - \Pr [\mathcal {A}(U_{{\lambda }},\mathsf {Keys}) = 1]| \le \mathsf {negl}({\lambda }) $$

  where $S \leftarrow \mathsf {KeyGen}_{\mathsf {PRF}}(1^{\lambda })$ and $\mathsf {Keys} = \{\mathsf {PrefixPunc}(S,x_{[i-1]}\Vert (1-x_i))\}_{i \in [{\mathsf {poly}}(\lambda )]}$ where $x_{[0]}$ denotes the empty string.

Remark 2

For brevity of notation, we will be denoting $\mathsf {PrefixPunc}(S,y)$ by $S_y$.

Garbled Circuits. We now define the circuit garbling scheme of Yao [Yao86] and state the required properties.

Definition 5

A circuit garbling scheme is a tuple of PPT algorithms given by $(\mathsf {Garb.Circuit},\mathsf {Garb.Eval})$ with the following syntax:

• $\mathsf {Garb.Circuit}(C)$: This is a randomized algorithm that takes in the circuit to be garbled and outputs garbled circuit and the set of garbled input labels: $\widetilde{C_{}},\{\mathsf {Inp}_{i,b_i}\}_{i \in [\lambda ],b_i \in \{0,1\}}$.

• $\mathsf {Garb.Eval}(\widetilde{C_{}},\{\mathsf {Inp}_{i,x_i}\}_{i \in [\lambda ]})$: This is a deterministic algorithm that takes in $\{\mathsf {Inp}_{i,x_i}\}_{i \in [\lambda ]}$ and $\widetilde{C_{}}$ as input and outputs a string y.

Definition 6

(Correctness). We say a circuit garbling scheme is correct if for all circuits C and for all inputs x:

$$ \Pr [\mathsf {Garb.Eval}(\widetilde{C_{}},\{\mathsf {Inp}_{i,x_i}\}_{i \in [\lambda ]}) = C(x)] = 1 $$

where $\widetilde{C_{}},\{\mathsf {Inp}_{i,b_i}\}_{i \in [\lambda ],b_i \in [\lambda ]} \leftarrow \mathsf {Garb.Circuit}(K,C)$.

Definition 7

(Security). There exists a simulator $\mathsf {Sim}$ such that for all circuits C and input x:

$$ \{\widetilde{C_{}},\{\mathsf {Inp}_{i,x_i}\}_{i \in [\lambda ]}\} \overset{c}{\approx }\{\mathsf {Sim}(1^{\lambda },C,C(x))\} $$

Lemma 1

[Yao86, LP09]. Assuming the existence of one-way functions there exists a circuit garbling scheme satisfying the security notion given in Definition 7.

4 Functional Encryption: Security and Efficiency

We recall the syntax and security notions of functional encryption [BSW11, O’N10].

A functional encryption $\mathsf {FE}$ with the message space $\{0,1\}^*$ and function space $\mathcal {F}$ is a tuple of PPT algorithms $(\mathsf {FE.Setup},\mathsf {FE.Enc},\mathsf {FE.KeyGen},\mathsf {FE.Dec})$ having the following syntax:

• $\mathsf {FE.Setup}(1^{\lambda })$: Takes as input the unary encoding of the security parameter $\lambda$ and outputs a public key $\mathsf {PK}$ and a master secret key $\mathsf {MSK}$.

• $\mathsf {FE.Enc}(\mathsf {PK},m)$: Takes as input a message $m \in \{0,1\}^*$ and outputs an encryption c of m under the public key $\mathsf {PK}$.

• $\mathsf {FE.KeyGen}(\mathsf {MSK},f)$: Takes as input the master secret key $\mathsf {MSK}$ and a function $f \in \mathcal {F}$ (given as a circuit) as input and outputs the function key $\mathsf {FSK}_f$.

• $\mathsf {FE.Dec}(\mathsf {FSK}_f,c)$: Takes as input the function key $\mathsf {FSK}_f$ and the ciphertext c and outputs a string y.

Definition 8

(Correctness). The functional encryption scheme $\mathsf {FE}$ is correct if for all $\lambda$ and for all messages $m \in \{0,1\}^*$ and for all $f \in \mathcal {F}$,

Security. We now give the formal definitions of the security notions. We start with the weakest notion of security namely weakly selective security.

Definition 9

(Weakly Selective Security). The functional encryption scheme is said to be multi-key, weakly selective secure if for all $\lambda$ and for all poly sized adversaries $\mathcal {A}$,

$$ \left| \Pr [\mathsf {Expt}_{\mathsf {Sel}^*,1^{\lambda },0,\mathcal {A}} = 1] - \Pr [\mathsf {Expt}_{\mathsf {Sel}^*,1^{\lambda },1,\mathcal {A}} = 1] \right| \le \mathsf {negl}(\lambda ) $$

where $\mathsf {Expt}_{\mathsf {Sel},1^{\lambda },b,\mathcal {A}}$ is defined below:

• Challenge Message Queries: The adversary $\mathcal {A}$ outputs two messages ${m}_0$, ${m}_1$ such that $|{m}_0| = |{m}_1|$ and a set of functions $f_1,\cdots ,f_{q} \in \mathcal {F}$ to the challenger. The parameter q is a priori unbounded.

• The challenger samples $(\mathsf {PK},\mathsf {MSK}) \leftarrow \mathsf {FE.Setup}(1^{\lambda })$ and generates the challenge ciphertext ${c} \leftarrow \mathsf {FE.Enc}(\mathsf {PK},{m}_b)$. The challenger also computes $\mathsf {FSK}_{f_i} \leftarrow \mathsf {FE.KeyGen}(\mathsf {MSK},f_i)$ for all $i \in [q]$. It then sends $(\mathsf {PK},{c}),\{\mathsf {FSK}_{f_i}\}_{i \in [q]}$ to $\mathcal {A}$.

• If $\mathcal {A}$ makes a query $f_j$ for some $j \in [q]$ to such that for any, $f_j(m_{0}) \ne f_j(m_{1})$, output of the experiment is $\bot$. Otherwise, the output is $b'$ which is the output of $\mathcal {A}$.

Remark 3

We say that the functional encryption scheme $\mathsf {FE}$ is single-key, weakly selectively secure if the adversary $\mathcal {A}$ in $\mathsf {Expt}_{\mathsf {Sel}^*,1^{\lambda },b,\mathcal {A}}$ is allowed to obtain the functional key for a single function f.

We now give the definition of selectively secure $\mathsf {FE}$.

Definition 10

(Selective Security). The functional encryption scheme is said to be multi-key, selectively secure $\mathsf {FE}$ if for all $\lambda$ and for all poly sized adversaries $\mathcal {A}$,

$$ \left| \Pr [\mathsf {Expt}_{\mathsf {Sel},1^{\lambda },0,\mathcal {A}} = 1] - \Pr [\mathsf {Expt}_{\mathsf {Sel},1^{\lambda },1,\mathcal {A}} = 1] \right| \le \mathsf {negl}(\lambda ) $$

where $\mathsf {Expt}_{\mathsf {Sel},1^{\lambda },b,\mathcal {A}}$ is defined below:

• Challenge Message Queries: The adversary $\mathcal {A}$ outputs two message vectors ${m}_0$, ${m}_1$ such that $|{m}_0| = |{m}_1|$ to the challenger.

• The challenger samples $(\mathsf {PK},\mathsf {MSK}) \leftarrow \mathsf {FE.Setup}(1^{\lambda })$ and generates the challenge ciphertext ${c} \leftarrow \mathsf {FE.Enc}(\mathsf {PK},{m}_b)$. It then sends $(\mathsf {PK},{c})$ to $\mathcal {A}$.

• Function Queries: $\mathcal {A}$ adaptively chooses a function $f \in \mathcal {F}$ and sends it to the challenger. The challenger responds with $\mathsf {FSK}_f \leftarrow \mathsf {FE.KeyGen}(\mathsf {MSK},f)$. The number of function queries made by the adversary is unbounded.

• If $\mathcal {A}$ makes a query f to functional key generation oracle such that, $f(m_{0}) \ne f(m_{1})$, output of the experiment is $\bot$. Otherwise, the output is $b'$ which is the output of $\mathcal {A}$.

Remark 4

In the adaptive variant, the adversary is allowed to give challenge messages after seeing the public parameters and functional secret key queries.

Efficiency. We now define the efficiency requirements of a $\mathsf {FE}$ scheme.

Definition 11

(Fully Compact). A functional encryption scheme $\mathsf {FE}$ is said to be fully compact if for all $\lambda \in \mathbb {N}$ and for all $m \in \{0,1\}^*$ the running time of the encryption algorithm $\mathsf {FE.Enc}$ is ${\mathsf {poly}}(\lambda ,|m|)$.

Definition 12

(Weakly Compact). A functional encryption scheme is said to be weakly compact if the running time of the encryption algorithm $\mathsf {FE.Enc}$ is $|\mathcal {F}|^{1-\epsilon }.{\mathsf {poly}}(\lambda ,|m|)$ for some $\epsilon > 0$ where $|\mathcal {F}| = \max _{f \in \mathcal {F}}{|C_f|}$ where $C_f$ is the circuit implementing f.

A functional encryption scheme is said to have non-compact ciphertexts if the running time of the encryption algorithm can depend arbitrarily on the maximum circuit size of the function family.

5 Our Transformation

In this section we describe our transformation from single-key, weakly selective secure functional encryption with fully compact ciphertexts to multi-key, selective secure functional encryption scheme. We later (in Sect. 6) show that it is sufficient for the single-key scheme to have weakly compact ciphertexts. We state the main theorem below.

Theorem 1

Assuming the existence of single-key, weakly selective secure $\mathsf {FE}$ scheme with fully compact ciphertexts, there exists a multi-key, selective secure $\mathsf {FE}$ scheme with fully compact ciphertexts.

The transformation from single-key, weakly selective secure $\mathsf {FE}$ scheme to multi-key, selective secure $\mathsf {FE}$ scheme uses the following primitives that are implied by single-key, weakly selective secure $\mathsf {FE}$.

• A single-key, weakly selective $\mathsf {FE}$ scheme $(\mathsf {FE.Setup},\mathsf {FE.KeyGen},\mathsf {FE.Enc},\mathsf {FE.Dec})$.

• A prefix puncturable PRF $(\mathsf {PPRF},\mathsf {KeyGen}_{\mathsf {PPRF}},\mathsf {PrefixPunc})$.

• A Circuit garbling scheme $(\mathsf {Garb.Circuit},\mathsf {Garb.Eval})$.

• A public key encryption scheme $(\mathsf {PK.KeyGen},\mathsf {PK.Enc},\mathsf {PK.Dec})$.

• A symmetric key encryption scheme $(\mathsf {SK.KeyGen},\mathsf {SK.Enc},\mathsf {SK.Dec})$ with disjoint range.

Notation. $\lambda$ will denote our security parameter. Let the length of the secret key output by $\mathsf {SK.KeyGen}$ be $\lambda _1$, let length of the key output by $\mathsf {KeyGen}_{\mathsf {PPRF}}$ be $\lambda _2$. We will denote length of public key output by $\mathsf {PK.KeyGen}$ to be $\kappa$. The message space is given by $\{0,1\}^{\gamma }$ and the function space is the set of all poly sized circuits taking $\gamma$-bit inputs.

The output of the transformation is a FE scheme $(\mathsf {MKFE.Setup}, \mathsf {MKFE.KeyGen},\mathsf {MKFE.Enc},\mathsf {MKFE.Dec})$. The formal description our construction appears in Fig. 5.

Fig. 5.

Transformation from single key to unbounded key secure

Fig. 6.

Auxiliary circuits

5.1 Correctness and Security

We first show correctness of our construction

Correctness. Recall that we need to show that if we decrypt a $\mathsf {FE}$ ciphertext encrypting m using a functional secret key for a function f then we obtain f(m). We first argue that our $\mathsf {FE}$ ciphertext is distributed as $(pk,\{\mathsf {PRF}(S_{pk},{i \Vert m_i})\}_{i \in [\kappa ]})$. From the correctness of $\mathsf {FE}$ decryption, we note that by iteratively decrypting $\mathsf {CT}_{\phi }$ under $\mathsf {FSK}_1,\cdots ,\mathsf {FSK}_{\kappa +1}$ using the bits of pk we obtain a public key encryption of $S_{pk}$ under public key pk. From the correctness of public key decryption, we correctly recover $S_{pk}$. Hence our $\mathsf {FE}$ ciphertext is distributed as $(pk,\{\mathsf {PRF}(S_{pk},{i \Vert m_i})\}_{i \in [\kappa ]})$.

We now look at the decryption procedure. We notice from the correctness of $\mathsf {FE}$ decryption procedure that by iteratively decrypting $\mathsf {CT}^f_{\phi }$ under $\mathsf {FSK}^f_1,\cdots \mathsf {FSK}^f_{\kappa +1}$ using the bits of pk, we obtain $\widetilde{C_{f}},\{c_{i,b_i}\}_{i \in [\gamma ],b_i \in \{0,1\}}$ where $c_{i,b_i} \leftarrow \mathsf {SK.Enc}(\mathsf {PRF}(S_{pk},i\Vert m_i),\mathsf {Inp}_{i,b_i})$ for every $i \in [\gamma ]$ and $b_i \in \{0,1\}$. It follows from the correctness of $\mathsf {SK.Dec}$ and the fact that the symmetric key encryption we use has disjoint ranges, we correctly obtain $\{\mathsf {Inp}_{i,m_i}\}_{i \in [\kappa ]}$. The correctness of our $\mathsf {MKFE}$ decryption now follows from the correctness of garbled circuit evaluation.

We note that length of the ciphertexts (and the size of the encryption circuit) in our $\mathsf {MKFE}$ scheme is independent of the circuit size of functions. Hence, the $\mathsf {MKFE}$ scheme has fully compact ciphertexts. We now state the main lemma for security.

Lemma 2

Assuming single-key, weakly selective security of $\mathsf {FE}$, semantic security of $\mathsf {SKE}$, semantic security of $\mathsf {PKE}$, and the security of prefix puncturable pseudorandom function $\mathsf {PPRF}$, the $\mathsf {MKFE}$ construction described in Fig. 5 is multi-key, selectively secure.

Before we describe the proof of Lemma 2, we first set up some notation.

Notation. Let $x \in \{0,1\}^{\kappa }$. Let ${\mathsf {Prefixes}}(x)$ denote the set of all prefixes ($\kappa$ in number) of the string x. Formally,

$$ {\mathsf {Prefixes}}(x) := \{x_{[i]}\}_{i \in [\kappa ]} $$

Let $\mathsf {Siblings}(x)$ denote the set of siblings of all prefixes of x. Formally,

$$ \mathsf {Siblings}(x) := \{y_{[i-1]} \Vert (1 - y_i) : \forall y \in {\mathsf {Prefixes}}(x), i \in [\kappa ] \text { where } |y| = i\} $$

Proof of Lemma 2 . The proof proceeds via a hybrid argument.

• $\mathsf {Hyb}_0$: In this hybrid, the adversary is given the challenge ciphertext encrypting the message $m_b$. To be more precise, the challenge ciphertext is given by $(pk^*,\{\mathsf {L}_{i,(m_b)_i}\}_{i \in [\kappa ]})$ where $(pk^*,sk^*) \leftarrow \mathsf {PK.KeyGen}(1^{\kappa })$ and $\mathsf {L}_{i,(m_b)_i} \leftarrow \mathsf {PRF}(S_{pk^*},i\Vert (m_b)_i)$ for all $i \in [\kappa ]$. All key generation queries are generated as per the construction described in Fig. 5.

• $\mathsf {Hyb}_1$: In this hybrid, we are going to “tunnel” through the path from root to the leaf node labeled $pk^*$ in the master public key. This step is realized through a couple of intermediate hybrids. Let $P_1 := {\mathsf {Prefixes}}(pk^*)$ and $Q_1 = \mathsf {Siblings}(pk^*) \setminus P_1$. For every $z \in P_1 \cup Q_1$, let $\mathsf {CT}_z$ be the result of the iterated decryption procedure on the master public key with z as input.³ Additionally, let $\mathsf {Val}_{pk^*}$ be the output of the decryption of $\mathsf {CT}_{pk^*}$ under $\mathsf {FSK}_{\kappa +1}$. Let

  $$ \mathsf {str}_{i} = \Vert _{z \in P_1 \cup Q_1 \wedge |z| = i}{(z,\mathsf {CT}_z)} $$
  $$ \mathsf {str}_{\lambda +1} = (pk^*,\mathsf {Val}^1_{pk^*}) $$

  We set $\mathsf {len}_i(\lambda )$ to be the maximum length of $\mathsf {str}_{i}$ over all choices of $pk^*$. We pad $\mathsf {str}_{i}$ to this size.

  • $\mathsf {Hyb}_{0,1}$: In this hybrid we are going to change how $\varPsi _i$ is generated. Instead of encrypting the all zeroes string of length $\mathsf {len}_i(\kappa )$, we encrypt $\mathsf {str}_{i}$. Indistinguishability follows from the semantic security of the symmetric key encryption since the key sk is not needed to simulate $\mathsf {Hyb}_0$ or $\mathsf {Hyb}_{0,1}$.

  • $\mathsf {Hyb}_{0,2}$: In this hybrid we change how $\mathsf {CT}_{\phi }$ is generated. Instead of generating $\mathsf {CT}_{\phi }$ to be $\mathsf {FE.Enc}(\mathsf {PK}_1,(\phi ,S,K_{\phi },0^{\lambda _1},0))$, we generate it as $\mathsf {FE.Enc}(\mathsf {PK}_1,(\phi ,0^{\lambda _2},0^{\lambda _2},sk,1))$. We now argue that $\mathsf {Hyb}_{0,2}$ is indistinguishable from $\mathsf {Hyb}_{0,1}$. Notice that output of $\mathsf {BitExt}_1[\varPsi _1,\mathsf {PK}_2]$ is same on $(\phi ,S,K_{\phi },0^{\lambda _1},0)$ and $(\phi ,0^{\lambda _2},0^{\lambda _2},sk,1)$. Also, the choice of the two messages and the functionality for which the secret key is obtained do not depend on the public parameters. Hence, it follows from the weakly selective security of $\mathsf {FE}$ scheme under $\mathsf {PK}_1$ that $\mathsf {Hyb}_{0,1}$ and $\mathsf {Hyb}_{0,2}$ are indistinguishable.

  • $\mathsf {Hyb}_{0,3}$: In this hybrid we are going to tunnel through the path from the root to the leaf labeled $pk^*$. To achieve this, we are going to change $\mathsf {CT}_z$ that is encrypted in $\varPsi _1$ for every $z \in P_1$. We don’t change the encryption when $z \in Q_1$. In particular, we change $\mathsf {CT}_z = \mathsf {FE.Enc}(\mathsf {PK}_{|z|+1},(z,S_z,K_z,0^{\lambda _1},0);{K'}_z)$ to $\mathsf {FE.Enc}(\mathsf {PK}_{|z|+1}, (z,0^{\lambda _2},0^{\lambda _2},sk,1);r_z)$ where $r_z$ is chosen uniformly at random. Notice that as a result $S_z$ for every z that is a strict prefix of $pk^*$ does not appear in the public key of our $\mathsf {MKFE}$ scheme.

    We first introduce an ordering of strings in $P_1$. For every string $x,y \in P_1$ $x \prec y$ if and only if $|x| < |y|$. This induces a partial ordering of the strings in $P_1$. We let $\mathsf {Hyb}_{0,2,x}$ to denote the hybrid where for all $z \prec x$, $\mathsf {CT}_z$ has been changed from $\mathsf {FE.Enc}(\mathsf {PK}_{|z|+1}, (z,S_z,K_z,0^{\lambda _1},0);{K'}_z)$ to $\mathsf {FE.Enc}(\mathsf {PK}_{|z|+1},(z,0^{\lambda _2},0^{\lambda _2},sk,1);r_z)$. We prove for any two adjacent strings $x,x'$ where $x' \prec x$ in ordered $P_1$ that $\mathsf {Hyb}_{0,2,x}$ is indistinguishable to $\mathsf {Hyb}_{0,2,x'}$. Since $|P_1| \le \kappa$, we get $\mathsf {Hyb}_{0,2}$ is indistinguishable to $\mathsf {Hyb}_{0,3}$ through a series a $\kappa$ hybrids.

    • * $\mathsf {Hyb}_{0,2,x',1}$: In this hybrid we change $\mathsf {CT}_x$ to $\mathsf {FE.Enc}(\mathsf {PK}_{|x|+1}, (x,S_x,K_x,0^{\lambda _1},0);r_x)$ where $r_x$ is chosen uniformly at random. Notice that for all strings y that are prefixes of x, $\mathsf {CT}_y$ has already been changed to $\mathsf {FE.Enc}(\mathsf {PK}_{|y|+1},(y,0^{\lambda _2},0^{\lambda _2},sk,1);r_y)$ because $y \prec x$ by our ordering. For every y that is a prefix of x, $K_{y}$ is not needed to simulate $\mathsf {Hyb}_{0,2,x'}$ and $\mathsf {Hyb}_{0,2,x',1}$. It follows from the pseudorandomness at prefix punctured point property of PRF key $K_{\phi }$ we have $\mathsf {Hyb}_{0,2,x'}$ is indistinguishable to $\mathsf {Hyb}_{0,2,x',1}$. Illustration for this hybrid change is given in Fig. 7.

    • * $\mathsf {Hyb}_{0,2,x',2}$: In this hybrid we change $\mathsf {CT}_x$ to $\mathsf {FE.Enc}(\mathsf {PK}_{|x|+1}, (x,0^{\lambda _2},0^{\lambda _2},sk,1);r_x)$. Notice that decrypting $\mathsf {FE.Enc}(\mathsf {PK}_{|x| + 1}, (x,0^{\lambda _2},0^{\lambda _2},sk,1);r_x))$ and $\mathsf {FE.Enc}(\mathsf {PK}_{|x|+1},(x,S_x,K_x,0^{\lambda _2},0))$ under the secret key $\mathsf {FSK}_{|x|+1}$ has the same output due to the choice of $\varPsi _{|x|+1}^*$. Also, the choice of the two messages and the functionality for which the secret key is obtained do not depend on the public parameters. Hence, it follows from the weakly selective security of $\mathsf {FE}$ scheme under $\mathsf {PK}_{|x|+1}$ that $\mathsf {Hyb}_{0,2,x',1}$ and $\mathsf {Hyb}_{0,2,x',2}$ are indistinguishable.

    Notice that $\mathsf {Hyb}_{0,2,x',2}$ is distributed identically to $\mathsf {Hyb}_{0,2,x}$.

• $\mathsf {Hyb}_2$: In this hybrid we are going to change $\mathsf {Val}_{pk^*}$ encrypted in $\varPsi ^*_1$. Notice that in $\mathsf {Hyb}_2$, $\mathsf {Val}_{pk^*}$ is set to be an public key encryption of $S_{pk^*}$ under the public key $pk^*$ (using pseudorandomly generated coins). In this hybrid we are going to change $\mathsf {Val}_{pk^*}$ to be an public key encryption of all zeroes string ($0^{\lambda }$) under $pk^*$.

  • $\mathsf {Hyb}_{1,1}$: In this hybrid we generate the randomness used for encrypting $S_{pk^*}$ under the public key $pk^*$ uniformly instead of generating it pseudorandomly using the key $K_{pk^*}$. Notice that $K_{z}$ for every z that is a prefix of $pk^*$ is not needed to simulate either $\mathsf {Hyb}_1$ or $\mathsf {Hyb}_{1,1}$. Therefore, from the pseudorandomness at prefix punctured point property of PRF under key $K_{\phi }$, $\mathsf {Hyb}_1$ is indistinguishable from $\mathsf {Hyb}_{1,1}$.

  • $\mathsf {Hyb}_{1,2}$: In this hybrid we change $\mathsf {Val}_{pk^*}$ to be an encryption of $0^{\kappa }$ under $pk^*$. Indistinguishability of $\mathsf {Hyb}_{1,1}$ and $\mathsf {Hyb}_{1,2}$ follows from the semantic security of public key encryption.

• $\mathsf {Hyb}_3$: In this hybrid we are going to tunnel through the paths from the root to the leaf $pk^*$ in each function secret key $\mathsf {FSK}_f$ that is queried by the adversary. We explain the details for a single function key $\mathsf {FSK}_f$ and we can extend to all function secret keys by a standard hybrid argument. The indistinguishability argument for a single function secret key $\mathsf {FSK}_f$ is similar to our argument to show indistinguishability between $\mathsf {Hyb}_0$ and $\mathsf {Hyb}_1$.

  Let $P_2 := {\mathsf {Prefixes}}(pk^*)$ and $Q_2 = \mathsf {Siblings}(pk^* )$. For every $z \in P_2 \cup Q_2$ let $\mathsf {CT}^f_z$ be the result of the iterated decryption procedure on the function secret key $\mathsf {FSK}_f$ with z as input. Additionally, let $\widetilde{C_{f}}, \{c_{i,b_i}\}_{i \in [\gamma ],b_i \in \{0,1\}}$ be the output of the decryption of $\mathsf {CT}_{pk^*}$ under $\mathsf {FSK}^f_{\kappa +1}$. Let

  $$ \mathsf {str}^f_i = \Vert _{z \in P_2 \cup Q_2 \wedge |z| = i}{(z,\mathsf {CT}_z)} $$
  $$ \mathsf {str}^f_{\kappa +1} = (pk^*,\widetilde{C_{f}},\{c_{i,b_i}\}_{i \in [\gamma ],b_i \in \{0,1\}}) $$

  We set $\mathsf {len}^f_i(\kappa )$ to be the maximum length of $\mathsf {str}^f_i$ over all choices of f. We pad $\mathsf {str}^f_i$ to this size.

  • $\mathsf {Hyb}_{2,1}$: In this hybrid we are going to change how $\varPsi ^f_i$ is generated. Instead of encrypting the all zeroes string of length $\mathsf {len}'_i(\kappa )$ we encrypt $\mathsf {str}^f_i$. Indistinguishability follows from the semantic security of the symmetric key encryption since the key $sk^f$ is not needed to simulate $\mathsf {Hyb}_2$ or $\mathsf {Hyb}_{2,1}$.

  • $\mathsf {Hyb}_{2,2}$: In this hybrid we change how $\mathsf {CT}^f_{\phi }$ is generated. Instead of generating $\mathsf {CT}^f_{\phi }$ to be $\mathsf {FE.Enc}(\mathsf {PK}^f_1,(\phi ,S,K^f_{\phi },0^{\lambda _1},0))$ we generate it as $\mathsf {FE.Enc}(\mathsf {PK}^f_1,(\phi ,0^{\lambda _2},0^{\lambda _2},sk^f,1))$. We now argue that $\mathsf {Hyb}_{2,2}$ is indistinguishable from $\mathsf {Hyb}_{2,1}$. Notice that output of $\mathsf {BitExt}_1[\varPsi ^*_f,\mathsf {PK}^f_2]$ is same on $(\phi ,S,K^f_{\phi },0^{\lambda _1},0)$ and $(\phi ,0^{\lambda _2},0^{\lambda _2},sk^f,1)$. Also, the choice of the two messages and the functionality for which the secret key is obtained do not depend on the public parameters. Hence, it follows from the weakly selective security of $\mathsf {FE}$ scheme under $\mathsf {PK}^f_1$ that $\mathsf {Hyb}_{2,1}$ and $\mathsf {Hyb}_{2,2}$ are indistinguishable.

  • $\mathsf {Hyb}_{2,3}$: In this hybrid we are going to tunnel through the paths from the root to the leaf labeled $pk^*$ in $\mathsf {FSK}_f$. To achieve this we are going to change $\mathsf {CT}_z$ that is encrypted in $\varPsi ^f_i$ for every $z \in P_2$. As before, we don’t change the encryption when $z \in Q_2$. In particular, we change $\mathsf {CT}^f_z = \mathsf {FE.Enc}(\mathsf {PK}^f_{|z|+1},(z,S_z,K^f_z,0^{\lambda _1},0);{K'}^f_z)$ to $\mathsf {FE.Enc}(\mathsf {PK}^f_{|z|+1},(z,0^{\lambda _2},0^{\lambda _2},sk^f;r_z)$ where $r_z$ is chosen uniformly at random. The proof of indistinguishability between $\mathsf {Hyb}_{2,2}$ and $\mathsf {Hyb}_{2,3}$ is exactly same as the one between $\mathsf {Hyb}_{0,2}$ and $\mathsf {Hyb}_{0,3}$.

• $\mathsf {Hyb}_4$: In this hybrid we are going to change $S_{pk^*}$ used to generate the challenge ciphertext to an uniformly chosen random $\kappa$-bit string $T^*$. We observe that for z that is a prefix of $pk^*$, $S_z$ is not needed to simulate either $\mathsf {Hyb}_3$ or $\mathsf {Hyb}_4$ because we have “tunneled” through from the root to leaf node $pk^*$ in the master public key and in all the function secret keys $\mathsf {FSK}_f$. Hence from the pseudorandomness at prefix punctured point property of the PRF under the key S, $\mathsf {Hyb}_4$ is computationally indistinguishable to $\mathsf {Hyb}_3$. Notice that this also implies (from the property of the pseudorandom function) that $\{\mathsf {L}_{i,{b}_i}\}$ for every $i \in [\gamma ]$ and for every $b_i \in \{0,1\}$ can be changed to uniformly chosen random strings. This change is made to challenge ciphertext as well as encryption keys used for generating $\{c_{i,b_i}\}_{i \in [\gamma ],b_i \in \{0,1\}}$ in $\varPsi ^f_{\kappa +1}$ in each functional secret key $\mathsf {FSK}_f$.

• $\mathsf {Hyb}_5$: In this hybrid we are going to change to change the randomness used for generating garbled circuit, the encryptions $c_{i,b_i}$ that are encrypted in $\varPsi ^f_{\kappa +1}$ and the randomness used for permuting $c_{i,b_i}$ in each of the function secret keys $\mathsf {FSK}_f$ to uniformly chosen random strings. Observe that since we have “tunneled” through $pk^*$ in each of the function secret keys it follows from pseudorandomness of prefix punctured point property of the PRF under the key $K^f_{\phi }$, $\mathsf {Hyb}_5$ is computationally indistinguishable to $\mathsf {Hyb}_4$.

• $\mathsf {Hyb}_6$: In this hybrid we are going to change $c_{i,1-(m_b)_i}$ to encrypting all zeroes string instead of encrypting $\mathsf {Inp}_{i,1 - (m_b)_i}$. This change is made in $\varPsi ^f_{\kappa +1}$ in each of the function secret keys $\mathsf {FSK}_f$. Indistinguishablity of $\mathsf {Hyb}_5$ and $\mathsf {Hyb}_6$ follows from the semantic security of secret key encryption under $\mathsf {L}_{i,1-(m_b)_i}$.

• $\mathsf {Hyb}_7$: In this hybrid we are going to change $\{\mathsf {Inp}_{i,(m_b)_i}\}_{i \in [\gamma ]},\widetilde{C_{f}}$ to be output of the simulator for the garbled circuit. This change is made in $\varPsi ^f_{\kappa +1}$ in each of the function secret keys $\mathsf {FSK}_f$. More precisely, we set $\{\mathsf {Inp}_{i,(m_b)_i}\}_{i \in [\gamma ]},\widetilde{C_{f}} \leftarrow \mathsf {Sim}(1^{\kappa },C_f,f(m_0))$ (note that $f(m_0) = f(m_b)$). Indistinguishability of $\mathsf {Hyb}_6$ and $\mathsf {Hyb}_7$ follows from the security of garbled circuits.

In $\mathsf {Hyb}_7$, the view of the adversary is independent of the challenge bit b. Hence the advantage that the adversary has in guessing the bit b is 0 in $\mathsf {Hyb}_7$.

Fig. 7.

Illustration for $\mathsf {Hyb}_{0,2,x',1}$ where $x' = 1$ and $x = 10$. The blackened nodes are not needed for simulation.

6 Efficiency Analysis

In this section we relax the requirement of full compactness from our single-key selectively secure $\mathsf {FE}$ scheme to weakly compact ciphertexts. Parts of this section are taken verbatim from Bitansky and Vaikuntanathan [BV15].

Recall that a $\mathsf {FE}$ scheme with weakly compact ciphertexts has an encryption circuit whose size grows sub-linearly with the circuit size of functions for which function secret keys are given.

Let $F_{1},F_2,\cdots ,F_{\kappa +1}$ be the functionalities implemented by the secret keys $\mathsf {FSK}^f_1,\cdots ,\mathsf {FSK}^f_{\kappa +1}$.⁴ Notice that for any $i = \{1,\cdots ,\kappa \}$, $F_i$ implements the encryption circuit $E_{i+1}$ for the functional encryption scheme under $\mathsf {PK}_{i+1}$, symmetric decryption circuit and a prefix puncturing circuit. The size of the functional encryption circuit and the symmetric decryption circuit is bounded by $|E_{i+1}|.{\mathsf {poly}}(\kappa )$ and the size of the prefix puncturing circuit is bounded by ${\mathsf {poly}}(\kappa )$. Therefore,

$$ |F_i| \le |E_{i+1}|.{\mathsf {poly}}(\kappa ) $$

From our assumption that the underlying $\mathsf {FE}$ scheme is weakly compact we get:

$$ |E_{i}| \le |F_{i}|^{1 - \epsilon } . {\mathsf {poly}}(\kappa ) $$

Notice that:

$$ |F_{\kappa +1}| \le |C_f| . {\mathsf {poly}}(\kappa ) $$

Hence we get:

$$ |E_i| \le |F_{i}|^{1 - \epsilon } . {\mathsf {poly}}(\kappa ) \le |E_{i+1}|^{1 - \epsilon }.({\mathsf {poly}}(\kappa ))^{1 - \epsilon } . {\mathsf {poly}}(\kappa ) $$

By recursively enumerating we get:

$$ |E_i| \le |C_f|^{1 - \epsilon } . {\mathsf {poly}}(\kappa ) . \prod _{j = 1} ^{\kappa +2 - i}{{\mathsf {poly}}(\kappa )^{(1-\epsilon )^j}} $$

We observe that:

$$ \prod _{j = 1} ^{\kappa +2 - i}{{\mathsf {poly}}(\kappa )^{(1-\epsilon )^j}} \le \prod _{j = 0} ^{\infty }{{\mathsf {poly}}(\kappa )^{(1-\epsilon )^j}} \le ({\mathsf {poly}}(\kappa ))^{\frac{1}{\epsilon }} $$

Hence, for all $i \in [\kappa +1]$ we get:

$$ |E_i| \le |C_f|^{1 - \epsilon } . {\mathsf {poly}}(\kappa )^{1 + \frac{1}{\epsilon }} $$

which implies efficiency of our underlying construction.