The Magic of ELFs

Abstract

We introduce the notion of an Extremely Lossy Function (ELF). An ELF is a family of functions with an image size that is tunable anywhere from injective to having a polynomial-sized image. Moreover, for any efficient adversary, for a sufficiently large polynomial r (necessarily chosen to be larger than the running time of the adversary), the adversary cannot distinguish the injective case from the case of image size r.

We develop a handful of techniques for using ELFs, and show that such extreme lossiness is useful for instantiating random oracles in several settings. In particular, we show how to use ELFs to build secure point function obfuscation with auxiliary input, as well as polynomially-many hardcore bits for any one-way function. Such applications were previously known from strong knowledge assumptions — for example polynomially-many hardcore bits were only know from differing inputs obfuscation, a notion whose plausibility has been seriously challenged. We also use ELFs to build a simple hash function with output intractability, a new notion we define that may be useful for generating common reference strings.

Next, we give a construction of ELFs relying on the exponential hardness of the decisional Diffie-Hellman problem, which is plausible in pairing-based groups. Combining with the applications above, our work gives several practical constructions relying on qualitatively different — and arguably better — assumptions than prior works.

M. Zhandry—This work was sponsored by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contract number W911NF-15-C-0226.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Hash functions are a ubiquitous tool in cryptography: they are used for password verification, proofs of work, and are central to a variety of cryptographic algorithms including efficient digital signatures and encryption schemes.

Unfortunately, formal justifications of many of the uses of hash functions have been elusive. The trouble stems from the difficulty of even defining what security properties a hash function should satisfy. On one extreme, a hash function can be assumed to have standard security properties such as one-wayness or collision resistance, which are useless for most of the applications above. On the other extreme, a hash function can be modeled as a truly random function, where it is assumed that an adversary only has black-box access. In the so-called random oracle model (ROM) [5], all of the above applications are secure. However, random oracles clearly do not exist and moreover provably cannot be replaced by any concrete hash function [16]. In this light, it is natural to ask:

What are useful properties of random oracles that can be realized by real-world hash functions.

Some attempts have been made to answer this question; however, many such attempts have serious limitations. For example Canetti et al. [16] propose the notion of correlation intractability as a specific feature of random oracles that could potentially have a standard model instantiation. However, they show that for some parameter settings such standard model hash functions cannot exist. The only known positive example [15] relies on extremely strong cryptographic assumptions such as general-purpose program obfuscation. For another example, Bellare et al. [4] define a security property for hash functions called Universal Computational Extractors (UCE), and show that hash functions with UCE security suffice for several uses of the random oracle model. While UCE’s present an important step toward understanding which hash function properties might be achievable and which are not, UCE’s have several limitations. For example, the formal definition of a UCE is somewhat complicated to even define. Moreover, UCE is not a single property, but a family or “framework” of assumptions. The most general form of UCE is trivially unattainable, and some of the natural restricted classes of UCE have been challenged [7, 13]. Therefore, it is unclear which versions of UCE should be trusted and which untrusted.

Similar weaknesses have been shown for other strong assumptions that can be cast as families of assumptions or as knowledge/extracting assumptions, such as extractable one-way functions (eOWFs) [8] and differing inputs obfuscation (diO) [2, 12, 21]. These weakness are part of a general pattern for strong assumptions such as UCE, eOWFs, and diO that are not specified by a cryptographic game. In particular, these assumptions do not meet standard notions of falsifiability ([22, 28]), and are not complexity assumptions in the sense of Goldwasser and Kalai [24]. We stress that such knowledge/extracting/framework assumptions are desirable as security properties. However, in order to trust that the property actually holds, it should be derived from a “nice” and trusted assumption. Therefore, an important question in this space is the following:

Are there primitives with “nice” (e.g. simple, well-established, game-based, falsifiable, complexity assumption, etc.) security properties that can be used to build hash functions suitable for instantiating random oracles for many protocols.

1.1 Our Work

Our Random Oracle Targets. We aim to base several applications of random oracles on concrete, “nice” assumptions with relatively simple instantiations.

• Boosting selective to adaptive security. A trivial application of random oracles is to boost selective to adaptive security in the case of signatures and identity-based encryption. This is done by first hashing the message/identity with the random oracle before signing/generating secret keys. There has been no standard-model security notion for hash functions that allows for this conversion to be secure, though in the case of signatures, chameleon hash functions [27] achieve this conversion with a small tweak.

• Password hashing. Another common use of hash functions is to securely store a password in “encrypted” form, allowing for the password to be verified, but hiding the actual password in case the password database is compromised. This use case is a special instance of point obfuscation (PO). In the case that there may be side information about the password, we have the notion of auxiliary input point obfuscation (AIPO). The only prior constructions of AIPO [9, 14] rely on very strong knowledge assumptions. The first is Canetti’s [14] strong knowledge variant of the decisional Diffie Hellman (DDH) assumption, whose plausibility has been called into question by a recent work showing it is incompatible with the existence of certain strong forms of obfuscation [7]. The second is a strong knowledge assumption about one-way permutations due to Bitansky and Paneth [9], which is a strengthening of Wee’s strong one-way permutation assumption [37]. To the best of our knowledge, the only currently known ways to instantiate the [9] assumption is to make the tautological assumption that a particular one-way permutation is secure. For reasons mentioned above, such tautological knowledge assumptions are generally considered undesirable in cryptography.

• Generating system parameters. A natural use case of hash functions is for generating common random strings (crs) in a trusted manner. More specifically, suppose a (potentially untrusted) authority is generating a crs for some protocol. Unfortunately, such a crs may admit a “trapdoor” that allows for breaking whatever protocol is using it (Dual_EC_DRBG is a prominent example of this). In order to ensure to untrusting parties that no trapdoor is known, the authority will generate the crs as an output of the hash function on some input. The authority may have some flexibility in choosing the input; we wish to guarantee that it cannot find an input such that it also knows a trapdoor for the corresponding output. In the random oracle model, this methodology is sound: the authority cannot choose an input so that it knows the trapdoor for the output. However, standard notions of security for hash functions give no guarantees for this setting. We propose (Sect. 5) the notion of output intractability as a standard-model security notion that captures this use case. Output intractability is related to, but incomparable with, the notion of correlation intractability mentioned above. As an assumption, our notion of output intractability takes the form of a knowledge assumption on hash functions; no construction based on “nice” assumptions is currently known.

• Hardcore bits for any one-way function. A random oracle serves as a good way to extract many hardcore bits for any one-way function. This fact gives rise to a simple public-key encryption scheme from trapdoor permutations. While it is known how to extract many hardcore bits for specific functions [1, 29, 34], extracting many bits for general one-way functions may be useful in settings where we cannot freely choose the function, such as if the function is required to be a trapdoor permutation. Unfortunately, for general one-way functions, the only known way to extract more than a logarithmic number of hardcore bits is to use very strong (and questionable [21]) knowledge assumptions: differing inputs obfuscation [6] (plus one-way functions) or extractable witness PRFs [39]. In the case of injective one-way functions, Bellare et al. [6] show that the weaker assumption of indistiguishability obfuscation (iO) (plus one-way functions) suffices. While weaker than diO, iO is still one of the strongest assumptions made in cryptography. Either way, the forms of obfuscation required are also completely impractical [3]. Another limitation of prior constructions is that randomness used to sample the hardcore function needs to be kept secret.

• Instantiating Full Domain Hash (FDH) signatures. Finally, we consider using random oracles to instantiate the Full Domain Hash (FDH) protocol transforming trapdoor permutations into signatures. Hohenberger et al. [26] show that (indistinguishability) obfuscating a (puncturable) pseudorandom function composed with the permutation is sufficient for FDH signatures. However, their proof has two important limitations. First, the resulting signature scheme is only selectively secure. Second, the instantiation depends on the particular trapdoor permutation used, as well as the public key of the signer. Thus, each signer needs a separate hash function, which needs to be appended to the signer’s public keys. To use their protocol, everyone will therefore need to publish new keys, even if they already have published keys for the trapdoor permutation.

Our approach. We take a novel approach to addressing the questions above. We isolate a (generally ignored) property of random oracles, namely that random oracles are indistinguishable from functions that are extremely lossy. More precisely, the following is possible in the random oracle model. Given any polynomial time oracle adversary ${{\mathcal {A}}}$ and an inverse polynomial $\delta$, we can choose the oracle such that (1) the image size of the oracle is a polynomial r (even for domain/range sizes where a truly random oracle will have exponential image size w.h.p.), and (2) ${{\mathcal {A}}}$ cannot tell the difference between such a lossy oracle and a truly random oracle, except with advantage smaller than $\delta$. Note that the tuning of the image size must be done with knowledge of the adversary’s running time — an adversary running in time $O(\sqrt{r})$ can with high probability find a collision, thereby distinguishing the lossy function from a truly random oracle. However, by setting $\sqrt{r}$ to be much larger than the adversary’s running time, the probability of finding a collision diminishes. We stress that any protocol would still use a truly random oracle and hence not depend on the adversary; the image size tuning would only appear in the security proof. Our observation of this property is inspired by prior works of Boneh and Zhandry [11, 38], who use it for the entirely different goal of giving security proofs in the so-called quantum random oracle model (random oracle instantiation was not a goal nor accomplishment of these prior works).

We next propose the notion of an Extremely Lossy Function (ELF) as a standard-model primitive that captures this tunable image size property. The definition is related to the notion of a lossy trapdoor function due to Peikert and Waters [30], with two important differences: we do not need any trapdoor, giving hope that ELFs could be constructed from symmetric primitives. On the other hand, we need the functions to be much, much more lossy, as standard lossy functions still have exponential image size.

On the surface, extreme lossiness without a trapdoor does not appear incredibly useful, since many interesting applications of standard lossy functions (e.g. CCA-secure public key encryption) require a trapdoor. Perhaps surprisingly, we show that this extremely lossy property, in conjunction with other tools — usually pairwise independence — can in fact quite powerful, and we use this power to give new solutions to each of the tasks above. Our results are as follows:

• (Section 3) We give a practical construction of ELFs assuming the exponential hardness of the decisional Diffie-Hellman (DDH) problem: roughly, that the best attack on DDH for groups of order p takes time $O(p^{c})$ for some constant c. More generally, our construction can be based on the exponential hardness of the k-Lin problem. Our construction is based on the lossy trapdoor functions due to Peikert and Waters [30] and Freeman et al. [20], though we do not need the trapdoor from those works. Our construction starts from a trapdoor-less version of the DDH-based construction of [20], and iterates it many times at different security levels, together with pairwise independent hashing to keep the output length from growing too large. Having many different security levels allows us to do the following: when switching the function to be lossy, we can do so at a security level that is just high enough to prevent the particular adversary from detecting the switch. Using the exponential DDH assumption, we show that the security level can be set low enough so that (1) the adversary cannot detect the switch, and (2) so that the resulting function has polynomial image size. We note that a couple prior works [10, 18] have used a similar technique of combining several “bounded adversary” instances at multiple security levels, and invoking the security of the instance with “just high enough” security. The main difference is that in prior works, “bounded adversary” refers to bounded queries, and the security parameter itself is kept constant across instances; in our work, “bounded adversary” refers to bounding the running time of the adversary, and the security parameter is what is varied across instances.

  Our iteration at multiple security levels is somewhat generic and would potentially apply to other constructions of lossy functions, such as those based on LWE. However, LWE-based constructions of lossy functions are not quite lossy enough for our needs since even “exponentially secure” LWE can be solved in time sub-exponential in the length of the secret.

  The exponential hardness of DDH is plausible on elliptic curve groups — despite over a decade of wide-spread use and cryptanalysis attempts, there are virtually no non-trivial attacks on most elliptic curve groups and the current best attacks on DDH take time $\varOmega (p^{1/2})$. In fact, the parameter settings for most real-world uses of the Diffie-Hellman problem are set assuming the Diffie-Hellman problem takes exponential time to solve. If our assumption turns out to be false, it would have significant ramifications as it would suggest that parameters for many cryptosystems in practice are set too aggressively. It would therefore be quite surprising if DDH turned out to not be exponentially hard on elliptic curves. While not a true falsifiable assumption in the sense of Naor [28] or Gentry and Wichs [22] due to the adversary being allowed to run in exponential time, the exponential DDH assumption is falsifiable in spirit and naturally fits within the complexity assumption framework of Goldwasser and Kalai [24].

  While our ELFs are built from public key tools, we believe such tools are unnecessary and we leave as an interesting open question the problem of constructing ELFs from symmetric or generic tools.

  We observe that our construction achieves a public coin notion, which is useful for obtaining public coin hash functions in applications¹.

• We give several different hash function instantiations based on ELFs ranging in complexity and the additional tools used. In doing so, we give new solutions to each of the problems above. Each construction uses the ELFs in different ways, and we develop new techniques for the analysis of these constructions. Thus we give an initial set of tools for using ELFs that we hope to be useful outside the immediate scope of this work.

  • The simplest instantiation is just to use an ELF itself as a hash function. Such a function can be used to generically boost selective security to adaptive security in signatures and identity-based encryption by first hashing the message/user identity (more details below).

  • (Section 4) The next simplest instantiation is to pre-compose the ELF with a pairwise independent hash function. This function gives rise to a simple (public coin) point function obfuscation (PO). Proving this uses a slight generalization of the “crooked leftover hash lemma” [17].

  • (Section 5) A slightly more complicated instantiation is given by post-composing and ELF with a k-wise independent function. We show that this construction satisfies our notion of output intractability. It is moreover public coin. This construction and analysis can be seen as a generalization of the result of [30] that post-composing a standard lossy function with a pairwise independent hash function gives a collision resistant function, though the details of the analysis are very different.

  • (Section 6) We then give an even more complicated construction, though still using ELF’s as the only underlying source of cryptographic hardness. The construction roughly follows a common paradigm used in leakage resilience [19]: apply a computational step (in our case, involving ELFs), compress with pairwise independence, and repeat. We note however that the details of the construction and analysis are new to this work.

    We demonstrate that our construction is a pseudorandom generator attaining a very strong notion of leakage resilience for the seed. This property strengthens the one-way notion of Bitansky and Paneth [9]. Our construction therefore shows how to instantiate the knowledge properties conjectured in their work using a more traditional-style assumption.

    An immediate consequences of our generator requirement is a (public coin) point function obfuscation that is secure even in the presence of auxiliary information (AIPO), which was previously known from either permutations satisfying [9]’s one-wayness requirement (our function is not a permutation), or from Canetti’s strong knowledge variant of DDH [9, 14]². Our AIPO construction is qualitatively very different from these existing constructions, and when plugging in our ELF construction, again relies on just exponential DDH.

    Our generator also immediately gives a family of (public coin) hardcore functions of arbitrary stretch for any one-way function. Unlike the previous obfuscation-based solutions, our is practical, and public coin, and ultimately based on a well-studied game-based assumption.

    Our analysis also demonstrates that our ELF-based function can be used in a standard random oracle public key encryption protocol [5].

  • In the full version [40], we give an instantiation useful for Full Domain Hash (FDH) signatures which involves obfuscating the composition of an ELF and a (puncturable) pseudorandom function using an indistinguishability obfuscator. Since we use obfuscation as in Hohenberger et al. [26] scheme, this construction is still completely impractical and therefore currently only of theoretical interest. We show that our construction can be used in the FDH protocol, solving some of the limitations in [26]. In particular, by composing with an ELF, we immediately get adaptive security as observed above. Our construction is moreover independent of the permutation (except for the size of the circuit computing it), and is also independent of the signer’s public key. Thus, our instantiation is universal and one instantiation can be used by any signer, even using existing keys. Similar to [26], this construction is still required to be secret coin, even if the underlying ELF is public coin.

Warm up: generically boosting selective to adaptive security. To give a sense for our techniques, we show how ELFs can be used to generically boost selective to adaptive security in signatures and identity-based encryption. We demonstrate the case for signatures; the case for identity based encryption is almost identical.

Recall that in selective security for signatures, the adversary commits to a message $m^*$ at the beginning of the experiment before seeing the public key. Then the adversary makes a polynomial q adaptive signing queries on messages $m_1,\dots ,m_q\ne m^*$, receiving signatures $\sigma _1,\dots ,\sigma _q$. Then, the adversary produces a forged signature $\sigma ^*$ on $m^*$, and security states that $\sigma ^*$ is with overwhelming probability invalid for any efficient adversary. Adaptive security, in contrast, allows the adversary to choose $m^*$ potentially after the q adaptive queries.

We now convert selective to adaptive security using ELFs: first hash the message using the ELF, and then sign. Adaptive security is proved through a sequence of hybrids. The first is the standard adaptive security game above. Toward contradiction, suppose that the adversary runs in polynomial time t and succeeds in forging a signature on $m^*$ with non-negligible probability $\epsilon$. Let $\delta$ be an inverse polynomial that lower bounds $\epsilon$ infinitely often. In the second hybrid, the ELF is selected to have polynomial image size r, where $r\ge 2q$ is chosen, say, so that no t-time adversary can distinguish between this ELF and an injective ELF, except with probability at most $\delta /2$. Thus, in this hybrid, the adversary still successfully forges with probability $\epsilon -\delta /2$. This is lower bounded by $\delta /2$ infinitely often, and is therefore non-negligible.

In the next hybrid, at the beginning of the experiment, one of the r image points of the ELF, $y^*$, is chosen at random³. Then we abort the experiment if the adversary’s chosen $m^*$ does not hash to $y^*$; with probability 1 / r, we do not abort⁴. This abort condition is independent of the adversary’s view, meaning that we do not abort, and the adversary successfully forges, with probability at least $(\epsilon -\delta /2)/r$, which again is non-negligible. Notice now that $y^*$ can be chosen at the beginning of the experiment. This is sufficient for obtaining an adversary for the selective security of the original signature scheme.

1.2 Complexity Absorption

It may be more reasonable to assume the (sub-)exponential hardness of an existing well-studied problem than to assume such hardness for new and untested problems. Moreover, there might be implementation issues (such as having to re-publish longer keys, see the full version [40] for a setting where this could happen) that make the sub-exponential hardness of certain primitives undesirable.

The application of ELFs to signatures and identity-based encryption above can be seen as an instance of a more general task of complexity absorption, where an extra complexity-absorbing primitive (in our case, and ELF) is introduced into the protocol. The original building blocks of the protocol (the underlying signature/identity-based encryption in this case) can be reduced from (sub)exponential security to polynomial security. Meanwhile, the complexity-absorbing primitive may still require exponential hardness as in our case, but hopefully such hardness is a reasonable assumption. Our hardcore function with arbitrary span can also be seen in this light: it is straightforward to extend Goldreich-Levin [23] to a hardcore function of polynomial span for exponentially-secure one-way functions. By introducing an ELF into the hardcore function, the ELF can absorb the complexity required of the one-way function, yielding a hardcore function for any one-way function, even one-way functions that are only polynomially secure. Similarly, our random oracle instantiation for Full Domain Hash can also be seen as an instance of complexity absorption.

Thus, our work can be seen as providing an initial set of tools and techniques for the task of complexity absorption that may be useful in other settings where some form of sub-exponential hardness is difficult or impossible to avoid. For example, Rao [32] argues that any proof of adaptive security for multiparty non-interactive key exchange (NIKE) will likely incur an exponential loss. As all current multiparty NIKE protocols are built from multilinear maps or obfuscation, which in turn rely on new, untested (and in many cases broken) hardness assumptions, assuming the sub-exponential security of the underlying primitives to attain adaptive security is undesirable. Hofheinz et al. [25] give a construction in the random oracle model that only has a polynomial loss; our work gives hope that a standard model construction based on ELFs may be possible where the ELF is the only primitive that needs stronger than polynomial hardness.

1.3 Non-black Box Simulation

Our proofs require knowledge of the adversary’s running time (and success probability). Thus, they do not make black box use of the adversary. Yet, this is the only non-black box part of our proofs — the reduction does not need to know the description or internal workings of the adversary. This is similar to Goldreich-Levin [23], where only the adversary’s success probability is needed. Thus our reductions are nearly black box, while potentially giving means to circumvent black-box impossibilities. For example, proving the security of AIPO is known to require non-black box access to the adversary [9, 37], and yet our reduction proves the security of AIPO knowing only the adversary’s running time and success probability. We leave it as an interesting open question to see if your techniques can be used to similarly circumvent other black box impossibilities.

1.4 On the Minimal Assumptions Needed to Build ELFs

We show how to construct extremely lossy functions from a specific assumption on elliptic curve groups. One could also hope for generic constructions of ELFs based on existing well-studied primitives. Unfortunately, this appears to be a difficult task, and there are several barriers to constructing ELFs. For example, lossy functions (even standard ones) readily imply collision resistance [30], which cannot be built from one-way functions in a black-box fashion [35]. Rosen and Segev [33] show a similar separation from functions that are secure under correlated products. Pietrzak et al. [31] show that efficiently amplifying lossiness in a black box way is impossible — this suggests that building ELFs from standard lossy functions will be difficult, if not impossible.

Perhaps an even stronger barrier to realizing ELFs from standard assumptions is the following. Our assumption, unfortunately, is about exponential-time adversaries, as opposed to typical assumptions about polynomial-time adversaries. One could hope for basing ELFs on standard polynomial assumptions, such as polynomial DDH. However, this would require major breakthroughs in complexity theory. Indeed, lossy and injective modes of an ELF can be distinguished very efficiently using a super-logarithmic amount of non-determinism as follows. Let $D=[2^{\omega (\log m)}]$ where m is the number of input bits to the ELF. In the injective mode, there will be no collisions when the domain is restricted to D. However, in the lossy mode for any polynomial image size $r=r(m)$, there is guaranteed to be a collision in D. Points in D can be specified by $\omega (\log m)$ bits. Therefore, we can distinguish the two modes by non-deterministically guessing two inputs in D (using $\omega (\log m)$ bits of non-determinism) and checking that they form a collision. Therefore, if $\mathtt {NP}$ restricted to some super-logarithmic amount of non-determinism was solvable in polynomial time, then this algorithm could be made efficient while removing all non-determinism. Such an algorithm would violate ELF security.

Theorem 1

If ELFs exist, then for any super-logarithmic function t, $\mathtt {NP}$ with t bits of non-determinism is not solvable in polynomial time.

Therefore, it seems implausible to base ELFs on any polynomially-secure primitive, since it is consistent with our current knowledge that $\mathtt {NP}$ with, say, $\log ^2$ bits of non-determinism is solvable in polynomial time, but polynomially-secure cryptographic primitives exist. This may seem to suggest that ELFs are too strong of a starting point for our applications; to the contrary, we argue that for most of our applications — point functions⁵ (Sect. 4), output intractability (Sect. 5), and polynomially-many hardcore bits for any one-way function (Sect. 6) — similar barriers are inherent to the applications. Therefore, this limitation of ELFs is shared with any primitive strong enough to realize the applications.

Therefore, instead of starting from standard polynomially-secure primitives, we may hope to build ELFs generically from, say, an exponentially secure primitive which has a similar limitation. Can we build ELFs from exponentially secure (injective) one-way functions? Exponentially-secure collision resistant hash functions? To what extent do the black-box barriers above extend into the regime of exponential hardness? We leave these as interesting open questions.

2 Preliminaries

Given a distribution ${\mathcal {D}}$ over a set ${\mathcal {X}}$, define the support of ${\mathcal {D}}$, ${\mathrm {Supp}}({\mathcal {D}})$, to be the set of points in ${\mathcal {X}}$ that occur with non-zero probability. For any $x\in {\mathcal {X}}$, let $\Pr [{\mathcal {D}}=x]$ be the probability that ${\mathcal {D}}$ selects x. For any set ${\mathcal {X}}$, define $U_{\mathcal {X}}$ to be the uniform distribution on ${\mathcal {X}}$. Define the collision probability of ${\mathcal {D}}$ to be $CP({\mathcal {D}})=\Pr [x_1=x_2:x_1,x_2\leftarrow {\mathcal {D}}]=\sum _{x\in {\mathcal {X}}}\Pr [{\mathcal {D}}=x]^2$. Given two distributions ${\mathcal {D}}_1,{\mathcal {D}}_2$, define the statistical distance between ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$ to be $\varDelta ({\mathcal {D}}_1,{\mathcal {D}}_2)=\frac{1}{2}\sum _{x\in {\mathcal {X}}}\big |\Pr [{\mathcal {D}}_1=x]-\Pr [{\mathcal {D}}_2=x]\big |$. Suppose ${\mathrm {Supp}}({\mathcal {D}}_1)\subseteq {\mathrm {Supp}}({\mathcal {D}}_2)$. Define the Rényi Divergence between ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$ to be $RD({\mathcal {D}}_1,{\mathcal {D}}_2)=\sum _{x\in \sup ({\mathcal {D}}_1)}\frac{\Pr [{\mathcal {D}}_1=x]^2}{\Pr [{\mathcal {D}}_2=x]}$ ⁶. The Rényi divergence is related to the statistical distance via the following lemma:

Lemma 1

For any distributions ${\mathcal {D}}_1,{\mathcal {D}}_2$ over a set ${\mathcal {Z}}$ such that ${\mathrm {Supp}}({\mathcal {D}}_1)\subseteq {\mathrm {Supp}}({\mathcal {D}}_2)$, $\varDelta ({\mathcal {D}}_1,{\mathcal {D}}_2)\le \frac{1}{2}\sqrt{RD({\mathcal {D}}_1,{\mathcal {D}}_2)-1}$.

Consider a distribution ${\mathcal {H}}$ over the set of functions $h:{\mathcal {X}}\rightarrow {\mathcal {Y}}$. We say that ${\mathcal {H}}$ is pairwise independent if, for any $x_1\ne x_2\in {\mathcal {X}}$, the random variables ${\mathcal {H}}(x_1)$ and ${\mathcal {H}}(x_2)$ are independent and identically distributed, though not necessarily uniform. Similarly define k-wise independence. We say that ${\mathcal {H}}$ has output distribution ${\mathcal {D}}$ if for all x, the random variable ${\mathcal {H}}(x)$ is identical to ${\mathcal {D}}$. Finally, we say that ${\mathcal {H}}$ is uniform if it has output distribution $U_{\mathcal {Y}}$ ⁷. We will sometimes abuse notation and say that a function h is a pairwise independent function (resp. uniform) if h is drawn from a pairwise independent (resp. uniform) distribution of functions.

We will say that a (potentially probabilistic) algorithm ${{\mathcal {A}}}$ outputting a bit b distinguishes two distributions ${\mathcal {D}}_0,{\mathcal {D}}_1$ with advantage $\epsilon$ if $\Pr [{{\mathcal {A}}}({\mathcal {D}}_b):b\leftarrow \{0,1\}]\in \left[ \frac{1}{2}-\epsilon ,\frac{1}{2}+\epsilon \right]$. This is equivalent to the random variables ${{\mathcal {A}}}({\mathcal {D}}_0)$ and ${{\mathcal {A}}}({\mathcal {D}}_1)$ have $2\epsilon$ statistical distance.

Unless otherwise stated, all cryptographic protocols will implicitly take a security parameter $\lambda$ as input. Moreover, any sets (such as message spaces, ciphertext spaces, etc.) will be implicitly indexed by $\lambda$, unless otherwise stated. In this context, when we say that an adversary is efficient, we mean its running time is polynomial in $\lambda$. A non-negative function $\epsilon =\epsilon (n)$ is negligible if, for any polynomial $p=p(\lambda )$, $\epsilon <1/p$ for all sufficiently large $\lambda$. When discussing cryptographic protocols, we say that a probability of an event or advantage of an adversary is negligible if it is negligible in $\lambda$. Two distributions ${\mathcal {D}}_0,{\mathcal {D}}_1$ (implicitly parameterized by $\lambda$) are computationally indistinguishable if any efficient algorithm has only negligible distinguishing advantage, and are statistically indistinguishable if the distributions have negligible statistical distance. In the statistical setting, we also sometimes say that ${\mathcal {D}}_0,{\mathcal {D}}_1$ are statistically close.

The Crooked Leftover Hash Lemma. Here we state a slight generalization of the “crooked Leftover Hash Lemma” of Dodis and Smith [17]; the proof is in the full version [40] and follows [17].

Lemma 2

Let H be a distribution on functions $h:{\mathcal {X}}\rightarrow {\mathcal {Y}}$ that is pairwise independent with output distribution ${\mathcal {E}}$, for some distribution ${\mathcal {E}}$ that is possibly non-uniform. Let ${\mathcal {D}}$ be an arbitrary distribution over ${\mathcal {X}}$. Then we have that $\varDelta \big ((H,H({\mathcal {D}}))\;,\; (H,{\mathcal {E}})\big )\le \frac{1}{2}\sqrt{CP({\mathcal {D}})\big (|{\mathrm {Supp}}({\mathcal {E}})|-1\big )}$.

3 Extremely Lossy Functions

Here, we define our notion of extremely lossy functions, or ELFs. A standard lossy function [30] is intuitively a function family with two modes: an injective mode where the function is injective, and a lossy mode where the image size of the function is much smaller than the domain. The standard security requirement is that no polynomial-time adversary can distinguish the two modes⁸.

An ELF is a lossy function with a much stronger security requirement. In the lossy mode, the image size can be taken to be a polynomial r. Clearly, such a lossy mode can be distinguished from injective by an adversary running in time $O(\sqrt{r})$ that simply evaluates the function on $\sqrt{r}$ inputs, looking for a collision. Therefore, we cannot have security against arbitrary polynomial-time attackers. Instead, we require security against $r^c$-time attackers, for some $c\le 1/2$. Moreover, we require that r is actually tunable, and can be chosen based on the adversary in question. This means that for any polynomial time attacker, we can set the lossy function to have domain r for some polynomial r, and the lossy function will be indistinguishable from injective to that particular attacker (note that the honest protocol will always use the injective mode, and therefore will not depend on the adversary in any way).

Definition 1

An extremely lossy function (ELF) consists of an algorithm ${\mathtt {ELF.Gen}}$, which takes as input integers M and $r\in [M]$. There is no security parameter here; instead, $\log M$ acts as the security parameter. ${\mathtt {ELF.Gen}}$ outputs the description of a function $f:[M]\rightarrow [N]$ such that:

• f is computable in time polynomial in the bit-length of its input, namely $\log M$. The running time is independent of r.

• If $r=M$, then f is injective with overwhelming probability (in $\log M$).

• For all $r\in [M]$, $|f([M])|\le r$ with overwhelming probability. That is, the function f has image size at most r.

• For any polynomial p and inverse polynomial function $\delta$ (in $\log M$), there is a polynomial q such that: for any adversary ${{\mathcal {A}}}$ running in time at most p, and any $r \in [q(\log M),M]$, we have that ${{\mathcal {A}}}$ distinguishes ${\mathtt {ELF.Gen}}(M,M)$ from ${\mathtt {ELF.Gen}}(M,r)$ with advantage less than $\delta$. Intuitively, no polynomial-time adversary ${{\mathcal {A}}}$ can distinguish an injective from polynomial image size (where the polynomial size depends on the adversary’s running time.).

For some applications, we will need an additional requirement for ELFs:

Definition 2

An ELF has an efficiently enumerable image space if there is a (potentially randomized) procedure running in time polynomial in r and $\log M$ that, given $f\leftarrow {\mathtt {ELF.Gen}}(M,r)$ and r, outputs a polynomial-sized set S of points in [N] such that, with overwhelming probability over the choice of f and the randomness of the procedure, $f([M])\subseteq S$.

Definition 3

An ELF has a efficiently sampleable image space if there is a polynomial s and a randomized polynomial time procedure (where “polynomial” means polynomial in r and $\log M$) such that the following holds. Given $f\leftarrow {\mathtt {ELF.Gen}}(M,r)$ and r, the procedure outputs a point $y\in [N]$ such that with overwhelming probability over the choice of f, the point y has a distribution that places weight at least 1 / s on each image point in f([M]).

Lemma 3

An ELF is efficiently sampleable iff it is efficiently enumerable.

Proof

In one direction, we just sample a random element from the polynomial-sized list S, obtaining each image point with probability 1 / |S|. In the other direction, by sampling $\lambda s$ points independently at random, except with negligible probability in $\lambda$, the set of sampled points will contain each of the r images.   $\square$

The following property will be useful for attaining ELFs with efficiently enumerable/sampleable image spaces:

Definition 4

An ELF is regular if, for all polynomial r, with overwhelming probability over the choice of $f\leftarrow {\mathtt {ELF.Gen}}(M,r)$, the distribution f(x) for a uniform $x\leftarrow [M]$ is statistically close to uniform over f([M]).

Lemma 4

If an ELF is regular, then it is efficiently sampleable/enumerable.

Proof

To sample, just apply the ELF to a random point. Notice that the sampled point is guaranteed to be an image point. Thus regularity actually implies a strong notion of enumerability where $S=f([M])$ with overwhelming probability.   $\square$

The final ELF property we define is public coin.

Definition 5

An ELF is public coin if the description of an injective mode f outputted by ${\mathtt {ELF.Gen}}(M,M)$ is simply the random coins used by ${\mathtt {ELF.Gen}}(M,M)$. The descriptions of lossy mode f’s outputted by ${\mathtt {ELF.Gen}}(M,r),r<M$ may (and in fact, must) be a more complicated function of the random coins.

3.1 Constructing ELFs

We now show how to construct ELFs. Our construction will have two steps: first, we will show that ELFs can be constructed from a weaker primitive called a bounded adversary ELF, which is basically and ELF that is only secure against a priori bounded adversaries. Then we show essentially that the DDH-based lossy function of [20], when the group size is taken to be polynomial, satisfies our notion of a bounded-adversary ELF.

Bounded Adversary ELFs

Definition 6

An bounded adversary extremely lossy function (bounded ELF) consists of an algorithm ${\mathtt {ELF.Gen}}'$, which takes as input integers M, $r\in [M]$, and $b\in \{0,1\}$. Here, b will indicate whether the function should be lossy, and r will specify the lossiness. Similar to regular ELFs, there is no security parameter here; instead, $\log M$ acts as the security parameter. ${\mathtt {ELF.Gen}}'$ outputs the description of a function $f:[M]\rightarrow [N]$ such that:

• f is computable in time polynomial in the bit-length of its input, namely $\log M$. The running time is independent of r.

• If $b=0$, then f is injective with overwhelming probability (in $\log M$).

• For all $r\in [M]$, if $b=1$, then $|f([M])|\le r$ with overwhelming probability. That is, the function f has image size at most r.

• For any polynomial p and inverse polynomial function $\delta$ (in $\log M$), there is a polynomial q such that: for any adversary ${{\mathcal {A}}}$ running in time at most p, and any $r \in [q(\log M),M]$, we have that ${{\mathcal {A}}}$ distinguishes ${\mathtt {ELF.Gen}}'(M,r,0)$ from ${\mathtt {ELF.Gen}}'(M,r,1)$ with advantage less than $\delta$.

Intuitively, the difference between a regular ELF and a bounded adversary ELF is that in a regular ELF, r can be chosen dynamically based on the adversary, whereas in a bounded adversary ELF, r must be chosen first, and then security only applies to adversaries whose running time is sufficiently small. In a bounded adversary ELF, the adversary may be able to learn r. We now show that bounded ELFs are sufficient for constructing full ELFs.

Construction 1

On input M, r, ${\mathtt {ELF.Gen}}$ does:

• For simplicity, assume M is a power of 2: $M=2^k$. Let $M'=M^3=2^{2k}$, and [N] be the co-domain of ${\mathtt {ELF.Gen}}'$ on domain $[M']$.

• Let $i^*$ be the integer such that $2^{i^*}\in (r/2,r]$. Set $b_{i^*}=1$ and $b_i=0$ for $i\ne i^*$

• For $i=1,\dots ,k-1$, let $f_i\leftarrow {\mathtt {ELF.Gen}}'(M',2^i,b_i)$.

• For $i=2,\dots ,k$, choose a pairwise independent random $h_i:[N']\rightarrow [M']$.

• Choose a pairwise independent random $h_1:[M]\rightarrow [M']$.

• Output the function $f=h_k\circ f_{k-1}\circ h_{k-1}\circ f_{k-2}\circ \dots \circ f_1\circ h_1$.

Fig. 1.

An example instantiation for $k=3$.

Theorem 2

If ${\mathtt {ELF.Gen}}'$ is a bounded-adversary ELF, then ${\mathtt {ELF.Gen}}$ is a (standard) ELF. If ${\mathtt {ELF.Gen}}'$ is public coin, then so is ${\mathtt {ELF.Gen}}$. If ${\mathtt {ELF.Gen}}'$ is enumerable, then so is ${\mathtt {ELF.Gen}}$. If ${\mathtt {ELF.Gen}}'$ is regular, then so is ${\mathtt {ELF.Gen}}$.

Proof

First, if $r=M$, then $i^*=k$, and so each of the $b_i$ will be 0. Thus each of the $f_i$ will be injective with overwhelming probability. Fix $h_1,f_i,\dots ,h_{i-1},f_{i-1}$, and let $S_i$ be the image of $f_{i-1}\circ h_{i-1}\circ f_{k-2}\circ \dots \circ f_1\circ h_1$. Since each of the functions $h_i$ have co-domain of size $M'=M^3$, by pairwise independence, $h_i$ will be injective on $S_i$ with overwhelming probability. Thus, with overwhelming probability, the entire evaluation of f will be injective.

Second, if $r< M$, the function $f_{i^*}$ is set to be lossy with image size $2^{i^*}\le r$. Thus, f will have image size at most r. Third, we need to argue security. Let p be a polynomial and $\sigma$ be an inverse polynomial (in $\log M$). Let $p'=p+c$ for some c to be determined later. We can think of $p',\sigma$ as being functions of $\log M'=3\log M$. Let q be the polynomial guaranteed by ${\mathtt {ELF.Gen}}'$ for $p'$ and $\sigma$. Then we can consider q to be a polynomial in $\log M$. Consider any adversary A for ${\mathtt {ELF.Gen}}$ running in time at most p. Let $r\in (q(\log M),M]$, and let $i^*$ be such that $2^{i^*}\in (r/2,r]$. We construct an adversary $A'$ for ${\mathtt {ELF.Gen}}'$: let $f_{i^*}$ be the f that $A'$ receives, where $f_{i^*}$ is either ${\mathtt {ELF.Gen}}(M,2^{i^*},0)$ or ${\mathtt {ELF.Gen}}(M,2^{i^*},1)$. $A'$ simulates the rest of f for itself, setting $b_i=0,f_i\leftarrow {\mathtt {ELF.Gen}}'(M,2^i,b_i)$ for $i\ne i^*$ as well as generating the $h_i$. $A'$ then runs A on the simulated f. Let c be the overhead of this reduction, so that $A'$ runs in time $p+c=p'$. Thus by the bounded-adversary security of ${\mathtt {ELF.Gen}}'$, $A'$ cannot distinguish injective or lossy mode, except with advantage $\sigma$. Moreover, if $f_{i^*}$ is generated as ${\mathtt {ELF.Gen}}(M,2^{i^*},0)$, then this corresponds to the injective mode of ${\mathtt {ELF.Gen}}$, and if $f_{i^*}$ is generated as ${\mathtt {ELF.Gen}}(M,2^{i^*},1)$, then this corresponds to ${\mathtt {ELF.Gen}}(M,r)$. Thus, $A'$ and A have the same distinguishing advantage, and therefore A cannot distinguish the two cases except with probability less than $\sigma$.

It remains to show that ${\mathtt {ELF.Gen}}$ inherits some of the properties of ${\mathtt {ELF.Gen}}'$. Being public coin is trivially inherited. To get a sampler for ${\mathtt {ELF.Gen}}$, apply the sampler for ${\mathtt {ELF.Gen}}'$ to the instance $f_{i^*}$ that is lossy, obtaining point $y^{(i^*)}$. Then compute $y=h_k\circ f_{k-1}\circ h_{k-1}\circ f_{k-2}\circ \dots \circ f_{i^*+1}\circ h_{i^*+1}(y^{(i^*)})$. Since any image of f is necessarily computed as $h_k\circ f_{k-1}\circ h_{k-1}\circ f_{k-2}\circ \dots \circ f_{i^*+1}\circ h_{i^*+1}(y^{(i^*)})$ for some $y_{i^*}$ in the image of $f_{i^*}$, and all other steps are injective with overwhelming probability, the result $x^{(k+1)}$ will hit each image point of f frequently as well. In the full version [40], we also show that regularity is inherited.   $\square$

Instantiation for Bounded Adversary ELFs. Our construction of bounded adversary ELFs is based on the DDH-based lossy trapdoor functions of Peikert and Waters [30] and Freeman et al. [20]. We stress that we do not need the trapdoor property of their construction, only the lossy property. Security will be based on the exponential hardness of the decisional Diffie-Hellman problem, or its k-linear generalizations.

Definition 7

A cryptographic group consists of an algorithm $\mathtt {GroupGen}$ that takes as input a security parameter $\lambda$, and outputs the description of a cyclic group $\mathbb {G}$ of prime order $p\in [2^\lambda ,2\times 2^\lambda )$, and a generator g for $\mathbb {G}$ such that:

• The group operation $\times :\mathbb {G}^2\rightarrow \mathbb {G}$ can be computed in time polynomial in $\lambda$.

• Exponentiation by elements in $\mathbb {Z}_p$ can be carried out in time polynomial in $\lambda$. This follows from the efficient group operation procedure by repeated doubling and the fact that $\log p\le \lambda +1$.

• The representation of a group element h has size polynomial in $\lambda$. This also follows implicitly from the assumption that the group operation is efficient.

We now introduce some notation. For vectors ${\mathbf {v}},{\mathbf {w}}\in \mathbb {Z}_p^n$, let ${\mathbf {v}}* {\mathbf {w}}$ denote the point-wise product of the two vectors. For a matrix ${\mathbf {A}}\in \mathbb {Z}_p^{m\times n}$, we write $g^{\mathbf {A}}\in \mathbb {G}^{m\times n}$ to be the $m\times n$ matrix of group elements $g^{A_{i,j}}$. Similarly define $g^{\mathbf {w}}$ for a vector ${\mathbf {w}}\in \mathbb {Z}_p^n$. Given a matrix $\hat{{\mathbf {A}}}\in \mathbb {G}^{m\times n}$ of group elements and a vector ${\mathbf {v}}\in \mathbb {Z}_p^n$, define $\hat{{\mathbf {A}}}\cdot {\mathbf {v}}$ to be $\hat{{\mathbf {w}}}\in \mathbb {G}^m$ where $\hat{w}_i=\prod _{j=1}^n \hat{A}_{i,j}^{v_j}$. Using this notation, $(g^{\mathbf {A}})\cdot {\mathbf {v}}=g^{{\mathbf {A}}\cdot {\mathbf {v}}}$. Therefore, the map $g^{\mathbf {A}},{\mathbf {v}}\mapsto g^{{\mathbf {A}}\cdot {\mathbf {v}}}$ is efficiently computable.

Definition 8

The exponential decisional k -linear assumption (k-eLin) on a cryptographic group specified by $\mathtt {GroupGen}$ holds if there is a polynomial $q(\cdot ,\cdot )$ such that the following is true. For any time bound t and probability $\epsilon$, let $\lambda =\log q(t,1/\epsilon )$. Then for any adversary ${{\mathcal {A}}}$ running in time at most t, the following two distributions are indistinguishable, except with advantage at most $\epsilon$:

$$\begin{aligned}&(\mathbb {G},g,g^{\mathbf {v}},g^{{\mathbf {v}}* {\mathbf {w}}},g^c):(\mathbb {G},g,p)\leftarrow \mathtt {GroupGen}(\lambda ),{\mathbf {v}},{\mathbf {w}}\leftarrow \mathbb {Z}_p^k,c\leftarrow \mathbb {Z}_p\text { and }\\&(\mathbb {G},g,g^{\mathbf {v}},g^{{\mathbf {v}}* {\mathbf {w}}},g^{\sum _{i=1}^k w_i}:(\mathbb {G},g,p)\leftarrow \mathtt {GroupGen}(\lambda ),{\mathbf {v}},{\mathbf {w}}\leftarrow \mathbb {Z}_p^k \end{aligned}$$

Definition 9

A cryptographic group is public coin if the following holds:

• The “description” of $\mathbb {G},g,p$ is just the random coins sampled by $\mathtt {GroupGen}$.

• There is a (potentially redundant) efficiently computable representation of group elements in $\mathbb {G}$ as strings in $\{0,1\}^n$ such that (1) a random string in $\{0,1\}^n$ corresponds to a random element in $\mathbb {G}$, and (2) a random representation of a random element in $\mathbb {G}$ is a random string in $\{0,1\}^n$.

A plausible candidate for a cryptographic group supporting the k-eLin assumption are groups based on elliptic curves. Despite over a decade or research, essentially no non-trivial attack is known on general elliptic curve groups. Therefore, the k-eLin assumption on these groups appears to be a reasonable assumption. We note that groups based on elliptic curves can be made public coin.

Construction 2

Our construction is as follows, and will be parameterized by k. ${\mathtt {ELF.Gen}}_k'(M,r,b)$ does the following.

• Let $\lambda$ be the largest integer such that $(2\times 2^\lambda )^k < r$. Run $(\mathbb {G},g,p)\leftarrow \mathtt {GroupGen}(\lambda )$.

• Assume for simplicity that $M=p^m$ for some integer m. Then associate the domain [M] with $\mathbb {Z}_p^m$. The more general case can be handled by hashing [M] into $\mathbb {Z}_p^m$ for some m using a pairwise independent hash function which is injective with overwhelming probability; we defer the analysis to the full version [40] and here focus on the simple case.

• Let $n\ge m$ be such that a random matrix sampled from $\mathbb {Z}_p^{n\times m}$ has rank m with overwhelming probability. For this, it suffices to set $n=2m$.

• If $b=0$, choose a random matrix of group elements $g^{\mathbf {A}}$. If $b=1$, choose a random rank-k matrix ${\mathbf {A}}\in \mathbb {Z}_p^{n\times m}$ and compute $g^{\mathbf {A}}$.

• Output the function $f(x)={\mathbf {A}}\cdot x$. The description of f will consist of $(\mathbb {G},p,{\mathbf {A}},m,n)$.

Theorem 3

If $\mathtt {GroupGen}$ is a group where the k-eLin assumption holds for some constant k, then ${\mathtt {ELF.Gen}}'_k$ is a regular bounded adversary ELF. If $\mathtt {GroupGen}$ is public coin, then so is ${\mathtt {ELF.Gen}}'$.

Proof

If ${\mathbf {A}}$ is full rank, then the map $\mathbf {y}\mapsto g^{{\mathbf {A}}\cdot \mathbf {y}}$ is injective. If ${\mathbf {A}}$ has rank k, then the map has image size $p^k<r$. For security, we just need to show that the two distributions on $g^{\mathbf {A}}$ are indistinguishable. Note that it is well known that the k-linear assumption implies that it is hard to distinguish $g^{\mathbf {B}}$ for a random ${\mathbf {B}}\in \mathbb {Z}_p^{k+1,k+1}$ from $g^{\mathbf {B}}$ for a random rank k matrix ${\mathbf {B}}$ with no loss in the security of the reduction. From here, it is straightforward to show that it is hard to distinguish the full rank and rank k cases of $g^{\mathbf {A}}$, with a loss of a factor of $m-k$. In fact, using the ideas of [36], the loss can even be made logarithmic in m, but we will use m as an upper bound on the loss for simplicity. Let q be the polynomial guaranteed by the k-eLin assumption. Let t be a polynomial and $\delta$ an inverse polynomial. Let $q'=4q(t+u,m/\delta )^k$, where u is the overhead in the reduction from k-eLin to the problem of distinguishing ranks of matrices. Suppose an adversary runs in time t and distinguishes the two distributions on $g^{\mathbf {A}}$ with advantage $\delta$. For any $r\ge q'$, we have that $\lambda \ge r^{1/k}/4 \ge q(t+u,m/\delta )$. This means no $(t+u)$-time adversary can break the k-eLin assumption with advantage greater than $\delta /m$. By our reduction from distinguishing ranks, this means no t-time adversary can distinguish the two cases of $g^{\mathbf {A}}$, except with advantage at most $\delta$, as desired.

Notice that if $\mathtt {GroupGen}$ is public coin, we can sample $g^{\mathbf {A}}$ directly in the injective mode since it is just a matrix of random group elements. Finally, note that the function $\mathbf {y}\mapsto g^{{\mathbf {A}}\cdot \mathbf {y}}$ is perfectly regular due to its linear structure.   $\square$

Corollary 1

If there exists a constant k and a cryptographic group where the k-eLin assumption holds, then there exists an ELF with efficiently sampleable/enumerable image. If the group is public coin, then so is the ELF.

4 Point Function Obfuscation

A (expanding) random oracle H serves as a good point function obfuscator: to obfuscate the point function $I_x(x')={\left\{ \begin{array}{ll}1&{}\text {if }x'=x\\ 0&{}\text {if }x'\ne x\end{array}\right. }$, simply output $y=H(x)$. Then to run the “program” on input $x'$, simply check that $H(x')=y$. For any x that is drawn from an source with super-logarithmic min-entropy, an adversary making a polynomial number of queries to H will not be able to determine x from y. Thus, x is hidden to all efficient adversaries.

In this section, we show how to use ELFs to implement a concrete function H for which the strategy above still yields a secure point obfuscation (PO).

Definition 10

A point obfuscator (PO) is an efficient probabilistic algorithm ${\mathcal {O}}$ with the following properties:

• (Almost Perfect Correctness) On input a point function $I_x$, with overwhelming probability over the random coins of ${\mathcal {O}}$, ${\mathcal {O}}$ outputs the description of a program P that is functionally equivalent to $I_x$. P must run in time polynomial in the length of x and the security parameter.

• (Secrecy) For any distribution ${\mathcal {D}}$ over a set ${\mathcal {X}}$ with super-logarithmic min-entropy, the distribution ${\mathcal {O}}(I_x)$ for $x\leftarrow {\mathcal {D}}$ is computationally indistinguishable from ${\mathcal {O}}(I_{x'})$ where $x'\leftarrow U_{\mathcal {X}}$.

Before giving our construction, we point out that a point obfuscator implies a separation from $\mathtt {NP}$ with super-logarithmic non-determinism and $\mathtt {P}$. Thus, any primitive used to build point obfuscation, such as ELFs, must necessarily imply such a separation. This is essentially the same statement as a theorem of Wee [37], and is proved in the full version [40].

Theorem 4

If Point Obfuscators exist, then for any super-logarithmic function t, $\mathtt {NP}$ with t bits of non-determinism is not solvable in polynomial time.

4.1 The Construction

Construction 3

Let ${\mathcal {X}}$ be the desired domain of H. To generate H,

• Let ${\mathcal {Z}}$ be some set such that $|{\mathcal {X}}|^2/|{\mathcal {Z}}|$ is negligible, and sample a hash function h from a uniform and pairwise independent function distribution from ${\mathcal {X}}$ to ${\mathcal {Z}}$. h will thus be injective with overwhelming probability.

• Let $f\leftarrow {\mathtt {ELF.Gen}}(|{\mathcal {Z}}|,|{\mathcal {Z}}|)$ to get an injective-mode f.

• Output $H=f\circ h$.

Fig. 2.

The function $H=f\circ h$.

Theorem 5

Assuming ${\mathtt {ELF}}$ is a secure ELF, H in Construction 3 gives a secure point obfuscator. If ${\mathtt {ELF}}$ is public coin, then so is H.

Proof

We will actually show something stronger: that the point function obfuscation of x is indistinguishable from an obfuscation of the all-zeros function. In particular, we will show that no efficient adversary can distinguish $y=f(h(x))$ from $y=f(z)$ for a uniformly random z. Notice that by injectivity of f, y has a pre-image under $H=f\circ h$ if and only if $z=f^{-1}(y)$ has a pre-image under h. Since we chose h to be expanding, when we sample z uniformly random, z will have no pre-image with overwhelming probability. Therefore, $y=f(z)$ has no pre-image with overwhelming probability.

The proof involves a sequence of hybrids. Suppose the adversary runs in time t and distinguishes $y=f(h(x))$ from $y=f(z)$ with non-negligible advantage $\epsilon$. This means there is an inverse polynomial $\delta$ such that $\epsilon \ge \delta$ infinitely often.

• Hybrid 0. This is the honestly generated $y=f(h(x))$ for f drawn in injective mode and x drawn from D.

• Hybrid 1. Now, we change f to be lossy. That is, we generate $f\leftarrow {\mathtt {ELF.Gen}}(|{\mathcal {Z}}|,r)$ where r is chosen so that no adversary running in time t can distinguish this lossy f from an injective f, except with advantage at most $\delta /3$. Thus by ELF security, the adversary cannot distinguish Hybrid 0 from Hybrid 1, except with probability $\delta /3$.

• Hybrid 2. Now we change y to be $y=f(z)$ for a random uniform $z\in {\mathcal {Z}}$. Fix f, and let E be the distribution of y. Then notice that by the pairwise independence and uniformity of h, the composition $H=f\circ h$ is pairwise independent and has output distribution E. Moreover, ${\mathrm {Supp}}(E)\le r$ is a polynomial. Therefore, by Lemma 2, we see that Hybrid 1 and Hybrid 2 are indistinguishable, except with probability $\frac{1}{2}\sqrt{CP(D)\big (|{\mathrm {Supp}}(E)|-1\big )}$. As long as the collision probability of ${\mathcal {X}}$ is negligible (which in particular happens when ${\mathcal {X}}$ has super-logarithmic min-entropy), this quantity will be negligible. In particular, the distinguishing advantage will be less than $\delta /3$.

• Hybrid 3. Now we change f to be injective again. The distinguishing advantage between Hybrid 2 and Hybrid 3 will be at most $\delta /3$. Notice that Hybrid 3 is exactly our all-zeros obfuscation. Therefore, Hybrid 0 and Hybrid 3 are indistinguishable, except with probability less than $\delta$, meaning $\epsilon <\delta$. This contradicts our assumption about the adversary.   $\square$

In Sect. 6, we will show how to strengthen our construction to get a point obfuscator that is secure even against auxiliary information about the point.

5 Output Intractability

Consider any $k+1$-ary relation R over ${\mathcal {Y}}^k\times {\mathcal {W}}$ that is computationally intractable: on a random input $\mathbf {y}\in {\mathcal {Y}}^k$, it is computationally infeasible to find a $w\in {\mathcal {W}}$ such that $R(\mathbf {y},w)$ outputs 1. If H is a random oracle, assuming k is a constant, it is computationally infeasible for find a set of distinct inputs x, $x_i\ne x_j\forall i\ne j$, and a $w\in {\mathcal {W}}$, such that $R(H(\mathbf{x }),w)=1$. We will now show how to build standard-model hash functions H that achieve the same property.

Definition 11

A family of hash functions $H:[M]\rightarrow {\mathcal {Y}}$ is k -ary output intractable if, for any computationally intractable $k+1$-ary relation $R:{\mathcal {Y}}^k\times {\mathcal {W}}\rightarrow \{0,1\}$, no efficient adversary, given H, can find a set of distinct inputs ${\mathbf {x}} \in [M]^k$ and an element $w\in {\mathcal {W}}$, such that $R(H({\mathbf {x}}),w)=1$.

Note that binary output intractability implies as a special case collision resistance. In the unary case, and if ${\mathcal {W}}$ is just a singleton set, then output intractability is a special case of correlation intractability, which allows the relation to additionally depend on the input.

The unary case captures the following use case of hash functions: a given protocol may require a common reference string (crs), but some or all instances of the crs may admit a trapdoor that allows breaking the protocol. Of course, such a trapdoor should be difficult to find for a random crs. To “prove” that the crs is generated so that the generator of the crs does not know a trapdoor, the generator sets the crs to be the output of a public hash function on an arbitrary point. Since the potentially malicious generator does not control the hash function, he should be unable to find an output along with a corresponding trapdoor. Modeling the hash function as a random oracle, this methodology is sound. However, standard notions of security do not prevent the crs generator from choosing the input in such a way so that it knows a trapdoor. Unary output intractability precludes this case. Of course, the hash function itself needs to be set up in a trusted manner; however, once the hash function is set up and trusted, it can be used to generate arbitrarily many different crs by even untrusted authorities.

We note, however, that the unary case on its own is not very interesting: the family of hash functions H parameterized by a string $y\in {\mathcal {Y}}$ where $H(x)=y$ for all x is clearly unary intractable. Depending on the application, one may want additional features such as collision resistance, which as noted above is implied by binary output intractability ($k=2$). Therefore, $k=2$ and above are likely to be the most interesting settings. In the full version [40], we argue that $k\ge 2$ inherently requires some sort of super-polynomial hardness:

Theorem 6

If binary output intractable hash functions exist, then for any super-logarithmic function t, $\mathtt {NP}$ with t bits of non-determinism is not solvable in polynomial time.

Trivial impossibility for arbitrary k. We note that no one family of hash functions H can satisfy k-ary output intractability for all k. That is, for different k, a different family will be required. Suppose to the contrary that a family H satisfied k-output intractability for all k. Let t be the size of the circuit computing H. Choose k so that $k\log |{\mathcal {Y}}|\ge t$. Then with overwhelming probability over the choice of random $\mathbf {y}\in {\mathcal {Y}}^k$, there is no circuit of size at most t that outputs $y_i$ on input $i\in [k]$. Therefore, let ${\mathcal {W}}$ be the set of circuits of size at most t, and let $R(\mathbf {y},C)$ output 1 if and only if $C(i)=y_i$ for each $i\in [k]$. Then R is computationally (in fact statistically) intractable. However, it is trivial to find an x, w that satisfy $R(H(\mathbf{x }), w)=1$: set x $=[k]$ and $w=H$. Therefore, output intractability is violated. We obtain the following:

Theorem 7

For any family $H:[M]\rightarrow {\mathcal {Y}}$ of hash functions, let t be the description size of H. Then H cannot be output intractable for any $k\ge t/\log |{\mathcal {Y}}|$.

In the following, we show that it is nonetheless possible to obtain output intractability for any given constant k. Our functions will be described by strings of length $k(\log |{\mathcal {Y}}|+ {\mathtt {poly}}(\log M))$, which in the case $|{\mathcal {Y}}|\gg M$ gives a near-optimal relationship between k and t.

5.1 The Construction

Construction 4

Let [M] be the desired domain of H, and ${\mathcal {Y}}$ the desired range. To generate H, to the following:

• Let $f\leftarrow {\mathtt {ELF.Gen}}(M,M)$ to get an injective-mode f, with codomain ${\mathcal {Z}}$.

• Let g be a k-wise independent and uniform function from ${\mathcal {Z}}$ to ${\mathcal {Y}}$.

• Output $H=g\circ f$.

Fig. 3.

The function $H=g\circ f$.

Theorem 8

If ${\mathtt {ELF}}$ is a secure ELF with an efficiently enumerable image, then for any constant k the hash function H in Construction 4 is k-ary output intractable. If ${\mathtt {ELF}}$ is public coin, then so is H.

Proof

Suppose toward contradiction that there is an intractable $k+1$-ary relation R and an adversary ${{\mathcal {A}}}$ that on input H finds a set of distinct inputs x and a value $w\in {\mathcal {W}}$ such that $R(H(\mathbf{x }),w)=1$ with non-negligible probability $\epsilon$. Let $\delta$ be an inverse polynomial such that $\epsilon \ge \delta$ infinitely often. We will switch to a lossy mode for f so that (1) f has polynomial image size, and (2) no adversary running in time t (for a t to be chosen later) can distinguish the lossy mode from injective, except with probability $\delta /3$. By choosing t to be larger than the running time of ${{\mathcal {A}}}$, we have that ${{\mathcal {A}}}$ still outputs x of distinct elements, and a string w, such that $R(H(\mathbf{x }),w)=1$ with probability $\epsilon -\delta /3$.

We first argue that each of the elements of f(x) are distinct except with probability $\delta /3$. Since this was true in the injective case (since x is distinct), if this is not true in the lossy case, then the injective and lossy modes could be easily distinguished by an adversary taking slightly more time than ${{\mathcal {A}}}$. Let t be this time, so that this distinguisher is impossible. Thus, the adversary succeeds and the elements of f(x) are distinct with probability at least $\epsilon -2\delta /3$. This probability is larger than $\delta /3$ infinitely often, and is therefore non-negligible. Let S be the polynomial-sized set of image points of f. Then in other words, the adversary comes up with an ordered set ${\mathbf {z}}$ of distinct elements in S, and a string w, such that $R(g({\mathbf {z}}),w)=1$.

Now, note that, for any ordered set ${\mathbf {z}}$ of k distinct inputs, $g({\mathbf {z}})$ is distributed uniformly at random, by the k-wise independence of g. Moreover, it is straightforward, given ${\mathbf {z}}$ and a vector $\mathbf {y}\in {\mathcal {Y}}^k$, to sample a random g conditioned on $g({\mathbf {z}})=\mathbf {y}$. Sampling random $\mathbf {y}$, and then g in this way, gives a correctly distributed g.

We now describe an algorithm ${{\mathcal {B}}}$ that breaks the intractability of R. ${{\mathcal {B}}}$, on input $\mathbf {y}\in {\mathcal {Y}}^k$, chooses lossy f as above, and then selects k distinct (potential) image points from the image sampling procedure. Let ${\mathbf {z}}$ be the ordered list of points. Next, it chooses a random g such that $g({\mathbf {z}})=\mathbf {y}$. Finally, it runs ${{\mathcal {A}}}$ on the hash function $H=g\circ f$. When ${{\mathcal {A}}}$ outputs x, w, if $f(\mathbf{x })={\mathbf {z}}$ (equivalently, $H(\mathbf{x })=\mathbf {y}$), ${{\mathcal {B}}}$ outputs w; otherwise it aborts.

Since $\mathbf {y}$ is hidden from ${{\mathcal {A}}}$’s view, g is distributed randomly according to the k-wise independent distribution. Therefore, ${{\mathcal {A}}}$ will output a valid w with probability at least $\epsilon -2\delta /3$. If ${{\mathcal {B}}}$’s guess for ${\mathbf {z}}$ was correct, then w will break the intractability of R on $\mathbf {y}$. Since ${\mathbf {z}}$ is independent of ${{\mathcal {A}}}$’s view, the probability of a good guess is at least $1/s^k$, where 1 / s is the inverse polynomial lower bound on the probability any image point is selected. Therefore, ${{\mathcal {B}}}$ breaks the intractability of R with probability $(\epsilon -2\delta /3)/s^k$, which is larger than $\delta /3s^k$ infinitely often, and is therefore non-negligible.   $\square$

6 Leakage-Resilient PRGs, AIPO and Poly-Many Hardcore Bits

In this section, we use ELFs to give arbitrarily-many hardcore bits for any one-way function, and for constructing point function obfuscation secure in the presence of auxiliary information. Both of these can be seen as special cases of a very strong security requirement for pseudorandom generators.

Definition 12

A distribution ${\mathcal {D}}$ on pairs $(x,z)\in {\mathcal {X}}\times {\mathcal {Z}}$ is computationally unpredictable if no efficient adversary can guess x given z.

Definition 13

A family of pseudorandom generators $H:{\mathcal {X}}\rightarrow {\mathcal {Y}}$ secure for computationally unpredictable seeds if, for any computationally unpredictable distribution on $({\mathcal {X}},{\mathcal {Z}})$, no efficient adversary can distinguish (H, z, H(x)) from (H, z, S) where $(x,z)\leftarrow {\mathcal {D}}$ and $S\leftarrow U_{\mathcal {Y}}$.

Basically, this requirement states that H is a secure pseudorandom generator for arbitrary distributions on the seed, and even remains secure in the presence of arbitrary leakage about the seed, so long as the seed remains computationally unpredictable. The only restriction is that the distribution on the seed and the leakage must be chosen independently of H. However, in the absence of other restrictions, this independence between the source ${\mathcal {D}}$ and function H can easily be seen to be necessary: if z contained a few bits of H(x), then it is trivial to distinguish H(x) from random.

6.1 The Construction

The intuition behind our construction is the following. The usual way of extracting pseudorandomness from computationally unpredictable source is to output a hardcore bit of the source, say using Goldreich-Levin [23]. While this can be used to generate a logarithmic number of pseudorandom bits, security is lost once a super-logarithmic number of hardcore bits have been generated in this way.

In order to get around this logarithmic barrier, we actually compute a polynomial number of Goldreich-Levin bits. Of course, we cannot output these in the clear or else the seed can be easily computed by linear algebra. Instead, we scramble the hardcore bits using a sequence of ELFs. We can argue that each of the (scrambled) hardcore bits really is “as good as” random, in the sense that we can replace each bit with a truly random bit before scrambling without detection. To do so, we use the lossiness of the ELFs to argue that, when the ith hardcore bit is incorporated into the scramble, enough information is lost about the previous bits that the ith bit actually still is hardcore. By iterating this for each bit, we replace each one with random. We now give the details.

Construction 5

Let q be the input length and m be the output length. Let $\lambda$ be a security parameter. We will consider inputs x as q-dimensional vectors ${\mathbf {x}}\in {\mathbb F}_2^q$. Let ${\mathtt {ELF}}$ be an ELF. Let $M=2^{m+\lambda +1}$, and let n be the bit-length of the ELF on input $m+1$. Set $N=2^{n}$. Let $\ell$ be some polynomial in $m,\lambda$ to be determined later. First, we will construct a function $H'$ as follows.

Choose random $f_1,\dots ,f_\ell \leftarrow {\mathtt {ELF.Gen}}(M,M)$ where $f_i:[M]\rightarrow [N]$, and let $h_1,\dots ,h_{\ell -1}:[N]\rightarrow [M/2]=[2^{m+\lambda }]$ and $h_\ell :[N]\rightarrow [2^m]$ be pairwise independent and uniform functions. Define ${\mathbf {f}}=\{f_1,\dots ,f_\ell \}$ and ${\mathbf {h}}=\{h_1,\dots ,h_\ell \}$. Define $H'_i:\{0,1\}^i\rightarrow [M/2]$ (and $H'_\ell :\{0,1\}^\ell \rightarrow [2^m]$) as follows:

• $H'_0()=y_1 = 1\in [2^{m+\lambda }]$

• $H'_i({\mathbf {b}}_{[1,i-1]},b_i)=y_{i+1}=h_i(z_i)$ where $y_i\leftarrow H'_{i-1}({\mathbf {b}}_{[1,i-1]}), z_i\leftarrow f_i(y_i||b_i)$.

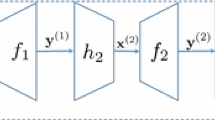
Then we set $H'=H'_\ell$. Then to define H, choose a random matrix ${\mathbf {R}}\in {\mathbb F}_2^{\ell \times q}$. The description of H consists of ${\mathbf {f}},{\mathbf {h}},{\mathbf {R}}$. Then set $H(x)=H'({\mathbf {R}}\cdot {\mathbf {x}})$. A diagram of H is given in Fig. 4.

Fig. 4.

An example instantiation for $\ell =3$. Notice that each iteration is identical, except for the final iteration, where $h_\ell$ has a smaller output.

We now prove several important facts about H and $H'$:

Claim

If $\ell \ge m+\lambda$, and if ${\mathbf {b}}$ is drawn uniformly at random, then $(H',H'({\mathbf {b}}))$ is statistically close to $(H',R)$ where R is uniformly random in $[2^m]$.

Proof

We will prove the case $\ell =m+\lambda$, the case of larger $\ell$ being similar. We will consider $f_1,\dots ,f_\ell$ as being fixed injective functions; since the $f_i$ are injective with overwhelming probability, the claim follows from this case. This means that the composition $h_i\circ f_i$ is pairwise independent, for all i.

Let $d_i(h_1,\dots ,h_i)$ be the collision probability of $y_{i+1}$ when $b_i\dots ,b_i$ are random bits, for fixed $h_1,\dots ,h_i$. Let $d_i$ be the expectation (over $h_1,\dots ,h_i$) of this value. There are two possibilities for a collision at $y_{i+1}$:

• There is a collision at $y_i$ and $b_i$. This happens with half the probability that there is a collision at $y_i$.

• There is not a collision at $y_i$ and $b_i$, but $h_i\circ f_i$ maps the two points to the same $y_{i+1}$. Conditioned on there being no collision at $(y_i,b_i)$, this occurs with probability $\frac{1}{2^{m+\lambda }}$ for $i<\ell$, and $\frac{1}{2^m}$ for $i=\ell$.

Then we have that $d_0=1$ and it is straightforward to show the following recurrence for $i<\ell$: $d_i=d_{i-1}\left( \frac{1}{2}-\frac{1}{2\times 2^{m+\lambda }}\right) +\frac{1}{2^{m+\lambda }}$. This recurrence has the form $d_i=a+b d_{i-1}$, which is solved by $d_i=b^i+a\frac{b^i-1}{b-1}$. Therefore, with some manipulation we have that $d_i=\frac{2}{2^{m+\lambda }+1}+\frac{(2^{m+\lambda }-1)^{i+1}}{2^{(m+\lambda )i}(2^{m+\lambda }+1)}$. Now, for $i=m+\lambda -1$, this becomes $d_{m+\lambda -1}=\frac{2\left( 1+\left( 1-2^{-m-\lambda }\right) ^{m+\lambda }\right) }{2^{m+\lambda }+1}\le \frac{4}{2^{m+\lambda }}$. Next, it is straightforward to adapt the above argument to show that $d_{m+\lambda }=d_{m+\lambda -1}\left( \frac{1}{2}-\frac{1}{2\times 2^{m}}\right) +\frac{1}{2^{m}}\le \frac{1}{2^m}+\frac{2}{2^{m+\lambda }}$. Now, the Rényi entropy of $y_{m+\lambda +1}$ is exactly the collision probability, scaled up by a factor of the $2^m$. Therefore, the expected Rényi entropy of $y_{m+\lambda +1}$ is at most $1+\frac{2}{2^\lambda }$. Finally, we relate the Rényi entropy to the statistical distance from uniform using Lemma 1:

$$\begin{aligned} \mathop {\mathbb E}_{h_1,\dots ,h_\ell } \varDelta (y_{\ell +1},R)\le \mathop {\mathbb E}\frac{1}{2}\sqrt{RE(y_{\ell +1})-1}\le \frac{1}{2}\sqrt{\mathop {\mathbb E}[ RE(y_{\ell +1})]-1}\le 2^{-(\lambda +1)/2} \end{aligned}$$

The statistical distance between $(H',H'({\mathbf {b}}))$ and $(H',R)$ is exactly this quantity, which is negligible in $\lambda$.   $\square$

We will thus set $\ell =m+\lambda$ in our construction of $H'$. Claim 6.1 will be crucial for our security proof for H. We also show our H is injective (with overwhelming probability) exactly when a truly random function with the same domain and co-domain is injective (with overwhelming probability).

Claim

If $2^{-(m-2q)}$ is negligible (in q), and $\ell \ge m$, then with overwhelming probability H is injective.

Proof

First, note that with overwhelming probability by our choice of $\ell \ge m\ge 2q$, ${\mathbf {R}}$ is full rank. Next, let ${\mathcal {Y}}_i$ be the set of possible $y_i$ values as we vary x, and ${\mathcal {Z}}_i$ be the set of possible $z_i$ values. By the injectivity of $f_i$, we have that $|{\mathcal {Z}}_i|\ge |{\mathcal {Y}}_i|$. Moreover, since $h_i$ is pairwise independent and uniform, with overwhelming probability $h_i$ is injective on ${\mathcal {Z}}_i$ since $|{\mathcal {Z}}_i|\le 2^q$ but the co-domain of $h_i$ has size at least $2^{m}\gg (2^q)^2$. Therefore $|{\mathcal {Y}}_{i+1}|= |{\mathcal {Z}}_i|\ge |{\mathcal {Y}}_i|$. This means that as we increase i, the image size never decreases (with overwhelming probability).

Now pick q linearly independent rows of ${\mathbf {R}}$. We will assume that the q rows constitute the first q rows of ${\mathbf {R}}$; the more general case is handled analogously. By performing an appropriate invertible transformation on the domain, we can assume that these q rows form the identity matrix. Therefore, we can take $b_i=x_i$ for $i\in [q]$. Next, observe that $y_i$ for $i\in [q]$ only depends on the first $i-1$ bits of x. Thus the set of possible pairs $(y_i,b_i)=(y_i,x_i)$ is exactly ${\mathcal {Y}}_i\times \{0,1\}$, which has size $2|{\mathcal {Y}}_i|$. By the injectivity of $f_i$, $|{\mathcal {Z}}_i|=2|{\mathcal {Y}}_i|$. Since $|{\mathcal {Y}}_{i+1}|=|{\mathcal {Z}}_i|=2|{\mathcal {Y}}_i|$, we have that the image size exactly doubles in each iteration for $i\in [q]$. Once we get to $i=q$, the image size is $2^q$, and the remaining iterations do not introduce any collisions. Thus the image size of H is $2^q$, meaning H is injective.   $\square$

Theorem 9

If ${\mathtt {ELF}}$ is a secure ELF, then H in Construction 5 is a pseudorandom generator secure for computationally unpredictable seeds. If ${\mathtt {ELF}}$ is public coin, then so is H.

Proof

Recall that $H(\mathbf{x })=H'({\mathbf {R}}\cdot \mathbf{x })$, and that $H'({\mathbf {b}})$ is (with overwhelming probability over the choice of $H'$) statistically close to random when ${\mathbf {b}}$ is random. Therefore, it suffices to show that the following distributions are indistinguishable: $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}},z,H'({\mathbf {R}}\cdot \mathbf{x }))\text { and }({\mathbf {f}},{\mathbf {h}},{\mathbf {R}},z,H'({\mathbf {b}}))$ for a uniformly random ${\mathbf {b}}$.

Suppose an adversary ${{\mathcal {A}}}$ has non-negligible advantage $\epsilon$ in distinguishing the two distributions. Define ${\mathbf {b}}^{(i)}$ so that the first i bits of ${\mathbf {b}}^{(i)}$ are equal to the first i bits of ${\mathbf {R}}\cdot \mathbf{x }$, and the remaining $\ell -i$ bits are chosen uniformly at random independently of x. Define Hybrid i to be the case where ${{\mathcal {A}}}$ is given the distribution $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}},z,H'({\mathbf {b}}^{(i)}))$.

Then ${{\mathcal {A}}}$ distinguishes Hybrid 0 from Hybrid $\ell$ with probability $\epsilon$. Thus there is an index $i\in [\ell ]$ such that the adversary distinguishes Hybrid $i-1$ from Hybird i with probability at least $\epsilon /\ell$. Next, observe that since bits $i+1$ through t are random in either case, they can be simulated independently of the challenge. Moreover, $H'({\mathbf {b}})$ can be computed given $H_{i-1}'({\mathbf {b}}_{[i-1]})$, $b_i$ (be it random or equal to ${\mathbf {R}}_i,$ x), and the random $b_{i+1},\dots ,b_\ell$. Thus, we can construct an adversary ${{\mathcal {A}}}'$ that distinguishes ${\mathbf {R}}_i\cdot \mathbf{x }$ from a random $b_i$ — given $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]},z,H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x }),{\mathbf {R}}_i)$ — with advantage $\epsilon /\ell$, where ${\mathbf {R}}_{[i-1]}$ consists of the first $i-1$ rows of ${\mathbf {R}}$, ${\mathbf {R}}_i$ is the ith row of ${\mathbf {R}}$, and $b_i$ is a random bit.

Next, since $\epsilon /3\ell$ is non-negligible, there is an inverse polynomial $\delta$ such that $\epsilon /3\ell \ge \delta$ infinitely often. Then, there is a polynomial r such ${{\mathcal {A}}}'$ cannot distinguish $f_i$ generated as ${\mathtt {ELF.Gen}}(M,r)$ from the honest $f_i$ generated from ${\mathtt {ELF.Gen}}(M,M)$, except with probability at most $\delta$. This means, if we generate $f_i\leftarrow {\mathtt {ELF.Gen}}(M,r)$, we have that ${{\mathcal {A}}}'$ still distinguishes ${\mathbf {R}}_i\cdot \mathbf{x }$ from a random $b_i$ — given $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]},z,H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x }),{\mathbf {R}}_i)$ — with advantage $\epsilon '=\epsilon /\ell -2\delta$. Put another way, given $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]},z,H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x }),{\mathbf {R}}_i)$, ${{\mathcal {A}}}'$ is able to compute ${\mathbf {R}}_i\cdot \mathbf{x }$ with probability $\frac{1}{2}+\epsilon '$. Note that $\epsilon '\ge \delta$ infinitely often, and is therefore non-negligible.

Now fix ${\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]}$, which fixes $H_{i-1}'$. Let $y_i=H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x })$. Notice that since ${\mathbf {f}},{\mathbf {h}}$ are fixed, there are at most r possible values for $y_i$, and recall that r is a polynomial. We now make the following claim:

Claim

Let ${\mathcal {D}}$ be a computationally unpredictable distribution on ${\mathcal {X}}\times {\mathcal {Z}}$. Suppose $T:{\mathcal {X}}\rightarrow {\mathcal {R}}$ is drawn from a family ${\mathcal {T}}$ of efficient functions where the size of the image of T is polynomial. Then the following distribution is also computationally unpredictable: $(x,\;(T,z,T(x)))$ where $T\leftarrow {\mathcal {T}}$, $(x,z)\leftarrow {\mathcal {D}}$.

Proof

Suppose we have an efficient adversary ${{\mathcal {B}}}$ that predicts x with non-negligible probability $\gamma$ given T, z, T(x), and suppose T has polynomial image size r. We then construct a new adversary ${{\mathcal {C}}}$ that, given x, samples a random T, samples $(x',z')\leftarrow {\mathcal {D}}$, and sets $a=T(x')$. It then runs ${{\mathcal {B}}}(T,z,a)$ to get a string $x''$, which it outputs. Notice that a is sampled from the same distribution as T(x), so with probability at least 1 / r, $a=T(x)$. In this case, $x''=x$ with probability $\gamma$. Therefore, ${{\mathcal {C}}}$ outputs x with probability $\gamma /r$, which is non-negligible.   $\square$

Using Claim 6.1 with $T=H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x })$, we see that $(x,({\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]},z, H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x })))$ is computationally unpredictable. Moreover, ${\mathbf {R}}_i\cdot \mathbf{x }$ is a Goldriech and Levin [23] hardcore bit for any computationally unpredictable source. Hence, no efficient adversary can predict ${\mathbf {R}}_x\cdot \mathbf{x }$ given $({\mathbf {f}},{\mathbf {h}},{\mathbf {R}}_{[i-1]},z, H_{i-1}'({\mathbf {R}}_{[i-1]}\cdot \mathbf{x }),{\mathbf {R}}_i)$. This contradicts the existence of ${{\mathcal {A}}}'$, proving the theorem.   $\square$

6.2 Applications

Polynomially-many hardcore bits for any one-way function. We see that H immediately gives us a hardcore function of arbitrary stretch for any computationally unpredictable distribution. This includes any one-way function. To the best of our knowledge, this is the first hardcore function of arbitrary stretch based on simple assumptions that applies to general computationally unpredictable sources. In the special case of one-way functions, the only prior constructions are due to Bellare et al. [6] using differing inputs obfuscation (diO), and of Zhandry [39] using extractable witness PRFs. Our construction offers an entirely different approach to constructing hardcore functions with arbitrary stretch, and is based on a very simple primitive.

Strong injective one-way functions. Bitansky and Paneth [9] conjecture the existence of a very strong one-way permutation family. We demonstrate that our function H meets this notion of security. Unfortunately, however, it is only injective, not a permutation.

Definition 14

A [9] permutation is a family of functions H such that for any computationally unpredictable distribution ${\mathcal {D}}$, the following two distributions are also unpredictable: $(x,\;(z,H,H(x))\;)$ and $(H(x),\;(z,H)\;)$ where $(x,z)\leftarrow {\mathcal {D}}$.

The first property is a generalization of a strong uninvertability assumption of Wee [37]. The second guarantees that if x is unpredictable, then so is H(x). In the full version [40], we show that H satisfies this definition:

Theorem 10

H constructed above using a secure ELF, when set to be injective as in Claim 6.1, is a [9]-injective one-way function.

The main application of Bitansky and Paneths [9] assumption is to build auxiliary input point function obfuscation (AIPO). Since H is not a permutation, it cannot be immediately plugged into their construction. Yet, next, we show that going through their construction is unnecessary in our case: we show that our function H gives an AIPO “out of the box” with no additional overhead.

Point function obfuscation with auxiliary input (AIPO). We now show how to achieve full AIPO using just the assumption of ELFs.

Definition 15

A auxiliary input point obfuscator (AIPO) is an efficient probabilistic algorithm ${\mathcal {O}}$ that saitsfies the almost perfect correctness requirement of Definition 10, as well as the following secrecy requirement: for any unpredictable distribution ${\mathcal {D}}$ over pairs $(x,z)\in {\mathcal {X}}\times {\mathcal {Z}}$, $({\mathcal {O}}(I_x),z)$ and $({\mathcal {O}}(I_{x'}),z)$ are computationally indistinguishable, where $(x,z)\leftarrow {\mathcal {D}}$ and $x'\leftarrow {\mathcal {X}}$.

As in Sect. 4, an expanding ideal hash function (random oracle) H gives a very natural AIPO: the obfuscation of a point function $I_x$ is simply $S=H(x)$. Injectivity of H gives (almost perfect) correctness. Moreover, security is easily proved in the random oracle model.

We now show that by choosing H to be as in the construction above, the same is true. In particular, by Claim 6.1, H is injective in the same regime of input/output sizes as a random oracle. For security, we have the following:

Theorem 11

The obfuscation construction described above is a secure AIPO assuming H is constructed as in Construction 5 using a secure ELF.

Proof

Note that since H is expanding, if we choose S at random from $[2^m]$, then with overwhelming probability there are no inputs x that map to S. Therefore, the obfuscated program corresponding to S is just the all-zeros function.

Let ${\mathcal {D}}$ be any computationally unpredictable source. We thus need to show that the following two distributions are indistinguishable: $(H,z,H({\mathbf {x}}))$ and (H, z, S) (where $({\mathbf {x}},z)\leftarrow {\mathcal {D}}$). This follows immediately from Theorem 9.   $\square$

Public key encryption from trapdoor permutations. In the full version [40], we show that our hardcore function can be used in a simple hybrid encryption scheme of Bellare and Rogaway [5].

6.3 Difficulty of Realizing Applications

Since AIPO implies PO, AIPO implies that $\mathtt {NP}$ with a super-logarithmic amount of non-determinism cannot be solved in polynomial time. Hence, this separation is inherent to the AIPO application. As an immediately corollary, we also have that our pseudorandom generator definition also implies such a separation. Since our pseudorandom generator definition is essentially equivalent to obtaining hardcore functions of arbitrary span for any unpredictable source, we also see that such a separation is inherent to such hardcore functions. In contrast, this separation does not extend to the special case of hardcore functions for any one-way function. It is consistent with our current knowledge that $\mathtt {NP}$ with, say, $\log ^2$ bits of non-determinism is solvable in polynomial time, and yet there are still hardcore functions of arbitrary stretch for any one-way function. However, in the full version [40], we still demonstrate some barriers to realizing this special case from polynomially-hard primitives.