Abstract
Fine-grained cryptographic primitives are ones that are secure against adversaries with an a-priori bounded polynomial amount of resources (time, space or parallel-time), where the honest algorithms use less resources than the adversaries they are designed to fool. Such primitives were previously studied in the context of time-bounded adversaries (Merkle, CACM 1978), space-bounded adversaries (Cachin and Maurer, CRYPTO 1997) and parallel-time-bounded adversaries (Håstad, IPL 1987). Our goal is come up with fine-grained primitives (in the setting of parallel-time-bounded adversaries) and to show unconditional security of these constructions when possible, or base security on widely believed separation of worst-case complexity classes. We show:
-
1.
\({\textsf {NC}^{1}}\)-cryptography: Under the assumption that
 , we construct one-way functions, pseudo-random generators (with sub-linear stretch), collision-resistant hash functions and most importantly, public-key encryption schemes, all computable in \({\textsf {NC}^{1}}\) and secure against all \({\textsf {NC}^{1}}\) circuits. Our results rely heavily on the notion of randomized encodings pioneered by Applebaum, Ishai and Kushilevitz, and crucially, make non-black-box use of randomized encodings for logspace classes.
, we construct one-way functions, pseudo-random generators (with sub-linear stretch), collision-resistant hash functions and most importantly, public-key encryption schemes, all computable in \({\textsf {NC}^{1}}\) and secure against all \({\textsf {NC}^{1}}\) circuits. Our results rely heavily on the notion of randomized encodings pioneered by Applebaum, Ishai and Kushilevitz, and crucially, make non-black-box use of randomized encodings for logspace classes. -
2.
\({\textsf {AC}^{0}}\)-cryptography: We construct (unconditionally secure) pseudo-random generators with arbitrary polynomial stretch, weak pseudo-random functions, secret-key encryption and perhaps most interestingly, collision-resistant hash functions, computable in \({\textsf {AC}^{0}}\) and secure against all \({\textsf {AC}^{0}}\) circuits. Previously, one-way permutations and pseudo-random generators (with linear stretch) computable in \({\textsf {AC}^{0}}\) and secure against \({\textsf {AC}^{0}}\) circuits were known from the works of Håstad and Braverman.
Research supported in part by NSF Grants CNS-1350619 and CNS-1414119, Alfred P. Sloan Research Fellowship, Microsoft Faculty Fellowship, the NEC Corporation, a Steven and Renee Finn Career Development Chair from MIT. This work was also sponsored in part by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The last four decades of research in the theory of cryptography has produced a host of fantastic notions, from public-key encryption [DH76, RSA78, GM82] and zero-knowledge proofs [GMR85] in the 1980s, to fully homomorphic encryption [RAD78, Gen09, BV11] and program obfuscation [BGI+01, GGH+13, SW14] in the modern day. Complexity theory is at the heart of these developments, playing a key role in coming up with precise mathematical definitions as well as constructions whose security can be reduced to precisely stated computational hardness assumptions.
However, the uncomfortable fact remains that a vast majority of cryptographic constructions rely on unproven assumptions. At the very least, one requires that \(\mathsf {NP} \nsubseteq \mathsf {BPP}\) [IL89], but that is hardly ever enough — when designing advanced cryptographic objects, cryptographers assume the existence of one-way functions as a given, move up a notch to assuming the hardness of specific problems such as factoring, discrete logarithms and the approximate shortest vector problem for lattices, and, more recently, even more exotic assumptions. While there are some generic transformations between primitives, such as from one-way functions to pseudo-random generators and symmetric encryption (e.g., [HILL99]), there are large gaps in our understanding of relationships between most others. In particular, it is a wide open question whether \(\mathsf {NP} \nsubseteq \mathsf {BPP}\) suffices to construct even the most basic cryptographic objects such as one-way functions, or whether it is possible to construct public-key encryption assuming only the existence of one-way functions (for some partial negative results, see [BT03, AGGM06, BB15, IR88]).
In this work, we ask if a weaker version of these cryptographic primitives can be constructed, with security against a bounded class of adversaries, based on either mild complexity-theoretic assumptions or no assumptions at all. Indeed, this question has been asked by several researchers in the past.
-
1.
Merkle [Mer78] constructed a non-interactive key exchange protocol (and thus, a public-key encryption scheme) where the honest parties run in linear time O(n) and security is shown against adversaries that run in time \(o(n^2)\). His assumption was the existence of a random function that both the honest parties and the adversary can access (essentially, the random oracle model [BR93]). Later, the assumption was improved to exponentially strong one-way functions [BGI08]. This work is timeless, not only because it jump-started public-key cryptography, but also because it showed how to obtain a primitive with much structure (trapdoors) from one that apparently has none (namely, random oracles and exponentially strong one-way functions).
-
2.
Maurer [Mau92] introduced the bounded storage model, which considers adversaries that have an a-priori bounded amount of space but unbounded computation time. Cachin and Maurer constructed symmetric-key encryption and key-exchange protocols that are unconditionally secure in this model [CM97] assuming that the honest parties have storage O(s) and the adversary has storage \(o(s^2)\) for some parameter s. There has been a rich line of work on this model [CM97, AR99, DM04] following [Mau92].
-
3.
Implicit in the work of Håstad [Has87] is a beautiful construction of a one-way permutation that can be computed in \({\textsf {NC}^{0}}\) (constant-depth circuits with AND and OR gates of unbounded fan-in and NOT gates), but inverting which is hard for any \({\textsf {AC}^{0}}\) circuit. Here is the function:
$$\begin{aligned} f(x_1,x_2,\ldots ,x_n) = \big ( x_1, x_1 \oplus x_2, x_2 \oplus x_3, \ldots , x_{n-1}\oplus x_n \big ) \end{aligned}$$Clearly, each output bit of this function depends on at most two input bits. Inverting the function implies in particular the ability to compute \(x_n\), which is the parity of all the output bits. This is hard for \({\textsf {AC}^{0}}\) circuits as per [FSS84, Ajt83, Hås86].
All these works share two common features. First, security is achieved against a class of adversaries with bounded resources (time, space and parallel time, respectively, in the three works above). Secondly, the honest algorithms use less resources than the class of adversaries they are trying to fool. We propose to call the broad study of such cryptographic constructions fine-grained cryptography, and construct several fine-grained cryptographic primitives secure against parallel-time-bounded adversaries.
We study two classes of low-depth circuits (as adversaries). The first is \({\textsf {AC}^{0}}\), which is the class of functions computable by constant-depth polynomial-sized circuits consisting of \(\mathsf {AND}\), \(\mathsf {OR}\), and \(\mathsf {NOT}\) gates of unbounded fan-in, and the second is \({\textsf {NC}^{1}}\), the class of functions computable by logarithmic-depth polynomial-sized circuits consisting of \(\mathsf {AND}\), \(\mathsf {OR}\), and \(\mathsf {NOT}\) gates of fan-in 2. In both cases, we mean the non-uniform versions of these classes. Note that this also covers the case of adversaries that are randomized circuits with these respective restrictions. This is because for any such randomized adversary \(\mathcal {A}\) there is a non-uniform adversary \(\mathcal {A}'\) that performs as well as \(\mathcal {A}\) – \(\mathcal {A}'\) is simply \(\mathcal {A}\) hard-coded with the randomness that worked best for it.
Early developments in circuit lower bounds [FSS84, Ajt83, Hås86] showed progressively better and average-case and exponential lower bounds for the PARITY function against \({\textsf {AC}^{0}}\) circuits. This has recently been sharpened to an average-case depth hierarchy theorem [RST15]. We already saw how these lower bounds translate to meaningful cryptography, namely one-way permutations against \({\textsf {AC}^{0}}\) adversaries. Extending this a little further, a reader familiar with Braverman’s breakthrough result [Bra10] (regarding the pseudorandomness of \(n^{\epsilon }\)-wise independent distributions against \({\textsf {AC}^{0}}\)) will notice that his result can be used to construct large-stretch pseudo-random generators that are computable by fixed-depth \({\textsf {AC}^{0}}\) circuits and are pseudo-random against arbitrary constant-depth \({\textsf {AC}^{0}}\) circuits. Can we do more? Can we construct secret-key encryption, collision-resistant hash functions, and even trapdoor functions, starting from known lower bounds against \({\textsf {AC}^{0}}\) circuits? Our first contribution is a positive answer to some of these questions.
Our second contribution is to study adversaries that live in \({\textsf {NC}^{1}}\). In this setting, as we do not know any lower bounds against \({\textsf {NC}^{1}}\), we are forced to rely on an unproven complexity-theoretic assumption; however, we aim to limit this to a worst-case, widely believed, separation of complexity classes. Here, we construct several cryptographic primitives from the worst-case hardness assumption that  , the most notable being an additively-homomorphic public-key encryption scheme where the key generation, encryption and decryption algorithms are all computable in \({\textsf {AC}^{0}}\)[2] (constant-depth circuits with \(\textsf {MOD}2\) gates; note that \({\textsf {AC}^{0}}\)[2] \(\subsetneq {\textsf {AC}^{0}}\) [Raz87, Smo87]), and the scheme is semantically secure against \({\textsf {NC}^{1}}\) adversaries. (
, the most notable being an additively-homomorphic public-key encryption scheme where the key generation, encryption and decryption algorithms are all computable in \({\textsf {AC}^{0}}\)[2] (constant-depth circuits with \(\textsf {MOD}2\) gates; note that \({\textsf {AC}^{0}}\)[2] \(\subsetneq {\textsf {AC}^{0}}\) [Raz87, Smo87]), and the scheme is semantically secure against \({\textsf {NC}^{1}}\) adversaries. ( can be thought of as the class of languages with polynomial-sized branching programs. Note that by Barrington’s Theorem [Bar86], all languages in \({\textsf {NC}^{1}}\) have polynomial-sized branching programs of constant width.)
can be thought of as the class of languages with polynomial-sized branching programs. Note that by Barrington’s Theorem [Bar86], all languages in \({\textsf {NC}^{1}}\) have polynomial-sized branching programs of constant width.)
Apart from theoretical interest stemming from the fact that these are rather natural objects, one possible application of such constructions (that was suggested to us independently by Ron Rothblum and Yuval Ishai) is in using them in conjunction with other constructions that are secure against polynomial-time adversaries under stronger assumptions. This could be done to get hybrids that are secure against polynomial-time adversaries under these stronger assumptions while also being secure against bounded adversaries unconditionally (or under minimal assumptions). For instance, consider an encryption scheme where the message is first encrypted using the \({\textsf {AC}^{0}}\)-encryption scheme from Sect. 5.3, and the resultant ciphertext is then encrypted using a scheme that works in \({\textsf {AC}^{0}}\) and is secure against polynomial-time adversaries under some standard assumptions (see [AIK04] for such schemes). This resultant scheme can be shown to be secure against polynomial-time adversaries under the same assumptions while being unconditionally secure against \({\textsf {AC}^{0}}\) adversaries.
We now briefly describe the relation between our results and the related work on randomized encodings [IK00, AIK04], and move on to describing the results in detail.
Relation to Randomized Encodings and Cryptography in \({\textsf {NC}^{0}}\) . Randomized encodings of Ishai and Kushilevitz [IK00, AIK04] are a key tool in our results against \({\textsf {NC}^{1}}\) adversaries. Using randomized encodings, Applebaum, Ishai and Kushilevitz [AIK04] showed how to convert several cryptographic primitives computable in logspace classes into ones that are computable in \({\textsf {NC}^{0}}\). The difference between their work and ours is two-fold: (1) Their starting points are cryptographic schemes secure against arbitrary polynomial-time adversaries, which rely on average-case hardness assumptions, whereas in our work, the focus is on achieving security either with no unproven assumptions or only worst-case assumptions; of course, our schemes are not secure against polynomial-time adversaries, but rather, limited adversarial classes; (2) In the case of public-key encryption, they manage to construct key generation and encryption algorithms that run in \({\textsf {NC}^{0}}\), but the decryption algorithm retains its high complexity. In contrast, in this work, we can construct public key encryption (against \(\mathsf {NC}^1\) adversaries) where the encryption algorithm can be computed in \({\textsf {NC}^{0}}\) and the key generation and decryption in \({\textsf {AC}^{0}}\)[2].
A Remark on Cryptographic vs. Non-cryptographic Constructions. An important desideratum for us is that the (honest) algorithms in our constructions can be implemented with fewer resources than the adversary that they are trying to fool. We call such constructions cryptographic in contrast to non-cryptographic constructions where this is not necessarily the case. Perhaps the clearest and the most well-known example of this distinction is the case of pseudo-random generators (PRGs) [BM84, Yao82, NW94]. Cryptographic PRGs, pioneered in the works of Blum, Micali and Yao [BM84, Yao82] are functions computable in a fixed polynomial time that produce outputs that are indistinguishable from random against any polynomial-time machine. The designer of the PRG does not know the precise power of the adversary: he knows that the adversary is polynomial-time, but not which polynomial. On the other hand, non-cryptographic (“Nisan-Wigderson type”) PRGs [NW94] take more time to compute than the adversaries they are designed to fool.
Our constructions will be exclusively in the cryptographic regime. For example, our one-way functions, pseudo-random generators and collision-resistant hash functions against \({\textsf {AC}^{0}}\) are computable by circuits of fixed polynomial size \(q(\lambda )\) and fixed (constant) depth d, and maintain security (in the appropriate sense) against adversarial circuits of size \(p'(\lambda )\) and depth \(d'\) for any polynomial function \(p'\) and any constant \(d'\).
1.1 Our Results and Techniques
Our results are grouped into two classes — primitives secure against \({\textsf {NC}^{1}}\) circuits based on minimal worst-case assumptions, and those that are unconditionally secure against \({\textsf {AC}^{0}}\) circuits. In the description below and throughout the rest of the paper, all algebra is over \(\mathbb {F}_{2}\).
Constructions Against \({\varvec{\textsf {NC}^{1}}}\) Adversaries. We construct one-way functions (OWFs), pseudo-random generators (PRGs), additively homomorphic public-key encryption (PKE), and collision-resistant hash functions (CRHFs) that are computable in \({\textsf {NC}^{1}}\) and are secure against \({\textsf {NC}^{1}}\) adversaries, based on the worst-case assumption that  . An important tool we use for these constructions is the notion of randomized encodings of functions introduced in [IK00].
. An important tool we use for these constructions is the notion of randomized encodings of functions introduced in [IK00].
A randomized encoding of a function f is a randomized function \(\hat{f}\) that is such that for any input x, the distribution of \(\hat{f}(x)\) reveals f(x), but nothing more about x. We know through the work of [IK00, AIK04] that there are randomized encodings for the class  that can be computed in (randomized, uniform) \({\textsf {NC}^{0}}\). Randomized encodings naturally offer a flavor of worst-to-average case reductions as they reduce the problem of evaluating a function on a given input to deciding some property of the distribution of its encoding. Our starting point is the observation, implicit in [AIK04, AR15], that they can be used to generically construct infinitely-often one-way functions and pseudo-random generators with additive stretch, computable in \({\textsf {NC}^{0}}\) and secure against \({\textsf {NC}^{1}}\) adversaries (assuming, again, that
that can be computed in (randomized, uniform) \({\textsf {NC}^{0}}\). Randomized encodings naturally offer a flavor of worst-to-average case reductions as they reduce the problem of evaluating a function on a given input to deciding some property of the distribution of its encoding. Our starting point is the observation, implicit in [AIK04, AR15], that they can be used to generically construct infinitely-often one-way functions and pseudo-random generators with additive stretch, computable in \({\textsf {NC}^{0}}\) and secure against \({\textsf {NC}^{1}}\) adversaries (assuming, again, that  ). We start with the following general theorem.
). We start with the following general theorem.
Theorem 1.1
(Informal). Let \(\mathcal {C}_1\) and \(\mathcal {C}_2\) be two classes such that \(\mathcal {C}_2 \not \subseteq \mathcal {C}_1\) and \(\mathcal {C}_2\) has perfect randomized encodings computable in \(\mathcal {C}_1\). Then, there are OWFs and PRGs that are computable in \(\mathcal {C}_1\) and are secure against arbitrary adversarial functions in \(\mathcal {C}_1\).
Informally, the argument for Theorem 1.1 is the following: Let L be the language in \(\mathcal {C}_2\) but not \(\mathcal {C}_1\). The PRG is a function that takes an input r and outputs the randomized encoding of the indicator function for membership in L on the input \(0^\lambda \), using r as the randomness (where \(\lambda \) is a security parameter). Any adversary that can distinguish the output of this function from random can be used to decide if a given x is in the language L by computing the randomized encoding of x and feeding it to the adversary. This gives us a PRG with a non-zero additive stretch (and also a OWF) if the randomized encoding has certain properties (they need to be perfect) — see Sect. 3 for details.
While we have one way functions and pseudorandom generators, a black-box construction of public key cryptosystems from randomized encodings seems elusive. Our first contribution in this work is to use the algebraic structure of the randomized encodings for  to construct an additively homomorphic public key encryption scheme secure against \({\textsf {NC}^{1}}\) circuits (assuming that
to construct an additively homomorphic public key encryption scheme secure against \({\textsf {NC}^{1}}\) circuits (assuming that  ).
).
Additively Homomorphic Public-Key Encryption. The key attribute of the randomized encodings of [IK00, AIK04] for  is that the encoding is not a structureless string. Rather, the randomized encodings of computations are matrices whose rank corresponds to the result of the computation. Our public-key encryption construction uses two observations:
is that the encoding is not a structureless string. Rather, the randomized encodings of computations are matrices whose rank corresponds to the result of the computation. Our public-key encryption construction uses two observations:
-
Under the assumption
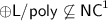 , there exist, for an infinite number of values of n, distributions \(D^n_0\) and \(D^n_1\) over \(n\times n\) matrices of rank \((n-1)\) and n, respectively, that are indistinguishable to \({\textsf {NC}^{1}}\) circuits.
, there exist, for an infinite number of values of n, distributions \(D^n_0\) and \(D^n_1\) over \(n\times n\) matrices of rank \((n-1)\) and n, respectively, that are indistinguishable to \({\textsf {NC}^{1}}\) circuits. -
It is possible to sample a matrix \(\mathbf {M}\) from \(D^n_0\) along with the non-zero vector \(\mathbf {k}\) in its kernel. The sampling can be accomplished in \({\textsf {NC}^{1}}\) or even \({\textsf {AC}^{0}}\)[2].
The public key in our scheme is such a matrix \(\mathbf {M}\), and the secret key is the corresponding \(\mathbf {k}\). Encryption of a bit b is a vector \(\mathbf {r}^T\mathbf {M}+ b\mathbf {t}^T\), where \(\mathbf {r}\) is a random vectorFootnote 1 and \(\mathbf {t}\) is a vector such that \(\langle \mathbf {t}, \mathbf {k} \rangle = 1\). In effect, the encryption of 0 is a random vector in the row-span of \(\mathbf {M}\) while the encryption of 1 is a random vector outside. Decryption of a ciphertext \(\mathbf {c}\) is simply the inner product \(\langle \mathbf {c}, \mathbf {k} \rangle \). Semantic security against \({\textsf {NC}^{1}}\) adversaries follows from the fact that \(D^n_0\) and \(D^n_1\) are indistinguishable to \({\textsf {NC}^{1}}\) circuits. In particular, (1) We can indistinguishably replace the public key by a random full rank matrix \(\mathbf {M}'\) chosen from \(D_n^1\); and (2) with \(\mathbf {M}'\) as the public key, encryptions of 0 are identically distributed to the encryptions of 1. The following is an informal restatement of Theorem 4.1.
Theorem 1.2
(Informal). If  , there is a public-key encryption scheme secure against \(\mathsf{NC}^{1}\) adversaries where key generation, encryption and decryption are all computable in (randomized) \(\mathsf{{AC}^{0}}[2]\).
, there is a public-key encryption scheme secure against \(\mathsf{NC}^{1}\) adversaries where key generation, encryption and decryption are all computable in (randomized) \(\mathsf{{AC}^{0}}[2]\).
The scheme above is additively homomorphic, and thus, collision-resistant hash functions (CRHF) against \({\textsf {NC}^{1}}\) follow immediately from the known generic transformations [IKO05] which work in \({\textsf {NC}^{1}}\).
Theorem 1.3
(Informal). If  , there is a family of collision-resistant hash functions that is secure against \(\mathsf{NC}^{1}\) adversaries where both sampling hash functions and evaluating them can be performed in (randomized) \(\mathsf{AC}^{0}[2]\).
, there is a family of collision-resistant hash functions that is secure against \(\mathsf{NC}^{1}\) adversaries where both sampling hash functions and evaluating them can be performed in (randomized) \(\mathsf{AC}^{0}[2]\).
We remark that in a recent work, Applebaum and Raykov [AR15] construct CRHFs against polynomial-time adversaries under the assumption that there are average-case hard functions with perfect randomized encodings. Their techniques also carry over to our setting and imply, for instance, the existence of CRHFs against \({\textsf {NC}^{1}}\) under the assumption that there is a language that is average-case hard for \({\textsf {NC}^{1}}\) that has perfect randomized encodings that can be computed in \({\textsf {NC}^{1}}\). This does not require any additional structure on the encodings apart from perfectness, but does require average-case hardness in place of our worst-case assumptions.
Constructions Against \({\varvec{\textsf {AC}^{0}}}\) Adversaries. We construct one-way functions (OWFs), pseudo-random generators (PRGs), weak pseudo-random functions (weak PRFs), symmetric-key encryption (SKE) and collision-resistant hash functions (CRHFs) that are computable in \({\textsf {AC}^{0}}\) and are unconditionally secure against arbitrary \({\textsf {AC}^{0}}\) circuits. While some constructions for OWFs and PRGs against \({\textsf {AC}^{0}}\) were already known [Hås86, Bra10], and the existence of weak PRFs and SKE, being minicrypt primitives, is not that surprising, the possibility of unconditionally secure CRHFs against \({\textsf {AC}^{0}}\) is somewhat surprising, and we consider this to be our primary contribution in this section. We also present a candidate construction for public-key encryption, but we are unable to prove its unconditional security against \({\textsf {AC}^{0}}\) circuits.
As we saw earlier, Håstad [Has87] constructed one-way permutations secure against \({\textsf {AC}^{0}}\) circuits based on the hardness of computing PARITY. When allowed polynomial running time, we have black-box constructions of pseudorandom generators [HILL99] and pseudorandom functions [GGM86] from one-way functions. But because these reductions are not implementable in \({\textsf {AC}^{0}}\), getting primitives computable in \({\textsf {AC}^{0}}\) requires more effort.
Our constructions against \({\textsf {AC}^{0}}\) adversaries are primarily based on the theorem of Braverman [Bra10] (and its recent sharpening by Tal [Tal14]) regarding the pseudo-randomness of polylog-wise independent distributions against constant depth circuits. We use this to show that \({\textsf {AC}^{0}}\) circuits cannot distinguish between the distribution \((\mathbf {A}, \mathbf {A}\mathbf {k})\), where \(\mathbf {A}\) is a random “sparse” matrix of dimension poly \((n) \times n\) and \(\mathbf {k}\) is a uniformly random secret vector, from the distribution \((\mathbf {A}, \mathbf {r})\), where \(\mathbf {r}\) is a uniformly random vector. Sparse here means that each row of \(\mathbf {A}\) has at most \(\mathsf {polylog}(n)\) many ones.
(This is shown as follows. It turns out that with high probability, a matrix chosen in this manner is such that any set of \({\textsf {polylog}}(n)\) rows is linearly independent (Lemma 2.5). Note that when a set of rows of \(\mathbf {A}\) is linearly independent, the corresponding set of bits in \(\mathbf {A}\mathbf {k}\) are uniformly distributed. This implies that if all polylog(n)-sized sets of rows of \(\mathbf {A}\) are linearly independent, then \(\mathbf {A}\mathbf {k}\) is \({\textsf {polylog}}(n)\)-wise independent. This fact, along with the theorems regarding pseudo-randomness mentioned above prove the indistinguishability by \({\textsf {AC}^{0}}\).)
We also crucially use the fact, from [AB84], that the inner product of an arbitrary vector with a sparse vector can be computed in constant depth.
OWFs and PRGs. This enables us to construct PRGs in \({\textsf {NC}^{0}}\) with constant multiplicative stretch and in \({\textsf {AC}^{0}}\) with polynomial multiplicative stretch. The construction is to fix a sparse matrix \(\mathbf {A}\) with the linear independence properties mentioned above, and the PRG output on seed \(\mathbf {k}\) is \(\mathbf {A}\mathbf {k}\). Pseudo-randomness follows from the indistinguishability arguments above. This is stated in the following informal restatement of Theorem 5.1. We need to show that there exist such matrices \(\mathbf {A}\) in which any polylog-sized set of rows are linearly independent, and yet are sparse. As we show in Sect. 2.3, there are indeed matrices that have these properties.
Theorem 1.4
(Informal). For any constant c, there is a family of circuits \(\left\{ C_n: \left\{ 0,1 \right\} ^n \rightarrow \left\{ 0,1 \right\} ^{n^c} \right\} \) such that for any n, each output bit of \(C_n\) depends on at most O(c) input bits. Further, for large enough n, \(\mathsf{AC}^{0}\) circuits cannot distinguish the output distribution \(C_n(U_n)\) from \(U_{n^c}\).
We note that similar techniques have been used in the past to construct PRGs that fool circuit families of a fixed constant depth - see, for instance, [Vio12].
Weak PRFs Against \({\textsf {AC}^{0}}\) . A Pseudo-Random Function family (PRF) is a collection of functions such that a function chosen at random from this collection is indistinguishable from a function chosen at random from the set of all functions (with the appropriate domain and range), based on just a polynomial number of evaluations of the respective functions. In a Strong PRF, the distinguisher is allowed to specify (even adaptively) the input points at which it wants the function to be evaluated. In a Weak PRF, the distinguisher is given function evaluations at input points chosen uniformly at random.
We construct Weak PRFs against \({\textsf {AC}^{0}}\) that are unconditionally secure. In our construction, each function in the family is described by a vector \(\mathbf {k}\). The computation of the pseudo-random function proceeds by mapping its input \(\mathbf {x}\) to a sparse vector \(\mathbf {a}\) and computing the inner product \(\langle \mathbf {a}, \mathbf {k}\rangle \) over \(\mathbb {F}_{2}\). Given polynomially many samples of the form \((\mathbf {a}, \langle \mathbf {a}, \mathbf {k}\rangle )\), one can write this as \((\mathbf {A}, \mathbf {A}\mathbf {k})\), where \(\mathbf {A}\) is a matrix with random sparse rows. Our mapping of \(\mathbf {x}\)’s to \(\mathbf {a}\)’s is such that \((\mathbf {A},\mathbf {A}\mathbf {k})\) is in some sense the only useful information contained in a set of random function evaluations. This is now indistinguishable from \((\mathbf {A},\mathbf {r})\) where \(\mathbf {r}\) is uniformly random, via the arguments mentioned earlier in this section. The following is an informal restatement of Theorem 5.2.
Theorem 1.5
(Informal). There is a Weak Pseudo-Random Function family secure against \(\mathsf{AC}^{0}\) adversaries and is such that both sampling a function at random and evaluating it can be performed in \(\mathsf{AC}^{0}\).
We note that while our construction only gives us quasi-polynomial security (that is, an adversary might be able to achieve an inverse quasi-polynomial advantage in telling our functions from random) as opposed to exponential security, we show that this is an inherent limitation of weak PRFs computable in \({\textsf {AC}^{0}}\). Roughly speaking, due to the work of [LMN93], we know that a constant fraction of the Fourier mass of any function on n inputs computable in \({\textsf {AC}^{0}}\) is concentrated on Fourier coefficients upto some \({\textsf {polylog}}(n)\). So there is at least one coefficient in the case of such a function that is at least  in absolute value, whereas in a random function any coefficient would be exponentially small. So, by guessing and estimating a Fourier coefficient of degree at most \({\textsf {polylog}}(n)\) (which can be done in \({\textsf {AC}^{0}}\)), one can distinguish functions computed in \({\textsf {AC}^{0}}\) from a random function with some
in absolute value, whereas in a random function any coefficient would be exponentially small. So, by guessing and estimating a Fourier coefficient of degree at most \({\textsf {polylog}}(n)\) (which can be done in \({\textsf {AC}^{0}}\)), one can distinguish functions computed in \({\textsf {AC}^{0}}\) from a random function with some  advantage.
advantage.
Symmetric Key Encryption Against \({\textsf {AC}^{0}}\) . In the case of polynomial-time adversaries and constructions, weak PRFs generically yield symmetric key encryption schemes, and this continues to hold in our setting. However, we present an alternative construction that has certain properties that make it useful in the construction of collision-resistant hash functions later on. The key in our scheme is again a random vector \(\mathbf {k}\). The encryption of a bit b is a random sparse vector \(\mathbf {c}\) such that \(\langle \mathbf {c}, \mathbf {k} \rangle = b\) over \(\mathbb {F}_2\). (Similar schemes, albeit without the sparsity, have been employed in the past in the leakage-resilience literature — see [GR12] and references therein.)
Encryption is performed by rejection sampling to find such a \(\mathbf {c}\), and decryption is performed by computing \(\langle \mathbf {c}, \mathbf {k} \rangle \), which can be done in constant depth owing to the sparsity of \(\mathbf {c}\). We reduce the semantic security of this construction to the indistinguishability of the distributions \((\mathbf {A},\mathbf {A}\mathbf {k})\) and \((\mathbf {A},\mathbf {r})\) mentioned earlier. Note that this scheme is additively homomorphic, a property that will be useful later. The following is an informal restatement of Theorem 5.3.
Theorem 1.6
(Informal). There is a Symmetric Key Encryption scheme that is secure against \(\mathsf{AC}^{0}\) adversaries and is such that key generation, encryption and decryption are all computable in (randomized) \(\mathsf{AC}^{0}\).
Collision Resistance Against \({\textsf {AC}^{0}}\) . Our most important construction against \({\textsf {AC}^{0}}\), which is what our encryption scheme was designed for, is that of Collision Resistant Hash Functions. Note that while there are generic transformations from additively homomorphic encryption schemes to CRHFs [IKO05], these transformations do not work in \({\textsf {AC}^{0}}\) and hence do not yield the construction we desire.
Our hash functions are described by matrices where each column is the encryption of a random bit under the above symmetric encryption scheme. Given such a matrix \(\mathbf {M}\) that consists of encryptions of the bits of a string m, the evaluation of the function on input \(\mathbf {x}\) is \(\mathbf {M}\mathbf {x}\). Note that we wish to perform this computation in constant depth, and this turns out to be possible to do correctly for most keys because of the sparsity of our ciphertexts.
Finding a collision for a given key \(\mathbf {M}\) is equivalent to finding a vector \(\mathbf {u}\) such that \(\mathbf {M}\mathbf {u}= 0\). By the additive homomorphism of the encryption scheme, and the fact that \(\mathbf {0}\) is a valid encryption of 0, this implies that \(\langle m, \mathbf {u} \rangle = 0\). But this is non-trivial information about m, and so should violate semantic security. However showing that this is indeed the case turns out to be somewhat non-trivial.
In order to do so, given an \({\textsf {AC}^{0}}\) adversary A that finds collisions for the hash function with some non-negligible probability, we will need to construct another \({\textsf {AC}^{0}}\) adversary, B, that breaks semantic security of the encryption scheme. The most straightforward attempt at this would be as follows. B selects messages \(\mathbf {m}_0\) and \(\mathbf {m}_1\) at random and sends them to the challenger who responds with \(\mathbf {M}= \mathsf {{Enc}}(\mathbf {m}_b)\). B then forwards this to A who would then return, with non-negligible probability, a vector \(\mathbf {u}\) such that \(\langle \mathbf {u}, \mathbf {m}_b \rangle = 0\). If B could compute \(\langle \mathbf {u}, \mathbf {m}_0 \rangle \) and \(\langle \mathbf {u}, \mathbf {m}_1 \rangle \), B would then be able to guess b correctly with non-negligible advantage. The problem with this approach is that \(\mathbf {u}\), \(\mathbf {m}_0\) and \(\mathbf {m}_1\) might all be of high Hamming weight, and this being the case, B would not be able to compute the above inner products.
The solution to this is to choose \(\mathbf {m}_0\) to be a sparse vector and \(\mathbf {m}_1\) to be a random vector and repeat the same procedure. This way, B can compute \(\langle \mathbf {u}, \mathbf {m}_0 \rangle \), and while it still cannot check whether \(\langle \mathbf {u}, \mathbf {m}_1 \rangle = 0\), it can instead check whether \(\mathbf {M}\mathbf {u}=\mathbf {0}\) and use this information. If it turns out that \(\mathbf {M}\mathbf {u}= \mathbf {0}\) and \(\langle \mathbf {u}, \mathbf {m}_0 \rangle \ne 0\), then B knows that \(b = 1\), due to the additive homomorphism of the encryption scheme. Also, when \(b=1\), since \(\mathbf {m}_0\) is independent of \(\mathbf {m}_1\), the probability that A outputs \(\mathbf {u}\) such that \(\langle \mathbf {u}, \mathbf {m}_0 \rangle \ne 0\) is non-negligible. Hence, by guessing \(b = 1\) when this happens and by guessing b at random otherwise, B can gain non-negligible advantage against semantic security. This achieves the desired contradiction and demonstrates the collision resistance of our construction. The following is an informal restatement of Theorem 5.4.
Theorem 1.7
(Informal). There is a family of Collision Resistant Hash Functions that is secure against \(\mathsf{AC}^{0}\) adversaries and is such that both sampling a hash function at random and evaluating it can be performed in (randomized) \(\mathsf{AC}^{0}\).
Candidate Public Key Encryption Against \({\textsf {AC}^{0}}\) . We also propose a candidate Public Key Encryption scheme whose security we cannot show. It is similar to the LPN-based cryptosystem in [Ale03]. The public key is a matrix of the form \(\mathbf {M}= (\mathbf {A}, \mathbf {A}\mathbf {k})\) where \(\mathbf {A}\) is a random \(n\times n\) matrix and \(\mathbf {k}\), which is also the secret key, is a random sparse vector of length n. To encrypt 0, we choose a random sparse vector \(\mathbf {r}\) and output \(\mathbf {c}^T = \mathbf {r}^T\mathbf {M}\), and to encrypt 1 we just output a random vector \(\mathbf {c}^T\) of length \((n+1)\). Decryption is simply the inner product of \(\mathbf {c}\) and the vector \((\mathbf {k}\ 1)^T\), and can be done in \({\textsf {AC}^{0}}\) because \(\mathbf {k}\) is sparse.
1.2 Other Related Work: Cryptography Against Bounded Adversaries
The big bang of public-key cryptography was the result of Merkle [Mer78] who constructed a key exchange protocol where the honest parties run in linear time O(n) and security is obtained against adversaries that run in time \(o(n^2)\). His assumption was the existence of a random function that both the honest parties and the adversary can access. Later, the assumption was improved to strong one-way functions [BGI08]. This is, indeed, a fine-grained cryptographic protocol in our sense.
The study of \(\epsilon \)-biased generators [AGHP93, MST06] is related to this work. In particular, \(\epsilon \)-biased generators with exponentially small \(\epsilon \) give us almost k-wise independent generators for large k, which in turn fool \({\textsf {AC}^{0}}\) circuits by a result of Braverman [Bra10]. This and other techniques have been used in the past to construct PRGs that fool circuits of a fixed constant depth, with the focus generally being on optimising the seed length [Vio12, TX13].
The notion of precise cryptography introduced by Micali and Pass [MP06] studies reductions between cryptographic primitives that can be computed in linear time. That is, they show constructions of primitive B from primitive A such that if there is a \(\mathsf {TIME}(f(n))\) algorithm that breaks primitive B, there is a \(\mathsf {TIME}(O(f(n)))\) algorithm that breaks A.
Maurer [Mau92] introduced the bounded storage model, which considers adversaries that have a bounded amount of space and unbounded computation time. There are many results known here [DM04, Vad04, AR99, CM97] and in particular, it is possible to construct Symmetric Key Encryption and Key Agreement protocols unconditionally in this model [CM97].
2 Preliminaries
In this section we establish notation that shall be used throughout the rest of the presentation and recall the notion of randomized encodings of functions. We state and prove some results about certain kinds of random matrices that turn out to be useful in Sect. 5. In Sects. 2.4 and 2.5, we present formal definitions of a general notion of adversaries with restricted computational power and also of several standard cryptographic primitives against such restricted adversaries (as opposed to the usual definitions, which are specific to probabilistic polynomial time adversaries).
2.1 Notation
For a distribution D, by \(x\leftarrow D\) we denote x being sampled according to D. Abusing notation, we denote by D(x) the probability mass of D on the element x. For a set S, by \(x\leftarrow S\), we denote x being sampled uniformly from S. We also denote the uniform distribution over S by \({U}_S\), and the uniform distribution over \(\left\{ 0,1 \right\} ^\lambda \) by \({U}_\lambda \). We use the notion of total variational distance between distributions, given by:
For distributions \(D_1\) and \(D_2\) over the same domain, by \(D_1\equiv D_2\) we mean that the distributions are the same, and by \(D_1\approx D_2\), we mean that \(\varDelta (D_1,D_2)\) is a negligible function of some parameter that will be clear from the context. Abusing notation, we also sometimes use random variables instead of their distributions in the above expressions.
For any \(n\in \mathbb {N}\), we denote by \(\left\lfloor n \right\rfloor _2\) the greatest power of 2 that is not more than n. For any n, k, and \(d \le k\), we denote by \(SpR_{k,d}\) the uniform distribution over the set of vectors in \(\left\{ 0,1 \right\} ^k\) with exactly d non-zero entries, and by \(SpM_{n,k,d}\) the distribution over the set of matrices in \(\left\{ 0,1 \right\} ^{n\times k}\) where each row is distributed independently according to \(SpR_{k,d}\).
We identify strings in \(\left\{ 0,1 \right\} ^n\) with vectors in \(\mathbb {F}_2^n\) in the natural manner. For a string (vector) x, \(\left||x \right||\) denotes its Hamming weight. Finally, we note that all arithmetic computations (such as inner products, matrix products, etc.) in this work will be over \(\mathbb {F}_2\), unless specified otherwise.
2.2 Constant-Depth Circuits
Here we state a few known results on the computational power of constant depth circuits that shall be useful in our constructions against \({\textsf {AC}^{0}}\) adversaries.
Theorem 2.1
(Hardness of Parity, [Hås14]). For any circuit C with n inputs, size s and depth d,

Theorem 2.2
(Partial Independence, [Bra10, Tal14]). Let D be a k-wise independent distribution over \(\left\{ 0,1 \right\} ^n\). For any circuit C with n inputs, size s and depth d,
The following lemma is implied by theorems proven in [AB84, RW91] regarding the computability of polylog thresholds by constant-depth circuits.
Lemma 2.3
(Polylog Inner Products). For any constant c and for any function \(t:\mathbb {N}\rightarrow \mathbb {N}\) such that \(t(\lambda ) = O(\log ^c{\lambda })\), there is an \(\mathsf{AC}^{0}\) family \(\mathcal {I}^t = \left\{ ip_\lambda ^t \right\} \) such that for any \(\lambda \),
-
\(ip_\lambda ^t\) takes inputs from \(\left\{ 0,1 \right\} ^\lambda \times \left\{ 0,1 \right\} ^\lambda \).
-
For any \(x, y \in \left\{ 0,1 \right\} ^\lambda \) such that \(\min (\left||x \right||, \left||y \right||) \le t(\lambda )\), \(ip_\lambda ^t(x, y) = \langle x, y \rangle \).
2.3 Sparse Matrices and Linear Codes
In this section we describe and prove some properties of a sampling procedure for random matrices. In interest of space, we will defer the proofs of the lemmas stated in this section to the full version.
We describe the following two sampling procedures that we shall use later. \(\mathsf {SRSamp}\) and \(\mathsf {SMSamp}\) abbreviate Sparse Row Sampler and Sparse Matrix Sampler, respectively. \(\mathsf {SRSamp}(k, d, r)\) samples unformly at random a vector from \(\left\{ 0,1 \right\} ^k\) with exactly d non-zero entries, using r for randomness – it chooses a set of d distinct indices between 0 to \(k-1\) (via rejection sampling) and outputs the vector in which the entries at those indices are 1 and the rest are 0. When we don’t specifically need to argue about the randomness, we drop the explicitly written r. \(\mathsf {SMSamp}(n, k, d)\) samples an \(n\times k\) matrix whose rows are samples from \(\mathsf {SRSamp}(k, d, r)\) using randomly and independently chosen r’s.

For any fixed k and \(d < k\), note that the function \(S_{k, d}:\left\{ 0,1 \right\} ^{d^2\left\lceil \log (k) \right\rceil } \rightarrow \left\{ 0,1 \right\} ^k\) given by \(S_{k,d}(x) = \mathsf {SRSamp}(k, d, x)\) can be easily seen to be computed by a circuit of size \(O((d^3+kd^2)\log (k))\) and depth 8. And so the family \(\mathcal {S} = \left\{ S_{\lambda , d(\lambda )} \right\} \) is in \({\textsf {AC}^{0}}\). When, in our constructions, we require computing \(\mathsf {SRSamp}(k, d, x)\), this is to be understood as being performed by the circuit for \(S_{k,d}\) that is given as input the prefix of x of length \(d^2\left\lceil \log (k) \right\rceil \). So if the rest of the construction is computed by polynomial-sized constant depth circuits, the calls to \(\mathsf {SRSamp}\) do not break this property.
Recall that we denote by \(SpR_{k,d}\) the uniform distribution over the set of vectors in \(\left\{ 0,1 \right\} ^k\) with exactly d non-zero entries, and by \(SpM_{n,k,d}\) the distribution over the set of matrices in \(\left\{ 0,1 \right\} ^{n\times k}\) where each row is sampled independently according to \(SpR_{k,d}\). The following lemma states that the above sampling procedures produce something close to these distributions.
Lemma 2.4
(Uniform Sparse Sampling). For any n, and \(d = \log ^2(k)\), there is a negligible function \(\nu \) such that for any k that is a power of two, when \(r\leftarrow \left\{ 0,1 \right\} ^{\log ^5(k)}\),
-
1.
\(\varDelta (\mathsf {SRSamp}(k, d, r),SpR_{k,d}) \le \nu (k)\)
-
2.
\(\varDelta (\mathsf {SMSamp}(n, k, d),SpM_{n,k,d}) \le n\nu (k)\)
The following property of the sampling procedures above is easiest proven in terms of expansion properties of bipartite graphs represented by the matrices sampled. The analysis closely follows that of Gallager [Gal62] from his early work on Low-Density Parity Check codes.
Lemma 2.5
(Sampling Codes). For any constant \(c > 0\), set \(n = k^c\), and \(d = \log ^2(k)\). For a matrix \(\mathbf {H}\), let \(\delta (\mathbf {H})\) denote the minimum distance of the code whose parity check matrix is \(\mathbf {H}\). Then, there is a negligible function \(\nu \) such that for any k that is a power of two,
Recall that a \(\delta \) -wise independent distribution over n bits is a distribution whose marginal distribution on any set of \(\delta \) bits is the uniform distribution.
Lemma 2.6
(Distance and Independence). Let \(\mathbf {H}\) (of dimension \(n\times k\)) be the parity check matrix of an \([n, (n-k)]_2\) linear code of minimum distance more than \(\delta \). Then, the distribution of \(\mathbf {H}\mathbf {x}\) is \(\delta \)-wise independent when \(\mathbf {x}\) is chosen uniformly at random from \(\left\{ 0,1 \right\} ^k\).
The following is immediately implied by Lemmas 2.5, 2.6 and Theorem 2.2. It effectively says that \({\textsf {AC}^{0}}\) circuits cannot distinguish between \((\mathbf {A}, \mathbf {A}\mathbf {s})\) and \((\mathbf {A}, \mathbf {r})\) when \(\mathbf {A}\) is sampled using \(\mathsf {SRSamp}\) and \(\mathbf {s}\) and \(\mathbf {r}\) are chosen uniformly at random.
Lemma 2.7
For any polynomial n, there is a negligible function \(\nu \) such that for any Boolean family  , and for any k that is a power of 2, when \(\mathbf {A}\leftarrow \mathsf {SMSamp}(n(k), k, \log ^2(k))\), \(\mathbf {s}\leftarrow \left\{ 0,1 \right\} ^k\) and \(\mathbf {r}\leftarrow \left\{ 0,1 \right\} ^{n(k)}\),
, and for any k that is a power of 2, when \(\mathbf {A}\leftarrow \mathsf {SMSamp}(n(k), k, \log ^2(k))\), \(\mathbf {s}\leftarrow \left\{ 0,1 \right\} ^k\) and \(\mathbf {r}\leftarrow \left\{ 0,1 \right\} ^{n(k)}\),
2.4 Adversaries
Definition 2.8
(Function Family). A function family is a family of (possibly randomized) functions \(\mathcal {F}= \{f_\lambda \}_{\lambda \in \mathbb {N}}\), where for each \(\lambda \), \(f_\lambda \) has domain \(D^f_\lambda \) and co-domain \(R^f_\lambda \).
In most of our considerations, \(D^f_\lambda \) and \(R^f_\lambda \) will be \(\left\{ 0,1 \right\} ^{d^f_\lambda }\) and \(\left\{ 0,1 \right\} ^{r^f_\lambda }\) for some sequences \(\{d^f_\lambda \}_{\lambda \in \mathbb {N}}\) and \(\{r^f_\lambda \}_{\lambda \in \mathbb {N}}\). Wherever function families are seen to act as adversaries to cryptographic objects, we shall use the terms adversary and function family interchangeably. The following are some examples of natural classes of function families.
Definition 2.9
( \(\mathsf{AC}^{0}\) ). The class of (non-uniform) \(\mathsf{AC}^{0}\) function families is the set of all function families \(\mathcal {F}= \left\{ f_\lambda \right\} \) for which there is a polynomial p and constant d such that for each \(\lambda \), \(f_\lambda \) can be computed by a (randomized) circuit of size \(p(\lambda )\), depth d and unbounded fan-in using \(\mathsf {AND}\), \(\mathsf {OR}\) and \(\mathsf {NOT}\) gates.
Definition 2.10
( \(\mathsf{NC}^{1}\) ). The class of (non-uniform) \(\mathsf{NC}^{1}\) function families is the set of all function families \(\mathcal {F}= \left\{ f_\lambda \right\} \) for which there is a polynomial p and constant c such that for each \(\lambda \), \(f_\lambda \) can be computed by a (randomized) circuit of size \(p(\lambda )\), depth \(c\log (\lambda )\) and fan-in 2 using \(\mathsf {AND}\), \(\mathsf {OR}\) and \(\mathsf {NOT}\) gates.
2.5 Primitives Against Bounded Adversaries
In this section, we generalize the standard definitions of several standard cryptographic primitives to talk about security against different classes of adversaries. In the following definitions, \(\mathcal {C}_1\) and \(\mathcal {C}_2\) are two function classes, and \(l, s: \mathbb {N}\rightarrow \mathbb {N}\) are some functions. Due to space constraints, we do not define all the primitives we talk about in the paper here, but the samples below illustrate how our definitions relate to the standard ones, and the rest are analogous. All definitions are present in the full version of the paper.
Implicit (and hence left unmentioned) in each definition are the following conditions:
-
Computability, which says that the function families that are part of the primitive are in the class \(\mathcal {C}_1\). Additional restrictions are specified when they apply.
-
Non-triviality, which says that the security condition in each definition is not vacuously satisfied – that there is at least one function family in \(\mathcal {C}_2\) whose input space corresponds to the output space of the appropriate function family in the primitive.
Definition 2.11
(One-Way Function). Let \(\mathcal {F}= \left\{ f_\lambda :\left\{ 0,1 \right\} ^\lambda \rightarrow \left\{ 0,1 \right\} ^{l(\lambda )} \right\} \) be a function family. \(\mathcal {F}\) is a \(\mathcal {C}_1\) -One-Way Function (OWF) against \(\mathcal {C}_2\) if:
-
Computability: For each \(\lambda \), \(f_\lambda \) is deterministic.
-
One-wayness: For any \(\mathcal {G}= \left\{ g_\lambda : \left\{ 0,1 \right\} ^{l(\lambda )} \rightarrow \left\{ 0,1 \right\} ^\lambda \right\} \in \mathcal {C}_2\), there is a negligible function \(\nu \) such that for any \(\lambda \in \mathbb {N}\):
$$\begin{aligned} \mathop {\mathrm{{Pr}}}_{x\leftarrow {U}_\lambda }{f_\lambda (g_\lambda (y)) = y\ |\ y \leftarrow f_\lambda (x)} \le \nu (\lambda ) \end{aligned}$$
For a function class \(\mathcal {C}\), we sometimes refer to a \(\mathcal {C}\)-OWF or an OWF against \(\mathcal {C}\). In both these cases, both \(\mathcal {C}_1\) and \(\mathcal {C}_2\) from the above definition are to be taken to be \(\mathcal {C}\). To be clear, this implies that there is a family \(\mathcal {F}\in \mathcal {C}\) that realizes the primitive and is secure against all \(\mathcal {G}\in \mathcal {C}\). We shall adopt this abbreviation also for other primitives defined in the above manner.
Definition 2.12
(Symmetric Key Encryption). Consider function families \({\mathcal KeyGen} = \left\{ \mathsf {KeyGen}_\lambda :\varnothing \rightarrow K_\lambda \right\} \), \({\mathcal Enc}\) \( = \left\{ \mathsf {{Enc}}_\lambda : K_\lambda \times \left\{ 0,1 \right\} \rightarrow C_\lambda \right\} \), and \({\mathcal Dec} = \left\{ \mathsf {Dec}_\lambda : K_\lambda \times C_\lambda \rightarrow \left\{ 0,1 \right\} \right\} \). \(({\mathcal KeyGen}, {\mathcal Enc}, {\mathcal Dec})\) is a \(\mathcal {C}_1\) -Symmetric Key Encryption Scheme against \(\mathcal {C}_2\) if:
-
Correctness: There is a negligible function \(\nu \) such that for any \(\lambda \in \mathbb {N}\) and any \(b\in \left\{ 0,1 \right\} \):
$$\begin{aligned} \Pr \left[ \mathsf {Dec}_\lambda \left( k, c\right) = b \left| \begin{array}{c} k \leftarrow \mathsf {KeyGen}_\lambda \\ c \leftarrow \mathsf {{Enc}}_\lambda (k, b)\end{array} \right. \right] \ge 1 - \nu (\lambda ) \end{aligned}$$ -
Semantic Security: For any polynomials \(n_0, n_1: \mathbb {N}\rightarrow \mathbb {N}\), and any family \(\mathcal {G}= \left\{ g_\lambda :C_\lambda ^{n_0(\lambda ) + n_1(\lambda ) + 1} \rightarrow \left\{ 0,1 \right\} \right\} \in \mathcal {C}_2\), there is a negligible function \(\nu '\) such that for any \(\lambda \in \mathbb {N}\):
$$\begin{aligned} \Pr \left[ g_\lambda \left( \left\{ c^0_i \right\} , \left\{ c^1_i \right\} , c\right) = b \left| \begin{array}{c} k \leftarrow \mathsf {KeyGen}_\lambda , b\leftarrow U_1 \\ c^0_1, \dots , c^0_{n_0(\lambda )} \leftarrow \mathsf {{Enc}}_\lambda (k, 0) \\ c^1_1, \dots , c^1_{n_1(\lambda )} \leftarrow \mathsf {{Enc}}_\lambda (k, 1) \\ c \leftarrow \mathsf {{Enc}}_\lambda (k, b)\end{array} \right. \right] \le \frac{1}{2}+ \nu '(\lambda ) \end{aligned}$$
2.6 Randomized Encodings
The notion of randomized encodings of functions was introduced by Ishai and Kushilevitz [IK00] in the context of secure multi-party computation. Roughly, a randomized encoding of a deterministic function f is another deterministic function \(\widehat{f}\) that is easier to compute by some measure, and is such that for any input x, the distribution of \(\widehat{f}(x,r)\) (when r is chosen uniformly at random) reveals the value of f(x) and nothing more. This reduces the computation of f(x) to determining some property of the distribution of \(\widehat{f}(x,r)\). Hence, randomized encodings offer a flavor of worst-to-average case reduction — from computing f(x) from x to that of computing f(x) from random samples of \(\widehat{f}(x,r)\).
We work with the following definition of Perfect Randomized Encodings from [App14]. We note that constructions of such encodings for  which are computable in \({\textsf {NC}^{0}}\) were presented in [IK00].
which are computable in \({\textsf {NC}^{0}}\) were presented in [IK00].
Definition 2.13
(Perfect Randomized Encodings). Consider a deterministic function \(f:\left\{ 0,1 \right\} ^n\rightarrow \left\{ 0,1 \right\} ^t\). We say that the deterministic function \(\widehat{f}:\left\{ 0,1 \right\} ^n\times \left\{ 0,1 \right\} ^m \rightarrow \left\{ 0,1 \right\} ^s\) is a Perfect Randomized Encoding (PRE) of f if the following conditions are satisfied.
-
Input independence: For every \(x,x'\in \left\{ 0,1 \right\} ^n\) such that \(f(x)=f(x')\), the random variables \(\widehat{f}(x,U_m)\) and \(\widehat{f}(x',U_m)\) are identically distributed.
-
Output disjointness: For every \(x, x'\in \left\{ 0,1 \right\} ^n\) such that \(f(x)\ne f(x')\), \(\text{ Supp }(\widehat{f}(x,U_m))\cap \text{ Supp }(\widehat{f}(x',U_m)) = \phi \).
-
Uniformity: For every x, \(\widehat{f}(x,U_m)\) is uniform on its support.
-
Balance: For every \(x,x'\in \left\{ 0,1 \right\} ^n\), \(\left| \text{ Supp }(\widehat{f}(x,U_m))\right| =\left| \text{ Supp }(\widehat{f}(x',U_m))\right| \)
-
Stretch preservation: \(s - (n+m) = t-n\)
Additionally, the PRE is said to be surjective if it also has the following property.
-
Surjectivity: For every \(y\in \left\{ 0,1 \right\} ^s\), there exist x and r such that \(\widehat{f}(x,r) = y\).
We naturally extend the definition of PREs to function families – a family \(\widehat{\mathcal {F}} = \left\{ \widehat{f}_\lambda \right\} \) is a PRE of another family \(\mathcal {F}= \left\{ f_\lambda \right\} \) if for all large enough \(\lambda \), \(\widehat{f}_\lambda \) is a PRE of \(f_\lambda \). Note that this notion only makes sense for deterministic functions, and the functions and families we assume or claim to have PREs are to be taken to be deterministic.
3 OWFs from Worst-Case Assumptions
In this section and in Sect. 4, we describe some constructions of cryptographic primitives against bounded adversaries starting from worst-case hardness assumptions. The existence of Perfect Randomized Encodings (PREs) can be leveraged to construct one-way functions and pseudo-random generators against bounded adversaries starting from a function that is hard in the worst-case for these adversaries. We describe this construction below.
Remark 3.1
(Infinitely Often Primitives). For a class \(\mathcal {C}\), the statement \(\mathcal {F}= \left\{ f_\lambda \right\} \not \in \mathcal {C}\) implies that for any family \(\mathcal {G}= \left\{ g_\lambda \right\} \) in \(\mathcal {C}\), there are an infinite number of values of \(\lambda \) such that \(f_\lambda \not \equiv g_\lambda \). Using such a worst case assumption, we only know how to obtain primitives whose security holds for an infinite number of values of \(\lambda \), as opposed to holding for all large enough \(\lambda \). Such primitives are called infinitely-often, and all primitives constructed in this section and Sect. 4 are infinitely-often primitives.
On the other hand, if we assume that for every \(\mathcal {G}\in \mathcal {C}\), there exists \(\lambda _0\) such that for all \(\lambda > \lambda _0\), \(f_\lambda \not \equiv g_\lambda \) we can achieve the regular stronger notion of security (that holds for all large enough security parameters) in each case by the same techniques.
Theorem 3.2
(OWFs, PRGs from PREs). Let \(\mathcal {C}_1\) and \(\mathcal {C}_2\) be two function classes satisfying the following conditions:
-
1.
Any function family in \(\mathcal {C}_2\) has a surjective PRE computable in \(\mathcal {C}_1\).
-
2.
\(\mathcal {C}_2 \not \subseteq \mathcal {C}_1\).
-
3.
\(\mathcal {C}_1\) is closed under a constant number of compositions.
-
4.
\(\mathcal {C}_1\) is non-uniform or randomized.
-
5.
\(\mathcal {C}_1\) can compute arbitrary thresholds.
Then:
-
1.
There is a \(\mathcal {C}_1\)-OWF against \(\mathcal {C}_1\).
-
2.
There is a \(\mathcal {C}_1\)-PRG against \(\mathcal {C}_1\) with non-zero additive stretch.
Theorem 3.2 in effect shows that the existence of a language with PREs outside \(\mathcal {C}_1\) implies the existence of one way functions and pseudorandom generators computable in \(\mathcal {C}_1\) secure against \(\mathcal {C}_1\). Instances of classes that satisfy its hypothesis (apart from \(\mathcal {C}_2 \not \subseteq \mathcal {C}_1\)) include \({\textsf {NC}^{1}}\) and \({\mathsf {BPP}}\). Note that this theorem does not provide constructions against \({\textsf {AC}^{0}}\) because \({\textsf {AC}^{0}}\) cannot compute arbitrary thresholds.
Proof Sketch. We start with a language in \(\mathcal {C}_2 \setminus \mathcal {C}_1\) described by a function family \(\mathcal {F}= \left\{ f_\lambda \right\} \). Let \(\widehat{\mathcal {F}} = \left\{ \widehat{f}_\lambda \right\} \) be its randomized encoding. Say \(f_\lambda \) takes inputs from \(\left\{ 0,1 \right\} ^\lambda \). Then the PRG/OWF for parameter \(\lambda \) is the function \(g_\lambda (r) = \widehat{f}_\lambda (0^\lambda ,r)\).
Without loss of generality, say \(f_\lambda (0^\lambda )=0\) and \(f_\lambda (z_1)=1\) for some \(z_1\). To show pseudorandomness, we first observe that, by the perfectness of the randomized encoding, the uniform distribution can be generated as an equal convex combination of \(\widehat{f}_\lambda (0^\lambda , r)\) and \(\widehat{f}_\lambda (z_1, r)\). The advantage in distinguishing \(g_\lambda (r) = \widehat{f}_\lambda (0^\lambda , r)\) from uniform can hence be used to decide if a given input x is in the language because an equal convex combination of \(\widehat{f}_\lambda (0^\lambda , r)\) and \(\widehat{f}_\lambda (x, r)\) will be identical to \(\widehat{f}_\lambda (0^\lambda ,r)\) if \(f_\lambda (x) = f_\lambda (0) = 0\), and otherwise will be identical to uniform.
We require the class to be closed under composition and to be able to compute thresholds in order to be able to amplify the success probability. The non-zero additive stretch comes from the fact that the PRE is stretch-preserving.
4 PKE Against \({\textsf {NC}}^{1}\) from Worst-Case Assumptions
In Theorem 3.2 we saw that we can construct one way functions and PRGs with a small stretch generically from Perfect Randomized Encodings (PREs) starting from worst-case hardness assumptions. We do not know how to construct Public Key Encryption (PKE) in a similar black-box fashion. In this section, we use certain algebraic properties of a specific construction of PREs for functions in  due to Ishai-Kushilevitz [IK00] to construct Public Key Encryption and Collision Resistant Hash Functions against \({\textsf {NC}^{1}}\) that are computable in \({\textsf {AC}^{0}}\)[2] under the assumption that
due to Ishai-Kushilevitz [IK00] to construct Public Key Encryption and Collision Resistant Hash Functions against \({\textsf {NC}^{1}}\) that are computable in \({\textsf {AC}^{0}}\)[2] under the assumption that  . We state the necessary implications of their work here. We start by describing sampling procedures for some relevant distributions in Construction 4.1.
. We state the necessary implications of their work here. We start by describing sampling procedures for some relevant distributions in Construction 4.1.
In the randomized encodings of [IK00], the output of the encoding of a function f on input x is a matrix \(\mathbf {M}\) sampled identically to \(\mathbf {R}_1 \mathbf {M}^\lambda _0 \mathbf {R}_2\) when \(f(x) = 0\) and identically to \(\mathbf {R}_1 \mathbf {M}^\lambda _1 \mathbf {R}_2\) when \(f(x) = 1\), where \(\mathbf {R}_1 \leftarrow \mathsf {LSamp}(\lambda )\) and \(\mathbf {R}_2\leftarrow \mathsf {RSamp}(\lambda )\). Notice that \(\mathbf {R}_1 \mathbf {M}^\lambda _1 \mathbf {R}_2\) is full rank, while \(\mathbf {R}_1 \mathbf {M}^\lambda _0 \mathbf {R}_2\) has rank \((\lambda -1)\). The public key in our encryption scheme is a sample \(\mathbf {M}\) from \(\mathbf {R}_1 \mathbf {M}^\lambda _0 \mathbf {R}_2\), and the secret key is a vector \(\mathbf {k}\) in the kernel of \(\mathbf {M}\). An encryption of 0 is a random vector in the row-span of \(\mathbf {M}\) (whose inner product with \(\mathbf {k}\) is hence 0), and an encryption of 1 is a random vector that is not in the row-span of \(\mathbf {M}\) (whose inner product with \(\mathbf {k}\) is non-zero). Decryption is simply inner product with \(\mathbf {k}\). (This is very similar to the cryptosystem in [ABW10] albeit without the noise that is added there.)
Security follows from the fact that under our hardness assumption \(\mathbf {M}\) is indistinguishable from \(\mathbf {R}_1 \mathbf {M}^\lambda _1 \mathbf {R}_2\) (see Theorem 4.2), which has an empty kernel, and so when used as the public key results in identical distributions of encryptions of 0 and 1.
Theorem 4.1
(Public Key Encryption Against \({\mathsf{NC}^{1}}\)
). Assume  . Then, the tuple of families \(({\mathcal KeyGen}, {\mathcal Enc}, {\mathcal Dec})\) defined in Construction 4.2 is an \(\mathsf{AC}^{0}[2]\)-Public Key Encryption Scheme against \(\mathsf{NC}^{1}\).
. Then, the tuple of families \(({\mathcal KeyGen}, {\mathcal Enc}, {\mathcal Dec})\) defined in Construction 4.2 is an \(\mathsf{AC}^{0}[2]\)-Public Key Encryption Scheme against \(\mathsf{NC}^{1}\).
Before beginning with the proof, we describe some properties of the construction. We first begin with two sampling procedures that correspond to sampling from \(\widehat{f}(x, \cdot )\) when \(f(x) = 0\) or \(f(x)= 1\) as described earlier. We describe these again in Construction 4.3.

Theorem 4.2
[IK00, AIK04]. For any boolean function family \(\mathcal {F}= \left\{ f_\lambda \right\} \) in  , there is a polynomial n such that for any \(\lambda \), \(f_\lambda \) has a PRE \(\widehat{f}_\lambda \) such that the distribution of \(\widehat{f}_\lambda (x)\) is identical to \(\mathsf {ZeroSamp}(n(\lambda ))\) when \(f_\lambda (x) = 0\) and is identical to \(\mathsf {OneSamp}(n(\lambda ))\) when \(f_\lambda (x) = 1\).
, there is a polynomial n such that for any \(\lambda \), \(f_\lambda \) has a PRE \(\widehat{f}_\lambda \) such that the distribution of \(\widehat{f}_\lambda (x)\) is identical to \(\mathsf {ZeroSamp}(n(\lambda ))\) when \(f_\lambda (x) = 0\) and is identical to \(\mathsf {OneSamp}(n(\lambda ))\) when \(f_\lambda (x) = 1\).
This implies that if some function in  is hard to compute on the worst-case then it is hard to distinguish between samples from \(\mathsf {ZeroSamp}\) and \(\mathsf {OneSamp}\). In particular, the following lemma follows immediately from the observation that \(\mathsf {ZeroSamp}\) and \(\mathsf {OneSamp}\) can be computed in \({\textsf {NC}^{1}}\).
is hard to compute on the worst-case then it is hard to distinguish between samples from \(\mathsf {ZeroSamp}\) and \(\mathsf {OneSamp}\). In particular, the following lemma follows immediately from the observation that \(\mathsf {ZeroSamp}\) and \(\mathsf {OneSamp}\) can be computed in \({\textsf {NC}^{1}}\).
Lemma 4.3
If  , then there is a polynomial n and a negligible function \(\nu \) such that for any family \(\mathcal {F}= \left\{ f_\lambda \right\} \) in \(\mathsf{NC}^{1}\), for an infinite number of values of \(\lambda \),
, then there is a polynomial n and a negligible function \(\nu \) such that for any family \(\mathcal {F}= \left\{ f_\lambda \right\} \) in \(\mathsf{NC}^{1}\), for an infinite number of values of \(\lambda \),

Lemma 4.3 can now be used to prove Theorem 4.1 as described in Sect. 1.1. We defer the details to the full version.


Remark 4.4
The computation of the PRE from [IK00] can be moved to \({\textsf {NC}^{0}}\) by techniques noted in [IK00] itself. Using similar techniques with Construction 4.2 gives us a Public Key Encryption scheme with encryption in \({\textsf {NC}^{0}}\) and decryption and key generation in \({\textsf {AC}^{0}}\)[2]. The impossibility of decryption in \({\textsf {NC}^{0}}\), as noted in [AIK04], continues to hold in our setting.
Remark 4.5
(This was pointed out to us by Abhishek Jain.) The above PKE scheme has what are called, in the terminology of [PVW08], “message-lossy” public keys – in this case, this is simply \(\mathbf {M}\) when sampled from \(\mathsf {OneSamp}\), as in the proof above. Such schemes may be used, again by results from [PVW08], to construct protocols for Oblivious Transfer where the honest parties are computable in \({\textsf {NC}^{1}}\) and which are secure against semi-honest \({\textsf {NC}^{1}}\) adversaries under the same assumptions (that \({{\oplus }{\mathsf {L}}/\mathsf {poly}\,{\not \subseteq }\,{\mathsf {NC}^{1}}}\)).
4.1 Collision Resistant Hashing
Note that again, due to the linearity of decryption, Construction 4.2 is additively homomorphic – if \(c_1\) and \(c_2\) are valid encryptions of \(m_1\) and \(m_2\), \((c_1\oplus c_2)\) is a valid encryption of \((m_1\oplus m_2)\). Furthermore, the size of ciphertexts does not increase when this operation is performed. Given these properties, we can use the generic transformation from additively homomorphic encryption to collision resistance due to [IKO05], along with the observation that all operations involved in the transformation can still be performed in \({\textsf {AC}^{0}}\)[2], to get the following.
Theorem 4.6
Assume \({{\oplus }{\mathsf {L}}/\mathsf {poly}\,{\not \subseteq }\,{\mathsf {NC}^{1}}}\). Then, for any constant \(c<1\) and function s such that \(s(n) = O(n^c)\), there exists an \(\mathsf{AC}^{0}[2]\)-CRHF against \(\mathsf{NC}^{1}\) with compression s.
5 Cryptography Without Assumptions
In this section, we present some constructions of primitives unconditionally secure against \({\textsf {AC}^{0}}\) adversaries that are computable in \({\textsf {AC}^{0}}\). This is almost the largest complexity class (after \({\textsf {AC}^{0}}\) with \(\textsf {MOD}\) gates) for which we can hope to get such unconditional results owing to a lack of better lower bounds. In this section, we present constructions of PRGs with arbitrary polynomial stretch, Weak PRFs, Symmetric Key Encryption, and Collision Resistant Hash Functions. We end with a candidate for Public Key Encryption against \({\textsf {AC}^{0}}\) that we are unable to prove secure, but also do not have an attack against.
5.1 High-Stretch Pseudo-Random Generators
We present here a construction of Pseudo-Random Generators against \({\textsf {AC}^{0}}\) with arbitrary polynomial stretch that can be computed in \({\textsf {AC}^{0}}\). In fact, the same techniques can be used to obtain constant stretch generators computable in \({\textsf {NC}^{0}}\)
The key idea behind the construction is the following: [Bra10] implies that for any constant \(\epsilon \), an \(n^{\epsilon }\)-wise independent distribution will fool \({\textsf {AC}^{0}}\) circuits of arbitrary constant depth. So, being able to sample such distributions in \({\textsf {AC}^{0}}\) suffices to construct good PRGs. As shown in Sect. 2.3, if \(\mathbf {H}\) is the parity-check matrix of a code with large distance d, then the distribution \(\mathbf {H}\mathbf {x}\) is d-wise independent for \(\mathbf {x}\) being a uniformly random vector (by Lemma 2.6). Further, as was also shown in Sect. 2.3, even for rather large d there are such matrices \(\mathbf {H}\) that are sparse, allowing us to compute the product \(\mathbf {H}\mathbf {x}\) in \({\textsf {AC}^{0}}\).
Theorem 5.1
(PRGs Against \(\mathsf{AC}^{0}\) ). For any polynomial l, the family \(\mathcal {F}^l\) from Construction 5.1 is an \(\mathsf{AC}^{0}\)-PRG with multiplicative stretch \(\left( \frac{l(\lambda )}{\lambda } \right) \).

Proof
For any l, the most that needs to be done to compute \(f^l_\lambda (x)\) is computing the product \(\mathbf {H}_{l,\lambda }\mathbf {x}\). We know that each row of \(\mathbf {H}_{l,\lambda }\) contains at most \(\log ^2(\lambda )\) non-zero entries. Hence, by Lemma 2.3, \(\mathcal {F}^l\) is in \({\textsf {AC}^{0}}\). The multiplicative stretch being \(\left( \frac{l(\lambda )}{\lambda } \right) \) is also easily verified.
For pseudo-randomness, we observe that the product \(\mathbf {H}_{l,\lambda } \mathbf {x}\) is \(\varOmega \left( \frac{\lambda }{\log ^3(\lambda )} \right) \)-wise independent, by Lemma 2.6. And hence, Theorem 2.2 implies that this distribution is pseudo-random to adversaries in \({\textsf {AC}^{0}}\).
5.2 Weak Pseudo-Random Functions
In this section, we describe our construction of Weak Pseudo-Random Functions against \({\textsf {AC}^{0}}\) computable in \({\textsf {AC}^{0}}\) (Construction 5.2). Roughly, we know that for a random sparse matrix \(\mathbf {H}\), \((\mathbf {H}, \mathbf {H}\mathbf {k})\) is indistinguishable from \((\mathbf {H}, \mathbf {r})\) where \(\mathbf {r}\) and \(\mathbf {k}\) are chosen uniformly at random. We choose the key of the PRF to be a random vector \(\mathbf {k}\). On an input \(\mathbf {x}\), the strategy is to use the input \(\mathbf {x}\) to generate a sparse vector \(\mathbf {y}\) and then take the inner product \(\langle \mathbf {y}, \mathbf {k} \rangle \).

Theorem 5.2
(PRFs Against \(\mathsf{AC}^{0}\) ). The pair of families \(({\mathcal KeyGen}, {\mathcal Eval})\) defined in Construction 5.2 is a Weak \(\mathsf{AC}^{0}\)-PRF against \(\mathsf{AC}^{0}\).
The intuitive reason one would think Construction 5.2 might be pseudo-random is that a collection of random function values from a randomly sampled key seems to contain the same information as \((\mathbf {H}, \mathbf {H}\mathbf {k})\) where \(\mathbf {k}\) is sampled uniformly at random and \(\mathbf {H}\) is sampled using \(\mathsf {SMSamp}\): a matrix with sparse rows. We know from Lemma 2.5 that except with negligible probability, \(\mathbf {H}\) is going to be the parity check matrix of a code with large distance, and when it is, the arguments from Sect. 5.1 show that \((\mathbf {H}, \mathbf {H}\mathbf {k})\) is indistinguishable from \((\mathbf {H}, \mathbf {r})\), where \(\mathbf {r}\) is sampled uniformly at random.
The only fact that prevents this from functioning as a proof is that what the adversary gets is not \((\mathbf {y}, \langle \mathbf {y}, \mathbf {k} \rangle )\) where \(\mathbf {y}\) is an output of \(\mathsf {SRSamp}\), but rather \((\mathbf {r}, \langle \mathbf {y}, \mathbf {k} \rangle )\), where \(\mathbf {r}\) is randomness that when used in \(\mathsf {SRSamp}\) gives \(\mathbf {y}\). One way to show that this is still pseudo-random is to reduce the case where the input is \((\mathbf {y}, \langle \mathbf {y}, \mathbf {x} \rangle )\) to the case where the input is \((\mathbf {r}, \langle \mathbf {y}, \mathbf {x} \rangle )\) using an \({\textsf {AC}^{0}}\)-reduction. To do this, one would need an \({\textsf {AC}^{0}}\) circuit that would, given \(\mathbf {y}\), sample from a distribution close to the uniform distribution over \(\mathbf {r}\)’s that cause \(\mathsf {SRSamp}\) to output \(\mathbf {y}\) when used as randomness. We implement this proof strategy in the full version.
Construction 5.2 of Weak PRFs achieves only quasi-polynomial security — that is, there is no guarantee that some \({\textsf {AC}^{0}}\) adversary may not have an inverse quasi-polynomial advantage in distinguishing between the PRF and a random function. Due to the seminal work of Linial-Mansour-Nisan [LMN93] and subsequent improvements in [Tal14], we know that this barrier is inherent and we cannot hope for exponential security
5.3 Symmetric Key Encryption
In this section, we present a Symmetric Key Encryption scheme against \({\textsf {AC}^{0}}\) computable in \({\textsf {AC}^{0}}\), which is also additively homomorphic – a property that shall be useful in constructing Collision Resistant Hash Functions later on.
In Sect. 5.2, we saw a construction of Weak PRFs. And Weak PRFs give us Symmetric Key Encryption generically (where \(\mathsf {Enc}(\mathsf {k}, b) = (\mathsf {r}, \mathsf {PRF}(\mathsf {k}, \mathsf {r}) \oplus b)\)). For the Weak PRF construction from Sect. 5.2, this implied scheme also happens to be additively homomorphic. But it has the issue that the last bit of the ciphertext is an almost unbiased bit and hence it is not feasible to do more than \({\textsf {polylog}(\lambda )}\) homomorphic evaluations on collections of ciphertexts in \({\textsf {AC}^{0}}\). So, we construct a different Symmetric Key Encryption scheme that does not suffer from this drawback and is still additively homomorphic. Then we will use this scheme to construct Collision Resistant Hash Functions. This scheme is described in Construction 5.3. In this scheme we choose the ciphertext by performing rejection sampling in parallel. For encrypting a bit b, we sample a ciphertext \(\mathbf {c}\) such that \(\mathbf {c}\) is sparse and \(\langle \mathbf {c}, \mathbf {k} \rangle = b\). This ensures that the we have an additively homomorphic scheme where all the bits are sparse.

Theorem 5.3
(Symmetric Encryption Against \(\mathsf{AC}^{0}\) ). The tuple of families \(({\mathcal KeyGen}, {\mathcal Enc}, {\mathcal Dec})\) defined in Construction 5.3 is an \(\mathsf{AC}^{0}\)-Symmetric-Key Encryption Scheme against \(\mathsf{AC}^{0}\).
The key idea behind the proof is showing that for most keys \(\mathbf {k}\), the distribution of a uniformly random bit along with its encryption, that is,
is statistically close to the distribution of a random sparse vector along with its inner product with \(\mathbf {k}\), that is,
The second distribution is similar to the one that came up in the security proof of the weak PRF construction earlier, where we effectively showed that we can replace \(\langle \mathbf {r}, \mathbf {k} \rangle \) with an independent random bit without being caught by \({\textsf {AC}^{0}}\) adversaries. We defer the complete proof to the full version.
5.4 Collision Resistant Hash Functions
To construct Collision Resistant Hash Functions (CRHFs), we use the additive homomorphism of the Symmetric Key Encryption scheme constructed in Sect. 5.3. Each function in the family of hash functions is given by a matrix whose columns are ciphertexts from the encryption scheme, and evaluation is done by treating the input as a column vector and computing its product with this matrix (effectively computing a linear combination of ciphertexts). To find collisions, the adversary needs to come up with a vector in the kernel of this matrix. We show that constant depth circuits of polynomial size cannot do this for most such matrices. This is because the all-zero vector is a valid encryption of 0 in our encryption scheme, and as this scheme is additively homomorphic, finding a subset of ciphertexts that sum to zero is roughly the same as finding a subset of the corresponding messages that sum to 0, and this is a violation of semantic security.

Theorem 5.4
(CRHFs Against \(\mathsf{AC}^{0}\) ). For any polylogarithmic function s, the pair of families \(({\mathcal KeyGen^s}, {\mathcal Eval^s})\), from Construction 5.4 is an \(\mathsf{AC}^{0}\)-CRHF with compression s.
We refer the reader to the sketch of the proof of Theorem 1.7 (an informal version of Theorem 5.4) towards the end of Sect. 1.1 and leave the proof of Theorem 5.4 to the full version.
5.5 Candidate Public Key Encryption Scheme
In Lemma 2.7 we showed that the distribution \((\mathbf {A}, \mathbf {A}\mathbf {k})\) where \(\mathbf {A}\) was sampled as a sparse matrix and \(\mathbf {k}\) was a random vector is indistinguishable from \((\mathbf {A},\mathbf {r})\) where \(\mathbf {r}\) is also a random vector, for a wide range of parameters. We need at least one of the two \(\mathbf {A}\) or \(\mathbf {k}\) to be sparse to enable the computation of \(\mathbf {A}\mathbf {k}\) in \({\textsf {AC}^{0}}\). If we make the analogous indistinguishability assumption with the key being sparse – that is, that \((\mathbf {A}, \mathbf {A}\mathbf {k})\) is indistinguishable from \((\mathbf {A}, \mathbf {r})\) where \(\mathbf {A}\leftarrow \left\{ 0,1 \right\} ^{\lambda \times \lambda }\), \(\mathbf {k}\leftarrow \mathsf {SRSamp}(\lambda , \log ^2 \lambda )\) and \(\mathbf {r}\leftarrow \left\{ 0,1 \right\} ^\lambda \) – this allows us to construct a Public Key Encryption scheme against \({\textsf {AC}^{0}}\) computable in \({\textsf {AC}^{0}}\).
This is presented in Construction 5.5, and is easily seen to be secure under Assumption 5.5. This candidate is very similar to the LPN based cryptosystem due to Alekhnovich [Ale03]. Note that while the correctness of decryption in Construction 5.5 is not very good, this may be easily amplified by repetition without losing security, as the error is one-sided.
Assumption 5.5
Distributions \(D_1 = (\mathbf {A}, \mathbf {A}\mathbf {k})\) where \(\mathbf {A}\leftarrow \left\{ 0,1 \right\} ^{\lambda \times \lambda }\), \(\mathbf {k}\leftarrow \mathsf {SRSamp}(\lambda , \log ^2 \lambda )\) and \(D_2 = (\mathbf {A}, \mathbf {r})\) where \(\mathbf {r}\leftarrow \left\{ 0,1 \right\} ^\lambda \) are indistinguishable by \(\mathsf{AC}^{0}\) adversaries with non-negligible advantage.

The most commonly used proof technique in this paper – showing k-wise independence for a large k – cannot be used to prove the security of this scheme because due to the sparsity of the key, the distribution \((\mathbf {A}, \mathbf {A}\mathbf {k})\) is not k-wise independent.
Conclusions and Open Questions. We construct various cryptographic primitives secure against parallel-time-bounded adversaries. Our constructions against \({\textsf {AC}^{0}}\) are unconditional whereas our constructions against \({\textsf {NC}^{1}}\) require the assumption that \({{\mathsf {NC}^{1}}\,{\ne }\,{\oplus }{\mathsf {L}}/\mathsf {poly}}\). Our constructions make use of circuit lower bounds [Bra10] and non-black-box use of randomized encodings for logspace classes [IK00].
There are several open questions that arise out of this work. Perhaps the most immediate are:
-
1.
Unconditional lower-bounds are known for slightly larger classes like \({\textsf {AC}^{0}}\)[p] when p is a prime power. Can we get cryptographic primitives from those lower-bounds?
-
2.
Construct a public key encryption scheme secure against \({\textsf {AC}^{0}}\), either by proving the security of our candidate proposal (see Sect. 5.5) or by completely different means. Natural ways of doing this lead us to a fascinating question about the complexity of \({\textsf {AC}^{0}}\) circuits. Braverman [Bra10] shows that any \(n^\epsilon \)-wise independent distribution fools all \({\textsf {AC}^{0}}\) circuits. Our candidate encryption, however, produces ciphertexts that come from a \(\log ^c(n)\)-wise distribution for some constant c. This raises the following question: Can we show some fixed polylog -wise independent distribution (that is not \(n^\epsilon \) -wise independent) that fools \({\textsf {AC}^{0}}\) circuits of arbitrary depth? (This question came up during discussions with Li-Yang Tan.)
-
3.
We relied on the assumption that \({{\oplus }{\mathsf {L}}/\mathsf {poly}\,{\not \subseteq }\,{\mathsf {NC}^{1}}}\) to construct primitives secure against \({\textsf {NC}^{1}}\). It would be desirable to relax the assumption to \({{\mathsf {P}}\,{\not \subseteq }\,{\mathsf {NC}^{1}}}\).
A related extension of Merkle’s work is to construct a public-key encryption scheme resistant against \(O(n^c)\) time adversaries (for some \(c>2\)) under worst-case hardness assumptions.
Notes
- 1.
We maintain the convention that all vectors are by default column vectors. For a vector \(\mathbf {r}\), the notation \(\mathbf {r}^T\) denotes the row vector that is the transpose of \(\mathbf {r}\).
References
Ajtai, M., Ben-Or, M.: A theorem on probabilistic constant depth computations. In: Proceedings of the 16th Annual ACM Symposium on Theory of Computing, April 30–May 2 1984, Washington, DC, USA, pp. 471–474 (1984)
Applebaum, B., Barak, B., Wigderson, A.: Public-key cryptography from different assumptions. In: Proceedings of the Forty-Second ACM Symposium on Theory of Computing, pp. 171–180. ACM (2010)
Akavia, A., Goldreich, O., Goldwasser, S., Moshkovitz, D.: On basing one-way functions on NP-hardness. In: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, May 21–23 2006, pp. 701–710 (2006)
Alon, N., Goldreich, O., Håstad, J., Peralta, R.: Addendum to “simple construction of almost k-wise independent random variables”. Random Struct. Algorithms 4(1), 119–120 (1993)
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in NC\(^0\). In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2004, 17–19 October 2004, Rome, Italy, p. 166. IEEE Computer Society Press (2004)
Ajtai, M.: 11-formulae on finite structures. Ann. Pure Appl. Logic 24(1), 1–48 (1983)
Alekhnovich, M.: More on average case vs approximation complexity. In: Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science, pp. 298–307. IEEE (2003)
Applebaum, B.: Cryptography in NC\(^0\). In: Applebaum, B. (ed.) Cryptography in Constant Parallel Time, pp. 33–78. Springer, Heidelberg (2014)
Aumann, Y., Rabin, M.O.: Information theoretically secure communication in the limited storage space model. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 65–79. Springer, Heidelberg (1999)
Applebaum, B., Raykov, P.: On the relationship between statistical zero-knowledge and statistical randomized encodings. Electron. Colloq. Comput. Complex. (ECCC) 22, 186 (2015)
Mix Barrington, D.A.: Bounded-width polynomial-size branching programs recognize exactly those languages in NC\({^1}\). In: Proceedings of the 18th Annual ACM Symposium on Theory of Computing, 28–30 May 1986, Berkeley, California, USA, pp. 1–5 (1986)
Bogdanov, A., Brzuska, C.: On basing size-verifiable one-way functions on NP-hardness. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 1–6. Springer, Heidelberg (2015)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (Im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, p. 1. Springer, Heidelberg (2001)
Biham, E., Goren, Y.J., Ishai, Y.: Basing weak public-key cryptography on strong one-way functions. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 55–72. Springer, Heidelberg (2008)
Blum, M., Micali, S.: How to generate cryptographically strong sequences of pseudo-random bits. SIAM J. Comput. 13(4), 850–864 (1984)
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Denning, D.E., Pyle, R., Ganesan, R., Sandhu, R.S., Ashby, V. (eds.) Proceedings of the 1st ACM Conference on Computer and Communications Security, CCS 1993, Fairfax, Virginia, USA, 3–5 November 1993, pp. 62–73. ACM (1993)
Braverman, M.: Polylogarithmic independence fools AC\({}^{\text{0 }}\) circuits. J. ACM 57(5), 28:1–28:10 (2010)
Bogdanov, A., Trevisan, L.: On worst-case to average-case reductions for NP problems. In: Proceedings of the 44th Symposium on Foundations of Computer Science (FOCS 2003), 11–14 October 2003, Cambridge, MA, USA, pp. 308–317. IEEE Computer Society (2003)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: Ostrovsky, R. (ed.) FOCS, pp. 97–106. IEEE (2011). Invited to SIAM Journal on Computing
Cachin, C., Maurer, U.M.: Unconditional security against memory-bounded adversaries. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 292–306. Springer, Heidelberg (1997)
Diffie, W., Hellman, M.E.: New directions in cryptography. IEEE Trans. Inf. Theor. 22(6), 644–654 (1976)
Dziembowski, S., Maurer, U.M.: On generating the initial key in the bounded-storage model. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 126–137. Springer, Heidelberg (2004)
Furst, M.L., Saxe, J.B., Sipser, M.: Parity, circuits, and the polynomial-time hierarchy. Math. Syst. Theor. 17(1), 13–27 (1984)
Gallager, R.G.: Low-density parity-check codes. IRE Trans. Inf. Theor. 8(1), 21–28 (1962)
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC, pp. 169–178 (2009)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS 2013, pp. 40–49 (2013)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM (JACM) 33(4), 792–807 (1986)
Goldwasser, S., Micali, S.: Probabilistic encryption and how to play mental poker keeping secret all partial information. In: STOC 1982, pp. 365–377 (1982)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems (extended abstract). In: Proceedings of the 17th Annual ACM Symposium on Theory of Computing, 6–8 May 1985, Providence, Rhode Island, USA, pp. 291–304 (1985)
Goldwasser, S., Rothblum, G.N.: How to compute in the presence of leakage. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS 2012, New Brunswick, NJ, USA, 20–23 October 2012, pp. 31–40 (2012)
Håstad, J.: Almost optimal lower bounds for small depth circuits. In: Proceedings of the 18th Annual ACM Symposium on Theory of Computing, 28–30 May 1986, Berkeley, California, USA, pp. 6–20 (1986)
Hastad, J.: One-way permutations in NC\(^0\). Inf. Process. Lett. 26(3), 153–155 (1987)
Håstad, J.: On the correlation of parity and small-depth circuits. SIAM J. Comput. 43(5), 1699–1708 (2014)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: Proceedings of the 41st Annual Symposium on Foundations of Computer Science, pp. 294–304. IEEE (2000)
Ishai, Y., Kushilevitz, E., Ostrovsky, R.: Sufficient conditions for collision-resistant hashing. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 445–456. Springer, Heidelberg (2005)
Impagliazzo, R., Luby, M.: One-way functions are essential for complexity based cryptography (extended abstract). In: 30th Annual Symposium on Foundations of Computer Science, Research Triangle Park, North Carolina, USA, 30 October–1 November 1989, pp. 230–235. IEEE Computer Society (1989)
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 8–26. Springer, Heidelberg (1990)
Linial, N., Mansour, Y., Nisan, N.: Constant depth circuits, fourier transform, and learnability. J. ACM (JACM) 40(3), 607–620 (1993)
Maurer, U.M.: Conditionally-perfect secrecy and a provably-secure randomized cipher. J. Cryptol. 5(1), 53–66 (1992)
Merkle, R.C.: Secure communications over insecure channels. Commun. ACM 21(4), 294–299 (1978)
Micali, S., Pass, R.: Local zero knowledge. In: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 21–23 May 2006, pp. 306–315 (2006)
Mossel, E., Shpilka, A., Trevisan, L.: On epsilon-biased generators in NC\({}^{\text{0 }}\). Random Struct. Algorithms 29(1), 56–81 (2006)
Nisan, N., Wigderson, A.: Hardness vs randomness. J. Comput. Syst. Sci. 49(2), 149–167 (1994)
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008)
Rivest, R., Adleman, L., Dertouzos, M.: On data banks and privacy homomorphisms. In: Foundations of Secure Computation, pp. 169–177. Academic Press (1978)
Razborov, A.A.: Lower bounds on the size of bounded depth circuits over a complete basis with logical addition. Math. Notes Acad. Sci. USSR 41(4), 333–338 (1987)
Rivest, R.L., Shamir, A., Adleman, L.M.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21(2), 120–126 (1978)
Rossman, B., Servedio, R.A., Tan, L.-Y.: An average-case depth hierarchy theorem for boolean circuits. Electron. Colloq. Comput. Complex. (ECCC) 22, 65 (2015)
Ragde, P., Wigderson, A.: Linear-size constant-depth polylog-treshold circuits. Inf. Process. Lett. 39(3), 143–146 (1991)
Smolensky, R.: Algebraic methods in the theory of lower bounds for boolean circuit complexity. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, New York, New York, USA, pp. 77–82 (1987)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) Symposium on Theory of Computing, STOC 2014, New York, NY, USA, May 31–June 03 2014, pp. 475–484. ACM (2014)
Tal, A.: Tight bounds on the fourier spectrum of AC\({}^{\text{0 }}\). Electron. Colloq. Comput. Complex. (ECCC) 21, 174 (2014)
Trevisan, L., Xue, T.: A derandomized switching lemma and an improved derandomization of AC\({}^{\text{0 }}\). In: Proceedings of the 28th Conference on Computational Complexity, CCC 2013, K.lo Alto, California, USA, 5–7 June 2013, pp. 242–247 (2013)
Vadhan, S.P.: Constructing locally computable extractors and cryptosystems in the bounded-storage model. J. Cryptol. 17(1), 43–77 (2004)
Viola, E.: The complexity of distributions. SIAM J. Comput. 41(1), 191–218 (2012)
Yao, A.C.: Theory and applications of trapdoor functions (extended abstract). In: 23rd Annual Symposium on Foundations of Computer Science, Chicago, Illinois, USA, 3–5 November 1982, pp. 80–91. IEEE Computer Society (1982)
Acknowledgements
We thank Prabhanjan Ananth for several useful discussions towards the beginning of the project. We would also like to thank the anonymous reviewers for their careful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Degwekar, A., Vaikuntanathan, V., Vasudevan, P.N. (2016). Fine-Grained Cryptography. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9816. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53015-3_19
Download citation
DOI: https://doi.org/10.1007/978-3-662-53015-3_19
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53014-6
Online ISBN: 978-3-662-53015-3
eBook Packages: Computer ScienceComputer Science (R0)


 , we construct one-way functions, pseudo-random generators (with sub-linear stretch), collision-resistant hash functions and most importantly, public-key encryption schemes, all computable in
, we construct one-way functions, pseudo-random generators (with sub-linear stretch), collision-resistant hash functions and most importantly, public-key encryption schemes, all computable in 


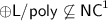 , there exist, for an infinite number of values of n, distributions
, there exist, for an infinite number of values of n, distributions 