Abstract
We construct a constant-round leakage-resilient zero-knowledge argument system under the existence of collision-resistant hash function family. That is, using collision-resistant hash functions, we construct a constant-round zero-knowledge argument system such that for any cheating verifier that can obtain arbitrary amount of leakage of the prover’s state, there exists a simulator that can simulate the adversary’s view by obtaining at most the same amount of leakage of the witness. Previously, leakage-resilient zero-knowledge protocols were constructed only under a relaxed security definition (Garg-Jain-Sahai, CRYPTO’11) or under the DDH assumption (Pandey, TCC’14).
Our leakage-resilient zero-knowledge argument system satisfies an additional property that it is simultaneously leakage-resilient zero-knowledge, meaning that both zero-knowledgeness and soundness hold in the presence of leakage.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Collision-resistant Hash Function Family
- Zero-knowledge Protocol
- Equivocal Commitment Scheme
- Leakage Queries
- Hamiltonicity Protocol
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Zero-knowledge (\(\mathrm {ZK}\)) proofs and arguments [14] are interactive proof/argument systems with which the prover can convince the verifier of the correctness of a mathematical statement while providing zero additional knowledge. This “zero additional knowledge” property is formalized thorough the simulation paradigm. Specifically, an interactive proof or argument is said to be zero-knowledge if for any adversarial verifier there exists a simulator that can output a simulated view of the adversary.
Recently, Garg et al. [12] introduced a new notion of zero-knowledgeness called leakage-resilient zero-knowledge (\(\mathrm {LRZK}\)). Roughly speaking, \(\mathrm {LRZK}\) is a notion of zero-knowledgeness in the setting where adversarial verifiers can obtain arbitrary leakage on the entire state of the honest prover (including the witness and the randomness) during the entire protocol execution. \(\mathrm {LRZK}\) is motivated by the studies of side-channel attacks (e.g., [2, 18, 27]), which demonstrated that adversaries might be able to obtain leakage of honest parties’ secret states by attacking physical implementations of cryptographic algorithms.
Informally speaking, \(\mathrm {LRZK}\) requires that the protocol does not reveal anything beyond the validity of the statement and the leakage that the adversary obtained. More formally, \(\mathrm {LRZK}\) is defined as follows. In the definition of \(\mathrm {LRZK}\), the cheating verifier is allowed to make arbitrary number of leakage queries during the interaction with a honest prover, where each leakage query f is answered by \(f(w, \mathsf {tape})\) for the witness w and the randomness \(\mathsf {tape}\) that the honest prover generated thus far. On the other hand, the simulator is allowed to make queries to the leakage oracle \(\mathcal {L}_w\), which is parametrized by the witness w of the honest prover and outputs f(w) on input any function f. \(\mathrm {LRZK}\) is then defined by requiring that for any cheating verifier \(V^*\) there exists a simulator \(\mathcal {S}\) such that for any \(\ell \in \mathbb {N}\), when \(V^*\) obtains \(\ell \) bits of leakage of the prover’s state via leakage queries, \(\mathcal {S}\) can simulate the view of \(V^*\) by obtaining \(\ell \) bits of leakage of the witness via queries to the leakage oracle \(\mathcal {L}_w\).Footnote 1
In [12], Garg et al. showed a proof system that satisfies a weaker notion of \(\mathrm {LRZK}\) called \((1+\epsilon )\)-\(\mathrm {LRZK}\). Specifically, they showed that for any \(\epsilon >0\), there exists a proof system such that when \(V^*\) obtains \(\ell \) bits of leakage from the prover, a simulator can simulate the verifier’s view by obtaining at most \((1+\epsilon )\cdot \ell \) bits of leakage from \(\mathcal {L}_w\). The round complexity of this protocol is at least \(\omega (\log n){\slash }\epsilon \), and its security is proven under a standard general assumption (the existence of statistically hiding commitment scheme that is public-coin w.r.t. the receiver).
A natural question left open by [12] is whether we can construct a \(\mathrm {LRZK}\) protocol without weakening the security requirement. That is, the question is whether we can reduce \(\epsilon \) to 0 in the protocol of [12]. This question is particularly of theoretical interest because reducing \(\epsilon \) to 0 is optimal in the sense that \(\lambda \)-\(\mathrm {LRZK}\) for \(\lambda <0\) is impossible to achieve in the plain model [12].
Recently, this question was solved affirmatively by Pandey [23], who constructed the first \(\mathrm {LRZK}\) argument system by using the DDH assumption and collision-resistant hash functions. Pandey’s protocol has only constant number of rounds; therefore, it follows that asymptotically optimal round complexity can be achievable even in the presence of leakage.
A question that is explicitly left open by Pandey [23, Section 1] is whether we can construct \(\mathrm {LRZK}\) protocols under a standard general assumption. In fact, although the protocol of Pandey [23] is superior to the protocol of Garg et al. [12] in terms of both leakage resilience (\(\mathrm {LRZK}\) v.s. \((1+\epsilon )\)-\(\mathrm {LRZK}\)) and round complexity (constant v.s. \(\omega (\log n){\slash }\epsilon \)), the assumption of the former is seemingly much stronger than that of the latter (the DDH assumption v.s. the existence of statistically hiding commitment scheme that is public-coin w.r.t. the receiver, which is implied by, say, the existence of collision-resistant hash function family or even the existence of one-way functionsFootnote 2).
Question. Can we construct a (constant-round) leakage-resilient zero-knowledge protocol under standard general assumptions?
1.1 Our Results
In this paper, we answer the above question affirmatively by constructing a \(\mathrm {LRZK}\) protocol from collision-resistant hash functions (CRHFs). Like the protocol of [23], our protocol has only constant number of rounds. Also, our protocol has an additional property that it is public coin (w.r.t. the verifier).
Theorem. Assume the existence of collision-resistant hash function family. Then, there exists a constant-round public-coin leakage-resilient zero-knowledge argument for \(\mathcal {NP}\).
Simultaneously Leakage-Resilient Zero-Knowledge. Our protocol has an additional property that it is simultaneously leakage-resilient zero-knowledge [12], meaning that not only zero-knowledgeness but also soundness holds in the presence of leakage. The leakage-resilient (LR) soundness (i.e., soundness in the presence of leakage) of our protocol follows immediately from its public-coin property. In fact, any public-coin interactive proof/argument system is \(\text {LR}\) sound for arbitrary amount of leakage of the verifier because the verifier has no secret state in public-coin protocols.
To the best of our knowledge, our protocol is the first simultaneously \(\mathrm {LRZK}\) protocol. The \((1+\epsilon )\)-\(\mathrm {LRZK}\) protocol of Garg et al. [12] is \(\text {LR}\) sound in a weak sense—it is \(\text {LR}\) sound when there is an a-priori upper bound on the amount of leakage—but is not \(\text {LR}\) sound when the amount of leakage is unbounded,Footnote 3 and similarly, the \(\mathrm {LRZK}\) protocol of Pandey [23] is also not \(\text {LR}\) sound with unbounded amount of leakage. In contrast, our protocol is sound even when cheating verifiers obtain arbitrary amount of leakage.
The summary of the previous results and ours is given in Table 1. In the table, “bounded-\(\text {LR}\) sound” means that the soundness holds when there is an a-priori upper bound on the amount of leakage from the verifier.
1.2 Related Works
Several works study interactive protocols in the presence of arbitrary leakage in the models other than the plain model, e.g., the work about leakage-tolerant UC-secure protocols in the CRS model [5], the work about non-transferable interactive proof systems in the CRS model with leak-free input encoding/updating phase [1], and the works about secure computation protocols in the CRS model with leak-free preprocessing/input-encoding phase and constant fraction of honest parties [6–8]. We remind the readers that, like [12, 23], this work considers \(\mathrm {LRZK}\) protocols in the plain model without any leak-free phase.
In [22], Ostrovsky et al. showed an impossibility result about black-box \(\mathrm {LRZK}\) in the model with only leak-free input-encoding phase (i.e., without CRS and preprocessing). We notice that this impossibility result does not contradict our result since the definition of \(\mathrm {LRZK}\) in [22] is different from the one we use (i.e., the definition given by [12]). Specifically, in the definition of [22], the simulator is not allowed to obtain any leakage, whereas in the definition that we use, the simulator can obtain the same amount of leakage as the cheating verifier. (In other words, Ostrovsky et al. [22] considers leakage resilience whereas we consider leakage tolerance; see Footnote 1.)
2 Overview of Our Techniques
2.1 Previous Techniques
Since our techniques rely on the techniques that are used in the previous \(\mathrm {LRZK}\) protocols of [12, 23], we start by recalling these protocols.
Protocol of [12]. In [12], Garg et al. constructed a \((1+\epsilon )\)-leakage-resilient zero-knowledge proof system, i.e., a proof system such that when \(V^*\) obtains \(\ell \) bits of leakage from the prover, its view can be simulated by obtaining at most \((1+\epsilon )\cdot \ell \) bits of leakage from \(\mathcal {L}_w\).
A key idea behind the protocol of [12] is to give the simulator two independent ways of cheating—one for simulating prover’s messages and the other for simulating leakages. Concretely, Garg et al. constructed their protocol by combining two well-known techniques of constant-round zero-knowledge protocols—the technique by Goldreich and Kahan [13] that requires the verifier to commit to its challenges in advance and the technique by Feige and Shamir [11] that uses equivocal commitment schemes. They then proved the security by considering a simulator that simulates the prover’s messages by extracting the challenges and simulates the leakages by using the equivocality of the commitment scheme.
In more details, the protocol of [12] consists of the following two phases. In the first phase, the verifier uses an extractable commitment scheme to commit to a challenge string ch of Blum’s Hamiltonicity protocol and trapdoor information td of an equivocal commitment scheme.Footnote 4 In the second phase, the prover and the verifier execute Blum’s Hamiltonicity protocol that is instantiated with the equivocal commitment scheme. In simulation, the simulator extracts ch and td in the first phase and then simulates the prover’s messages and the leakages in the second phase by using the knowledge of ch and td in the following way. (For simplicity, we assume that Blum’s protocol is executed only once instead of many times in parallel.)
-
When the extracted challenge \({{\varvec{ch}}}\) is \({\mathbf{0}}\), the simulator commits to a randomly permuted graph of statement G, and after \(V^*\) decommits the challenge ch (which must be 0), the simulator decommits the commitment to the permuted graph of G. Notice that the simulator does exactly the same things as a honest prover. Hence, the simulator can simulate prover’s randomness \(\mathsf {tape}\) easily and therefore can answer any leakage query f from \(V^*\) by querying \(f(\cdot , \mathsf {tape})\) to \(\mathcal {L}_w\).
-
When the extracted challenge \({{\varvec{ch}}}\) is \(\mathbf{1}\), the simulator commits to a randomly chosen cycle graph H at the beginning and then partially decommits it in the last step so that only the edges on the cycle are revealed.
When \(V^*\) makes a leakage query, the simulator answers it by using w and td to compute randomness that “explains” the commitment to H as a commitment to a permuted graph of G. (Recall that the prover is supposed to commit to a permuted graph of G.) Specifically, the simulator answers a leakage query f from \(V^*\) by querying the following function \(\widetilde{f}(\cdot )\) to \(\mathcal {L}_w\).
-
1.
On input w, function \(\widetilde{f}\) first computes a permutation \(\pi \) that maps the Hamiltonian cycle w in G to the cycle in H (i.e., computes \(\pi \) such that \(\pi (G)\) has the same cycle as H).
-
2.
Then, by using equivocalityFootnote 5 with trapdoor td, it computes randomness \(\mathsf {tape}\) that explains the commitment to H as a commitment to \(\pi (G)\) (i.e., it computes \(\mathsf {tape}\) such that committing to \(\pi (G)\) with randomness \(\mathsf {tape}\) will generate the same commitment as the one that the simulator has sent to \(V^*\) by committing to H).
-
3.
Finally, it outputs \(f(w, \mathsf {tape})\).
Notice that since \(\pi (G)\) has the same cycle as H, the simulated leakages (from which \(V^*\) may be able to compute \(\pi (G)\)) are consistent with the cycle of H that is decommitted by the simulator in the last step.
-
1.
We remark that the reason why the protocol of [12] satisfies only \((1+\epsilon )\)-\(\mathrm {LRZK}\) (rather than standard \(\mathrm {LRZK}\)) is that the extraction of ch and td involves the rewinding of \(V^*\). In fact, since \(V^*\) can make new leakage queries after being rewound, the simulator need to obtain new leakages from \(\mathcal {L}_w\) in each rewinding and hence the simulator need to obtain more bits of leakage than \(V^*\).
Protocol of [23]. In [23], Pandey constructed a constant-round \(\mathrm {LRZK}\) argument system under the DDH assumption. Roughly speaking, Pandey’s idea is to replace the rewinding simulation technique in the protocol of [12] with the “straight-line” simulation technique of Barak [3]. In particular, Pandey replaced the first phase of the protocol of [12] with the following one.
-
1.
First, the prover and the verifier execute an encrypted version of so called Barak’s preamble [3, 24, 25], which determines a “fake statement” that is false except with negligible probability.
-
2.
Next, the prover and the verifier execute Yao’s garbled circuit protocol [28] in which the prover can obtain ch and td only when it has a valid witness for the fake statement.
From the security of the encrypted Barak’s preamble, no cheating prover can make the fake statement true; hence, ch and td are hidden from the cheating prover. In contrast, a non-black-box simulator can make the fake statement true by using the knowledge of the code of the verifier; hence, the simulator can obtain ch and td without rewinding \(V^*\). An issue is that, to guarantee leakage resilience, it is required that Yao’s protocol is executed in a way that all prover’s messages are pseudorandom (since otherwise it is hard to simulate randomness that explains the simulated prover’s messages as honest prover’s messages during the simulation of the leakages). Since Yao’s protocol involves executions of an oblivious transfer protocol (in which the prover behaves as a receiver), this property is hard to satisfy. Pandey solved this problem by using the DDH assumption, under which there exists an oblivious transfer protocol such that all receiver’s messages are indistinguishable from random group elements.
2.2 Our Techniques
The reason why the protocols of [12, 23] either guarantee only weaker security or rely on a stronger assumption is that the simulation involves extraction from \(V^*\). In fact, in [12], the simulator need to obtain more amount of leakage than \(V^*\) because it rewinds \(V^*\) during extraction, and in [23], the DDH assumption is required because Yao’s protocol is used for extraction.
Based on this observation, our strategy is to modify the protocols of [12, 23] so that no extraction is required in simulation. We first remove the extraction of trapdoor td and next remove the extraction of challenge ch.
Removing Extraction of Trapdoor \({{\varvec{td.}}}\) We first modify the protocols of [12, 23] so that leakages can be simulated without extracting the trapdoor td of an equivocal commitment scheme.
Our main tool is Hamiltonicity commitment scheme \(\mathsf {H}\text {-}\mathsf {Com}\) [9, 11], which is a well-known instance-dependent equivocal commitment scheme based on Blum’s Hamiltonicity protocol. \(\mathsf {H}\text {-}\mathsf {Com}\) is parametrized by a graph G with \(q = \mathsf {poly}(n)\) vertices. To commit to 0, the committer chooses a random permutation \(\pi \) and commits to the adjacent matrix of \(\pi (G)\) using any commitment scheme \(\mathsf {Com}\); to decommit, the committer reveals \(\pi \) and decommits all the entries of the matrix. To commit to 1, the committer commits to the adjacent matrix of a random q-cycle graph; to decommit, the committer decommits only the entries that corresponds to the edges on the cycle. \(\mathsf {H}\text {-}\mathsf {Com}\) satisfies equivocality when G has a Hamiltonian cycle; this is because after committing to 0, the committer can decommit it to both 0 and 1 given a Hamiltonian cycle w in G.
Given \(\mathsf {H}\text {-}\mathsf {Com}\), we remove the extraction of td by combining \(\mathsf {H}\text {-}\mathsf {Com}\) with an encrypted variant of Barak’s preamble. Specifically, we replace the equivocal commitment scheme in the protocols of [12, 23] with \(\mathsf {H}\text {-}\mathsf {Com}\) that depends on the fake statement \(G'\) that is obtained by the encrypted Barak’s preamble. From the security of Barak’s preamble, any cheating prover cannot make \(G'\) true and hence it cannot use the equivocality of \(\mathsf {H}\text {-}\mathsf {Com}\), whereas the simulator can make \(G'\) true and hence it can use the equivocality of \(\mathsf {H}\text {-}\mathsf {Com}\) as desired.
Remark 1
As observed in [23], it is not straightforward to use the encrypted Barak’s preamble in the presence of leakage. Roughly speaking, in the encrypted Barak’s preamble, the prover commits to its messages instead of sending them in clear, and in the proof of soundness, it is required that the prover’s messages are extractable from the commitments. The problem is that it is not easy to guarantee this extractability in the presence of leakage (this is because the prover’s messages are typically not pseudorandom in the techniques of extractability). Pandey [23] solved this problem by having the prover use a specific extractable commitment scheme based on the DDH assumption. In this paper, we instead have the prover use a commitment scheme that satisfies only very weak extractability but the prover’s messages of which are pseudorandom and the security of which is based on the existence of CRHFs.Footnote 6 For details, see Sect. 4.1.
Removing Extraction of Challenge \({{\varvec{ch.}}}\) Next, we modify the protocols of [12, 23] so that prover’s messages can be simulated without extracting the challenge ch of Hamiltonicity protocol.
We first notice that although the simulator can use equivocality without extraction as shown above, it is not easy for the simulator to use equivocality for simulating prover’s messages. This is because when the leakages to \(V^*\) includes the randomness that is used for commitments, \(V^*\) may be able to determine the committed values from the leakages and therefore equivocation may be detected by \(V^*\).
As our main technical tool, then, we introduce a specific instance-dependent equivocal commitment scheme \(\mathsf {GJS}\text {-}\mathsf {Com}\) that we obtain by considering the technique of [12] on Hamiltonicity protocol in the context of \(\mathsf {H}\text {-}\mathsf {Com}\). Recall that, as explained in Sect. 2.1, in [12] Garg et al. use Blum’s Hamiltonicity protocol that is instantiated with an equivocal commitment scheme. Here, we use \(\mathsf {H}\text {-}\mathsf {Com}\) that is instantiated with an equivocal commitment scheme (i.e., we use \(\mathsf {H}\text {-}\mathsf {Com}\) in which the adjacent matrix is committed to by an equivocal commitment scheme). The equivocal commitment scheme that we use here is, as above, \(\mathsf {H}\text {-}\mathsf {Com}\) that depends on the fake statement generated by the encrypted Barak’s preamble.Footnote 7 Hence, the commitment scheme \(\mathsf {GJS}\text {-}\mathsf {Com}\) is a version of \(\mathsf {H}\text {-}\mathsf {Com}\) that is instantiated by using \(\mathsf {H}\text {-}\mathsf {Com}\) itself as the underling commitment scheme.Footnote 8 \(\mathsf {GJS}\text {-}\mathsf {Com}\) depends on two statements of the Hamiltonicity problem: The “outer” \(\mathsf {H}\text {-}\mathsf {Com}\) (the \(\mathsf {H}\text {-}\mathsf {Com}\) that is implemented with \(\mathsf {H}\text {-}\mathsf {Com}\)) depends on the real statement G, and the “inner” \(\mathsf {H}\text {-}\mathsf {Com}\) (the \(\mathsf {H}\text {-}\mathsf {Com}\) that is used to implement \(\mathsf {H}\text {-}\mathsf {Com}\)) depends on the fake statement \(G'\). \(\mathsf {GJS}\text {-}\mathsf {Com}\) inherits equivocality from the outer \(\mathsf {H}\text {-}\mathsf {Com}\), i.e., given a witness for the real statement G, a \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment to 0 can be decommitted to both 0 and 1.
Since \(\mathsf {GJS}\text {-}\mathsf {Com}\) is obtained by considering the technique of [12] in the context of \(\mathsf {H}\text {-}\mathsf {Com}\), it satisfies a property that is useful for proving \(\mathrm {LRZK}\) property. First, observe that given \(\mathsf {GJS}\text {-}\mathsf {Com}\), the second phase of the \(\mathrm {LRZK}\) protocol of [12] (i.e., Hamiltonicity protocol phase) can be viewed as follows.
-
1.
The prover commits to 0 by using \(\mathsf {GJS}\text {-}\mathsf {Com}\).
-
2.
The verifier reveals the challenge \(ch\in \{0,1 \}\) that is committed to in the first phase.
-
3.
When \(ch = 0\), the prover decommits the \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment to 0 honestly, and when \(ch = 1\), the prover decommits it to 1 by using the equivocality with the knowledge of Hamiltonian cycle w in G.
When the second phase of the protocol of [12] is viewed in this way, the key property that is used in the simulation of the leakages in [12] is the following.
-
Given a Hamiltonian cycles in G and \(G'\), a \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment to 1 (in which a random cycle graph is committed) can be “explained” as a commitment to 0 (in which a permutation of G is committed) by using the equivocality of the inner \(\mathsf {H}\text {-}\mathsf {Com}\).
Furthermore, even after being explained as a commitment to 0, the commitment can later be decommitted to 1 in a consistent way with the explained randomness (cf. function \(\widetilde{f}\) in Sect. 2.1).
Because of this property, even when the simulator commits to 1 instead of 0 using \(\mathsf {GJS}\text {-}\mathsf {Com}\) to simulate the messages, the simulator can answer any leakage query f from \(V^*\) by querying \(\mathcal {L}_w\) a function \(\widetilde{f}\) that, on input w, computes randomness \(\mathsf {tape}\) that explains the commitment to 1 as a commitment to 0 and then outputs \(f(w, \mathsf {tape})\).
A problem of this property is that it can be used only in a very limited situation. Specifically, this property can be used only when the simulator knows which \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment will be decommitted to 1, and this is the reason why the extraction of ch is required in the simulation strategy of [12, 23]. Hence, to remove the extraction of ch, we need to use \(\mathsf {GJS}\text {-}\mathsf {Com}\) in a way that, given a witness for the fake statement, the simulator can predict which value each \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment will be decommitted to.
Our key observation is that we can use this property if we use \(\mathsf {GJS}\text {-}\mathsf {Com}\) to implement the Hamiltonicity protocol in which the fake statement is proven. Concretely, we consider the following protocol.
-
1.
The prover and the verifier execute an encrypted variant of Barak’s preamble. Let \(G'\) be the fake statement and let \(q'\) be the number of the nodes of \(G'\).
-
2.
-
(a)
The prover commits to a \(q'\times q'\) zero matrix by using \(\mathsf {GJS}\text {-}\mathsf {Com}\).
-
(b)
The verifier sends a challenge \(ch\in \{0,1 \}\).
-
(c)
When \(ch=0\), the prover sends a random permutation \(\pi \) over \(G'\) to the verifier and then decommit the \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitments to the adjacent matrix of \(\pi (G')\) by using the equivocality of \(\mathsf {GJS}\text {-}\mathsf {Com}\) with the knowledge of a witness for the real statement.
When \(ch=1\), the prover chooses a random \(q'\)-cycle graph H and decommits some of the \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitments to 1 by using the equivocality of \(\mathsf {GJS}\text {-}\mathsf {Com}\) so that the decommitted entries of the matrix correspond to the cycle in H.
-
(d)
When \(ch=0\), the verifier verifies whether the decommitted graph is \(\pi (G')\). When \(ch=1\), the verifier verifies whether the decommitted entries corresponds to a \(q'\)-cycle in a graph.
-
(a)
Since any charting prover cannot make the fake statement \(G'\) true, \(\mathsf {GJS}\text {-}\mathsf {Com}\) is statistically binding when the real statement G is false, and hence soundness follows. In contrast, the simulator can cheat in Barak’s preamble so that it knows a Hamiltonian cycle \(w'\) in the fake statement \(G'\), and therefore it can simulate the prover’s messages by “honestly” proving the fake statement, i.e., by committing to \(\pi (G')\) in step 2(a) for a randomly chosen \(\pi \) and then revealing the entire graph \(\pi (G')\) or only the cycle \(\pi (w')\) depending on the value of ch. Furthermore, since in step 2(a) the simulator do know which value each \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment will be decommitted to (the commitments to the edges on \(\pi (w')\) will be always decommitted to 1 and others will be decommitted honestly or will not be decommitted), the simulator can simulate the leakage in the same way as in the protocol of [12] by using the property of \(\mathsf {GJS}\text {-}\mathsf {Com}\) described above.
This completes the overview of our techniques. The details are given in what follows.
3 Preliminaries
3.1 Notations
We use \(n\) to denote the security parameter. For any \(k\in \mathbb {N}\), we use [k] to denote the set \(\{1,\ldots ,k \}\). For any randomized algorithm \(\mathsf {Algo}\), we use \(\mathsf {Algo}(x; r)\) to denote the execution of \(\mathsf {Algo}\) with input x and randomness r, and we use \(\mathsf {Algo}(x)\) to denote the execution of \(\mathsf {Algo}\) with input x and uniform randomness.
We use \(\mathbf L _{\mathrm {HC}}\) to denote the languages of the Hamiltonian graphs. For any \(G\in \mathbf L _{\mathrm {HC}}\), we use \(\mathbf R _{\mathrm {HC}}(G)\) to denote the set of the Hamiltonian cycles in G. Generally, for any language \(\mathbf L \) and any instance \(x\in \mathbf L \), we use \(\mathbf R _\mathbf{L }(x)\) to denote the set of the witnesses for \(x\in \mathbf L \).
For any two-party protocol \(\langle A, B \rangle \), we use \(\mathsf {trans}\left[ A(x) \leftrightarrow B(y) \right] \) to denote a random variable representing the transcript of the interaction between A and B with input x and y respectively, and use \(\mathsf {output}_{A}\left[ A(x) \leftrightarrow B(y) \right] \) (resp., \(\mathsf {output}_{B}\left[ A(x) \leftrightarrow B(y) \right] \)) to denote a random variable representing the output of A (resp., B) in the interaction between A and B with input x and y respectively.
3.2 Leakage-Resilient Zero-Knowledge
We recall the definition of leakage-resilient zero-knowledgeness [12]. For convenience, we use a slightly different formulation of the definition.
For any interactive proof system \(\langle P, V \rangle \), any \(\textsc {ppt} \) cheating receiver \(V^*\), any statement \(x\in \mathbf L \), any witness \(w\in \mathbf R _\mathbf{L }(x)\), and any oracle machine \(\mathcal {S}\) called simulator, consider the following two experiments.
-
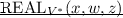
-
1.
Execute \(V^*(x, z)\) with a honest prover P(x, w) of \(\langle P, V \rangle \).
During the interaction, \(V^*\) can make arbitrary number of adaptive leakage queries on the state of P. A leakage query consists of an efficiently compatible function \(f_i\) (described as a circuit) and it is answered with \(f_i(w, \mathsf {tape})\), where \(\mathsf {tape}\) is the randomness used by P so far.
-
2.
Output the view of \(V^*\).
-
1.
-

-
1.
Execute \(\mathcal {S}(x, z)\) with access to a leakage oracle \(\mathcal {L}_w\). A query to \(\mathcal {L}_w\) consists of an efficiently computable function f and answered with f(w). Let \(\tau \) be the output of \(\mathcal {S}\).
-
2.
If \(\tau \) is not a valid view of \(V^*\), the output of the experiment is \(\bot \). Otherwise, let \(\ell \) be the total length of the leakage that \(V^*\) obtains in \(\tau \). If the total length of the answers that \(\mathcal {S}\) obtained from \(\mathcal {L}_w\) is larger than \(\ell \), the output of the experiment is \(\bot \). Otherwise, the output is \(\tau \).
-
1.
Let \(\mathsf {REAL}_{V^*}(x,w,z)\) be the random variable representing the output of \(\mathrm {REAL}_{V^*}(x,w,z)\) and \(\mathsf {IDEAL}_{\mathcal {S}}(x,w,z)\) be the random variable representing the output of \(\mathrm {IDEAL}_{\mathcal {S}}(x,w,z)\).
Definition 1
An interactive argument system \(\langle P, V \rangle \) for a language \(\mathbf L \) with witness relation \(\mathbf R \) is leakage-resilient zero knowledge if for every ppt machine \(V^*\) and every sequence \(\{w_x \}_{x\in \mathbf L }\) such that \((x, w_x)\in \mathbf R _\mathbf{L }\), there exists a \(\textsc {ppt} \) oracle machine \(\mathcal {S}\) such that the following hold.
-
Indistinguishability Condition
$$\begin{aligned} \left\{ \mathsf {REAL}_{V^*}(x, w_x, z) \right\} _{x\in \mathbf L , z\in \{0,1 \}^{*}} \approx \left\{ \mathsf {IDEAL}_{\mathcal {S}}(x, w_x, z) \right\} _{x\in \mathbf L , z\in \{0,1 \}^{*}}. \end{aligned}$$ -
Leakage-length condition. For every \(x\in \mathbf L \) and \(z\in \{0,1 \}^*\),
$$\begin{aligned} \Pr \left[ \mathsf {IDEAL}_{\mathcal {S}}(x, w_x, z) = \bot \right] = 0. \end{aligned}$$
3.3 Commitment Scheme
Recall that commitment schemes are two-party protocols between a committer C and a receiver R. We say that a commitment is valid if there exists a value to which it can be decommitted. We denote by \(\mathsf {value}(\cdot )\) a function that, on input a commitment (i.e., a transcript in the commit phase), outputs its committed value if it is uniquely determined and outputs \(\bot \) otherwise.
3.4 Naor’s Commitment
We recall Naor’s statistically binding commitment scheme \(\mathsf {Com}\), which can be constructed from one-way functions [16, 20].
Commit Phase. The commit phase consists of two rounds. In the first round, the receiver sends a random \(3n\)-bit string \(r\in \{0,1 \}^{3n}\). In the second round, the committer chooses a random seed \(s\in \{0,1 \}^{n}\) for a pseudorandom generator \(\mathsf {PRG}:\{0,1 \}^{n} \rightarrow \{0,1 \}^{3n}\) and then sends \(\mathsf {PRG}(s)\) if it wants to commit to 0 and sends \(\mathsf {PRG}(s) \oplus r\) if it wants to commit to 1.
We use \(\mathsf {Com}_r(\cdot )\) to denote an algorithm that, on input \(b\in \{0,1 \}\), computes a commitment to b as above by using r as the first-round message.
Decommit Phase. In the decommit phase, the committer reveals the seed s.
Security. \(\mathsf {Com}\) is statistically binding and computational hiding. Furthermore, the binding and hiding property hold even when the same first-round message r is used in multiple commitments.
Committing to Strings. For any \(\ell \in \mathbb {N}\), we can commit to an \(\ell \)-bit string by simply committing to each bit using \(\mathsf {Com}\). We notice that the same first-round message r can be used in all the commitments.
We abuse the notation and use \(\mathsf {Com}_r(\cdot )\) to denote an algorithm that, on input \(m\in \{0,1 \}^*\), computes a commitment to m as above by using r as the first-round message. Notice that \(\mathsf {Com}_r(\cdot )\) has pseudorandom range. Thus, by using an algorithm \(\mathsf {Com}_{\mathrm {pub}}\) that outputs a random \(3n\ell \)-bit string on input \(1^{\ell }\), we can obtain a “fake commitment” that is indistinguishable from a real commitment.
3.5 Hamiltonicity Commitment
We recall a well-known instance-dependent commitment scheme \(\mathsf {H}\text {-}\mathsf {Com}\) [9, 11] that is based on Blum’s zero-knowledge proof for Hamiltonicity.
Commit Phase. \(\mathsf {H}\text {-}\mathsf {Com}\) is parametrized by a graph G. Let q be the number of its vertices. To commit to 0, the committer chooses a random permutation \(\pi \) over the vertices of G and then commits to the adjacent matrix of \(\pi (G)\) by using \(\mathsf {Com}\). To commit to 1, the committer chooses a random q-cycle graph and then commits to its adjacent matrix by using \(\mathsf {Com}\).
We use \(\mathsf {H}\text {-}\mathsf {Com}_{G,r}(\cdot )\) to denote an algorithm that, on input \(b\in \{0,1 \}\), computes a commitment to b as above by using r as the first-round message of all the \(\mathsf {Com}\) commitments.
Decommit Phase. When the committer committed to 0, it reveals \(\pi \), and also reveals all the entries of the adjacent matrix by decommitting all the \(\mathsf {Com}\) commitments. When the committer committed to 1, it reveals only the entries corresponding to the edges on the q-cycle by decommitting the \(\mathsf {Com}\) commitments in which these entries are committed.
Security. \(\mathsf {H}\text {-}\mathsf {Com}\) is computationally hiding, and it is statistically binding when \(G\not \in \mathbf L _{\mathrm {HC}}\).
Equivocality. When \(G\in \mathbf L _{\mathrm {HC}}\), a commitment to 0 can be decommitted to 1 given a Hamiltonian cycle \(w\in \mathbf R _{\mathrm {HC}}(G)\) in G. Specifically, a commitment to 0 can be decommitted to 1 by decommitting the entries that corresponds to the edges on \(\pi (w)\) (i.e., the cycle that is obtained by applying \(\pi \) on w).
3.6 Adaptive Hamiltonicity Commitment
We recall the adaptively secure Hamiltonicity commitment scheme \(\mathsf {AH}\text {-}\mathsf {Com}\), which was used in, e.g., [9, 19].
Commit Phase. \(\mathsf {AH}\text {-}\mathsf {Com}\) is parametrized by a graph G. Let q be the number of its vertices. To commit to 0, the committer does the same things as in \(\mathsf {H}\text {-}\mathsf {Com}\); i.e., it chooses a random permutation \(\pi \) over the vertices of G and then commits to the adjacent matrix of \(\pi (G)\) by using \(\mathsf {Com}\). To commit to 1, the committer chooses a random q-cycle graph and then commits to its adjacent matrix in the following way: For all the entries corresponding to the edges on the q-cycle, it commits to 1 by using \(\mathsf {Com}\), and for all the other entries, it simply sends random \(3n\)-bit strings instead of committing to 0. (Since \(\mathsf {Com}\) has pseudorandom range, random \(3n\)-bit strings are indistinguishable from \(\mathsf {Com}\) commitments.)
We use \(\mathsf {AH}\text {-}\mathsf {Com}_{G,r}(\cdot )\) to denote an algorithm that, on input \(b\in \{0,1 \}\), computes a commitment to b as above by using r as the first-round message of all the \(\mathsf {Com}\) commitments.
Decommit Phase. To decommit, the committer reveals all the randomness used in the commit phase. We use \(\mathsf {AH}\text {-}\mathsf {Dec}_r(\cdot , \cdot , \cdot )\) to denote an algorithm that, on input \(c, b, \rho \) such that \(\mathsf {AH}\text {-}\mathsf {Com}_r(b; \rho ) = c\), outputs a decommitment d as above.
Security. Like \(\mathsf {H}\text {-}\mathsf {Com}\), \(\mathsf {AH}\text {-}\mathsf {Com}\) is computationally hiding both when \(G\in \mathbf L _{\mathrm {HC}}\) and when \(G\not \in \mathbf L _{\mathrm {HC}}\), and it is statistically binding when \(G\not \in \mathbf L _{\mathrm {HC}}\).
Adaptive Security. When \(G\in \mathbf L _{\mathrm {HC}}\), a commitment to 0 can be “explained” as a valid commitment to 1 given a witness \(w\in \mathbf R _{\mathrm {HC}}(G)\). Specifically, for a commitment c to 0, we can compute \(\rho \) such that \(\mathsf {AH}\text {-}\mathsf {Com}(1; \rho ) = c\). This is because commitments to the entries that do not correspond to the edges on \(\pi (w)\) are indistinguishable from random strings.
Formally, there exists an algorithm AH-ExplainAsOne such that for security parameter \(n\in \mathbb {N}\), graphs \(G\in \mathbf L _{\mathrm {HC}}\), witness \(w\in \mathbf R _{\mathrm {HC}}(G)\), and string \(r\in \{0,1 \}^{3n}\), the following hold.
-
Correctness. Given witness \(w\in \mathbf R _{\mathrm {HC}}(G)\) and c, \(\rho \) such that \(\mathsf {AH}\text {-}\mathsf {Com}_{G,r}(0; \rho ) = c\), \(\mathsf{AH}\text {-}\mathsf{ExplainAsOne}_{G, r}\) outputs \(\rho '\) such that \(\mathsf {AH}\text {-}\mathsf {Com}_{G,r}(1; \rho ') = c\).
-
Indistinguishability. Consider the following two probabilistic experiments.
-

/* \(\;\mathtt {commit}\;\mathtt {to}\) 1 \(\mathtt {and}\; \mathtt {reveal}\; \mathtt {randomness}\;\texttt {*/}\)
-
1.
Computes \(c \leftarrow \mathsf {AH}\text {-}\mathsf {Com}_{G, r}(1)\).
Let \(\rho _1\) be the randomness used in \(\mathsf {AH}\text {-}\mathsf {Com}\).
-
2.
Output \((c, \rho _1)\).
-
1.
-

/* \(\mathtt {commit\;to}\) 0 \(\mathtt {and\;explain\;it\;as\;commitment\;to}\) 1 */
-
1.
Computes \(c \leftarrow \mathsf {AH}\text {-}\mathsf {Com}_{G, r}(0)\).
Let \(\rho _0\) be the randomness used in \(\mathsf {AH}\text {-}\mathsf {Com}\).
Compute \(\rho _1 := \mathsf{AH}\text {-}\mathsf{ExplainAsOne}_{G, r}(w, c, \rho _0)\).
-
2.
Output \((c, \rho _1)\).
-
1.
Let \(\mathsf {EXP}^{\mathrm {AH}}_b(n, G, w, r)\) be the random variable representing the output of \(\mathrm {EXP}^{\mathrm {AH}}_b(n, G, w, r)\) for each \(b\in \{0,1 \}\). Then, the following two ensembles are computationally indistinguishable.
-
\(\left\{ \mathsf {EXP}^{\mathrm {AH}}_0(n,G,w,r) \right\} _{n\in \mathbb {N}, G\in \mathbf L _{\mathrm {HC}}, w\in \mathbf R _{\mathrm {HC}}(G), r\in \{0,1 \}^{3n}}\)
-
\(\left\{ \mathsf {EXP}^{\mathrm {AH}}_1(n,G,w,r) \right\} _{n\in \mathbb {N}, G\in \mathbf L _{\mathrm {HC}}, w\in \mathbf R _{\mathrm {HC}}(G), r\in \{0,1 \}^{3n}}\)
-
3.7 Barak’s Non-black-box Zero-Knowledge Protocols
As explained in Sect. 2, in our \(\mathrm {LRZK}\) protocol, we use a variant of so called “encrypted” Barak’s preamble [24, 25], which is based on the preamble stage of Barak’s non-black-box zero-knowledge protocol [3]. In this section, we recall Barak’s non-black-box zero-knowledge protocol. Our variant of encrypted Barak’s preamble is described in Sect. 4.1.
Barak’s non-black-box zero-knowledge protocol is constructed from any collision-resilient hash function family \(\mathcal {H}\). Informally speaking, Barak’s protocol \(\mathsf {BarakZK}\) proceeds as follows.
-
1.
The verifier V sends a random hash function \(h\in \mathcal {H}\) and the first-round message \(r_1\in \{0,1 \}^{3n}\) of \(\mathsf {Com}\) to the prover P.
-
2.
P sends \(c \leftarrow \mathsf {Com}_{r_1}(0^{n})\) to V. Then, V sends random string \(r_2\) to P.
-
3.
P proves the following statement by a witness-indistinguishable argument.
-
\(x \in L\), or
-
\((h, c, r_2)\in \varLambda \), where \((h, c, r_2) \in \varLambda \) holds if and only if there exists a machine \(\mathrm {\mathrm {\Pi }}\) such that c is a commitment to \(h(\mathrm {\mathrm {\Pi }})\) and \(\mathrm {\mathrm {\Pi }}\) outputs \(r_2\) in \(n^{\log \log n}\) steps.
-
Note that the statement proven in the last step is not in \(\mathcal {NP}\). Thus, P proves this statement by a witness-indistinguishable universal argument (WIUA), with which P can prove any statement in \(\mathcal {NEXP}\). Intuitively, \(\mathsf {BarakZK}\) is sound since \(\mathrm {\mathrm {\Pi }}(c) \ne r\) holds with overwhelming probability even when a cheating prover \(P^*\) commits to \(h(\mathrm {\mathrm {\Pi }})\) for a machine \(\mathrm {\mathrm {\Pi }}\). On the other hand, the zero-knowledge property can be proven by using a simulator that commits to \(h(\mathrm {\mathrm {\Pi }})\) such that \(\mathrm {\mathrm {\Pi }}\) is a machine that emulates the cheating verifier \(V^*\); since \(\mathrm {\mathrm {\Pi }}(c) = V^*(c) = r\) holds from the definition, the simulator can give a valid proof in the last step.
For our purpose, it is convenient to consider a variant of \(\mathsf {BarakZK}\) that we denote by \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \). \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) is the same as \(\mathsf {BarakZK}\) except that in the last step, instead of proving \(x \in L \vee (h, c, r_2)\in \varLambda \) by using WIUA, P proves \((h, c, r_2)\in \varLambda \) by using four-round public-coin universal argument system \(\mathsf {UA}\) [4]. (Hence, \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) is no longer zero-knowledge protocol.) The formal description of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) is shown in Fig. 1. We remark that in \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \), the language proven in the last step is replaced with a slightly more complex language as in, e.g., [3, 23–25]. This replacement is important for using \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) in the setting of leakage-resilient zero-knowledge, because the cheating verifier can obtain arbitrary information (i.e., leakage) before sending \(r_2\).
In essentially the same way as the soundness of \(\mathsf {BarakZK}\), we can prove the following lemma on \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \), which roughly states that there exists a “hard” language \(\mathbf L _{\mathrm {B}}\) on the transcript of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) such that no cheating prover can generate a transcript that is included in \(\mathbf L _{\mathrm {B}}\).
Lemma 1
(Soundness). Let \(\mathbf L _{\mathrm {B}}\) be the language defined in Fig. 2. Then, for any cheating prover \(P^*\) against \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \), any \(n\in \mathbb {N}\), and any \(z\in \{0,1 \}^*\),
A proof sketch of this lemma is given in the full version of this paper [17].
3.8 Somewhat Extractable Commitment Scheme
As we mentioned in Remark 1 in Sect. 2.2, in our variant of encrypted Barak’s preamble, we use a commitment scheme that satisfies only very weak extractability, which we call somewhat extractability. An important point is that since only very weak extractability is required, we can construct a somewhat extractable commitment scheme such that the committer sends only pseudorandom messages. Furthermore, we can construct such a scheme from one-way functions.
Concretely, we consider the commitment scheme \(\mathsf {SWExtCom}\) in Fig. 3. \(\mathsf {SWExtCom}\) is the same as the extractable commitment scheme of [26] except that in the last step, the committer simply reveals the values that it committed to in the first step (instead of decommitting the commitments). Because of this simplification, \(\mathsf {SWExtCom}\) does not satisfy extractability in the standard sense. Still, it is not hard to see that \(\mathsf {SWExtCom}\) satisfies extractability in the sense that, given two valid commitments c and \(c'\) such that the transcripts of the commit stage are identical but those of the challenge stage are different, the committed value of c can be extracted. Formally, \(\mathsf {SWExtCom}\) satisfies the following extractability.
Lemma 2
(Somewhat Extractability). Let us say that two commitments \(c = (\{c_{i,b} \}_{i\in [n], b\in \{0,1 \}}, \{e_i \}_{i\in [n]}, \{a_{i,e_i} \}_{i\in [n]})\) and \(c' = (\{c'_{i,b} \}_{i\in [n], b\in \{0,1 \}}, \{e'_i \}_{i\in [n]}, \{a'_{i,e_i} \}_{i\in [n]})\) are admissible if
-
\(c_{i,b} = c'_{i,b}\) for every \(i\in [n]\) and \(b\in \{0,1 \}\),
-
there exists \(i^*\in [n]\) such that \(e_{i^*} \ne e'_{i^*}\), and
-
the committed value of \(c_{i,b}\) is uniquely determined for every \(i\in [n]\) and \(b\in \{0,1 \}\).
Let \(\mathsf {Extract}(\cdot , \cdot )\) be the algorithm shown in Fig. 3. Then, for any two admissible commitments c and \(c'\), if both c and \(c'\) are valid, \(\widetilde{v} \mathop {=}\limits ^\mathrm{def}\mathsf {Extract}(c, c')\) is equal to \(\mathsf {value}(c)\) (i.e., \(\widetilde{v}\) is the committed value of c).
Proof
First, when c and \(c'\) are valid, \(a_{i^*, e_{i^*}}\) and \(a'_{i^*, e'_{i^*}}\) are the committed values of \(c_{i^*, e_{i^*}}\) and \(c_{i^*, e'_{i^*}}\) (since otherwise, any decommitments of c and \(c'\) would be rejected because the decommitted values of \(c_{i^*, e_{i^*}}\) and \(c_{i^*, e'_{i^*}}\) are not consistent with \(a_{i^*, e_{i^*}}\) and \(a'_{i^*, e'_{i^*}}\)). Second, when c and \(c'\) are valid, the committed value of c can be computed by XORing the committed values of \(c_{i^*, e_{i^*}}\) and \(c_{i^*, e'_{i^*}}\) (since otherwise, any decommitments of c and \(c'\) would be rejected). From these, the lemma follows. \(\square \)
A nice property of \(\mathsf {SWExtCom}\) is that all the messages that the committer sends in the commit phase are pseudorandom. Formally, we have the following lemma.
Lemma 3
(Existence of Public-Coin Fake Committing Algorithm). Let C be a honest committer algorithm of \(\mathsf {SWExtCom}\). There exists a \(\textsc {ppt} \) public-coin algorithm \(C_{\mathrm {pub}}\) such that for any \(\textsc {ppt} \) cheating receiver \(R^*\) that interacts with C in the commit phase of \(\mathsf {SWExtCom}\), the following ensembles are computationally indistinguishable.
-
\(\left\{ \mathsf {output}_{R^*}\left[ C(v) \leftrightarrow R^*(1^{n}, z) \right] \right\} _{n\in \mathbb {N}, v\in \{0,1 \}^{n}, z\in \{0,1 \}^{*}}\)
-
\(\left\{ \mathsf {output}_{R^*}\left[ C_{\mathrm {pub}}(1^{n}) \leftrightarrow R^*(1^{n}, z) \right] \right\} _{n\in \mathbb {N}, v\in \{0,1 \}^{n}, z\in \{0,1 \}^{*}}\)
Proof
(sketch). \(C_{\mathrm {pub}}\) is an algorithm that is the same as C except that, instead of sending commitments of \(\mathsf {Com}\), it sends fake commitments of \(\mathsf {Com}\) using \(\mathsf {Com}_{\mathrm {pub}}\) (i.e., sends random strings with the same length as the \(\mathsf {Com}\) commitments). Since \(\mathsf {Com}\) has pseudorandom range, the indistinguishability can be proven by using a standard hybrid argument (in which the commitments of \(\mathsf {Com}\) are replaced with random strings one by one). The formal proof is omitted. \(\square \)
4 Building Blocks
4.1 Special-Purpose Encrypted Barak’s Preamble
In our \(\mathrm {LRZK}\) protocol, we use a variant of so called “encrypted” Barak’s preamble [24, 25]. The encrypted Barak’s preamble is the same as (a variant of) Barak’s non-black-box zero-knowledge protocol \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) in Sect. 3.7 except that \(P_{\mathrm {B}}\) commits to its \(\mathsf {UA}\) messages \(\beta \) and \(\delta \) instead of sending them in clear. In this paper, we use a variant in which, instead of giving valid commitments, \(P_{\mathrm {B}}\) gives fake commitments of \(\mathsf {Com}\) and \(\mathsf {SWExtCom}\) by using \(\mathsf {Com}_{\mathrm {pub}}\) and \(C_{\mathrm {pub}}\). A nice property of this variant is that the prover sends only random strings; as will become clear later, this property is useful for constructing leakage-resilient protocols. The formal description of this variant, which we denote by \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \), is shown in Fig. 4.
We first show that, as in the case of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \), there exists a “hard” language on the transcript of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \).
Lemma 4
(Soundness). Let \(\mathbb {L}_{\mathrm {B}}\) be the language defined in Fig. 5. Then, for any cheating prover \(\mathbb {P}^*\) against \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \), any \(n\in \mathbb {N}\), and any \(z\in \{0,1 \}^*\),
Proof
Assume for contradiction that there exists \(\mathbb {P}^*\) such that for infinitely many \(n\)’s, there exists \(z\in \{0,1 \}^*\) such that
for a polynomial \(p(\cdot )\). We use \(\mathbb {P}^*\) to construct a cheating prover \(P^*\) against \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) and show that it contradicts the soundness of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) (i.e., Lemma 1).
Consider the following cheating prover \(P^*\) against \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \). First, \(P^*\) internally invokes \(\mathbb {P}^*\). Then, while externally interacting with a honest \(V_{\mathrm {B}}\) of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \), \(P^*\) interacts with internal \(\mathbb {P}^*\) as a verifier of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) in the following way.
-
In Stage 1 and 2 (of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \)), \(P^*\) forwards all messages from external \(V_{\mathrm {B}}\) to internal \(\mathbb {P}^*\) and forwards all messages from internal \(\mathbb {P}^*\) to external \(V_{\mathrm {B}}\). (Notice that the verifier of \(\langle P_{\mathrm {B}}, V_{\mathrm {B}} \rangle \) and that of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) are identical.) Let \((h, r_1, c, r_2)\) be the transcript of these stages.
-
In Stage 3-1, \(P^*\) forwards \(\alpha \) from external \(V_{\mathrm {B}}\) to internal \(\mathbb {P}^*\).
-
In Stage 3-2, \(P^*\) interacts with internal \(\mathbb {P}^*\) as a honest receiver of \(\mathsf {SWExtCom}\) and obtains \(\widehat{\beta }_1\). Let \(\mathsf {st}\) be the current state of \(\mathbb {P}^*\). Then, \(P^*\) rewinds \(\mathbb {P}^*\) to the point just before the challenge stage of \(\mathsf {SWExtCom}\), interacts with \(\mathbb {P}^*\) again, and obtains \(\widehat{\beta }_2\). Then, \(P^*\) computes a potential committed value \(\widetilde{\beta } \mathop {=}\limits ^\mathrm{def}\mathsf {Extract}(\widehat{\beta }_1, \widehat{\beta }_2)\) of \(\widehat{\beta }_1\) (recall that \(\mathsf {Extract}\) is the extracting algorithm of \(\mathsf {SWExtCom}\) shown in Fig. 3) and sends \(\widetilde{\beta }\) to external \(V_{\mathrm {B}}\).
-
In Stage 3-3, \(P^*\) receives \(\gamma \) from \(V_{\mathrm {B}}\) and sends it to internal \(\mathbb {P}^*\) (which is restarted from state \(\mathsf {st}\)).
-
In Stage 3-4, \(P^*\) interacts with internal \(\mathbb {P}^*\) as a honest receiver of \(\mathsf {SWExtCom}\) and obtains \(\widehat{\delta }_1\). Then, \(P^*\) rewinds \(\mathbb {P}^*\) to the point just before the challenge stage of \(\mathsf {SWExtCom}\), interacts with \(\mathbb {P}^*\) again, and obtains \(\widehat{\delta }_2\). Then, \(P^*\) computes \(\widetilde{\delta } := \mathsf {Extract}(\widehat{\delta }_1, \widehat{\delta }_2)\) and sends \(\widetilde{\delta }\) to external \(V_{\mathrm {B}}\).
Whenever internal \(\mathbb {P}^*\) aborts, \(P^*\) also aborts.
Before analyzing the success probability of \(P^*\), we first introduce some terminologies regarding the internally emulated interaction between \(\mathbb {P}^*\) and \(\mathbb {V}_{\mathrm {B}}\). Let \(\tau = (h, r_1, c, r_2, \alpha , \widehat{\beta }_1, \gamma , \widehat{\delta }_1)\) be its transcript. Notice that since \(P^*\) emulates \(\mathbb {V}_{\mathrm {B}}\) for internal \(\mathbb {P}^*\) perfectly, we have \(\tau \in \mathbb {L}_{\mathrm {B}}\) with probability at least \(1{\slash }p(n)\).
-
We say that a transcript \(\tau _1\) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-2 is good if under the condition that \(\tau _1\) is a prefix of \(\tau \), the probability that \(\tau \in \mathbb {L}_{\mathrm {B}}\) holds is at least \(1{\slash }2p(n)\).
-
We say that a transcript \(\tau _2\) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-4 is good if (1) a prefix of \(\tau _2\) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-2 is good and (2) under the condition that \(\tau _2\) is a prefix of \(\tau \), the probability that \(\tau \in \mathbb {L}_{\mathrm {B}}\) holds is at least \(1{\slash }4p(n)\).
We then analyze the success probability of \(P^*\) as follows. Let  be the event that a prefix of \(\tau \) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-2 is good, and let
be the event that a prefix of \(\tau \) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-2 is good, and let  be the event that a prefix of \(\tau \) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-4 is good. From an average argument, we have
be the event that a prefix of \(\tau \) up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-4 is good. From an average argument, we have

Hence, we have

Also, from the definition of  , we have
, we have

Hence, from Eqs. (1) and (2), we have

Next, we observe that when the transcript up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-2 is good, \(\mathbb {P}^*\) gives a valid commitment of \(\mathsf {SWExtCom}\) in Stage 3-2 with probability at least \(1{\slash }2p(n)\), and similarly, when the transcript up until the commit stage of \(\mathsf {SWExtCom}\) in Stage 3-4 is good, \(\mathbb {P}^*\) gives a valid commitment of \(\mathsf {SWExtCom}\) in Stage 3-4 with probability at least \(1{\slash }4p(n)\). (This is because when the transcript is in \(\mathbb {L}_{\mathrm {B}}\), the \(\mathsf {SWExtCom}\) commitments in Stage 3-2 and 3-4 are valid.) Hence, under the condition that  , the probability that both of \(\widehat{\beta }_2\) and \(\widehat{\delta }_2\) are valid is at least \(1{\slash }8(p(n))^2\). Also, from the definition of \(\mathbb {L}_{\mathrm {B}}\), both of \(\widehat{\beta }_1\) and \(\widehat{\delta }_1\) are valid when \(\tau \in \mathbb {L}_{\mathrm {B}}\), and furthermore, \(\widehat{\beta }_1\) and \(\widehat{\beta }_2\) (resp, \(\widehat{\delta }_1\) and \(\widehat{\delta }_2\)) are admissible except with negligible probability. Hence, from Lemma 2, for \(\widetilde{\beta } = \mathsf {Extract}(\widehat{\beta }_1, \widehat{\beta }_2)\) and \(\widetilde{\delta } = \mathsf {Extract}(\widehat{\delta }_1, \widehat{\delta }_2)\) we have
, the probability that both of \(\widehat{\beta }_2\) and \(\widehat{\delta }_2\) are valid is at least \(1{\slash }8(p(n))^2\). Also, from the definition of \(\mathbb {L}_{\mathrm {B}}\), both of \(\widehat{\beta }_1\) and \(\widehat{\delta }_1\) are valid when \(\tau \in \mathbb {L}_{\mathrm {B}}\), and furthermore, \(\widehat{\beta }_1\) and \(\widehat{\beta }_2\) (resp, \(\widehat{\delta }_1\) and \(\widehat{\delta }_2\)) are admissible except with negligible probability. Hence, from Lemma 2, for \(\widetilde{\beta } = \mathsf {Extract}(\widehat{\beta }_1, \widehat{\beta }_2)\) and \(\widetilde{\delta } = \mathsf {Extract}(\widehat{\delta }_1, \widehat{\delta }_2)\) we have

Hence, from Eqs. (3) and (4), we have

Notice that from the definition of \(\mathbb {L}_{\mathrm {B}}\), when \(\tau \in \mathbb {L}_{\mathrm {B}}\wedge \widetilde{\beta } = \mathsf {value}(\widehat{\beta }_1) \wedge \widetilde{\delta } = \mathsf {value}(\widehat{\delta }_1)\), it holds that \((\alpha , \widetilde{\beta }, \gamma , \widetilde{\delta })\) is an accepting \(\mathsf {UA}\) proof for \((h, r_1, c, r_2)\in \varLambda \). Hence, we have
which contradicts Lemma 1. \(\square \)
We next note that a non-black-box simulator can simulate the transcript \(\tau \) in such a way that \(\tau \in \mathbb {L}_{\mathrm {B}}\) holds, and the simulator can additionally output a witness for \(\tau \in \mathbb {L}_{\mathrm {B}}\).
Lemma 5
(Simulatability). Let \(\mathbb {L}_{\mathrm {B}}\) be the language defined in Fig. 5. Then, for any \(\textsc {ppt} \) cheating verifier \(\mathbb {V}^*\) against \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \), there exists a \(\textsc {ppt} \) simulator \(\mathcal {S}\) such that the following hold.
-
Let \(\mathcal {S}_1(x, z)\) be the random variable representing the first output of \(\mathcal {S}(x, z)\). Then, the following indistinguishability holds.
$$\begin{aligned} \left\{ \mathsf {view}_{\mathbb {V}^*}\left[ \mathbb {P}_{\mathrm {B}}(1^{n}) \leftrightarrow \mathbb {V}^*(1^{n}, z) \right] \right\} _{n\in \mathbb {N}, z\in \{0,1 \}^{*}} \approx \left\{ \mathcal {S}_1(1^{n}, z) \right\} _{n\in \mathbb {N}, z\in \{0,1 \}^{*}} \end{aligned}$$ -
For any \(n\in \mathbb {N}\) and \(z\in \{0,1 \}^*\), the following holds.
$$\begin{aligned} \Pr \left[ \begin{array}{l} (v, w) \leftarrow \mathcal {S}(1^{n}, z);\\ reconstruct\;transcript\;\tau \;from\;view\; v\;of\;\mathbb {V}^*\end{array} : w \in \mathbf R _{\mathbb {L}_{\mathrm {B}}}(\tau ) \right] \ge 1 - \mathsf {negl}(n) \end{aligned}$$
This lemma can be proven in essentially the same way as the zero-knowledge property of Barak’s non-black-box zero-knowledge protocol. A proof sketch is given in the full version [17].
4.2 Special-Purpose Instance-Dependent Commitment
In our \(\mathrm {LRZK}\) protocol, we use a special-purpose instance-dependent commitment scheme \(\mathsf {GJS}\text {-}\mathsf {Com}\), which is shown in Fig. 6. \(\mathsf {GJS}\text {-}\mathsf {Com}\) is parametrized by two graphs, G and \(G'\), and obtained by modifying Hamiltonicity commitment scheme \(\mathsf {H}\text {-}\mathsf {Com}_{G,r}\) in such a way that the adjacent matrix is committed to by using \(\mathsf {AH}\text {-}\mathsf {Com}_{G',r}\) instead of \(\mathsf {Com}_r\). \(\mathsf {GJS}\text {-}\mathsf {Com}\) inherits many properties from \(\mathsf {H}\text {-}\mathsf {Com}\)—hiding, binding, and equivocality—and additionally, thanks to the adaptive security of \(\mathsf {AH}\text {-}\mathsf {Com}\), it provides adaptive security in the following sense: When \(G\in \mathbf L _{\mathrm {HC}}\) and \(G'\in \mathbf L _{\mathrm {HC}}\), a commitment to 1 can be explained as a valid commitment to 0, and furthermore, even after being explained as a commitment to 0, it can be decommitted to 1 in a consistent way. Details follow.
Lemma 6
(Hiding and Binding). \(\mathsf {GJS}\text {-}\mathsf {Com}\) is computationally hiding. Furthermore, it is statistically binding when \(G\not \in \mathbf L _{\mathrm {HC}}\) and \(G'\not \in \mathbf L _{\mathrm {HC}}\).
Lemma 7
(Equivocality). There exists an algorithm \(\mathsf {GJS}\text {-}\mathsf {EquivToOne}\) that is parametrized by graphs \(G, G'\) and a string \(r\in \{0,1 \}^{3n}\) and satisfies the following: When \(G\in \mathbf L _{\mathrm {HC}}\), on input any \(w\in \mathbf R _{\mathrm {HC}}(G)\) and any c and \(\rho \) such that \(\mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}(0; \rho ) = c\), \(\mathsf {GJS}\text {-}\mathsf {EquivToOne}_{G, G', r}\) outputs a valid decommitment of c to 1.
Proofs of these two lemmas are straightforward. We give the proofs in the full version [17].
Lemma 8
(Adaptive Security). There exists an algorithm \(\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}\) that is parametrized by graphs \(G, G'\) and a string \(r\in \{0,1 \}^{3n}\) and satisfies the following.
-
Correctness. When \(G, G'\in \mathbf L _{\mathrm {HC}}\), on input any \(w\in \mathbf R _{\mathrm {HC}}(G)\) and \(w'\in \mathbf R _{\mathrm {HC}}(G')\) and any c and \(\rho _1\) such that \(\mathsf {GJS}\text {-}\mathsf {Com}_{G,G',r}(1; \rho _1) = c\), \(\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}_{G,G',r}\) outputs \(\rho _0\) such that \(\mathsf {GJS}\text {-}\mathsf {Com}_{G,G',r}(0; \rho _0) = c\).
-
Indistinguishability. For security parameter \(n\in \mathbb {N}\), graphs \(G,G'\in \mathbf L _{\mathrm {HC}}\), witnesses \(w\in \mathbf R _{\mathrm {HC}}(G)\) and \(w'\in \mathbf R _{\mathrm {HC}}(G')\), and string \(r\in \{0,1 \}^{3n}\), consider the following two probabilistic experiments.
-

/* \(\mathtt {commit\;to}\) 0 \(\mathtt {and\;decommit\;it\;to}\) 1 \(\mathtt {using\;equivocality}\) */
-
1.
Compute \(c \leftarrow \mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}(0)\).
Let \(\rho _0\) be the randomness used in \(\mathsf {GJS}\text {-}\mathsf {Com}\).
-
2.
Compute \(d_1 := \mathsf {GJS}\text {-}\mathsf {EquivToOne}_{G, G', r}(c, w, \rho _0)\).
-
3.
Output \((c, \rho _0, d_1)\).
-
1.
-
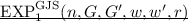
/* \( \mathtt {commit\; \& \;decommit\;to}\) 1 \(\mathtt {and\;explain\;it\;as\;commitment\;to}\) 0 */
-
1.
Compute \(c \leftarrow \mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}(1)\).
Let \(\rho _1\) be the randomness used in \(\mathsf {GJS}\text {-}\mathsf {Com}\).
Compute \(d_1 := \mathsf {GJS}\text {-}\mathsf {Dec}_{G, G', r}(c, 1, \rho )\).
-
2.
Compute \(\rho _0 := \mathsf {GJS}\text {-}\mathsf {ExplainAsZero}_{G, G', r}(c, w, w', \rho _1)\).
-
3.
Output \((c, \rho _0, d_1)\).
-
1.
Let \(\mathsf {EXP}^{\mathrm {GJS}}_b(n, G, G', w, w', r)\) be the random variable representing the output of \(\mathrm {EXP}^{\mathrm {GJS}}_b(n, G, G', w, w', r)\) for each \(b\in \{0,1 \}\). Then, the following two ensembles are computationally indistinguishable.
-
\(\left\{ \mathsf {EXP}^{\mathrm {GJS}}_0(n,G,G',w,w',r) \right\} _{n\in \mathbb {N}, G,G'\in \mathbf L _{\mathrm {HC}}, w\in \mathbf R _{\mathrm {HC}}(G), w'\in \mathbf R _{\mathrm {HC}}(G'), r\in \{0,1 \}^{3n}}\)
-
\(\left\{ \mathsf {EXP}^{\mathrm {GJS}}_1(n,G,G',w,w',r) \right\} _{n\in \mathbb {N}, G,G'\in \mathbf L _{\mathrm {HC}}, w\in \mathbf R _{\mathrm {HC}}(G), w'\in \mathbf R _{\mathrm {HC}}(G'), r\in \{0,1 \}^{3n}}\)
-
Proof
(sketch). \(\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}\) is shown in Fig. 7. A key idea is that given the ability to explain \(\mathsf {AH}\text {-}\mathsf {Com}\) commitments to 0 as \(\mathsf {AH}\text {-}\mathsf {Com}\) commitments to 1, we can explain a \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment to 1 (which is \(\mathsf {AH}\text {-}\mathsf {Com}\) commitments to the adjacent matrix of a cycle graph) as a \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitment to 0 (which is \(\mathsf {AH}\text {-}\mathsf {Com}\) commitments to the adjacent matrix of a Hamiltonian graph G). Intuitively, this is because a cycle graph can be transformed to any Hamiltonian graph by appropriately adding edges (which corresponds to changing some entries of the adjacent matrix from 0 to 1). A formal proof is given in the full version [17]. \(\square \)
5 Our Leakage-Resilient Zero-Knowledge Argument
Theorem 1
Assume the existence of collision-resistant hash function family. Then, there exists a constant-round public-coin leakage-resilient zero-knowledge argument system \(\mathsf {LR}\text {-}\mathsf {ZK}\).
Proof
\(\mathsf {LR}\text {-}\mathsf {ZK}\) is shown in Fig. 8. Since \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) can be constructed from any collision-resistant hash function family, and \(\mathsf {SWExtCom}\) can be constructed from any one-way function (which can be obtained from any collision-resistant hash function family), \(\mathsf {LR}\text {-}\mathsf {ZK}\) can be constructed from any collision-resistant hash function family. Also, by inspection, it can be seen that \(\mathsf {LR}\text {-}\mathsf {ZK}\) is public-coin and has constant number of rounds.
Roughly speaking, the soundness of \(\mathsf {LR}\text {-}\mathsf {ZK}\) can be proven as follows. From the soundness of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \), we have \(\tau \not \in \mathbb {L}_{\mathrm {B}}\) (and hence \(G'\not \in \mathbf L _{\mathrm {HC}}\)) in Stage 1 except with negligible probability. Hence, \(\mathsf {GJS}\text {-}\mathsf {Com}_{G, G'}\) is statistically binding except with negligible probability, and thus we can use essentially the same argument as in the proof of the soundness of Blum’s Hamiltonicity protocol to show that any cheating prover can give valid response in Stage 2-3 of all \(n\) iterations only with negligible probability. The formal proof is given in the full version [17].
In the following, we prove leakage-resilient zero-knowledgeness.
Lemma 9
\(\mathsf {LR}\text {-}\mathsf {ZK}\) is leakage-resilient zero-knowledge.
In the following, we prove this lemma only w.r.t. a simplified version of \(\mathsf {LR}\text {-}\mathsf {ZK}\) in which Stage 2-1, 2-2, and 2-3 are executed only once (instead of executed \(n\) times in parallel). The proof w.r.t. \(\mathsf {LR}\text {-}\mathsf {ZK}\) can be obtained by modifying the following proof in a straight-forward way.
Proof
Without loss of generality, we assume that after receiving each message from the prover, the cheating verifier makes exactly a single leakage query. To see that we indeed do not lose generality, observe that instead of making two queries \(f_1\) and \(f_2\), the cheating verifier can always query a single query f such that, on input witness w and prover’s randomness \(\mathsf {tape}\), it computes the first leakage \(L_1 := f_1(w, \mathsf {tape})\), chooses the second query \(f_2\) adaptively, computes the second leakage \(L_2 := f_2(w, \mathsf {tape})\), and outputs \((L_1, L_2)\).
Description of the Simulator. Given access to leakage oracle \(\mathcal {L}_{w}\) and input (G, z), our simulator \(\mathcal {S}\) simulates the view of cheating verifier \(V^*\) by internally invoking \(V^*(G, z)\) and interacting with it as follows.
Simulating Messages and Leakages in Stage 1. Roughly speaking, \(\mathcal {S}\) simulates the messages in Stage 1 by interacting with \(V^*\) in the same way as the simulator of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) (cf. Lemma 5). To simulate the leakages in Stage 1, \(\mathcal {S}\) uses the fact that Stage 1 of \(\mathsf {LR}\text {-}\mathsf {ZK}\) is public coin w.r.t. the prover and therefore all the randomness that a honest prover generates during Stage 1 is the messages themselves. Specifically, \(\mathcal {S}\) simulates the leakages by considering the messages \(\mathsf {msgs}\) that it has sent to \(V^*\) thus far as the randomness of the prover. An issue is that due to the existence of leakage queries, \(\mathcal {S}\) cannot use the simulator of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) in a modular way. Nonetheless, \(\mathcal {S}\) can still use the technique used in the simulator of \(\langle \mathbb {P}_{\mathrm {B}}, \mathbb {V}_{\mathrm {B}} \rangle \) as long as the length of the leakages is bounded by \(n^2\). (Notice that when the length of leakage exceeds \(n^2\), \(\mathcal {S}\) can simply obtain a Hamiltonian cycle w of G from \(\mathcal {L}_w\).)
Formally, \(\mathcal {S}\) interacts with \(V^*\) as follows.
-
1.
After receiving h and \(r_1\) from \(V^*\), \(\mathcal {S}\) sends \(c\leftarrow \mathsf {Com}_{r_1}(h(V^*))\) to \(V^*\). Let \(\mathsf {rand}\) be the randomness that was used in this step.
Leakage query: When \(V^*\) makes a leakage query f, \(\mathcal {S}\) does the following.
-
Let \(\mathsf {tape}:= c\).
-
If the output length of f is more than \(n^2\), \(\mathcal {S}\) obtains w from \(\mathcal {L}_w\) and returns \(f(w \!\parallel \! \mathsf {tape})\) to \(V^*\).
-
Otherwise, \(\mathcal {S}\) queries \(f(\cdot , \mathsf {tape})\) to \(\mathcal {L}_w\), obtains reply L from \(\mathcal {L}_w\), and forwards L to \(V^*\).
If \(\mathcal {S}\) obtained w, from now on \(\mathcal {S}\) interacts with \(V^*\) in exactly the same way as a honest prover. Otherwise, do the following.
-
-
2.
After receiving \(r_2\) and \(\alpha \) from \(V^*\), \(\mathcal {S}\) computes the second-round \(\mathsf {UA}\) message \(\beta \) by using witness \((V^*, \mathsf {rand}, L)\) and then honestly commits to \(\beta \) by using \(\mathsf {SWExtCom}\). Let \(\widehat{\beta }\) be the commitment and \(d_1\) be the decommitment.
Leakage query: When \(V^*\) makes a leakage query f, \(\mathcal {S}\) sets \(\mathsf {tape}:= \mathsf {msgs}\), queries \(f(\cdot , \mathsf {tape})\) to \(\mathcal {L}_w\), and forwards the reply from \(\mathcal {L}_w\) to \(V^*\), where \(\mathsf {msgs}\) are the messages that \(\mathcal {S}\) has sent to \(V^*\) thus far.
-
3.
After receiving \(\gamma \) from \(V^*\), \(\mathcal {S}\) computes the fourth-round \(\mathsf {UA}\) message \(\delta \) and then honestly commits to \(\delta \) by using \(\mathsf {SWExtCom}\). Let \(\widehat{\delta }\) be the commitment and \(d_2\) be the decommitment.
Leakage query: When \(V^*\) makes a leakage query f, \(\mathcal {S}\) answers it in exactly the same way as above.
Let \(\tau \mathop {=}\limits ^\mathrm{def}(h, r_1, c, r_2, \alpha , \widehat{\beta }, \gamma , \widehat{\delta })\) and \(\bar{w} \mathop {=}\limits ^\mathrm{def}(d_1, d_2, \beta , \delta )\). Since \((V^*, \mathsf {rand}, L)\) is a valid witness for \((h, r_1, c, r_2)\in \varLambda \), we have \(\tau \in \mathbb {L}_{\mathrm {B}}\) and \(\bar{w}\in \mathbf R _{\mathbb {L}_{\mathrm {B}}}(\tau )\). Let \(G'\) and \(w'\) be the graph and its Hamiltonian cycle that are obtained by reducing statement “\(\tau \in \mathbb {L}_{\mathrm {B}}\)” to Hamiltonicity problem through the \(\mathcal {NP}\) reduction.
Simulating Messages Stage 2. If \(\mathcal {S}\) obtained w during Stage 1, it interacts with \(V^*\) in the same way as a honest prover. Otherwise, \(\mathcal {S}\) interacts with \(V^*\) as follows. The idea is that, since \(\mathcal {S}\) know a witness \(w'\) for \(G'\in \mathbf L _{\mathrm {HC}}\), \(\mathcal {S}\) can correctly respond to the challenge for both \(ch=0\) and \(ch=1\) by committing to a random permutation of \(G'\) in the first step.
-
1.
\(\mathcal {S}\) chooses a random permutation \(\pi \) and computes \(H := \pi (G')\). Then, \(\mathcal {S}\) commits to the adjacent matrix \(A = \{a_{i, j} \}_{i,j\in [q']}\) of H by using \(\mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}\). That is, \(\mathcal {S}\) sends \(c_{i,j} \leftarrow \mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}(a_{i,j})\) to \(V^*\) for every \(i,j\in [q']\).
Let \(\{\rho _{i,j} \}_{i,j\in [q']}\) be the randomness used in the \(\mathsf {GJS}\text {-}\mathsf {Com}\) commitments and \(\pi (w')\) be the Hamiltonian cycle in H that is obtained by applying \(\pi \) on Hamiltonian cycle \(w'\) in \(G'\).
-
2.
\(\mathcal {S}\) receives a random bit \(ch\in \{0,1 \}\) from \(V^*\).
-
3.
-
When \({\varvec{ch = 0}}\varvec{,}\) \(\mathcal {S}\) sends \(\pi \) to V and decommits \(c_{i, j}\) to \(a_{i, j}\) honestly for every \(i,j\in [q']\). That is, \(\mathcal {S}\) sends \(d_{i,j} := \mathsf {GJS}\text {-}\mathsf {Dec}_{G, G', r}(c_{i,j}, a_{i,j}, \rho _{i,j})\) to V for every \(i,j\in [q']\).
-
When \({\varvec{ch = 1}}\varvec{,}\) \(\mathcal {S}\) decommits \(c_{i, j}\) to 1 honestly for every i, j such that edge (i, j) is on the Hamiltonian cycle \(\pi (w')\) in H. That is, for every such i and j, \(\mathcal {S}\) sends \(d_{i,j} := \mathsf {GJS}\text {-}\mathsf {Dec}_{G, G', r}(c_{i,j}, a_{i,j}, \rho _{i,j})\) to \(V^*\).
-
Simulating Leakage Queries in Stage 2. When \(V^*\) makes a leakage query f, \(\mathcal {S}\) simulates the leakage as follows. Recall that in Stage 2-1, a honest prover commits to a \(q' \times q'\) zero matrix whereas \(\mathcal {S}\) commits to the adjacent matrix of H. Hence, \(\mathcal {S}\) simulates the leakage by “explaining” commitments \(\{c_{i,j} \}_{i,j\in [q']}\) to \(\{a_{i,j} \}_{i,j\in [q']}\) as commitments to \(\{0 \}\) by using the adaptive security of \(\mathsf {GJS}\text {-}\mathsf {Com}\) and the knowledge of \(w'\). Concretely, \(\mathcal {S}\) does the following.
-
First, for each \(i,j\in [q']\), \(\mathcal {S}\) constructs a function \(F_{i,j}(\cdot )\) such that on input w, it outputs \(\widetilde{\rho }_{i, j}\) such that \(\mathsf {GJS}\text {-}\mathsf {Com}_{G, G', r}(0; \widetilde{\rho }_{i,j}) = c_{i,j}\). Concretely, when \(a_{i,j} = 0\), \(F_{i,j}(\cdot )\) is a function that always outputs \(\rho _{i,j}\), and when \(a_{i,j} = 1\), \(F_{i,j}(\cdot ) \mathop {=}\limits ^\mathrm{def}\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}_{G,G',r}(c_{i,j}, \cdot , w', \rho _{i,j})\).
-
Next, \(\mathcal {S}\) constructs a function \(\widetilde{f}\) such that on input w, it computes \(\mathsf {tape}:= \mathsf {msgs} \!\parallel \! \{F_{i,j}(w) \}_{i,j\in [q']} \) and outputs \(f(w, \mathsf {tape})\).
-
Finally, \(\mathcal {S}\) queries \(\widetilde{f}\) to \(\mathcal {L}_w\) and forwards the reply from \(\mathcal {L}_w\) to \(V^*\).
Amount of Total Leakage. From the construction of \(\mathcal {S}\), it always obtains at most the same amount of leakages as \(V^*\).
Indistinguishability of Views. For any cheating verifier \(V^*\) and any sequence \(\{w_G \}_{G\in \mathbf L _{\mathrm {HC}}}\) such that \(w_G\in \mathbf R _{\mathrm {HC}}(G)\), we show the following indistinguishability.
Toward this end, we consider the following hybrid experiments.
-
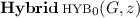 is identical with experiment \(\mathrm {REAL}_{V^*}(G, w, z)\). That is, \(V^*\) interacts with honest P(G, w) and obtains leakage that is computed honestly based on witness w and the prover’s randomness. The outputs of this hybrid is the view of \(V^*\).
is identical with experiment \(\mathrm {REAL}_{V^*}(G, w, z)\). That is, \(V^*\) interacts with honest P(G, w) and obtains leakage that is computed honestly based on witness w and the prover’s randomness. The outputs of this hybrid is the view of \(V^*\). -
 is the same as
is the same as  except for the following.
except for the following.-
– In Stage 1, a honest prover is replaced with the simulator. That is, c is computed by committing to \(h(V^*)\), \(\widehat{\beta }\) is computed by committing to \(\beta \), and \(\widehat{\delta }\) is computed by committing to \(\delta \).
Let \(\tau \) and \(\bar{w}\) be the statement and the witness generated in it. Let \(G'\) and \(w'\) be the graph and its Hamiltonian cycle that are obtained by reducing statement “\(\tau \in \mathbb {L}_{\mathrm {B}}\)” to Hamiltonicity problem through the \(\mathcal {NP}\) reduction.
-
– The leakage queries are answered by considering that the randomness generated by the prover during Stage 1 is equal to the messages sent to \(V^*\) during Stage 1.
-
-
 is the same as
is the same as  except for the following.
except for the following.-
– As in \(\mathcal {S}\), a random permutation \(\pi \) is chosen randomly at the beginning of Stage 2-1. Let \(H \mathop {=}\limits ^\mathrm{def}\pi (G')\), and \(A = \{a_{i,j} \}_{i,j\in [q']}\) be the adjacent matrix of H. Let \(\pi (w')\) be the Hamiltonian cycle in H that is obtained by applying \(\pi \) on Hamiltonian cycle \(w'\) in \(G'\).
We remark that in this hybrid, the prover still commits to a \(q' \times q'\) zero matrix as in
 . Also, the leakage query immediately after Stage 2-1 is answered in exactly the same way as in
. Also, the leakage query immediately after Stage 2-1 is answered in exactly the same way as in 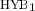 . In particular, when the leakage query is answered, \(\pi \) is not included in the randomness generated by the prover in Stage 2-1.
. In particular, when the leakage query is answered, \(\pi \) is not included in the randomness generated by the prover in Stage 2-1. -
– In Stage 2-3, graph \(H_0\) or \(H_1\) is chosen as follows.
-
When \({\varvec{ch = 0}}\varvec{,}\) \(H_0 := H\).
-
When \({\varvec{ch = 1}}\varvec{,}\) \(H_1\) is the graph that is obtained by removing every edge in H except for the ones on Hamiltonian cycle \(\pi (w')\).
The leakage query immediately after Stage 2-3 is answered in the same way as in
 by considering that \(H_0\) or \(H_1\) was chosen during Stage 2-3 as in
by considering that \(H_0\) or \(H_1\) was chosen during Stage 2-3 as in 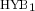 .
. -
-
-
 is the same as
is the same as  except for the following.
except for the following.-
– In Stage 2-1, for every \(i,j\in [q']\), commitment \(c_{i,j}\) is computed by committing to \(a_{i,j}\) (instead of 0), i.e., \(c_{i,j} \leftarrow \mathsf {GJS}\text {-}\mathsf {Com}_{G,G',r}(a_{i,j})\).
-
– In Stage 2-3, for every \(i,j\in [q']\), if commitment \(c_{i,j}\) need to be decommitted, it is decommitted to \(a_{i,j}\) honestly.
-
– When the leakage queries are answered during Stage 2, the randomness \(\rho _{i,j}\) used for computing \(c_{i,j}\) is simulated by \(\widetilde{\rho }_{i,j}\) that is computed by function \(F_{i,j}\) as in \(\mathcal {S}\) for every \(i,j\in [q']\).
-
-
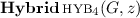 is identical with \(\mathrm {IDEAL}_{\mathcal {S}}(x, w, z)\). That is, \(\mathcal {S}(G, z)\) is executed given access to \(\mathcal {L}_{w}\). The outputs of this hybrid is that of \(\mathcal {S}\).
is identical with \(\mathrm {IDEAL}_{\mathcal {S}}(x, w, z)\). That is, \(\mathcal {S}(G, z)\) is executed given access to \(\mathcal {L}_{w}\). The outputs of this hybrid is that of \(\mathcal {S}\).
Claim 1
The output of  and that of
and that of  are computationally indistinguishable.
are computationally indistinguishable.
Proof
 differs from
differs from  only in that fake commitments of \(\mathsf {Com}\) and \(\mathsf {SWExtCom}\) are replaced with real commitments. Hence, the indistinguishability follows from the security of \(\mathsf {Com}_{\mathrm {pub}}\) and \(C_{\mathrm {pub}}\) (see Sects. 3.4 and 3.8). \(\square \)
only in that fake commitments of \(\mathsf {Com}\) and \(\mathsf {SWExtCom}\) are replaced with real commitments. Hence, the indistinguishability follows from the security of \(\mathsf {Com}_{\mathrm {pub}}\) and \(C_{\mathrm {pub}}\) (see Sects. 3.4 and 3.8). \(\square \)
Claim 2
The output of  and that of
and that of  are computationally indistinguishable.
are computationally indistinguishable.
Proof
This claim can be proven by inspection. Observe that  differs from
differs from  only in the way graph \(H_0\) or \(H_1\) is chosen in Stage 2. When \(ch = 0\), the distribution of \(H_0\) in
only in the way graph \(H_0\) or \(H_1\) is chosen in Stage 2. When \(ch = 0\), the distribution of \(H_0\) in  is the same as that in
is the same as that in  since \(H_0\) is obtained both in
since \(H_0\) is obtained both in  and
and  by applying a random permutation on \(G'\). When \(ch = 1\), the distribution of \(H_1\) in
by applying a random permutation on \(G'\). When \(ch = 1\), the distribution of \(H_1\) in  is the same as that in
is the same as that in  since the Hamiltonian cycle \(w'\) in \(G'\) is mapped to a random q-cycle by \(\pi \). Hence, the output of
since the Hamiltonian cycle \(w'\) in \(G'\) is mapped to a random q-cycle by \(\pi \). Hence, the output of  is identically distributed with that of
is identically distributed with that of  . \(\square \)
. \(\square \)
Claim 3
The output of  and that of
and that of  are computationally indistinguishable.
are computationally indistinguishable.
Proof
Assume for contradiction that for infinitely many \(G\in \mathbf L _{\mathrm {HC}}\), there exists \(z\in \{0,1 \}^*\) such that a distinguisher \(\mathcal {D}\) distinguishes the output of  and that of
and that of  with advantage \(1{\slash }p(n)\) for a polynomial \(p(\cdot )\). Fix any such G and z. To derive a contradiction, we consider the following intermediate hybrids.
with advantage \(1{\slash }p(n)\) for a polynomial \(p(\cdot )\). Fix any such G and z. To derive a contradiction, we consider the following intermediate hybrids.
-
 is identical with
is identical with  .
. -
 , where \(k\in [q'^2]\), is the same as
, where \(k\in [q'^2]\), is the same as  except for the following. Let \(u \mathop {=}\limits ^\mathrm{def}\lfloor (k-1){\slash }q' \rfloor + 1\) and \(v \mathop {=}\limits ^\mathrm{def}k - \lfloor (k-1){\slash }q' \rfloor \cdot q'\).
except for the following. Let \(u \mathop {=}\limits ^\mathrm{def}\lfloor (k-1){\slash }q' \rfloor + 1\) and \(v \mathop {=}\limits ^\mathrm{def}k - \lfloor (k-1){\slash }q' \rfloor \cdot q'\).-
– In Stage 2-1, commitment \(c_{u,v}\) is computed by committing to \(a_{u,v}\) (instead of 0), i.e., \(c_{u,v} \leftarrow \mathsf {GJS}\text {-}\mathsf {Com}_{G,G',r}(a_{u,v})\).
-
– In Stage 2-3, if commitment \(c_{u,v}\) need to be decommitted, it is decommitted to \(a_{u,v}\) honestly.
-
– When the leakage queries are answered during Stage 2, the randomness \(\rho _{u,v}\) used for computing \(c_{u,v}\) is simulated by \(\widetilde{\rho }_{u,v}\) that is computed by function \(F_{u,v}\) as in \(\mathcal {S}\).
-
Clearly,  is identical with
is identical with  . Hence, there exists \(k^*\in [q'^2]\) such that the output of
. Hence, there exists \(k^*\in [q'^2]\) such that the output of  and that of
and that of  can be distinguished with advantage \(1{\slash }q'^2p(n)\). Furthermore, from an average argument, there exists a prefix \(\sigma \) of the execution of
can be distinguished with advantage \(1{\slash }q'^2p(n)\). Furthermore, from an average argument, there exists a prefix \(\sigma \) of the execution of  up until permutation \(\pi \) is chosen in Stage 2-1 (i.e., just before \(\{c_{i,j} \}_{i,j\in [q']}\) is sent to \(V^*\)) such that under the condition that a prefix of the execution is \(\sigma \), the output of
up until permutation \(\pi \) is chosen in Stage 2-1 (i.e., just before \(\{c_{i,j} \}_{i,j\in [q']}\) is sent to \(V^*\)) such that under the condition that a prefix of the execution is \(\sigma \), the output of  and that of
and that of  can be distinguished with advantage \(1{\slash }q'^2p(n)\). Notice that \(\sigma \) determines \(G'\), \(w'\), r, \(\{a_{i,j} \}_{i,j\in [q']}\).
can be distinguished with advantage \(1{\slash }q'^2p(n)\). Notice that \(\sigma \) determines \(G'\), \(w'\), r, \(\{a_{i,j} \}_{i,j\in [q']}\).
We derive a contradiction by showing that we can break the adaptive security of \(\mathsf {GJS}\text {-}\mathsf {Com}\) (Lemma 8). Specifically, we show that \(\mathsf {EXP}^{\mathrm {GJS}}_0(n, G, G', w, w', r)\) and \(\mathsf {EXP}^{\mathrm {GJS}}_1(n, G, G', w, w', r)\) can be distinguished with advantage \(1{\slash }q'^2p(n)\). Toward this end, consider the following distinguisher \(\mathcal {D}'\).
-
Externally, \(\mathcal {D}'\) takes \((c, \rho _0, d_1)\) as well as \((n, G, G', w, w', r)\) as input. \(\mathcal {D}'\) also takes \((\sigma , z)\) as non-uniform input.
-
Internally, \(\mathcal {D}'\) invokes \(V^*\) and simulates
 for \(V^*\) from \(\sigma \) honestly except for the following. Let \(u^* \mathop {=}\limits ^\mathrm{def}\lfloor (k^*-1){\slash }q' \rfloor + 1\) and \(v^* \mathop {=}\limits ^\mathrm{def}k^* - \lfloor (k^*-1){\slash }q' \rfloor \cdot q'\). Notice that it must hold that \(a_{u^*,v^*} = 1\) since
for \(V^*\) from \(\sigma \) honestly except for the following. Let \(u^* \mathop {=}\limits ^\mathrm{def}\lfloor (k^*-1){\slash }q' \rfloor + 1\) and \(v^* \mathop {=}\limits ^\mathrm{def}k^* - \lfloor (k^*-1){\slash }q' \rfloor \cdot q'\). Notice that it must hold that \(a_{u^*,v^*} = 1\) since  is identical with
is identical with  when \(a_{u^*,v^*} = 0\).
when \(a_{u^*,v^*} = 0\).-
In Stage 2-1, commitment \(c_{u^*,v^*}\) is defined by setting \(c_{u^*,v^*} := c\).
-
In Stage 2-3, when commitment \(c_{u^*,v^*}\) is decommitted, it is decommitted to \(a_{u^*,v^*} = 1\) by sending \(d_1\).
-
When the leakage queries are answered during Stage 2, the randomness \(\rho _{u^*,v^*}\) used for computing \(c_{u^*,v^*}\) is simulated by setting \(\widetilde{\rho }_{u^*,v^*} := \rho _0\).
Let \(\mathsf {view}\) be the view of \(V^*\). Then, \(\mathcal {D}'\) outputs \(\mathcal {D}(\mathsf {view})\).
-
When \((c, \rho _0, d_1) \leftarrow \mathsf {EXP}^{\mathrm {GJS}}_0(n, G, G', w, w', r)\) (i.e., when c is a commitment to 0, \(\rho _0\) is the randomness that is used to generate c, and \(d_1\) is a decommitment to 1 that is computed by \(\mathsf {GJS}\text {-}\mathsf {EquivToOne}\)), \(\mathcal {D}'\) emulates  for \(V^*\) perfectly. On the other hand, when \((c, \rho _0, d_1) \leftarrow \mathsf {EXP}^{\mathrm {GJS}}_1(n, G, G', w, w', r)\) (i.e., when c is a commitment to 1, \(\rho _0\) is randomness that is computed by \(\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}\), and \(d_1\) is a decommitment to 1 that is computed honestly), \(\mathcal {D}'\) emulates
for \(V^*\) perfectly. On the other hand, when \((c, \rho _0, d_1) \leftarrow \mathsf {EXP}^{\mathrm {GJS}}_1(n, G, G', w, w', r)\) (i.e., when c is a commitment to 1, \(\rho _0\) is randomness that is computed by \(\mathsf {GJS}\text {-}\mathsf {ExplainAsZero}\), and \(d_1\) is a decommitment to 1 that is computed honestly), \(\mathcal {D}'\) emulates  for \(V^*\) perfectly. Hence, from our assumption, \(\mathcal {D}'\) distinguishes \(\mathsf {EXP}^{\mathrm {GJS}}_0(n, G, G', w, w', r)\) and \(\mathsf {EXP}^{\mathrm {GJS}}_1(n,G,G',w,w',r)\) with advantage \(1{\slash }q'^2p(n)\), and therefore we reach a contradiction. \(\square \)
for \(V^*\) perfectly. Hence, from our assumption, \(\mathcal {D}'\) distinguishes \(\mathsf {EXP}^{\mathrm {GJS}}_0(n, G, G', w, w', r)\) and \(\mathsf {EXP}^{\mathrm {GJS}}_1(n,G,G',w,w',r)\) with advantage \(1{\slash }q'^2p(n)\), and therefore we reach a contradiction. \(\square \)
Claim 4
The output of  and that of
and that of  are computationally indistinguishable.
are computationally indistinguishable.
Proof
In  , the prover interacts with \(V^*\) in exactly the same way as \(\mathcal {S}\). Hence, the claim follows. \(\square \)
, the prover interacts with \(V^*\) in exactly the same way as \(\mathcal {S}\). Hence, the claim follows. \(\square \)
Equation (5) follows from these claims. This concludes the proof of Lemma 9. \(\square \)
This concludes the proof of Theorem 1. \(\square \)
Notes
- 1.
- 2.
- 3.
This is because in the protocol of [12], the verifier commits to the challenge bits of Blum’s Hamiltonicity protocol in advance and hence an cheating prover can easily break the soundness by obtaining the challenge bits via leakage.
- 4.
Actually, there is a coin-tossing protocol that determines the parameter of the equivocal commitment, and td is the trapdoor for biasing the outcome of the coin-tossing.
- 5.
What is actually used here is adaptive security, which guarantees that for each underlying commitment, it is possible to compute randomness \(\mathsf {tape}_0\) and \(\mathsf {tape}_1\) such that \(\mathsf {tape}_b\) explains the commitment as a commitment to b for each \(b\in \{0,1 \}\).
- 6.
This extractability is used only in the proof of soundness. Hence, the proof of zero-knowledgeness works even in the presence of this extractable commitment scheme.
- 7.
- 8.
In the “inner” \(\mathsf {H}\text {-}\mathsf {Com}\), the underlying commitment scheme is \(\mathsf {Com}\) as before.
References
Ananth, P., Goyal, V., Pandey, O.: Interactive proofs under continual memory leakage. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 164–182. Springer, Heidelberg (2014)
Anderson, R., Kuhn, M.: Tamper resistance: a cautionary note. In: WOEC, pp. 1–11 (1996)
Barak, B.: How to go beyond the black-box simulation barrier. In: FOCS, pp. 106–115 (2001)
Barak, B., Goldreich, O.: Universal arguments and their applications. SIAM J. Comput. 38(5), 1661–1694 (2008)
Bitansky, N., Canetti, R., Halevi, S.: Leakage-tolerant interactive protocols. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 266–284. Springer, Heidelberg (2012)
Bitansky, N., Dachman-Soled, D., Lin, H.: Leakage-tolerant computation with input-independent preprocessing. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 146–163. Springer, Heidelberg (2014)
Boyle, E., Garg, S., Jain, A., Kalai, Y.T., Sahai, A.: Secure computation against adaptive auxiliary information. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 316–334. Springer, Heidelberg (2013)
Boyle, E., Goldwasser, S., Jain, A., Kalai, Y.T.: Multiparty computation secure against continual memory leakage. In: STOC, pp. 1235–1254 (2012)
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: STOC, pp. 494–503 (2002)
Damgård, I., Pedersen, T.P., Pfitzmann, B.: Statistical secrecy and multibit commitments. IEEE Trans. Inf. Theor. 44(3), 1143–1151 (1998)
Feige, U., Shamir, A.: Zero knowledge proofs of knowledge in two rounds. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 526–544. Springer, Heidelberg (1990)
Garg, S., Jain, A., Sahai, A.: Leakage-resilient zero knowledge. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 297–315. Springer, Heidelberg (2011)
Goldreich, O., Kahan, A.: How to construct constant-round zero-knowledge proof systems for NP. J. Cryptol. 9(3), 167–190 (1996)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Haitner, I., Nguyen, M., Ong, S.J., Reingold, O., Vadhan, S.P.: Statistically hiding commitments and statistical zero-knowledge arguments from any one-way function. SIAM J. Comput. 39(3), 1153–1218 (2009)
Håstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Kiyoshima, S.: Constant-round leakage-resilient zero-knowledge from collision resistance. Cryptology ePrint Archive, Report 2015/1235 (2015). http://eprint.iacr.org/
Kocher, P.C.: Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 104–113. Springer, Heidelberg (1996)
Lindell, Y., Zarosim, H.: Adaptive zero-knowledge proofs and adaptively secure oblivious transfer. J. Cryptol. 24(4), 761–799 (2011)
Naor, M.: Bit commitment using pseudorandomness. J. Cryptol. 4(2), 151–158 (1991)
Naor, M., Yung, M.: Universal one-way hash functions and their cryptographic applications. In: STOC, pp. 33–43 (1989)
Ostrovsky, R., Persiano, G., Visconti, I.: Impossibility of black-box simulation against leakage attacks. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 130–149. Springer, Heidelberg (2015)
Pandey, O.: Achieving constant round leakage-resilient zero-knowledge. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 146–166. Springer, Heidelberg (2014)
Pass, R., Rosen, A.: Concurrent non-malleable commitments. In: FOCS, pp. 563–572 (2005)
Pass, R., Rosen, A.: New and improved constructions of non-malleable cryptographic protocols. In: STOC, pp. 533–542 (2005)
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009)
Quisquater, J., Samyde, D.: ElectroMagnetic Analysis (EMA): measures and counter-measures for smart cards. In: Attali, I., Jensen, T. (eds.) E-smart 2001. LNCS, vol. 2140, pp. 200–210. Springer, Heidelberg (2001)
Yao, A.C.C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Acknowledgments
The author would like to thank the anonymous reviewers for their helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Kiyoshima, S. (2016). Constant-Round Leakage-Resilient Zero-Knowledge from Collision Resistance. In: Fischlin, M., Coron, JS. (eds) Advances in Cryptology – EUROCRYPT 2016. EUROCRYPT 2016. Lecture Notes in Computer Science(), vol 9666. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49896-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-662-49896-5_4
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49895-8
Online ISBN: 978-3-662-49896-5
eBook Packages: Computer ScienceComputer Science (R0)





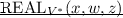











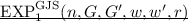


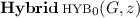 is identical with experiment
is identical with experiment  is the same as
is the same as  except for the following.
except for the following. is the same as
is the same as  except for the following.
except for the following. . Also, the leakage query immediately after Stage 2-1 is answered in exactly the same way as in
. Also, the leakage query immediately after Stage 2-1 is answered in exactly the same way as in 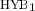 . In particular, when the leakage query is answered,
. In particular, when the leakage query is answered,  by considering that
by considering that 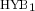 .
. is the same as
is the same as  except for the following.
except for the following.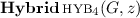 is identical with
is identical with  is identical with
is identical with  .
. , where
, where  except for the following. Let
except for the following. Let  for
for  is identical with
is identical with 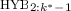 when
when