Abstract
The goal of leakage-resilient cryptography is to construct cryptographic algorithms that are secure even if the devices on which they are implemented leak information to the adversary. One of the main parameters for designing leakage resilient constructions is the leakage rate, i.e., a proportion between the amount of leaked information and the complexity of the computation carried out by the construction. We focus on the so-called circuit compilers, which is an important tool for transforming any cryptographic algorithm (represented as a circuit) into one that is secure against the leakage attack. Our model is the “probing attack” where the adversary learns the values on some (chosen by him) wires of the circuit.
Our results can be summarized as follows. First, we construct circuit compilers with perfect security and leakage rate \(O(1/\log (n))\), where n denotes the security parameter (previously known constructions achieved rate O(1 / n)). Moreover, for the circuits that have only affine gates we obtain a construction with a constant leakage rate. In particular, our techniques can be used to obtain constant-rate leakage-resilient schemes for refreshing an encoded secret (previously known schemes could tolerate leakage rates O(1 / n)).
We also show that our main construction is secure against constant-rate leakage in the random probing leakage model, where the leaking wires are chosen randomly.
M. Andrychowicz and S. Dziembowski—Supported by the WELCOME/2010-4/2 grant founded within the framework of the EU Innovative Economy (National Cohesion Strategy) Operational Programme.
S. Faust—In part supported by the Emmy Noether Program FA 1320/1-1 of the German Research Foundation (DFG).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Side-channel attacks are an omnipresent threat for the security of cryptographic implementations. In contrast to traditional cryptanalytical attacks that attempt to break the mathematical properties of the cryptographic algorithm, a side-channel adversary targets the implementation by, e.g., observing the running time of a device [29] or measuring its power consumption [30]. An important countermeasure against side-channel attacks – in particular against power analysis attacks – is the so-called masking countermeasure. A masking scheme randomizes the intermediate values of the computation in order to conceal sensitive information.
Circuit Compilers and the Probing Model. A formalization of the masking countermeasure has been introduced in the seminal work of Ishai et al. [26] with the concept of leakage resilient circuit compilers. At a high-level, a circuit compiler takes as input a description of a circuit \(\varGamma \) and compiles it into a protected circuit \(\widehat{\varGamma }\) that has the same functionality as \(\varGamma \) but additionally is secure in a well-defined leakage model. One of the most prominent leakage models is the so-called t-threshold probing model of Ishai et al., where the adversary is allowed to observe up to t intermediate values computed by \(\widehat{\varGamma }\). The threshold probing model is widely used in practice to analyze the soundness of a masking scheme against higher order attacks [3–5, 8, 9, 22, 28, 32].
On the Importance of the Leakage Rate. An important parameter to evaluate the security of a masking scheme in the probing model is the value of t. At first sight it may seem that a higher value for t automatically implies a higher level of security as the adversary obtains more knowledge about the internals. To see why such an approach may not always lead to better security imagine two compilers that on an input circuit \(\varGamma \) output the following: the first one produces a circuit \(\varGamma _1\) that has 1 thousand gates and tolerates leakage of 10 wires, while the second one produces a circuit \(\varGamma _2\) of size 1 million gates that tolerates leakage of 100 wires. Which construction provides a higher level of security (even discarding the production costs)? The first one has to be implemented on hardware that leaks at most 1 % of its wires, while the second one requires hardware that leaks at most 0.01 % of the wires! Therefore, the second construction is actually weaker (although it “tolerates more leakage” in absolute terms). The above simple example illustrates that in many case it may be more natural to look at the leakage rate of a given construction (i.e.: the “amount of leakage” divided by the circuit size), than at the “total amount of leakage” itself.Footnote 1
Despite the practical importance of the threshold probing model it is not well-understood how close we can get to the optimal leakage rate of O(1). Indeed, the best known construction is still the circuit compiler of Ishai et al., which remains secure if the adversary learns a O(1 / n)-fraction of the wires in the transformed circuit \(\widehat{\varGamma }\) (for security parameter n). The main contribution of our work is to significantly improve this rate and build new leakage resilient circuit compilers that achieve \(O(1/\log (n))\) leakage rate, and if the circuit \(\varGamma \) is only affine computation we achieve the optimal leakage rate of O(1).
At this point, we want to briefly comment about what we mean by “optimality” of leakage rate and the efficiency of our constructions. First, it shall be clear that we cannot leak everything and, hence, a leakage rate of O(1) is asymptotically optimal. Of course, concretely there can be big differences depending on the hidden constants. Some of our constructions are asymptotically optimal (for affine circuits), but their constants are far from the optimal 1. We believe it is an important question for future work to optimize these constants. We sometimes also talk about optimality in terms of efficiency. In this case, we mean optimality for circuit compilers that compute with encodings and offer information theoretic security. One may get asymptotically better efficiency by using solutions based on FHE.Footnote 2
1.1 The Work of Ishai, Sahai and Wagner
The Threshold Probing Model. Ishai et al. consider two different types of probing adversaries: the first type of adversary is allowed to probe up to t intermediate values in the entire transformed circuit \(\widehat{\varGamma }\). Notice that this implies that for a growing number of gates in the circuit \(\widehat{\varGamma }\) the number of corrupted wires stays the same, and hence the fraction of wires of the circuit that are corrupted decreases. To improve the leakage rate, [26] also considers a significantly stronger adversary where the transformed circuit is structured into so-called regions and the adversary can probe up to t wires in each such region. In the following we call the later model the t-region probing model, which will be the focus of our work. Notice that in the following a region will correspond to a sub-circuit of the transformed circuit, and we will describe below how we structure the transformed circuit into such regions.
The Circuit Compiler of Ishai, Sahai and Wagner (ISW). Ishai et al. consider Boolean circuits \(\varGamma \) with internal state m, which can, e.g., store the secret key of an AES. The basic ingredient of the compiler of Ishai et al. is a leakage resilient encoding scheme \(\text {Enc}(.)\) that encodes the computation in \(\widehat{\varGamma }\). For a fixed number of probes t define the security parameter \(n = O(t)\).Footnote 3 In the transformed circuit each intermediate wire (including the state m) which carries a bit x in the original circuit \(\varGamma \) is represented by n wires \(\text {Enc}(x) = (X_1,\ldots , X_n)\) that are chosen uniformly at random such that \(\sum _i X_i = x\) (the sum here represents Boolean XOR, but the encoding scheme can be defined over an arbitrary finite field). Since the above encoding scheme is a perfect \((n-1)\) out of n secret sharing scheme, it is easy to see that an adversary that learns up to \(t=n-1\) values of the codeword X obtains no information about the secret x.
The main difficulty in developing a secure circuit compiler is the transformation of the gates, i.e., the transformation of the AND and XOR gate in the case of ISW. In \(\widehat{\varGamma }\) gates are represented by so-called gadgets. A gadget, e.g., an AND gadget, takes as input two encodings \(\text {Enc}(a)\) and \(\text {Enc}(b)\) and outputs \(\text {Enc}(c)\) such that \(c=ab\). Of course, besides correctness, the gadgets have to be specifically tailored such that they withstand t-region probing attacks, where for the ISW construction each gadget corresponds to a region.
Security against t-region probing attacks is formalized by a simulation-based argument. That is, any information that can be learnt by an adversary with t-region probing access to \(\widehat{\varGamma }\), can also be obtained by an adversary that has only black-box access to \(\varGamma \). More formally, Ishai et al. show that for any t-region probing adversary \({\mathcal A}\) against \(\widehat{\varGamma }\) there exists a simulator \({\mathsf {Sim}}\) that can simulate answers to all probes with just black-box access to \(\varGamma \). Notice that the simulation is assumed to be perfect, i.e., the distribution that an adversary obtains by applying a t-probing attack against \(\widehat{\varGamma }\) is identical to the distribution that the simulator produces. The ISW compiler achieves security against a probing rate of at least \(\varOmega (1/n)\) of the wires. In fact, it is easy to see that this bound is tight for the construction of ISW due to the way in which transformed AND gadgets are computed.Footnote 4 Hence, to further improve the leakage rate, we need to develop a new circuit transformation.
1.2 Our Contributions
Protecting Affine Circuits. We first consider the seemingly simpler problem of how to protect only affine operations against t-region probing adversaries. We use the simple encoding function described above, i.e., a secret \(x \in {\mathbb F}\) is encoded by a random vector \(X:=(X_1, \ldots , X_n)\) such that \(\sum _i X_i = x\). It is easy to see that the addition of two encoded values and multiplication by a constant can be done efficiently requiring only O(n) operations. Hence, if we consider only a single affine operation, then the adversary may learn up to \(t=O(n)\) wires from such an operation without violating security. Unfortunately, the above does not easily scale for larger circuits. If we allow the adversary to probe in each gadget t wires then the adversary may eventually reveal secret information.
To avoid this problem, the construction of Ishai et al. (and essentially any leakage resilient circuit compiler) uses a so-called \(\mathsf {refresh}\) algorithm that refreshes the encoding by introducing new randomness into X, thereby rendering previous leakage on X useless. The basic idea of the algorithm \(Y \leftarrow \mathsf {refresh}(X)\) is to sample \(Z \leftarrow \text {Enc}(0)\) and compute \(Y =X + Z\). Of course, the main difficulty is to generate Z in a way that is secure against t-region probing adversaries. Ishai et al. propose an implementation of the \(\mathsf {refresh}\) algorithm that requires \(O(n^2)\) operations leading to a leakage rate of \(O(n^{-1})\). Surprisingly, it is non-trivial to improve the complexity of \(\mathsf {refresh}\) to O(n) – in fact, we are not aware of any secure \(\mathsf {refresh}\) algorithm that has the optimal complexity of O(n). The first contribution of our work is to propose the first refreshing algorithm that is perfectly secure against O(n) adversarial chosen probes and has (asymptotically) optimal complexity and randomness usage of O(n). Inspired by the work of Ajtai [1] who studies security against the weaker model of random probing attacks (we will compare our work with the work of Ajtai below), we build our refreshing scheme from expander graphs with constant degree. We emphasize that while our refreshing scheme is similar to the one used by Ajtai, the security proofs differ significantly as we show security in the much stronger model of adaptive probing attacks.
Using the above expander-based scheme for refreshing and combining it with the fact that transformed gadgets for affine operations have complexity O(n), we obtain the first compiler for affine circuits that asymptotically achieves both the optimal complexity of O(n) and remains secure against t-region probing adversaries for \(t = O(n)\), where each region is of size O(n).
Protecting Any Circuit Against Probing Attacks. To extend our result to work for arbitrary circuits, we need to develop a secure transformation for the multiplication operation. Notice that the transformed multiplication gadget of ISW can be broken when the adversary can probe \(\varOmega (n)\) wires.Footnote 5 Our construction borrows techniques from perfectly secure multiparty computation [14] and combines them in a novel way with our transformation for affine circuits from the previous paragraph. We give some more details below.
Instead of using the simple additive encoding scheme that can be used to protect affine computation, we use a linear secret sharing scheme that has the multiplicative property [11]. Informally speaking, a linear secret sharing scheme is multiplicative if from two encodings X, Y, we can compute the product xy just by computing a linear combination of all the values \(Z_i = X_i \cdot Y_i\) and then taking a linear combination of \(Z_i\) to compute xy. An example of a secret sharing scheme that satisfies the above property is Shamir’s scheme. In Shamir’s scheme a secret x from some field \({\mathbb F}\) is encoded into \(n=2t+1\) shares such that any \((t+1)\) shares can be used to reconstruct the secret x but any subset of at most t shares reveals no information about x. In the following we denote a multiplicative sharing of a secret x with threshold t by \([x]_{t}\). Notice that since the above encoding scheme is linear, we can easily implement t-region probing resistant addition and multiplication by a constant. We now turn to the description of the protected multiplication operation.
To simplify exposition, let us first assume that the transformed multiplication has access to a leak-free source of randomness that outputs for a random field element \(r \in {\mathbb F}\) random encodings \([r]_{t}\) and \([r]_{2t}\) for Shamir’s scheme. In this setting, we can use ideas from [14] to carry out the multiplication. On input two vectors \(A = [a]_{t}\) and \(B=[b]_{t}\), first compute \(Z_i = X_i \cdot Y_i\). It is easy to see that \(Z_i\) defines shares that lie on a polynomial of degree 2t with the shared secret being xy, i.e., we have \(Z = [xy]_{2t}\). The good news is that the vector Z already yields an encoding of the desired value xy, however, the threshold for Z has increased by a factor 2. To solve this problem we use the encodings \([r]_{t}\) and \([r]_{2t}\) output by the leak-free component, which enables us to decrease the degree of the encoding \([xy]_{t}\). Similar techniques have been used in the context of circuit compilers by [2, 23], but it is easy to see that their constructions are not secure when \(\omega (1/n)\) of the wires are corrupted.
Assuming that \([r]_{t}\) and \([r]_{2t}\) are produced by the leak-free gates, we can prove that the above construction remains secure in the presence of an adversary that learns up to t wires where \(n= 2t+1\). Of course, for our final transformation we do not want to assume that the computation of \([r]_{t}\) and \([r]_{2t}\) is done in a leak-free way. Instead, we seek for a t-region probing resistant implementation of it. The crucial observation to achieve this goal is the fact that the encodings \([r]_{t}\) and \([r]_{2t}\) can be produced by a circuit solely consisting of affine operations (for Shamir’s scheme Lagrange polynomial interpolation – but this can be easily generalized). Hence, the problem of protecting arbitrary computation, can be reduced to protecting the affine computation against t-region probing attacks! As the later can be solved by the expander-based transformation described above, we obtain a circuit transformation that works for arbitrary circuits \(\varGamma \) and produces protected circuits \(\widehat{\varGamma }\) that remain perfectly secure even if in each region of size O(n) the adversary can learn \(O(n/\log (n))\) wires.
The above description omits several technical challenges – in particular, when combining the protected computation operating with the multiplicative secret sharing with our expander-based transformation for affine computation. One problem that we need to address is how to do a secure “conversion” between different types of encodings. More precisely, when we apply our transformation for affine computation in a naive way, then the resulting circuit outputs “encodings of encodings” (so-called “double-encodings”). That is, each share of \([r]_{t}\) and \([r]_{2t}\) is again encoded using the simple additive sharing used by our affine compiler. Hence, we need to design a t-probing resistant way to “peal-off” the outer layer of the “double-encoding” without revealing the secret value r. To this end, we propose special sub-circuits – so-called tree decoders – that can do the decoding without breaking security in the presence of an adversary that probes a \(O(n/\log (n))\)-fraction of the wires.Footnote 6
On the Relation to the Noisy Leakage Model. An important leakage model that has recently been considered in several works is the noisy leakage model [6, 17, 20, 31]. The noisy leakage model matches with the engineering perspective as it is closely related to what happens in real-world side-channel attacks based on the power consumption [31]. Recently, it was shown by Duc et al. [16] that security in the probing model can be translated into security in the noisy leakage model. In particular, using a Chernoff bound and the reduction of [16] security in the t-region probing model implies security in the noisy leakage model of [31]. As the noise parameter is directly related to the leakage rate, by improving the leakage rate, we also get quantitatively better bounds for the Prouff-Rivain noise parameter. More precisely, by applying [16] we directly achieve security when we set the PR noise parameter to \(O(1/\log (n)|{\mathbb F}|)\) (compared to \(O(1/n|{\mathbb F}|)\)). We also show in Sect. 6 that by a more careful analysis our construction actually achieves security for \(O(1/|{\mathbb F}|)\) noise level. This is done by showing that our construction is actually secure in the p-random probing model when p is a constant. Using the reduction in [16] and instantiating the multiplicative secret sharing with codes based on algebraic geometry [7], we obtain circuit compilers that are secure for the optimal noise rate of O(1).
On Perfect Security and Adaptive Probing Attacks. We notice that all our result in the t-region probing model achieve perfect security, i.e., there is no statistical error in the theorem statements. This is important, as from a practical point of view such a statistical error term often matters as for small values of the security parameter the error term can be significant.
Another advantage that perfect security has (over statistical security, say) is that one can show that security against adaptive and non-adaptive probing attacks is equivalent. Indeed, in our security analysis we typically consider an adversary that chooses together with the input to the circuit a set of probes \({\mathcal P}\) that specifies for which wires the adversary will learn the corresponding value when the circuit is evaluated. While the adversary can choose a different set of probes \({\mathcal P}\) before each execution of the circuit, most of our analysis does not explicitly allow the adversary to adaptively choose the position of the probes within one execution (i.e., the adversary cannot observe the value of some wire and then depending on the value on that wire decide which wire to probe next). Since all our constructions achieve perfect security, we can apply results from [10] to get security even against fully adaptive probing adversaries.
On the Efficiency of Our Construction. Our basic construction blows up the size of the circuit by a factor of \(O(n^3)\). In contrast the construction of Ishai et al. achieves better efficiency and only increases the size of the circuit by a factor of \(O(n^2)\). We note that the efficiency of our construction can most likely be improved by a linear factor by using packed secret sharing as the multiplicative encoding scheme (in a similar way as recently done in [2, 23]), hence asymptotically achieving the same efficiency as the construction of Ishai et al. We omit the details in this extended abstract.
1.3 Comparison to Other Related Work
Due to space limitations we only compare with the most relevant literature on circuit compilers. Notice also that our focus is not on protecting against active attacks – so-called fault attacks [12, 19, 25], and hence, we omit a detailed comparison.
The Work of Ishai et al. [26]. Besides the main construction that was already outlined above, Ishai et al. propose a second transformation that achieves improved leakage rate with statistical security (i.e., with a small error probability a probing adversary will break security). In particular, from Theorem 3 of [26] one gets statistical security against \(t := O(n)\) probes with a circuit of size \(s\cdot {O}(n\log (n)) \cdot \mathsf {poly}(k)\), where k is the statistical security parameter and s the size of the initial circuit \(\varGamma \). The above result can be transformed to the t-region probing model considered in our work. In this case, one obtains gadgets of size \(n(\log n) \mathsf {poly}(k)\). Since each region is represented by a gadget this yields asymptotically a leakage rate of \(O(1/\log n)\), which is as in our paper. There are, however, several important differences:
-
1.
While [26] achieve statistical security, we obtain perfect security. Perfect security is important as it gives full adaptivity for free.
-
2.
The “constant” in \(O(1/\log n)\) depends on the statistical security parameter, i.e., it is \(\mathsf {poly}(k)\).
-
3.
The results from [26] do not easily generalize to the noisy leakage model. The reason for this comes from the statistical security loss \(\mathsf {poly}(k)\) that is hidden in the O(.) notation.
-
4.
Compared to our main construction that has complexity blow-up \(O(n^3)\) per multiplication, [26] obtains asymptotically better efficiency of \(O(n\log (n))\). We notice, however, that we can trivially improve efficiency of our construction to \(O(n^2\log (n))\), and further efficiency improvements are probably possible using the packed secret sharing.
The Work of Ajtai [1]. At STOC’11 Ajtai proposed a construction that achieves constant rate in the so-called p-random probing model. Ajtai’s construction achieves statistical security for “sufficiently” large n and “sufficiently” small constant p, and hence in total a constant fraction of the wires is corrupted. While similar to Ajtai, we use expander graphs to refresh additive encodings, our construction for the transformed multiplication follows a different path. In particular, it is not clear if Ajtai’s involved construction for the multiplication operation can be proven secure in the much stronger t-region probing model. Besides the fact that we prove security in the strictly stronger adversarial model, where the adversary can control which wires he wants to corrupt, our construction also improves the efficiency of Ajtai’s construction by a factor \(O(n\log (n))\) and our security proof is significantly simpler. Hence, one contribution of our work is to simplify and generalize the important work of Ajtai [1].
The Use of Shamir’s Secret Sharing in Context of Leakage-Resilient Compliers. Shamir’s secret sharing was used in this context before [9, 22], however what is achieved there is the leakage rate of O(1 / n). Let us stress that the combination of Shamir secret sharing and the expander-based circuit compiler for affine computation was not known before and can be interesting on its own (before it was not known how to get the O(n) overhead and constant fraction rate even for affine computation).
Circuit Compilers in Other Leakage Models. Various other works [13, 18, 21, 27] build circuit compilers in leakage models that are different from the threshold probing model. We notice that all these works achieve security with leakage rate O(1 / n) or worse. The work of [13] also gives a nice overview of compilers for the bounded independent leakage model (which is more general than the probing model).
2 Definitions
For two field elements \(a,b \in {\mathbb F}\), addition and multiplication in \({\mathbb F}\) are denoted by \(a + b\) and ab. For two vectors \(A,B \in {\mathbb F}^n\), \(A + B\) is the vector-wise addition in \({\mathbb F}\). For a constant \(c \in {\mathbb F}\), we denote by \(cA = (cA_1, \ldots , cA_n)\), i.e., component-wise multiplication with the constant c. Let \([n] =\{1,\ldots ,n\}\) and \([a,b]=\{a,\ldots ,b\}\). If \(S \subseteq [n]\) and \(X \in {\mathbb F}^n\) then \(X_S = \{X_i\}_{i \in S}\). We write \(M \in {\mathbb F}^{r \times c}\) for a matrix \(\{m_{i,j}\}_{i \in [r]}^{j \in [c]}\) with r rows and c columns. For distinct elements \(z_1, \ldots , z_r \in {\mathbb F}\) we use \(\mathsf {Van}^{r \times c}(z_1, \ldots , z_r)\) to denote the Vandermonde matrix \(\{z_{i}^j\}_{i \in [r]}^{j \in [c]}\).
2.1 Leakage Resilient Encoding Schemes
An important building block to construct a circuit with resilience to leakage is a leakage resilient encoding scheme [15]. An encoding scheme \(\varPi = (\mathsf {Enc},\mathsf {Dec})\) consists of two algorithms. The probabilistic \(\mathsf {Enc}\) algorithm takes as input some secret \(x \in {\mathbb F}\) for a field \({\mathbb F}\) and produces a codeword \(X = (X_1, \ldots , X_n) \in {\mathbb F}^n\), where \(X_i\) are called the shares of the encoding. The deterministic decoding function \(\mathsf {Dec}\) takes as input a codeword and outputs the encoded message. A coding scheme satisfies the correctness property if for any \(x \in {\mathbb F}\) we have \(\Pr [\mathsf {Dec}(\mathsf {Enc}(x))) = x] = 1\). Moreover, we want that the encoding scheme is secure against t-probing attacks. An encoding scheme is t-probing secure if for any \(x,x' \in {\mathbb F}\) the adversary cannot distinguish t shares of \(\mathsf {Enc}(x)\), from t shares of \(\mathsf {Enc}(x')\). In this paper we will be interested in two different probing resilient encoding schemes.
Additive Encoding Schemes. The most simple encoding scheme is to encode a secret element \(x \in {\mathbb F}\) by a vector X sampled uniformly at random from \({\mathbb F}^n\) such that \(\sum _i X_i = x\). Formally, we define the additive encoding scheme  as:
as:
-
\(\mathsf {EncAE}: {\mathbb F}\rightarrow {\mathbb F}^n\): On input \(x \in {\mathbb F}\) choose \(X_1,\ldots , X_{n-1}\) uniformly at random and compute \(X_n = x - X_1 - \ldots - X_{n-1}\). Output \(X = (X_1, \ldots , X_n)\).
-
\(\mathsf {DecAE}: {\mathbb F}^n \rightarrow {\mathbb F}\) works as follows: On input a vector \(X \in {\mathbb F}^n\) output \(x = \sum _i X_i\).
It is easy to see that any adversary that learns up to \(n-1\) shares of X has no knowledge about the secret x.
Encoding Based on Multiplicative Secret Sharing. Additionally to  which will mainly be used in Sect. 4 to protect affine computation against t-region probing attacks, we need an additional code for protecting arbitrary circuits. In particular, we need a linear secret sharing scheme that additionally satisfies the multiplicative property [11]. Informally speaking, a linear secret sharing scheme is multiplicative if from two encodings X, Y, we can compute the product xy just by computing a linear combination of all the values \(Z_i = X_i Y_i\). We formally define the encoding scheme
which will mainly be used in Sect. 4 to protect affine computation against t-region probing attacks, we need an additional code for protecting arbitrary circuits. In particular, we need a linear secret sharing scheme that additionally satisfies the multiplicative property [11]. Informally speaking, a linear secret sharing scheme is multiplicative if from two encodings X, Y, we can compute the product xy just by computing a linear combination of all the values \(Z_i = X_i Y_i\). We formally define the encoding scheme  with \(n=2t+1\) and M being the generator matrix of the linear code (representing the secret sharing scheme) as follows:
with \(n=2t+1\) and M being the generator matrix of the linear code (representing the secret sharing scheme) as follows:
-
\(\mathsf {EncMSS}: {\mathbb F}\rightarrow {\mathbb F}^n\): On input \(x \in {\mathbb F}\) choose uniformly at random \((a_1, \ldots , a_t) \leftarrow {\mathbb F}^t\) and compute \(X = (x_1, \ldots ,x_n) = M \cdot (x, a_1, \ldots , a_t)\). We will often denote encodings of \(x \in {\mathbb F}\) using
 with \([x]_{t}\).
with \([x]_{t}\). -
\(\mathsf {DecMSS}: {\mathbb F}^n \rightarrow {\mathbb F}\): On input \(X \in {\mathbb F}^n\) compute \(X \cdot M^{-1}\in {\mathbb F}^{t+1}\), where the first element represents the recovered secret.
We require that  is multiplicative meaning that there exists a n-elements vector \(R \in {\mathbb F}^n\) such that \(\sum _i R_i X_i Y_i\), where all operations are in \({\mathbb F}\).Footnote 7 If two encodings \([x]_{t}\) and \([y]_{t}\) are multiplied then we obtain \([xy]_{2t}\), where the decoding now requires a slightly adjusted generator matrix \(\tilde{M}\).
is multiplicative meaning that there exists a n-elements vector \(R \in {\mathbb F}^n\) such that \(\sum _i R_i X_i Y_i\), where all operations are in \({\mathbb F}\).Footnote 7 If two encodings \([x]_{t}\) and \([y]_{t}\) are multiplied then we obtain \([xy]_{2t}\), where the decoding now requires a slightly adjusted generator matrix \(\tilde{M}\).
To simplify exposition, for most of this paper the reader may think of the code as the standard code representing Shamir’s secret sharing and as M of the Vandermonde matrix \(\mathsf {Van}^{n \times (t+1)}( z_1, \ldots , z_n)\) for distinct elements \(z_i\). Using alternative codes, e.g., packed secret sharing schemes or codes based on algebraic geometry, we can improve the efficiency and the tolerated leakage rate of our construction in the case of random probing from Boolean circuits (we discuss this briefly in Sect. 7). It is easy to see that the encoding scheme  based on Shamir’s scheme is secure against any t-probing adversary, when \(n=2t+1\). To simplify notation we omit the parameters \({\mathbb F}\) and M and simply denote this scheme
based on Shamir’s scheme is secure against any t-probing adversary, when \(n=2t+1\). To simplify notation we omit the parameters \({\mathbb F}\) and M and simply denote this scheme  .
.
2.2 Circuit Transformations
We recall the formalization of circuit transformation of [20, 26]. A circuit transformation \(\mathsf {TR}\) takes as input a security parameter n, a circuit \(\varGamma \), and an initial state \(m_0\) and produces a new circuit \(\widehat{\varGamma }\) and a new initial state \(\widehat{M}_0\).
The Original Circuit \(\varGamma \) . We assume that the original circuit \(\varGamma \) carries values from an (arbitrary) finite field \({\mathbb F}\) on its wires and is composed of the following gates (in addition to the memory gates which will be discussed later):
-
\(+, -\), and \(*\), which compute, respectively, the sum, difference, and product in \({\mathbb F}\), of their two inputs; moreover, for every \(\alpha \in {\mathbb F}\), the constant gate \(\mathsf {Const}_\alpha \), which has no inputs and simply outputs \(\alpha \).
-
the “coin flip” gate \(\mathsf {Rand}\), which has no inputs and produces a uniformly random independently chosen element of \({\mathbb F}\).
Fan-out in \(\varGamma \) is handled by a special \(\mathsf {Copy}\) gate that takes as input a single value and outputs two copies. Circuits that only contain the above types of gates are called stateless.
Stateful Circuits. In addition to the gates described above, stateful circuits also contain memory gates, each of which has a single incoming and a single outgoing edge. Memory gates maintain state between the consecutive executions of the circuit. At any execution of the circuit (called a round or a cycle), a memory gate sends its current state down its outgoing edge and updates it according to the value of its incoming edge. Let \(m_i\) be the state of all memory gates of the circuit after the i-th round and \(m_0\) be the initial state of the circuit. During the i-th round the circuit is run in the state \(m_{i-1}\) on the input \(x_i\) and the execution results in the output \(y_i\) and the new state \(m_i\). The above execution will be denoted as \((y_i,m_i) \leftarrow \varGamma [m_{i-1}](x_i)\) for the circuit \(\varGamma \). For instance, the state \(m_0\) of an AES circuit may be its secret key.
The Transformed Circuit \(\widehat{\varGamma }\) . Our circuit transformation \(\mathsf {TR}\) is encoding-based, i.e., it uses as a main building block an encoding scheme that is resilient to t-probing adversaries. \(\mathsf {TR}\) takes as input \((C,m_0)\) and outputs a protected state \(\widehat{M}_0\) and the description of the protected circuit \(\widehat{\varGamma }\). As in earlier work the transformation of the initial state \(m_0\) is easy: instead of storing \(m_0\) we store an encoding of \(m_0\) using a leakage resilient encoding described in the previous section. We denote the transformed state by \(\widehat{M}_0\). The transformation of the gates in \(\varGamma \) works gate-by-gate: each gate in the original circuit \(\varGamma \) is represented by a sub-circuit – a so-called gadget – that carries out the same computation as the corresponding gate in \(\varGamma \) in encoded form. Notice that the transformed circuit also uses special sub-circuits to encode the input \(x_i\) and decode the output of the circuit. As in previous works [20] we deal with this situation with so-called \(\mathsf {Decoder}\) and \(\mathsf {Encoder}\) gates. These gadgets are simple and just execute the underlying decoding, respectively, encoding function of the underlying leakage resilient encoding scheme.
2.3 Probing Attacks Against Circuits
As discussed in the introduction, we are interested in security against so-called t-region probing adversaries, i.e., adversaries that learn up to t wires in a region of a transformed circuit \(\widehat{\varGamma }\). Typically, a region is a sub-circuit of size O(n) (this is the same in the case of the work of [26]) of the transformed circuit, where in most cases in our transformation a region corresponds naturally to a transformed gadget. We will call a set of probes \({\mathcal P}\) t-region admissible if \({\mathcal P}\) contains at most t probes for each region of the transformed circuit.
Security against a t-region probing adversary is formalized by a simulation-based argument and given in Definition 1. To this end, we first define a real and ideal security game shown in Fig. 1. In the following, we use \(\mathcal {W}_{\widehat{\varGamma }}(X|Y)\) to denote the wire assignment of \(\widehat{\varGamma }\) when run on inputs \(X=(x_i,\widehat{M}_{i-1})\) conditioned that the output is \(Y = (y_i,\widehat{M}_{i})\). The set \({\mathcal P}_i\) denotes the set of wires that the adversary wants to probe in the i-th clock cycle and \({\mathcal P}_i(\mathcal {W}_{\widehat{\varGamma }}(X|Y))\) the leakage during the i-th clock cycle.
Definition 1
(Security of Circuit Transformation). Recall that n is the security parameter. A circuit transformation \(\mathsf {TR}\) is (perfectly) t-region probing secure if for any t-region probing adversary \({\mathcal A}\) there exists a PPT simulator \({\mathsf {Sim}}\) such that for any (stateful) circuit \(\varGamma \) with initial state \(m_0\) the distributions \(\mathsf {Real}_{\mathsf {TR}}({\mathcal A},n,\varGamma ,m_0)\) and \(\mathsf {Ideal}_{\mathsf {TR}}({\mathsf {Sim}}, {\mathcal A},n,\varGamma , m_0)\) are identical, where the probabilities are taken over all the coin tosses.
Leakage from Stateless Circuits. In spirit of earlier works on leakage resilient circuit compilers [20, 26] the main difficulty for proving that a compiler satisfies Definition 1 is to show that leakage from stateless transformed circuits can be simulated with probing access to just its encoded inputs and outputs. In the following we will focus on proving such a simulation property for stateless circuits and only provide a high-level discussion how this property can be extended to prove that the circuit transformation is secure according to Definition 1.
We adapt the notion of reconstructability from Faust et al. [20] to the probing setting with perfect security. To this end we define a leakage oracle \(\varOmega (X^{(1)}, X^{(2)}, \ldots )\) for some sequence of encodings \((X^{(1)}, X^{(2)}, \ldots )\). The oracle can be queried on (i, j), and returns the value \(X^{(i)}_j\), i.e., the j-th position of the i-th encoding. We will use the notation \({\mathsf {Sim}}^{\varOmega (X^{(1)}, X^{(2)}, \ldots )}\) to denote the run of the simulator \({\mathsf {Sim}}\) with the access to the oracle \(\varOmega (X^{(1)}, X^{(2)}, \ldots )\). We call the simulator q-bounded if for each of the input encodings given to the oracle he queries at most for q different elements of the encoding.
Definition 2
(( t , q )-region reconstructible). Let \(\widehat{\varGamma }\) be a (transformed) stateless circuit with \(\varsigma \) input encodings and producing \(\tau \) output encodings. We say that a pair of strings (X, Y) is plausible for \(\widehat{\varGamma }\) if \(\widehat{\varGamma }\) might output \(Y = (Y^{(1)}, \ldots , Y^{(\tau )})\) on input \(X = (X^{(1)}, \ldots , X^{(\varsigma )})\), i.e., if \(\Pr [\widehat{\varGamma }(X)=Y]>0\). We say that \(\widehat{\varGamma }\) is (t, q)-region reconstructible, if for any t-region admissible set of probes \({\mathcal P}\), there exists q-bounded simulator \({\mathsf {Sim}}_{\widehat{\varGamma }}\) such that for any plausible (X, Y), the following two distributions are identical: \({\mathcal P}(\mathcal {W}_{\widehat{\varGamma }}(X|Y))\) and \({\mathsf {Sim}}_{\widehat{\varGamma }}^{\varOmega (X,Y)}({\mathcal P})\).
To better understand the above definition, consider the transformed multiplication gadget. The multiplication gadget takes as input two encoded inputs A, B and produces an encoding C such that \(\mathsf {Dec}(C) = \mathsf {Dec}(A) \cdot \mathsf {Dec}(B)\). If the multiplication gadget is (t, q)-region reconstructible, then we need to show that for any t-region admissible set of probes \({\mathcal P}\) and any plausible inputs/outputs ((A, B), C) there exists a q-bounded simulator \({\mathsf {Sim}}\) such that the following holds: \( {\mathcal P}(\mathcal {W}_{\widehat{\varGamma }}((A,B)|C)) \equiv {\mathsf {Sim}}_{\widehat{\varGamma }}^{\varOmega (A,B,C)}({\mathcal P}). \)
In addition to the region-reconstructible property we need that gadgets are re-randomizing [20]. Informally, this means that the output encoding of a gadget is independent from the input encodings, except that it encodes the correct result. Before we describe our new circuit compiler we present in the next section our new refreshing scheme that achieves optimal parameters both in terms of complexity and leakage rate.
3 Leakage Resilient Refreshing from Expander Graphs
A fundamental building block of any leakage resilient circuit compiler is a leakage resilient refreshing scheme. Informally, a refreshing scheme updates the encoding of a secret value such that continuous/repeated leakage from the execution of the \(\mathsf {refresh}\) procedure does not reveal the encoded secret. More precisely, for a secret \(x \in {\mathbb F}\) let \(X \leftarrow \mathsf {Enc}(x)\) be an encoding of x. A refreshing scheme \(\mathsf {refresh}\) is a randomized algorithm that takes as input X and outputs \(Y \leftarrow \mathsf {refresh}(X)\) such that Y is a fresh encoding of x. Informally, a refreshing scheme \(\mathsf {refresh}\) is said to be secure if even given continuous probing leakage from the refreshing procedure the adversary cannot distinguish the leakage from an encoding of any two secrets \(x,x' \in {\mathbb F}\).
The refreshing procedure of [26] is described by a circuit of size \(\varTheta (n^2)\) which uses \(\varTheta (n^2)\) fresh random values per \(\mathsf {refresh}\) execution and achieves security against a t-probing adversary when \(n=2t+1\). While it is easy to construct refreshing schemes that achieve security against a O(1 / n) fraction of probes per execution, it appears to be much harder to construct a refreshing scheme that achieves the optimal size of \(\varTheta (n)\) and requires only \(\varTheta (n)\) random field elements while tolerating \(t=\varOmega (n)\) probes. This is quite surprising as various candidate schemes look secure at first sight.
As outlined in the introduction the main ingredient of our refreshing scheme (and essentially of most leakage resilient refreshing schemes) is a method to sample form \(\mathsf {EncAE}(0)\). Given a “leakage resilient way” to sample \(R\leftarrow \mathsf {EncAE}(0)\) we can implement a refreshing algorithm in a simple way: to refresh \(X^{(i-1)}\) we compute \(X^{(i)} = X^{(i-1)} + R\), where R is sampled from \(\mathsf {EncAE}(0)\). Our construction to sample from \(\mathsf {EncAE}(0)\) uses a undirected expander graph \({\mathcal G}= (V,E)\), with \(V = \{1,\ldots ,n\}\) (see, e.g., [24] for an excellent exposition). Informally speaking expander graphs are sparse graphs with strong connectivity properties. Let \(\mathcal {G}=(V,E)\) be an undirected graph with V being the set of vertices and E being a set of edges (hence E is a multiset). Assume \({\mathcal G}\) can have self-loops and parallel edges. We define the edge expansion of the graph as: \( \min _{S \subset V: |S| \le |V|/2} \frac{|\partial (S)|}{|S|}, \) where \(\partial (S)\) denotes the edge boundary of S in \({\mathcal G}\), i.e., the set of edges with exactly one endpoint in S. We say that an undirected d-regular graph \({\mathcal G}\) is an (d, h)-expander if \(d > 0\) and its edge expansion is at least h.
To describe our construction we will write the edges of \({\mathcal G}\) as ordered pairs (i, j) where always \(i \le j\). Given such a \({\mathcal G}\) one can construct an arithmetic circuit \(\mathsf {RefSamp}_{\mathcal {G}}(1^n)\) (over some additive field \({\mathbb F}\)) that produces random additive encodings \((X_1,\ldots ,X_n)\) of zero. This is done as follows. The circuit \(\mathsf {RefSamp}_{\mathcal {G}}(1^n)\) consists of |E| coin flip gates \(\mathsf {Rand}\) — to each \(e \in E\) we associate one of them. Let \(r_e\) denote the output of each \(\mathsf {Rand}_e\). To compute the encoding \((X_1,\ldots ,X_n)\) we start with each \(X_i := 0\) and for every edge \((i,j) \in E\) we add \(r_e\) to it, and for every edge \((j,i) \in E\) we subtract \(r_e\) from it. In other words each \(X_i\) is defined as follows:
The gate-level implementation of the sum computations in (1) is pretty straightforward: we attach a \(\mathsf {Copy}\) gate to each \(\mathsf {Rand}_e\) gate. Let \(v_e\) and \(w_e\) be the output wires of this gate. Then we sum and subtract the appropriate \(v_e\)’s and \(w_e\)’s in order to compute the sums in (1). It is easy to see that every \(r_{(i,j)}\) is counted twice in the sum \(X_1 + \ldots + X_n\): once with a “plus” sign (for the vertex i), and once with a “minus” sign (for the vertex j). Therefore \((X_1,\ldots ,X_n)\) is an additive encoding of zero.
3.1 Reconstructibility of \(\mathsf {RefSamp}_{\mathcal {G}}\)
In this section we show that the circuit \(\mathsf {RefSamp}_{\mathcal {G}}\) is (t, q)-region reconstructible for an appropriate choice of t and q. To this end, we start by giving some useful properties about the connectivity of expander graphs and the circuit \(\mathsf {RefSamp}_{\mathcal {G}}\). Recall that a connected component of a graph is a subgraph in which any two vertices are connected to each other by a path, and which is connected to no additional vertices. It will be useful to analyze the properties of expanders and their connected components when some number T of their edges is removed (for some parameter T). Call a set of vertices \(S \subset V\) small if \(|S| \le T/h\), call it medium if \(T/h < |S| < n - T/h\), and call it large otherwise. We can then show the following simple lemma about the sizes of connected components when T vertices are removed from the expander graph. We can then show the following simple lemma about the sizes of connected components when T vertices are removed from the expander graph.
Lemma 1
Suppose \(T < nh/3\) and \({\mathcal G}\) is an (d, h)-expander. Let \({\mathcal G}'\) be an arbitrary graph that resulted from removing up to T edges from \({\mathcal G}\). Then \({\mathcal G}'\) contains exactly one large connected component.
Proof
We first prove that \({\mathcal G}'\) contains no medium components. We actually show something slightly stronger, namely, that for every medium subset of vertices S there exists an edge in \({\mathcal G}'\) between S and \(V \setminus S\). Take such a medium S and consider two cases. First, assume that \(S \le n/2\). From the definition of edge expansion we get that the number x of edges between S and \(V \setminus S\) in the original graph \({\mathcal G}\) is equal at least \(h \cdot |S|\). Since we assumed that S is medium, thus \(|S| > T/h\), and hence \(x > T\). It is also easy to see that if \(|S| > n/2\), then we can use a symmetric reasoning, as \(|S| < n - T/h\) implies that \(|V \setminus S| > T/h\). Hence, also in this case we get that \(x \ge h \cdot |V \setminus S| > T\). In other words: that there are more than T edges between S and \(V \setminus S\) in \({\mathcal G}\). Thus, even if we remove at most T edges from \({\mathcal G}\) there is still one edge remaining. Hence there must be an edge between S and \(V \setminus S\) in \({\mathcal G}'\).
Therefore \({\mathcal G}'\) cannot have medium connected components, and hence each connected component has to be either small or large. Recall that we defined a large subgraph to have more than \(n-T/h\) vertices. Since we assumed that \(T < nh/3\), which implies that \(T/h < n/3\), thus a large connected component must have more than 2n / 3 vertices, which means that there can be at most one such a component (as obviously two connected components cannot overlap). To finish the proof we need to show that there is at least one large component. For the sake of contradiction suppose there is no large connected component. Hence, all the connected components need to be small. Let \(V_1,\ldots ,V_m \subset V\) be these small components. Obviously \(\left| V_1 \cup \cdots \cup V_m\right| = n\). Since each \(V_i\) is such that \(|V_i| \le T/h < n/3\), thus there has to exists j such that \(n/3 < \left| V_1 \cup \cdots \cup V_j\right| < 2n/3\). Hence \(V_1 \cup \cdots \cup V_j\) is a medium set. Therefore, from what we have shown at the beginning of this proof, there has to exist an edge in \({\mathcal G}'\) connecting this union with a vertex outside of it. Hence at least one of the sets \(V_1,\ldots ,V_j\) cannot be a connected component. This yields a contradiction. \(\square \)
We next give a lemma that states that after removing edges from the expander graph, the circuit induced by the remaining connected component results into a random additive encoding of a fixed constant value. More technically, we have:
Lemma 2
Suppose \({\mathcal G}^* = (V^*,E^*)\) is a connected subgraph of \({\mathcal G}\), where \({\mathcal G}\) is as in Lemma 1. Let \((X_1,\ldots ,X_n) \leftarrow \mathsf {RefSamp}_{{\mathcal G}}(1^n)\) and let \(v_1 \le \cdots \le v_{m}\) be the elements of \(V^*\). Consider an adversary \({\mathcal A}\) that learns all \(r_e\)’s corresponding to \({\mathcal G}\)’s edges that are not in \({\mathcal G}^*\). Note that in particular he knows \(X_{v}\) for every \(v \not \in V^*\) and can compute \(C = \sum _{v \not \in V^*} X_{v}\). Then, from \({\mathcal A}\)’s point of view \((X_{v_1},\ldots ,X_{v_m})\) is distributed uniformly over the set \(U^{-C}_m := \{(x_{v_1},\ldots ,x_{v_m}): x_{v_1} + \cdots +x_{v_m} = -C \}\).
Before we give a proof of Lemma 2 let us first show that the expander based-construction indeed outputs random encodings of 0. To this end, we need the following auxiliary lemma.
Lemma 3
Let \({\mathcal G}^* = (V^*,E^*)\) be a graph as above except that the set of vertices is a subset of \(\{1,\ldots ,n\}\). Let \(v_1 \le \cdots \le v_{m}\) be the elements of \(V^*\). Suppose \({\mathcal G}^*\) is connected. Then the variable \((Y_{v_1},\ldots ,Y_{v_m}) \leftarrow \mathsf {RefSamp}_{{\mathcal G}^*}(1^n)\) is distributed uniformly over the set \(U_m^0 := \{(y_{v_1},\ldots ,y_{v_m}) \in {\mathbb F}^m: y_{v_1} + \ldots +y_{v_m} = 0\}\).
This fact will be useful, since if \({\mathcal G}'\) results from removing some edges from an expander, then (by Lemma 1) it is guaranteed to contain a large connected component \({\mathcal G}^*\), and hence the variables \(Y_{v_1},\ldots ,Y_{v_m}\) obtained by “summing” the \(r_e\)’s from \({\mathcal G}^*\) will have a uniform distribution over \(U^0_m\).
Proof
(of Lemma 3 ). Induction over m. Consider the base case \(m=1\) first. In this case \({\mathcal G}^*\) contains one node v and no edges. Then clearly \(Y_{v} = 0\) what is distributed uniformly over the set \(U_m^0=\{0\}\).
Now suppose we know that the lemma holds for some m, and let us prove it for \(m+1\). Let v be an arbitrary leaf in an arbitrary spanning tree of \({\mathcal G}^*\). Notice that the graph \({\mathcal G}^*\) with the vertex v (and all edges adjacent to it) removed is connected. To simplify the notation we will assume that \(v=v_{m+1}\). Let \(R_1,\ldots ,R_b\) be all the values produced by the \(\mathsf {Rand}\) gates corresponding to the edges in \({\mathcal G}^*\) with one endpoint being \(v_{m+1}\). Clearly \(Y_{v_{m+1}} = - \sum _{i=1} R_i\), and hence it is uniform. On the other hand, by the induction hypothesis \((Y_{v_1},\ldots ,Y_{v_m})\) is uniformly distributed over \(U_m^0\) if one does not consider the edges going to \(v_{m+1}\), i.e., if one does not count the values \(R_1,\ldots ,R_b\) in the sums. Therefore, if we consider also these values then \((Y_{v_1},\ldots ,Y_{v_m})\) will be uniformly distributed over the set \(\{(y_{v_1},\ldots ,y_{v_m}): y_{v_1} + \cdots +y_{v_m} = \sum _{i=1} R_i \}\). Hence, altogether \((Y_{v_1},\ldots ,Y_{v_{m+1}})\) is uniformly distributed over \(U_{m+1}^0\). This concludes the proof. \(\square \)
The Lemma 2 is a consequence on Lemma 3. The proof is given below.
Proof
(of Lemma 2 ). Look at the graph \({\mathcal G}^{**} := (V,E \setminus E^*)\). Each \(X_{v_i}\) can be expressed as \(X_{v_i}^*\) + \(X_{v_i}^{**}\), where \(X_{v_i}^*\) and \(X_{v_i}^{**}\) denote the sum of \(r_e\)’s from respectively \({\mathcal G}^*\) and \({\mathcal G}^{**}\). Since all \(r_e\)’s that correspond to the edges of \({\mathcal G}^{**}\) are known to \({\mathcal A}\), thus for each \(v_i\) he can compute \(X^{**}_{v_i}\). Clearly \(X^{**}_{v_1} + \cdots + X^{**}_{v_m} = -C\). Moreover, by Lemma 3 the distribution of \((X_{v_1}^*,\ldots ,X_{v_m}^*)\) is uniform over \(U_m^0\). Hence the distribution of \((X_{v_1},\ldots ,X_{v_m})\) is uniform over \(U_m^{-C}\). \(\square \)
Finally, we need the following simple fact, where we denote by \(\Pr _{X|Y}\) the conditional distribution of X conditioned on Y.
Lemma 4
Consider an execution of \((X_1,\ldots ,X_n) \leftarrow \mathsf {RefSamp}_{\mathcal G}(1^n)\). Let \(\{R_e\}_{e \in E}\) denote the random variables corresponding to the \(r_e\) values in the circuit computing \(\mathsf {RefSamp}_{\mathcal G}(1^n)\). Take some \(W \subseteq \{1,\ldots ,n\}\). Then there exists an efficient procedure that for every input \(\{x_i\}_{i \in W}\) produces as output \(\{r'_e\}_{e \in E}\) distributed according to the conditional distribution \(\Pr _{\{R_e\}_{e \in E} | \forall _{i \in W} X_i = x_i}\).
Proof
Clearly every \(X_i\) is a linear combination o the \(r_e\)’s. Hence the condition \(\forall _{i \in W} X_i = x_i\) can be understood as a system of linear equations (with \(r_e\)’s being the unknowns), and the set of its solutions is a linear subspace \(\mathcal {L}\) whose base can be efficiently computed. To sample a random value of \(\Pr _{\{R_e\}_{e \in E} | \forall _{i \in W} X_i = x_i}\) one can simply output a uniform vector from \(\mathcal {L}\). \(\square \)
We are now ready to prove our first technical theorem.
Theorem 1
Let \(n\in {\mathbb N}\) be the security parameter, \(\mathcal {G}=(V,E)\) be a d-regular graph with edge expansion \(h>0\). Then for any \(t < \frac{n h}{3 d}\) the gadget \(\mathsf {RefSamp}_\mathcal {G}\) treated as one region is (t, q)-region reconstructible for \(q=\lfloor td/h \rfloor \).
Proof
Let X be a plausible output of \(\mathsf {RefSamp}_{\mathcal {G}}(1^n)\), i.e., \(\sum _i X_i = 0\). The simulator \(\mathsf {SimRefSamp}^{\varOmega (X)}_\mathcal {G}\) has to simulate the leakage from a t-admissible set of probes \({\mathcal P}\) from the execution of \(X \leftarrow \mathsf {RefSamp}_\mathcal {G}(1^n)\) with only q-bounded access to its oracle \(\varOmega (X)\) where \(q=\lfloor td/h \rfloor \). We will sketch it now informally, the full description is presented on Fig. 2. The simulator \(\mathsf {SimRefSamp}_\mathcal {G}\) computes the set of edges \(L \subset E\) s.t. the values of the random gates associated with the edges from L are sufficient to compute the values on all leaking wires. Then, it computes the large connected subgraph \({\mathcal G}^* = (V^*,E^*)\) such that the output variables with indices in \(V^*\) are independent of the leakage, he then probes the output variables with \(X_i\) for \(i \in V \setminus V^*\) from its oracle \(\varOmega (X)\), and simulates a random execution consistent with the probed values \(X_i\).
We start by proving that \(\mathsf {SimRefSamp}_\mathcal {G}\) is indeed \(\lfloor td/h \rfloor \)-bounded. To this end we analyse the possible sizes of connected components in the graph \(\mathcal {G}'\). It is easy to see that each wire that is revealed according to the set of probes \({\mathcal P}\) increases the set L by at most d elements, and therefore \(|L| \le t d\). Since we assumed that \(t < n h/ (3 d)\), thus \(|L| < nh/3\). We can therefore apply Lemma 1 to \({\mathcal G}'\) with \(T = |L|\). In this way we obtain that the number of vertices in the largest component \({\mathcal G}^*\) in \({\mathcal G}'\) is at least \(n - |L|/h\), which is clearly at least \(n - td/h\). Therefore the number of vertices in \(V \setminus V^*\) is smaller than td / h. Since these are exactly the indexes probed by the simulator \(\mathsf {SimRefSamp}_\mathcal {G}\), thus it is \(\lfloor td/h \rfloor \)-bounded.
The definition of reconstructability states that for each fixed \(X_1,\ldots ,X_n\) s.t. \(X_1+\ldots +X_n=0\) the distribution of the leakage in the execution of the real circuit \(\mathsf {RefSamp}_\mathcal {G}(1^n)\) assuming that it outputted the sequence \(X_1,\ldots ,X_n\) is identical to the distribution produced by the simulator \(\mathsf {SimRefSamp}_\mathcal {G}({\mathcal P})\) that uses q-probing leakage from \(X_1,\ldots ,X_n\). This is equivalent to saying that the joint distribution of the output \((X_1,\ldots ,X_n)\) and the leakage is the same in the real and simulated case (this follows from the definition of conditional probability). Let us define the two joint distributions more formally by considering two experiments. In the first one the values \((X^\mathsf {REAL}_1,\ldots ,X^\mathsf {REAL}_n)\) are sampled using \(X^\mathsf {REAL}\leftarrow \mathsf {RefSamp}_\mathcal {G}(1^n)\) and the leakage obtained from this execution is denoted by \({\mathcal P}(\mathcal {W}_{\mathsf {RefSamp}_\mathcal {G}}(X^\mathsf {REAL}))\), where \({\mathcal P}\) are a set of probes that is t-region admissible. In the simulated case the values \((X^\mathsf {SIM}_1,\ldots ,X^\mathsf {SIM}_n)\) are drawn using \(X^\mathsf {SIM}\leftarrow \mathsf {EncAE}(0)\) and the leakage is computed by the simulator leaking from \(X^\mathsf {SIM}\) and denoted \(\mathsf {SimRefSamp}_\mathcal {G}^{\varOmega (X^\mathsf {SIM})}({\mathcal P})\). Hence, we need to show that
First observe that
and
are identically distributed. This is because \(\mathsf {SimRefSamp}_\mathcal {G}^{\varOmega (X^\mathsf {SIM})}({\mathcal P})\) is computed based on the perfect simulation given in Lemma 4 using the values \(X^\mathsf {SIM}_{V^* \setminus V}\), which are leaked and hence distributed appropriately. Let \(U_m^{-C}\) be as in Lemma 2. Clearly, given (2) the remaining values \(X^\mathsf {SIM}_{V^*}\) have a uniform distribution over the set \(U_{|V^*|}^{-C}\), where \(C = \sum _{i \in V \setminus V^*} X^\mathsf {SIM}_i\), because they have not been leaked. By Lemma 2 also \(X^\mathsf {REAL}_{V^*}\) have a uniform distribution over the set \(U_{|V^*|}^{-C}\), where \(C = \sum _{i \in V \setminus V^*} X^\mathsf {REAL}_i\) given \(X^\mathsf {REAL}_{V \setminus V^*}\) and all the \(r_e\) values corresponding to the edges in the set \(E \setminus E^*\). Since these values fully determine \({\mathcal P}(\mathcal {W}_{\mathsf {RefSamp}_\mathcal {G}}(X^\mathsf {REAL}))\) thus \(X^\mathsf {REAL}_{V^*}\) have a uniform distribution over the set \(U_{|V^*|}^{-C}\) given (3). This finishes the proof. \(\square \)
4 Circuits for Affine Computation
In this section we build a circuit transformation \(\mathsf {TR}^{\mathsf {Aff}}\) that allows to transform arbitrary circuits implementing affine computation into protected circuits that are resilient to t-region probing adversaries. In the transformed circuit \(\widehat{\varGamma }\) that are produced by \(\mathsf {TR}^{\mathsf {Aff}}\) each region is represented by a gadget. Hence, if the original circuit \(\varGamma \) has size s then \(\widehat{\varGamma }\leftarrow \mathsf {TR}^{\mathsf {Aff}}(1^n, \varGamma )\) has s regions. Notice that we assume that the input and output encoding of each gadget are part of two consecutive regions, and consequently the adversary may leak twice from them.
4.1 The Transformation \(\mathsf {TR}^{\mathsf {Aff}}\)
Our transformation \(\mathsf {TR}^{\mathsf {Aff}}\) is an encoding-based transformation as described in Sect. 2.2. The transformation uses as building blocks the additive encoding scheme  . The initial state \(m_0\) of the original circuit \(\varGamma \) will be stored in encoded form using the code
. The initial state \(m_0\) of the original circuit \(\varGamma \) will be stored in encoded form using the code  , i.e., \(\widehat{M}_0 \leftarrow \mathsf {EncAE}(1^n, m_0)\). One can view the encoded state as an initial encoded input that is given as input to the transformed circuit, and hence security of stateful circuits is just a special case of security of stateless circuits.
, i.e., \(\widehat{M}_0 \leftarrow \mathsf {EncAE}(1^n, m_0)\). One can view the encoded state as an initial encoded input that is given as input to the transformed circuit, and hence security of stateful circuits is just a special case of security of stateless circuits.
We need to define transformations for the basic operations of affine computation. Let \(\varGamma \) be a circuit that takes \(\varsigma \) inputs \(x_1, \ldots , x_\varsigma \) and produces \(\tau \) outputs \(y_1, \ldots , y_\tau \). The outputs are computed from the inputs using solely the following types of operations:
-
1.
Addition in \({\mathbb F}\) and multiplication by a (known) constant \(x \in {\mathbb F}\).
-
2.
The randomness gate \(\mathsf {Rand}\) that outputs a random element \(r \in {\mathbb F}\).
-
3.
The constant gate \(\mathsf {Const}_x\) that for a constant \(x \in {\mathbb F}\) outputs x.
-
4.
The copy gate \(\mathsf {Copy}\) that for input x outputs two wires carrying the value x. Notice that the \(\mathsf {Copy}\) gate in \(\varGamma \) is needed for fan-out.
Our transformation \(\mathsf {TR}^{\mathsf {Aff}}\) is very simple. Each gate of the above form is replaced by a gadget from Fig. 3. The wires connecting the gadgets are called wire bundles and carry the corresponding encoding of the values using the code  . The gadgets presented in Fig. 3 use as a sub-circuit \(X \leftarrow \mathsf {RefSamp}_{{\mathcal G}}(1^n)\) for some expander graph \({\mathcal G}\). In the following, we will omit to mention explicitly the graph \({\mathcal G}\) and assume that \({\mathcal G}\) is d-regular with edge expansion h. We will assume that it is fixed once and for all.
. The gadgets presented in Fig. 3 use as a sub-circuit \(X \leftarrow \mathsf {RefSamp}_{{\mathcal G}}(1^n)\) for some expander graph \({\mathcal G}\). In the following, we will omit to mention explicitly the graph \({\mathcal G}\) and assume that \({\mathcal G}\) is d-regular with edge expansion h. We will assume that it is fixed once and for all.
4.2 (t, q)-reconstructability of Gadgets in \(\mathsf {TR}^{\mathsf {Aff}}\)
In this section, we show that the operations of \(\mathsf {TR}^{\mathsf {Aff}}\) from Fig. 3 are (t, q)-region reconstructible and re-randomizing. The proofs are given in the full version.
Lemma 5
Recall that \(n \in {\mathbb N}\) is the security parameter and let d and h be constants defining the underlying expander graph on n vertices. For any \(t<\frac{nh}{3d}\) we set \(q=\lfloor td/h \rfloor \). The gadget \(\mathsf {PlusAE}\) is (t, q)-region reconstructible and re-randomizing, where the region is defined by the gadget itself.
We can also show that the remaining gates are region reconstructible.
Lemma 6
The gadgets \(\mathsf {MultAE}_x\), \(\mathsf {ConstAE}_x\), \(\mathsf {CoinAE}\) and \(\mathsf {CopyAE}\) are (t, q)-region reconstructible and re-randomizing, where the region is defined by each gadget itself.
4.3 Security of Composed Circuits
In this section we discuss briefly that arbitrary composed circuits build from the transformed gadgets defined in Sect. 4.2 are (t, q)-region reconstructible, where in the composed transformed circuit \(\widehat{\varGamma }\) each gadget corresponds to a region. We state the lemma in a slightly more general form (similar to Lemma 13 from [20]). This will allow us to later apply it when we consider circuits that are made out of arbitrary transformed gadgets.
Lemma 7
Recall that n is the security parameter and q and t are functions in n. Let \(\varGamma \) be a stateless circuit over some finite field \({\mathbb F}\) with \(\varsigma \) inputs, \(\tau \) outputs and s gates. Assume that the gates in \(\varGamma \) all have fan-in and fan-out at most 2 elements in \({\mathbb F}\). Let \(\varPi = (\mathsf {Enc},\mathsf {Dec})\) be a 2q-probing resilient code. Let \(\widehat{\varGamma }\leftarrow \mathsf {TR}(1^n,\varGamma )\) be the transformation of \(\varGamma \) based on \(\varPi = (\mathsf {Enc},\mathsf {Dec})\) and let \(\widehat{\varGamma }\) be composed from (t, q)-probing reconstructible and re-randomizing gadgets, then \(\widehat{\varGamma }\) is (t, q)-probing reconstructible and re-randomizing.
The proof uses a hybrid argument and is provided in the full version. The above lemma together with Lemmas 5 and 6 immediately implies that any stateless circuit \(\widehat{\varGamma }\leftarrow \mathsf {TR}^{\mathsf {Aff}}(1^n, \varGamma )\) is (t, q)-reconstructible for choices of t and q that are given in the lemma below.
Lemma 8
Recall that n is the security parameter and let d and h be constants defining the underlying expander graph on n vertices. Let \(\varGamma \) be a stateless circuit over field \({\mathbb F}\) using only affine operations. Then, the transformed circuit \(\widehat{\varGamma }\leftarrow \mathsf {TR}^{\mathsf {Aff}}(1^n, \varGamma )\) is re-randomizable and (t, q)-reconstructible for \(t < \frac{nh}{3d}\) and \(q=\lfloor td/h \rfloor \) and regions that correspond to gadgets in \(\widehat{\varGamma }\).
It is easy to see that all transformed gadgets have size O(n) which together with \(t < \frac{nh}{3d}\) for constants h and d asymptotically shows that a constant fraction of all wires in \(\widehat{\varGamma }\) can be learnt by the adversary.
5 Circuits for Arbitrary Computation
To protect non-affine computation, we also need a transformation for multiplication in the underlying field. Before we present our transformation \(\mathsf {TR}\), we first discuss a special protected circuit called \(\mathsf {RandSamp}(1^n)\) that is mostly produced by \(\mathsf {TR}^{\mathsf {Aff}}\) and will be used in the transformed multiplication operation as an important building block. In the following, for some \(\tau \in {\mathbb N}\) we let \(n=2\tau +1\) be the security parameter and require that \(|{\mathbb F}| > n\) such that we can use the coding scheme  based on Shamir secret sharing as described in Sect. 2.1 (as we mentioned we can use other encoding schemes to improve the asymptotic complexity of our construction).
based on Shamir secret sharing as described in Sect. 2.1 (as we mentioned we can use other encoding schemes to improve the asymptotic complexity of our construction).
5.1 The Circuit \(\mathsf {RandSamp}\)
The goal of the circuit \(\mathsf {RandSamp}(1^n)\) is to sample correlated randomness that can be used in the transformed multiplication operation even in the presence of a t-region probing adversary. More precisely, the randomized circuit \(\mathsf {RandSamp}(1^n)\) takes no inputs and outputs two random encodings \([r]_{\tau } \leftarrow \mathsf {EncMSS}_{n,\tau }(r)\) and \([r]_{2\tau } \leftarrow \mathsf {EncMSS}_{n,2\tau }(r)\) Footnote 8, where \(r \leftarrow {\mathbb F}\) is a uniformly and independently chosen field element. The main difficulty is to ensure that the computation of \([r]_{\tau }\) and \([r]_{2\tau }\) do not reveal anything about r even in the presence of a t-region probing adversary. Hence, the goal is to design a circuit that samples these two encodings in an oblivious way. Our main observation that enables us to achieve this goal is the fact that \([r]_{\tau }\) and \([r]_{2\tau }\) can be computed (in a natural way) by an affine circuit \(\varGamma '\) that can be protected using \(\mathsf {TR}^{\mathsf {Aff}}\).
A technical difficulty is that the sub-circuit \(\mathsf {RandSamp}'(1^n) \leftarrow \mathsf {TR}^{\mathsf {Aff}}(1^n,\varGamma ')\) outputs additive encodings of \(([r]_{\tau }\), \([r]_{2\tau })\), i.e., \((\mathsf {EncAE}([r]_{\tau }), \mathsf {EncAE}([r]_{2\tau }))\). The protected multiplication operation, however, requires access to \(([r]_{\tau }\), \([r]_{2\tau })\). To decode one level of the “double-encoding” and obtain the final circuit \(\mathsf {RandSamp}\), we append two \(\mathsf {MultiDecoder}\) sub-circuits to the output of \(\mathsf {RandSamp}'\) to decode \(\mathsf {EncAE}([r]_{\tau })\) and \(\mathsf {EncAE}([r]_{2\tau })\), respectively. A \(\mathsf {MultiDecoder}\) sub-circuit takes as input a double encoding \(\mathsf {EncAE}([r]_{\tau })\) and outputs \([r]_{\tau }\) by “peeling off” one layer of the code. More precisely, we let \((U_1, \ldots , U_n) := [r]_{\tau }\) and \((X^{(1)}, \ldots , X^{(n)}) := (\mathsf {EncAE}(U_1), \ldots , \mathsf {EncAE}(U_n))\). The deterministic \(\mathsf {MultiDecoder}\) circuit takes as input \((X^{(1)}, \ldots , X^{(n)})\) and outputs \((U_1,\ldots , U_n)\). To this end, it runs n \(\mathsf {Decoder}\) sub-circuits (corresponding to the decoding function of the code  ), where each such sub-circuit takes as input an encoding \(X^{(i)}\) and outputs \(U_i\). For the security of our construction it will be important that each such \(\mathsf {Decoder}\) circuit computes the sum of the shares in a natural way by representing the summation as a binary tree. More precisely, the shares of \(X^{(i)}\) represent the leaves of the tree, the internal nodes of the tree correspond to the sum of the values assigned to its children and the root is the corresponding result of the decoding procedure. The high-level structure of the \(\mathsf {RandSamp}\) circuit is given in Fig. 4.
), where each such sub-circuit takes as input an encoding \(X^{(i)}\) and outputs \(U_i\). For the security of our construction it will be important that each such \(\mathsf {Decoder}\) circuit computes the sum of the shares in a natural way by representing the summation as a binary tree. More precisely, the shares of \(X^{(i)}\) represent the leaves of the tree, the internal nodes of the tree correspond to the sum of the values assigned to its children and the root is the corresponding result of the decoding procedure. The high-level structure of the \(\mathsf {RandSamp}\) circuit is given in Fig. 4.
The architecture of the \(\mathsf {RandSamp}\) and \(\mathsf {MultiDecoder}\) circuit. The \(\mathsf {RandSamp}\) circuit consists of the \(\mathsf {RandSamp}'\) sub-circuit and two \(\mathsf {MultiDecoder}\) sub-circuits. Each \(\mathsf {MultiDecoder}\) circuit consists of n \(\mathsf {Decoder}\) sub-circuits. Notice that regions in the \(\mathsf {MultiDecoder}\) circuit does not correspond to the \(\mathsf {Decoder}\) sub-circuits. More precisely, each region in the \(\mathsf {MultiDecoder}\) circuit consists of n wires — one in each of the \(\mathsf {Decoder}\) sub-circuits, such that each of them correspond to the same edge in the summing tree. For example, both dotted wires on the figure belong to the same region.
It remains to discuss how \(\mathsf {RandSamp}\) is structured into regions. First notice that for \(\mathsf {RandSamp}'\) the structure of the regions is inherited from the compiler \(\mathsf {TR}^{\mathsf {Aff}}\). Hence, the regions in \(\mathsf {RandSamp}'\) correspond to a transformed gadget in \(\mathsf {RandSamp}'\). Next, notice that each of the decoder sub-circuits \(\mathsf {MultiDecoder}\) has size \(\varTheta (n^2)\), and we need an appropriate way to structure its computation into regions of size \(\varOmega (n)\). To illustrate, why for the \(\mathsf {MultiDecoder}\) we cannot use a natural representation where each region corresponds to a computation of one output value \(U_i\), consider the following example. Let the decoding process of the n encodings be structured into n regions, where each region corresponds to a \(\mathsf {Decoder}\) gadgets that decodes \(X^{(i)}\) into \(U_i\). Unfortunately, however, it is easy to see that already a single probe in each such region allows the adversary to learn the entire output of the \(\mathsf {MultiDecoder}\) circuit, i.e., the adversary may learn \(U_i\) in the i-th region, which allows to recover the secret value r. To prevent this attack, we instead structure the computation of the \(\mathsf {MultiDecoder}\) in regions of size O(n), where each region corresponds to one node (or one edge) in each of the n \(\mathsf {Decoder}\) trees.Footnote 9 Recall that the \(\mathsf {MultiDecoder}\) consists of n \(\mathsf {Decoder}\) trees. The i-th region in \(\mathsf {MultiDecoder}\) contains the wires associated with the output of the i-th gate in each of the n \(\mathsf {Decoder}\) trees. Given the above structuring into regions, we can show the following property about the \(\mathsf {RandSamp}\) circuit.
Lemma 9
Recall that \(n \in {\mathbb N}\) is the security parameter and let d and h be constants defining the underlying expander graph on n vertices. For any \(t < \frac{nh}{3d}\) the circuit \(\mathsf {RandSamp}(1^n)\) is (t, q)-region reconstructible for \(q=\frac{3}{2}t (\lceil \log (n) \rceil + 1)\), where the regions are defined as described above in the description of \(\mathsf {RandSamp}'\) and the \(\mathsf {MultiDecoder}\) sub-circuit. Moreover, \(\mathsf {RandSamp}\) has circuit size \(O(n^3)\).
A consequence of the above lemma is that in order to guarantee that the encoded random values r produced (in encoded form) by \(([r]_{\tau },[r]_{2\tau }) \leftarrow \mathsf {RandSamp}(1^n)\) are hidden for a t-probing adversary, we need to set: \(t < \frac{n}{3 (\lceil \log (n) \rceil +1)}.\) Notice that we need an additional factor of 1 / 2 since the code  is only resilient against \(\tau <n/2\) probes.
is only resilient against \(\tau <n/2\) probes.
5.2 Protecting Arbitrary Computation Against Probing
Our final transformation follows the general paradigm of encoding-based circuit transformations from Sect. 2, where we use as the underlying code the scheme  with \(n=2\tau +1\). The initial state \(m_0\) of the circuit is transformed into \(\widehat{M}_0 \leftarrow \mathsf {EncMSS}(m_0)\), and the wires in \(\varGamma \) are represented in \(\widehat{\varGamma }\) by wire bundles carrying an encoding of the value carried on the wire in \(\varGamma \). The transformation for the individual operations is presented in Figs. 5, 6 and 7. In Fig. 5, we present the main ingredient of our new transformation – the transformation for the multiplication operation, which we describe in further detail below.
with \(n=2\tau +1\). The initial state \(m_0\) of the circuit is transformed into \(\widehat{M}_0 \leftarrow \mathsf {EncMSS}(m_0)\), and the wires in \(\varGamma \) are represented in \(\widehat{\varGamma }\) by wire bundles carrying an encoding of the value carried on the wire in \(\varGamma \). The transformation for the individual operations is presented in Figs. 5, 6 and 7. In Fig. 5, we present the main ingredient of our new transformation – the transformation for the multiplication operation, which we describe in further detail below.
The transformation for the multiplication operation in \({\mathbb F}\). \(\mathsf {RandSamp}(1^n)\) samples \(([r]_{\tau }, [r]_{2\tau })\) as described in Sect. 5.1.
The transformation for the multiplication uses ideas from secure multiparty computation – in particular, the use of \([r]_{\tau }, [r]_{2\tau }\) that allows to decode \(W = T + V\) without revealing sensitive information follows the approach from [14]. There are two important differences to the protocol of [14] – most notably, for our purposes we need to sample \(([r]_{\tau }, [r]_{2\tau })\) in a way that is secure against t-region probing adversaries. Second, in Step 4 of Fig. 5 we use a trivial encoding of the value w with the code  . In particular, instead of using \(\mathsf {EncMSS}(w)\) to sample Z, we just use the trivial encoding of w as n-elements vector \(Z:=(w,\ldots , w)\). While clearly this encoding procedure does not offer any security, it guarantees that we can encode w in complexity O(n). This will be relevant when we structure the computation of \(\mathsf {MultSS}\) into region, which will be explained next.
. In particular, instead of using \(\mathsf {EncMSS}(w)\) to sample Z, we just use the trivial encoding of w as n-elements vector \(Z:=(w,\ldots , w)\). While clearly this encoding procedure does not offer any security, it guarantees that we can encode w in complexity O(n). This will be relevant when we structure the computation of \(\mathsf {MultSS}\) into region, which will be explained next.
We structure \(\mathsf {MultSS}\) into the following regions. The first set of regions corresponds to Step 1 when \(\mathsf {MultSS}\) queries the external source \(\mathsf {RandSamp}(1^k)\) for (U, V) and corresponds to the set of regions defined in the previous section. Besides the regions that are naturally inherited from \(\mathsf {RandSamp}\), we introduce one additional region that includes all operations of \(\mathsf {MultSS}\) from Step 2–4. Clearly, this region has size of O(n), which will be important for our security argument.
To complete the description of the transformation it remains to propose constructions for the addition operation, the \(\mathsf {Rand}\) operation and how to implement fan-out. The transformation is rather straightforward and details are given in Fig. 7. Notice that the transformations from Fig. 7 use the multiplication gadget as a sub-routine to implement a refreshing scheme for the  encoding scheme. The refreshing algorithm for
encoding scheme. The refreshing algorithm for  works as follows. We first sample once and for all a fixed encoding \(D \leftarrow \mathsf {EncMSS}(1)\), where 1 denotes the multiplicative identity in \({\mathbb F}\). To refresh X, we compute \(Z \leftarrow \mathsf {MultSS}(X,D)\).Footnote 10
works as follows. We first sample once and for all a fixed encoding \(D \leftarrow \mathsf {EncMSS}(1)\), where 1 denotes the multiplicative identity in \({\mathbb F}\). To refresh X, we compute \(Z \leftarrow \mathsf {MultSS}(X,D)\).Footnote 10
Finally, notice that each gadget of Fig. 7 represents a single region, where the execution of \(\mathsf {MultSS}(.,D)\) to refresh the output of the gadgets is structured into regions as explained above (and not part of the region of the gadgets itself). This completes the description of the transformation \(\mathsf {TR}\) and the structuring of computation into regions. We can show the following about the above construction.
Theorem 2
Let n be the security parameter and d, h be constants defining the underlying expander graph on n vertices. The transformation \(\mathsf {TR}\) described above is perfectly t-region probing secure for \(t < \frac{n}{12(\lceil \log (n) \rceil +1)}.\) Moreover, for a circuit \(\varGamma \) of size s, the transformed circuit \(\widehat{\varGamma }\leftarrow \mathsf {TR}(\varGamma , 1^n)\) has size \(O(sn^3)\).
We notice that it is straightforward to improve the complexity of the construction to \(O(sn^2\log n)\) using FFT. Moreover, as mentioned in the introduction, further improvements of the efficiency are possible using packed secret sharing.
6 Application to the Noisy Leakage Model
As shown by Duc et al. [16] security in the so-called p-random probing model implies security in the noisy leakage model. In the random probing model the adversary has no control over the choice of the probes and instead corrupts each wire of the circuit independently with a probability p. By applying Chernoff, it is straightforward that security in the threshold probing model with rate r implies security in the random probing model with \(p=cr\) for some constant \(c < 1\). Hence, applying Theorem 2, we straightforwardly get security in the p-random probing model for \(p = O(\log ^{-1}(n))\). As argued in the introduction we can further improve p to a constant when we directly prove security in the p-random probing model instead of taking the detour via the much stronger threshold probing model. In particular, we can get the following result.
Theorem 3
The transformation \(\mathsf {TR}\) described in Sect. 5 is p-random probing secure for a sufficiently small constant \(p < 1/12\). For a circuit \(\varGamma \) of size s, the transformed circuit \(\widehat{\varGamma }\leftarrow \mathsf {TR}(\varGamma , 1^n)\) has complexity \(O(sn^3)\).
Proof
To distinguish the random probing model from the t-region probing model that we discussed in the last section, we will call the later in the following the t-threshold probing model. To show security against a p-random probing adversary observe that clearly security against a t-region probing adversary for regions of size O(n) and \(t=\varOmega (n)\) probes implies security in the random probing model for a constant p. This worst-case to average case reduction is a straightforward application of the Chernoff bound. Recall that in our transformation \(\mathsf {TR}\) from Sect. 5 all parts of the transformed circuit tolerate a constant corruption rate in the threshold probing modelFootnote 11 except for the \(\mathsf {MultiDecoder}\) sub-circuits, which are the reason that we only can allow \(O(n / \log (n))\) probes (cf. Sect. 5.1). Therefore, to show that our construction achieves security in the random probing model for constant p we only need to show that the \(\mathsf {MultiDecoder}\) sub-circuits remain secure in the p-random probing model for a constant p. To this end, we need the following fact:
Lemma 10
Let \(\mathsf {MultiDecoder}\) be a deterministic circuit as described in Sect. 5.1 that takes as input n encodings \(X:=(X^{(1)}, \ldots , X^{(n)})\) and outputs their decodings \(U := (U_1,\ldots ,U_n)\). Let \({\mathcal P}\) be a set of probes for \(\mathsf {MultiDecoder}\) drawn by a p-random probing adversary. There exists a simulator \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}\) such that for any plausible inputs \(X:=(X^{(1)}, \ldots , X^{(n)})\) and corresponding output vector \(U := (U_1,\ldots ,U_n)\), we have:
Moreover, for each \(i \in [n]\) (independently) we have the following: the probability (over sampling of the set \({\mathcal P}\)) that the value \(X^{(i)}\) is fully leaked by the \({\mathsf {Sim}}_{\mathsf {Decoder}}^{\varOmega (X)}({\mathcal P})\) (i.e., the value \(X^{(i)}_j\) is leaked for every \(j \in [n]\)) is equal at most \(\frac{p}{1-p}\).
The proof is given in the full version.
We now continue the proof of Theorem 3. Note the only requirement we have in Lemma 10 is that for each i (independently) it holds that with probability at least \(1-p/(1-p)\) the t-th \(\mathsf {Decoder}\) is not fully covered. Hence, we also need to prove (as in was done in Lemma 9) that not too many of the input encodings to the \(\mathsf {Decoder}\) are fully leaked by the simulator for the composed circuit \(\mathsf {RandSamp}'\). Fix one input encodings \(X^{(i)}\) to one of the \(\mathsf {Decoder}\) sub-circuits. Recall that there are two simulator, which leak from the encoding \(X^{(i)}\): \({\mathsf {Sim}}_{\mathsf {Decoder}}^{\varOmega (X)}({\mathcal P})\) and the simulator for the gadget, which outputs \(X^{(i)}\) in \(\mathsf {RandSamp}'\), which will be denoted \({\mathsf {Sim}}'\).
Recall that all gadgets except the \(\mathsf {MultiDecoder}\) sub-circuit are (t, q)-reconstructible for \(t=cn\) and \(q=c'n\) for an appropriate choice of constants \(c,c' < 1/6\). Since all regions are of size O(n) (where the O-notation only hides small constants), there exists a constant \(p < p/(1-p) < 1/6\) such that with overwhelming probability a set of probes \({\mathcal P}\) when sampled by a p-random probing adversary is t-region admissible. Therefore, with overwhelming probability (over the choice of \({\mathcal P}\)) at most q positions are leaked from \(X^{(i)}\) by the simulator \({\mathsf {Sim}}'\) in order to simulate answers to the probes in the part of \(\mathsf {RandSamp}'\) producing \(X^{(i)}\). To simplify the description, we assume that \({\mathcal P}\) produced by the p-random probing adversary is indeed t-admissible, and we do not explicitly mention the bad event when it is not (as this event is negligible anyway).
From Lemma 10 we know that with probability at least \(1-\frac{p}{1-p} \ge \frac{5}{6}\) there exists a random j, s.t. the value \(X^{(i)}_j\) is not queried by the simulator \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}^{\varOmega (X)}({\mathcal P})\). Notice, that the index j of the share, which is not leaked by the \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}^{\varOmega (X)}({\mathcal P})\) is uniformly random over [n] due to the symmetry of the \(\mathsf {MultiDecoder}\) sub-circuit with respect to the input shares indexesFootnote 12. Hence, the probability that the particular value \(X^{(i)}_j\) (recall that j was drawn at random) is queried by the \({\mathsf {Sim}}'\) is equal at most \(\frac{q}{n}<c' <\frac{1}{6}\). Therefore, the probability that the encoding \(X^{(i)}\) is fully leaked by both simulators is not greater than \(\frac{1}{6} + \frac{5}{6} \cdot \frac{1}{6} < \frac{1}{3}\), where the first term in the sum comes from Lemma 10 and the fact that with probability 1 / 6 the simulator \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}\) reveals the entire encoding, and the second term comes from the analysis above (i.e., with probability 5 / 6 we have at least one random share \(X^{(i)}_j\) that is not queried by \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}\) and \({\mathsf {Sim}}'\) only asks for a 1 / 6 fraction to its leakage oracle. Given this bound, we can now use again Chernoff to prove that with overwhelming probability (in n) less than \(\frac{1}{2}\) of all the input encodings to the \(\mathsf {MultiDecoder}\) circuit are fully leaked. The rest of the security proof is analogous to the case of the threshold probing adversary. Putting the above together we obtain Theorem 3. \(\square \)
We emphasize that the above is mainly a feasibility result and the constant is rather small due to the properties of the expander graph.
7 Extensions
7.1 Security of Boolean Circuits
As outlined in the introduction our transformation \(\mathsf {TR}\) presented in the last section requires that the computation is carried out over a field \({\mathbb F}\) of size O(n). This implies that the values carried on the wires are from \({\mathbb F}\) and the basic gates used in \(\widehat{\varGamma }\) represent the operations from the underlying field \({\mathbb F}\). Notice that the later also means that we require leak-free operations that are of size \(O(\log (n)\log \log (n))\), which is required to carry out, e.g., the multiplication in the field \({\mathbb F}\). While we emphasize that this assumption is used by most works that consider leakage resilient circuit transformations, we observe that for our particular construction we can eliminate this assumption by getting slightly weaker parameters (weaker by a constant factor only). The basic idea to achieve this is as follows: instead of using Shamir’s secret sharing as underlying code, we can use codes based on algebraic geometry that exhibit the multiplicative property. Such codes are for instance constructed in the work of Chen and Cramer [7]. These codes operate over fields of constant size and hence there basic operations can be implemented by constant size Boolean circuits.
The above is in particular useful for Theorem 3 where we obtain security against constant random probing rate. Using algebraic geometric codes the corruption probability p stays constant even if \(\widehat{\varGamma }\) is implemented with Boolean gates – which is optimal.
7.2 From Non-adaptive to Adaptive Security
In our analysis we assumed that for each clock cycle the adversary chooses a set of \({\mathcal P}_i\) that defines what wires leak. This implies that within a clock cycle the adversary is non-adaptive and cannot change the position of his probes, e.g., he cannot learn the first share of an encoding and upon the value of this share decide what wire he wants to probe next. Fortunately, we can easily get fully adaptive security since our construction achieves perfect security against a threshold probing adversary [10]. We stress that the same does not hold for construction that are only statistical secure [10].
Notes
- 1.
We note that this model still ignores many aspects of the side channel attacks, for example the fact that some operations (like writing bits to the memory) leak more information than some other ones (like the arithmetic operations). We stress that a certain level of abstraction is inevitable in every formal model. Moreover, the fact that a wire w leaks more information than the wires can be reflected by having several copies of w in \(\varGamma \) (where \(\varGamma \) is an input for the circuit compiler, see Sect. 1.1 for more on the circuit compilers).
- 2.
Notice that even for such solutions our construction offers asymptotic improvements over earlier works since the decryption circuit of the FHE scheme has to be protected with an encoding-based circuit compiler.
- 3.
In the rest of the work we will mostly give a concrete relation between the number of probes t and the security parameter n, which determine the blow-up of the transformed circuit.
- 4.
For readers familiar with the construction of [26] the transformation for the AND gate computes on input \(A=(A_1, \ldots ,A_n)\) and \(B=(B_1, \ldots ,B_n)\) the values \(A_i\cdot B_j\) for all \(i,j \in [n]\). Hence, each share \(A_i\) appears at least n times and hence it is impossible to obtain leakage rate better than \(O(n^{-1})\).
- 5.
One may object that by structuring the computation of the ISW AND transformation into regions of size O(n) one can achieve an improved probing rate. However, it is easy to see by a counting argument that such structuring is impossible.
- 6.
Notice that the tree-decoding is also the technical reason why we do not achieve the optimal rate of O(1).
- 7.
The above can be generalized but we stick to this simple requirement for simplicity.
- 8.
We present here the parameters n, t to indicate that the value \([r]_{2\tau }\) comes from the encoding
 (and not
(and not 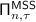 ).
). - 9.
Notice that in reality regions constitute a partition of wires, not gates. Whenever, we say that a particular gate is in a particular region, it simply means that gate’s output is in that region.
- 10.
We note that the expander-based refreshing from Sect. 3 unfortunately does not easily transfer to a refreshing scheme for the code
 .
. - 11.
This is true for all gadgets of the transformation \(\mathsf {TR}\) as well as for \(\mathsf {RandSamp}'\).
- 12.
Recall that we assume that n is a power of two and T is then a full binary tree. Moreover, the simulator \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}^{\varOmega (X)}({\mathcal P})\) is also symmetric with respect to the input share indexes. Furthermore, if there is more than one index j, s.t. the value \(X^{(i)}_j\) is not leaked by the \({\mathsf {Sim}}_{\mathsf {MultiDecoder}}^{\varOmega (X)}({\mathcal P})\) we pick one of them uniformly at random.
References
Ajtai, M.: Secure computation with information leaking to an adversary. In: Fortnow, L., Vadhan, S.P. (eds.) Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC 2011, San Jose, CA, USA, 6–8 June 2011, pp. 715–724. ACM (2011)
Andrychowicz, M., Damgård, I., Dziembowski, S., Faust, S., Polychroniadou, A.: Efficient leakage resilient circuit compilers. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 311–329. Springer, Heidelberg (2015)
Balasch, J., Faust, S., Gierlichs, B.: Inner product masking revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 486–510. Springer, Heidelberg (2015)
Barthe, G., Crespo, J.M., Lakhnech, Y., Schmidt, B.: Mind the gap: modular machine-checked proofs of one-round key exchange protocols. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 689–718. Springer, Heidelberg (2015)
Carlet, C., Goubin, L., Prouff, E., Quisquater, M., Rivain, M.: Higher-order masking schemes for S-boxes. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 366–384. Springer, Heidelberg (2012)
Chari, S., Jutla, C.S., Rao, J.R., Rohatgi, P.: Towards sound approaches to counteract power-analysis attacks. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 398–412. Springer, Heidelberg (1999)
Chen, H., Cramer, R.: Algebraic geometric secret sharing schemes and secure multi-party computations over small fields. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 521–536. Springer, Heidelberg (2006)
Coron, J.-S., Großschädl, J., Vadnala, P.K.: Secure conversion between boolean and arithmetic masking of any order. In: Batina, L., Robshaw, M. (eds.) CHES 2014. LNCS, vol. 8731, pp. 188–205. Springer, Heidelberg (2014)
Coron, J.-S., Prouff, E., Roche, T.: On the use of Shamir’s secret sharing against side-channel analysis. In: Mangard, S. (ed.) CARDIS 2012. LNCS, vol. 7771, pp. 77–90. Springer, Heidelberg (2013)
Cramer, R., Damgård, I., Dziembowski, S., Hirt, M., Rabin, T.: Efficient multiparty computations secure against an adaptive adversary. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 311–326. Springer, Heidelberg (1999)
Cramer, R., Damgård, I., Maurer, U.M.: General secure multi-party computation from any linear secret-sharing scheme. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, p. 316. Springer, Heidelberg (2000)
Dachman-Soled, D., Kalai, Y.T.: Securing circuits against constant-rate tampering. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 533–551. Springer, Heidelberg (2012)
Dachman-Soled, D., Liu, F.-H., Zhou, H.-S.: Leakage-resilient circuits revisited – optimal number of computing components without leak-free hardware. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 131–158. Springer, Heidelberg (2015)
Damgård, I., Ishai, Y., Krøigaard, M.: Perfectly secure multiparty computation and the computational overhead of cryptography. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 445–465. Springer, Heidelberg (2010)
Davì, F., Dziembowski, S., Venturi, D.: Leakage-resilient storage. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 121–137. Springer, Heidelberg (2010)
Duc, A., Dziembowski, S., Faust, S.: Unifying leakage models: from probing attacks to noisy leakage. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 423–440. Springer, Heidelberg (2014)
Duc, A., Faust, S., Standaert, F.-X.: Making masking security proofs concrete - or how to evaluate the security of any leaking device. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 401–429. Springer, Heidelberg (2015)
Dziembowski, S., Faust, S.: Leakage-resilient circuits without computational assumptions. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 230–247. Springer, Heidelberg (2012)
Faust, S., Pietrzak, K., Venturi, D.: Tamper-proof circuits: how to trade leakage for tamper-resilience. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011, Part I. LNCS, vol. 6755, pp. 391–402. Springer, Heidelberg (2011)
Faust, S., Rabin, T., Reyzin, L., Tromer, E., Vaikuntanathan, V.: Protecting circuits from leakage: the computationally-bounded and noisy cases. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 135–156. Springer, Heidelberg (2010)
Goldwasser, S., Rothblum, G.N.: How to compute in the presence of leakage. In: 53rd FOCS, pp. 31–40, New Brunswick, NJ, USA, 20–23 October 2012. IEEE Computer Society Press (2012)
Goubin, L., Martinelli, A.: Protecting AES with Shamir’s secret sharing scheme. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 79–94. Springer, Heidelberg (2011)
Grosso, V., Standaert, F.-X., Faust, S.: Masking vs. multiparty computation: how large is the gap for AES? In: Bertoni, G., Coron, J.-S. (eds.) CHES 2013. LNCS, vol. 8086, pp. 400–416. Springer, Heidelberg (2013)
Hoory, S., Linial, N., Wigderson, A., Overview, A.: Expander graphs, their applications. Bull. Am. Math. Soc. (N.S) 43, 439–561 (2006)
Ishai, Y., Prabhakaran, M., Sahai, A., Wagner, D.: Private circuits II: keeping secrets in tamperable circuits. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 308–327. Springer, Heidelberg (2006)
Ishai, Y., Sahai, A., Wagner, D.: Private circuits: securing hardware against probing attacks. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 463–481. Springer, Heidelberg (2003)
Juma, A., Vahlis, Y.: Protecting cryptographic keys against continual leakage. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 41–58. Springer, Heidelberg (2010)
Kim, H., Hong, S., Lim, J.: A fast and provably secure higher-order masking of AES S-box. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 95–107. Springer, Heidelberg (2011)
Kocher, P.C.: Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 104–113. Springer, Heidelberg (1996)
Kocher, P.C., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999)
Prouff, E., Rivain, M.: Masking against side-channel attacks: a formal security proof. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 142–159. Springer, Heidelberg (2013)
Rivain, M., Prouff, E.: Provably secure higher-order masking of AES. In: Mangard, S., Standaert, F.-X. (eds.) CHES 2010. LNCS, vol. 6225, pp. 413–427. Springer, Heidelberg (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Andrychowicz, M., Dziembowski, S., Faust, S. (2016). Circuit Compilers with \(O(1/\log (n))\) Leakage Rate. In: Fischlin, M., Coron, JS. (eds) Advances in Cryptology – EUROCRYPT 2016. EUROCRYPT 2016. Lecture Notes in Computer Science(), vol 9666. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49896-5_21
Download citation
DOI: https://doi.org/10.1007/978-3-662-49896-5_21
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49895-8
Online ISBN: 978-3-662-49896-5
eBook Packages: Computer ScienceComputer Science (R0)


 with
with 






 (and not
(and not 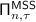 ).
). .
.