On the Influence of Message Length in PMAC’s Security Bounds

Abstract

Many MAC (Message Authentication Code) algorithms have security bounds which degrade linearly with the message length. Often there are attacks that confirm the linear dependence on the message length, yet PMAC has remained without attacks. Our results show that PMAC’s message length dependence in security bounds is non-trivial. We start by studying a generalization of PMAC in order to focus on PMAC’s basic structure. By abstracting away details, we are able to show that there are two possibilities: either there are infinitely many instantiations of generic PMAC with security bounds independent of the message length, or finding an attack against generic PMAC which establishes message length dependence is computationally hard. The latter statement relies on a conjecture on the difficulty of finding subsets of a finite field summing to zero or satisfying a binary quadratic form. Using the insights gained from studying PMAC’s basic structure, we then shift our attention to the original instantiation of PMAC, namely, with Gray codes. Despite the initial results on generic PMAC, we show that PMAC with Gray codes is one of the more insecure instantiations of PMAC, by illustrating an attack which roughly establishes a linear dependence on the message length.

1 Introduction

When searching for optimal cryptographic schemes, security bounds provide an important tool for selecting the right parameters. Security bounds, as formalized by Bellare et al. [1], capture the concept of explicitly measuring the effect of an adversary’s resources on its success probability in breaking the scheme. They enable one to determine how intensively a scheme can be used in a session. Therefore, provably reducing the impact of an adversary’s resources from, say, a quadratic to a linear term, can mean an order of magnitude increase in a scheme’s lifetime. Conversely, finding attacks which confirm an adversary’s success rate, relative to its allotted resources, prove claims of security bound optimality.

MAC algorithms provide a good example of schemes which have been studied extensively to determine optimal bounds. A MAC’s longevity is defined as the number of times the MAC can be used under a single key: it can be measured as a function of the number of tagging queries, q, and the largest message length, $\ell$, used before a first forgery attempt is successful. The impact of an adversary’s resources, q and $\ell$, on its success probability in breaking a MAC is then described via an upper bound of the form $f(q, \ell )\cdot \epsilon$, where f is a function, often a polynomial, and $\epsilon$ is a quantity dependent on the MAC’s parameters. The maximum number of queries $q_{\max }$ with length $\ell _{\max }$ one can make under a key is computed by determining when $f(q_{\max },\ell _{\max })\cdot \epsilon$ is less than some threshold success probability. For example, if one is comfortable with adversaries which have a one in a million chance of breaking the scheme, but no more, then one would determine $q_{\max }$ and $\ell _{\max }$ via

$$\begin{aligned} f(q_{\max }, \ell _{\max })\cdot \epsilon \le 10^{-6}\,. \end{aligned}$$

(1)

Given that $q_{\max }$ and $\ell _{\max }$ depend only on f, it becomes important to find the f which establishes the tightest upper bound on the success probability.

The optimality of f depends on the environment in which the MAC operates, or in other words, the assumptions made on the MAC. For instance, stateful MACs, such as the Wegman-Carter construction [21], can achieve bounds independent of q and $\ell$. In this case, an adversary’s success remains negligible regardless of q and $\ell$, as long as the construction receives nonces, that is, additional unique input. Therefore, determining $q_{\max }$ and $\ell _{\max }$ for Wegman-Carter MACs amounts to solving $\epsilon \ll 1$, which is true under the assumption that nonces are unique. Similarly, XOR MAC [3] with nonces achieves a security upper bound of $\epsilon = 1/2^\tau$, with $\tau$ the tag length in bits, which is the optimal bound for any MAC. Randomized, but stateless MACs can achieve bounds similar to stateful MACs, as shown by Minematsu [14].

In contrast, deterministic and stateless MACs necessarily have a lower bound of $q^2/2^n$, where n is the inner state size, due to a generic attack by Preneel and van Oorschot [18]. This means that for any f,

$$\begin{aligned} f(q,\ell )\cdot \epsilon \ge \frac{q^2}{2^n}\,, \end{aligned}$$

(2)

hence any deterministic, stateless MAC must use fewer than $2^{n/2}$ tagging queries per key.

Given this lower limit on f, one would perhaps expect to find schemes for which the proven upper bound is $q^2/2^n$. Yet many deterministic, stateless MACs have upper bounds including an $\ell$-factor. Block cipher based MACs, such as CBC-MAC [4], OMAC [12], and PMAC [7], were originally proven with an upper bound on the order of $q^2\ell ^2/2^n$, growing quadratically as a function of $\ell$. Much effort has been placed in improving the bounds to a linear dependence on $\ell$, resulting in bounds of the form $q^2\ell /2^n$ [5, 11, 15, 16].

For certain deterministic, stateless schemes the dependence on $\ell$ has been proven to be necessary. Dodis and Pietrzak [9] point out that this is the case for polynomial based MACs, and try to avoid the dependence by introducing randomness. Pietrzak [17] notes that the EMAC bound must depend on $\ell$. Gazi, Pietrzak, and Rybár [10] give an attack on NMAC showing its dependence on $\ell$. Nevertheless, there are no known generic attacks establishing a lower bound of the form $\ell ^\epsilon /2^n$ for any $\epsilon > 0$.

PMAC, introduced by Black and Rogaway [7], stands out as a construction for which little analysis has been performed showing the necessity of $\ell$ in the bound. It significantly differs in structure from other MACs (see Fig. 1 and Definition 3), which gives it many advantages:

• 1. it is efficient, since nearly all block cipher calls can be made in parallel,

• 2. it is simple, which in turn enables simple analysis,

• 3. and its basic structure lends itself to high-security extensions, such as PMAC-Plus [22], PMAC-with-Parity [23], and PMACX [24].

The disadvantage of having such a different structure is that no known attacks can help to establish $\ell$-dependency.

Contributions. We start by abstracting away some details of PMAC in order to focus on its basic structure. We do so by considering generic PMAC, which is a generalized version of PMAC accepting an arbitrary block cipher and constants, and with an additional independent key. We prove that one of the following two statements is true:

• 1. either there are infinitely many instances of generic PMAC for which there are no attacks with success probability greater than $2q^2/2^n$,

• 2. or finding an attack against generic PMAC with success probability greater than $2q^2/2^n$ is computationally hard.

The second statement relies on a conjecture which we explain below.

Then we focus on an instantiation of generic PMAC, namely PMAC with Gray codes, introduced by Black and Rogaway [7]. We show that PMAC with Gray codes is an instantiation which does not meet the optimal bound of $2q^2/2^n$, by finding an attack with success probability $(2^{k-1}-1)/2^{n}$ with $\ell = 2^k$, establishing a dependence on $\ell$ for every power of two.

Approach. Proving the above results requires viewing the inputs to PMAC’s block cipher calls in a novel way: as a set of points $\mathsf {P}$ lying in a finite affine plane. Keys are identified as slopes of lines in the affine plane. A collision is guaranteed to occur under a specific key w if and only if each line with slope w covers an even number of points in $\mathsf {P}$; in this case we say that w evenly covers $\mathsf {P}$.

Maximizing the collision probability means finding a set of points $\mathsf {P}$ for which there is large set of slopes $\mathsf {W}$ evenly covering $\mathsf {P}$. But finding such a set $\mathsf {W}$ is non-trivial: the x-coordinates of the points in $\mathsf {P}$ must either contain a subset summing to zero, or satisfying some quadratic form.

Finding a subset summing to zero is the subset sum (SS) problem, which is known to be NP-complete. The second problem we call the binary quadratic form (BQF) problem (see Definition 9), and there is reason to believe this problem is NP-complete as well (see Appendix B). As a result, we conjecture that finding solutions to the union of the two problems is computationally hard.

By reducing SS and the BQF problem to finding slopes $\mathsf {W}$ evenly covering points $\mathsf {P}$, we establish our results.

Related Work. Rogaway [19] has shown that the dependence on $\ell$ disappears if you consider a version of PMAC with an ideal tweakable block cipher. PMAC’s basic structure has also been used to design schemes where the impact of $\ell$ is reduced by construction: Yasuda’s PMAC-with-Parity [23] and Zhang’s PMACX [24] get bounds of the form $q^2\ell ^2/2^{2n}$.

For EMAC, Pietrzak [17] proved that if $\ell \le 2^{n/8}$ and $q\ge \ell ^2$, then the bound’s order of growth is independent of $\ell$. The proven bound is

$$\begin{aligned} 128\cdot \frac{q^2\ell ^8}{2^{2n}} + 16\cdot \frac{q^2}{2^n} + \frac{q(q-1)}{2^{n+1}}\,. \end{aligned}$$

(3)

Note that the condition on $\ell$ means that EMAC’s bound is not truly independent of $\ell$. An example of a construction which has a bound which is truly independent of $\ell$ is a variant of PMAC described by Yasuda [23, Sect. 1]. This construction achieves a bound that does not grow as a function of $\ell$, with the limitation that $\ell \le 2^{n/2}$ and at a rate of two block cipher calls per block of message. The construction works by splitting the message into half blocks, and then appending a counter to each half-block, to create a full block. Each full block is input into a block cipher, and all the block cipher outputs are XORed together, and finally input into a last, independent block cipher.

2 Preliminaries

2.1 Notation

If $\mathsf {X}$ is a set then $\overline{\mathsf {X}}$ is its complement, $\mathsf {X}^q$ is the Cartesian product of q copies of $\mathsf {X}$, $\mathsf {X}^{\le \ell } = \bigcup _{i=1}^\ell \mathsf {X}^i$, and $\mathsf {X}^+ = \bigcup _{i=1}^\infty \mathsf {X}^i$. If ${\varvec{x}}\in \mathsf {X}^q$, then its coordinates are $(x_1, x_2, \ldots , x_q)$. If $f:\mathsf {X}\rightarrow \mathsf {Y}$ then define $\widetilde{f}:\mathsf {X}^+\rightarrow \mathsf {Y}^+$ to be the mapping

$$\begin{aligned} \widetilde{f}(x_1,\ldots ,x_q) = (f(x_1),\ldots ,f(x_q)). \end{aligned}$$

(4)

If ${\varvec{a}}\in \mathsf {X}^{\ell _1}$ and ${\varvec{b}}\in \mathsf {X}^{\ell _2}$, then ${\varvec{a}}\Vert {\varvec{b}}$ is the concatenation of ${\varvec{a}}$ and ${\varvec{b}}$, that is,

$$\begin{aligned} {\varvec{a}}\Vert {\varvec{b}} :=(a_1,a_2,\ldots ,a_{\ell _1},b_1,b_2,\ldots ,b_{\ell _2})\in \mathsf {X}^{\ell _1+\ell _2}\,. \end{aligned}$$

(5)

If ${\varvec{a}}\in \mathsf {X}^\ell$ and $\mu \le \ell$, then ${\varvec{a}}_{\le \mu }:=(a_1,a_2,\ldots ,a_\mu )$. If $\mathsf {X}$ is a field, then for ${\varvec{a}}\in \mathsf {X}^\ell$, $\mathbf{1}\cdot {{\varvec{a}}} = \sum _{i=1}^\ell a_i$. Furthermore, when considering elements (x, y) of $\mathsf {X}^2$, we call the left coordinate of the pair the x-coordinate, and the other the y-coordinate.

2.2 Primitives

A uniformly distributed random function (URF) from $\mathsf {M}$ to $\mathsf {T}$ is a uniformly distributed random variable over the set of all functions from $\mathsf {M}$ to $\mathsf {T}$. A uniformly distributed random permutation (URP) on $\mathsf {X}$ is a uniformly distributed random variable over the set of all permutations on $\mathsf {X}$.

A pseudo-random function (PRF) is a function $\varPhi :\mathsf {K}\times \mathsf {M}\rightarrow \mathsf {T}$ defined on a set of keys $\mathsf {K}$ and messages $\mathsf {M}$ with output in $\mathsf {T}$. We write $\varPhi _k(m)$ for $\varPhi (k,m)$. The PRF-advantage of an adversary A against the PRF $\varPhi$ is the probability that A distinguishes $\varPhi _k$ from $\$$, where k is a uniformly distributed random variable over $\mathsf {K}$, and $\$$ is a URF. More formally, the advantage of A can be described as

$$\begin{aligned} \left|\mathbf {Pr}_{}\left[ A^{\varPhi _k} = 1\right] - \mathbf {Pr}_{}\left[ A^{\$} = 1\right] \right|\,, \end{aligned}$$

(6)

where $A^O = 1$ is the event that A outputs 1 given access to oracle O.

A pseudorandom permutation (PRP) is a function $E:\mathsf {K}\times \mathsf {X}\rightarrow \mathsf {X}$ defined on a set of keys $\mathsf {K}$, where $E(k,\cdot )$ is a permutation for each $k\in \mathsf {K}$. As with PRFs, we write $E_k(x)$ for E(k, x). The PRP-advantage of an adversary A versus E is defined similarly to the PRF-advantage, and can be described as follows:

$$\begin{aligned} \left|\mathbf {Pr}_{}\left[ A^{E_k}=1\right] - \mathbf {Pr}_{}\left[ A^{\pi }=1\right] \right|\,, \end{aligned}$$

(7)

where k is uniformly distributed over $\mathsf {K}$, and $\pi$ is a URP.

2.3 Message Authentication

A MAC consists of a tagging and a verification algorithm. The tagging algorithm accepts messages from some message set $\mathsf {M}$ and produces tags from a tag set $\mathsf {T}$. The verification algorithm receives message-tag pairs (m, t) as input, and outputs 1 if the pair (m, t) is valid, and 0 otherwise. The insecurity of a MAC is measured as follows.

Definition 1

Let A be an adversary with access to a MAC. The advantage of A in breaking the MAC is the probability that A is able to produce a message-tag pair (m, t) for which the verification algorithm outputs 1, where m has not been previously queried to the tagging algorithm.

PRF-based MACs use a PRF $\varPhi :\mathsf {K}\times \mathsf {M}\rightarrow \mathsf {T}$ to define the tagging algorithm. The verification algorithm outputs 1 if $\varPhi _k(m) = t$, and 0 otherwise. As shown by the following theorem, the insecurity of a PRF-based MAC can be reduced to the insecurity of the PRF, allowing us to focus on $\varPhi$.

Theorem 1

([2]). Let $\alpha$ denote the advantage of adversary A in breaking a PRF-based MAC with underlying PRF $\varPhi$. Say that A makes q tagging queries and v verification queries. Then there exists a PRF-adversary B making $q+v$ PRF queries such that

$$\begin{aligned} \alpha \le \frac{v}{\left|\mathsf {T}\right|} + \beta \,, \end{aligned}$$

(8)

where $\beta$ is the advantage of B.

Some PRFs are constructed using a smaller PRP $E_k:\mathsf {K}\times \mathsf {X}\rightarrow \mathsf {X}$. If $\varPhi ^{E_k}$ denotes a PRF using $E_k$, then one can reduce the PRF-advantage of an adversary against $\varPhi ^{E_k}$ to the PRF-advantage of an adversary against $\varPhi ^{\pi }$, where $\pi$ is a URP over $\mathsf {X}$. The result is well-known, and used, for example, to prove the security of PMAC [7].

Theorem 2

Let $\alpha$ denote the PRF-advantage of adversary A against $\varPhi ^{E_k}$. Say that A makes q queries to the PRF. Then there exists a PRF-adversary B against $\varPhi ^\pi$ making q queries and a PRP-adversary C against E such that

$$\begin{aligned} \alpha \le \beta + \gamma \,, \end{aligned}$$

(9)

where $\beta$ is the advantage of B and $\gamma$ is the advantage of C.

The above theorem lets us focus on PRFs built with URPs instead of PRPs.

3 PMAC

PMAC is a PRF-based MAC, which means we can focus on the underlying PRF. Throughout this paper we identify PMAC with its PRF. Furthermore, we focus on PMAC defined with a URP.

The original PMAC specifications [7, 19] have as message space the set of arbitrary length strings. Although our results focus on the dependency of PMAC on message length, it will suffice to consider strings with length a multiple of some block size in order to illustrate how the security bounds evolve as a function of message length. With this in mind, we define PHASH, first introduced by Minematsu and Matsushima [15]. Figure 1 depicts a diagram of PHASH.

Definition 2

(PHASH). Let $\mathsf {X}$ be a finite field of characteristic two with N elements. Let $\mathsf {M}:=\mathsf {X}^{\le N}$ and let ${\varvec{c}}\in \mathsf {X}^N$ be a sequence containing all elements of $\mathsf {X}$. Let $\pi$ be a URP over $\mathsf {X}$. Let $\omega = \pi (0)$, then ${PHASH}:\mathsf {M}\rightarrow \mathsf {X}$ is defined to be

$$\begin{aligned} {PHASH}({\varvec{m}}) :=\mathbf{1}\cdot {\widetilde{\pi }\left( {\varvec{m}}+\omega {\varvec{c}}_{\le \ell }\right) }\,, \end{aligned}$$

(10)

where ${\varvec{m}}$ has length $\ell$.

Fig. 1.

PHASH evaluated on a message $m = (m_1,m_2,m_3,m_4)$.

PHASH maps messages to a single block. PMAC sends this block through a last transformation, whose output will be the tag. We describe two different generic versions of PMAC, one in which the last transformation is independent of PHASH, and one in which it is not.

Definition 3

(PMAC). Consider ${PHASH}:\mathsf {M}\rightarrow \mathsf {X}$ with URP $\pi$ and let $c^*$ denote the last element of ${\varvec{c}}$. If y is the output of PHASH under message ${\varvec{m}}$, PMAC evaluated on ${\varvec{m}}$ is $\pi (y + c^*\omega )$.

Definition 4

(PMAC*). Consider ${PHASH}:\mathsf {M}\rightarrow \mathsf {X}$ with URP $\pi$. Let $\phi :\mathsf {X}\rightarrow \mathsf {X}$ be an independent URF. Then PMAC* is the composition of PHASH with $\phi$.

Although PMAC* is defined with an independent outer URF instead of a URP, all the results in the paper hold with slight modifications to the bounds if a URP is used.

The two specifications of PMAC define the sequence ${\varvec{c}}$ differently. Our attack against PMAC applies to the specification with Gray codes [7], which we will define in Sect. 6.4. As pointed out by Nandi and Mandal [16], in order to get a PRF-advantage upper bound of the form $q^2\ell /N$, the only requirement on ${\varvec{c}}$ is that each of its components are distinct.

4 PHASH Collision Probability

Definition 5

The collision probability of PHASH is

$$\begin{aligned} \max _{{\varvec{m}}^1,{\varvec{m}}^2\in \mathsf {M}, {\varvec{m}}^1\ne {\varvec{m}}^2}\mathbf {Pr}_{}\left[ {PHASH}({\varvec{m}}^1) = {PHASH}({\varvec{m}}^2)\right] . \end{aligned}$$

(11)

PHASH’s collision probability is closely linked with the security of PMAC and PMAC*. In particular, if an adversary finds a collision in PHASH, then it is able to distinguish PMAC and PMAC* from a URF. The converse is true for PMAC*, which is a well-known result; see for example Dodis and Pietrzak [9]. Concluding that a distinguishing attack against PMAC results in a collision found for PHASH has not been proven and is outside of the scope of the paper, although we conjecture that the statement holds. In either case, understanding the effect of the message length on PHASH’s collision probability will give us a good understanding of PMAC’s message length dependence.

In this section we compute bounds on the collision probability for PHASH. Minematsu and Matsushima [15] prove an upper bound for the collision probability of PHASH. We use their proof techniques and provide a lower bound as well.

Throughout this section we fix two different messages ${\varvec{m}}^1$ and ${\varvec{m}}^2$ in $\mathsf {M}$ of length $\ell _1$ and $\ell _2$, respectively, and consider the collision probability over these messages. Let ${\varvec{m}} = {\varvec{m}}^1\Vert {\varvec{m}}^2$ and ${\varvec{d}} = {\varvec{c}}_{\le \ell _1}\Vert {\varvec{c}}_{\le \ell _2}$.

If there exists i such that $m_i^1 = m_i^2$, then these blocks will cancel each other out in Eq. (11) and will not affect the collision probability, hence we remove them. Let $i_1, i_2,\ldots , i_k$ denote the indices of the blocks for which ${\varvec{m}}^1$ equals ${\varvec{m}}^2$, then define ${\varvec{m}}^*$ to be ${\varvec{m}}$ with the entries indexed by $i_1, i_2,\ldots , i_k$ and $i_1+\ell _1, i_2+\ell _1, \ldots , i_k+\ell _1$ removed; ${\varvec{d}}^*$ is defined similarly and $\ell ^*$ denotes the length of ${\varvec{m}}^*$ and ${\varvec{d}}^*$.

Let ${\varvec{x}}^w :={\varvec{m}}^* + w{\varvec{d}}^*$ for $w\in \mathsf {X}$. The vector ${\varvec{x}}^w$ represents the inputs to the permutation $\pi$ when $\pi (0)$ equals w, meaning the equality $\text {PHASH}({\varvec{m}}^1) = \text {PHASH}({\varvec{m}}^2)$ can be written as

$$\begin{aligned} \mathbf{1}\cdot {\widetilde{\pi }\left( {\varvec{x}}^w\right) }&= 0\,, \end{aligned}$$

(12)

given that $\pi (0) = w$. If there is a component of ${\varvec{x}}^w$ which does not equal any of the other components, then Eq. (12) will contain a $\pi$-output which is roughly independent of the other outputs, thereby making a collision unlikely when $\pi (0) = w$. For example, say that ${\varvec{x}}^w = (a, b, c, b)$, then Eq. (12) becomes $\pi (a)+\pi (b)+\pi (c)+\pi (b) = \pi (a)+\pi (c)$, which equals 0 with negligible probability.

Similarly, if there are an odd number of components of ${\varvec{x}}^w$ which equal each other, but do not equal any other components, then they will not cancel out, resulting again in an unlikely collision. For example, if ${\varvec{x}}^w = (a,a,a,b,b)$, then Eq. (12) becomes $\pi (a)$. In fact, a collision is only guaranteed under a given key w when each component of ${\varvec{x}}^w$ is paired with another component so that each pair cancels each other out in Eq. (12). Bounding the collision probability in Eq. (11) amounts to determining how many keys w there are for which each component of ${\varvec{x}}^w$ is paired.

We formalize these “equality classes” of components of ${\varvec{x}}^w$ as follows. Define I to be the set of integers from 1 to $\ell ^*$, $\left\{ 1,\ldots ,\ell ^*\right\}$, then the components of ${\varvec{x}}^w = (x_1^w, x_2^w,\ldots ,x_{\ell ^*}^w)$, induce the following equivalence relation on I: i is equivalent to j if and only if $x^w_i = x^w_j$. For $i\in I$, let [i] denote i’s equivalence class, and $\#[i]$ the number of elements in [i]. Let $R^w$ denote the set of equivalence class representatives where each representative is the smallest element of its class. Let $R_e^w$ be those $i\in R^w$ such that $\#[i]$ is even, and $R_o^w$ the complement of $R_e^w$ in $R^w$. Taking the example ${\varvec{x}}^w = (c,c,c,b,b,b,b,a)$, then $R^w$ would equal $\{1,4,8\}$ and $R_e^w$ is $\{4\}$.

Define $\mathbf {W}$ to be the set of $w\in \mathsf {X}$ such that $R_o^w$ is empty. In other words, the set $\mathbf {W}$ is the set of keys w for which ${\varvec{m}}^1$ and ${\varvec{m}}^2$ are guaranteed to collide.

Proposition 1

Let $F = {PHASH}$, then

$$\begin{aligned} \frac{\left|\mathbf {W}\right|}{N}\le \mathbf {Pr}_{}\left[ F({\varvec{m}}^1) = F({\varvec{m}}^2)\right] \le \frac{\left|\mathbf {W}\right|}{N}+ \frac{1}{N-\ell ^*+1}. \end{aligned}$$

(13)

Proof

Let $\varPi$ be the set of permutations on $\mathsf {X}$. Let $\delta _w$ be the number of distinct components in $0\Vert {\varvec{x}}^w$ and let $S_w$ be the set of ${\varvec{y}}$ such that $\mathbf{1}\cdot {{\varvec{y}}} = 0$ and $w\Vert {\varvec{y}}$ matches $0\Vert {\varvec{x}}^w$, where two sequences ${\varvec{a}}$ and ${\varvec{b}}$ of the same length match if $a_i = a_j$ if and only if $b_i = b_j$, for all i, j. We have that

$$\begin{aligned} \mathbf {Pr}_{}\left[ F({\varvec{m}}^1)+F({\varvec{m}}^2) = 0\right]&= \mathbf {Pr}_{}\left[ \mathbf{1}\cdot {\widetilde{\pi }({\varvec{x}}^\omega )} = 0\right] \end{aligned}$$

(14)

$$\begin{aligned}&= \frac{1}{N!}\cdot \left|\left\{ p\in \varPi \mid \mathbf{1}\cdot {\widetilde{p}\left( {\varvec{x}}^{p(0)}\right) } = 0\right\} \right|\end{aligned}$$

(15)

$$\begin{aligned}&= \frac{1}{N!}\cdot \sum _{w\in \mathsf {X}}\sum _{{\varvec{y}}\in S_w}\left|\left\{ p\in \varPi \mid \widetilde{p}(0\Vert {\varvec{x}}^w) = w\Vert {\varvec{y}}\right\} \right|\,. \end{aligned}$$

(16)

Note that for all w and ${\varvec{y}}\in S_w$,

$$\begin{aligned} \left|\left\{ p\in \varPi \mid \widetilde{p}(0\Vert {\varvec{x}}^w) = w\Vert {\varvec{y}}\right\} \right| = (N-\delta _w)!, \end{aligned}$$

(17)

hence we get

$$\begin{aligned} \mathbf {Pr}_{}\left[ F({\varvec{m}}^1) = F({\varvec{m}}^2)\right]&= \frac{1}{N!}\cdot \sum _{w\in \mathsf {X}}(N-\delta _w)!\cdot \left|S_w\right|. \end{aligned}$$

(18)

Let ${\varvec{y}}$ be such that $w\Vert {\varvec{y}}$ matches $0\Vert {\varvec{x}}^w$. Note that $y_i = y_j$ if and only if i is equivalent to j, and for any $i\in R^w$,

$$\begin{aligned} \sum _{j\in [i]}y_j&= {\left\{ \begin{array}{ll} 0 &{}\text { if }\#[i]\text { is even}\\ y_i &{}\text { otherwise}\,. \end{array}\right. } \end{aligned}$$

(19)

Then ${\varvec{y}}\in S_w$ if and only if $w\Vert {\varvec{y}}$ matches $0\Vert {\varvec{x}}^w$ and $\sum _{i\in R^w_o}y_i = 0$.

Let w be such that $x_i^w\ne 0$ for all i. The number of ${\varvec{y}}$ such that $w\Vert {\varvec{y}}$ matches $0\Vert {\varvec{x}}^w$ and $\sum _{i\in R^w_o}y_i = 0$ can be counted as follows. Consider ${\varvec{y}} = (y_1,\ldots ,y_{\ell ^*})$ satisfying the requirements, and enumerate the values in $R^w_e$: $i_1,i_2,\ldots , i_k$. By fixing $y_{i_1}, y_{i_2}, \ldots , y_{i_k}$, we determine all components of ${\varvec{y}}$ contained in the equivalence classes of $R^w_e$. Since $y_{i_1}, y_{i_2}, \ldots , y_{i_k}$ is a sequence of k distinct values, all different from w, there are $(N-1)!/(N-k-1)!$ possibilities for $y_{i_1}, y_{i_2}, \ldots , y_{i_k}$. If $R^w_o\ne \emptyset$, then we enumerate the elements of $R^w_o$: $j_1,j_2,\ldots ,j_l$. Similar to $R^w_e$, by determining $y_{j_1},y_{j_2},\ldots , y_{j_l}$ we will determine the remaining components of ${\varvec{y}}$. The sequence $y_{j_1}, y_{j_2},\ldots , y_{j_l}$ contains l distinct values, all different from $y_{i_1}, y_{i_2},\ldots , y_{i_k}$ and w, and such that $y_{j_1}+y_{j_2}+\cdots +y_{j_l} = 0$, resulting in at most $(N-k-1)!/(N-k-l)!$ possibilities. Putting this together, and observing that $k+l = \left|R^w_e\right|+\left|R^w_o\right| = \delta _w-1$, we get $\left|S_w\right| \le \frac{(N-1)!}{(N-\delta _w+1)!}$ when $R^w_o\ne \emptyset$ and $x_i^w\ne 0$ for all i. If $R^w_o=\emptyset$, then $\left|S_w\right| = \frac{(N-1)!}{(N-\delta _w)!}$.

By following similar reasoning, we get that if w is such that there exists $x_i^w = 0$, $\left|S_w\right|\le \frac{(N-1)!}{(N-\delta _w+1)!}$ when $R^w_o\ne \emptyset$, and $\left|S_w\right| = \frac{(N-1)!}{(N-\delta _w)!}$ otherwise.

Putting the above together, we have

$$\begin{aligned} \mathbf {Pr}_{}\left[ F({\varvec{m}}^1) = F({\varvec{m}}^2)\right]&\le \frac{\left|\mathbf {W}\right|}{N}+ \frac{1}{N}\sum _{w\in \overline{\mathbf {W}}}\frac{1}{N-\delta _w+1}, \end{aligned}$$

(20)

and since the computation of $\left|S_w\right|$ is exact when $R^w_o=\emptyset$, we get

$$\begin{aligned} \frac{\left|\mathbf {W}\right|}{N}\le \mathbf {Pr}_{}\left[ F({\varvec{m}}^1) = F({\varvec{m}}^2)\right] . \end{aligned}$$

(21)

$\quad \square$

5 Necessary Conditions for a Collision

This section provides a geometric interpretation of the set $\mathbf {W}$ which facilitates finding necessary conditions for $\mathbf {W}$ to contain more than two elements.

5.1 Evenly Covered Sets

Recall that an element w of $\mathsf {X}$ is in $\mathbf {W}$ only if $R^w_o = \emptyset$, meaning $\#[i]$ is even for all $i\in R^w$. Two components $x_i^w$ and $x_j^w$ of ${\varvec{x}}^w$ are equal if and only if

$$\begin{aligned} w = \frac{m_i^*-m_j^*}{d_j^*-d_i^*}, \end{aligned}$$

(22)

since the points such that $(d_i,m_i) = (d_j,m_j)$ were removed earlier when forming ${\varvec{m}}^*$ from ${\varvec{m}}$. In particular, Eq. (22) says that $x_i^w$ equals $x_j^w$ if and only if the points $(d_i^*,m_i^*)$ and $(d_j^*,m_j^*)$ lie on a line with slope w. Since $\#[i]$ is even, we know that there are an even number of points on the line through $(d_i^*,m_i^*)$ with slope w, which motivates the following definition.

Definition 6

Let $\mathsf {P}\subset \mathsf {X}^2$ be a set of points. A line evenly covers $\mathsf {P}$ if it contains an even number of points from $\mathsf {P}$. A slope $w\in \mathsf {X}$ evenly covers $\mathsf {P}$ if all lines with slope w evenly cover $\mathsf {P}$. A subset of $\mathsf {X}$ evenly covers $\mathsf {P}$ if all slopes in the subset evenly cover $\mathsf {P}$.

We let $\mathbf {P}$ denote the set of points $(d_i, m_i)$ for $1\le i\le \ell$. Applying the above definition together with Eq. (22), we get the following proposition.

Proposition 2

An element $w\in \mathsf {X}$ is in $\mathbf {W}$ if and only if w evenly covers $\mathbf {P}$.

Using this geometric interpretation, we obtain the upper bound proved by Minematsu and Matsushima [15] for the collision probability of PHASH.

Proposition 3

$$\begin{aligned} \left|\mathbf {W}\right|&\le \ell ^*-1 \end{aligned}$$

(23)

Proof

Given a point $p_0\in \mathbf {P}$, all possible slopes connecting $p_0$ to another point in $\mathbf {P}$ can be generated from the lines connecting the points. This results in at most $\left|\mathbf {P}\right|-1$ different slopes covering $\mathbf {P}$, hence an upper bound for $\left|\mathbf {W}\right|$ is $\left|\mathbf {P}\right|-1 = \ell ^*-1$. $\quad \square$

It is easy to construct sets evenly covered by two slopes. Consider $\mathsf {P}:=\left\{ (x_1, 0), (x_1, 1), (x_2,0), (x_2,1)\right\}$, depicted in Fig. 2. The possible slopes are 0 and $(x_1+x_2)^{-1}$. Throughout the paper we do not consider $\infty$ to be a slope, since such a slope would only be possible if $d_i^* = d_j^*$ in Eq. (22), which happens only if $m^*_i = m^*_j$. The lines with slope 0, from $(x_1,0)$ to $(x_2,0)$ and from $(x_1,1)$ to $(x_2,1)$, evenly cover $\mathsf {P}$. Similarly, the lines with slope $(x_1+x_2)^{-1}$, from $(x_1,0)$ to $(x_2,1)$ and from $(x_1,1)$ to $(x_2,0)$, also evenly cover $\mathsf {P}$. Therefore $\mathsf {P}$ is evenly covered by $\left\{ 0,(x_1+x_2)^{-1}\right\}$.

Fig. 2.

A set of four points evenly covered by the slopes 0 and $(x_1+x_2)^{-1}$. The x-coordinates of the points are $x_1$ and $x_2$, and the y-coordinates are 0 and 1.

The above set can be converted into two messages: ${\varvec{m}}_1 = (0,0)$ and ${\varvec{m}}_2 = (1,1)$. Setting $x_1 = c_1$ and $x_2 = c_2$, then we know that the collision probability of ${\varvec{m}}_1$ and ${\varvec{m}}_2$ is at least .

Proposition 4

There exist messages ${\varvec{m}}_1$ and ${\varvec{m}}_2$ such that $\left|\mathbf {W}\right|\ge 2$.

Note that $\mathbf {P}$ constructed from ${\varvec{m}}^*$ contains at most two points per x-coordinate.

5.2 Properties of Evenly Covered Sets

Although Proposition 3 gives a good upper bound for the collision probability of PHASH, it does not use any of the structure of evenly covered sets. In this section we explore various properties of evenly covered sets, allowing us to relate their discovery to NP-hard problems in Sect. 5.3.

The following lemma shows that removing an evenly covered subset from an evenly covered set results in an evenly covered set.

Lemma 1

Let $\mathsf {P}\subset \mathsf {X}^2$ and let $\mathsf {W}\subset \mathsf {X}$ be a set evenly covering $\mathsf {P}$. Say that $\mathsf {P}$ contains a subset $\mathsf {P}'$ evenly covered by $\mathsf {W}$ as well, then $\mathsf {P}\setminus \mathsf {P}'$ is evenly covered by $\mathsf {W}$.

Proof

Let $\mathsf {Q}:=\mathsf {P}\setminus \mathsf {P}'$. The set $\mathsf {W}$ evenly covers $\mathsf {Q}$ if and only if every line with slope $w\in \mathsf {W}$ contains an even number of points in $\mathsf {Q}$. Let $p\in \mathsf {Q}$ and $w\in \mathsf {W}$ and consider the line $\lambda$ with slope w through point p. By hypothesis, $\lambda$ evenly covers $\mathsf {P}$ and $\mathsf {P}'$. By removing $\mathsf {P}'$ from $\mathsf {P}$, an even number of points are removed from $\lambda$, resulting in $\lambda$ evenly covering $\mathsf {Q}$. $\quad \square$

If a set $\mathsf {P}$ is evenly covered by at least two slopes u and v, then all the points in the set lie in a loop.

Definition 7

Let $\mathsf {P}\subset \mathsf {X}^2$ be evenly covered by $\mathsf {W}\subset \mathsf {X}$. A (u, v)-loop in $(\mathsf {W},\mathsf {P})$ is a sequence of points $(p_1, p_2,\ldots ,p_k)$ with two different slopes $u,v\in \mathsf {W}$ such that $p_i$ and $p_{i+1\pmod {k}}$ lie on a line with slope u for i odd, and on a line with slope v otherwise.

The set from Fig. 2 contains $(0,(x_1+x_2)^{-1})$-loops. In fact, there are always at least four points in any (u, v)-loop. Note that there must be at least three points since there are two distinct slopes. If there are only three points then $p_1$ is connected to $p_2$ via u, $p_2$ is connected to $p_3$ via v, and $p_3$ must be connected to $p_1$ via u, resulting in all three lying on the same line with slope u, but also $p_2$ lying on a line with slope v with $p_3$, resulting in a contradiction. Figure 3 shows a set with more complicated loops, including two which loop over all points in the set.

Lemma 2

Let $\mathsf {P}\subset \mathsf {X}^2$ be evenly covered by $\mathsf {W}\subset \mathsf {X}$. Let $u,v\in \mathsf {W}$, then every point in $\mathsf {P}$ is in a (u, v)-loop starting with slope u and ending with slope v.

Proof

Let $p_0\in \mathsf {P}$, then by hypothesis there is another point $p_1$ in $\mathsf {P}$ lying on a line with slope u connecting to $p_0$. Similarly, there is a point $p_2$ different from $p_0$ and $p_1$ lying on a line with slope v connected to $p_1$. Continuing like this, we can create a sequence of points $p_0, p_1, \ldots , p_k$ until $p_{k+1} = p_i$ for some $i\le k$, with the property that adjacent points in the sequence are connected by lines alternating with slope u and v.

If $i = 0$, then we are done. Otherwise, consider $p_{i-1}$, $p_i$, $p_{i+1}$, and $p_k$. Say that $p_{i-1}$ is connected to $p_i$ via a line with slope u, so that $p_i$ is connected to $p_{i+1}$ via a line with slope v. If $p_k$ is connected to $p_i$ via a line with slope v, then there are three points on the same line with slope v: $p_i, p_{i+1}$, and $p_k$. This means there is a fourth point $p^*$ on the same line. Since $p_k$ is connected to $p_{i+1}$ via v, the sequence $p_{i+1},p_{i+2}, \ldots , p_k$ forms a (u, v)-loop. We remove the (u, v)-loop from $\mathsf {P}$, which is evenly covered by u and v, resulting in a set evenly covered by u and v, and we continue by induction. Similar reasoning can be applied when $p_k$ is connected to $p_i$ via u. $\quad \square$

Proposition 5

The sum of the x-coordinates in a (u, v)-loop must be zero.

Proof

Say that $(x_1,y_1), (x_2,y_2), \ldots , (x_k,y_k)$ are the points in the loop. Then

$$\begin{aligned} y_i + y_{i+1} = \delta _i(x_i+x_{i+1\,(\text {mod }k)})\,, \end{aligned}$$

(24)

where $\delta _i$ is u if i is odd, and v otherwise. Since

$$\begin{aligned} (y_1 + y_2) + (y_2 + y_3) + \cdots + (y_{k-1}+y_k) + (y_k+y_1) = 0\,, \end{aligned}$$

(25)

we have that

$$\begin{aligned}&u(x_1+x_2) + v(x_2+x_3) + u(x_3+x_4) + \cdots \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \quad + u(x_{k-1}+x_{k}) + v(x_k+x_1) = 0\,, \end{aligned}$$

(26)

therefore

$$\begin{aligned} (u+v)(x_1+x_2+\cdots +x_k) = 0\,. \end{aligned}$$

(27)

Since $u\ne v$, it must be the case that $x_1+x_2+\cdots +x_k = 0$. $\quad \square$

Fig. 3.

A set of points evenly covered by the slopes u, v, and w. Each point is accompanied by another point with the same x-coordinate. The x-coordinates of the pairs are indicated below the lower points.

Adversaries can only construct sets $\mathsf {P}$ where there are at most two points per x-coordinate. Therefore, either all loops only contain points (x, y) for which there is exactly one other point $(x,y')$ with the same x-coordinate, or there exists a loop with a point which is the only one with that x-coordinate. For example, Figs. 2 and 3 depict evenly covered sets where every loop always contains all x-coordinate pairs. If we consider the only loop in Fig. 2, then we get

$$\begin{aligned} 0\cdot (x_1+x_2) + (x_1+x_2)^{-1}(x_2+x_1) + 0\cdot (x_1+x_2) + (x_1+x_2)^{-1}(x_2+x_1)\,, \end{aligned}$$

(28)

which trivially equals zero. All loops in Fig. 3 also trivially sum to zero.

Fig. 4.

A set of points evenly covered by the slopes u, v, and w. None of the points are accompanied by another point with the same x-coordinate. The points are labelled by their x-coordinates.

In contrast, Fig. 4 depicts an evenly covered set in which we get a non-trivial sum of the x-coordinates:

$$\begin{aligned} u\cdot a + v(a+c) + u(c+b) + v\cdot b = (u+v)(a+b+c) = 0\,, \end{aligned}$$

(29)

hence such a set only exists if $a+b+c = 0$.

Therefore, Proposition 5 only poses a non-trivial restriction on the x-coordinates if there is a loop which contains a point without another point sharing its x-coordinate. If the loop contains all pairs of points with the same x-coordinates, then the x-coordinates will trivially sum to zero. This is why in the case of Fig. 2 there are no restrictions on the x-coordinates, other than the fact that they must be distinct, resulting in the existence of sets evenly covered by two slopes.

Fig. 5.

Illustration of loops with three slopes.

In the case of Fig. 3 however, there are additional restrictions on the x-coordinates. Consider the two points at x-coordinate 0. Then there is part of a (u, v)-loop connecting them, and part of a (u, w)-loop connecting them, and combining both parts we get a full loop using all three slopes; see the left hand side of Fig. 5. A similar loop involving all three slopes can be constructed around the points with x-coordinate b. Using these two loops, we get the following equations. From the left hand side of Fig. 5 we have

$$\begin{aligned} ua + va&= wb + u(b+c) + w(a+c) + ua\end{aligned}$$

(30)

$$\begin{aligned} (u+v)a&= (w+u)(a+b+c)\,. \end{aligned}$$

(31)

From the right hand side of Fig. 5 we have

$$\begin{aligned} (u+v)(b+c)&= wb + ua + w(a+b)\end{aligned}$$

(32)

$$\begin{aligned} (u+v)(b+c)&= (w+u)a\,. \end{aligned}$$

(33)

Combining both, we get the following:

$$\begin{aligned} \frac{a+b+c}{a}&= \frac{a}{b+c}\end{aligned}$$

(34)

$$\begin{aligned} a^2 + b^2 + c^2 + ab + ac&= 0\,. \end{aligned}$$

(35)

The last equation above can be described as a so-called quadratic form. A quadratic form over $\mathsf {X}$ is a homogeneous multivariate polynomial of degree two. In our case, the quadratic form can be written as ${\varvec{x}}^TQ{\varvec{x}}$, where ${\varvec{x}}\in \mathsf {X}^n$ is the list of variables, and $Q\in \{0,1\}^{n\times n}$ is a matrix with entries in $\left\{ 0,1\right\}$. We say that ${\varvec{x}}_*$ is a solution to Q if ${\varvec{x}}_*^TQ{\varvec{x}}_* = 0$, and the quadratic form Q is non-trivial if there exists ${\varvec{x}}\ne 0$ such that ${\varvec{x}}^TQ{\varvec{x}} \ne 0$.

So the evenly covered set from Fig. 3 only exists if the x-coordinates satisfy some non-trivial quadratic form. The same is true for any evenly covered set where all loops always contain pairs of points with the same x-coordinate.

Proposition 6

Let $\mathsf {P}\subset \mathsf {X}^2$ be evenly covered by $\mathsf {W}\subset \mathsf {X}$ with $\mathsf {W}\ge 3$. Say that all loops in $\mathsf {P}$ contain only pairs of points with the same x-coordinates. Then there exists a subset S of k x-coordinates, and a non-trivial quadratic form described by a matrix $Q\in \left\{ 0,1\right\} ^{k\times k}$ over k variables, such that when the k elements of S are placed in a vector ${\varvec{x}}_*\in \mathsf {X}^k$, ${\varvec{x}}_*^TQ{\varvec{x}}_* = 0$.

Proof

Pick three slopes, u, v, w in $\mathsf {W}$. We know that there are at least four points in $\mathsf {P}$. Pick two pairs of points with the same x-coordinates: $(p,p')$ and $(q,q')$. Consider the (u, v)-loop starting at p. By hypothesis it must contain $p'$. We let ${\varvec{a}} = (a_1,a_2,\ldots ,a_{k_a})$ denote the sequence of x-coordinates of the part of the (u, v)-loop from p to $p'$. Note that $a_1$ equals $a_{k_a}$ since p and $p'$ have the same x-coordinates. Similarly, the (u, v)-loop starting at q must contain $q'$, and we denote the sequence of x-coordinates of the part of the (u, v)-loop from q to $q'$ by ${\varvec{b}} = (b_1,b_2,\ldots ,b_{k_b})$. The same holds for the (v, w)-loops containing p and q, and we define the x-coordinate sequences ${\varvec{e}}$ and ${\varvec{f}}$ similarly.

Let y denote the difference in the y-coordinates of p and $p'$. For ${\varvec{a}}$ we have the following:

$$\begin{aligned} u(a_1+a_2) + v(a_2+a_3) + \cdots + \delta (u,v)_{k_a}(a_{k_a-1}+a_{k_a}) = y\,, \end{aligned}$$

(36)

where $\delta (u,v)_{k_a}$ is u if $k_a$ is even and v otherwise. Collecting the terms, if $k_a$ is even, we get

$$\begin{aligned} u(a_1+a_2+\cdots +a_{k_a-1}+a_{k_a}) + v(a_2+\cdots +a_{k_a-1}) = y\,, \end{aligned}$$

(37)

and since $a_1 = a_{k_a}$, we know that

$$\begin{aligned} (u+v)(a_2+\cdots +a_{k_a-1}) = y\,. \end{aligned}$$

(38)

If $k_a$ is odd, then we get

$$\begin{aligned} (u+v)(a_1+a_2+\cdots +a_{k_a-1}) = y\,. \end{aligned}$$

(39)

Note that it cannot be the case that $\sum a_i = 0$, since $y\ne 0$.

Similar reasoning applied to ${\varvec{b}}$ gives

$$\begin{aligned} \begin{array}{cc} (v+w)(b_2+\cdots +b_{k_b-1}) = y &{} \text { if }k_b \text { is even}\\ (v+w)(b_1+\cdots +b_{k_b-1}) = y &{} \text {otherwise}\,. \end{array} \end{aligned}$$

(40)

Regardless of $k_a$ and $k_b$’s parities, setting both equations equal to each other results in the following equation:

$$\begin{aligned} \frac{u+v}{v+w} = \frac{\sum b_i}{\sum a_i}\,. \end{aligned}$$

(41)

Applying the same result to ${\varvec{e}}$ and ${\varvec{f}}$, we get

$$\begin{aligned} \frac{u+v}{v+w} = \frac{\sum f_i}{\sum e_i}\,. \end{aligned}$$

(42)

As a result, we have

$$\begin{aligned} \left( \sum b_i\right) \left( \sum e_i\right) + \left( \sum a_i\right) \left( \sum f_i\right) = 0\,, \end{aligned}$$

(43)

which is the solution to a quadratic form. $\quad \square$

5.3 Computational Hardness

As shown in Propositions 5 and 6, either there is a loop where the x-coordinates non-trivally sum to zero, or there is a subset of the x-coordinates which form the solution to some non-trivial quadratic form. The former is Subset Sum (SS), whereas the latter we name the binary quadratic form (BQF) problem.

Definition 8

(Subset Sum Problem ( SS )). Given a finite field $\mathsf {X}$ of characteristic two and a subset $S\subset \mathsf {X}$, determine whether there is a subset $S_0\subset S$ such that $\sum _{x\in S_0}x = 0$.

Definition 9

(Binary Quadratic Form Problem ( BQF )). Given a finite field $\mathsf {X}$ of characteristic two and a subset $S\subset \mathsf {X}$, determine whether there is a non-trivial quadratic form $Q\in \left\{ 0,1\right\} ^{k\times k}$ with a solution ${\varvec{x}}_*$ made up of distinct components from S.

SS is know to be NP-complete. In Appendix B we show that BQF-t, a generalization of BQF, is NP-complete as well. The problem of finding either a subset summing to zero or a non-trivial quadratic form we call the SS-or-BQF problem.

Conjecture 1

There do not exist polynomial time algorithms solving SS-or-BQF.

Definition 10

(PHASH Problem). Given a finite field $\mathsf {X}$ of characteristic two and a sequence of masks ${\varvec{c}}$, determine whether there is a collision in PHASH with probability greater than , where $N = \left|\mathsf {X}\right|$.

Given a collision in PHASH one can easily find a solution to SS-or-BQF. The converse does not necessarily hold, which means SS-or-BQF cannot be reduced to the PHASH problem in general, although we can conclude the following.

Theorem 3

One of the following two statements holds.

• 1. There are infinitely many input sizes for which the PHASH problem does not have a solution, but SS-or-BQF does.

• 2. For sufficiently large input sizes, SS-or-BQF can be reduced to the PHASH problem.

Proof

Both the PHASH and SS-or-BQF problems are decision problems, so the output of the algorithms solving the problems is a yes or a no, indicating whether the problems have a solution or not. Note that the inputs to both problems are identical. The reductions consist of simply converting the input to one problem into the input of the other, and then directly using the output of the algorithm solving the problem.

We proved that a yes instance for PHASH becomes a yes instance for SS-or-BQF: if you have an instance of SS-or-BQF, then you can convert it into a PHASH problem, and if you are able to determine that PHASH has a collision with sufficient probability, then SS-or-BQF has a solution. Similarly, a no instance for SS-or-BQF means a no instance for PHASH.

The issue is when there exists a no instance for PHASH and a yes instance for SS-or-BQF for a particular input size. If there are finitely many input sizes for which there is a no instance for PHASH and a yes instance for SS-or-BQF simultaneously, then there exists an r such that for all input sizes greater than r a no instance for PHASH occurs if and only if a no instance for SS-or-BQF occurs, and a yes instance for PHASH occurs if and only if a yes instance for SS-or-BQF occurs. Therefore, an algorithm which receives a no instance for PHASH can say that the corresponding SS-or-BQF problem is a no instance, and similarly for the yes instances, which is our reduction. Otherwise there are infinitely many input sizes for which PHASH is a no instance, and SS-or-BQF is a yes instance. $\quad \square$

If statement 1 holds, then there are infinitely many candidates for an instantiation of PMAC* with security bound independent of the message length. If statement 2 holds, and we assume that SS-or-BQF is hard to solve, then finding a collision for generic PHASH is computationally hard.

6 Finding Evenly Covered Sets

The previous section focused on determining necessary conditions for the existence of evenly covered sets, illustrating the difficulty with which such sets are found. Nevertheless, finding evenly covered sets becomes feasible in certain situations. In this section we provide an alternative description of evenly covered sets in order to find sufficient conditions for their existence.

6.1 Distance Matrices

Let $(x_1, y_1), (x_2,y_2), \ldots , (x_n, y_n)$ be an enumeration of the elements of $\mathsf {P}\subset \mathsf {X}^2$. If $w\in \mathsf {X}$ covers $\mathsf {P}$ evenly, then the line with equation $y = w(x-x_1) + y_1$ must meet $\mathsf {P}$ in an even number of points. In particular, there must be an even number of $x_i$ values for which $w(x_i-x_1) + y_1 = y_i$, or in other words, the vector

$$\begin{aligned} w\cdot (x_1-x_1, x_2-x_1, \ldots , x_{n}-x_1) \end{aligned}$$

(44)

must equal

$$\begin{aligned} (y_1-y_1, y_2-y_1, \ldots , y_n-y_1) \end{aligned}$$

(45)

in an even number of coordinates. The same must hold for the lines starting from all other points in $\mathsf {P}$.

Let $\varDelta ^{{\varvec{x}}}$ be the matrix with (i, j) entry equal to $x_i-x_j$ and $\varDelta ^{{\varvec{y}}}$ the matrix with (i, j) entry equal to $y_i-y_j$. We write $A\sim B$ if matrix $A\in \mathsf {X}^{n\times n}$ equals matrix $B\in \mathsf {X}^{n\times n}$ in an even number of entries in each row. Then, following the reasoning from above, we have that $w\in \mathsf {X}$ covers $\mathsf {P}$ evenly only if $\varDelta ^{{\varvec{y}}}\sim w\varDelta ^{{\varvec{x}}}$.

The matrices $\varDelta ^{{\varvec{x}}}$ and $\varDelta ^{{\varvec{y}}}$ are so-called distance matrices, that is, symmetric matrices with zero diagonal. Entry (i, j) in these distance matrices represents the “distance” between $x_i$ and $x_j$, or $y_i$ and $y_j$. In fact, starting from distance matrices M and D such that $M\sim wD$ we can also recover a set $\mathsf {P}$ evenly covered by w: interpret the matrices M and D as the distances between the points in the set $\mathsf {P}$. This proves the following lemma.

Lemma 3

Let $k\le n-1$ and let $\mathsf {W}\subset \mathsf {X}$ be a set of size k. There exist n by n distance matrices M and D such that $M\sim wD$ for all $w\in \mathsf {W}$ if and only if there exists $\mathsf {P}$ with $\left|\mathsf {P}\right| = n$ and $\mathsf {W}$ evenly covers $\mathsf {P}$.

From the above lemma we can conclude that the existence of $\mathsf {P}\subset \mathsf {X}^2$ evenly covered by $\mathsf {W}\subset \mathsf {X}$ is not affected by the following transformations:

• 1. Translating the set $\mathsf {P}$ by any vector in $\mathsf {X}^2$. This also preserves the set $\mathsf {W}$.

• 2. Subtracting any element $w_0\in \mathsf {W}$ from the set $\mathsf {W}$.

• 3. Scaling the set $\mathsf {P}$ in either x or y-direction by a non-zero scalar in $\mathsf {X}$.

• 4. Scaling the set $\mathsf {W}$ by any non-zero element of $\mathsf {X}$.

Fig. 6.

Non-trivial example of a set with 12 points evenly covered by three slopes. Horizontal points lie on the same y-coordinate, and vertical points on the same x-coordinate. Since there are six points on a line with slope u, the natural graph is not regular.

6.2 Connection with Graphs

Let $\mathsf {P}\subset \mathsf {X}^2$ be evenly covered by $\mathsf {W}\subset \mathsf {P}$. The pair $(\mathsf {P}, \mathsf {W})$ has a natural graph structure with vertices $\mathsf {P}$ and an edge connecting two vertices $p_1$ and $p_2$ if and only if the line connecting them has slope in $\mathsf {W}$. Figures 2 and 3 provide diagrams which can also be viewed as examples of the natural graph structure. In this section we connect the existence of evenly covered sets with so-called factorizations of a graph. See Appendix A for a review of the basic graph theoretic definitions used in this section.

Each vertex in the natural graph has at least $\left|\mathsf {W}\right|$ neighbours, and if there are two points per line in $\mathsf {P}$, then the graph is $\left|\mathsf {W}\right|$-regular. Vertices have more than $\left|\mathsf {W}\right|$ neighbours only if they are on a line with more than two points. Since we are not interested in the redundancy from connecting a point with all points on the same line, we only consider graphs without the additional edges.

Definition 11

A graph associated to $(\mathsf {P},\mathsf {W})$ is a $\left|\mathsf {W}\right|$-regular graph G with $\mathsf {P}$ as its set of vertices and an edge between two vertices $p_1$ and $p_2$ only if the line connecting $p_1$ with $p_2$ has slope in $\mathsf {W}$.

Any graph associated to $(\mathsf {P}, \mathsf {W})$ is a subgraph of the natural graph structure described above, and there could be multiple associated graphs, depending upon what edges are chosen to connect multiple points lying on the same line. For example, Fig. 6 depicts an evenly covered set with twelve points, six of which lie on the same line. As depicted in Fig. 7, it can easily be converted into an associated graph.

Fig. 7.

The diagram from Fig. 6 converted into an associated graph. The slopes u, v, and w induce a natural 1-factorization of the graph.

The following definition allows us to describe another property that associated graphs have.

Definition 12

A k-factor of a graph G is a k-regular subgraph with the same vertex set as G. A k-factorization partitions the edges of a graph in disjoint k-factors.

Associated graphs have a 1-factorization induced by $\mathsf {W}$, where each 1-factor is composed of the edges associated to the same slope in $\mathsf {W}$. See Fig. 7 for an example.

We know that every pair $(\mathsf {P},\mathsf {W})$ has an associated $\left|\mathsf {W}\right|$-regular graph with 1-factorization. In order to determine the existence of evenly covered sets we need to consider when a k-regular graph with 1-factorization describes the structure of some pair $(\mathsf {P},\mathsf {W})$ with $\left|\mathsf {W}\right| = k$. By first fixing a graph with a 1-factorization, it is possible to set up a system of equations to determine the existence of distance matrices M and D, and slopes $\mathsf {W}$ such that $M\sim wD$ for all $w\in \mathsf {W}$. Then, by applying Lemma 3, we will have our desired pair $(\mathsf {P},\mathsf {W})$.

Definition 13

Let G be a regular graph with vertices $(v_1,\ldots ,v_n)$ and a 1-factorization, and let $\mathsf {X}^{n\times n}$ denote the set of matrices over $\mathsf {X}$. Define $\mathbf {S}_G\subset \mathsf {X}^{n\times n}$ to be the matrices where entry (i, j) equals entry (k, l) if and only if the edges $(v_i,v_j)$ and $(v_k,v_l)$ are in the same 1-factor of G.

Proposition 7

There exists a set $\mathsf {P}\subset \mathsf {X}^2$ with n elements evenly covered by $\mathsf {W}\subset \mathsf {X}$ with $\left|\mathsf {W}\right| = k$ if and only if there exists a k-regular graph G of order n with a 1-factorization such that there is a solution to

$$\begin{aligned} M = S\circ D\,, \end{aligned}$$

(46)

where $S\in \mathbf {S}_G$, $M, D\in \mathsf {X}^{n\times n}$ are distance matrices, and $\circ$ denotes elementwise multiplication.

Therefore by picking a regular graph with a 1-factorization and solving a system of equations, we can determine the existence of pairs $(\mathsf {P},\mathsf {W})$ for various sizes, in order to determine a lower bound for PHASH’s collision probability.

6.3 Latin Squares and Abelian Subgroups

In this section we consider what happens when we solve Eq. (46) with a 1-factorization of the complete graph of order n. Since we look at complete graphs, finding a solution would imply the existence of sets with n points evenly covered by $n-1$ slopes, the optimal number as shown by Proposition 3. We describe a necessary and sufficient condition on the matrix D from Eq. (46), which in turn becomes a condition on the x-coordinates of the evenly covered sets.

As described by Laywine and Mullen [13, Sect. 7.3], 1-factorizations of a complete graph G of order n, with n even, are in one-to-one correspondence with reduced, symmetric, and unipotent Latin squares, that is, n by n matrices with entries in $\mathbb {N}$ such that

• 1. the first row enumerates the numbers from 1 to n,

• 2. the matrix is symmetric, that is, entry (i, j) equals entry (j, i),

• 3. the diagonal consists of just ones,

• 4. and each natural number from 1 to n appears just once in every row and column.

The correspondence between 1-factorizations of complete graphs and Latin squares works by identifying row i and column i with a vertex in the graph, labelling the 1-factor containing edge (1, i) with i, and then setting entry (i, j) equal to the label of the 1-factor containing edge (i, j). This is exactly the structure of the matrices in $\mathbf {S}_G$.

Let n be a power of two. The abelian 2-group of order n is a commutative group in which every element has order two, that is, $a+a = 0$ for all elements a in the group. The Cayley table of the abelian 2-group of order n can be written as a reduced, symmetric, and unipotent Latin square.

Definition 14

The (i, j) entry of the Cayley table of the abelian 2-group with $\ell$ elements is denoted $\gamma (i,j)$.

Lemma 4

$\gamma (i,\gamma (i,j)) = j$.

Proposition 8

Let G denote the complete graph of order n, where n is a power of two, with 1-factorization induced by the Cayley table of the abelian 2-group of order n. Then Eq. (46) has a solution if and only if the first row of D forms an additive subgroup of $\mathsf {X}$ of order n.

The above proposition shows that the graph structure corresponding to the abelian 2-group induces the same additive structure on the x-coordinates of the evenly covered set. This transfer of structure only works with this particular 1-factorization of the complete graph. In general, reduced, symmetric, and unipotent Latin squares do not even correspond to the Cayley table of some group: associativity is not guaranteed. Furthermore, 1-factorizations of non-complete graphs do not necessarily even form Latin squares; see for example Fig. 6.

Proof

Denote the first row of S by $s_1, s_2, \ldots , s_n$, and the first row of D by $d_1, \ldots , d_n$. Note that D is entirely determined by its first row, since the (i, j) entry of D is $d_i+d_j$, and since S follows the form of $\gamma$, it is entirely determined by its first row as well. In particular, the (i, j) entry of S is $s_{\gamma (i,j)}$, where $\gamma (i,j)$ is the (i, j) entry of the Cayley table.

We need to determine the conditions under which $S\circ D$ is a distance matrix, as a function of $s_1,\ldots , s_n$ and $d_1,\ldots , d_n$. This happens if and only if the (i, j) entry of $S\circ D$ is equal to $s_id_i + s_jd_j$:

$$\begin{aligned} s_id_i + s_jd_j&= s_{\gamma (i,j)}(d_i+d_j)\,. \end{aligned}$$

(47)

Furthermore, it must be the case that

$$\begin{aligned} s_id_i + s_{\gamma (i,j)}d_{\gamma (i,j)}&= s_{j}(d_i + d_{\gamma (i,j)})\,, \end{aligned}$$

(48)

since $\gamma (i, \gamma (i,j)) = j$. Therefore

$$\begin{aligned} s_jd_j + s_{\gamma (i,j)}d_{\gamma (i,j)}&= s_{\gamma (i,j)}(d_i+d_j) + s_j(d_i+d_{\gamma (i,j)})\end{aligned}$$

(49)

$$\begin{aligned} (s_j+s_{\gamma (i,j)})(d_i+d_j+d_{\gamma (i,j)})&= 0\,. \end{aligned}$$

(50)

Since S must follow the Latin square structure, the first row of S must consist of n distinct entries, hence $s_j\ne s_{\gamma (i,j)}$ and so $d_i+d_j+d_{\gamma (i,j)} = 0$. Therefore, $d_1,\ldots ,d_n$ satisfies the equations of the Cayley table, hence they form an additive subgroup of $\mathsf {X}$.

Continuing, we have the following equations:

$$\begin{aligned} s_id_i + s_jd_j + s_{\gamma (i,j)}d_{\gamma (i,j)} = 0\,. \end{aligned}$$

(51)

In order for these equations to be satisfied, $s_1d_1, \ldots , s_nd_n$ must form an additive subgroup of $\mathsf {X}$ as well. In particular, there must exist an isomorphism $\phi$ mapping $d_i$ to $s_id_i$, which can be written as $d_i^{-1}\phi (d_i) = s_i$ for $i > 1$. The only requirement for the existence of such an isomorphism is that $x^{-1}\phi (x)$ must map to distinct values. Picking $x\mapsto x^2$ as the isomorphism, we have our desired result. Note that the $d_i$ must be distinct, otherwise the $s_i$ are not distinct, contradicting the fact that S follows the Latin square structure. $\quad \square$

6.4 Application to PMAC

Before we present an attack, we first need the following lemma.

Lemma 5

Let $\mathsf {P}$ and $\mathsf {P}'$ be disjoint subsets of $\mathsf {X}^2$ evenly covered by $\mathsf {W}\subset \mathsf {X}$. Then $\mathsf {P}\cup \mathsf {P}'$ is evenly covered by $\mathsf {W}$.

A collision in PHASH with probability $(\ell -1)/N$ can be found as follows. Take ${\varvec{c}}$ and let k be the smallest index such that ${\varvec{c}}_{\le k}$ contains a subsequence ${\varvec{c}}'$ of length $\ell$ such that the elements $\left\{ c'_1+c'_1, c'_1+c'_2, \ldots , c'_1+c'_\ell \right\}$ form an additive subgroup of $\mathsf {X}$. Let $\mu$ be the mapping which maps indices of ${\varvec{c}}'$ onto indices of ${\varvec{c}}$, so that $c'_i = c_{\mu (i)}$.

Let D be a distance matrix in $\mathsf {X}^{\ell \times \ell }$ such that its first row is equal to $(c'_1+c'_1, c'_1+c'_2, \ldots , c'_1+c'_\ell )$; recall that a distance matrix is completely determined by its first row. Let G be the complete graph of order $\ell$ with 1-factorization determined by the abelian 2-group of order $\ell$. Solve Eq. (46), that is, find a distance matrix M such that there exists $S\in \mathbf {S}_G$ where

$$\begin{aligned} M = S\circ D\,. \end{aligned}$$

(52)

Let ${\varvec{m}}^1$ denote the first row of M, and let $\mathsf {W}$ denote the elements making up the first row of S, without the first row element. Then the set $\mathsf {P}:=\left\{ (c_1',m_1^1), \ldots , (c_\ell ',m_\ell ^1)\right\}$ is evenly covered by $\mathsf {W}$, which contains $\ell -1$ slopes.

By translating $\mathsf {P}$ vertically by some constant, say 1, construct the disjoint set $\mathsf {P}'$, which is also evenly covered by $\mathsf {W}$. Therefore, by Lemma 5, the union of $\mathsf {P}$ and $\mathsf {P}'$ is evenly covered by $\mathsf {W}$. Let ${\varvec{m}}^2$ denote the y-coordinates of $\mathsf {P}'$.

Define $\overline{{\varvec{m}}^1}$ to be the vector of length k where for all $i\le \ell$, $\overline{m^1}_{\mu (i)} = m^1_i$, and for all i not in the range of $\mu$, $\overline{m^1}_i = 0$. Define $\overline{{\varvec{m}}^2}$ similarly. Then $\overline{{\varvec{m}}^1}$ and $\overline{{\varvec{m}}^2}$ collide with probability $(\ell -1)/N$.

For sufficiently large k, ${\varvec{c}}_{\le k}$ will always contain additive subgroups. In particular, one can find such subgroups in PMAC with Gray codes [7], where ${\varvec{c}}$ is defined as follows. In this case $\mathsf {X}:=\left\{ 0,1\right\} ^\nu$ is the set of $\nu$-bit strings, identified in some way with a finite field of size $2^\nu$. We define the following sequence of vectors $\lambda ^\nu$:

$$\begin{aligned} \lambda ^1&= (0, 1)\end{aligned}$$

(53)

$$\begin{aligned} \lambda ^{\nu +1}&= (0\Vert \lambda ^{\nu }_1, 0\Vert \lambda ^{\nu }_2, \ldots , 0\Vert \lambda ^{\nu }_{2^\nu }, 1\Vert \lambda ^{\nu }_{2^\nu }, \ldots , 1\Vert \lambda ^\nu _2, 1\Vert \lambda ^\nu _1)\,. \end{aligned}$$

(54)

Note that $\lambda ^\nu$ contains all strings in $\mathsf {X}$. Then ${\varvec{c}}$ is $\lambda ^\nu$ without the first component, meaning ${\varvec{c}}$ contains all strings in $\mathsf {X}$ without the zero string. Similarly, the sequence $(c_1, \ldots , c_{2^\kappa })$ contains all strings starting with $\nu -\kappa$ zeros, i.e. $0^{\nu -\kappa }\Vert \left\{ 0,1\right\} ^{\kappa }$, excluding the zero string. Note that $c_1 = 0^{\nu -1}1$. The sequence $(c_1+c_1, c_1+c_2, \ldots , c_1+c_{2^\kappa })$ contains all strings in $0^{\nu -\kappa }\Vert \left\{ 0,1\right\} ^{\kappa }$ except for $c_1$, meaning it contains an additive subgroup of order $2^{\kappa -1}$. This results in an attack using messages of length $k = 2^\kappa$ with success probability $(2^\kappa -1)/2^\nu$.

Appendices

A Basic Graph Theoretic Definitions

• 1. A neighbour of a vertex v in a graph G is a vertex with an edge connecting it to v.

• 2. A graph G is said to be k-regular if every vertex of G has exactly k neighbours.

• 3. A subgraph of a graph G is a graph with vertex set and edge set subsets of G’s vertex and edge sets, respectively.

• 4. A complete graph is a graph in which every vertex is connected to every other vertex via an edge.

B BQF-t is NP-complete

Definition 15

( BQF -t). Given a finite field $\mathsf {X}$ with characteristic 2 and a vector $\varvec{x}_* \in \mathsf {X}^k$ and a target element $t \in \mathsf {X}$, determine if there is a non-trivial binary quadratic form $Q \in \{0,1\}^{k\times {}k}$ such that $\varvec{x}_*^T Q \varvec{x}_* = t$.

Note. The word ‘binary’ in our use of the term ‘binary quadratic form’ refers to the coefficients of the quadratic form matrix Q and not to the number of variables.

Proposition 9

BQF-t $\in \mathbf {NP}$

Proof

Given a BQF-t yes-instance $(\mathsf {X}, \varvec{x}_*, t)$ of $(k+2) \times \ell$ bits, there exists a certificate of $k^2 \times \ell$ bits that proves it is a yes-instance, namely the matrix Q such that $\varvec{x}_*^T Q \varvec{x}_* = t$. Moreover, the validity of this certificate can be verified by computing $\varvec{x}_*^T Q \varvec{x}_*$ and testing if it is indeed equal to t. This evaluation requires $(n+1) \times n$ multiplications and the same number of additions in the finite field $\mathsf {X}$. After testing equality, the non-triviality of Q is verified by testing whether $Q^T + Q \ne 0$, costing another $n^2$ finite field additions and as many equality tests. Thus, for every yes-instance of BQF-t, there exists a polynomial-size certificate whose validity is verifiable in polynomial time. Hence, BQF-t $\in \mathbf {NP}$. $\quad \square$

Proposition 10

BQF-t is $\mathbf {NP}$-hard.

Proof

We show that BQF-t is $\mathbf {NP}$-hard by reducing the subset-sum problem SS, another $\mathbf {NP}$-hard problem, to it. In particular, we show that SS $\le$ BQF-t under deterministic polynomial-time Karp reductions.

Given an instance $(\mathsf {X},S)$ of SS, the goal is to find a subset $S_0 \subset S$ such that $\sum _{x \in S_0}x = 1$. Note the target of SS can be changed without loss of generality. We transform this problem instance to an instance $(\mathsf {X}', \varvec{x}_*, t)$ of BQF-t as follows.

Let $k = \#S$, the number of elements in S and let each unique element $s_i$ of S be indexed by $i \in \{1, \ldots , k\}$. Choose a degree $2k+1$ irreducible polynomial $\psi (z) \in \mathsf {X}[z]$ and define the extension field $\mathsf {X}' = \mathsf {X}[z] / \langle \psi (z) \rangle$. Then define the vector $\varvec{x}_*$ as follows:

$$ \varvec{x}_* = \left( \begin{matrix} z^{1}s_1 \\ z^{2}s_2 \\ \vdots \\ z^{k}s_k \\ z^{-1} \\ z^{-2} \\ \vdots \\ z^{-k} \\ \end{matrix} \right) . $$

The BQF-t instance is $(\mathsf {X}', \varvec{x}_*, 1)$. It now remains to be shown that (1) this transformation is computable in polynomial time; (2) if the SS problem instance is a yes-instance, then the BQF-t problem instance is yes-instance; (3) conversely, if the SS problem instance is a no-instance, then the BQF-t problem instance is a no-instance.

• 1. It is known to be possible to deterministically select an irreducible polynomial over a finite field of small characteristic in polynomial time [20]. After selecting the polynomials, the inverse of z is computed using the polynomial-time extended GCD algorithm and all the necessary powers of z and $z^{-1}$ are found after two times k multiplications. Lastly, the proper powers of z are combined with the $s_i$ elements using k multiplications for the construction of the first half of the vector $\varvec{x}_*$; the second half of this vector has already been computed. So since this transformation consists of a polynomial-number of polynomial-time steps, its total running time is also polynomial.

• 2. If the SS instance is a yes-instance, then there exist k binary weights ${w_i \in \{0,1\}}$ for all $i \in \{1, \ldots , k\}$ such that $\sum _{i=1}^k w_i s_i = 1$. The existence of these weights imply the existence of the matrix Q, as defined below. This matrix consists of four $k \times k$ submatrices and only the diagonal of the upper right submatrix is nonzero. In fact, this diagonal is where the weights $w_i$ appear.

  

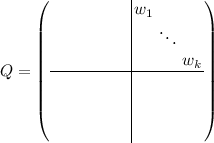  (55)

  Indeed, the BQF-t instance is guaranteed to be a yes-instance as

  $$\begin{aligned} \varvec{x}_*^T Q \varvec{x}_* = \sum _{i=1}^{k} z^{i}s_iw_iz^{-i} = 1 \end{aligned}$$

  if and only if

  $$ \sum _{i=1}^kw_is_i = 1 ,$$

  which is the solution to the SS problem. Also, Q is non-trivial if there exists at least one nonzero weight $w_i$.

• 3. If the SS instance is a no-instance, then no set of weights $w_i$ such that $\sum _{i=1}^kw_is_i = 1$ exists. Consequently, no Q satisfying $\varvec{x}_*^T Q \varvec{x}_* = 1$ can exist. The reason is that all the elements of the Q-matrix except for the upper right diagonal are multiplied with higher or lower powers of z, which make them linearly independent from 1. Hence, neither the upper right diagonal nor any other set of nonzero elements in Q can make the total quadratic form equal to one.$\quad \square$   $\square$

Corollary 1

BQF-t is $\mathbf {NP}$-complete.