Characteristic Formulae for Session Types

Abstract

Subtyping is a crucial ingredient of session type theory and its applications, notably to programming language implementations. In this paper, we study effective ways to check whether a session type is a subtype of another by applying a characteristic formulae approach to the problem. Our core contribution is an algorithm to generate a modal $\mu$-calculus formula that characterises all the supertypes (or subtypes) of a given type. Subtyping checks can then be off-loaded to model checkers, thus incidentally yielding an efficient algorithm to check safety of session types, soundly and completely. We have implemented our theory and compared its cost with other classical subtyping algorithms.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Motivations. Session types [25, 26, 41] have emerged as a fundamental theory to reason about concurrent programs, whereby not only the data aspects of programs are typed, but also their behaviours wrt. communication. Recent applications of session types to the reverse-engineering of large and complex distributed systems [13, 30] have led to the need of handling potentially large and complex session types. Analogously to the current trend of modern compilers to rely on external tools such as SMT-solvers to solve complex constraints and offer strong guarantees [17, 24, 32, 33], state-of-the-art model checkers can be used to off-load expensive tasks from session type tools such as [30, 38, 43].

A typical use case for session types in software (reverse-) engineering is to compare the type of an existing program with a candidate replacement, so to ensure that both are “compatible”. In this context, a crucial ingredient of session type theory is the notion of subtyping [10, 15, 20] which plays a key role to guarantee safety of concurrent programs while allowing for the refinement of specifications and implementations. Subtyping for session types relates to many classical theories such as simulations and pre-orders in automata and process algebra theories; but also to subtyping for recursive types in the $\lambda$-calculus [5]. The characteristic formulae approach [1–3, 12, 22, 39, 40], which has been studied since the late eighties as a method to compute simulation-like relations in process algebra and automata, appears then as an evident link between subtyping in session type theory and model checking theories. In this paper, we make the first formal connection between session type and model checking theories, to the best of our knowledge. We introduce a novel approach to session types subtyping based on characteristic formulae; and thus establish that subtyping for session types can be decided in quadratic time wrt. the size of the types. This improves significantly on the classical algorithm [21]. Subtyping can then be reduced to a model checking problem and thus be discharged to powerful model checkers. Consequently, any advance in model checking technology has an impact on subtyping.

Example. Let us illustrate what session types are and what subtyping covers. Consider a simple protocol between a server and a client, from the point of view of the server. The client sends a message of type $request$ to the server who decides whether or not the request can be processed by replying $ok$ or $ko$, respectively. If the request is rejected, the client is offered another chance to send another request, and so on. This may be described by the session type below

$$\begin{aligned} U_1 = \mathtt {rec}\, \mathbf {\mathbf {x}} . {{\mathrm{?}}} request .\{{{\mathrm{!}}} ok .\mathtt {end}\oplus {{\mathrm{!}}} ko .\mathbf {x}\} \end{aligned}$$

(1)

where $\mathtt {rec}\, \mathbf {\mathbf {x}}$ binds variable $\mathbf {x}$ in the rest of the type, ${{\mathrm{?}}} msg$ (resp. ${{\mathrm{!}}} msg$) specifies the reception (resp. emission) of a message $msg$, $\oplus$ indicates an internal choice between two behaviours, and $\mathtt {end}$ signifies the termination of the conversation. An implementation of a server can then be type-checked against $U_1$.

The client’s perspective of the protocol may be specified by the dual of $U_1$:

(2)

where indicates an external choice, i.e., the client expects two possible behaviours from the server. A classical result in session type theory essentially says that if the types of two programs are dual of each other, then their parallel composition is free of errors (e.g., deadlock).

Generally, when we say that $\mathtt {integer}$ is a subtype of $\mathtt {float}$, we mean that one can safely use an $\mathtt {integer}$ when a $\mathtt {float}$ is required. Similarly, in session type theory, if T is a subtype of a type U (written $T {{\mathrm{\leqslant }}}U$), then T can be used whenever U is required. Intuitively, a type T is a subtype of a type U if T is ready to receive no fewer messages than U, and T may not send more messages than U [10, 15]. For instance, we have

(3)

A server of type $T_1$ can be used whenever a server of type $U_1$ (1) is required ($T_1$ is a more refined version of $U_1$, which always accepts the request). A client of type $T_2$ can be used whenever a client of type $U_2$ (2) is required since $T_2$ is a type that can deal with (strictly) more messages than $U_2$.

In Sect. 3.2, we will see that a session type can be naturally transformed into a $\mu$-calculus formula that characterises all its subtypes. The transformation notably relies on the diamond modality to make some branches mandatory, and the box modality to allow some branches to be made optional; see Example 2.

Contribution and Synopsis. In Sect. 2 we recall session types and give a new abstract presentation of subtyping. In Sect. 3 we present a fragment of the modal $\mu$-calculus and, following [39], we give a simple algorithm to generate a $\mu$-calculus formula from a session type that characterises either all its subtypes or all its supertypes. In Sect. 4, building on results from [10], we give a sound and complete model-checking characterisation of safety for session types. In Sect. 5, we present two other subtyping algorithms for session types: Gay and Hole’s classical algorithm [21] based on inference rules that unfold types explicitly; and an adaptation of Kozen et al.’s automata-theoretic Algorithm [28]. In Sect. 6, we evaluate the cost of our approach by comparing its performances against the two algorithms from Sect. 5. Our performance analysis is notably based on a tool that generates arbitrary well-formed session types. We conclude and discuss related works in Sect. 7. Due to lack of space, full proofs are relegated to an online appendix [31]. Our tool and detailed benchmark results are available online [29].

2 Session Types and Subtyping

Session types are abstractions of the behaviour of a program wrt. the communication of this program on a given session (or conversation), through which it interacts with another program (or component).

2.1 Session Types

We use a two-party version of the multiparty session types in [16]. For the sake of simplicity, we focus on first order session types (that is, types that carry only simple types (sorts) or values and not other session types). We discuss how to lift this restriction in Sect. 7. Let $\mathcal {V}$ be a countable set of variables (ranged over by $\mathbf {x}, \mathbf {y}$, etc.); let $\mathbb {A}$ be a (finite) alphabet, ranged over by a, b, etc.; and $\mathcal {A}$ be the set defined as $\{ {{\mathrm{!}}} a \, \mid \,a \in \mathbb {A}\} \cup \{ {{\mathrm{?}}} a \, \mid \,a \in \mathbb {A}\}$. We let ${{\mathrm{\dagger }}}$ range over elements of $\{ !, ? \}$, so that ${{{\mathrm{\dagger }}} a}$ ranges over $\mathcal {A}$. The syntax of session types is given by

where $I \ne \varnothing$ is finite, $a_i \in \mathbb {A}$ for all $i \in I$, $a _i \ne a _j$ for $i \ne j$, and $\mathbf {x}\in \mathcal {V}$. Type $\mathtt {end}$ indicates the end of a session. Type $\bigoplus _{i \in I} {{{\mathrm{!}}} a _{i}} . \, {T}_{i}$ specifies an internal choice, indicating that the program chooses to send one of the $a _i$ messages, then behaves as $T_i$. Type specifies an external choice, saying that the program waits to receive one of the $a _i$ messages, then behaves as $T_i$. Types $\mathtt {rec}\, \mathbf {\mathbf {x}} . T$ and $\mathbf {x}$ are used to specify recursive behaviours. We often write, e.g., $\{{{\mathrm{!}}} a _1. T_1 \oplus {\ldots } \oplus {{\mathrm{!}}} a _k . T_k \}$ for $\bigoplus _{1 \le i \le k} { {{\mathrm{!}}} a _i . T_i}$, write ${{\mathrm{!}}} a_1 . T_1$ when $k =1$, similarly for , and omit trailing occurrences of $\mathtt {end}$.

The sets of free and bound variables of a type T are defined as usual (the unique binder is the recursion operator $\mathtt {rec}\, \mathbf {\mathbf {x}} . T$). For each type T, we assume that two distinct occurrences of a recursion operator bind different variables, and that no variable has both free and bound occurrences. In coinductive definitions, we take an equi-recursive view of types, not distinguishing between a type and its unfolding . We assume that each type T is contractive [35], e.g., is not a type. Let $\mathcal {T}$ be the set of all (contractive) session types and $\mathcal {T}_{ c }\subseteq \mathcal {T}$ the set of all closed session types (i.e., which do not contain free variables).

Fig. 1.

LTS for session types in $\mathcal {T}_{ c }$

A session type $T \in \mathcal {T}_{ c }$ induces a (finite) labelled transition system (LTS) according to the rules in Fig. 1. We write $T \xrightarrow {{{{\mathrm{\dagger }}} a}}$ if there is $T' \in \mathcal {T}$ such that $T \xrightarrow {{{{\mathrm{\dagger }}} a}} T'$ and write $T \!\!\nrightarrow$ if $\forall {{{\mathrm{\dagger }}} a}\in \mathcal {A}\, : \,\lnot (T \xrightarrow {{{{\mathrm{\dagger }}} a}} )$.

2.2 Subtyping for Session Types

Subtyping for session types was first studied in [20] and further studied in [10, 15]. It is a crucial notion for practical applications of session types, as it allows for programs to be refined while preserving safety.

We give a definition of subtyping which is parameterised wrt. operators $\oplus$ and , so to allow us to give a common characteristic formula construction for both the subtype and the supertype relations, cf. Sect. 3.2. Below, we let $\maltese$ range over . When writing , we take the convention that ${{\mathrm{\dagger }}}$ refers to ! iff $\maltese$ refers to $\oplus$ (and vice-versa for ? and ). We define the (idempotent) duality operator as follows: , , $\overline{!} \overset{{\text {def}}}{=}?$, and $\overline{?} \overset{{\text {def}}}{=}!$.

Definition 1

(Subtyping). Fix , is the largest relation that contains the rules:

The double line in the rules indicates that the rules should be interpreted coinductively. Recall that we are assuming an equi-recursive view of types.    $\diamond$

We comment Definition 1 assuming that $\maltese$ is set to $\oplus$. Rule says that a type can be replaced by a type that offers no more messages, e.g., ${{\mathrm{!}}} a {{\mathrm{\unlhd }}}^{{\small \,\oplus }} {{\mathrm{!}}} a \oplus {{\mathrm{!}}} b$. Rule says that a type can be replaced by a type that is ready to receive at least the same messages, e.g., . Rule is trivial. It is easy to see that . In fact, we can recover the subtyping of [10, 15] (resp. [20, 21]) from , by instantiating $\maltese$ to $\oplus$ (resp. ).

Example 1

Consider the session types from (3), we have $T_1 {{\mathrm{\unlhd }}}^{{\small \,\oplus }} U_1$, , $T_2 {{\mathrm{\unlhd }}}^{{\small \,\oplus }} U_2$, and .

Hereafter, we will write ${{\mathrm{\leqslant }}}$ (resp. ${{\mathrm{\geqslant }}}$) for the pre-order ${{\mathrm{\unlhd }}}^{{\small \,\oplus }}$ (resp. ).

3 Characteristic Formulae for Subtyping

We give the core construction of this paper: a function that given a (closed) session type T returns a modal $\mu$-calculus formula [27] that characterises either all the supertypes of T or all its subtypes. Technically, we “translate” a session type T into a modal $\mu$-calculus formula $\phi$, so that $\phi$ characterises all the supertypes of T (resp. all its subtypes). Doing so, checking whether T is a subtype (resp. supertype) of U can be reduced to checking whether U is a model of $\phi$, i.e., whether $U \models \phi$ holds.

The constructions presented here follow the theory first established in [39]; which gives a characteristic formulae approach for (bi-)simulation-like relations over finite-state processes, notably for CCS processes.

3.1 Modal $\mu$-calculus

In order to encode subtyping for session types as a model checking problem it is enough to consider the fragment of the modal $\mu$ calculus below:

Modal operators $[ {{{\mathrm{\dagger }}} a} ]$ and $\langle {{{\mathrm{\dagger }}} a} \rangle$ have precedence over Boolean binary operators $\wedge$ and $\vee$; the greatest fixpoint point operator $\nu \mathbf {\mathbf {x}}$ has the lowest precedence (and its scope extends as far to the right as possible). Let $\mathcal {F}$ be the set of all (contractive) modal $\mu$-calculus formulae and $\mathcal {F}_{ c }\subseteq \mathcal {F}$ be the set of all closed formulae. Given a set of actions $A \subseteq \mathcal {A}$, we write $\lnot {A}$ for $\mathcal {A}\setminus A$, and $[ A ] \phi$ for $\bigwedge _{{{{\mathrm{\dagger }}} a}\in A}[ {{{\mathrm{\dagger }}} a} ] \phi$.

The $n^{th}$ approximation of a fixpoint formula is defined as follows:

A closed formula $\phi$ is interpreted on the labelled transition system induced by a session type T. The satisfaction relation $\models$ between session types and formulae is inductively defined as follows:

Intuitively, $\top$ holds for every T (while $\bot$ never holds). Formula $\phi _1 \wedge \phi _2$ (resp. $\phi _1 \vee \phi _2$) holds if both components (resp. at least one component) of the formula hold in T. The construct $[ {{{\mathrm{\dagger }}} a} ] \phi$ is a modal operator that is satisfied if for each ${{{\mathrm{\dagger }}} a}$-derivative $T'$ of T, the formula $\phi$ holds in $T'$. The dual modality is $\langle {{{\mathrm{\dagger }}} a} \rangle \phi$ which holds if there is an ${{{\mathrm{\dagger }}} a}$-derivative $T'$ of T such that $\phi$ holds in $T'$. Construct $\nu \mathbf {\mathbf {x}} .\, \phi$ is the greatest fixpoint operator (binding $\mathbf {x}$ in $\phi$).

3.2 Characteristic Formulae

We now construct a $\mu$-calculus formula from a (closed) session types, parameterised wrt. a constructor $\maltese$. This construction is somewhat reminiscent of the characteristic functional of [39].

Definition 2

(Characteristic formulae). The characteristic formulae of $T \in \mathcal {T}_{ c }$ on $\maltese$ is given by function , defined as:

   $\diamond$

Given $T \in \mathcal {T}_{ c }$, $\,{{{\varvec{F}}}}(T,\oplus )$ is a $\mu$-calculus formula that characterises all the supertypes of T; while characterises all its subtypes. For the sake of clarity, we comment on Definition 2 assuming that $\maltese$ is set to . The first case of the definition makes every branch mandatory. If $T = \bigoplus _{i \in I} {{{\mathrm{!}}} a _{i}} . \, {T}_{i}$, then every internal choice branch that T can select must also be offered by a supertype, and the relation must hold after each selection. The second case makes every branch optional but requires at least one branch to be implemented. If , then (i) for each of the ${{\mathrm{?}}} a_i$-branch offered by a supertype, the relation must hold in its ${{\mathrm{?}}} a_i$-derivative, (ii) a supertype must offer at least one of the ${{\mathrm{?}}} a_i$ branches, and (iii) a supertype cannot offer anything else but the ${{\mathrm{?}}} a_i$ branches. If $T = \mathtt {end}$, then a supertype cannot offer any behaviour (recall that $\bot$ does not hold for any type). Recursive types are mapped to greatest fixpoint constructions.

Lemma 1 below states the compositionality of the construction, while Theorem 1, our main result, reduces subtyping checking to a model checking problem. A consequence of Theorem 1 is that the characteristic formula of a session type precisely specifies the set of its subtypes or supertypes.

Lemma 1

The proof is by structural induction, see appendix [31].

Theorem 1

The proof essentially follows the techniques of [39], see appendix [31].

Corollary 1

The following holds:

The proof is by Theorem 1 and ${{\mathrm{\leqslant }}}= {{\mathrm{\unlhd }}}^{{\small \,\oplus }}$, , ${{\mathrm{\leqslant }}}= {{\mathrm{\geqslant }}}^{-1}$, and .

Proposition 1

For all $T, U \in \mathcal {T}_{ c }$, deciding whether or not $U \models \,{{{\varvec{F}}}}(T,\maltese )$ holds can be done in time complexity of $\mathcal {O}(|T |\times |U |)$, in the worst case; where $|T |$ stands for the number of states in the LTS induced by T.

This follows from [12], since the size of $\,{{{\varvec{F}}}}(T,\maltese )$ increases linearly with $|T |$.

Example 2

Consider session types $T_1$ and $U_1$ from (1) and (3) and fix $\mathcal {A}= \{ {{\mathrm{?}}} request , {{\mathrm{!}}} ok , {{\mathrm{!}}} ko \}$. Following Definition 2, we obtain:

We have and , as expected (recall tat $T_1 {{\mathrm{\leqslant }}}U_1$).

4 Safety and Duality in Session Types

A key ingredient of session type theory is the notion of duality between types. In this section, we study the relation between duality of session types, characteristic formulae, and safety (i.e., error freedom). In particular, building on recent work [10] which studies the preciseness of subtyping for session types, we show how characteristic formulae can be used to guarantee safety. A system (of session types) is a pair of session types T and U that interact with each other by synchronising over messages. We write $T {{\mathrm{\, | \,}}}U$ for a system consisting of T and U and let S range over systems of session types.

Definition 3

(Synchronous semantics). The synchronous semantics of a system of session types $T {{\mathrm{\, | \,}}}U$ is given by the rule below, in conjunction with the rules of Fig. 1.

We write $\xrightarrow {}^{*}$ for the reflexive transitive closure of $\xrightarrow {}$.   $\diamond$

Definition 3 says that two types interact whenever they fire dual operations.

Example 3

Consider the following execution of system $T_1 {{\mathrm{\, | \,}}}U_2$, from (3):

Definition 4

(Error [10] and safety). A system $T_1 {{\mathrm{\, | \,}}}T_2$ is an error if, either:

• (a) and , with $\maltese$ fixed;

• (b) and ; and $\exists i \in I \, : \,\forall j \in J \, : \,a_i \ne a_j$, with $h \ne g \in \{1,2\}$; or

• (c) $T_h = \mathtt {end}$ and , with $h \ne g \in \{1,2\}$.

We say that $S = T {{\mathrm{\, | \,}}}U$ is safe if for all $S' \, : \,S \xrightarrow {}^{*}S'$, $S'$ is not an error.   $\diamond$

A system of the form (a) is an error since both types are either attempting to send (resp. receive) messages. An error of type (b) indicates that some of the messages cannot be received by one of the types. An error of type (c) indicates a system where one of the types has terminated while the other still expects to send or receive messages.

Definition 5

(Duality). The dual of a formula $\phi \in \mathcal {F}$, written $\overline{\phi }$ (resp. of a session type $T \in \mathcal {T}$, written $\overline{T}$), is defined recursively as follows:

   $\diamond$

In Definition 5, notice that the dual of a formula only rename labels.

Lemma 2

For all $T \in \mathcal {T}_{ c }$ and $\phi \in \mathcal {F}_{ c }$, $T \models \phi \iff \overline{T} \models \overline{\phi }$.

The proof is direct using the definitions of $\overline{T}$ and $\overline{\phi }$.

Theorem 2

For all $T \in \mathcal {T}\, : \,\overline{\,{{{\varvec{F}}}}(T,\maltese )} = \,{{{\varvec{F}}}}(\overline{T},\overline{\maltese })$.

The proof of Theorem 2 is by structural induction on T, see appendix [31]. Theorem 3 follows straightforwardly from [10] and allows us to obtain a sound and complete model-checking based condition for safety, cf. Theorem 4.

Theorem 3

(Safety). $T {{\mathrm{\, | \,}}}U$ is safe $\iff$ $(T {{\mathrm{\leqslant }}}\overline{U} \vee U {{\mathrm{\leqslant }}}\overline{T})$.

The proof for $(\Longrightarrow )$ follows from [10, Table 7], while the direction $(\Longleftarrow )$ is by coinduction on the derivations of $T {{\mathrm{\leqslant }}}\overline{U}$ and $U {{\mathrm{\leqslant }}}\overline{T}$. See [31] for details.

Theorem 4, below, is a consequence of Corollary 1 and Theorems 2 and 3.

Theorem 4

The following statements are equivalent: $\; (a) {\;\,} T {{\mathrm{\, | \,}}}U \text { is safe }$

5 Alternative Algorithms for Subtyping

In order to compare the cost of checking the subtyping relation via characteristic formulae to other approaches, we present two other algorithms: the original algorithm as given by Gay and Hole in [21] and an adaptation of Kozen, Palsberg, and Schwartzbach’s algorithm [28] for recursive subtyping for the $\lambda$-calculus.

5.1 Gay and Hole’s Algorithm

The inference rules of Gay and Hole’s algorithm are given in Fig. 2 (adapted to our setting). The rules essentially follow those of Definition 1 but deal explicitly with recursion. They use judgments $\varGamma \vdash T {{\mathrm{\leqslant }}}_{c}U$ in which T and U are (closed) session types and $\varGamma$ is a sequence of assumed instances of the subtyping relation, i.e., $\varGamma = T_1 {{\mathrm{\leqslant }}}_{c}U_1, {\scriptstyle \ldots }, T_k {{\mathrm{\leqslant }}}_{c}U_k$, saying that each pair $T_i {{\mathrm{\leqslant }}}_{c}U_i$ has been visited. To guarantee termination, rule should always be used if it is applicable.

Fig. 2.

Algorithmic subtyping rules [21]

Theorem 5

(Correspondence [21, Corollary 2]). $T {{\mathrm{\leqslant }}}U$ if and only if $\varnothing \vdash T {{\mathrm{\leqslant }}}_{c}U$ is derivable from the rules in Fig. 2.

Proposition 2, a contribution of this paper, states the algorithm’s complexity.

Proposition 2

For all $T, U \in \mathcal {T}_{ c }$, the problem of deciding whether or not $\varnothing \vdash T {{\mathrm{\leqslant }}}_{c}U$ is derivable has an $\mathcal {O}(n^{2^n})$ time complexity, in the worst case; where n is the number of nodes in the parsing tree of the T or U (whichever is bigger).

Proof

Assume the bigger session type is T and its size is n (the number of nodes in its parsing tree). Observe that the algorithm in Fig. 2 needs to visit every node of T and relies on explicit unfolding of recursive types. Given a type of size n, its unfolding is of size $\mathcal {O}(n^2)$, in the worst case. Hence, we have a chain $\mathcal {O}(n) + \mathcal {O}(n^2) + \mathcal {O}(n^4) + \ldots$, or $\mathcal {O}(\sum _{1 \le i \le k} n^{2^i})$, where k is a bound on the number of derivations needed for the algorithm to terminate. According to [21, Lemma 10], the number of derivations is bounded by the number of sub-terms of T, which is $\mathcal {O}(n)$. Thus, we obtain a worst case time complexity of $\mathcal {O}(n^{2^n})$.    $\square$

5.2 Kozen, Palsberg, and Schwartzbach’s Algorithm

Considering that the results of [28] “generalise to an arbitrary signature of type constructors (...)”, we adapt Kozen et al.’s algorithm, originally designed for subtyping recursive types in the $\lambda$-calculus. Intuitively, the algorithm reduces the problem of subtyping to checking the language emptiness of an automaton given by the product of two (session) types. The intuition of the theory behind the algorithm is that “two types are ordered if no common path detects a counterexample”. We give the details of our instantiation below.

The set of type constructors over $\mathcal {A}$, written $\mathfrak {C}_\mathcal {A}$, is defined as follows:

Definition 6

(Term automata). A term automaton over $\mathcal {A}$ is a tuple $\mathcal {M}= (Q, \, \mathfrak {C}_\mathcal {A}, \, q_0, \, \delta , \, \ell )$ where

• $Q$ is a (finite) set of states,

• $q_0 \in Q$ is the initial state,

• $\delta : Q\times \mathcal {A}\rightarrow Q$ is a (partial) function (the transition function), and

• $\ell : Q\rightarrow \mathfrak {C}_\mathcal {A}$ is a (total) labelling function

such that for any $q\in Q$, if , then $\delta (q, {{{\mathrm{\dagger }}} a})$ is defined for all ${{{\mathrm{\dagger }}} a}\in A$; and for any $q\in Q$ such that $\ell (q) = \mathtt {end}$, $\delta (q, {{{\mathrm{\dagger }}} a})$ is undefined for all ${{{\mathrm{\dagger }}} a}\in \mathcal {A}$. We decorate $Q$, $\delta$, etc. with a superscript, e.g., $\mathcal {M}$, where necessary.   $\diamond$

We assume that session types have been “translated” to term automata, the transformation is straightforward (see, [16] for a similar transformation). Given a session type $T \in \mathcal {T}_{ c }$, we write $\mathcal {M}(T)$ for its corresponding term automaton.

Definition 7

(Subtyping). $\sqsubseteq$ is the smallest binary relation on $\mathfrak {C}_\mathcal {A}$ such that:

Definition 7 essentially maps the rules of Definition 1 to type constructors. The order $\sqsubseteq$ is used in the product automaton to identify final states, see below.

Definition 8

(Product automaton). Given two term automata $\mathcal {M}$ and $\mathcal {N}$ over $\mathcal {A}$, their product automaton $\mathcal {M} \blacktriangleleft \mathcal {N} = (P, \, p_0, \, \varDelta , \, F)$ is such that

• $P= Q^{\mathcal {M}} \times Q^{\mathcal {N}}$ are the states of $\mathcal {M} \blacktriangleleft \mathcal {N}$,

• $p_0 = (q_0^{\mathcal {M}}, q_0^{\mathcal {N}})$ is the initial state,

• $\varDelta : P\times \mathcal {A}\rightarrow P$ is the partial function which for $q_1 \in Q^{\mathcal {M}}$ and $q_2 \in Q^{\mathcal {N}}$ gives

  $$ \varDelta ( ( q_1, q_2 ), {{{\mathrm{\dagger }}} a}) = ( \delta ^{\mathcal {M}}(q_1, {{{\mathrm{\dagger }}} a}) , \delta ^{\mathcal {N}}(q_2, {{{\mathrm{\dagger }}} a}) ) $$

• $F\subseteq P$ is the set of accepting states:

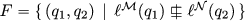
Note that $\varDelta ( ( q_1, q_2 ), {{{\mathrm{\dagger }}} a})$ is defined iff $\delta ^{\mathcal {M}}(q_1, {{{\mathrm{\dagger }}} a})$ and $\delta ^{\mathcal {N}}(q_2, {{{\mathrm{\dagger }}} a})$ are defined.   $\diamond$

Following [28], we obtain Theorem 6.

Theorem 6

Let $T, U \in \mathcal {T}_{ c }$, $T {{\mathrm{\leqslant }}}U$ iff the language of $\mathcal {M}(T) \blacktriangleleft \mathcal {M}(U)$ is empty.

Theorem 6 essentially says that $T {{\mathrm{\leqslant }}}U$ iff one cannot find a “common path” in T and U that leads to nodes whose labels are not related by $\sqsubseteq$, i.e., one cannot find a counterexample for them not being in the subtyping relation.

Example 4

Below we show the constructions for $T_1$ (1) and $U_1$ (3).

 

Where initial states are shaded and accepting states are denoted by a double line. Note that the language of $\mathcal {M}(T_1) \blacktriangleleft \mathcal {M}(U_1)$ is empty (no accepting states).

Fig. 3.

Benchmarks (1)

Proposition 3

For all $T, U \in \mathcal {T}_{ c }$, the problem of deciding whether or not the language of $\mathcal {M}(T) \blacktriangleleft \mathcal {M}(U)$ is empty has a worst case complexity of $\mathcal {O}(|T |\times |U |)$; where $|T |$ stands for the number of states in the term automaton $\mathcal {M}(T)$.

Proof

Follows from the fact that the algorithm in [28] has a complexity of $\mathcal {O}(n^2)$, see [28, Theorem 18]. This complexity result applies also to our instantiation, assuming that checking membership of $\sqsubseteq$ is relatively inexpensive, i.e., $|A |\ll |Q^\mathcal {M}|$ for each $q$ such that .   $\square$

6 Experimental Evaluation

Proposition 2 states that Gay and Hole’s classical algorithm has an exponential complexity; while the other approaches have a quadratic complexity (Propositions 1 and 3). The rest of this section presents several experiments that give a better perspective of the practical cost of these approaches.

6.1 Implementation Overview and Metrics

We have implemented three different approaches to checking whether two given session types are in the subtyping relation given in Definition 1. The tool [29], written in Haskell, consists of three main parts: (i) A module that translates session types to the mCRL2 specification language [23] and generates a characteristic formula (cf. Definition 2), respectively; (ii) A module implementing the algorithm of [21], which relies on the Haskell $\mathtt {bound}$ library to make session types unfolding as efficient as possible. (iii) A module implementing our adaptation of Kozen et al.’s algorithm [28]. Additionally, we have developed an accessory tool which generates arbitrary session types using Haskell’s QuickCheck library [11].

The tool invokes the mCRL2 toolset [14] (release version 201409.1) to check the validity of a $\mu$-calculus formula on a given model. We experimented invoking mCRL2 with several parameters and concluded that the default parameters gave us the best performance overall. Following discussions with mCRL2 developers, we observed that the addition of “dummy fixpoints” while generating the characteristic formulae gave us the best results overall. The tool is thus based on a slight modification of Definition 2 where a modal operator $[ {{{\mathrm{\dagger }}} a} ] \phi$ becomes $[ {{{\mathrm{\dagger }}} a} ] \nu \mathbf {\mathbf {t}} .\,\phi$ (with $\mathbf {t}$ fresh and unused) and similarly for $\langle {{{\mathrm{\dagger }}} a} \rangle \phi$. Note that this modification does not change the semantics of the generated formulae.

We use the following functions to measure the size of a session type.

Function $num (T)$ returns the number of messages in T. Letting $|T |_{\mathbf {x}}$ be the number of times variable $\mathbf {x}$ appears free in session type T, function $unf (T)$ returns the number of messages in the unfolding of T. Function $unf (T)$ takes into account the structure of a type wrt. recursive definitions and calls (by unfolding once every recursion variable).

Fig. 4.

Benchmarks (2)

6.2 Benchmark Results

The first set of benchmarks compares the performances of the three approaches when the pair of types given are identical, i.e., we measure the time it takes for an algorithm to check whether $T {{\mathrm{\leqslant }}}T$ holds. The second set of benchmarks considers types that are “unfolded”, so that types have different sizes. Note that checking whether two equal types are in the subtyping relation is one of the most costly cases of subtyping since every branch of a choice must be visited.

Our results below show the performances of four algorithms: (i) our Haskell implementation of Gay and Hole’s algorithm (GH), (ii) our implementation of Kozen, Palsberg, and Schwartzbach’s algorithm (KPS), (iii) an invocation to mCRL2 to check whether holds, and (iv) an invocation to mCRL2 to check whether holds.

All the benchmarks were conducted on a 3.40 GHz Intel i7 computer with 16 GB of RAM. Unless specified otherwise, the tests have been executed with a timeout set to 2 h (7200 s). A gap appears in the plots whenever an algorithm reached the timeout. Times (y-axis) are plotted on a logarithmic scale, the scale used for the size of types (x-axis) is specified below each plot.

Arbitrary Session Types. Plots (a) and (b) in Fig. 3 shows how the algorithms perform with randomly generated session types. Plot (a) shows clearly that the execution time of KPS, , and mostly depends on $num (T)$; while plot (b) shows that GH is mostly affected by the number of messages in the unfolding of a type ($unf (T)$).

Unsurprisingly, GH performs better for smaller session types, but starts reaching the timeout when $num (T) \approx 700$. The other three algorithms have roughly similar performances, with the model checking based ones performing slightly better for large session types. Note that both and have roughly the same execution time.

Non-recursive Arbitrary Session Types. Plot (c) in Fig. 3 shows how the algorithms perform with arbitrary types that do not feature any recursive definition (randomly generated by our tool), i.e., the types are of the form:

The plot shows that GH performs much better than the other three algorithms (terminating under 1s for each invocation), indeed there is no recursion hence no need to unfold types. Observe that the model checking based algorithms perform better than KPS for large session types. Again, and behave similarly.

Handcrafted Session Types. Plots (d) and (e) in Fig. 4 shows how the algorithms deal with “super-recursive” types, i.e., types of the form:

where $num (T) = k(k+2)$ for each T. Plot (d) shows the results of experiments with $\maltese$ set to $\oplus$ and ${{\mathrm{\dagger }}}$ to ${{\mathrm{!}}}$; while $\maltese$ is set to and ${{\mathrm{\dagger }}}$ to ${{\mathrm{?}}}$ in plot (e).

The exponential time complexity of GH appears clearly in both plots: GH starts reaching the timeout when $num (T) = 80$ ($k=8$). However, the other three algorithms deal well with larger session types of this form. Interestingly, due to the nature of these session types (consisting of either only internal choices or only external choices), the two model checking based algorithms perform slightly differently. This is explained by Definition 2 where the formula generated with for an internal choice is larger than for an external choice, and vice-versa for $\,{{{\varvec{F}}}}(T,\oplus )$. Observe that, (resp. ) performs better than KPS for large session types in plot (d) (resp. plot (e)).

Unfolded Types. The last set of benchmarks evaluates the performances of the four algorithms to check whether holds, where $\mathbf {x}$ is fixed and ${V}$ (randomly generated) is of the form:

Plots (f) in Fig. 4 shows the results of our experiments (with a timeout set to 6 hours). Observe that $U \models \,{{{\varvec{F}}}}(T,\oplus )$ starts reaching the timeout quickly. In this case, the model (i.e., U) is generally much larger than the formula (i.e., $\,{{{\varvec{F}}}}(T,\oplus )$). After discussing with the mCRL2 team, this discrepancy seems to originate from internal optimisations of the model checker that can be diminished (or exacerbated) by tweaking the parameters of the tool-set. The good performance of GH in this case can be explained by the fact that there is only one recursion variable in these types; hence the size of their unfolding does not grow very fast.

7 Related Work and Conclusions

Related Work. Subtyping for recursive types has been studied for many years. Amadio and Cardelli [5] introduced the first subtyping algorithm for recursive types for the $\lambda$-calculus. Kozen et al. gave a quadratic subtyping algorithm in [28], which we have adapted for session types, cf. Sect. 5.2. A good introduction to the theory and history of the field is in [19]. Pierce and Sangiori [36] introduced subtyping for IO types in the $\pi$-calculus, which later became a foundation for the algorithm of Gay and Hole who first introduced subtyping for session types in the $\pi$-calculus in [21]. The paper [15] studied an abstract encoding between linear types and session types, with a focus on subtyping. Chen et al. [10] studied the notion of preciseness of subtyping relations for session types. The present work is the first to study the algorithmic aspect of the problem.

Characteristic formulae for finite processes were first studied in [22], then in [39] for finite-state processes. Since then the theory has been studied extensively [1–3, 12, 18, 34, 40] for most of the van Glabbeek’s spectrum [42] and in different settings (e.g., time [4] and probabilistic [37]). See [2, 3] for a detailed historical account of the field. This is the first time characteristic formulae are applied to the field of session types. A recent work [3] proposes a general framework to obtain characteristic formula constructions for simulation-like relation “for free”. We chose to follow [39] as it was a better fit for session types as they allow for a straightforward inductive construction of a characteristic formula.

Chaki et al. [9] propose a framework consisting of a behavioural type-and-effect system for the $\pi$-calculus and an assume-guarantee principle that allows (LTL) properties of $\pi$-calculus processes to be checked via a model checker.

Conclusions. In this paper, we gave a first connection between session types and model checking, through a characteristic formulae approach based on the $\mu$-calculus. We gave three new algorithms for subtyping: two are based on model checking and one is an instantiation of an algorithm for the $\lambda$-calculus [28]. All of which have a quadratic complexity in the worst case and behave well in practice.

Our approach can be easily: (i) adapted to types for the $\lambda$-calculus (see appendix [31]) and (ii) extended to session types that carry other (closed) session types, e.g., see [10, 21], by simply applying the algorithm recursively on the carried types. For instance, to check one can check the subtyping for the outer-most types, while building constraints, i.e., , to be checked later on, by re-applying the algorithm.

The present work paves the way for new connections between session types and modal fixpoint logic or model checking theories. It is a basis for upcoming connections between model checking and classical problems of session types, such as the asynchronous subtyping of [10] and multiparty compatibility checking [16, 30]. We are also considering applying model checking approaches to session types with probabilistic, logical [6], or time [7, 8] annotations. Finally, we remark that [10] also establishes that subtyping (cf. Definition 1) is sound (but not complete) wrt. the asynchronous semantics of session types, which models programs that communicate through FIFO buffers. Thus, our new conditions (items (b)-(e) of Theorem 4) also imply safety (a) in the asynchronous setting.