Abstraction Refinement and Antichains for Trace Inclusion of Infinite State Systems

Abstract

A data automaton is a finite automaton equipped with variables (counters or registers) ranging over infinite data domains. A trace of a data automaton is an alternating sequence of alphabet symbols and values taken by the counters during an execution of the automaton. The problem addressed in this paper is the inclusion between the sets of traces (data languages) recognized by such automata. Since the problem is undecidable in general, we give a semi-algorithm based on abstraction refinement, which is proved to be sound and complete modulo termination. Due to the undecidability of the trace inclusion problem, our procedure is not guaranteed to terminate. We have implemented our technique in a prototype tool and show promising results on several non-trivial examples.

R. Iosif—Supported by the French National Research Agency project VECOLIB (ANR-14-CE28-0018).

A. Rogalewicz and T. Vojnar—Supported by the Czech Science Foundation project 14-11384S, the IT4IXS: IT4Innovations Excellence in Science project (LQ1602), and the internal BUT project FIT-S-14-2486.

1 Introduction

In this paper, we address a trace inclusion problem for infinite-state systems. Given (i) a network of data automata $\mathcal {A}={\langle A_1,\ldots ,A_N \rangle }$ that communicate via a set of shared variables ${\mathbf {x}}_{\mathcal {A}}$, ranging over an infinite data domain, and a set of input events $\Sigma _{\mathcal {A}}$, and (ii) a data automaton B whose set of variables ${\mathbf {x}}_B$ is a subset of ${\mathbf {x}}_{\mathcal {A}}$, does the set of (finite) traces of B contain the traces of $\mathcal {A}$? Here, by a trace, we understand an alternating sequence of valuations of the variables from the set ${\mathbf {x}}_B$ and input events from the set $\Sigma _{\mathcal {A}} \cap \Sigma _B$, starting and ending with a valuation. Typically, the network of automata $\mathcal {A}$ is an implementation of a concurrent system and B is a specification of the set of good behaviors of the system.

Fig. 1.

An instance of the trace inclusion problem.

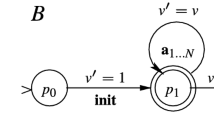
Consider, for instance, the network ${\langle A_1, \ldots , A_N \rangle }$ of data automata equipped with the integer-valued variables x and $\nu$ shown in Fig. 1 (left). The automata synchronize on the $\mathbf {init}$ symbol and interleave their $\mathbf {a}_{1,\ldots ,N}$ actions. Each automaton $A_i$ increases the shared variable x and writes its identifier i into the shared variable $\nu$ as long as the value of x is in the interval $[(i-1)\Delta ,i\Delta -1]$, and it is inactive outside this interval, where $\Delta \geqslant 1$ is an unbounded parameter of the network. A possible specification for this network might require that each firing sequence is of the form $\mathbf {init}~ \mathbf {a}_{1,\ldots ,N}^* ~\mathbf {a}_2~ \mathbf {a}_{2,\ldots ,N}^* \ldots \mathbf {a}_i~ \mathbf {a}_i^*$ for some $1 \leqslant i \leqslant N$, and that $\nu$ is increased only on the first occurrence of the events $\mathbf {a}_2,\ldots ,\mathbf {a}_i$, in this order. This condition is encoded by the automaton B (Fig. 1, right). Observe that only the $\nu$ variable is shared between the network ${\langle A_1,\ldots ,A_N \rangle }$ and the specification automaton B—we say that $\nu$ is observable in this case. An example of a trace, for $\Delta =2$ and $N\geqslant 3$, is: $(v=0) ~\mathbf {init}~ (v=1) ~\mathbf {a}_1~ (v=1) ~\mathbf {a}_1~ (v=1) \mathbf {a}_2~ (v=2) ~\mathbf {a}_2~ (v=2) ~\mathbf {a}_3~ (v=3)$. Our problem is to check that this, and all other traces of the network, are included in the language of the specification automaton, called the observer.

The trace inclusion problem has several applications, some of which we detail next. As the first potential application domain, we mention decision procedures for logics describing array structures in imperative programs [16, 17] that use a translation of array formulae to integer counter automata, which encode the set of array models of a formula. The expressiveness of such logics is currently limited by the decidability of the emptiness (reachability) problem for counter automata. If we give up on decidability, we can reduce an entailment between two array formulae to the trace inclusion of two integer counter automata, and use the method presented in this paper as a semi-decision procedure. To assess this claim, we have applied our trace inclusion method to several verification conditions for programs with unbounded arrays of integers [7].

Another application is within the theory of timed automata and regular specifications of timed languages [2] that can be both represented by finite automata extended with real-valued variables [14]. The verification problem boils down to the trace inclusion of two real-valued data automata. Our method has been tested on several timed verification problems, including communication protocols and boolean circuits [27].

When developing a method for checking the inclusion between trace languages of automata extended with variables ranging over infinite data domains, the first problem is the lack of determinization and/or complementation results. In fact, certain classes of infinite state systems, such as timed automata [2], cannot be determinized and are provably not closed under complement. This is the case due to the fact that the clock variables of a timed automaton are not observable in its timed language, which records only the time lapses between successive events. However, if we require that the values of all variables of a data automaton be part of its trace language, we obtain a determinization result, which generalizes the classical subset construction by taking into account the data valuations. Building on this first result, we define the complement of a data language and reduce the trace inclusion problem to the emptiness of a product data automaton $\mathcal {L}(A \times \overline{B}) = \varnothing$. It is crucial, for this reduction, that the variables ${\mathbf {x}}_B$ of the right-hand side data automaton B (the one being determinized) are also controlled by the left-hand side automaton A, in other words, that B has no hidden variables.

The language emptiness problem for data automata is, in general, undecidable [23]. Nevertheless, several semi-algorithms and tools for this problem (better known as the reachability problem) have been developed [3, 15, 19, 22]. Among those, the technique of lazy predicate abstraction [19] combined with counterexample-driven refinement using interpolants [22] has been shown to be particularly successful in proving emptiness of rather large infinite-state systems. Moreover, this technique shares similar aspects with the antichain-based algorithm for language inclusion in the case of a finite alphabet [1]. An important similarity is that both techniques use a partial order on states, to prune the state space during the search.

The main result of this paper is a semi-algorithm that combines the principle of the antichain-based language inclusion algorithm [1] with the interpolant-based abstraction refinement semi-algorithm [22], via a general notion of language-based subsumption relation. We have implemented our semi-algorithm in a prototype tool and carried out a number of experiments, involving hardware, real-time systems, and array logic problems. Since our procedure tests inclusion within a set of good traces, instead of empty intersection with a set of error traces, we can encode rather complex verification conditions concisely, by avoiding the blowup caused by an a-priori complementation of the automaton encoding the property.

Fig. 2.

Sample run of our semi-algorithm.

1.1 Overview

We introduce the reader to our trace inclusion method by means of an example. For space reasons, all proofs are given in an extended version of the paper [21].

Let us consider the network of data automata ${\langle A_1,A_2 \rangle }$ and the data automaton B from Fig. 1. We prove that, for any value of $\Delta$, any trace of the network ${\langle A_1,A_2 \rangle }$, obtained as an interleaving of the actions of $A_1$ and $A_2$, is also a trace of the observer B. To this end, our procedure will fire increasingly longer sequences of input events, in search for a counterexample trace. We keep a set of predicates associated with each state $({\langle q_1,q_2 \rangle },P)$ of the product automaton where $q_i$ is a state of $A_i$ and P is a set of states of B. These predicates are formulae that define over-approximations of the data values reached simultaneously by the network, when $A_i$ is the state $q_i$, and by the observer B, in every state from P.

The first input event is $\mathbf {init}$, on which $A_1$ and $A_2$ synchronize, moving together from the initial state ${\langle q_0^1, q_0^2 \rangle }$ to ${\langle q_1^1,q_1^2 \rangle }$. In response, B can chose to either (i) move from ${\left\{ p_0 \right\} }$ to ${\left\{ p_1 \right\} }$, matching the only transition rule from $p_0$, or (ii) ignore the transition rule and move to the empty set. In the first case, the values of $\nu$ match the relation of the rule $p_0 \xrightarrow {{\scriptscriptstyle \mathbf {init},v'=1}}{} p_1$, while in the second case, these values match the negated relation $\lnot (v'=1)$. The second case is impossible because the action of the network requires $x'=0 \wedge v'=1$. The only successor state is thus $({\langle q_1^1,q_1^2 \rangle },{\left\{ p_1 \right\} })$ in Fig. 2(a). Since no predicates are initially available at this state, the best over-approximation of the set of reachable data valuations is the universal set ($\top$).

The second input event is $\mathbf {a}_1$, on which $A_1$ moves from $q_1^1$ back to itself, while $A_2$ makes an idle step because no transition with $\mathbf {a}_1$ is enabled from $q^2_1$. Again, B has the choice between moving from ${\left\{ p_1 \right\} }$ either to $\varnothing$ or ${\left\{ p_1 \right\} }$. Let us consider the first case, in which the successor state is $({\langle q_1^1,q_1^2 \rangle }, \varnothing , \top )$. Since $q_1^1$ and $q^2_1$ are final states of $A_1$ and $A_2$, respectively, and no final state of B is present in $\varnothing$, we say that the state is accepting. If the accepting state (in dashed boxes in Fig. 2) is reachable according to the transition constraints along the input sequence $\mathbf {init}.\mathbf {a}_1$, we have found a counterexample trace that is in the language of ${\langle A_1,A_2 \rangle }$ but not in the language of B.

To verify the reachability of the accepting state, we check the satisfiability of the path formula corresponding to the composition of the transition constraints $x'=0\wedge v'=1$ ($\mathbf {init}$) and $0 \leqslant x < \Delta \wedge x'=x+1 \wedge v'=1 \wedge \lnot (v'=v)$ ($\mathbf {a}_1$) in Fig. 2(a). This formula is unsatisfiable, and the proof of infeasibility provides the interpolant ${\langle v=1 \rangle }$. This formula is an explanation for the infeasibility of the path because it is implied by the first constraint and it is unsatisfiable in conjunction with the second constraint. By associating the new predicate $v=1$ with the state $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_1 \right\} })$, we ensure that the same spurious path will never be explored again.

We delete the spurious counterexample and recompute the states along the input sequence $\mathbf {init}.\mathbf {a}_1$ with the new predicate. In this case, $({\langle q_1^1,q_1^2 \rangle }, \varnothing )$ is unreachable, and the outcome is $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_1 \right\} },v=1)$. However, this state was first encountered after the sequence $\mathbf {init}$, so there is no need to store a second occurrence of this state in the tree. We say that $\mathbf {init}.\mathbf {a}_1$ is subsumed by $\mathbf {init}$, depicted by a dashed arrow in Fig. 2(b).

We continue with $\mathbf {a}_2$ from the state $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_1 \right\} },v=1)$. In this case, $A_1$ makes an idle step and $A_2$ moves from $q_1^2$ to itself. In response, B has the choice between moving from ${\left\{ p_1 \right\} }$ to either (i) ${\left\{ p_1 \right\} }$ with the constraint $v'=v$, (ii) ${\left\{ p_2 \right\} }$ with the constraint $v'=v+1$, (iii) ${\left\{ p_1,p_2 \right\} }$ with the constraint $v'=v \wedge v'=v+1 \rightarrow \bot$ (this possibility is discarded), (iv) $\varnothing$ for data values that satisfy $\lnot (v'=v) \wedge \lnot (v'=v+1)$. The last case is also discarded because the value of $\nu$ after $\mathbf {init}$ constrained to 1 and the $A_2$ imposes further the constraint $v'=2$ and $v=1 \wedge v'=2 \wedge \lnot (v'=v) \wedge \lnot (v'=v+1) \rightarrow \bot$. Hence, the only $\mathbf {a}_2$-successor of $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_1 \right\} },v=1)$ is $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_2 \right\} },\top )$, in Fig. 2(b).

By firing the event $\mathbf {a}_1$ from this state, we reach $({\langle q_1^1,q_1^2 \rangle }, \varnothing ,v=1)$, which is, again, accepting. We check whether the path $\mathbf {init}.\mathbf {a}_2.\mathbf {a}_1$ is feasible, which turns out not to be the case. For efficiency reasons, we find the shortest suffix of this path that can be proved infeasible. It turns out that the sequence $\mathbf {a}_2.\mathbf {a}_1$ is infeasible starting from the state $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_1 \right\} },v=1)$, which is called the pivot. This proof of infeasibility yields the interpolant ${\langle v=1,\Delta <x \rangle }$, and a new predicate $\Delta <x$ is associated with $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_2 \right\} })$. The refinement phase rebuilds only the subtree rooted at the pivot state, in Fig. 2(b).

The procedure then builds the tree on Fig. 2(c) starting from the pivot node and finds the accepting state $({\langle q_1^1,q_1^2 \rangle }, \varnothing ,\Delta <x)$ as the result of firing the sequence $\mathbf {init}.\mathbf {a}_2.\mathbf {a}_2$. This path is spurious, and the new predicate $v=2$ is associated with the location $({\langle q_1^1,q_1^2 \rangle }, {\left\{ p_2 \right\} })$. The pivot node is the same as in Fig. 2(b), and, by recomputing the subtree rooted at this node with the new predicates, we obtain the tree in Fig. 2(d), in which all frontier nodes are subsumed by their predecessors. Thus, no new event needs to be fired, and the procedure can stop reporting that the trace inclusion holds.

Related Work. The trace inclusion problem has been previously addressed in the context of timed automata [25]. Although the problem is undecidable in general, decidability is recovered when the left-hand side automaton has at most one clock, or the only constant appearing in the clock constraints is zero. These are essentially the only known decidable cases of language inclusion for timed automata.

The study of data automata [5, 6] usually deals with decision problems in logics describing data languages for simple theories, typically infinite data domains with equality. Although our notions of data words and data languages are similar to the classical ones in the literature [5, 6], the data automata defined in this paper are different from [5], as well as [6]. The main difference consists in the fact that the existing notions of data automata are controlled by equivalence relations of finite index, whereas in our case, the transitions are defined by unrestricted formulae in the first-order theory of the data domain. Moreover, the emptiness problems [5, 6] are decidable, whereas we consider an undecidable model that subsumes the existing ones.

Data words are also studied in the context of symbolic visibly pushdown automata (SVPA) [11]. Language inclusion is decidable for SVPAs with transition guards from a decidable theory because SVPAs are closed under complement and the emptiness can be reduced to a finite number of queries expressible in the underlying theory of guards. Decidability comes here at the cost of reducing the expressiveness and forbidding comparisons between adjacent positions in the input (only comparisons between matching call/return positions of the input nested words are allowed).

Another related model is that of predicate automata [13], which recognize languages over integer data by labeling the words with conjunctions of uninterpreted predicates. The emptiness problem is undecidable for this model and becomes decidable when all predicates are monadic. Exploring further the connection between predicate automata and our definition of data automata could also provide interesting examples for our method, stemming from verification problems for parallel programs.

Finally, several works on model checking infinite-state systems against CTL [4] and CTL* [9] specifications are related to our problem as they check inclusion between the set of computation trees of an infinite-state system and the set of trees defined by a branching temporal logic specification. The verification of existential CTL formulae [4] is reduced to solving forall-exists quantified Horn clauses by applying counterexample guided refinement to discover witnesses for existentially quantified variables. The work [9] on CTL* verification of infinite systems is based on partial symbolic determinization, using prophecy variables to summarize the future program execution. For finite-state systems, automata are a strictly more expressive formalism than temporal logics¹. Such a comparison is, however, non-trivial for infinite-state systems. Nevertheless, we found the data automata considered in this paper to be a natural tool for specifying verification conditions of array programs [7, 16, 17] and regular properties of timed languages [2].

2 Data Automata

Let $\mathbf{\mathbb {N}}$ denote the set of non-negative integers including zero. For any $k,\ell \in \mathbf{\mathbb {N}}$, $k \leqslant \ell$, we write $[k,\ell ]$ for the set ${\left\{ k,k+1,\ldots ,\ell \right\} }$. We write $\bot$ and $\top$ for the boolean constants false and true, respectively. Given a possibly infinite data domain $\mathcal {D}$, we denote by $\text{ Th }(\mathcal {D})={\langle \mathcal {D}, p_1,\ldots ,p_n, f_1,\ldots ,f_m \rangle }$ the set of syntactically correct first-order formulae with predicate symbols $p_1,\ldots ,p_n$ and function symbols $f_1,\ldots ,f_m$. A variable x is said to be free in a formula $\upphi$, denoted as $\upphi (x)$, iff it does not occur under the scope of a quantifier.

Let ${\mathbf {x}} = {\left\{ x_1,\ldots ,x_n \right\} }$ be a finite set of variables. A valuation $\nu : {\mathbf {x}} \rightarrow \mathcal {D}$ is an assignment of the variables in ${\mathbf {x}}$ with values from $\mathcal {D}$. We denote by $\mathcal {D}^{\mathbf {x}}$ the set of such valuations. For a formula $\upphi ({\mathbf {x}})$, we denote by $\nu \models _\mathrm{{\tiny Th}(\mathcal {D})}\upphi$ the fact that substituting each variable $x \in {\mathbf {x}}$ by $\nu (x)$ yields a valid formula in the theory $\text{ Th }(\mathcal {D})$. In this case, $\nu$ is said to be a model of $\upphi$. A formula is said to be satisfiable iff it has a model. For a formula $\upphi ({\mathbf {x}}, {\mathbf {x'}})$ where ${\mathbf {x'}} = {\left\{ x' ~|~ x \in {\mathbf {x}} \right\} }$ and two valuations $\nu ,\nu ' \in \mathcal {D}^{{\mathbf {x}}}$, we denote by $(\nu ,\nu ') \models _\mathrm{{\tiny Th}(\mathcal {D})}\upphi$ the fact that the formula obtained from $\upphi$ by substituting each x with $\nu (x)$ and each $x'$ with $\nu '(x')$ is valid in $\text{ Th }(\mathcal {D})$.

Data Automata. Data Automata (DA) are extensions of non-deterministic finite automata with variables ranging over an infinite data domain $\mathcal {D}$, equipped with a first order theory $\text{ Th }(\mathcal {D})$. Formally, a DA is a tuple $A ={\langle \mathcal {D}, \Sigma , {\mathbf {x}}, Q, \iota , F, \Delta \rangle }$, where:

• $\Sigma$ is a finite alphabet of input events and $\diamond \in \Sigma$ is a special padding symbol,

• ${\mathbf {x}} = {\left\{ x_1,\ldots ,x_n \right\} }$ is a set of variables,

• Q is a finite set of states, $\iota \in Q$ is an initial state, $F \subseteq Q$ are final states, and

• $\Delta$ is a set of rules of the form $q \xrightarrow {{\scriptscriptstyle \sigma ,\upphi ({\mathbf {x}}, {\mathbf {x'}})}} q'$ where $\sigma \in \Sigma$ is an alphabet symbol and $\upphi ({\mathbf {x}},{\mathbf {x'}})$ is a formula in $\text{ Th }(\mathcal {D})$.

A configuration of A is a pair $(q,\nu ) \in Q \times \mathcal {D}^{{\mathbf {x}}}$. We say that a configuration $(q',\nu ')$ is a successor of $(q,\nu )$ if and only if there exists a rule $q \xrightarrow {{\scriptscriptstyle \sigma ,\upphi }}{} q' \in \Delta$ and $(\nu ,\nu ') \models _\mathrm{{\tiny Th}(\mathcal {D})}\upphi$. We denote the successor relation by $(q,\nu ) \xrightarrow {{\scriptscriptstyle \sigma ,\upphi }}{}_A (q',\nu ')$, and we omit writing $\upphi$ and A when no confusion may arise. We denote by $succ _A(q,\nu ) = \{(q',\nu ') \mid (q,\nu ) \xrightarrow {{\scriptscriptstyle }}{}_A (q',\nu ')\}$ the set of successors of a configuration $(q,\nu )$.

A trace is a finite sequence $w=(\nu _0,\sigma _0), \ldots , (\nu _{n-1},\sigma _{n-1}),(\nu _n,\diamond )$ of pairs $(\nu _i,\sigma _i)$ taken from the infinite alphabet $\mathcal {D}^{{\mathbf {x}}} \times \Sigma$. A run of A over the trace w is a sequence of configurations $\pi : (q_0,\nu _0) \xrightarrow {{\scriptscriptstyle \sigma _0}}{} (q_1,\nu _1) \xrightarrow {{\scriptscriptstyle \sigma _1}}{} \ldots \xrightarrow {{\scriptscriptstyle \sigma _{n-1}}}{} (q_n,\nu _n)$. We say that the run $\pi$ is accepting if and only if $q_n \in F$, in which case A accepts w. The language of A, denoted $\mathcal {L}(A)$, is the set of traces accepted by A.

Data Automata Networks. A data automata network (DAN) is a non-empty tuple $\mathcal {A} = {\langle A_1,\ldots ,A_N \rangle }$ of data automata $A_i = {\langle \mathcal {D},\Sigma _i,{\mathbf {x}}_i,Q_i,\iota _i,F_i,\Delta _i \rangle }$, $i\in [1,N]$ whose sets of states are pairwise disjoint. A DAN is a succinct representation of an exponentially larger DA $\mathcal {A}^e={\langle \mathcal {D},\Sigma _{\mathcal {A}}, {\mathbf {x}}_{\mathcal {A}}, Q_{\mathcal {A}}, \iota _{\mathcal {A}}, F_{\mathcal {A}}, \Delta _{\mathcal {A}} \rangle }$, called the expansion of $\mathcal {A}$, where:

• $\Sigma _{\mathcal {A}} = \Sigma _1 \cup \ldots \cup \Sigma _N$ and ${\mathbf {x}}_{\mathcal {A}} = {\mathbf {x}}_1 \cup \ldots \cup {\mathbf {x}}_N$,

• $Q_{\mathcal {A}} = Q_1 \times \ldots \times Q_N$, $\iota _{\mathcal {A}} = {\langle \iota _1, \ldots , \iota _N \rangle }$ and $F_{\mathcal {A}} = F_1 \times \ldots \times F_N$,

• ${\langle q_1, \ldots , q_N \rangle } \xrightarrow {{\scriptscriptstyle \sigma ,\varphi }}{} {\langle q'_1, \ldots , q'_N \rangle }$ if and only if (i) for each $i \in I$, there exists $\varphi _i \in \text{ Th }(\mathcal {D})$ such that $q_i \xrightarrow {{\scriptscriptstyle \sigma ,\varphi _i}}{} q'_i \in \Delta _i$, (ii) for all $i \not \in I$, $q_i = q'_i$, and (iii) $\varphi \equiv \bigwedge _{i\in I} \varphi _i \wedge \bigwedge _{j \not \in I} \tau _j$, where $I = \{i \in [1,N] \mid q_i \xrightarrow {{\scriptscriptstyle \sigma ,\varphi _i}}{} q'_i \in \Delta _i\}$ is the set of DA that can move from $q_i$ to $q'_i$ while reading the input symbol $\sigma$, and $\tau _j \equiv \bigwedge _{x \in {\mathbf {x}}_j \setminus \left( \bigcup _{i \in I} {\mathbf {x}}_i\right) } x'=x$ propagates the values of the local variables in $A_j$ that are not updated by ${\left\{ A_i \right\} }_{i\in I}$.

Intuitively, all automata that can read an input symbol synchronize their actions on that symbol whereas the rest of the automata make an idle step and copy the values of their local variables which are not updated by the active automata. The language of the DAN $\mathcal {A}$ is defined as the language of its expansion DA, i.e. $\mathcal {L}(\mathcal {A}) = \mathcal {L}(\mathcal {A}^e)$.

Trace Inclusion. Let $\mathcal {A}$ be a DAN and $\mathcal {A}^e={\langle \mathcal {D},\Sigma , {\mathbf {x}}_{\mathcal {A}}, Q_{\mathcal {A}}, \iota _{\mathcal {A}}, F_{\mathcal {A}}, \Delta _{\mathcal {A}} \rangle }$ be its expansion. For a set of variables ${\mathbf {y}}\subseteq {\mathbf {x}}_{\mathcal {A}}$, we denote by $\nu \varvec{\downarrow }_{{\mathbf {y}}}$ the restriction of a valuation $\nu \in \mathcal {D}^{{\mathbf {x}}_{\mathcal {A}}}$ to the variables in ${\mathbf {y}}$. For a trace $w=(\nu _0,\sigma _0), \ldots , (\nu _n,\diamond )\in \!\!\left( \mathcal {D}^{{\mathbf {x}}_{\mathcal {A}}} \times \Sigma _{\mathcal {A}}\right) ^*$, we denote by $w\!\varvec{\downarrow }_{{\mathbf {y}}}$ the trace $(\nu _0\varvec{\downarrow }_{{\mathbf {y}}},\sigma _0), \ldots , (\nu _{n-1}\varvec{\downarrow }_{{\mathbf {y}}},\sigma _{n-1}), (\nu _n\!\!\varvec{\downarrow }_{{\mathbf {y}}},\diamond ) \in \left( \mathcal {D}^{{\mathbf {y}}} \times \Sigma \right) ^*$. We lift this notion to sets of words in the natural way, by defining $\mathcal {L}(\mathcal {A}) \varvec{\downarrow }_{{\mathbf {y}}} = {\left\{ w \varvec{\downarrow }_{{\mathbf {y}}} \mid w \in \mathcal {L}(\mathcal {A}) \right\} }$.

We are now ready to define the trace inclusion problem on which we focus in this paper. Given a DAN $\mathcal {A}$ as before and a DA $B={\langle \mathcal {D},\Sigma ,{\mathbf {x}}_B,Q_B,\iota _B,F_B,\Delta _B \rangle }$ such that ${\mathbf {x}}_B \subseteq {\mathbf {x}}_{\mathcal {A}}$, the trace inclusion problem asks whether $\mathcal {L}(\mathcal {A})\varvec{\downarrow }_{{\mathbf {x}}_B} \subseteq \mathcal {L}(B)$? The right-hand side DA B is called observer, and the variables in ${\mathbf {x}}_B$ are called observable variables.

2.1 Boolean Closure Properties of Data Automata

Let $A = {\langle \mathcal {D}, \Sigma , {\mathbf {x}}, Q, \iota , F, \Delta \rangle }$ be a DA for the rest of this section. A is said to be deterministic if and only if, for each trace $w \in \mathcal {L}(A)$, A has at most one run over w. The first result of this section is that, interestingly, any DA can be determinized while preserving its language. The determinization procedure is a generalization of the classical subset construction for Rabin-Scott word automata on finite alphabets. The reason why determinization is possible for automata over an infinite data alphabet $\mathcal {D}^{{\mathbf {x}}} \times \Sigma$ is that the successive values taken by each variable $x\in {\mathbf {x}}$ are tracked by the language $\mathcal {L}(A) \subseteq \left( \mathcal {D}^{{\mathbf {x}}} \times \Sigma \right) ^*$. This assumption is crucial: a typical example of automata over an infinite alphabet, that cannot be determinized, are timed automata [2], where only the elapsed time is reflected in the language, and not the values of the variables (clocks).

Formally, the deterministic DA accepting the language $\mathcal {L}(A)$ is defined as $A^d = {\langle \mathcal {D}, \Sigma , {\mathbf {x}}, Q^d, \iota ^d, F^d, \Delta ^d \rangle }$, where $Q^d=2^Q$, $\iota ^d={\left\{ \iota \right\} }$, $F^d={\left\{ P \subseteq Q \mid P \cap F \ne \varnothing \right\} }$ and $\Delta ^d$ is the set of rules $P \xrightarrow {{\scriptscriptstyle \sigma ,\theta }}{} P'$ such that:

• for all $p' \in P'$ there exists $p \in P$ and a rule $p \xrightarrow {{\scriptscriptstyle \sigma ,\psi }}{} p' \in \Delta$,

• $\theta ({\mathbf {x}},{\mathbf {x}}') \equiv \bigwedge _{\scriptscriptstyle {p' \in P'}} \bigvee _{\begin{array}{l} {\scriptscriptstyle {p \xrightarrow {{\scriptscriptstyle \sigma ,\psi }}{} p' \in \Delta }}\\ {\scriptscriptstyle {p \in P}} \end{array}} \psi \wedge \bigwedge _{\scriptscriptstyle {p' \in Q \setminus P'}} \bigwedge _{\begin{array}{l} \scriptscriptstyle {p \xrightarrow {{\scriptscriptstyle \sigma ,\varphi }}{} p' \in \Delta }\\ \scriptscriptstyle {p \in P} \end{array}}\lnot \varphi .$

The main difference with the classical subset construction for Rabin-Scott automata is that here we consider all sets $P'$ of states that have a predecessor in P, not just the maximal such set. The reason is that a set $P'$ is not automatically subsumed by the union of all such sets due to the data constraints on the variables ${\mathbf {x}}$. Observe, moreover, that $A^d$ can be built for any theory $\text{ Th }(\mathcal {D})$ that is closed under conjunction and negation.

Lemma 1

Given a DA $A = {\langle \mathcal {D}, \Sigma , {\mathbf {x}}, Q, \iota , F, \Delta \rangle }$, (1) for any $w \in \left( \mathcal {D}^{{\mathbf {x}}} \times \Sigma \right) ^*$ and $P \in Q^d$, $A^d$ has exactly one run on w that starts in P, and (2) $\mathcal {L}(A)=\mathcal {L}(A^d)$.

The construction of a deterministic DA recognizing the language of A is key to defining a DA that recognizes the complement of A. Let $\overline{A} = {\langle \mathcal {D},\Sigma ,{\mathbf {x}},Q^d,\iota ^d,Q^d\setminus F^d,\Delta ^d \rangle }$. In other words, $\overline{A}$ has the same structure as $A^d$, and the set of final states consists of those subsets that contain no final state, i.e. ${\left\{ P \subseteq Q \mid P \cap F = \varnothing \right\} }$. Using Lemma 1, it is not difficult to show that $\mathcal {L}(\overline{A}) = \left( \mathcal {D}^{{\mathbf {x}}} \times \Sigma \right) ^* \setminus \mathcal {L}(A)$.

Next, we show closure of DA under intersection. Let $B = {\langle \mathcal {D},\Sigma ,{\mathbf {x}},Q',\iota ',F',\Delta ' \rangle }$ be a DA and define $A \times B = {\langle \mathcal {D},\Sigma ,{\mathbf {x}},Q \times Q',(\iota ,\iota '), F \times F',\Delta ^\times \rangle }$, where $(q,q') \xrightarrow {{\scriptscriptstyle \sigma ,\varphi }}{} (p,p') \in \Delta ^\times$ if and only if $q \xrightarrow {{\scriptscriptstyle \sigma ,\upphi }}{} p \in \Delta$, $q' \xrightarrow {{\scriptscriptstyle \sigma ,\psi }}{} p' \in \Delta '$ and $\varphi \equiv \upphi \wedge \psi$. It is easy to show that $\mathcal {L}(A \times B) = \mathcal {L}(A) \cap \mathcal {L}(B)$. DA are also closed under union, since $\mathcal {L}(A) \cup \mathcal {L}(B) = \mathcal {L}(\overline{\overline{A} \times \overline{B}})$.

Let us turn now to the trace inclusion problem. The following lemma shows that this problem can be effectively reduced to an equivalent language emptiness problem. However, note that this reduction does not work when the trace inclusion problem is generalized by removing the condition ${\mathbf {x}}_B \subseteq {\mathbf {x}}_A$. In other words, if the observer uses local variables not shared with the network², i.e. ${\mathbf {x}}_B \setminus {\mathbf {x}}_A \ne \varnothing$, the generalized trace inclusion problem $\mathcal {L}(A)\varvec{\downarrow }_{{\mathbf {x}}_A \cap {\mathbf {x}}_B} \subseteq \mathcal {L}(B)\varvec{\downarrow }_{{\mathbf {x}}_A \cap {\mathbf {x}}_B}$ has a negative answer iff there exists a trace $w = (\nu _0,\sigma _0), \ldots , (\nu _n,\diamond ) \in \mathcal {L}(A)$ such that, for all valuations $\mu _0,\ldots ,\mu _n\in \mathcal {D}^{{\mathbf {x}}_B\setminus {\mathbf {x}}_A}$, we have $w'=(\nu _0\varvec{\downarrow }_{{\mathbf {x}}_A \cap {\mathbf {x}}_B}\cup ~\mu _0,\sigma _0), \ldots , (\nu _n\varvec{\downarrow }_{{\mathbf {x}}_A \cap {\mathbf {x}}_B}\cup ~\mu _n,\diamond ) \not \in \mathcal {L}(B)$. This kind of quantifier alternation cannot be easily accommodated within the framework of language emptiness, in which only one type of (existential) quantifier occurs.

Lemma 2

Given DA $A = {\langle \mathcal {D},\Sigma ,{\mathbf {x}}_A,Q_A,\iota _A,F_A,\Delta _A \rangle }$ and $B = {\langle \mathcal {D},\Sigma ,{\mathbf {x}}_B,Q_B,\iota _B,F_B,\Delta _B \rangle }$ such that ${\mathbf {x}}_B \subseteq {\mathbf {x}}_A$. Then $\mathcal {L}(A)\varvec{\downarrow }_{{\mathbf {x}}_B} \subseteq \mathcal {L}(B)$ if and only if $\mathcal {L}(A \times \overline{B}) = \varnothing$.

The trace inclusion problem is undecidable, which can be shown by reduction from the language emptiness problem for DA (take B such that $\mathcal {L}(B)=\varnothing$). However the above lemma shows that any semi-decision procedure for the language emptiness problem can also be used to deal with the trace inclusion problem.

3 Abstract, Check, and Refine for Trace Inclusion

This section describes our semi-algorithm for checking the trace inclusion between a given network $\mathcal {A}$ and an observer B. Let $\mathcal {A}^e$ denote the expansion of $\mathcal {A}$, defined in the previous. In the light of Lemma 2, the trace inclusion problem $\mathcal {L}(\mathcal {A})\varvec{\downarrow }_{{\mathbf {x}}_B} \subseteq \mathcal {L}(B)$, where the set of observable variables ${\mathbf {x}}_B$ is included in the set of network variables, can be reduced to the language emptiness problem $\mathcal {L}(\mathcal {A}^e \times \overline{B}) = \varnothing$.

Although language emptiness is undecidable for data automata [23], several cost-effective semi-algorithms and tools [3, 15, 18, 22] have been developed, showing that it is possible, in many practical cases, to provide a yes/no answer to this problem. However, to apply one of the existing off-the-shelf tools to our problem, one needs to build the product automaton $\mathcal {A}^e \times \overline{B}$ prior to the analysis. Due to the inherent state explosion caused by the interleaving semantics of the network as well as by the complementation of the observer, such a solution would not be efficient in practice.

To avoid building the product automaton, our procedure builds on-the-fly an over-approximation of the (possibly infinite) set of reachable configurations of $\mathcal {A}^e \times \overline{B}$. This over-approximation is defined using the approach of lazy predicate abstraction [18], combined with counterexample-driven abstraction refinement using interpolants [22]. We store the explored abstract states in a structure called an antichain tree. In general, antichain-based algorithms [28] store only states which are incomparable w.r.t. a partial order called subsumption. Our method can be thus seen as an extension of the antichain-based language inclusion algorithm [1] to infinite-state systems by means of predicate abstraction and interpolation-based refinement. Since the trace inclusion problem is undecidable in general, termination of our procedure is not guaranteed; in the following, we shall, however, call our procedure an algorithm for the sake of brevity.

3.1 Antichain Trees

We define antichain trees, which are the main data structure of the trace inclusion procedure. Let $\mathcal {A} = {\langle A_1,\ldots ,A_N \rangle }$ be a network of automata where $A_i = {\langle \mathcal {D},\Sigma _i,{\mathbf {x}}_i,Q_i,\iota _i,F_i,\Delta _i \rangle }$, for all $i \in [1,N]$, and let $B = {\langle \mathcal {D},\Sigma ,{\mathbf {x}}_B,Q_B,\iota _B,F_B,\Delta _B \rangle }$ be an observer such that ${\mathbf {x}}_B \subseteq \bigcup _{i=1}^N{\mathbf {x}}_i$. We also denote by $\mathcal {A}^e = {\langle \mathcal {D}, \Sigma _{\mathcal {A}}, {\mathbf {x}}_{\mathcal {A}}, Q_{\mathcal {A}}, \iota _{\mathcal {A}}, F_{\mathcal {A}}, \Delta _{\mathcal {A}} \rangle }$ the expansion of the network $\mathcal {A}$ and by $\mathcal {A}^e \times \overline{B} = {\langle \mathcal {D}, \Sigma _{\mathcal {A}}, {\mathbf {x}}_{\mathcal {A}}, Q^p, \iota ^p, F^p, \Delta ^p \rangle }$ the product automaton used for checking language inclusion.

An antichain tree for the network $\mathcal {A}$ and the observer B is a tree whose nodes are labeled by product states (see Fig. 2 for examples). Intuitively, a product state is an over-approximation of the set of configurations of the product automaton $\mathcal {A}^e \times \overline{B}$ that share the same control state. Formally, a product state for $\mathcal {A}$ and B is a tuple $s=({\mathbf {q}},P,\Phi )$ where (i) $({\mathbf {q}},P)$ is a state of $\mathcal {A}^e \times \overline{B}$ with ${\mathbf {q}}={\langle q_1,\ldots ,q_N \rangle }$ being a state of the network expansion $\mathcal {A}^e$ and P being a set of states of the observer B, and (ii) $\Phi ({\mathbf {x}}_{\mathcal {A}}) \in \text{ Th }(\mathcal {D})$ is a formula which defines an over-approximation of the set of valuations of the variables ${\mathbf {x}}_{\mathcal {A}}$ that reach the state $({\mathbf {q}},P)$ in $\mathcal {A}^e \times \overline{B}$. A product state $s=({\mathbf {q}},P,\Phi )$ is a finite representation of a possibly infinite set of configurations of $\mathcal {A}^e \times \overline{B}$, denoted as $\mathbf{[\![}s \mathbf{]\!]} = \{({\mathbf {q}},P,\nu ) \mid \nu \models _\mathrm{{\tiny Th}(\mathcal {D})}\Phi \}$.

To build an over-approximation of the set of reachable states of the product automaton, we need to compute, for a product state s, an over-approximation of the set of configurations that can be reached in one step from s. To this end, we define first a finite abstract domain of product states, based on the notion of predicate map. A predicate map is a partial function that associates sets of facts about the values of the variables used in the product automaton, called predicates, with components of a product state, called substates. The reason behind the distribution of predicates over substates is two-fold. First, we would like the abstraction to be local, i.e. the predicates needed to define a certain subtree in the antichain must be associated with the labels of that subtree only. Second, once a predicate appears in the context of a substate, it should be subsequently reused whenever that same substate occurs as part of another product state.

Formally, a substate of a state $({\langle q_1,\ldots ,q_N \rangle },P) \in Q^p$ of the product automaton $\mathcal {A}^e \times \overline{B}$ is a pair $({\langle q_{i_1},\ldots ,q_{i_k} \rangle },S)$ such that (i) ${\langle q_{i_1},\ldots ,q_{i_k} \rangle }$ is a subsequence of ${\langle q_1,\ldots ,q_N \rangle }$, and (ii) $S \ne \varnothing$ only if $S \cap P \ne \varnothing$. We denote the substate relation by $({\langle q_{i_1},\ldots ,q_{i_k} \rangle },S) \vartriangleleft ({\langle q_1,\ldots ,q_N \rangle },P)$. The substate relation requires the automata $A_{i_1}, \ldots , A_{i_k}$ of the network $\mathcal {A}$ to be in the control states $q_{i_1},\ldots ,q_{i_k}$ simultaneously, and the observer B to be in at least some state of S provided $S\ne \varnothing$ (if $S=\varnothing$, the state of B is considered to be irrelevant). Let $\mathcal {S}_{{\langle \mathcal {A},B \rangle }} = {\left\{ r \mid \exists q \in Q^p ~.~ r \vartriangleleft q \right\} }$ be the set of substates of a state of $\mathcal {A}^e \times \overline{B}$.

A predicate map $\Pi : \mathcal {S}_{{\langle \mathcal {A},B \rangle }} \rightarrow 2^\mathrm{{\tiny Th}(\mathcal {D})}$ associates each substate $({\mathbf {r}},S) \in Q_{i_1} \times \ldots \times Q_{i_k} \times 2^{Q_B}$ with a set of formulae $\pi ({\mathbf {x}})$ where (i) ${\mathbf {x}} = {\mathbf {x}}_{i_1} \cup \ldots \cup {\mathbf {x}}_{i_k} \cup {\mathbf {x}}_B$ if $S \ne \varnothing$, and (ii) ${\mathbf {x}} = {\mathbf {x}}_{i_1} \cup \ldots \cup {\mathbf {x}}_{i_k}$ if $S = \varnothing$. Notice that a predicate associated with a substate refers only to the local variables of those network components $A_{i_1}, \ldots , A_{i_k}$ and of the observer B that occur in the particular substate.

We are now ready to define the abstract semantics of the product automaton $\mathcal {A}^e \times \overline{B}$, induced by a given predicate map. For convenience, we define first a set $Post (s)$ of concrete successors of a product state $s=({\mathbf {q}},P,\Phi )$ such that $({\mathbf {r}},S,\Psi ) \in Post (s)$ if and only if (i) the product automaton $\mathcal {A}^e \times \overline{B}$ has a rule $({\mathbf {q}},P) \xrightarrow {{\scriptscriptstyle \sigma ,\theta }}{} ({\mathbf {r}},S) \in \Delta ^p$ and $\Psi ({\mathbf {x}}_{\mathcal {A}}) \not \rightarrow \bot$, where $\Psi ({\mathbf {x}}_{\mathcal {A}}) \equiv \exists {\mathbf {x}}'_{\mathcal {A}} ~.~ \Phi ({\mathbf {x}}'_{\mathcal {A}}) \wedge \theta ({\mathbf {x}}'_{\mathcal {A}}, {\mathbf {x}}_{\mathcal {A}})$. The set of concrete successors does not contain states with empty set of valuations; these states are unreachable in $\mathcal {A}^e \times \overline{B}$.

Given a predicate map $\Pi$, the set $Post _\Pi (s)$ of abstract successors of a product state s is defined as follows: $({\mathbf {r}},S,\Psi ^\sharp ) \in Post _\Pi (s)$ if and only if (i) there exists a product state $({\mathbf {r}},S,\Psi ) \in Post (s)$ and (ii) $\Psi ^\sharp ({\mathbf {x}}_{\mathcal {A}}) \equiv \bigwedge _{r \vartriangleleft ({\mathbf {r}},S)} \bigwedge {\left\{ \pi \in \Pi (r) \mid \Psi \rightarrow \pi \right\} }$. In other words, the set of data valuations that are reachable by an abstract successor is the tightest over-approximation of the concrete set of reachable valuations, obtained as the conjunction of the available predicates from the predicate map that over-approximate this set.

Finally, an antichain tree (or, simply antichain) $\mathcal {T}$ for $\mathcal {A}$ and B is a tree whose nodes are labeled with product states and whose edges are labeled by input symbols and concrete transition relations. Let $\mathbf{\mathbb {N}}^*$ be the set of finite sequences of natural numbers that denote the positions in the tree. For a tree position $p \in \mathbf{\mathbb {N}}^*$ and $i \in \mathbf{\mathbb {N}}$, the position p.i is a child of p. A set $S \subseteq \mathbf{\mathbb {N}}^*$ is said to be prefix-closed if and only if, for each $p \in S$ and each prefix q of p, we have $q \in S$ as well. The root is denoted by the empty sequence $\varepsilon$.

Formally, an antichain $\mathcal {T}$ is a set of pairs ${\langle s,p \rangle }$, where s is a product state and $p\in \mathbf{\mathbb {N}}^*$ is a tree position, such that (1) for each position $p \in \mathbf{\mathbb {N}}^*$ there exists at most one product state s such that ${\langle s,p \rangle } \in \mathcal {T}$, (2) the set ${\left\{ p \mid {\langle s,p \rangle } \in \mathcal {T} \right\} }$ is prefix-closed, (3) $( root _{{\langle \mathcal {A},B \rangle }},\varepsilon ) \in \mathcal {T}$ where $root _{{\langle \mathcal {A},B \rangle }}=({\langle \iota _1,\ldots ,\iota _N \rangle }, {\left\{ \iota _B \right\} }, \top )$ is the label of the root, and (4) for each edge $({\langle s,p \rangle },{\langle t,p.i \rangle })$ in $\mathcal {T}$, there exists a predicate map $\Pi$ such that $t \in Post _\Pi (s)$. For the latter condition, if $s=({\mathbf {q}},P,\Phi )$ and $t=({\mathbf {r}},S,\Psi )$, there exists a unique rule $({\mathbf {q}},P) \xrightarrow {{\scriptscriptstyle \sigma ,\theta }}{} ({\mathbf {r}},S) \in \Delta ^p$, and we shall sometimes denote the edge as $s \xrightarrow {{\scriptscriptstyle \sigma ,\theta }}{} t$ or simply $s \xrightarrow {{\scriptscriptstyle \theta }}{} t$ when the tree positions are not important.

Each antichain node $n=(s,d_1\ldots d_k) \in \mathcal {T}$ is naturally associated with a path from the root to itself $\rho :n_0 \xrightarrow {{\scriptscriptstyle \sigma _1,\theta _1}}{} n_1 \xrightarrow {{\scriptscriptstyle \sigma _2,\theta _2}}{} \ldots \xrightarrow {{\scriptscriptstyle \sigma _2,\theta _k}}{} n_k$. We denote by $\rho _i$ the node $n_i$ for each $i\in [0,k]$, and by ${|{\rho }|}=k$ the length of the path. The path formula associated with $\rho$ is $\Theta (\rho ) \equiv \bigwedge _{i=1}^k \theta ({\mathbf {x}}_{\mathcal {A}}^{i-1},{\mathbf {x}}_{\mathcal {A}}^i)$ where ${\mathbf {x}}_{\mathcal {A}}^i = {\left\{ x^i \mid x \in {\mathbf {x}}_{\mathcal {A}} \right\} }$ is a set of indexed variables.

3.2 Counterexample-Driven Abstraction Refinement

A counterexample is a path from the root of the antichain to a node which is labeled by an accepting product state. A product state $({\mathbf {q}},P,\Phi )$ is said to be accepting iff $({\mathbf {q}},P)$ is an accepting state of the product automaton $\mathcal {A}^e \times \overline{B}$, i.e. ${\mathbf {q}} \in F_{\mathcal {A}}$ and $P \cap F_B = \varnothing$. A counterexample is said to be spurious if its path formula is unsatisfiable, i.e. the path does not correspond to a concrete execution of $\mathcal {A}^e \times \overline{B}$. In this case, we need to (i) remove the path $\rho$ from the current antichain and (ii) refine the abstract domain in order to exclude the occurrence of $\rho$ from future state space exploration.

Let $\rho : root _{{\langle \mathcal {A},B \rangle }} = ({\mathbf {q}}_0,P_0,\Phi _0) \xrightarrow {{\scriptscriptstyle \theta _1}}{} ({\mathbf {q}}_1,P_1,\Phi _1) \xrightarrow {{\scriptscriptstyle \theta _2}}{} \ldots \xrightarrow {{\scriptscriptstyle \theta _k}}{} ({\mathbf {q}}_k,P_k,\Phi _k)$ be a spurious counterexample in the following. For efficiency reasons, we would like to save as much work as possible and remove only the smallest suffix of $\rho$ which caused the spuriousness. For some $j \in [0,k]$, let $\Theta ^j(\rho ) \equiv \Phi _j({\mathbf {x}}^0_{\mathcal {A}}) \wedge \bigwedge _{i=j}^k \theta _i({\mathbf {x}}^{i-j}_{\mathcal {A}}, {\mathbf {x}}^{i-j+1}_{\mathcal {A}})$ be the formula defining all sequences of data valuations that start in the set $\Phi _j$ and proceed along the suffix $({\mathbf {q}}_j,P_j,\Phi _j) \xrightarrow {{\scriptscriptstyle }}{} \ldots \xrightarrow {{\scriptscriptstyle }}{} ({\mathbf {q}}_k,P_k,\Phi _k)$ of $\rho$. The pivot of a path $\rho$ is the maximal position $j\in [0,k]$ such that $\Theta ^j(\rho ) = \bot$, and $-1$ if $\rho$ is not spurious.

Finally, we describe the refinement of the predicate map, which ensures that a given spurious counterexample will never be found in a future iteration of the abstract state space exploration. The refinement is based on the notion of interpolant [22].

Definition 1

Given a formula $\Phi ({\mathbf {x}})$ and a sequence ${\langle \theta _1({\mathbf {x}},{\mathbf {x}}'), \ldots , \theta _k({\mathbf {x}},{\mathbf {x}}') \rangle }$ of formulae, an interpolant is a sequence of formulae $\mathbf {I} = {\langle I_0({\mathbf {x}}), \ldots , I_{k}({\mathbf {x}}) \rangle }$ where: (1) $\Phi \rightarrow I_0$, (2) $I_k \rightarrow \bot$, and (3) $I_{i-1}({\mathbf {x}}) \wedge \theta _i({\mathbf {x}},{\mathbf {x}}') \rightarrow I_i({\mathbf {x}}')$ for all $i \in [1,k]$.

Any given interpolant is a witness for the unsatisfiability of a (suffix) path formula $\Theta ^j(\rho )$. Dually, if Craig’s Interpolation Lemma [10] holds for the considered first-order data theory $\text{ Th }(\mathcal {D})$, any infeasible path formula is guaranteed to have an interpolant.

Given a spurious counterexample $\rho$ with pivot $j\geqslant 0$, an interpolant $\mathbf {I}={\langle I_0, \ldots , I_{k-j} \rangle }$ for the infeasible path formula $\Theta ^j(\rho )$ can be used to refine the abstract domain by augmenting the predicate map $\Pi$. As an effect of this refinement, the antichain construction algorithm will avoid every path with the suffix $({\mathbf {q}}_j,P_j,\Phi _j) \xrightarrow {{\scriptscriptstyle }}{} \ldots \xrightarrow {{\scriptscriptstyle }}{} ({\mathbf {q}}_k,P_k,\Phi _k)$ in a future iteration. If $I_i \iff C_i^1({\mathbf {y}}_1) \wedge \ldots \wedge C_i^{m_i}({\mathbf {y}}_{m_i})$ is a conjunctive normal form (CNF) of the i-th component of the interpolant, we consider the substate $({\mathbf {r}}_i^\ell ,S_i^\ell )$ for each $C_i^\ell ({\mathbf {y}}_\ell )$ where $l \in [1,m_i]$:

• ${\mathbf {r}}_i^\ell = {\langle q_{i_1}, \ldots , q_{i_h} \rangle }$ where $1 \leqslant i_1< \ldots < i_h \leqslant N$ is the largest sequence of indices such that ${\mathbf {x}}_{i_g} \cap {\mathbf {y}}_\ell \ne \varnothing$ for each $g\in [1,h]$ and the set ${\mathbf {x}}_{i_g}$ of variables of the network component DA $A_{i_g}$,

• $S_i^\ell = P_j$ if ${\mathbf {x}}_B \cap {\mathbf {y}}_\ell \ne \varnothing$, and $S_i^\ell =\varnothing$, otherwise.

A predicate map $\Pi$ is said to be compatible with a spurious path $\rho : s_0 \xrightarrow {{\scriptscriptstyle \theta _1}}{} \ldots \xrightarrow {{\scriptscriptstyle \theta _k}}{} s_k$ with pivot $j\geqslant 0$ if $s_j=({\mathbf {q}}_j,P_j,\Phi _j)$ and there is an interpolant $\mathbf {I}={\langle I_0,\ldots ,I_{k-j} \rangle }$ of the suffix ${\langle \theta _1,\ldots ,\theta _k \rangle }$ wrt. $\Phi _j$ such that, for each clause C of some equivalent CNF of $I_i$, $i \in [0,k-j]$, it holds that $C\in \Pi (r)$ for some substate $r \vartriangleleft s_{i+j}$. The following lemma proves that, under a predicate map compatible with a spurious path $\rho$, the antichain construction will exclude further paths that share the suffix of $\rho$ starting with its pivot.

Lemma 3

Let $\rho : ({\mathbf {q}}_0,P_0,\Phi _0) \xrightarrow {{\scriptscriptstyle \theta _0}}{} ({\mathbf {q}}_1,P_1,\Phi _1) \xrightarrow {{\scriptscriptstyle \theta _1}}{} \ldots \xrightarrow {{\scriptscriptstyle \theta _{k-1}}}{} ({\mathbf {q}}_k,P_k,\Phi _k)$ be a spurious counterexample and $\Pi$ be a predicate map compatible with $\rho$. Then, there is no sequence of product states $({\mathbf {q}}_j,P_j,\Psi _0), \ldots , ({\mathbf {q}}_k,P_k,\Psi _{k-j})$ such that: (1) $\Psi _0 \rightarrow \Phi _j$ and (2) $({\mathbf {q}}_{i+1},P_{i+1},\Psi _{i-j+1}) \in Post _\Pi (({\mathbf {q}}_i,P_i,\Psi _{i-j}))$ for all $i\in [j,k-1]$.

Observe that the refinement induced by interpolation is local since $\Pi$ associates sets of predicates with substates of the states in $\mathcal {A}^e \times \overline{B}$, and the update impacts only the states occurring within the suffix of that particular spurious counterexample.

3.3 Subsumption

The main optimization of antichain-based algorithms [1] for checking language inclusion of automata over finite alphabets is that product states that are subsets of already visited states are never stored in the antichain. On the other hand, language emptiness semi-algorithms, based on predicate abstraction [22] use a similar notion to cover newly generated abstract successor states by those that were visited sooner and that represent larger sets of configurations. In this case, state coverage does not only increase efficiency but also ensures termination of the semi-algorithm in many practical cases.

In this section, we generalize the subset relation used in classical antichain algorithms with the notion of coverage from predicate abstraction, and we define a more general notion of subsumption for data automata. Given a state $({\mathbf {q}},P)$ of the product automaton $\mathcal {A}^e \times \overline{B}$ and a valuation $\nu \in \mathcal {D}^{{\mathbf {x}}_{\mathcal {A}}}$, the residual language $\mathcal {L}_{({\mathbf {q}},P,\nu )}(\mathcal {A}^e \times \overline{B})$ is the set of traces w accepted by $\mathcal {A}^e \times \overline{B}$ from the state $({\mathbf {q}},P)$ such that $\nu$ is the first valuation which occurs on w. This notion is then lifted to product states as follows: $\mathcal {L}_s(\mathcal {A}^e \times \overline{B}) = \bigcup _{({\mathbf {q}},P,\nu )\in \mathbf{[\![}s \mathbf{]\!]}} \mathcal {L}_{({\mathbf {q}},P,\nu )}(\mathcal {A}^e \times \overline{B})$ where $\mathbf{[\![}s \mathbf{]\!]}$ is the set of configurations of the product automaton $\mathcal {A}^e \times \overline{B}$ represented by the given product state s.

Definition 2

Given a DAN $\mathcal {A}$ and a DA B, a partial order $\sqsubseteq$ is a subsumption provided that, for any two product states s and t, we have $s \sqsubseteq t$ only if $\mathcal {L}_s(\mathcal {A}^e \times \overline{B}) \subseteq \mathcal {L}_t(\mathcal {A}^e \times \overline{B})$.

A procedure for checking the emptiness of $\mathcal {A}^e \times \overline{B}$ needs not continue the search from a product state s if it has already visited a product state t that subsumes s. The intuition is that any counterexample discovered from s can also be discovered from t. The trace inclusion semi-algorithm described below in Sect. 3.4 works, in principle, with any given subsumption relation. In practice, our implementation uses the subsumption relation defined by the lemma below:

Lemma 4

The relation defined s.t. $({\mathbf {q}},P,\Phi ) \sqsubseteq _{ img } ({\mathbf {r}},S,\Psi ) \iff {\mathbf {q}}={\mathbf {r}},~ P \supseteq S \text {, and } \Phi \rightarrow \Psi$ is a subsumption.

3.4 The Trace Inclusion Semi-algorithm

With the previous definitions, Algorithm 1 describes the procedure for checking trace inclusion. It uses a classical work-list iteration loop (lines 2-30) that builds an antichain tree by simultaneously unfolding the expansion $\mathcal {A}^e$ of the network $\mathcal {A}$ and the complement $\overline{B}$ of the observer B, while searching for a counterexample trace $w \in \mathcal {L}(\mathcal {A}^e \times \overline{B})$. Both $\mathcal {A}^e$ and $\overline{B}$ are built on-the-fly, during the abstract state space exploration.

The processed antichain nodes are kept in the set $\mathtt{Visited}$, and their abstract successors, not yet processed, are kept in the set $\mathtt{Next}$. Initially, $\mathtt{Visited}=\varnothing$ and $\mathtt{Next}={\left\{ root _{\mathcal {A},B} \right\} }$. The algorithm uses a predicate map $\Pi$, which is initially empty (line 1). We keep a set of subsumption edges $\mathtt{Subsume} \subseteq \mathtt{Visited} \times \left( \mathtt{Visited} \cup \mathtt{Next}\right)$ with the following meaning: $({\langle s,p \rangle },{\langle t,q \rangle }) \in \mathtt{Subsume}$ for two antichain nodes, where s, t are product states and $p,q \in \mathbf{\mathbb {N}}^*$ are tree positions, if and only if there exists an abstract successor $s' \in Post _\Pi (s)$ such that $s' \sqsubseteq t$ (Definition 2). Observe that we do not explicitly store a subsumed successor of a product state s from the antichain; instead, we add a subsumption edge between the node labeled with s and the node that subsumes that particular successor. The algorithm terminates when each abstract successors of a node from $\mathtt{Next}$ is subsumed by some node from $\mathtt{Visited}$.

An iteration of Algorithm 1 starts by choosing an antichain node $\mathtt{curr}={\langle s,p \rangle }$ from $\mathtt{Next}$ and moving it to $\mathtt{Visited}$ (line 3). If the product state s is accepting (line 5) we check the counterexample path $\rho$, from the root of the antichain to $\mathtt{curr}$, for spuriousness, by computing its pivot k. If $k\geqslant 0$, then $\rho$ is a spurious counterexample (line 7), and the path formula of the suffix of $\rho$, which starts with position k, is infeasible. In this case, we compute an interpolant for the suffix and refine the current predicate map $\Pi$ by adding the predicates from the interpolant to the corresponding substates of the product states from the suffix (line 8).

The computation of the interpolant and the update of the predicate map are done by the refinePredicateMapByInterpolation function using the approach described in Sect. 3.2. Subsequently, we remove (line 12) from the current antichain the subtree rooted at the pivot node $\rho _k$, i.e. the k-th node on the path $\rho$ (line 9), and add $\rho _k$ to $\mathtt{Next}$ in order to trigger a recomputation of this subtree with the new predicate map. Moreover, all nodes with a successor previously subsumed by a node in the removed subtree are moved from $\mathtt{Visited}$ back to $\mathtt{Next}$ in order to reprocess them (line 11).

On the other hand, if the counterexample $\rho$ is found to be real ($k=-1$), any valuation $\nu \in \bigcup _{i=0}^{{|{\rho }|}}\mathcal {D}^{{\mathbf {x}}_{\mathcal {A}}^i}$ that satisfies the path formula $\Theta (\rho )$ yields a counterexample trace $w \in \mathcal {L}(\mathcal {A})\varvec{\downarrow }_{{\mathbf {x}}_B} \setminus \mathcal {L}(B)$, obtained by ignoring all variables from ${\mathbf {x}}_{\mathcal {A}} \setminus {\mathbf {x}}_B$ (line 15).

If the current node is not accepting, we generate its abstract successors (line 18). In order to keep in the antichain only nodes that are incomparable w.r.t. the subsumption relation $\sqsubseteq$, we add a successor t of s to $\mathtt{Next}$ (lines 23 and 30) only if it is not subsumed by another product state from a node $m\in \mathtt{Visited}$. Otherwise, we add a subsumption edge $(\mathtt{curr},m)$ to the set $\mathtt{Subsume}$ (line 20). Furthermore, if t is not subsumed by another state in $\mathtt{Visited}$, we remove from $\mathtt{Next}$ all nodes ${\langle t',p' \rangle }$ such that t strictly subsumes $t'$ (lines 22 and 29) and add subsumption edges to the node storing t from all nodes with a removed successor (line 26) or a removed subsumption edge (line 28).

The following theorem shows completeness modulo termination.

Theorem 1

Let $\mathcal {A} = {\langle A_1,\ldots ,A_N \rangle }$ be a DAN such that $A_i = {\langle \mathcal {D},\Sigma _i,{\mathbf {x}}_i,Q_i,\iota _i,F_i,\Delta _i \rangle }$ for all $i \in [1,N]$, and let $B = {\langle \mathcal {D},\Sigma ,{\mathbf {x}}_B,Q_B,\iota _B,F_B,\Delta _B \rangle }$ be a DA such that ${\mathbf {x}}_B \subseteq \bigcup _{i=1}^N{\mathbf {x}}_i$. If Algorithm 1 terminates and returns true on input $\mathcal {A}$ and B, then $\mathcal {L}(\mathcal {A})\varvec{\downarrow }_{{\mathbf {x}}_B} \subseteq \mathcal {L}(B)$.

The soundness question “if there exists a counterexample trace $w \in \mathcal {L}(\mathcal {A})\varvec{\downarrow }_{{\mathbf {x}}_B} \setminus \mathcal {L}(B)$, will Algorithm 1 discover it?” has a positive answer, when exploring paths in breadth-first order³. The reason is that any real counterexample corresponds to a finite path in the antichain, which will be eventually processed. Moreover, a real counterexample always results in an abstract counterexample, for any given predicate map.

4 Experimental Results

We have implemented Algorithm 1 in a prototype tool⁴ using the MathSat SMT solver [8] for answering the satisfiability queries and computing the interpolants. The results of the experiments are given in Tables 1 and  2. The results were obtained on an Intel i7-4770 CPU @ 3.40 GHz machine with 32 GB RAM.

Table 1. Experiments with single-component networks.

Table 1 contains experiments where the network $\mathcal {A}$ consists of a single component. We applied the tool on several verification conditions generated from imperative programs with arrays [7] (Array shift, Array rotation 1+2, Array split) available online [24]. Then, we applied it on models of hardware circuits (HW Counter 1+2, Synchronous LIFO) [26]. Finally, we checked two versions (correct and faulty) of the timed Alternating Bit Protocol [29].

Table 2. Experiments with multiple-component networks (e.g., $2\times 2/2 + 2\times 3/3$ in column $\mathcal {A}$ means that $\mathcal {A}$ is a network with 4 components, of which 2 DA with 2 states and 2 rules, and 2 DA with 3 states and 3 rules).

Table 2 provides a list of experiments where the network $\mathcal {A}$ has $N>1$ components. First, we have the example of Fig. 1 (Running). Next, we have several examples of real-time verification problems [27]: a controller of a railroad crossing [20] (Train) with T trains, the Fischer Mutual Exclusion protocol with deadlines $\Delta$ and $\Gamma$ (Fischer), and a hardware communication circuit with K stages, composed of timed NOR gates (Stari). Third, we have modelled a Producer-Consumer example [12] with a fixed buffer size B. Fourth, we have experimented with several models of parallel programs that manipulate arrays (Array init, Array copy, Array join) with window size $\Delta$.

For the time being, our implementation is a proof-of-concept prototype that leaves plenty of room for optimization (e.g. caching intermediate computation results) likely to improve the performance on more complicated examples. Despite that, we found the results from Tables 1 and 2 rather encouraging.

5 Conclusions

We have presented an interpolation-based abstraction refinement method for trace inclusion between a network of data automata and an observer where the variables used by the observer are a subset of those used by the network. The procedure builds on a new determinization result for DAs and combines in a novel way predicate abstraction and interpolation with antichain-based inclusion checking. The procedure has been successfully applied to several examples, including verification problems for array programs, real-time systems, and hardware designs. Future work includes an extension of the method to data tree automata and its application to logics for heaps with data. Also, we foresee an extension of the method to handle infinite traces.