Abstract
The Parameterized Compositional Model Checking Problem (PCMCP) is to decide, using compositional proofs, whether a property holds for every instance of a parameterized family of process networks. Compositional analysis focuses attention on the neighborhood structure of processes in the network family. For the verification of safety properties, the PCMCP is shown to be much more tractable than the more general Parameterized Model Checking Problem (PMCP). For example, the PMCP is undecidable for ring networks while the PCMCP is decidable in polynomial time. This result generalizes to toroidal mesh networks and related networks for describing parallel architectures. Decidable models of the PCMCP are also shown for networks of control and user processes. The results are based on the demonstration of compositional cutoffs; that is, small instances whose compositional proofs generalize to the entire parametric family. There are, however, control-user models where the PCMCP and the PMCP are both undecidable.
K.S. Namjoshi—Supported, in part, by DARPA under agreement number FA8750-12-C-0166. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of DARPA or the U.S. Government.
R.J. Trefler—Supported in part by a Natural Sciences and Engineering Research Council of Canada Discovery Grant.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Distributed network protocols and shared-memory concurrent programs are often parameterized by the number of processes or threads in a configured instance. State explosion generally limits model checking to protocol instances that are much smaller than those that arise in practice. It becomes important, therefore, to consider the question of determining “once and for all” if the entire unbounded family of instances satisfies a specification. This is referred to as the parameterized model checking problem (PMCP). The problem is, however, generally undecidable [5].
Faced with this obstacle, much of the work to date on the PMCP has explored two avenues. One is to restrict the structure of processes or their communication patterns in order to obtain decidability. Such restrictions, however, can limit applications to real protocols. The second is to analyze each protocol individually, with manually chosen abstractions applied to the global state space. In contrast, we explore a new and different form of parameterized verification, which is based instead on restricting the shape of a correctness proof. The formulation, which is referred to as the parametric compositional model checking problem (PCMCP), asks whether a parameterized family has a compositional proof that the specification is met for all instances.
Compositional analysis focuses the technical problem away from that of representing global states to one of representing local, neighborhood states. One might intuitively expect this to be easier to do. Indeed, our results show that the PCMCP is much more tractable than the PMCP. The following results are for the verification of quantified safety properties. To obtain precise statements of complexity, the internal state space of a process is assumed to be finite, and independent of the parameter n, the number of processes in an instance.
-
1.
For regular network families, such as the ring, torus, and cube-connected cycles, the PCMCP is decidable in polynomial time. In contrast, the PMCP is generally undecidable and decidable only under strong restrictions [9].
-
2.
For the synchronous control-user networks of German and Sistla [13], the PCMCP is decidable in polynomial time. In contrast, deciding the PMCP requires exponential time in the size of the processes.
-
3.
For asynchronous shared-memory networks from [11], the PCMCP is decidable in polynomial time. The PMCP is decidable but coNP-complete.
-
4.
For distributed memory control-user networks with an index-oblivious control process (defined later), the PCMCP is decidable in polynomial time. Decidability of the PMCP is unknown.
The positive results are based on symmetry arguments that establish the existence of compositional cutoffs: small instances whose compositional verification induces invariants that hold for the entire family. However, the PCMCP is not always decidable: we show that for a control-user system with a non-oblivious controller, both the PMCP and the PCMCP are undecidable.
As this is a new formulation of parameterized verification, we discuss some of the implications in more depth. First, the notion of modular proof is of intrinsic interest, practically as well as mathematically. In practice, several protocols have modular proofs, a recent example is given by a verification of the AODVv2 routing protocol by the authors [24, 25]. Mathematically, modular proofs (e.g., in the Owicki-Gries or assume-guarantee sense) are interesting as they limit the state information which is correlated across processes. These limits make it possible to find neighborhood symmetries which collapse the verification for an entire family on to a smaller cutoff instance. The topology of neighborhoods is usually less complicated than that of the entire graph, which simplifies verification.
Secondly, the PCMCP is an approximate form of the PMCP and could be used as such. That is, if the PCMCP answer is “yes” (there is a modular proof), then the PMCP answer must also be “yes”. Given the generally lower complexity of the PCMCP, it is advantageous to try to answer that question before attempting the PMCP. In this regard, the PCMCP is a new kind of approximation: methods for approximating the PMCP, such as counter abstraction, abstract the global state space; while the PCMCP, in contrast, restricts the structure of the proof. (Other restrictions on proof structure, such as bounding proof depth, might also be worth consideration.)
Finally, the cutoff results and modularity of the PCMCP could form a new basis for the synthesis of parameterized protocols, analogous to the application of cutoff theorems for the PMCP for that purpose (cf. [17]).
2 Preliminaries
We base the PCMCP on the formulation of compositional reasoning for invariance by Owicki-Gries [26] and Lamport [19] (equivalently “Modular” or “Assume-guarantee” reasoning). A compositional invariant is one where each process in a process network has its own invariant assertion, which is also guaranteed to be preserved under the actions of neighboring processes. This immunity to neighborhood “interference” (as it is called) ensures that the local per-process invariants combine to form a global program invariant.
Processes and Inductive Invariants. A process P is defined by a tuple (V, I, T), where V is a set of (typed) variables which induce a state space S that is the set of all possible valuations to V; I is a subset of S, the initial set of states, represented in logic by a predicate I(V); and T is a transition relation, a subset of \(S \times S\), represented by a predicate \(T(V,V')\), where \(V'\) is a copy of V describing a valuation to V in the next state. The transition relation and initial condition induce a set of reachable states (i.e., states which are obtained from an initial state through a sequence of transitions). An invariant is a predicate (i.e., a set of states) which holds of all reachable states.
An inductive invariant is a predicate that includes all initial states and is closed under the transition relation. That isFootnote 1, \(\theta \) is an inductive invariant of \(P=(V,I,T)\) if (1) \(\theta \) includes all initial states, i.e., \([I(V) \;\Rightarrow \;\theta (V)]\), and (2) \(\theta \) is closed under transitions, i.e., \([\theta (V) \;\wedge \;T(V,V') \;\Rightarrow \;\theta (V')]\). To show invariance of a predicate f, one determines an inductive invariant \(\theta \) which is a subset of f, i.e., \([\theta (V) \;\Rightarrow \;f(V)]\). In the sequel, we focus on inductive invariants.
Interleaved Composition of Processes. An asynchronous, interleaved composition of processes \(P_1=(V_1,I_1,T_1)\) and \(P_2=(V_2,I_2,T_2)\), written \(P=P_1\,//\,P_2\), is defined as the process \(P=(V,I,T)\), where:
-
The set of variables, V, is \(V_1 \cup V_2\). The set of shared variables is \(V_1 \cap V_2\).
-
I, the set of initial states, is a predicate on V such that its projection on \(V_1\) is in \(I_1\) and the projection on \(V_2\) is in \(I_2\).
-
The transition relation T interleaves transitions of \(P_1\) and \(P_2\), where transitions of one process leave the internal variables of the other process unchanged. That is, \(T(V,V')= (T_1(V_1,V'_1) \;\wedge \; unch (V\backslash V_1)) \;\vee \;(T_2(V_2,V'_2) \;\wedge \; unch (V\backslash V_2))\). The predicate \( unch (W)\) says that the values of all variables in the set W are unchanged, that is, it is the predicate \((\bigwedge w: w \in W: w'=w)\).
This definition extends to compositions \(P_1 \,//\,P_2 \ldots \,//\,P_N\) in a similar manner.
Compositional Invariants. There are several formulations of compositional reasoning, but all share the crucial characteristic that the reasoning centers on a process and its neighborhood. In the formulation we use here, there is a predicate, \(\theta _i\), for each process \(P_i\); this is a set of local states of \(P_i\). Each local state can be written in the form (x, y), where x is an internal state of \(P_i\) and y is the state of the neighborhood of \(P_i\). The neighborhood of a process is the set of variables which are shared between the process and other processes. (E.g., the neighborhood of a node i in a ring network of size n is defined by the variables shared between that node and its left neighbor, with index \((i-1)\,\mathsf {mod}\,n\), and its right neighbor, with index \((i+1)\,\mathsf {mod}\,n\).)
In a network of processes, the neighborhoods of processes overlap (e.g., in a ring, nodes i and \((i+1)\,\mathsf {mod}\,n\) share state). Hence, the natural formulation of the constraints on the \(\theta \)’s is through mutual induction, often referred to as (syntactically) “circular reasoning”. The constraints which the \(\{\theta _i\}\) predicates must satisfy to be called a compositional invariant are as follows.
-
(init) \(\theta _i\) includes the initial states of \(P_i\). That is, \([I(V) \;\Rightarrow \;\theta _i(V_i)]\), and
-
(step) \(\theta _i\) is inductive for \(P_i\). That is, \([\theta _i(V_i) \;\wedge \;T_i(V_i,V'_i) \;\Rightarrow \;\theta _i(V'_i)]\), and
-
(non-interference) the actions of a neighboring process, \(P_j\), do not falsify \(\theta _i\). That is, \([\theta _i(V_i) \;\wedge \;\theta _j(V_j) \;\wedge \;T_j(V_j,V'_j) \;\wedge \; unch (V\backslash V_j) \;\Rightarrow \;\theta _i(V'_i)]\).
The following theorem connects compositional to global invariance:
Theorem 1
If the set \(\{\theta _i\}\) is a compositional invariant, then \((\forall i: \theta _i)\) is a global inductive invariant of the program \((\,//\,i: P_i)\).
Compositionality as a Fixed Point. Let \(F_i\) be the disjunction of the predicates I, \((\theta _i \;\wedge \;T_i)\), and \((\theta _i \;\wedge \;\theta _j \;\wedge \;T_j \;\wedge \; unch (V\backslash V_j))\) for all neighbors j of i. The compositional constraints can be rearranged into the set of validities \(\{[F_i(\theta ) \;\Rightarrow \;\theta _i]\}\). Considering \(\theta =(\theta _1,\theta _2,\ldots )\) as a vector in the predicate lattice ordered by implication, \(F_i\) is monotone in \(\theta \). By the Knaster-Tarski theorem, there is a least fixpoint solution, which defines the strongest compositional invariant. This is the limit of the sequence \(X^0=( false , false ,\ldots )\), \(X^{i+1} = (F_1(X^i), F_2(X^i),\ldots )\). For finite-state processes, the limit can be computed in polynomial time in the number of processes and in the size of the state spaces of each process.
Proving Invariance. We focus on quantified assertions of the form \((\forall i: \xi (i))\), where \(\xi (i)\) is a predicate on the local state of process i. To compositionally prove this assertion to be an invariant, one checks the constraints:
-
(adequacy) \(\theta (i)\) is a subset of \(\xi (i)\), for all i, written as \([\theta (i) \;\Rightarrow \;\xi (i)]\).
It follows that \([(\forall i: \theta (i)) \;\Rightarrow \;(\forall i: \xi (i))]\). As \((\forall i: \theta (i))\) is a global inductive invariant of the program (by Theorem 1), \((\forall i: \xi (i))\) is a program invariant.
Parameterized Compositional Invariants. A compositional invariant for a parameterized family is defined using an unbounded set of compositional constraints. There is a \(\theta \)-component for each node i in each network N of the family; this is denoted as \(\theta _{(i,N)}\). The components must meet the previously defined constraints for compositional invariance:
-
(init) \(\theta _{(i,N)}\) includes the initial states of \(P_{(i,N)}\),
-
(step) \(\theta _{(i,N)}\) is inductive for \(P_{(i,N)}\), and
-
(non-interference) the actions of a neighboring process (j, N) in network N do not falsify \(\theta _{(i,N)}\).
Although the vector \(\theta \) is unbounded, there is still a strongest fixpoint solution. As processes from different instances do not influence one another, this fixpoint is the collection of strongest fixpoints for each instance. The decidability results in this paper are obtained by collapsing the unbounded collection of constraints to a bounded set through the identification of local (i.e., neighborhood) symmetries. This leads to the concept of a compositional cutoff.
Compositional Cutoff. Several of the network families examined in this paper have the following property: there is a limit, say K, such that the strongest compositional invariants in networks of size greater than K are identical (up to neighborhood isomorphism) to the strongest compositional invariants in networks of size at most K. We then refer to K as a compositional cutoff.
As a concrete illustration, any pair of nodes in the family of ring networks are locally symmetric – each has one neighbor to the left and one to the right – so that the strongest compositional solutions are isomorphic across the family, and the cutoff instance for the family is the smallest ring instance, of size 2.
3 Rings, Tori and Other Regular Networks
We recall results connecting compositional verification to local symmetry given in [22] and use those to show that the PCMCP is decidable in polynomial time for arbitrary protocols on rings, tori and other regular networks.
Networks. A network is formally defined as a pair (N, E) where N is a set of nodes and E is a set of edges. Processes are placed on nodes, and shared state on edges. Each edge, e, is associated with a set of input nodes, \( ins (e) \subseteq N\) and a set of output nodes, \( outs (e) \subseteq N\). For a node n, the set \( In (n) = \{e \;|\;n \in outs (e)\}\) describes the input edges to n and \( Out (n) = \{e \;|\;n \in ins (e)\}\) describes the output edges for n. The notation \( InOut (n)\) represents the union of those sets and it forms the neighborhood of n. We say that node m points to node n (written \(m \in pt (n)\)) if there is an output edge of m that is also in \( InOut (n)\).
Symmetry Groupoids. Two nodes m and n are locally similar, written \(m \simeq _{IO}n\), if there is a bijective function \(\beta \) that maps \( In (m)\) to \( In (n)\), and maps \( Out (m)\) to \( Out (n)\). I.e., the neighborhood of m is isomorphic to the neighborhood of n through \(\beta \). Tuples of the form \((m,\beta ,n)\) where \(\beta \) is a witnessing bijection for \(m \simeq _{IO}n\), are called local symmetries. Following [14], we call this the symmetry groupoidFootnote 2 of the network and denote it by \(\mathcal {G}_{IO}\).
A groupoid induces an orbit relation: nodes m and n are related if there is a groupoid element \((m, \beta , n)\). From the groupoid properties, this is an equivalence relation. The orbit relation for the symmetry groupoid is \(\simeq _{IO}\).
For a local symmetry \((m, \beta , n)\), the isomorphism \(\beta \) maps the neighborhood of m onto the neighborhood of n. We now lift this definition on structure to include the processes running at m and n. Thus \(\beta \) maps a local state (x, y) of m to a local state \((x,\beta (y))\) of n (recall that x is the internal state and y is the neighborhood state), and it similarly maps a local transition \(((x,y),(x',y'))\) of m to a local transition \(((x,\beta (y)),(x',\beta (y')))\) of n. This is lifted to sets of states and transitions in the standard way. An assignment of processes to nodes is valid for \(B \subseteq \mathcal {G}_{IO}\) if it respects the local symmetries in B: that is, for every \((m,\beta ,n) \in B\), it should hold that \([T_n \;\equiv \;\beta (T_m)]\) and \([I_n \;\equiv \;\beta (I_m)]\).
Balance. Intuitively, as the compositional constraints for a node refer only to its neighbors, one might expect that nodes that are locally symmetric have isomorphic invariants. This is not quite true: it is also necessary for the neighbors related by the isomorphism to be (recursively) locally symmetric. That is captured in a bisimulation-like definition of balance.
Definition 1
(Balance) ([14, 22]). A balance relation B is a set of local symmetries satisfying the following properties. For any \((m,\beta ,n)\) in B:
-
1.
Its inverse, \((n,\beta ^{-1},m)\), is also in B, and
-
2.
For any j which points to m, there is k which points to n and \(\delta \) such that (a) \((j,\delta ,k)\) is in B and (b) \(\beta \) and \(\delta \) agree on common edges. I.e., for every edge f in \( InOut (j) \cap InOut (m)\), \(\delta (f)= \beta (f)\).
We say that a vector \(\theta \) of per-process predicates respects a balance relation B if for all \((m,\beta ,n)\) in B, \([\theta _n \;\equiv \;\beta (\theta _m)]\). We can now state the main theorem connecting balance and local symmetry to compositional reasoning.
Theorem 2
(Symmetry Reduction) [22]. Given a balance relation, B, and a valid program assignment, the strongest compositional invariant \(\theta ^*\) respects B.
That is, balanced nodes have isomorphic strongest compositional invariants. Hence, it suffices to find a balance relation that is a groupoid (there is always one such, the greatest balance relation), pick one representative in each equivalence class of its orbit and compute an invariant for that representative. The invariants for all other nodes in the class will be isomorphic by Theorem 2.
For example, ring networks have only O(n) global symmetries [6, 10] which limits global state-space reduction. However, any two ring nodes are locally symmetric and, in fact, balanced. Thus, it suffices to compute a compositional invariant for a single node, the others will be isomorphic. To generalize this observation, we recall a result connecting global symmetry with balance.
Theorem 3
([22]). For a network with global symmetry group G, the set \(\mathsf {Local}(G)\) \( = \{(m,\beta ,n) \;|\;\beta \in G \;\wedge \;\beta (m)=n\}\) is a balance relation and a groupoid.
A network with a transitive global symmetry group of automorphisms (i.e., one where any pair of nodes is connected by an automorphism) is called vertex-transitive. We have the following corollary.
Corollary 1
In a vertex-transitive network, any pair of nodes is balanced and there is a single equivalence class.
Proof: Consider any pair of nodes m, n. As the network has a transitive symmetry group G, there is an automorphism \(\beta \) in G such that \(\beta (m)=n\). In that case, the triple \((m,\beta ,n)\) is in \(\mathsf {Local}(G)\) by definition. As \(\mathsf {Local}(G)\) is a balance relation, m and n are balanced and, as it is a groupoid, the orbit relation is an equivalence, so that m and n are in the same equivalence class of \(\mathsf {Local}(G)\). Hence, there is a single equivalence class. EndProof.
This corollary implies that for a vertex-transitive network, it suffices to compute a compositional invariant for a single representative node in order to obtain the compositional invariant for all other nodes. Such networks are common: rings, tori, toroidal meshes, hypercube and cube-connected-cycles (CCCs) all have transitive symmetry groups. In order to extend this symmetry reduction to a whole family of networks, say that a family of process networks, \(\mathcal {N}\), is uniform if (1) each network in the family is vertex-transitive, (2) for every pair (M, N) of networks, there is a pair of nodes, \(m\in M\) and \(n \in N\), that are locally symmetric, and (3) nodes that are locally symmetric are assigned isomorphic processes, whose state space is independent of network size. We say that a quantified assertion \((\forall n,N: n \in N: \xi _{(n,N)})\) is uniform if its components are locally symmetric. I.e., for any pair of nodes (m, M) and (n, N) which are locally symmetric through \(\beta \), it is the case that \([\beta (\xi _{(m,M)}) \;\equiv \;\xi _{(n,N)}]\).
Theorem 4
For a uniform family of networks, and a uniform quantified assertion \((\forall n,N: n \in N: \xi _{(n,N)})\), the PCMCP is decidable in polynomial time.
Proof: By condition (1) of uniformity and Corollary 1, any pair of nodes in a network N of the family are balanced. From condition (2), any pair of nodes in the family are locally symmetric. To see this, consider a node n in network N and m in network M. Then n (resp., m) is locally symmetric to all nodes in N (resp., M), and condition (2) says that there is a pair of nodes from M and N that are locally symmetric. Thus, m and n are locally symmetric by transitivity.
That, in turn, implies that all nodes in the family have isomorphic neighborhoods, of a size which is a constant independent of the network size. Moreover, for a network M, its compositional invariant can be computed on the neighborhood of a representative node \(m \in M\), and similarly for network N and its representative, \(n\in N\). However, as m and n have isomorphic neighborhoods and identical processes by condition (3), those invariants are isomorphic. Therefore, it suffices to compute the strongest compositional invariant on a single representative node from a single network of the family. As the size of the neighborhood is constant, this computation is in polynomial time in the local state space of the process on the node. Hence, the strongest per-node compositional invariant can be computed in polynomial time. As this is the strongest assertion, the adequacy tests succeed for some invariant if, and only if, it succeeds for the strongest one.
Consider the unbounded number of adequacy tests, each having the form \([\theta _{(n,N)} \;\Rightarrow \;\xi _{(n,N)}]\). Let (r, R) be a representative node for the family. It suffices to test whether \([\theta _{(r,R)} \;\Rightarrow \;\xi _{(r,R)}]\). Assuming this holds, consider any node (n, N), and let \(\beta \) be the local symmetry from (r, R) to (n, N). From the symmetry properties, it follows that \(\theta _{(n,N)} \;\equiv \;\beta (\theta _{(r,R)}) \;\Rightarrow \;\beta (\xi _{(r,R)}) \;\equiv \;\xi _{(n,N)}\), so that \([\theta _{(n,N)} \;\Rightarrow \;\xi _{(n,N)}]\) is also a validity. As the invariant computation and the adequacy test can be performed on the representative node in polynomial time, the PCMCP is decidable in polynomial time. EndProof.
This rather abstract result has a number of practical consequences. It implies that the PCMCP is polynomial-time decidable for ring, tori, toroidal mesh, and the hypercube-like cube-connected cycles (CCC) networks. The hypercube networks are excluded as the degree of a node increases as \(\log (k)\) with network size k. We show below that the other networks meet the uniformity condition of the theorem. Note that for each of these networks, the PMCP is undecidable, which follows from the basic result on ring networks by Apt and Kozen [5].
Ring Networks. The symmetry group of a ring network is transitive, as any node can be mapped to any other by an appropriate circular rotation. Furthermore, the nodes with index 0 in ring networks of size m and n are locally symmetric. Hence, the family of bidirectional (and unidirectional) ring networks is uniform and its PCMCP is decidable in polynomial time.
Mesh/Toroidal Networks. Our next examples of regular topologies are generalizations of the mesh structure. For instance, the \(\mathcal {N}(k, 2)\) meshes are the tori formed by gluing together two k length cycles and wrapping the rings into a cycle of length two at every interconnection point.
This parameterized topology can be extended for any \( k, a \in \mathbb {N}\), where \(0 < k\) and \(0 < a\) so that \(\mathcal {N}(k, a)\), is the parameterized set of wrap-around toroidal meshes with a ring like sections, each section having k nodes, each node connected to 4 neighbors. These mesh networks are examples of torus interconnection network architectures.
Here we generalize these structures to allow regular, but fixed rectangular interconnection networks. Our first example is that of a wrap around, right rectangular toroidal mesh, that contains arbitrary, parameterized numbers of nodes. For example, in \(\mathcal {N}(k_{1}, k_{2}, k_{3})\), the \(k_{i}\) range over positive elements of \(\mathbb {N}\). For any fixed \(k_{1}, k_{2},\) and \(k_{3}\), there are \(k_{3}\) toroidal mesh structures with \(k_{1}k_{2}\) nodes, stacked on top of each other. For all \(a \in [0..k_{1}-1]\), \(b \in [0..k_{2}-1]\), \(c \in [0..k_{3}-1]\), node (a, b, c) of mesh c is connected to nodes \((a, b, c+1)\) and \((a, b, c-1)\) (where addition and subtraction are modulo \(k_{3}\)). Within mesh c, the nodes are connected in the standard way, node (a, b, c) has neighbors \((a+1, b, c), (a-1, b, c), (a, b+1, c),\) and \((a, b-1, c)\), where the addition, respectively subtraction, are modulo \(k_1\), respectively \(k_{2}\). As in the tori of early sections we require that they be wrap-around, so that, for instance, \(((k_{1}-1, b, c), (0, b, c))\) is an edge in \((N(k_{1}, k_{2}, k_{3}), E)\). Note that for any fixed \(k_{1}\), \(k_{2}\) there are an unbounded number of right rectangular tori \((N(k_{1}, k_{2}, k_{3}), E)\).
Theorem 5
Every wrap-around toroidal mesh network, \((N(k_{1}, k_{2}, k_{3}), E)\), is vertex transitive.
Proof Sketch: Fix any of the two dimensions. Letting the third dimensional variable vary, the edge set of \((N(k_{1}, k_{2}, k_{3}), E)\) forms a ring. For each pair of fixed values of the two chosen dimensions, a ring is formed by the varying third dimension. Notice that for any two pairs of values the two rings are disjoint. In each of the different rings, the nodes are related by cyclic permutations. By keeping all other dimensional relationships constant, the cyclic permutations form automorphisms of the rings, and therefore the structure as a whole. Sequential composition of the ring-like automorphisms from the different dimensions, again form automorphisms of the wrap-around, right rectangular toroidal mesh structure. Thus for any (a, b, c) and \((a', b', c')\) in \(N(k_{1}, k_{2}, k_{3})\) there is an automorphism, \(\pi \), of \((N(k_{1}, k_{2}, k_{3}), E)\) such that \(\pi (a, b, c) = (a', b', c')\). EndSketch.
From the definition of the mesh, each node in an instance, regardless of the instance size, has degree 6. Hence, for a uniform family of mesh networks, all nodes in different instances are locally symmetric. Therefore it follows that the PCMCP is decidable, in polynomial time, for uniform families of mesh/toroidal networks of the form \(\mathcal {N}(k_{1}, k_{2}, k_{3})\). Similarly, the PCMCP is decidable in polynomial time for uniform families of mesh/toroidal networks of the form \(\mathcal {N}(k_{1}, a)\) for any fixed a. These results also generalize to uniform families of polytopes of the form \(\mathcal {N}(k_{1}, \ldots , k_{a})\), for fixed a.
Cube-Connected Cycles (CCC). CCC [28] are a parameterized topology used to describe interconnections of processors in parallel computing networks.
For \(k \ge 3\) the \( CCC (k)\) has \(k 2^{k}\) nodes. The nodes are indexed by pairs (x, y) where \(0 \le x < 2^{k}\) and \(0 \le y < k\). Each node (x, y) is connected to 3 neighbors: \((x, (y + 1) \,\mathsf {mod}\,k), (x, (y - 1) \,\mathsf {mod}\,k),\) and \((x \oplus 2^{y}, y)\). Here, \(\oplus \) denotes bitwise exclusive-or on binary numbers. Nodes \((x, (y+1) \,\mathsf {mod}\,k)\) and \((x, (y - 1) \,\mathsf {mod}\,k)\) are on the same cycle as node (x, y), while node \((x \oplus 2^{y}, y)\) is on a neighboring cycle. Intuitively, a CCC is obtained by taking a hypercube and expanding each node into a cycle, so that each node has only a constant out degree of 3.
Theorem 6
([3]). \( CCC (k)\) is vertex-transitive for all k.
From the definition of the CCC, each node in an instance, regardless of the instance size, has degree 3. Hence, nodes in different instances are locally symmetric. From this, it follows that the CCC is a uniform family of networks and, therefore, its PCMCP is decidable in polynomial time.
4 Control-User Networks
There are several decidability results on the PMCP for networks with a single distinguished process (the “control” process) and many identical “user” processes; however, the decision procedures have high complexity. We show that the PCMCP is decidable efficiently, in polynomial time in the size of these processes for two such network types. We prove decidability for a new index-oblivious model. However, we also give an undecidability result for a stronger control process.
4.1 Synchronized Control-User Networks
We consider the synchronized (CCS-like) control-user formulation analyzed by German and Sistla in their pioneering paper on parameterized verification [13]. For this formulation, deciding whether the control process satisfies an invariant can be done in double exponential time in the sizes of the control and user processes. We show that the PCMCP is decidable in polynomial time in the sizes of these processes. German and Sistla also define a simpler model without a control process and show that the PMCP is decidable in polynomial time, it is interesting that their algorithmFootnote 3 is identical to the least fixpoint computation of the compositional invariant, and therefore solves the PCMCP as well.
The control and user processes synchronize with CCS semantics. That is, a step of the system consists of either an internal step by one of the processes, or a pairwise synchronization of two processes (i.e., control-user or user-user). In the simplest compositional formulation, we define two invariants: \(\theta _C\), which represents local states of the control process, C, and \(\theta _U\), which represents local states of the user processes, U. A compositional calculation for an instance of the system with N users would have invariants \(\theta _{U_i}\), for each of the user processes with i ranging over \(1\ldots N\). However, we choose a formulation where the user processes in each instance, and across instances, are treated alike, and therefore have a single invariant, \(\theta _U\). This choice is justified by a “compositional cutoff” result based on local symmetries showing that the user invariants for instances of size 3 or more are identical.
The states in \(\theta _C\) are control states, while those in \(\theta _U\) are user states. As the system is built around pairwise synchronization, the interference rules are slightly different from those given in Sect. 2.
-
(Initial) All initial states of C are in \(\theta _C\), and all initial states of U are in \(\theta _U\),
-
(Step) If \(c \in \theta _C\) and \((c,\tau ,d)\) is an internal transition of C, then \(d \in \theta _C\). Similarly, if \(u \in \theta _U\) and \((u,\tau ,v)\) is an internal transition of U, then \(v \in \theta _U\).
-
(Interference) If \(c \in \theta _C\) and \(u \in \theta _U\) and (c, a, d) and \((u,\overline{a},v)\) are transitions in C and U respectively, then \(d \in \theta _C\) and \(v \in \theta _U\). This represents control-user interference. A similar clause applies to user-user interference.
Theorem 7
The PCMCP for the synchronous control-user system is decidable in polynomial time for uniform quantified assertions.
Proof: The strongest \((\theta _C,\theta _U)\) pair can be calculated by turning the compositional rules into a simultaneous least fixpoint formulation, as described in Sect. 2, and iterating until convergence. The computation time is polynomial in the number of states of C and of U. The target invariant has the form \((\forall n,N: n \in N: \xi _{(n,N)})\), which is uniform by assumption. With the strongest compositional invariant in hand, it suffices to check adequacy for a representative user node (r, R), i.e., to check \([\theta _U \;\Rightarrow \;\xi _{(r,R))}]\), which can be done in polynomial time. This suffices as, by the cutoff theorem, all other user nodes have isomorphic values of \(\theta _U\), and \(\xi \) is invariant under isomorphism by the uniformity requirement. Hence, the PCMCP is decidable in polynomial time. EndProof.
We now consider a different control-user model analyzed in [11]. Here, a system has a single control process (a “leader” in [11]) and an unbounded number of user processes (the “contributors”), that communicate only by reading and writing to a shared memory. There are no locks or atomic test-and-set actions. If the control and user processes are finite state, the PMCP is decidable and is co-NP complete [11]. In contrast, using symmetry arguments similar to those used above, the PCMCP is decidable in polynomial time.
Theorem 8
The PCMCP is decidable in polynomial time for the model of asynchronous, shared-memory control-user networks and uniform assertions.
4.2 Asynchronous, Distributed Memory Networks
We consider a control-user network more akin to a client-server system. The control maintains a finite, per-user state. Each user interacts with the control process through their mutually shared state, but not directly with other users. The network structure looks like a star, the control at the center and each user at the end of a spoke, with the shared control-user state along the spokeFootnote 4.
Within this general structure, many variations are possible based on the capabilities given to the controller. We show that the PCMCP itself is undecidable for a rather reasonable variation. The control process has two capabilities. First, it can perform a universal (dually, existential) test on its adjacent edges of the form \((\forall i: f(e_i))\) (dually, \((\exists i: f(e_i))\)). Second, it can carry out a non-deterministic guarded command on its edges, of the form \(([] i: f(e_i) \rightarrow e_i := v)\). This chooses an edge-state \(e_i\) for which \(f(e_i)\) is true, and updates it to hold a value v. The command blocks if no such edge can be found. Notice that all guards and actions are fully symmetric. The user processes are finite-state. Still, both the PMCP and the PCMCP are undecidable.
Theorem 9
Both the PMCP and the PCMCP are undecidable for this asynchronous, distributed memory control-user system.
Proof Sketch: The proof is a reduction from the undecidability of halting for two-counter machines (2CMs) [21]. We show how to simulate a 2CM using the control process alone. The user processes do nothing; they have a single internal state with a skip action. EndSketch.
4.3 A Decidable Asynchronous, Distributed Memory Network
We give a positive result for the PCMCP for a restricted control process, whose actions are “oblivious” to the user indices, i.e., one cannot target a specific index. The action either does nothing (skip) or it assigns a value v to all edges, written as  (or
(or  for short). This structure is inspired by that of a specific Dining Philosophers protocol over arbitrary graphs, where nodes are assigned philosophers and edges forks. A philosopher eats if it is hungry and “owns all neighboring forks” (a universal guard); after eating, it “releases all neighboring forks” (a universal action). Its compositional analysis [23] focuses on a generic graph node with an arbitrary number of neighbors. This looks like a control-user system. We now show that the PCMCP is decidableFootnote 5.
for short). This structure is inspired by that of a specific Dining Philosophers protocol over arbitrary graphs, where nodes are assigned philosophers and edges forks. A philosopher eats if it is hungry and “owns all neighboring forks” (a universal guard); after eating, it “releases all neighboring forks” (a universal action). Its compositional analysis [23] focuses on a generic graph node with an arbitrary number of neighbors. This looks like a control-user system. We now show that the PCMCP is decidableFootnote 5.
The pair of invariants \(\theta _C\) and \(\theta _U\) apply to the entire family, so \(\theta _C\) contains local states for the control process over all instances, and \(\theta _U\) contains neighborhood states for all users in all instances. A state in \(\theta _U\) is a pair (a, k) where a is an edge value, and k is a state of the user process. A state in \(\theta _C\) is a pair (c, x), where c is an internal state of the control process, and x is a vector of values for its adjacent edges. As \(\theta _C\) represents local states in all instances, the length of x is unbounded. We define an abstraction of the system and show that its compositional invariant is sufficiently precise to solve the PCMCP.
The abstraction is only for the control process, user processes have finite local state and are unabstracted. The abstraction is a Galois connection \((\alpha ,\gamma )\), where \(\alpha (c,x) = (c,s)\), where s is the set of edge-values which are in x, and \(\gamma (c,s) = \{(c,x) \;|\;\alpha (c,x)=(c,s)\}\). In the abstract system, the transitions of the control process are abstracted to operate on sets in the standard manner: the abstract version of transition t is given by \(\alpha \circ t \circ \gamma \). This can be simplified as follows. For a concrete transition from internal state c to \(c'\) with guard g and action act, the abstract equivalent is the following:
-
If g is \((\exists i: f(e_i))\), then \(\overline{g}\) applied to (c, s) is \((\exists a: a \in s: f(a))\). Similarly, if g is \((\forall i: f(e_i))\), then \(\overline{g}\) applied to (c, s) is \((\forall a: a \in s: f(a))\).
-
If act is skip, then \(\overline{act}\) is skip. If act is
 then \(\overline{act}\) is \(s := \{v\}\).
then \(\overline{act}\) is \(s := \{v\}\).
The abstract interference transitions operate in a similar manner. We refer to the strongest compositional invariants on the abstract system as \(\varDelta _C\) and \(\varDelta _U\).
-
(control-to-user) If there is an abstract transition with action
 from (c, s) to \((c',s')\), and (a, k) is a state in \(\varDelta _U\) and \(a \in s\), the interference state is (v, k).
from (c, s) to \((c',s')\), and (a, k) is a state in \(\varDelta _U\) and \(a \in s\), the interference state is (v, k). -
(user-to-control) If there is an abstract user transition from (a, k) to \((a',k')\), and (c, s) is a state in \(\varDelta _C\), and \(a \in s\), the interference successors are \((c,s \cup \{a'\})\) (i.e., \(a'\) is added to s) and \((c, (s\backslash \{a\}) \cup \{a'\})\) (i.e., \(a'\) replaces a in s).
The connections between \((\theta _C,\theta _U)\) and \((\varDelta _C,\varDelta _U)\) are laid out in the following lemmas. The first lemma says that the compositional invariants of the abstract system over-approximate those of the concrete one. This proof is by induction on the fixpoint stages of the computation of \(\theta \).
Lemma 1
For each state in \(\theta _C\) there is an \(\alpha \)-related state in \(\varDelta _C\). Every state in \(\theta _U\) is in \(\varDelta _U\).
The next lemma shows that the abstraction is not too abstract. The simpler statement \(\gamma (\varDelta _C)=\theta _C\) need not hold, as some abstract interference transitions are matched only by concrete states with sufficiently many components.
Lemma 2
For any k, \(\varDelta ^k_U \subseteq \theta _U\). For every state (c, s) in \(\varDelta ^k_C\) and any \(l \ge 1\), there is a related state (c, x) in \(\theta _C\) where for each value a in s, at least l edges of x have value a.
Proof: By induction on k.
Basis (stage 0): \(\varDelta ^0_C\) is just the state \((c_0,\{\bot \})\), while \(\varDelta ^0_U\) is the state \((u_0,\bot )\), where \(c_0\) and \(u_0\) are the initial states of the control and user process. So \(\varDelta ^0_U = \theta ^0_U\). By definition, \(\theta ^0_C\) consists of all states of the form \((c_0,x)\) where x is a vector of \(\bot \) entries. Hence, the hypothesis holds for \(\varDelta ^0_C\).
Control Step (stage \(k+1\) ): Consider an abstract state \((c',s')\) of stage \(k+1\) obtained through a step by C from a state (c, s) at stage k. We consider the various step transitions separately. We use the notation \(\varSigma (x)\) to represent the set of values on the edge vector x. First, note that for any (c, x) related by \(\gamma \) to (c, s), a concrete transition guard is enabled at (c, x) if and only if the corresponding abstract guard is enabled at (c, s), because \(\varSigma (x)=s\). Hence, we can focus on the effect of the actions.
(1) the action is “skip”. Then \(s'=s\). Consider any \(l>0\). By inductive hypothesis, there is a state (c, x) related to (c, s) where x has at least l components with value a for all a in s. Construct the state \((c',x)\). This is a step-successor of (c, x) by the skip action, so it is in \(\theta _C\) by closure under step. As \(s'=s\), the vector x in \((c',x)\) satisfies the condition required of l.
(2) the action is an ( ) action. Then \(s'=\{v\}\). Consider any \(l>0\). By the inductive hypothesis, there is a state (c, x) related to (c, s) by \(\gamma \), with at least l components for x. Let \((c',x')\) be its successor with the
) action. Then \(s'=\{v\}\). Consider any \(l>0\). By the inductive hypothesis, there is a state (c, x) related to (c, s) by \(\gamma \), with at least l components for x. Let \((c',x')\) be its successor with the  action. Then this state belongs to \(\theta _C\) and \(x'\) is a vector of v-values of length at least l, so it satisfies the condition required.
action. Then this state belongs to \(\theta _C\) and \(x'\) is a vector of v-values of length at least l, so it satisfies the condition required.
User Step (stage \(k+1\) ): Consider an abstract state \((a',m')\) of stage \(k+1\) obtained through a step by U from a state (a, m) at stage k. As (a, m) is in \(\theta _U\) by assumption, the state \((a',m')\) is also in \(\theta _U\) by closure under step transitions.
User-to-Control Interference (stage \(k+1\) ): Suppose there is a user transition from (a, m) to \((a',m')\), and (c, s) is a state in \(\varDelta ^k_C\) with \(a \in s\). There are two interference successors: \((c,s \cup \{a'\})\) and \((c, (s\backslash \{a\}) \cup \{a'\})\).
Consider the first successor. Let \(l>0\). By the inductive hypothesis, there is a state (c, x) in \(\gamma (c,s)\) and in \(\theta _C\), where x has at least 2l components with value w for every w in s. Apply a sequence of l concrete interference steps to x, each changing one of the components in x with value “a” to “\(a'\)”. The end state, \((c,x')\), is in \(\theta _C\), by closure under interference. Notice that \(\varSigma (x')=s \cup \{a'\}\) by construction, and that every value in \(x'\) is replicated at least l times. Hence, the inductive hypothesis holds for the first successor.
Now consider the second successor, and let \(l>0\). By the inductive hypothesis, there is a state (c, x) in \(\gamma (c,s)\) and in \(\theta _C\), where x has at least l components with value w for every w in S. Apply a sequence of concrete interference steps to x, each changing one of the a components in x to \(a'\) until all a-values are converted to \(a'\). The result of this sequence, \((c,x')\), is in \(\theta _C\), by closure under interference. Notice that \(\varSigma (x')=s\backslash \{a\} \cup \{a'\}\) by construction, and that every value in \(x'\) is replicated at least l times. Hence, the inductive hypothesis holds for the second successor.
Control-to-User Interference (stage \(k+1\)
): Consider an  abstract transition from (c, s) to \((c',s')\) in \(\varDelta ^k_C\), let (a, k) be in \(\varDelta ^k_U\), with \(a \in s\). Let (v, k) be the interference state. By inductive assumption, there is a state (c, x) in \(\gamma (c,s)\) which is in \(\theta _C\), and therefore an
abstract transition from (c, s) to \((c',s')\) in \(\varDelta ^k_C\), let (a, k) be in \(\varDelta ^k_U\), with \(a \in s\). Let (v, k) be the interference state. By inductive assumption, there is a state (c, x) in \(\gamma (c,s)\) which is in \(\theta _C\), and therefore an  successor \((c',x')\) that is in \(\gamma (c',s')\) and in \(\theta _C\). Also by the inductive assumption, the state (a, k) is in \(\theta _U\). Hence, there is a matching interference transition in the concrete system, so that (v, k) must be in \(\theta _U\), by closure under interference. EndProof.
successor \((c',x')\) that is in \(\gamma (c',s')\) and in \(\theta _C\). Also by the inductive assumption, the state (a, k) is in \(\theta _U\). Hence, there is a matching interference transition in the concrete system, so that (v, k) must be in \(\theta _U\), by closure under interference. EndProof.
Theorem 10
The PCMCP is decidable for this control-user system for properties on the internal state of the control process.
Proof: The decision procedure is to (1) construct \(\varDelta _U\) and \(\varDelta _C\) through the standard fixpoint calculation; then (2) to check if all states of \(\varDelta _C\) satisfy the invariant \(\varphi \). (Note that \(\varphi \) is a predicate on the internal state of C.)
Soundness: We show that all states of \(\theta _C\) also satisfy \(\varphi \). By way of contradiction, suppose there is a state (c, x) in \(\theta _C\) for which \(\varphi (c)\) is false. By Lemma1, there is an \(\alpha \)-related state (c, s) in \(\varDelta _C\), so the check in step (2) would not succeed, a contradiction.
Completeness: If there is a compositional proof of \(\varphi \), then, as \(\theta \) is the strongest compositional invariant, all states (c, x) in \(\theta _C\) must satisfy \(\varphi (c)\). Consider a state (c, s) in \(\varDelta _C\). By Lemma 2, there is a state (c, x) in \(\theta _C\) which is \(\alpha \)-related to (c, s). Hence, (c, s) satisfies \(\varphi (c)\) as well, so step (2) succeeds. EndProof.
The complexity of calculating \(\varDelta \) is polynomial in the number of internal states of the control and user processes, and exponential in the number of edge values.
5 Related Work and Conclusions
Analysis questions for families of regular networks running locally symmetric progrrams were studied. In particular, the algorithms introduced here are designed to decide whether all processes in a protocol family satisfy local safety properties expressed as local invariants. This form of local invariant analysis is related to the global invariant analysis techniques studied in [20]. The focus on local reasoning allows for relatively efficient analysis, given that the processes and neighborhoods are all finite state. For the protocols studied here, the local symmetry conditions ensure that all processes of the parametrized family are locally symmetric.
The work in [29] and [30] uses satisfiability modulo theories in the design of parametrized reasoning techniques for systems of many processes. That work provides semi-decision procedures and is designed for situations where the many different process types may not be locally (or globally) symmetric.
We have shown that by restricting attention to modular proofs, parameterized verification problems become simpler and more decidable. There are several positive results on the PMCP, however they require limits on process structure or communication patterns. Examples are the requirement of a single token for a token-ring [9] – two tokens result in undecidability – and the requirement of a well-quasi-ordered global state set and monotonic transition functions in [1]. Modular proofs create a number of advantages. First, there is less need to constrain process structure or communication. Second, compositional analysis naturally splits a global state into a number of local process neighborhoods, which are considered more or less independently. As neighborhood structure is typically simpler than global structure, this suggests that the decision problem should be easier. The results in this paper show that to be the case.
The PCMCP requires a choice of the modular proof system. We have considered the Owicki-Gries kind of proof system, based on local invariance. This is known to be incomplete, in that it may be necessary to expose auxiliary state in order to obtain a correctness proof. A fascinating question for future work is to consider variants of the PCMCP which search for modular proofs with limits on auxiliary state (e.g., “at most k bits of auxiliary state”). Alternative modular proof systems are based on auxiliary automata (which implicitly include auxiliary state) as in [4, 18]. The shape of these proof rules is usually as follows: in order to show \(P_1 || P_2 \models \varphi \), one finds auxiliary automata \(A_1\) and \(A_2\) such that \(P_1 || A_2 \preceq A_1\), \(P_2 || A_1 \preceq A_2\), and \(A_1 || A_2 \models \varphi \), where \(\preceq \) is usually the simulation pre-order, or language inclusion. The PCMCP formulation for this strategy would be to decide whether there are automata \(A_1,A_2,\ldots \) which meet the conditions of such a rule.
Motivation for introducing the PCMCP as a decision problem also comes from results on approximate procedures for obtaining parameterized proofs, several of which are based on localized analysis. For instance, environment abstraction methods [7] analyze a process along with an abstraction of its environment; the method of invisible invariants [27] and invisible ranking [12] generalizes invariants and rank functions from small instances to the parameterized family; and the work in [2] uses abstract interpretation on views, typically single processes or pairs of processes, to obtain a parameterized invariant. In our own work [22–24] we have used compositional methods along with localized symmetry and abstraction to build parametric proofs of protocols or families. By turning from such approximate constructions to a decision problem, the PCMCP offers a different perspective on the parameterized verification question.
Our results on the decidability of the PCMCP in the cases of mesh and CCC architectures cover two forms of parallel communication architectures. In the future, we plan to investigate PCMCP approaches for related architectures, including hypercubes (c.f. [16, 31]) and Message Passing Interface designs that are built on mesh architectures (c.f. [15, 32, 33]).
There are several promising directions to pursue. One that has already been mentioned is to strengthen the modular reasoning methods by allowing for auxiliary state and extending the decision procedures to liveness properties. Another is to examine whether abstraction methods, such as those developed in Sect. 4.3, lead to decision procedures for regular networks such as hypercubes where the degree of a node depends on the parameter n. A third direction is to explore other constraints on proof structure, such as depth or context-switch bounds.
Notes
- 1.
The notation is from Dijkstra-Scholten [8]: \([\varphi ]\) means that \(\varphi \) is valid.
- 2.
A groupoid is roughly a group with a partial composition operation. The network symmetry groupoid meets the conditions required of a groupoid: (1) \((m, \iota , m)\) is a symmetry for each node m, where \(\iota \) is the identity map; (2) if \((m,\beta ,n)\) is a symmetry so is the inverse \((n,\beta ^{-1},m)\); and (3) the composition of symmetries \((m,\beta ,n)\) and \((n',\gamma ,o)\), given by \((m,\gamma \beta ,o)\) if \(n = n'\), is also a symmetry.
- 3.
The algorithm in [13] considers checking Linear Temporal Logic formulae on networks of processes, in contrast we restrict attention to checking safety properties.
- 4.
Unlike the other cases, the local state space of the control process is unbounded as it has the form (c, x) where c is its internal state (which is bounded), and x is the vector of neighboring edge-values, which can have arbitrary length.
- 5.
We do not know the status of the PMCP. The powerful WQO theory of [1] appears not to apply due to the presence of universal guards. A more general assignment action,
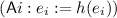 , also preserves the decidability of PCMCP. Allowing the dual action of assigning a value to some edge makes the PMCP undecidable (a reduction from 2CM). We do not know whether it also makes the PCMCP undecidable.
, also preserves the decidability of PCMCP. Allowing the dual action of assigning a value to some edge makes the PMCP undecidable (a reduction from 2CM). We do not know whether it also makes the PCMCP undecidable.
References
Abdulla, P.A., Cerans, K., Jonsson, B., Tsay, Y.-K.: General decidability theorems for infinite-state systems. In: LICS, pp. 313–321. IEEE Computer Society (1996)
Abdulla, P.A., Haziza, F., Holík, L.: All for the price of few. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 476–495. Springer, Heidelberg (2013)
Akers, S.B., Krishnamurthy, B.: A group-theoretic model for symmetric interconnection networks. IEEE Trans. Comput. 38(4), 555–566 (1989)
Alur, R., Henzinger, T.: Reactive modules. In: IEEE LICS (1996)
Apt, K.R., Kozen, D.: Limits for automatic verification of finite-state concurrent systems. Inf. Process. Lett. 22(6), 307–309 (1986)
Clarke, E., Enders, R., Filkorn, T., Jha, S.: Exploiting symmetry in temporal logic model checking. Formal Methods Syst. Des. 9(1/2), 77–104 (1996)
Clarke, E., Talupur, M., Veith, H.: Environment abstraction for parameterized verification. In: Emerson, E.A., Namjoshi, K.S. (eds.) VMCAI 2006. LNCS, vol. 3855, pp. 126–141. Springer, Heidelberg (2006)
Dijkstra, E., Scholten, C.: Predicate Calculus and Program Semantics. Springer, New York (1990)
Emerson, E., Namjoshi, K.: Reasoning about rings. In: ACM Symposium on Principles of Programming Languages (1995)
Emerson, E., Sistla, A.: Symmetry and model checking. Formal Methods in System Design 9(1/2), 105–131 (1996)
Esparza, J., Ganty, P., Majumdar, R.: Parameterized verification of asynchronous shared-memory systems. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 124–140. Springer, Heidelberg (2013)
Fang, Y., Piterman, N., Pnueli, A., Zuck, L.D.: Liveness with Invisible Ranking. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 223–238. Springer, Heidelberg (2004)
German, S., Sistla, A.: Reasoning about systems with many processes. J. ACM 39(3), 675–735 (1992)
Golubitsky, M., Stewart, I.: Nonlinear dynamics of networks: the groupoid formalism. Bull. Amer. Math. Soc. 43, 305–364 (2006)
Gopalakrishnan, G., Kriby, R.M., Siegel, S.F., Thakur, R., Gropp, W., Lusk, E., De Supinski, B.R., Schulz, M., Bronevetsky, G.: Formal analysis of MPI-based parallel programs. Commun. of the ACM 54, 82–91 (2011)
Hayes, J.P., Mudge, T.N., Stout, Q.F., Colley, S., Palmer, J.: Architecture of a hypercube supercomputer. In: Conference on Parallel Processing, pp. 653–660 (1986)
Jacobs, S., Bloem, R.: Parameterized synthesis. Logical Methods Comput. Sci. 10(1), 1–29 (2014)
Kurshan, R.: Computer-Aided Verification of Coordinating Processes: TheAutomata-Theoretic Approach. Princeton University Press, Princeton (1994)
Lamport, L.: Proving the correctness of multiprocess programs. IEEE Trans. Softw. Eng. 3(2), 125–143 (1977)
Manna, Z., Pnueli, A.: Temporal Verification of Reactive Systems: Safety. Springer, New York (1995)
Minsky, M.: Computation: finite and infinite machines. Prentice-Hall, Englewood Cliffs (1967)
Namjoshi, K.S., Trefler, R.J.: Local symmetry and compositional verification. In: Kuncak, V., Rybalchenko, A. (eds.) VMCAI 2012. LNCS, vol. 7148, pp. 348–362. Springer, Heidelberg (2012)
Namjoshi, K.S., Trefler, R.J.: Uncovering symmetries in irregular process networks. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 496–514. Springer, Heidelberg (2013)
Namjoshi, K.S., Trefler, R.J.: Analysis of dynamic process networks. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 164–178. Springer, Heidelberg (2015)
Namjoshi, K.S., Trefler, R.J.: Loop freedom in AODVv2. In: Graf, S., Viswanathan, M. (eds.) Formal Techniques for Distributed Objects, Components, and Systems. LNCS, vol. 9039, pp. 98–112. Springer, Heidelberg (2015)
Owicki, S.S., Gries, D.: Verifying properties of parallel programs: An axiomatic approach. Commun. ACM 19(5), 279–285 (1976)
Pnueli, A., Ruah, S., Zuck, L.D.: Automatic deductive verification with invisible invariants. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 82–97. Springer, Heidelberg (2001)
Preparata, F.P., Vuillemin, J.: The cube-connected cycles: a versatile network for parallel computation. CACM 24(5), 300–309 (1981)
Sánchez, A., Sánchez, C.: LEAP: a tool for the parametrized verification of concurrent datatypes. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 620–627. Springer, Heidelberg (2014)
Sanchez, A., Sanchez, C.: Parametrized invariance for infinite state processes. Acta Informatica 52(6), 525–557 (2015)
Seitz, C.L.: The cosmic cube. Commun. ACM 28, 22–33 (1985)
Siegel, S.F., Avrunin, G.S.: Verification of MPI-based software for scientific computation. In: Graf, S., Mounier, L. (eds.) SPIN 2004. LNCS, vol. 2989, pp. 286–303. Springer, Heidelberg (2004)
Siegel, S.F., Gopalakrishnan, G.: Formal analysis of message passing. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 2–18. Springer, Heidelberg (2011)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Namjoshi, K.S., Trefler, R.J. (2016). Parameterized Compositional Model Checking. In: Chechik, M., Raskin, JF. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2016. Lecture Notes in Computer Science(), vol 9636. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49674-9_39
Download citation
DOI: https://doi.org/10.1007/978-3-662-49674-9_39
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49673-2
Online ISBN: 978-3-662-49674-9
eBook Packages: Computer ScienceComputer Science (R0)




 then
then  from (c, s) to
from (c, s) to 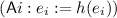 , also preserves the decidability of PCMCP. Allowing the dual action of assigning a value to some edge makes the PMCP undecidable (a reduction from 2CM). We do not know whether it also makes the PCMCP undecidable.
, also preserves the decidability of PCMCP. Allowing the dual action of assigning a value to some edge makes the PMCP undecidable (a reduction from 2CM). We do not know whether it also makes the PCMCP undecidable.