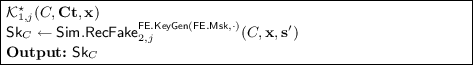Abstract
Deniable encryption, first introduced by Canetti et al. [14], allows a sender and/or receiver of encrypted communication to produce fake but authentic-looking coins and/or secret keys that “open” the communication to a different message. Here we initiate its study for the more general case of functional encryption (FE), as introduced by Boneh et al. [12], wherein a receiver in possession of a key k can compute from any encryption of a message x the value F(k, x) according to the scheme’s functionality F. Our results are summarized as follows: We put forth and motivate the concept of deniable FE, for which we consider two models. In the first model, as previously considered by O’Neill et al. [31] in the case of identity-based encryption, a receiver gets assistance from the master authority to generate a fake secret key. In the second model, there are “normal” and “deniable” secret keys, and a receiver in possession of a deniable secret key can produce a fake but authentic-looking normal key on its own. This parallels the “multi-distributional” model of deniability previously considered for public-key encryption.
In the first model, we show that any FE scheme for the general circuit functionality (as several recent candidate construction achieve) can be converted into an FE scheme having receiver deniability, without introducing any additional assumptions. In addition we show an efficient receiver deniable FE for Boolean Formulae from bilinear maps. In the second (multi-distributional) model, we show a specific FE scheme for the general circuit functionality having receiver deniability. This result additionally assumes differing-inputs obfuscation and relies on a new technique we call delayed trapdoor circuits. To our knowledge, a scheme in the multi-distributional model was not previously known even in the simpler case of identity-based encryption.
Finally, we show that receiver deniability for FE implies some form of simulation security, further motivating study of the latter and implying optimality of our results.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Encryption schemes meeting standard security notions (e.g., semantic security [22]) may be committing in the sense that they tie the sender and receiver to having communicated a particular message. This is potentially damaging in the context of coercion, whereby for example the receiver’s secret key becomes revealed (say under subpoena). Deniable encryption, formalized by Canetti et al. in 1997 [14], mitigates this threat by allowing the sender and/or receiver, after having already exchanged an encrypted message, to produce fake but authentic-looking random coins that “open” the ciphertext to a different message. That is, they can produce random coins (from which in particular a secret key can be computed) that make it look like they communicated some other message. The study of deniable encryption has seen a renewed interest. In particular, O’Neill et al. [31] construct “bideniable” public-key encryption schemes, namely where the sender and receiver can simultaneously equivocate without coordination, albeit in a relaxed, “multidistributional” model where there are special “deniable” algorithms that the sender and receiver must run in order to later be able to do so (in which case it looks like they ran the “normal” prescribed algorithms all along). Following [14, 31], we call schemes where only the sender can equivocate “sender deniable,” where only the receiver can equivocate “receiver deniable,” and where both can equivocate “bideniable”. Bendlin et al. [8] show that (non-interactive) receiver-deniable public-key encryption is impossible unless one works in the multidistributional model. Finally, a recent breakthrough work of Sahai and Waters [32] constructs sender-deniable public-key encryption without relying on the multidistributional model.
Deniability for Functional Encryption. In this paper, we initiate the study of deniability for much more advanced cryptosystems, as captured under the umbrella concept of functional encryption (FE) [12]. (Deniability for identity-based encryption was also previously considered by [31].) Whereas in traditional public-key encryption decryption is an all-or-nothing affair (i.e., a receiver is either able to recover the entire message using its key, or nothing), in FE is possible to finely control the amount of information that is revealed by a ciphertext to a given receiver. Somewhat more precisely, in a functional encryption scheme for functionality F, each secret key (generated by a master authority) is associated with some value k. Anyone can encrypt via the public parameters. When a ciphertext \(\mathsf{Ct}_x\) that encrypts x is decrypted using a secret key \(\mathsf{Sk}_k\) for value k, the result is F(k, x). Intuitively, security requires that a receiver in possession of \(\mathsf{Sk}_k\) learns nothing beyond this. We contend that deniability is an important property to consider in the context of FE. For example, consider a large organization using FE in which members have different keys. Suppose the police coerces one of the members of the organization into revealing its key or requesting a key for some value k. A deniable FE scheme in the sense we consider would allow this member to provide the police with a key \(\widetilde{SK}_k\) that “opens” a ciphertext \(\mathsf{Ct}_x\) as above to any apparent value of F(k, x) it likes. Another interesting application would be an encrypted email server that uses FE, where the server is in possession of keys that allow it to do searches, spam filtering, targeted advertising, etc. If the government coerces the email server to provide its keys or requests additional keys from the client, the server can do so in a way that again reveals any apparent values it likes. As another scenario, consider a secure routing protocol implemented with FE, where any node receives an encrypted packet and using a secret key corresponding to its routing table can forward the packet to the right port without knowing the next destinations of the packet. The NSA could coerce the nodes to reveal their respective routing tables to trace the final destinations of the packet. If the FE system is receiver deniable, there is no reason for the NSA to coerce them as the nodes could reveal a fake secret key.
Model and Definitions. More specifically, we propose the concept of receiver-deniable FE. For intuition, suppose the coercer has observed \(\mathsf{Ct}_x\) as above. Informally, receiver-deniable FE allows the sender to produce “fake” secret key \(\mathsf{Sk}'_k\) (we assume the coercer knows k) that makes equivocate \(\mathsf{Ct}_x\) as encryption of any other \(x'\) so that the secret key decrypts to \(F(k,x')\). But this intuition for the definition hides several points. First, what if the coercer is able to coerce many receivers, thus seeing many secret keys? In the case of identity-based encryption, it was previously observed by O’Neill et al. [31] that this case is equivalent via a hybrid argument to equivocation of a single ciphertext and secret key. However, this hybrid argument fails in our more general setting. Therefore, in our modeling we consider what we call \((n_c,n_k)\) -receiver-deniability, meaning the coercer requests \(n_c\) challenge ciphertexts (for which no underlying randomness is revealed) and \(n_k\) secret keys (i.e., receiver-coerce queries) adaptively. Second, and more interesting, O’Neill et al. [31] noted that an impossibility result of [8] implies that, even in the simpler case of identity-based encryption, “full” receiver deniability inherently requires that a receiver get assistance from the master authority to produce a fake secret key. While this may seem like the strongest possible model (indeed, [31] conveys the intuition that it is necessary for deniability), we propose an alternative, “multi-distributional” model as well, where there are “normal” and “deniable” secret keys, and a receiver in possession of a deniable secret key can produce a fake but authentic-looking normal one without any assistance. Here we envision that a user tells the authority initially whether it wants a normal or deniable secret key, and can later claim to a coercer that it requested a normal one even if it did not. We consider both models for deniable FE in this work. Note that the models are incomparable: on the one hand, the first (“full”) model requires the receiver to get assistance from the master authority, but a receiver does not have to choose one or the other type of key to request initially as in the second (“multi-distributional”) model. Getting assistance from the master authority to equivocate may not be feasible in many cases, making the second model particularly compelling, especially in light of the arguments of [31] for the meaningfulness of the multi-distributional model in the basic case of public-key encryption.
“Full” Receiver Deniability from Trapdoor Circuits. Next we show how to transform any “IND-secure” FE scheme for general circuits (i.e., where its functionality F computes general boolean circuits on some input length) into a FE for the same functionality that is \((n_c, \mathsf{poly})\)-receiver-deniable in the full model (but where the receiver gets assistance from the master authority to equivocate) without introducing any additional assumption. In particular, recent works [13, 19, 21, 34] show IND-secure FE for general circuits whose security is based either on indistinguishable obfuscation and its variants or polynomial hardness of simple assumptions on multi-linear maps. We can use any of these schemes in our construction. We present a direct black-box transformation, making use of the “trapdoor circuits” technique, introduced by De Caro et al. [17] to show how to bootstrap IND-secure for circuits to the stronger notion of simulation security (SIM-security). The idea of the trapdoor mechanism is to replace the original circuit C with a trapdoor circuit \(\mathsf{Trap}[C]\) that the receiver faking algorithm can then use to program the output in some way.
To give some intuition, let us consider for simplicity the case of equivocating a single ciphertext and secret key. Then, a plaintext will have two slots where the first slot will be the actual message \({x}\). The second slot will be a random string s, some sort of tag used to identify the ciphertext. On the other hand, \(\mathsf{Trap}[C]\), where for simplicity we restrict C to be one-bit output circuit, will have two slots embedded in it, let us call them trapdoor values. Both the slots will be random strings \(r_1,r_2\) used as formal variables to represent Boolean values 0 and 1. Now, if it happens that \(s=r_1\) then \(\mathsf{Trap}[C]\) returns 0, if \(s=r_2\) then it returns 1, otherwise \(\mathsf{Trap}[C]\) returns \(C({x})\). Notice that, when \(s,r_1\) and \(r_2\) are chosen uniformly and independently at the random then the above events happen with negligible probability thus this trapdoor mechanism does not influence the correctness of the scheme. On the other hand, it is easy to see how the receiver faking algorithm works by setting \(r_1\) or \(r_2\) to s depending on the expected faked output. Clearly, the receiver needs the master authority to generate a new secret key, corresponding to circuit \(\mathsf{Trap}[C]\), with tailored embedded \(r_1\) and \(r_2\). Moreover, the above solution fails when more secret keys have to be equivocated. In fact, s then would appear in all the faked secret keys and this would be easily recognizable by the adversary. A trivial fix is to put in the ciphertexts as many different s’s as the number of secret keys to be faked but this will create an unnecessary dependence that can be removed by using a PRF as a compact source of randomness. In Sect. 3 we present the result in full details.
Efficient Receiver Deniable FE for Boolean Formulae. We explore the possibility of achieving receiver deniability for weaker classes of functionalities that still support some form of trapdoor mechanism and for which a functional encryption scheme can be constructed assuming standard assumptions. We show how to do this for Boolean formulae, namely we show how to transform any IND-secure FE scheme for Boolean formulate into one that is \((n_c,n_d)\)-receiver deniable. Note that Katz, Sahai and Waters [27] show how to construct an FE scheme for Boolean formulae given an FE scheme for the inner-product predicate whose security, by the result of Okamoto and Takashima [29], can be based on the Decisional Linear Assumption in bilinear groups. An interesting point, however, is that these schemes for boolean formulae allow polynomials in t variables with degree at most d in each variable, as long as \(d^t\) is polynomial in the security parameter. This will mean that in order for our scheme to be efficient the trapdoor mechanism will have a non-negligible probability of being activated by an honest encryption (i.e., completeness is non-negligible). We fix this issue by using parallel repetition. The resulting scheme is \((n_c,n_k)\)-receiver deniable but we do not know how to achieve \(n_k=\mathsf{poly}\). The result is presented in Sect. 4.
“Multi-distributional” Receiver Deniability from “Delayed Trapdoor Circuits”. In our first result, the receiver crucially relies on the assistance of the master authority to generate a new secret key with tailored embedded \(r_1\) and \(r_2\), the trapdoor values. To avoid this, we need to find a way for the central authority to release a fake key that allows the receiver to modify the trapdoor values later on when required. This is solved using the new technique of delayed trapdoor circuits. Instead of embedding directly the trapdoor values in the \(\mathsf{Trap}[C]\), they are externalised. The trapdoor values are encrypted using an IND-CCA encryption scheme to avoid that the adversary can maul those values and learn something it should not learn. The resulting ciphertext, let us call it \(\mathsf{Ct}'\), is then linked to the corresponding \(\mathsf{Trap}[C]\) by using a one-way function f in this way: a fresh random value z in the domain of f will be encrypted together with the trapdoor values, \(t=f(z)\) will be embedded in trapdoor circuit. \(\mathsf{Trap}[C]\) then will take in input also \(\mathsf{Ct}'\) and verify that it encrypts a pre-image of t, before proceeding more. It is easy to see then that the fake key we were looking for is z. Knowing z allows to generate a new \(\mathsf{Ct}'\) for different trapdoor values. Our construction starts from that of Garg et al. [19] but departs from it in many technicalities needed to face the challenges met in the hybrid experiments. Namely, a ciphertext of the functional encryption scheme for x corresponds to a double encryption, à la Naor-Yung [28], of x, using a statistical simulation-soundness NIZK. A secret key for circuit C is the differing-input obfuscation [2, 4, 13] of a trapdoor circuit \(\mathsf{Trap}[C]\) that takes in input the double encryption of x and the double encryption of the trapdoor values related to \(\mathsf{Trap}[C]\). Intuitively, differing-input obfuscation is required because there are certain \(\mathsf{Ct}'\) that allows to understand, for example, which secret key \(\mathsf{Trap}[C]\) is using to decrypt the double encryption of x. The actual construction is much more complicated, and is presented in full details in Sect. 3. We point out that in a concurrent work Apon et al. [3] construct a bi-deniable FE scheme for the inner-product predicate in the multidistributional model from LWE.
Relation to Simulation-Based Security. As observed by [31], in the case of PKE, deniability implies a scheme is also non-committing [15, 16] and secure under key-revealing selective-opening attacks (SOA-K) [6, 18]. On the other hand, it was recently observed by [7] that the notion of simulation-based (SIM) security for FE implicitly incorporates SOA-K. SIM-security is a stronger notion of security for FE than IND-security and has been the subject of multiple recent works [1, 5, 7, 12, 17, 23, 30]. Very roughly, in both notions the adversary makes key-derivation queries, then queries for challenge ciphertexts, then again makes key-derivation queries. SIM-security asks that the “view” of the adversary can be simulated by a simulator given neither ciphertexts nor keys but only the corresponding outputs of the functionality on the underlying plaintexts, whereas IND-security only asks that it cannot distinguish the encryptions of messages that it cannot trivially distinguish using its requested keys. This leads to the interesting result that a receiver-deniable FE scheme necessarily achieves some form of SIM-security. To formalize it, recall from [17] that \((q_1, \ell , q_2)\)-SIM security denotes SIM-security where the adversary is allowed to make at most \(q_1\) non-adaptive key queries, \(\ell \) encryption queries (challenge ciphertexts), and \(q_2\) adaptive key queries. We show that an \((n_c,n_k)\)-receiver deniable FE scheme is also \((0,n_c,n_k)\)-SIM-secure (see Appendix A for a formal theorem and proof). On the other hand we stress deniability is stronger in the respect that equivocable ciphertexts and keys must decrypt correctly in the real system. Our results on receiver deniability can be seen as showing that the techniques of [17] are sufficient not just for achieving SIM-security but for deniability as well. Moreover, this implication implies that known impossibility results for SIM-secure FE [1, 7, 12, 17] mean that in the receiver deniable case \((n_c,\mathsf{poly})\)-deniability (which we achieve assuming IND-secure FE for the circuit functionality) is in fact optimal. These impossibility results hold only in the standard model and not in the (programmable) RO model [26], but in the case of deniability it is unclear how programmable ROs could help since programmability only helps in a simulation whereas deniability refers to the behaviour of the real system.
What About Sender Deniability? In this work we choose to focus on receiver deniability rather than sender deniability. Receiver deniability is arguably more important than sender deniability in practice — it is plausible that the sender erases its coins, but not that the receiver erases its key. We believe sender deniability can also be added to our schemes, however, by applying the techniques of Sahai and Waters [32] used to achieve sender-deniable public-key encryption. We investigated sender deniability for FE but we did not include the results in this version.
2 Definitions
We start by giving formal definition of functional encryption [12, 20], and its security, and deniable functional encryption and its security. Due to space constraints we defer to [2, 4, 13] for definitions of differing-inputs obfuscation, and to Garg et al. [19] for the definition of statistical simulation-sound non-interactive zero-knowledge proofs (SSS-NIZK, in short).
Functional Encryption. We define the primitive and its security following Boneh et al. [12] notation.
Definition 1
[Functionality] A functionality \(F=\{F_n\}_{n>0}\) is a family of functions \(F_n:K_n\times X_n\rightarrow \varSigma \) where \(K_n\) is the key space for parameter n, \(X_n\) is the message space for parameter n and \(\varSigma \) is the output space. Sometimes we will refer to functionality F as a function from \(F:K\times X\rightarrow \varSigma \) with \(K=\cup _n K_n\) and \(X=\cup _n X_n\).
Notice that, when \(\varvec{x}=(x_1,\ldots ,x_\ell )\) is a vector of messages, for any \(k\in K\), we denote by \(F(k,\varvec{x})\) the vector of evaluations \((F(k,x_1), \ldots ,F(k,x_\ell ))\).
Definition 2
[Functional Encryption Scheme] A functional encryption scheme for functionality F defined over (K, X) is a tuple \(\mathsf{FE}=(\mathsf{Setup}, \mathsf{KeyGen},\mathsf{Enc},\mathsf{Dec})\) of 4 algorithms with the following syntax:
-
1.
\(\mathsf{Setup}(1^\lambda ,1^n)\) outputs public and master secret keys \((\mathsf{Mpk},\mathsf{Msk})\) for security parameter \(\lambda \) and length parameter n that are polynomially related.
-
2.
\(\mathsf{KeyGen}(\mathsf{Msk},k)\), on input \(\mathsf{Msk}\) and \(k\in K_n\) outputs secret key \(\mathsf{Sk}\).
-
3.
\(\mathsf{Enc}(\mathsf{Mpk},{x})\), on input \(\mathsf{Mpk}\) and \({x}\in X_n\) outputs ciphertext \(\mathsf{Ct}\);
-
4.
\(\mathsf{Dec}(\mathsf{Mpk},\mathsf{Ct},\mathsf{Sk})\) outputs \(y \in \varSigma \cup \{ \perp \}\).
In addition we make the following correctness requirement: for all \((\mathsf{Mpk},\mathsf{Msk})\leftarrow \mathsf{Setup}(1^\lambda ,1^n)\), all \(k\in K_n\) and \({x}\in X_n\), for \(\mathsf{Sk}\leftarrow \mathsf{KeyGen}(\mathsf{Msk},k)\) and \(\mathsf{Ct}\leftarrow \mathsf{Enc}(\mathsf{Mpk},x)\), we have that \(\mathsf{Dec}(\mathsf{Mpk},\mathsf{Ct},\mathsf{Sk}) =F(k,x)\) whenever \(F(k,x) \ne \bot \), except with negligible probability. (See [7] for a discussion about this condition.)
Definition 3
[Circuit Functionality] The Circuit functionality has key space \(K_n\) equals to the set of all n-input Boolean circuits and message space \(X_n\) the set \(\{0,1\}^n\) of n-bit strings. For \(C\in K_n\) and \({x}\in X_n\), we have \(\mathsf{Circuit}(C,{x})= C({x})\), that is, the output of circuit C on input \({x}\).
Indistinguishability-Based Security. The indistinguishability-based notion of security for functional encryption scheme \(\mathsf{FE}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Enc},\mathsf{Dec})\) for functionality F defined over (K, X) is formalized by means of the following game \(\mathsf{IND}^\mathsf{FE}_\mathcal{A}\) between an adversary \(\mathcal{A}=(\mathcal{A}_0,\mathcal{A}_1)\) and a challenger \(\mathcal {C}\).

The advantage of adversary \(\mathcal {A}\) in the above game is defined as
Definition 4
We say that \(\mathsf{FE}\) is \((q_1,\ell ,q_2)\)-indistinguishably secure (\((q_1,\ell ,q_2)\)-IND-Secure, for short) where \(q_1 = q_1(\lambda ),\ell = \ell (\lambda ) q_2 = q_2(\lambda )\) are polynomials in the security parameter \(\lambda \) that are fixed a priori, if all probabilistic polynomial-time adversaries \(\mathcal{A}\) issuing at most \(q_1\) non-adaptive key queries, \(q_2\) adaptive key queries and output challenge message vectors of length and most \(\ell \), have at most negligible advantage in the above game. Notice that, in the case that a parameter is an unbounded polynomial we use the notation \(\mathsf{poly}\). If a parameter is not specified then it assumed to be \(\mathsf{poly}\).
Receiver-Deniable Functional Encryption Scheme. We define the primitive and its security in the following way:
Definition 5
[Receiver-Deniable Functional Encryption Scheme] A \((n_c,n_k)\)- receiver-deniable functional encryption scheme for functionality F defined over (K, X), where \(n_c = n_c(\lambda ), n_k = n_k(\lambda )\) are polynomials in the security parameter \(\lambda \) that are fixed a priori, is made up of the algorithms \(\mathsf{RecDenFE}=(\mathsf{Setup},\mathsf{Enc}, \mathsf{KeyGen},\mathsf{Dec})\) of a standard \(\mathsf{FE}\) scheme for F (Definition 2) and in addition the following algorithm:
-
\(\mathsf{RecFake}(\mathsf{Msk},k,\mathbf{Ct},\mathbf{x})\). The receiver faking algorithm, on input the master secret key \(\mathsf{Msk}\), a key k, at most \(n_c\) ciphertexts \(\mathbf{Ct}=(\mathsf{Ct}_1,\ldots ,\mathsf{Ct}_{n_c})\) and messages \(\mathbf{x}=(x_1,\ldots ,x_{n_c})\), outputs faked secret key \(\mathsf{Sk}_C\).
Correctness is defined as in Definition 2 and indistinguishability as in Definition 4.
Definition 6
[Receiver-Deniability] We require that for every PPT adversary \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\), issuing at most \(n_k\) receiver-coerce oracle queries, the following two experiments are computationally indistinguishable.

where \(\mathbf{x}^\star =({x}_1^\star ,\ldots ,{x}_{n_c}^\star )\), \(\mathbf{y}^\star =(y_1^\star ,\ldots ,y_{n_c}^\star )\), and \(\mathbf{Ct}^\star =(\mathsf{Ct}_1^\star ,\ldots ,\mathsf{Ct}_{n_c}^\star )\). \((\mathcal {K}_1,\mathcal {K}_2)\) are the receiver-coerce oracles.
All the oracles declared above are defined as follows:

In the above experiments, we require the following:
-
1.
There is no query (k, x, y) issued to \(\mathcal {O}_1\) and at same time a query \((k,\mathbf{Ct}^\star ,\mathbf{x})\) for some \(\mathbf{x}\) issued to \(\mathcal {K}_1\) and there is no query (k, x, y) issued to \(\mathcal {O}_2\) and at same time a query \((k,\mathbf{Ct}^\star ,\mathbf{x})\) for some \(\mathbf{x}\) issued to \(\mathcal {K}_2\), where we consider all queries issued during the entire course of the experiment; i.e., when counting all the queries made by \(\mathcal {A}_0\) and \(\mathcal {A}_1\) together.
-
2.
For any query issued by \(\mathcal {A}_1\) to its oracle \(\mathcal {K}_1\) or \(\mathcal {K}_2\) oracle for key \(k^\star \), neither \(\mathcal {A}_0\) nor \(\mathcal {A}_1\) query \(k^\star \) to either of their oracles \(\mathcal {O}_1,\mathcal {O}_2\); i.e., they do not make any query \((k^\star ,x,y)\) for any x, y to \(\mathcal {O}_1\) or \(\mathcal {O}_2\).
-
3.
For each key k different from any of the challenge keys \(k_i^\star \) queried by \(\mathcal {A}_0\) and \(\mathcal {A}_1\) to oracles \(\mathcal {O}_1\) or \(\mathcal {O}_2\), it holds that \(F(k,\mathbf{x}^\star )=F(k,\mathbf{y}^\star )\).
2.1 Multi-distributional Receiver-Deniable Functional Encryption Scheme
Definition 7
[Multi-Distributional Receiver-Deniable FE] A \((n_c,n_k)\)-multi-distributional receiver-deniable functional encryption scheme for functionality F defined over (K, X), where \(n_c = n_c(\lambda ), n_k = n_k(\lambda )\) are polynomials in the security parameter \(\lambda \) that are fixed a priori, is made up of the algorithms \(\mathsf{MDRecDenFE}=(\mathsf{Setup},\mathsf{Enc},\mathsf{KeyGen},\mathsf{Dec})\) of a standard \(\mathsf{FE}\) scheme for F (Definition 2) and in addition the following two algorithms:
-
\(\mathsf{DenKeyGen}(\mathsf{Msk},k)\). The deniable key generation algorithm, on input the master secret key \(\mathsf{Msk}\), and key k, outputs secret key \(\mathsf{Sk}_k\) and fake key \(\mathsf{Fk}_k\).
-
\(\mathsf{RecFake}(\mathsf{Sk}_k,\mathsf{Fk}_k,\mathbf{Ct},\mathbf{x})\). The receiver faking algorithm, on input secret key and fake key \(\mathsf{Sk}_k,\mathsf{Fk}_k\) for key k, at most \(n_c\) ciphertexts \(\mathbf{Ct}=(\mathsf{Ct}_1,\ldots ,\mathsf{Ct}_{n_c})\) and messages \(\mathbf{x}=(x_1,\ldots ,x_{n_c})\), outputs faked secret key \(\mathsf{Sk}'_k\).
Correctness is defined as in Definition 2 and indistinguishability as in Definition 4. We also require the following security property.
Definition 8
[Multi-Distributional Receiver Deniability] We require that for every PPT adversary \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\), issuing at most \(n_k\) receiver-coerce oracle queries, the following two experiments are computationally indistinguishable.

where \(\mathbf{x}^\star =({x}_1^\star ,\ldots ,{x}_{n_c}^\star )\), \(\mathbf{y}^\star =(y_1^\star ,\ldots ,y_{n_c}^\star )\), and \(\mathbf{Ct}^\star =(\mathsf{Ct}_1^\star ,\ldots ,\mathsf{Ct}_{n_c}^\star )\). \((\mathcal {K}_1,\mathcal {K}_2)\) are the receiver-coerce oracles.
All the oracle declared above are defined as follows:

In the above experiments, we require the following:
-
1.
There is no query (k, x, y) issued to \(\mathcal {O}_1\) and at same time a query \((k,\mathbf{Ct}^\star ,\mathbf{x})\) for some \(\mathbf{x}\) issued to \(\mathcal {K}_1\) and there is no query (k, x, y) issued to \(\mathcal {O}_2\) and at same time a query \((k,\mathbf{Ct}^\star ,\mathbf{x})\) for some \(\mathbf{x}\) issued to \(\mathcal {K}_2\), where we consider all queries issued during the entire course of the experiment; i.e., when counting all the queries made by \(\mathcal {A}_0\) and \(\mathcal {A}_1\) together.
-
2.
For any query issued by \(\mathcal {A}_1\) to its oracle \(\mathcal {K}_1\) or \(\mathcal {K}_2\) for key \(k^\star \), neither \(\mathcal {A}_0\) nor \(\mathcal {A}_1\) query \(k^\star \) to either of their oracles \(\mathcal {O}_1,\mathcal {O}_2\); i.e., they do not make any query \((k^\star ,x,y)\) for any x, y to \(\mathcal {O}_1\) or \(\mathcal {O}_2\).
-
3.
For each key k different from any of the challenge keys \(k_i^\star \) queried by \(\mathcal {A}\) to oracles \(\mathcal {O}_1\) or \(\mathcal {O}_2\), it holds that \(F(k,\mathbf{x}^\star )=F(k,\mathbf{y}^\star )\).
Remark 9
Our security notion is selective, in that the adversary commits to (x, y) before it sees \(\mathsf{Mpk}\). It is possible to bootstrap selectively-secure scheme to full security using standard complexity leveraging arguments [10, 24] at the price of a \(2^{|x|}\) loss in the security reduction.
3 Receiver Deniable FE from Trapdoor Circuits
In this section, we present a construction of a \((n_c,\mathsf{poly})\)-receiver deniable functional encryption scheme for Circuit, \(\mathsf{RecDenFE}\).
Overview. To construct our \(\mathsf{RecDenFE}\) scheme, we start from an IND-Secure FE scheme for Circuit. During the key generation, we replace the original circuit with a trapdoor one that the receiver faking algorithm can then use to program the output in some way. More specifically, we put additional “slots” in the plaintexts and secret keys that will be critically used by the receiver faking algorithm. A plaintext will have two slots where the first slot will be the actual message \({x}\). The second slot will be a random string s, some sort of tag used to identify the ciphertext that will serve as seed of a PRF. On the other hand, a secret key for circuit C has \(4\cdot n_c\) slots consisting of random strings \(t_i,z_i,t'_i,z'_i\), for \(i\in [n_c]\), used as formal variables to represent Boolean values 0 and 1. Specifically:
Definition 10
[Trapdoor Circuit] Let C be a Boolean circuit on n-bits and 1-bit output, \(\mathcal {F}= \{f_s:s\in \{0,1\}^\lambda \}_{\lambda \in {{\mathbb N}}}\) be a \((l(\lambda ),L(\lambda ))\)-pseudo-random function family. For any \(\mathbf{t}= (t_i\in \{0,1\}^{l(\lambda )})_{i\in [n_c]}, \mathbf{z}= (z_i\in \{0,1\}^{L(\lambda )})_{i\in [n_c]}\) and \(\mathbf{t}' = (t'_i\in \{0,1\}^{l(\lambda )})_{i\in [n_c]}, \mathbf{z}'= (z'_i\in \{0,1\}^{L(\lambda )})_{i\in [n_c]}\), define the corresponding trapdoor circuit \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}\) on \((n+\lambda )\)-bit inputs and 1-bit output as follows:

We are now ready to present our \(\mathsf{RecDenFE}\) scheme.
Construction 11
[Receiver Deniable Functional Encryption] Let \(\mathsf{FE}=(\mathsf{FE}.\mathsf{Setup}, \mathsf{FE}.\mathsf{Enc},\mathsf{FE}. \mathsf{KeyGen},\mathsf{FE}.\mathsf{Dec})\) be a functional encryption scheme for the functionality Circuit and \(\mathcal {F}= \{f_s:s\in \{0,1\}^\lambda \}_{\lambda \in {{\mathbb N}}}\) be a \((l(\lambda ),L(\lambda ))\)-pseudo-random function family. We define our receiver deniable functional encryption scheme \(\mathsf{RecDenFE}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Enc}, \mathsf{Dec},\mathsf{RecFake})\) for Circuit as follows.
-
\(\mathsf{Setup}(1^\lambda ,1^n)\) runs \(\mathsf{FE}.\mathsf{Setup}(1^\lambda ,1^{n+\lambda })\) to get the pair \((\mathsf{FE}.\mathsf{Mpk},\mathsf{FE}.\mathsf{Msk})\). Then, the master public key is \(\mathsf{Mpk}=\mathsf{FE}.\mathsf{Mpk}\) and the master secret key is \(\mathsf{Msk}=\mathsf{FE}.\mathsf{Msk}\). The algorithm returns the pair \((\mathsf{Mpk},\mathsf{Msk})\).
-
\(\mathsf{Enc}(\mathsf{Mpk},{x})\) on input master public key \(\mathsf{Mpk}=\mathsf{FE}.\mathsf{Mpk}\), and message \({x}\in \{0,1\}^n\), chooses a random \(s\in \{0,1\}^\lambda \) and sets \({x}'=({x},s)\). Then the algorithm computes and returns the ciphertext \(\mathsf{Ct}=\mathsf{FE}.\mathsf{Enc}(\mathsf{FE}.\mathsf{Mpk},{x}')\).
-
\(\mathsf{KeyGen}(\mathsf{Msk},C)\) on input master secret key \(\mathsf{Msk}=\mathsf{FE}.\mathsf{Msk}\) and a n-input Boolean circuit C, chooses, for \(i\in [n_c]\), random strings \(t_i,t'_i\in \{0,1\}^{l(\lambda )}\), \(z_i,z'_i\in \{0,1\}^{L(\lambda )}\) and computes \(\mathsf{FE}.\mathsf{Sk}_C=\mathsf{FE}.\mathsf{KeyGen}(\mathsf{FE}.\mathsf{Msk}, \mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z}, \mathbf{t}',\mathbf{z}'})\). The algorithm returns the secret key \(\mathsf{Sk}_C=(\mathbf{t},\mathbf{z}, \mathbf{t}',\mathbf{z}',\mathsf{FE}.\mathsf{Sk}_C)\).
-
\(\mathsf{Dec}(\mathsf{Mpk},\mathsf{Ct},\mathsf{Sk}_C)\) on input master public key \(\mathsf{Mpk}=\mathsf{FE}.\mathsf{Mpk}\), \(\mathsf{Ct}\) and secret key \(\mathsf{Sk}_C=(\mathbf{t},\mathbf{z}, \mathbf{t}',\mathbf{z}',\mathsf{FE}.\mathsf{Sk}_C)\) for circuit C, returns the output of \(\mathsf{FE}.\mathsf{Dec}(\mathsf{FE}.\mathsf{Mpk},\mathsf{Ct},\mathsf{FE}.\mathsf{Sk}_C)\).
-
\(\mathsf{RecFake}(\mathsf{Msk},C,\mathbf{Ct},\mathbf{x})\) on input the master secret key \(\mathsf{Msk}=\mathsf{FE}.\mathsf{Msk}\), a Boolean circuit C on n-bits input and 1-bit output, at most \(n_c\) ciphertexts \(\mathbf{Ct}=(\mathsf{Ct}_1,\ldots ,\mathsf{Ct}_\ell )\) and messages \(\mathbf{x}=({x}_1,\ldots ,{x}_\ell )\), extracts \(s_i\) from each ciphertext \(\mathsf{Ct}_i\) by using \(\mathsf{FE}.\mathsf{Msk}\). Then, for each \(i\in [\ell ]\), \(\mathsf{RecFake}\) chooses random \(t_i\) and \(t'_i\) in \(\{0,1\}^{l(\lambda )}\) and distinguishes between the following two case:
-
If \(C({x}_i)=1\), it sets \(z_i=f_{s_i}(t_i)\) and chooses random \(z'_i\in \{0,1\}^{L(\lambda )}\).
-
If \(C({x}_i)=0\), it sets \(z'_i=f_{s_i}(t'_i)\) and chooses random \(z_i\in \{0,1\}^{L(\lambda )}\).
Finally, \(\mathsf{RecFake}\) computes \(\mathsf{FE}.\mathsf{Sk}_C=\mathsf{FE}. \mathsf{KeyGen}(\mathsf{FE}.\mathsf{Msk},\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'})\), and returns secret key \(\mathsf{Sk}_C=(\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}',\mathsf{FE}.\mathsf{Sk}_C)\).
-
Correctness of our \(\mathsf{RecDenFE}\) scheme follows from the correctness of \(\mathsf{FE}\) and from the observation that, for randomly chosen \(\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'\) and s and for all \({x}\), \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'} ({x},s)=C({x})\) except with negligible probability.
Security. The proof of security can be found in Appendix B.
4 Receiver Deniable FE for Boolean Formulae
We have seen in the previous section how to construct a receiver deniable functional encryption scheme for circuits assuming the existence of an IND-Secure FE scheme for the same functionality. To the best of our knowledge, the only way to construct an IND-Secure FE for circuits is by using obfuscation and its variants.
In this section we explore the possibility of achieving receiver deniability for weaker classes of functionalities that still support some form of trapdoor mechanism and for which a functional encryption scheme can be constructed assuming standard assumptions. Namely, we are interested in constructing a receiver deniable FE for Boolean formulae. In [27], Katz et al, show how to construct a functional encryption scheme for Boolean formulae given a functional encryption scheme for the inner-product whose security, by the result of Okamoto and Takashima [29], can be based on the Decisional Linear Assumption in bilinear groups. To construct a functional encryption scheme for Boolean formulae, [27] first shows how to construct functional encryption schemes for predicates corresponding to univariate polynomials whose degree d is polynomial in the security parameter. This can be generalized to the case of polynomials in t variables, and degree at most d in each variable, as long as \(d^t\) is polynomial in the security parameter. Given the polynomial-based construction, [27] shows that for Boolean variables it is possible to handle arbitrary CNF or DNF formulas by noting that the predicate \(\textsf {OR}_{I_1 ,I_2}\), where \(\textsf {OR}_{I_1,I_2}(x_1, x_2) = 1\) iff either \(x_1 = I_1\) or \(x_2 = I_2\), can be encoded as the bivariate polynomial \(p(x_1,x_2)=(x_1-I_1)\cdot (x_2-I_2)\) and the predicate \(\textsf {AND}_{I_1,I_2}\), where \(\textsf {AND}_{I_1,I_2}(x_1,x_2) = 1\) if both \(x_1 = I_1\) and \(x_2 = I_2\), correspond to the polynomial \(p(x_1,x_2)=(x_1-I_1)+(x_2-I_2)\). (Notice that, for non-Boolean variables it is not known how to directly handle negation.) The complexity of the resulting scheme depends polynomially on \(d^t\), where t is the number of variables and d is the maximum degree of the resulting polynomial in each variable. This bound will critically influence our construction of receiver deniable scheme as we will show in the next section. Specifically, the length of the additional slots used in trapdoor mechanism of the previous section will be fixed and independent of the security parameter to avoid the exponential blowup of the complexity of the resulting scheme. As a consequence, the trapdoor mechanism has a non-negligible probability of being active in the real scheme thus influencing the decryption error probability. Parallel repetition will fix this issue.
4.1 Our Construction
Overview. The trapdoor formula will follow the same design lines of the trapdoor circuit we used in the previous section with the main difference being the length of the slots which will be here constant and independent from the security parameter to avoid the exponential blowup in the [27] construction. Thus, as in the previous section, we will have additional slots in the plaintexts and secret keys that will be critically used by the receiver faking algorithm. The plaintext will have two slots where the first slot will be the actual message \({x}\). The second slot will be a random string s. On the other hand, a secret key for Boolean formula f will also have two slots to represent Boolean values 0 and 1. Specifically:
Construction 12
[Trapdoor Boolean Formula] Let f be a Boolean formula on n-bits. For any two strings \(r_0,r_1\in \{0,1\}^\ell \), define the corresponding trapdoor boolean formula \(\mathsf{Trap}[f]^{r_0,r_1}\) on \((n+\ell )\)-bit inputs as follows: \(\mathbf{Formula} \mathsf{Trap}[f]^{r_0,r_1}(x,s) := (s=r_1)\vee \left[ f(x)\wedge \lnot (s=r_0)\right] \), where the expression \((s=r)\) is the comparison bit-a-bit.
We are now ready to present our \(\mathsf{RecDenFE}\) scheme.
Construction 13
[Receiver Deniable Functional Encryption for Boolean Formulae] Let \(\mathsf{FE}=(\mathsf{FE}.\mathsf{Setup},\mathsf{FE}.\mathsf{Enc},\mathsf{FE}.\mathsf{KeyGen},\mathsf{FE}.\mathsf{Eval})\) be the functional encryption scheme for the functionality Boolean Formulae. For any constant \(\ell > 3\), we define our receiver deniable functional encryption scheme \(\mathsf{RecDenFE}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Enc}, \mathsf{Dec},\mathsf{RecFake})\) for Boolean formulae as follows.
-
\(\mathsf{Setup}(1^\lambda ,1^n,1^m)\), for each \({i\in [m]}\), runs \(\mathsf{FE}.\mathsf{Setup}(1^\lambda ,1^{n+\ell })\) to get the pair \((\mathsf{FE}.\mathsf{Mpk}_i,\mathsf{FE}.\mathsf{Msk}_i)\). Then, the master public key is \(\mathsf{Mpk}=(\mathsf{FE}.\mathsf{Mpk})_{i\in [m]}\) and the master secret key is \(\mathsf{Msk}=(\mathsf{FE}.\mathsf{Msk})_{i\in [m]}\). The algorithm returns the pair \((\mathsf{Mpk},\mathsf{Msk})\).
-
\(\mathsf{Enc}(\mathsf{Mpk},{x})\), on input master public key \(\mathsf{Mpk}=(\mathsf{FE}.\mathsf{Mpk}_i)_{i\in [m]}\) and message \({x}\in \{0,1\}^n\), for each \(i\in [m]\), chooses a random \(s_i\in \{0,1\}^\ell \) and sets \(\mathsf{Ct}_i=\mathsf{FE}.\mathsf{Enc}(\mathsf{FE}.\mathsf{Mpk}_i,(x,s_i))\). The algorithm returns the ciphertext \(\mathsf{Ct}=(\mathsf{Ct}_i)_{i\in [m]}\).
-
\(\mathsf{KeyGen}(\mathsf{Msk},f)\), on input master secret key \(\mathsf{Msk}=(\mathsf{FE}.\mathsf{Msk})_{i\in [m]}\) and a n-input Boolean formula f, for each \(i\in [m]\), chooses two random strings \(r_0^i,r_1^i\in \{0,1\}^\ell \), such that \(r_0^i\ne r_1^i\), and computes secret key \(\mathsf{FE}.\mathsf{Sk}_f^i=\mathsf{FE}.\mathsf{KeyGen}(\mathsf{FE}.\mathsf{Msk}_i, \mathsf{Trap}[f]^{r_0^i,r_1^i})\). The algorithm returns the secret key \(\mathsf{Sk}_f=(r_0^i,r_1^i,\mathsf{FE}.\mathsf{Sk}_f^i)_{i\in [m]}\).
-
\(\mathsf{Dec}(\mathsf{Mpk},\mathsf{Ct},\mathsf{Sk}_f)\), on input master public key \(\mathsf{Mpk}=(\mathsf{FE}.\mathsf{Mpk})_{i\in [m]}\), \(\mathsf{Ct}=(\mathsf{Ct}_i)_{i\in [m]}\) and secret key \(\mathsf{Sk}_f=(r_0^i,r_1^i,\mathsf{FE}.\mathsf{Sk}_f^i)_{i\in [m]}\) for Boolean formula f, for \(i\in [m]\), computes Boolean value \(b_i=\mathsf{FE}.\mathsf{Eval}(\mathsf{FE}.\mathsf{Mpk}_i,\mathsf{Ct}_i,\mathsf{FE}.\mathsf{Sk}_f^i)\), and returns as output the Boolean value on which the majority of \(b_i\)’s have agreed on.
-
\(\mathsf{RecFake}(\mathsf{Msk},f,\mathsf{Ct},{x}')\), on input the master secret key \(\mathsf{Msk}=(\mathsf{FE}.\mathsf{Msk}_i)_{i\in [m]}\), an n-input Boolean formula f, ciphertext \(\mathsf{Ct}=(\mathsf{Ct}_i)_{i\in [m]}\) and message \({x}'\), for all \(i\in [m]\), the algorithm extracts \(s_i\) from \(\mathsf{Ct}_i\) by using \(\mathsf{FE}.\mathsf{Msk}_i\). Now, \(\mathsf{RecFake}\) chooses the \(r_0^i\)’s and \(r_1^i\)’s by following a binomial distribution with number of trials equals to m and success probability \(p=(1-2^{-\ell })\). Specifically, \(\mathsf{RecFake}\) distinguishes between the following two cases. Let \(b'=f({x}')\), for each \(i\in [m]\), if there is a success in the i-th trial then \(\mathsf{RecFake}\) sets \(r_{b'}^i=s_i\) and \(r^i_{1-b}\) to a random value different from \(s_i\). Otherwise, \(\mathsf{RecFake}\) sets \(r_{1-b'}^i=s_i\) and \(r_{b}\) to a random value different from \(s_i\). Finally, \(\mathsf{RecFake}\) computes secret key \(\mathsf{FE}.\mathsf{Sk}_f^i=\mathsf{FE}.\mathsf{KeyGen}(\mathsf{FE}.\mathsf{Msk}_i,\mathsf{Trap}[f]^{r_0^i,r_1^i})\), and returns the secret key \(\mathsf{Sk}_f=(r_0^i,r_1^i,\mathsf{FE}.\mathsf{Sk}_f^i)_{i\in [m]}\) as faking key.
Correctness. Notice that for any \(i\in [m]\), the probability that \(s_i=r_0^i \vee s_i=r_1^i\) is at most \(2^{-\ell +1}\). Thus the output of the decryption is correct, i.e. \(\mathsf{Trap}[f]^{r_0^i,r_1^i}({x},s_i)=f({x})\), with probability at least \(1-2^{-\ell +1}\).
Thus on average, an \((1-2^{-\ell +1})\) fraction of the ciphertexts will be decrypted to the correct value and for large enough m, the Chernoff bound guarantees that the correctness of \(\mathsf{RecDenFE}\) hold with overwhelming probability.
Security. The proof that \(\mathsf{RecDenFE}\) is a (1, 1)-receiver deniable functional encryption scheme for Boolean formulae is essentially that of Theorem 20 and we omit further details.
We note that one can extend the scheme to \((n_c,n_k)\)-receiver deniability in a simple way but we cannot achieve \(n_k = \mathsf{poly}\) in this case, however, because we cannot use symmetric encryption (at least in a straightforward way).
5 Multi-distributional Receiver Deniable FE from \(\mathsf{di}\mathcal{O}\)
In order to avoid to overburden the notation and to make the presentation easy to follow, we present a construction of a (1, 1)-multi-distributional receiver deniable functional encryption scheme for Circuit.
Overview. Our construction resembles that of Garg et al. [19]. Namely, a ciphertext of the functional encryption scheme for x corresponds to a double encryption, à la Naor-Yung [28], of x, using a statistical simulation-soundness NIZK. A secret key for circuit C is the differing-input obfuscation of a trapdoor circuit \(\mathsf{Trap}[C]\) that takes in input the double encryption of x and the double encryption of the trapdoor values.
Construction 14
[Multi-Distributional Receiver Deniable FE] Given an IND-CPA PKE system \(\mathcal {E}=(\mathcal {E}.\mathsf{Setup},\mathcal {E}.\mathsf{Enc},\mathcal {E}.\mathsf{Dec})\) with perfect correctness, a differing-inputs obfuscator \(\mathsf{di}\mathcal{O}\), an SSS-NIZK proof system \(\mathsf{NIZK}=(\mathsf{NIZK}.\mathsf{Setup},\mathsf{NIZK}.\mathsf{Prove},\mathsf{NIZK}.\mathsf{Verify},\mathsf{NIZK}.\mathsf{Sim})\) and a one-way function f, we define our multi-distributional receiver deniable functional encryption \(\mathsf{MDRecDenFE}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Enc},\mathsf{DenKeyGen},\mathsf{RecFake},\mathsf{Dec})\) as follows:
-
1.
\(\mathsf{Setup}(1^\lambda )\) takes in input the security parameter \(\lambda \) and computes the following: For \(i\in [4]\), \((\mathsf{pk}_i,\mathsf{sk}_i)\leftarrow {\mathcal {E}}.\mathsf{Setup}(1^\lambda )\). Then, \(\mathsf{crs}\leftarrow \mathsf{NIZK}.\mathsf{Setup}(1^\lambda )\). The algorithm sets \(\mathsf{Mpk}=((\mathsf{pk}_i)_{i\in [4]},f,\mathsf{crs})\), \(\mathsf{Msk}=((\mathsf{sk}_i)_{i\in [4]})\).
-
2.
\(\mathsf{KeyGen}(\mathsf{Msk},C)\) takes in input master secret key \(\mathsf{Msk}=((\mathsf{sk}_i)_{i\in [4]})\), and circuit C, and does the following: Computes common reference string \(\mathsf{crs}'\leftarrow \mathsf{NIZK}.\mathsf{Setup}(1^\lambda )\). Then, sample random z in the domain of f and set \(t=f(z)\) and compute \(\mathsf{Ct}' := (\mathsf{ct}_{3},\mathsf{ct}_{4},\pi _2)\), where \(\mathsf{ct}_{3}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_3, (z,0^n,0^\lambda );r_3)\) and \(\mathsf{ct}_{4}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_4, (z,0^n,0^\lambda );r_4)\), and \(\pi _2\) is a NIZK proof of Eq. 2. Finally, the algorithm computes a differing-input obfuscation \(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}}\) for the trapdoor circuit \(\mathsf{Trap}_{1,3}[C,\mathsf{crs},\mathsf{crs}',\mathsf{sk}_i,\mathsf{sk}_j,f,t]\). The algorithm outputs secret key for the circuit C, \(\mathsf{Sk}_C=(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}},t,\mathsf{Ct}')\).
-
3.
\(\mathsf{DenKeyGen}(\mathsf{Msk},C)\) takes in input\(\mathsf{Msk}=((\mathsf{sk}_i)_{i\in [4]})\) and circuit C, and computes \(\mathsf{Sk}_C=\mathsf{KeyGen}(\mathsf{Msk},C)\). The algorithm outputs \(\mathsf{Sk}_C\) as the secret key for the circuit C and \(\mathsf{Fk}_C=z\).
-
4.
\(\mathsf{Enc}(\mathsf{Mpk},{x})\), on input master public key \(\mathsf{Mpk}=((\mathsf{pk}_i)_{i\in [4]},f,\mathsf{crs})\) and messages \({x}\in X_n\), computes \(\mathsf{Ct}=(\mathsf{ct}_{1},\mathsf{ct}_{2},\pi _1)\), where \(\mathsf{ct}_{1}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_1, x;r_1)\) and \(\mathsf{ct}_{2}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_2,x;r_2)\) and \(\pi _1\) is a NIZK proof of Eq. 1. The algorithm outputs ciphertext \(\mathsf{Ct}\).
-
5.
\(\mathsf{Dec}(\mathsf{Sk}_C,\mathsf{Ct})\) on input secret key \(\mathsf{Sk}_C=(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}},t,\mathsf{Ct}')\) and ciphertext \(\mathsf{Ct}\), the algorithm outputs \(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}}(\mathsf{Ct},\mathsf{Ct}')\).
-
6.
\(\mathsf{RecFake}(\mathsf{Sk}_C,\mathsf{Fk}_C,\mathsf{Ct},{x})\) on input secret key \(\mathsf{Sk}_C=(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}},t,\mathsf{Ct}')\), fake key \(\mathsf{Fk}_C=z\), where \(t=f(z)\), ciphertext \(\mathsf{Ct}=(\mathsf{ct}_{1},\mathsf{ct}_{2},\pi _1)\) and message \({x}\), does the following: Compute \({\hat{\mathsf{Ct}}} := ({\hat{\mathsf{ct}}_{3}},{\hat{\mathsf{ct}}_{4}},{\hat{\pi }_2})\), where \({\hat{\mathsf{ct}}_{3}}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_3, (z,\mathsf{Ct},{x});r_3)\) and \({\hat{\mathsf{ct}}_{4}}\leftarrow {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_4, (z,\mathsf{Ct},{x}); r_4)\) and \({\hat{\pi }_2}\) is a NIZK proof of Eq. 2. The new secret key for circuit C is \(\mathsf{Sk}_C=(\mathsf{di}\mathcal{O}_{\mathsf{Trap}_{1,3}},t,\hat{\mathsf{Ct}})\).
Correctness follows immediately from the correctness of the \(\mathsf{di}\mathcal{O}\), PKE, SSS-NIZK, and the description of the trapdoor circuits described below.

Remark 15
To allow a secret key to support faking against \(n_c\) ciphertexts, like we do in Sect. 3, we attach to a secret key \(n_c\) ciphertexts \(\mathsf{Ct}_i'\) each being the double encryption of \((z_i,0^n,0^\lambda )\) for different \(z_i\)’s. Then, \(\mathsf{Trap}_{i,j}\) will contain the images under f of all \(z_i\)’s.
Proof of Security. We prove the following main theorem.
Theorem 16
If \(\mathsf{di}\mathcal{O}\) is an differing-input obfuscator, \({\mathcal {E}}\) is IND-CPA and f is a one-way function then \(\mathsf{MDRecDenFE}\) is a (1, 1)-multi-distributional receiver deniable in the sense of Definition 6.
To prove the above theorem, we prove the indistinguishability of the following hybrid experiments. Recall that, for simplicity, we prove (1, 1)-security. Extending the proof of security to \(n_c\) being any constant and \(n_k=\mathsf{poly}\) resorts to add more hybrids to switch the challenge ciphertexts and the secret keys generated by the receiver-coerce oracle to the target distribution.
Hybrid \({\varvec{H}}_\mathbf{1}\) . This is the \(\mathsf{RealMDRecDenExp}\) experiment where the receiver-coerce oracle is \(\mathcal {K}_1\).
Hybrid \({\varvec{H}}_\mathbf{2}\) . It is identical to \(H_1\) except that: (1) \((\mathsf{crs},\pi _1^\star )\) is simulated as \((\mathsf{crs},\pi _1^\star )\leftarrow \mathsf{NIZK}.\mathsf{Sim}(1^\lambda , \exists x,r_1,r_2 : \mathsf{ct}_1^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_1,x;r_1) \text { and } \mathsf{ct}_2^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_2,x;r_2)) \) where \(\mathsf{ct}_1^\star ,\mathsf{ct}_2^\star \) is part of the challenge ciphertext. Note that, in the selective security game the challenge ciphertext can be given out simultaneously with the public parameters. (2) \((\mathsf{crs}',\pi _2)\), generated by the receiver-coerce oracle, is simulated as \((\mathsf{crs}',\pi _2)\leftarrow \mathsf{NIZK}.\mathsf{Sim}(1^\lambda , \exists z,c,x,r_3,r_4 : \mathsf{ct}_3 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_3,(z,c,x);r_3) \wedge \mathsf{ct}_4 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_4,(z,c,x);r_4) \wedge f(z)=t) \). Notice that the \(\mathsf{crs}\) of the secret keys generated by \(\mathcal {O}_1\) and \(\mathcal {O}_2\) are not simulated. The indistinguishability of \(H_2\) from \(H_1\) follows from the ZK property of the NIZK system and by a standard hybrid argument.
Hybrid \({\varvec{H}}_\mathbf{3}\) . It is identical to \(H_2\) except that \(\mathsf{ct}_2^\star \) encrypts y. The NIZK’s are still simulated. The indistinguishability of \(H_3\) from \(H_2\) follows from the IND-CPA security of \((\mathsf{pk}_2,\mathsf{sk}_2)\).
Hybrid \({\varvec{H}}_\mathbf{4}\) . It is identical to \(H_3\) except that \(\mathsf{ct}_4\), generated by the receiver-coerce oracle, encrypts \((0^k,\mathsf{Ct}^\star ,x)\). The NIZK’s are still simulated. The indistinguishability of \(H_4\) from \(H_3\) follows from the IND-CPA security of \((\mathsf{pk}_4,\mathsf{sk}_4)\).
Hybrid \({\varvec{H}}_\mathbf{5}\) . It is identical to \(H_4\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{1,4}\). The indistinguishability of \(H_5\) from \(H_4\) follows from the security of \(\mathsf{di}\mathcal{O}\) noticing that \(\mathsf{Trap}_{1,3}\) and \(\mathsf{Trap}_{1,4}\) compute the same function. This follows: (1) by the statistical simulation-soundness of the NIZK system that guarantees that \(\mathsf{Ct}'\), as generated by the receiver-coerce oracle, used in both experiments, is the only one to contain a NIZK proof for a false statement accepted by the verifier and (2) by the fact that by definition of \(\mathsf{Trap}_{1,3}\), \(\mathsf{Trap}_{1,4}\) and \(\mathsf{Ct}'\), it holds that: \(\mathsf{Trap}_{1,3}(\mathsf{Ct}^\star ,\mathsf{Ct}')=C({\mathcal {E}}.\mathsf{Dec}(\mathsf{sk}_1,\mathsf{ct}_1))=C(x)=C({\mathcal {E}}.\mathsf{Dec}(\mathsf{sk}_4,\mathsf{ct}_4))=\mathsf{Trap}_{1,4}(\mathsf{Ct}^\star ,\mathsf{Ct}')\).
Hybrid \({\varvec{H}}_\mathbf{6}\) . It is identical to \(H_5\) except that the secret keys, generated by \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{1,4}\). The indistinguishability of \(H_6\) from \(H_5\) follows from the security of \(\mathsf{di}\mathcal{O}\) noticing that \(\mathsf{Trap}_{1,3}\) and \(\mathsf{Trap}_{1,4}\) compute the same function. The statistical simulation-soundness of the NIZK system guarantees that there is no \(\mathsf{Ct}'\) for a false statement that the verifier accepts.
Hybrid \({\varvec{H}}_\mathbf{7}\) . It is identical to \(H_6\) except that \(\mathsf{ct}_3\), generated by the receiver-coerce oracle, encrypts \((0^k,\mathsf{Ct}^\star ,x)\). The NIZK’s are still simulated. The indistinguishability of \(H_7\) from \(H_6\) follows from the IND-CPA security of \((\mathsf{pk}_3,\mathsf{sk}_3)\).
Hybrid \({\varvec{H}}_\mathbf{8}\) . It is identical to \(H_7\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{1,3}\). The indistinguishability of \(H_8\) from \(H_7\) is symmetrical to that of \(H_5\) from \(H_4\).
Hybrid \({\varvec{H}}_\mathbf{9}\) . It is identical to \(H_8\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,3}\).
Overview: by the statistical simulation-soundness of the NIZK proof system and by definition of \(\mathsf{Trap}_{2,3}\), the inputs that distinguish \(\mathsf{Trap}_{2,3}\) from \(\mathsf{Trap}_{1,3}\) have the form \((\mathsf{Ct}^\star ,\hat{\mathsf{Ct}})\) where: (1) \(\hat{\mathsf{Ct}}=(\hat{\mathsf{ct}}_3,\hat{\mathsf{ct}}_4,\hat{\pi }_2)\ne \mathsf{Ct}'\). (2) \(\hat{\mathsf{ct}}_3\) and \(\hat{\mathsf{ct}}_4\) encrypt the same value (this follows by the statistical simulation-soundness of the NIZK system and from the fact that, being \(\mathsf{Ct}'\) the only false statement with accepting proof, it must hold that \(\hat{\mathsf{Ct}}\ne \mathsf{Ct}'\)), and (3) \(\hat{\mathsf{ct}}_3\) encrypts a string of the form \((z',c',x')\) with \(f(z')=t\).
To prove the indistinguishability of \(H_8\) from \(H_7\), we proceed in two steps: Let \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\) be any multi-distributional receiver deniability adversary, in the first step we show that there exists a sampling algorithm \(\mathsf{Sampler}^\mathcal {A}\) that samples a circuit family \(\mathcal {C}\) (containing \(\mathsf{Trap}_{2,3}\) and \(\mathsf{Trap}_{1,3}\)), that it is differing-inputs under the one-wayness of f. In the second step, we show that if \(\mathcal {A}\) can distinguish the two experiments, then it is possible to construct a distinguisher that breaks the security of \(\mathsf{di}\mathcal{O}\).
First Step: We define a circuit family \(\mathcal {C}\) associated with a PPT \(\mathsf{Sampler}^\mathcal {A}\) and show that it is differing-inputs under the one-wayness of f. \(\mathsf{Sampler}^\mathcal {A}\) takes in input the security parameter, the description of the OWF f and the challenge of the one-way security game \(t^\star \), and does the following:
-
1.
Runs \(\mathcal {A}_0\) on input \(1^\lambda \) to obtain \((x^\star ,y^\star ,\mathtt{st}_\mathcal {A})\).
-
2.
Computes, for \(i\in [4]\), \((\mathsf{pk}_i,\mathsf{sk}_i)\leftarrow {\mathcal {E}}.\mathsf{Setup}(1^\lambda )\), and \( \mathsf{ct}_1^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_1,x^\star ) \text { and } \mathsf{ct}_2^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_1,y^\star ) \) and \((\mathsf{crs},\pi _1^\star )\leftarrow \mathsf{NIZK}.\mathsf{Sim}(1^\lambda , \exists x,r_1,r_2 : \mathsf{ct}_1^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_1,x;r_1) \text { and } \mathsf{ct}_2^\star = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_2,x;r_2)) \). Sets the master public key and the challenge ciphertext as \( \mathsf{Mpk}=((\mathsf{pk}_i)_{i\in [4]},f,\mathsf{crs})\), \(\mathsf{Ct}^\star =(\mathsf{ct}_1^\star ,\mathsf{ct}_2^\star ,\pi _1^\star )\). The master secret key is then \(\mathsf{Msk}=(\mathsf{sk}_i)\).
Finally, runs \(\mathcal {A}_1\) on input \((\mathsf{Mpk}, \mathsf{Ct}^\star , \mathtt{st}_\mathcal {A})\), simulating oracles \(\mathcal {O}_1,\mathcal {O}_2\) and \(\mathcal {K}(\cdot ,\mathsf{Ct}^\star , x^\star )\) in the following way:
-
1.
\(\mathcal {O}_1(k,x,y), \mathcal {O}_2(k,x,y)\): Given \(\mathsf{Mpk}\) and \(\mathsf{Msk}\), the output distributions of these oracles is easy to generate.
-
2.
\(\mathcal {K}(C,\mathsf{Ct}^\star , x^\star )\): \(\mathsf{Sampler}^\mathcal {A}\) computes \( \mathsf{ct}_3 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_3,(0^\lambda ,\mathsf{Ct}^\star ,x^\star )) \) and \(\mathsf{ct}_4 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_4,(0^\lambda ,\mathsf{Ct}^\star ,x^\star ))\), and \((\mathsf{crs}',\pi _2)\leftarrow \mathsf{NIZK}.\mathsf{Sim}( \exists z, c,x,r_3,r_4 : \mathsf{ct}_3 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_3,(z,c,x);r_3) \text { and } \mathsf{ct}_4 = {\mathcal {E}}.\mathsf{Enc}(\mathsf{pk}_4,(z,c,x);r_4) \text{ and } f(z)=t^\star )\). At this point the algorithm interrupts the execution of \(\mathcal {A}\) and returns \((\mathsf{Trap}_{1,3}[C,\mathsf{crs},\mathsf{crs}',\mathsf{sk}_1,\mathsf{sk}_3,f,t],\mathsf{Trap}_{2,3}[C,\mathsf{crs},\mathsf{crs}',\mathsf{sk}_2,\mathsf{sk}_3,f,t],\mathtt{st})\), where \(\mathtt{st}\) contains its entire computation.
-
1.
This terminates the description of \(\mathsf{Sampler}^\mathcal {A}\). Now, suppose there exists an adversary \(\mathcal {B}\) that takes in input \((1^\lambda ,\mathsf{Trap}_{1,3},\mathsf{Trap}_{2,3},\mathtt{st})\) and finds an input on which \(\mathsf{Trap}_{1,3},\mathsf{Trap}_{2,3}\) are different, meaning \(\mathcal {B}\) finds a \(\hat{\mathsf{Ct}}=(\hat{\mathsf{ct}}_3,\hat{\mathsf{ct}}_4,\hat{\pi }_2)\) as defined above. Then, by using \(\mathsf{sk}_3\) in \(\mathtt{st}\), \(\mathcal {B}\) can decrypt \(\hat{\mathsf{ct}}_3\) and extract a pre-image of \(t^\star \).
Second Step: Suppose that \(\mathcal {A}\) distinguishes \(H_9\) and \(H_8\) with non-negligible advantage then we can construct a distinguisher \(\mathcal{D}^\mathcal {A}\), for the differing-input circuit family defined above, that breaks the security of \(\mathsf{di}\mathcal{O}\). The distinguisher \(\mathcal{D}^\mathcal {A}\) taks in \((C,\mathtt{st})\) where C is the differing-input obfuscation of either \(\mathsf{Trap}_{1,3}\) or \(\mathsf{Trap}_{2,3}\) and does the following: (1) Restart from the position where \(\mathsf{Sampler}^\mathcal {A}\) stopped and uses C to generate the output of the receiver-coerce oracle. Specifically, \(\mathcal{D}\) returns \((C,t^\star ,\mathsf{Ct}')\), where \(\mathsf{Ct}'=(\mathsf{ct}_3,\mathsf{ct}_4,\pi _2)\). (2) \(\mathcal{D}\) continues to respond to the oracle invocations as \(\mathsf{Sampler}^\mathcal {A}\) does. (3) Finally, when \(\mathcal {A}\) has completed its execution, it returns a bit that become \(\mathcal{D}\)’s output.
This terminates the description of \(\mathcal{D}^\mathcal {A}\). Now, if C is the differing-input obfuscation of \(\mathsf{Trap}_{1,3}\) then \((\mathsf{Sampler}^\mathcal {A},\mathcal{D}^\mathcal {A})\) have simulated \(H_8\). On the other hand, if C is the differing-input obfuscation of \(\mathsf{Trap}_{2,3}\) then \((\mathsf{Sampler}^\mathcal {A},\mathcal{D}^\mathcal {A})\) have simulated \(H_9\).
Hybrid \({\varvec{H}}_\mathbf{10}\) . It is identical to \(H_9\) except that the secret keys, generated by the \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,4}\). The indistinguishability of \(H_{10}\) from \(H_9\) follows from the security of \(\mathsf{di}\mathcal{O}\) noticing that \(\mathsf{Trap}_{1,4}\) and \(\mathsf{Trap}_{2,4}\) compute the same function. The statistical simulation-soundness of the NIZK system guarantees that there is no \(\mathsf{Ct}\) for a false statement that the verifier accepts. Moreover when considering \(\mathsf{Ct}^\star \), the security game constraints guarantee that the secret keys asked to \(\mathcal {O}_1\) and \(\mathcal {O}_2\) evaluate to the same value on the challenge messages.
Hybrid \({\varvec{H}}_\mathbf{11}\) . It is identical to \(H_{10}\) except that \(\mathsf{ct}_1^\star \) encrypts y, The indistinguishability of \(H_{11}\) from \(H_{10}\) follows from the IND-CPA security of \((\mathsf{pk}_1,\mathsf{sk}_1)\).
Hybrid \({\varvec{H}}_\mathbf{12}\) . It is identical to \(H_{11}\) except that the secret keys, generated by the \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,3}\). The indistinguishability of \(H_{12}\) from \(H_{11}\) is symmetrical to that of \(H_6\) from \(H_5\).
Hybrid \({\varvec{H}}_\mathbf{13}\) . It is identical to \(H_{12}\) except that \(\mathsf{ct}_4\), generated by the receiver-coerce oracle, encrypts \((z,\mathsf{Ct}^\star ,x)\), The indistinguishability of \(H_{13}\) from \(H_{12}\) follows from the IND-CPA security of \((\mathsf{pk}_4,\mathsf{sk}_4)\).
Hybrid \({\varvec{H}}_\mathbf{14}\) . It is identical to \(H_{13}\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,4}\). The indistinguishability of \(H_{14}\) from \(H_{13}\) is symmetrical to that of \(H_5\) from \(H_4\).
Hybrid \({\varvec{H}}_\mathbf{15}\) . It is identical to \(H_{14}\) except that the secret keys, generated by the \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,4}\). The indistinguishability of \(H_{15}\) from \(H_{14}\) is symmetrical to that of \(H_6\) from \(H_5\).
Hybrid \({\varvec{H}}_\mathbf{16}\) . It is identical to \(H_{15}\) except that \(\mathsf{ct}_3\), generated by the receiver-coerce oracle, encrypts \((z,\mathsf{Ct}^\star ,x)\). The indistinguishability of \(H_{16}\) from \(H_{15}\) follows from the IND-CPA security of \((\mathsf{pk}_3,\mathsf{sk}_3)\).
Hybrid \({\varvec{H}}_\mathbf{17}\) . It is identical to \(H_{16}\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,3}\). The indistinguishability of \(H_{17}\) from \(H_{16}\) is symmetrical to that of \(H_5\) from \(H_4\).
Hybrid \({\varvec{H}}_\mathbf{18}\) . It is identical to \(H_{17}\) except that the secret keys, generated by the receiver-coerce oracle, contain the differing-input obfuscation of the program \(\mathsf{Trap}_{1,3}\). The indistinguishability of \(H_{18}\) from \(H_{17}\) is symmetrical to that of \(H_5\) from \(H_4\).
Hybrid \({\varvec{H}}_\mathbf{19}\) . It is identical to \(H_{18}\) except that the secret keys, generated by the \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{2,3}\). The indistinguishability of \(H_{19}\) from \(H_{18}\) is symmetrical to that of \(H_6\) from \(H_5\).
Hybrid \({\varvec{H}}_\mathbf{20}\) . It is identical to \(H_{19}\) except that the secret keys, generated by the \(\mathcal {O}_1\) and \(\mathcal {O}_2\), contain the differing-input obfuscation of the program \(\mathsf{Trap}_{1,3}\). The indistinguishability of \(H_{20}\) from \(H_{19}\) is symmetrical to that of \(H_{10}\) from \(H_{9}\).
Hybrid \({\varvec{H}}_\mathbf{21}\) . It is identical to \(H_{20}\) except that all \(\mathsf{crs}\)’s are honestly generated. The indistinguishability of \(H_{21}\) from \(H_{20}\) follows from the zero-knowledge of the NIZK system and by a standard hybrid argument. It remains to notice that \(H_{21}\) corresponds to \(\mathsf{FakeDenExp}\) where the receiver-coerce oracle is \(\mathcal {K}_2\).
6 Open Problems and Future Work
References
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013)
Ananth, P., Boneh, D., Garg, S., Sahai, A., Zhandry, M.: Differing-inputs obfuscation and applications. Cryptology ePrint Archive, Report 2013/689 (2013). http://eprint.iacr.org/2013/689
Apon, D., Fan, X., Liu, F.: Bi-deniable inner product encryption from LWE. IACR Cryptology ePrint Archive 2015:993 (2015)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (Im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, p. 1. Springer, Heidelberg (2001)
Barbosa, M., Farshim, P.: On the semantic security of functional encryption schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 143–161. Springer, Heidelberg (2013)
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009)
Bellare, M., O’Neill, A.: Semantically-secure functional encryption: possibility results, impossibility results and the quest for a general definition. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 218–234. Springer, Heidelberg (2013)
Bendlin, R., Nielsen, J.B., Nordholt, P.S., Orlandi, C.: Lower and upper bounds for deniable public-key encryption. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 125–142. Springer, Heidelberg (2011)
Blundo, C., Iovino, V., Persiano, G.: Predicate encryption with partial public keys. In: Heng, S.-H., Wright, R.N., Goi, B.-M. (eds.) CANS 2010. LNCS, vol. 6467, pp. 298–313. Springer, Heidelberg (2010)
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004)
Boneh, D., Raghunathan, A., Segev, G.: Function-private identity-based encryption: hiding the function in functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 461–478. Springer, Heidelberg (2013)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011)
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014)
Canetti, R., Dwork, C., Naor, M., Ostrovsky, R.: Deniable encryption. In: Kaliski Jr., B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 90–104. Springer, Heidelberg (1997)
Canetti, R., Feige, U., Goldreich, O., Naor, M.: Adaptively secure multi-party computation. In: 28th Annual ACM Symposium on Theory of Computing, pp. 639–648. ACM Press, May 1996
Damgård, I.B., Nielsen, J.B.: Improved non-committing encryption schemes based on a general complexity assumption. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 432–450. Springer, Heidelberg (2000)
De Caro, A., Iovino, V., Jain, A., O’Neill, A., Paneth, O., Persiano, G.: On the achievability of simulation-based security for functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 519–535. Springer, Heidelberg (2013)
Dwork, C., Naor, M., Reingold, O., Stockmeyer, L.J.: Magic functions. In: 40th Annual Symposium on Foundations of Computer Science, pp. 523–534. IEEE Computer Society Press, October 1999
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual Symposium on Foundations of Computer Science, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Gentry, C., Halevi, S., Sahai, A., Waters, B.: Attribute-based encryption for circuits from multilinear maps. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 479–499. Springer, Heidelberg (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Fully secure attribute based encryption from multilinear maps. Cryptology ePrint Archive, Report 2014/622 (2014). http://eprint.iacr.org/2014/622
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th Annual ACM Symposium on Theory of Computing, pp. 545–554. ACM Press, June 2013
Iovino, V., Tang, Q., Żebrowski, K.: On the power of public-key functional encryption with function privacy. IACR Cryptology ePrint Archive 2015:470 (2015)
Iovino, V., Żebroski, K.: Simulation-based secure functional encryption in the random oracle model. In: Lauter, K., Rodríguez-Henríquez, F. (eds.) LatinCrypt 2015. LNCS, vol. 9230, pp. 21–39. Springer, Heidelberg (2015)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008)
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd Annual ACM Symposium on Theory of Computing, pp. 427–437. ACM Press, May 1990
Okamoto, T., Takashima, K.: Adaptively attribute-hiding (Hierarchical) inner product encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 591–608. Springer, Heidelberg (2012)
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). http://eprint.iacr.org/
O’Neill, A., Peikert, C., Waters, B.: Bi-deniable public-key encryption. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 525–542. Springer, Heidelberg (2011)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, pp. 475–484. ACM Press, May/June 2014
Shen, E., Shi, E., Waters, B.: Predicate privacy in encryption systems. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 457–473. Springer, Heidelberg (2009)
Waters, B.: A punctured programming approach to adaptively secure functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 678–697. Springer, Heidelberg (2015)
Acknowledgments
Vincenzo Iovino is supported by the National Research Fund of Luxembourg and made part of this work while was at the University of Warsaw supported by the WELCOME/2010-4/2 grant founded within the framework of the EU Innovative Economy Operational Programme.
Angelo de Caro’s work was partly supported by the EU H2020 TREDISEC project, funded by the European Commission under grant agreement no. 644412.
We thank Anna Sorrentino and the anonymous reviewers for useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Simulation-Based Security for FE and Its Relation to Receiver-Deniability
Definition 17
[De Caro et al. [17] Simulation-Based Definition] A FE scheme \(\mathsf{FE}=(\mathsf{Setup}, \mathsf{KeyGen},\mathsf{Enc},\mathsf{Eval})\) for functionality F defined over (K, X) is \((q_1,\ell ,q_2)\)-simulation-secure (\((q_1,\ell ,q_2)\)-SIM-Secure, for short), where \(q_1 = q_1(\lambda ), \ell = \ell (\lambda ), q_2 = q_2(\lambda )\) are polynomials in the security parameter \(\lambda \) that are fixed a priori, if there exists a PPT simulator algorithm \(\mathsf{Sim}=(\mathsf{Sim}_0,\mathsf{Sim}_1)\) such that for all PPT adversary algorithms \(\mathcal{A}=(\mathcal{A}_0,\mathcal{A}_1)\), issuing at most \(q_1\) non-adaptive key queries, \(q_2\) adaptive key queries and output challenge message vector of length and most \(\ell \), the outputs of the following two experiments are computationally indistinguishable.

Here, the \((k_i)\)’s correspond to the key-generation queries of the adversary. Further, oracle \(\mathcal {O}(\cdot )\) is the second stage of the simulator, namely algorithm \(\mathsf{Sim}_1(\mathsf{Msk},\mathtt{st}',\cdot , \cdot )\). Algorithm \(\mathsf{Sim}_1\) receives as third argument a key \(k_j\) for which the adversary queries a secret key, and as fourth argument the output value \(F(k_j,\varvec{{x}})\). Further, note that the simulator algorithm \(\mathsf{Sim}_1\) is stateful in that after each invocation, it updates the state \(\mathtt{st}'\) which is carried over to its next invocation. (Notice that, in the case that a parameter is an unbounded polynomial we use the notation \(\mathsf{poly}\).)
\((n_c,n_k)\) -receiver-deniability \(\implies \) \((0,n_c,n_k)\) - SIM -Security.
Theorem 18
Suppose that \(\mathsf{RecDenFE}\) is a \((n_c,n_k)\)-receiver-deniable functional encryption scheme for functionality F defined over (K, X) then \(\mathsf{RecDenFE}\) is \((0,n_c,n_k)\)-SIM-Secure (Definition 17) as well.
Proof
We start by constructing the simulator required by the SIM-Security. \(\mathsf{Sim}=(\mathsf{Sim}_0,\mathsf{Sim}_1)\) is defined as follow. \(\mathsf{Sim}_0\) on input master public key \(\mathsf{Mpk}\), remember that non-adaptive key generation queries are not allowed in the setting we are considering, chooses random vector \(\varvec{{x}}^\star \) of \(n_c\) messages and, for \(i\in n_c\), generated ciphertext \(\mathsf{Ct}_i^\star =\mathsf{Enc}(\mathsf{Mpk},{x}^\star _i)\) and returns \(( \varvec{\mathsf{Ct}}^\star , \mathtt{st}=(\varvec{\mathsf{Ct}}^\star ))\). \(\mathsf{Sim}_1\) on input master secret key \(\mathsf{Msk}\), status \(\mathtt{st}'\), and tuple \((k,\mathsf{Sk}_C,F(k,\varvec{{x}})))\) does the following. \(\mathsf{Sim}_1\) invokes the receiver faking algorithm to generate the secret key for k, namely \(\mathsf{Sk}_k=\mathsf{RecFake}(\mathsf{Msk},k,\varvec{\mathsf{Ct}}^\star , F(k,\varvec{{x}}))\). Finally, \(\mathsf{Sim}_1\) returns \(\mathsf{Sk}_k\) as its own output.
Now, for the sake of contradiction, let \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\) and \(\mathcal{D}\) be an adversary and a distinguisher that break the \((0,n_c,n_k)\)-SIM-Security of \(\mathsf{RecDenFE}\), meaning that \((\mathcal {A},\mathcal{D})\) can distinguish between \(\mathsf{RealExp}\) and \(\mathsf{IdealExp}\). Then, we construct and adversary \(\mathcal {B}=(\mathcal {B}_0,\mathcal {B}_1)\) and distinguisher \(\mathcal{D}'\) that break the \((n_c,n_k)\)-receiver-deniable security of \(\mathsf{RecDenFE}\). Specifically, \(\mathcal {B}\) is defined as follows: \(\mathcal {B}_0\) on input master public key \(\mathsf{Mpk}\) runs \(\mathcal {A}_0\) on input \(\mathsf{Mpk}\). Notice that, \(\mathcal {A}_0\) does not issue any key generation query. At some point \(\mathcal {A}_0\) returns challenge messages \(\varvec{{x}}\) and status \(\mathtt{st}_\mathcal {A}\). \(\mathcal {B}_0\) chooses random messages \(\varvec{{x}}'\) and returns \((\varvec{{x}},\varvec{{x}}', \mathtt{st}=(\mathtt{st}_\mathcal {A}, \varvec{{x}}))\).
\(\mathcal {B}_1\) on input \(\varvec{\mathsf{Ct}}^\star \) and status \(\mathtt{st}\) (notice that in this case \(\varvec{r}_S\) is a zero-length vector) runs \(\mathcal {A}_1\) on input \(\varvec{\mathsf{Ct}}^\star \) and status \(\mathtt{st}_\mathcal {A}\). When \(\mathcal {A}_1\) issue a key-generation query for key k, \(\mathcal {B}\) invokes its \(\mathcal {O}^K\) oracle on input k, \(\varvec{\mathsf{Ct}}^\star \) and \(F(k,\varvec{{x}})\) to obtain \(\mathsf{Sk}_k\) that is given back to \(\mathcal {A}_1\). At some point \(A_1\) returns some output \(\alpha \) and \(\mathcal {B}_1\) returns \(\alpha \) as its own output.
On the other hand, the distinguisher \(\mathcal{D}'\) is exactly \(\mathcal{D}\).
Now notice that, if \(\mathcal {B}\) is playing the \(\mathsf{RealRecDenExp}\) experiment then \(\mathcal {A}\) is playing the \(\mathsf{RealExp}\). On the other side, if \(\mathcal {B}\) is playing the \(\mathsf{FakeRecDenExp}\) experiment then \(\mathcal {A}\) is playing the \(\mathsf{IdealExp}\). This concludes the proof.
B Proof of Security of Construction 11
In this section, we prove the following main theorems
Theorem 19
If \(\mathsf{FE}\) is IND-Secure, then \(\mathsf{RecDenFE}\) is IND-Secure as well.
The proof of Theorem 19 is straightforward and we omit it.
Theorem 20
If \(\mathsf{FE}\) is \((\mathsf{poly},1,\mathsf{poly})\)-IND-Secure then \(\mathsf{RecDenFE}\) is a \((n_c,\mathsf{poly})\)-receiver deniable in the sense of Definition 6, for any constant \(n_c\).
Proof
We prove security via a sequence of hybrid experiments. To do so, we will make use of the following simulation receiver faking algorithm.

We are now ready to describe the hybrids. The change between the presented hybrid and the previous will be denoted by boxing the modified parts.
Hybrid \({\varvec{H}}_\mathbf{1}\) : Consider the following two oracles:

Then, hybrid \(H_1\) is the real experiment \(\mathsf{RealDenExp}\) where the challenge ciphertexts are created by oracle \(\mathcal {E}^\star _1\), and the receiver-coerce oracle is \(\mathcal {K}^\star _1\).
Notice that \(\mathcal {E}^\star _1\) is exactly \(\mathcal {E}_1\) with the only difference that we have unrolled the call to the \(\mathsf{RecDenFE}\) encryption algorithm for the sake of clarity, and \(\mathcal {K}^\star _1=\mathcal {K}_1\).
Hybrid \({\varvec{H}}_\mathbf{2}\) : Consider the following oracles:

where \(\mathbf{s}'=(s'_1,\ldots ,s'_{n_c})\) is the randomness sampled by \(\mathcal {E}^\star _2\).
Then, experiment \(H_2\) is the same as \(H_1\) except that the oracle \(\mathcal {E}^\star _1\) is replaced by \(\mathcal {E}^\star _2\) and receiver-coerce oracle is modified as above.
Hybrid \({\varvec{H}}_\mathbf{3}\) : Consider the following oracles:

Then, experiment \(H_3\) is the same as \(H_2\) except that the oracle \(\mathcal {E}^\star _2\) is replaced by \(\mathcal {E}^\star _3\) and receiver-coerce oracle is modified as above.
Finally, notice that \(H_3\) is exactly the faking experiment FakeDenExp where \(\mathcal {E}_2=\mathcal {E}^\star _3\) and \(\mathcal {K}_2=\mathcal {K}^\star _3\).
We now show that the relevant distinguishing probabilities between adjacent hybrids are negligible, which completes the proof.
Indistinguishability of \({\varvec{H}}_\mathbf{1}\) and \({\varvec{H}}_\mathbf{2}\) : To prove indistinguishability we use the following sequence of hybrid experiments.
-
Hybrid \(H_{1,j}\), for \(1\le j \le n_c+1\): This is the same as \(H_1\) except that \(\mathcal {E}^\star _2\) is used instead of \(\mathcal {E}^\star _1\) and the following new receiver-coercer oracle is used:
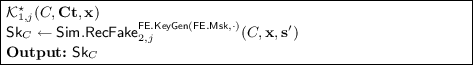
where \(\mathbf{s}'\) is chosen by oracle \(\mathcal {E}^\star _1\) and \(\mathsf{Sim}.\mathsf{RecFake}_2\) is defined as follow:

Then, notice that \(H_1=H_{1,1}\) and \(H_2=H_{1,n_c+1}\). Thus, it is sufficient to prove that \(H_{1,k}\) is computational indistinguishable from \(H_{1,k+1}\). This can be reduced to the security of the family of pseudo-random functions. In fact, notice that \(H_{1,k+1}\) is the same as \(H_{1,k}\) except that to set \(z_k\) (or \(z_k'\) deeding on \(C(x_k)\)), the PRF is used on input seed \(s_k'\) which is never used in any other part of the simulation.
More formally, suppose there exists a distinguisher \(\mathcal{D}\) and adversary \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\) for which \(H_{1,k}\) and \(H_{1,k+1}\) are not computationally indistinguishable. Then \(\mathcal {A}\) and \(\mathcal{D}\) can be used to construct a successful adversary \(\mathcal{B}\) for the pseudo-randomness of \(\mathcal {F}\).
Specifically, \(\mathcal{B}\) on input the security parameter \(\lambda \) an having oracle access to a function \(\hat{f}\) which is either \(f_s\) for random seed \(s\leftarrow \{0,1\}^\lambda \) or \(F \leftarrow \mathcal{R}(l(\lambda ),L(\lambda ))\) where \(\mathcal{R}(l(\lambda ),L(\lambda ))\) is the space of all possible functions \(F:\{0,1\}^{l(\lambda )}\rightarrow \{0,1\}^{L(\lambda )}\), does the following.
-
\(\mathcal{B}\), generates \((\mathsf{Mpk},\mathsf{Msk})\) by invoking the setup algorithm of \(\mathsf{FE}\). \(\mathcal {B}\) runs \(\mathcal {A}_0\) on input master public key \(\mathsf{Mpk}\) and answers \(\mathcal {A}_0\)’s queries to \(\mathcal {O}_1\) and \(\mathcal {O}_2\) by using \((\mathsf{Mpk},\mathsf{Msk})\). Eventually, \(\mathcal {A}_0\) outputs \(\mathbf{x}^\star =(x^\star _1,\ldots ,x^\star _{n_c}), \mathbf{y}^\star =(y^\star _1,\ldots ,y^\star _{n_c})\) and its state \(\mathtt{st}\). Then \(\mathcal {B}\), generates the challenge ciphertexts \(\mathsf{Ct}^\star _1,\ldots ,\mathsf{Ct}^\star _{n_c}\) by using \(\mathsf{Mpk}\), encrypting \(\mathbf{x}\) or \(\mathbf{y}\) depending on a chosen random bit b. Finally, \(\mathcal {B}\) runs \(\mathcal {A}_1\) on input challenge ciphertexts \(\mathsf{Ct}^\star _1,\ldots ,\mathsf{Ct}^\star _{n_c}\) and answers \(\mathcal {A}_1\)’s queries to \(\mathcal {O}_1\) and \(\mathcal {O}_2\) by using \((\mathsf{Mpk},\mathsf{Msk})\). To answer receiver-coerce oracle queries, \(\mathcal {B}\) first chooses \((s_i'\leftarrow \{0,1\}^\lambda )_{i\in [n_c]\setminus \{k\}}\), then on input a receiver-coerce query of the form \((C,\mathbf{Ct},\mathbf{x})\), where \(\mathbf{x}=(x_1,\ldots ,x_{n_c})\), \(\mathcal {B}\) does the following: For each \(i\in [n_c]\setminus \{k\}\), \(\mathcal {B}\) chooses random \(t_i\) and \(t'_i\) in \(\{0,1\}^{l(\lambda )}\). Then,
-
1.
\(i<k\): \(\mathcal {B}\) distinguishes between the following two cases: (a) If \(C({x}_i)=1\), it sets \(z_i=f_{s_i'}(t_i)\) and chooses random \(z'_i\in \{0,1\}^{L(\lambda )}\). (b) If \(C({x}_i)=0\), it sets \(z'_i=f_{s_i'}(t'_i)\) and chooses random \(z_i\in \{0,1\}^{L(\lambda )}\).
-
2.
\(i=k\): \(\mathcal {B}\) uses its own oracle \(\hat{f}\) as follows:
-
If \(C({x}_i)=1\), it sets \(z_i=\hat{f}(t_i)\) and chooses random \(z'_i\in \{0,1\}^{L(\lambda )}\).
-
If \(C({x}_i)=0\), it sets \(z'_i=\hat{f}(t'_i)\) and chooses random \(z_i\in \{0,1\}^{L(\lambda )}\).
-
-
3.
\(i\ge k\): \(\mathcal {B}\) chooses random \(z_i, z'_i\in \{0,1\}^{L(\lambda )}\).
Finally, \(\mathcal {B}\) computes \(\mathsf{FE}.\mathsf{Sk}_C= \mathsf{FE}.\mathsf{KeyGen}(\mathsf{FE}.\mathsf{Msk},\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'})\), and returns secret key \(\mathsf{Sk}_C=(\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}',\mathsf{FE}.\mathsf{Sk}_C)\) as the answer of oracle \(\mathcal {E}^\star _1\). Eventually, \(\mathcal {A}_1\) returns its output and \(\mathcal {B}\) passes it to the distinguisher \(\mathcal{D}\) and returns \(\mathcal{D}\)’s output as its own output.
-
1.
Now notice that if \(\hat{f}=F\) then \(\mathcal {B}\) is simulating Game \(H_{1,k}\). On the other hand, if \(\hat{f}=f_s\) then \(\mathcal {B}\) is simulating Game \(H_{1,k+1}\)
Indistinguishability of \({\varvec{H}}_\mathbf{2}\) and \({\varvec{H}}_\mathbf{3}\) : To prove indistinguishability we use the following sequence of hybrid experiments.
-
Hybrid \(H_{2,j}\), for \(1\le j \le n_c+1\): This is the same as \(H_2\) except that the following new oracle \(\mathcal {E}^\star _{2,j}\) is used:

Then, notice then that \(H_2=H_{2,1}\) and \(H_3=H_{2,n_c+1}\). Thus, it is sufficient to prove that \(H_{2,k}\) is computational indistinguishable from \(H_{2,k+1}\). This follows from the assumed IND-Security of \(\mathsf{FE}\). In fact, notice that \(H_{2,k+1}\) is the same as \(H_{2,k}\) except that the k-th challenge ciphertext is for message \((y_k,s_k')\) instead of \((x_k,s_k)\). Moreover, notice that for all the faked secret keys generated using the algorithm \(\mathsf{Sim}.\mathsf{RecFake}_{2,n_c+1}\) it holds than \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}(x_k,s_k)=C(x_k)=\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}(y_k,s_k')\).
More formally, suppose there exists a distinguisher \(\mathcal{D}\) and adversary \(\mathcal {A}=(\mathcal {A}_0,\mathcal {A}_1)\) for which \(H_{2,k}\) and \(H_{2,k+1}\) are not computationally indistinguishable. Then \(\mathcal {A}\) and \(\mathcal{D}\) can be used to construct a successful \(\mathsf{IND}\) adversary \(\mathcal{B}\) for \(\mathsf{FE}\). Specifically, \(\mathcal{B}= (\mathcal{B}_0,\mathcal{B}_1)\) does the following.
-
\(\mathcal{B}_0\) on input \(\mathsf{FE}\) master public key \(\mathsf{Mpk}\) and having oracle access to the \(\mathsf{FE}\) key generation algorithm, runs \(\mathcal {A}_0\) on input master public key \(\mathsf{Mpk}\) and answers \(\mathcal {A}_0\)’s queries to \(\mathcal {O}_1\) and \(\mathcal {O}_2\) by using \(\mathsf{Mpk}\) and its key generation oracle. Eventually, \(\mathcal {A}_0\) outputs \(\mathbf{x}^\star =(x^\star _1,\ldots ,x^\star _{n_c}), \mathbf{y}^\star =(y^\star _1,\ldots ,y^\star _{n_c})\) and its state \(\mathtt{st}\). Them \(\mathcal {B}_0\), chooses \((s_i\leftarrow \{0,1\}^\lambda )_{i\in [n_c]}\) and \((s_i'\leftarrow \{0,1\}^\lambda )_{i\in [n_c]}\), and returns as its challenge messages \((y^\star _k,s_k')\) and \((x^\star _k,s_k)\) and put in its state the state of \(\mathcal {A}_0\) and its entire computation.
-
\(\mathcal {B}_1\) on input ciphertext \(\mathsf{Ct}^\star \), which is the encryption of \((y^\star _k,s_k')\) or \((x^\star _k,s_k)\), and having oracle access to the \(\mathsf{FE}\) key generation algorithm, generates challenge ciphertexts in the following way: For \(j<k\), \(\mathcal {B}_1\) sets \(\mathsf{Ct}^\star _j=\mathsf{Encrypt}(\mathsf{Mpk},(y_j^\star ,s_j'))\), for \(j>k\), \(\mathcal {B}_1\) sets \(\mathsf{Ct}^\star _j=\mathsf{Encrypt}(\mathsf{Mpk},(x_j^\star ,s_j))\), and for \(j=k\), \(\mathcal {B}_0\) set \(\mathsf{Ct}^\star _k=\mathsf{Ct}^\star \). Finally, \(\mathcal {B}_1\) runs \(\mathcal {A}_1\) on input challenge ciphertexts \(\mathsf{Ct}^\star _1,\ldots ,\mathsf{Ct}^\star _{n_c}\) and answers \(\mathcal {A}_1\)’s queries to \(\mathcal {O}_1\) and \(\mathcal {O}_2\) and to the receiver-coerce oracle \(\mathcal {K}\), which is implemented at this stage by \(\mathsf{Sim}.\mathsf{RecFake}_{2,n_c+1}\), by using \(\mathsf{Mpk}\) and its own key generation oracle. Eventually, \(\mathcal {A}_1\) returns its output and \(\mathcal {B}_1\) passes it to the distinguisher \(\mathcal{D}\) and returns \(\mathcal{D}\)’s output as its own output.
It remains to verify that \(\mathcal {B}\) is valid IND adversary, meaning that all the key queries issued by \(\mathcal {B}\) satisfy the game constraints with the respect to the challenge messages \((y^\star _k,s_k')\) and \((x^\star _k,s_k)\). We have the following two cases: (1) For query made by \(\mathcal {A}\) to \(\mathcal {O}_1\) or \(\mathcal {O}_2\) of the form (C, x, y), \(\mathcal {B}\) generates a ciphertext with the respect to a freshly chosen seed \(\hat{s}\) and issues a secret key query to its oracle for circuit \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}\), where \(\mathbf{z}\) and \(\mathbf{z}'\) are related to \(\hat{s}\) It holds then, under the constraints of the receiver deniable security game, \(C(y^\star _k)=C(x^\star _k)\) then with overwhelming probability \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}((y^\star _k,s_k'))= C(y^\star _k)=C(x^\star _k) =\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}((x^\star _k,s_k))\), by definition of the trapdoor circuit and by noting that \(s_k,s_k',\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'\) are uncorrelated. (2) For a query issued to the receiver-coerce oracle for a circuit C, the corresponding secret key is generated by the algorithm \(\mathsf{Sim}.\mathsf{RecFake}_{2,n_c+1}\). By definition of this algorithm it holds that \(\mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}(x_k^\star ,s_k)=C(x_k)= \mathsf{Trap}[C,\mathcal {F}]^{\mathbf{t},\mathbf{z},\mathbf{t}',\mathbf{z}'}(y_k^\star ,s_k')\). This concludes the proof.
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
De Caro, A., Iovino, V., O’Neill, A. (2016). Deniable Functional Encryption. In: Cheng, CM., Chung, KM., Persiano, G., Yang, BY. (eds) Public-Key Cryptography – PKC 2016. Lecture Notes in Computer Science(), vol 9614. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49384-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-662-49384-7_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49383-0
Online ISBN: 978-3-662-49384-7
eBook Packages: Computer ScienceComputer Science (R0)