Abstract
We initiate the study of cryptography for parallel RAM (PRAM) programs. The PRAM model captures modern multi-core architectures and cluster computing models, where several processors execute in parallel and make accesses to shared memory, and provides the “best of both” circuit and RAM models, supporting both cheap random access and parallelism.
We propose and attain the notion of Oblivious PRAM. We present a compiler taking any PRAM into one whose distribution of memory accesses is statistically independent of the data (with negligible error), while only incurring a polylogarithmic slowdown (in both total and parallel complexity). We discuss applications of such a compiler, building upon recent advances relying on Oblivious (sequential) RAM (Goldreich Ostrovsky JACM’12). In particular, we demonstrate the construction of a garbled PRAM compiler based on an OPRAM compiler and secure identity-based encryption.
E. Boyle—The research of the first author has received funding from the European Union’s Tenth Framework Programme (FP10/ 2010-2016) under grant agreement no. 259426 ERC-CaC, and ISF grant 1709/14. Supported by the ERC under the EU’s Seventh Framework Programme (FP/2007-2013) ERC Grant Agreement n. 307952.
K.-M. Chung—supported in part by Ministry of Science and Technology, Taiwan, under Grant no. MOST 103-2221-E-001-022-MY3.
R. Pass—Work supported in part by a Microsoft Faculty Fellowship, Google Faculty Award, NSF Award CNS-1217821, NSF Award CCF-1214844, AFOSR Award FA9550-15-1-0262 and DARPA and AFRL under contract FA8750-11-2-0211. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Defense Advanced Research Projects Agency or the US Government.
R. Pass—This work was done in part while the authors were visiting the Simons Institute for the Theory of Computing, supported by the Simons Foundation and by the DIMACS/Simons Collaboration in Cryptography through NSF grant #CNS-1523467.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Completeness results in cryptography provide general transformations from arbitrary functionalities described in a particular computational model, to solutions for executing the functionality securely within a desired adversarial model. Classic results, stemming from [Yao82, GMW87], modeled computation as boolean circuits, and showed how to emulate the circuit securely gate by gate.
As the complexity of modern computing tasks scales at tremendous rates, it has become clear that the circuit model is not appropriate: Converting “lightweight,” optimized programs first into a circuit in order to obtain security is not a viable option. Large effort has recently been focused on enabling direct support of functionalities modeled as Turing machines or random-access machines (RAM) (e.g., [OS97, GKK+12, LO13, GKP+13, GHRW14, GHL+14, GLOS15, CHJV15, BGL+15, KLW15]). This approach avoids several sources of expensive overhead in converting modern programs into circuit representations. However, it actually introduces a different dimension of inefficiency. RAM (and single-tape Turing) machines do not support parallelism: thus, even if an insecure program can be heavily parallelized, its secure version will be inherently sequential.
Modern computing architectures are better captured by the notion of a Parallel RAM (PRAM). In the PRAM model of computation, several (polynomially many) CPUs are simultaneously running, accessing the same shared “external” memory. Note that PRAM CPUs can model physical processors within a single multicore system, as well as distinct computing entities within a distributed computing environment. We consider an expressive model where the number of active CPUs may vary over time (as long as the pattern of activation is fixed a priori). In this sense, PRAMs capture the “best of both” RAM and the circuit models: A RAM program handles random access but is entirely sequential, circuits handle parallelism with variable number of parallel resources (i.e., the circuit width), but not random access; variable CPU PRAMs capture both random access and variable parallel resources. We thus put forth the challenge of designing cryptographic primitives that directly support PRAM computations, while preserving computational resources (total computational complexity and parallel time) up to poly logarithmic, while using the same number of parallel processors.
Oblivious Parallel RAM (OPRAM). A core step toward this goal is to ensure that secret information is not leaked via the memory access patterns of the resulting program execution.
A machine is said to be memory oblivious, or simply oblivious, if the sequences of memory accesses made by the machine on two inputs with the same running time are identically (or close to identically) distributed. In the late 1970s, Pippenger and Fischer [PF79] showed that any Turing Machine \(\varPi \) can be compiled into an oblivious one \(\varPi '\) (where “memory accesses” correspond to the movement of the head on the tape) with only a logarithmic slowdown in running-time. Roughly ten years later, Goldreich and Ostrovsky [Gol87, GO96] proposed the notion of Oblivious RAM (ORAM), and showed a similar transformation result with polylogarithmic slowdown. In recent years, ORAM compilers have become a central tool in developing cryptography for RAM programs, and a great deal of research has gone toward improving both the asymptotic and concrete efficiency of ORAM compilers (e.g., [Ajt10, DMN11, GMOT11, KLO12, CP13, CLP14, GGH+13, SvDS+13, CLP14, WHC+14, RFK+14, WCS14]). However, for all such compilers, the resulting program is inherently sequential.
In this work, we propose the notion of Oblivious Parallel RAM (OPRAM). We present the first OPRAM compiler, converting any PRAM into an oblivious PRAM, while only inducing a polylogarithmic slowdown to both the total and parallel complexities of the program.
Theorem 1
(OPRAM – Informally Stated). There exists an OPRAM compiler with \(O(\log (m) \log ^3(n))\) worst-case overhead in total and parallel computation, and f(n) memory overhead for any \(f \in \omega (1)\), where n is the memory size and m is an upper-bound on the number of CPUs in the PRAM.
We emphasize that applying even the most highly optimized ORAM compiler to an m-processor PRAM program inherently inflicts \(\varOmega (m \log (n))\) overhead in the parallel runtime, in comparison to our \(O(\log (m) \mathsf{polylog}(n))\). When restricted to single-CPU programs, our construction incurs slightly greater logarithmic overhead than the best optimized ORAM compilers (achieving \(O(\log n)\) overhead for optimal block sizes); we leave as an interesting open question how to optimize parameters. (As we will elaborate on shortly, some very interesting results towards addressing this has been obtained in the follow-up work of [CLT15].)
1.1 Applications of OPRAM
ORAM lies at the base of a wide range of applications. In many cases, we can directly replace the underlying ORAM with an OPRAM to enable parallelism within the corresponding secure application. For others, simply replacing ORAM with OPRAM does not suffice; nevertheless, in this paper, we demontrate one application (garbling of PRAM programs) where they can be overcome; follow-up works show further applications (secure computation and obfuscation).
Direct Applications of OPRAM. We briefly describe some direct applications of OPRAM.
-
Improved/Parallelized Outsourced Data. Standard ORAM has been shown to yield effective, practical solutions for securely outsourcing data storage to an untrusted server (e.g., the ObliviStore system of [SS13]). Efficient OPRAM compilers will enable these systems to support secure efficient parallel accesses to outsourced data. For example, OPRAM procedures securely aggregate parallel data requests and resolve conflicts client-side, minimizing expensive client-server communications (as was explored in [WST12], at a smaller scale). As network latency is a major bottleneck in ORAM implementations, such parallelization may yield significant improvements in efficiency.
-
Multi-client Outsourced Data. In a similar vein, use of OPRAM further enables secure access and manipulation of outsourced shared data by multiple (mutually trusting) clients. Here, each client can simply act as an independent CPU, and will execute the OPRAM-compiled program corresponding to the parallel concatenation of their independent tasks.
-
Secure Multi-processor Architecture. Much recent work has gone toward implementing secure hardware architectures by using ORAM to prevent information leakage via access patterns of the secure processor to the potentially insecure memory (e.g., the Ascend project of [FDD12]). Relying instead on OPRAM opens the door to achieving secure hardware in the multi-processor setting.
Garbled PRAM (GPRAM). Garbled circuits [Yao82] allow a user to convert a circuit C and input x into garbled versions \(\tilde{C}\) and \(\tilde{x}\), in such a way that \(\tilde{C}\) can be evaluated on \(\tilde{x}\) to reveal the output C(x), but without revealing further information on C or x. Garbling schemes have found countless applications in cryptography, ranging from delegation of computation to secure multi-party protocols (see below). It was recently shown (using ORAM) how to directly garble RAM programs [GHL+14, GLOS15], where the cost of evaluating a garbled program \(\tilde{P}\) scales with its RAM (and not circuit) complexity.
In the full version of this paper, we show how to employ any OPRAM compiler to attain a garbled PRAM (GPRAM), where the time to generate and evaluate the garbled PRAM program \(\tilde{P}\) scales with the parallel time complexity of P. Our construction is based on one of the construction of [GHL+14] and extends it using some of the techniques developed for our OPRAM. Plugging in our (unconditional) OPRAM construction, we obtain:
Theorem 2
(Garbled PRAM – Informally Stated). Assuming identity-based encryption, there exists a secure garbled PRAM scheme with total and parallel overhead \(\mathsf{poly}(\kappa ) \cdot \mathsf{polylog}(n)\), where \(\kappa \) is the security parameter of the IBE and n is the size of the garbled data.
Secure Two-Party and Multi-party Computation of PRAMs. Secure multi-party computation (MPC) enables mutually distrusting parties to jointly evaluate functions on their secret inputs, without revealing information on the inputs beyond the desired function output. ORAM has become a central tool in achieving efficient MPC protocols for securely evaluating RAM programs. By instead relying on OPRAM, these protocols can leverage parallelizability of the evaluated programs.
Our garbled PRAM construction mentioned above yields constant-round secure protocols where the time to execute the protocol scales with the parallel time of the program being evaluated. In a companion paper [BCP15], we further demonstrates how to use OPRAM to obtain efficient protocols for securely evaluating PRAMs in the multi-party setting; see [BCP15] for further details.
Obfuscation for PRAMs. In a follow-up work, Chen et al. [CCC+15] rely on our specific OPRAM construction (and show that it satisfies an additional “puncturability” property) to achieve obfuscation for PRAMs.
1.2 Technical Overview
Begin by considering the simplest idea toward memory obliviousness: Suppose data is stored in random(-looking) shuffled order, and for each data query i, the lookup is performed to its permuted location, \(\sigma (i)\). One can see this provides some level of hiding, but clearly does not suffice for general programs. The problem with the simple solution is in correlated lookups over time—as soon as item i is queried again, this collision will be directly revealed. Indeed, hiding correlated lookups while maintaining efficiency is perhaps the core challenge in building oblivious RAMs. In order to bypass this problem, ORAM compilers heavily depend on the ability of the CPU to move data around, and to update its secret state after each memory access.
However, in the parallel setting, we find ourselves back at square one. Suppose in some time step, a group of processors all wish to access data item i. Having all processors attempt to perform the lookup directly within a standard ORAM construction corresponds to running the ORAM several times without moving data or updating state. This immediately breaks security in all existing ORAM compiler constructions. On the other hand, we cannot afford for the CPUs to “take turns,” accessing and updating the data sequentially.
In this overview, we discuss our techniques for overcoming this and further challenges. We describe our solution somewhat abstractly, building on a sequential ORAM compiler with a tree-based structure as introduced by Shi et al. [SCSL11]. In our formal construction and analysis, we rely on the specific tree-based ORAM compiler of Chung and Pass [CP13] that enjoys a particularly clean description and analysis.
Tree-Based ORAM Compilers. We begin by roughly describing the structure of tree-based ORAMs, originating in the work of [SCSL11]. At a high level, data is stored in the structure of a binary tree, where each node of the tree corresponds to a fixed-size bucket that may hold a collection of data items. Each memory cell \(\mathsf{addr}\) in the original database is associated with a random path (equivalently, leaf) within a binary tree, as specified by a position map  .
.
The schemes maintain three invariants: (1) The content of memory cell \(\mathsf{addr}\) will be found in one of the buckets along the path  . (2) Given the view of the adversary (i.e., memory accesses) up to any point in time, the current mapping Pos appears uniformly random. And, (3) with overwhelming probability, no node in the binary tree will ever “overflow,” in the sense that its corresponding memory bucket is instructed to store more items than its fixed capacity.
. (2) Given the view of the adversary (i.e., memory accesses) up to any point in time, the current mapping Pos appears uniformly random. And, (3) with overwhelming probability, no node in the binary tree will ever “overflow,” in the sense that its corresponding memory bucket is instructed to store more items than its fixed capacity.
These invariants are maintained by the following general steps:
-
1.
Lookup: To access a memory item \(\mathsf{addr}\), the CPU accesses all buckets down the path
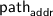 , and removes it where found.
, and removes it where found. -
2.
Data “put-back”: At the conclusion of the access, the memory item \(\mathsf{addr}\) is assigned a freshly random path
 , and is returned to the root node of the tree.
, and is returned to the root node of the tree. -
3.
Data flush: To ensure the root (and any other bucket) does not overflow, data is “flushed” down the tree via some procedure. For example, in [SCSL11], the flush takes place by selecting and emptying two random buckets from each level into their appropriate children; in [CP13], it takes place by choosing an independent path in the tree and pushing data items down this path as far as they will go (see Fig. 1 in Sect. 2.2).
Extending to Parallel RAMs. We must address the following problems with attempting to access a tree-based ORAM in parallel.
-
Parallel Memory Lookups: As discussed, a core challenge is in hiding correlations in parallel CPU accesses. In tree-based ORAMs, if CPUs access different data items in a time step, they will access different paths in the tree, whereas if they attempt to simultaneously access the same data item, they will each access the same path in the tree, blatantly revealing a collision.
To solve this problem, before each lookup we insert a CPU-coordination phase. We observe that in tree-based ORAM schemes, this problem only manifests when CPUs access exactly the same item, otherwise items are associated with independent leaf nodes, and there are no bad correlations. We thus resolve this issue by letting the CPUs check—through an oblivious aggregation operation—whether two (or more) of them wish to access the same data item; if so, a representative is selected (the CPU with the smallest id) to actually perform the memory access, and all the others merely perform “dummy” lookups. Finally, the representative CPU needs to communicate the read value back to all the other CPUs that wanted to access the same data item; this is done using an oblivious multi-cast operation.
The challenge is in doing so without introducing too much overhead—namely, allowing only (per-CPU) memory, computation, and parallel time polylogarithmic in both the database size and the number of CPUs—and that itself retains memory obliviousness.
-
Parallel “Put-backs”: After a memory cell is accessed, the (possibly updated) data is assigned a fresh random path and is reinserted to the tree structure. To maintain the required invariants, the item must be inserted somewhere along its new path, without revealing any information about the path. In tree-based ORAMs, this is done by reinserting at the root node of the tree. However, this single node can hold only a small bounded number of elements (corresponding to the fixed bucket size), whereas the number of processors m—each with an item to reinsert—may be significantly larger.
To overcome this problem, instead of returning data items to the root, we directly insert them into level \(\log m\) of the tree, while ensuring that they are placed into the correct bucket along their assigned path. Note that level \(\log m\) contains m buckets, and since the m items are each assigned to random leaves, each bucket will in expectation be assigned exactly 1 item.
The challenge in this step is specifying how the m CPUs can insert elements into the tree while maintaining memory obliviousness. For example, if each CPU simply inserts their own item into its assigned node, we immediately leak information about its destination leaf node. To resolve this issue, we have the CPUs obliviously route items between each other, so that eventually the ith CPU holds the items to be insert to the ith node, and all CPUs finally perform either a real or a dummy write to their corresponding node.
-
Preventing Overflows: To ensure that no new overflows are introduced after inserting m items, we now flush m times instead of once, and all these m flushes are done in parallel: each CPU simply performs an independent flush. These parallel flushes may lead to conflicts in nodes accessed (e.g., each flush operation will likely access the root node). As before, we resolve this issue by having the CPUs elect some representative to perform the appropriate operations for each accessed node; note, however, that this step is required only for correctness, and not for security.
Our construction takes a modular approach. We first specify and analyze our compiler within a simplified setting, where oblivious communication between CPUs is “for free.” We then show how to efficiently instantiate the required CPU communication procedures oblivious routing, oblivious aggregation, and oblivious multi-cast, and describe the final compiler making use of these procedures. In this extended abstract, we defer the first step to Appendix 3.1, and focus on the remaining steps.
1.3 Related Work
Restricted cases of parallelism in Oblivious RAM have appeared in a handful of prior works. It was observed by Williams, Sion, and Tomescu [WST12] in their PrivateFS work that existing ORAM compilers can support parallelization across data accesses up to the “size of the top level,”Footnote 1 (in particular, at most \(\log n\)), when coordinated through a central trusted entity. We remark that central coordination is not available in the PRAM model. Goodrich and Mitzenmacher [GM11] showed that parallel programs in MapReduce format can be made oblivious by simply replacing the “shuffle” phase (in which data items with a given key are routed to the corresponding CPU) with a fixed-topology sorting network. The goal of improving the parallel overhead of ORAM was studied by Lorch et al. [LPM+13], but does not support compilation of PRAMs without first sequentializing.
Follow-up Work. As mentioned above, our OPRAM compiler has been used in the recent works of Boyle, Chung, and Pass [BCP15] and Chen et al. [CCC+15] to obtain secure multi-party computation for PRAM, and indistinguishability obfuscation for PRAM, respectively. A different follow-up work by Nayak et al. [NWI+15] provides targeted optimizations and an implementation for secure computation of specific parallel tasks.
Very recently, an exciting follow-up work of Chen, Lin, and Tessaro [CLT15] builds upon our techniques to obtain two new construction: an OPRAM compiler whose overhead in expectation matches that of the best current sequential ORAM [SvDS+13]; and, a general transformation taking any generic ORAM compiler to an OPRAM compiler with \(\log n\) overhead in expectation. Their OPRAM constructions, however, only apply to the special case of PRAM with a fixed number of processors being activated at every step (whereas our notion of a PRAM requires handling also a variable number of processorsFootnote 2); for the case of variable CPU PRAMs, the results of [CLT15] incurr an additional multlicative overhead of m in terms of computational complexity, and thus the bounds obtained are incomparable.
2 Preliminaries
2.1 Parallel RAM (PRAM) Programs
We consider the most general case of Concurrent Read Concurrent Write (CRCW) PRAMs. An m-processor CRCW parallel random-access machine (PRAM) with memory size \(n\) consists of numbered processors \(CPU_1,\ldots ,CPU_m\), each with local memory registers of size \(\log n\), which operate synchronously in parallel and can make access to shared “external” memory of size \(n\).
A PRAM program \(\varPi \) (given \(m,n\), and some input x stored in shared memory) provides CPU-specific execution instructions, which can access the shared data via commands \(\mathsf{Access}(r,v)\), where \(r \in [n]\) is an index to a memory location, and v is a word (of size \(\log n\)) or \(\bot \). Each \(\mathsf{Access}(r,v)\) instruction is executed as:
-
1.
Read from shared memory cell address r; denote value by \(v_\mathsf{old}\).
-
2.
Write value \(v \ne \bot \) to address r (if \(v = \bot \), then take no action).
-
3.
Return \(v_\mathsf{old}\).
In the case that two or more processors simultaneously initiate \(\mathsf{Access}(r,v_i)\) with the same address r, then all requesting processors receive the previously existing memory value \(v_\mathsf{old}\), and the memory is rewritten with the value \(v_i\) corresponding to the lowest-numbered CPU i for which \(v_i \ne \bot \).
We more generally support PRAM programs with a dynamic number of processors (i.e., \(m_i\) processors required for each time step i of the computation), as long as this sequence of processor numbers \(m_1,m_2,\dots \) is public information. The complexity of our OPRAM solution will scale with the number of required processors in each round, instead of the maximum number of required processors.
The (parallel) time complexity of a PRAM program \(\varPi \) is the maximum number of time steps taken by any processor to evaluate \(\varPi \), where each \(\mathsf{Access}\) execution is charged as a single step. The PRAM complexity of a function f is defined as the minimal parallel time complexity of any PRAM program which evaluates f. We remark that the PRAM complexity of any function f is bounded above by its circuit depth complexity.
Remark 1
(CPU-to-CPU Communication). It will be sometimes convenient notationally to assume that CPUs may communicate directly amongst themselves. When the identities of sending and receiving CPUs is known a priori (which will always be the case in our constructions), such communication can be emulated in the standard PRAM model with constant overhead by communicating through memory. That is, each action “CPU1 sends message m to CPU2” is implemented in two time steps: First, CPU1 writes m into a special designated memory location \(\mathsf{addr}_{CPU1}\); in the following time step, CPU2 performs a read access to \(\mathsf{addr}_{CPU1}\) to learn the value m.
2.2 Tree-Based ORAM
Concretely, our solution relies on the ORAM due to Chung and Pass [CP13], which in turn closely follows the tree-based ORAM construction of Shi et al. [SCSL11]. We now recall the [CP13] construction in greater detail, in order to introduce notation for the remainder of the paper.
The [CP13] construction (as with [SCSL11]) proceeds by first presenting an intermediate solution achieving obliviousness, but in which the CPU must maintain a large number of registers (specifically, providing a means for securely storing \(n\) data items requiring CPU state size \(\tilde{\varTheta }(n/\alpha )\), where \(\alpha >1\) is any constant). Then, this solution is recursively applied \(\log _\alpha n\) times to store the resulting CPU state, until finally reaching a CPU state size \(\mathsf{polylog}(n)\), while only blowing up the computational overhead by a factor \(\log _\alpha n\). The overall compiler is fully specified by describing one level of this recursion.
Step 1: Basic ORAM with \(O(n)\) Registers. The compiler ORAM on input \(n\in \mathbb {N}\) and a program \(\varPi \) with memory size \(n\) outputs a program \(\varPi '\) that is identical to \(\varPi \) but each \(\mathsf{Read}(r)\) or \(\mathsf{Write}(r,val)\) is replaced by corresponding commands \(\mathsf{ORead}(r)\), \(\mathsf{OWrite}(r,val)\) to be specified shortly. \(\varPi '\) has the same registers as \(\varPi \) and additionally has \(n/\alpha \) registers used to store a position map \(\mathsf{Pos}\) plus a polylogarithmic number of additional work registers used by \(\mathsf{ORead}\) and \(\mathsf{OWrite}\). In its external memory, \(\varPi '\) will maintain a complete binary tree \(\varGamma \) of depth \(\ell =\log (n/\alpha )\); we index nodes in the tree by a binary string of length at most \(\ell \), where the root is indexed by the empty string \(\lambda \), and each node indexed by \(\gamma \) has left and right children indexed \(\gamma 0\) and \(\gamma 1\), respectively. Each memory cell r will be associated with a random leaf pos in the tree, specified by the position map \(\mathsf{Pos}\); as we shall see shortly, the memory cell r will be stored at one of the nodes on the path from the root \(\lambda \) to the leaf pos. To ensure that the position map is smaller than the memory size, we assign a block of \(\alpha \) consecutive memory cells to the same leaf; thus memory cell r corresponding to block \(b=\lfloor r/\alpha \rfloor \) will be associated with leaf \(pos = \mathsf{Pos}(b)\).
Illustration of the basic [CP13] ORAM construction.
Each node in the tree is associated with a bucket which stores (at most) K tuples (b, pos, v), where v is the content of block b and pos is the leaf associated with the block b, and \(K \in \omega (\log n) \cap \mathsf{polylog}(n)\) is a parameter that will determine the security of the ORAM (thus each bucket stores \(K(\alpha +2 )\) words). We assume that all registers and memory cells are initialized with a special symbol \(\perp \).
The following is a specification of the \(\mathsf{ORead}(r)\) procedure:
-
Fetch: Let \(b=\lfloor r/\alpha \rfloor \) be the block containing memory cell r (in the original database), and let \(i = r \mod \alpha \) be r’s component within the block b. We first look up the position of the block b using the position map: \(pos = \mathsf{Pos}(b)\); if \(\mathsf{Pos}(b)=\perp \), set \(pos \leftarrow [n/\alpha ]\) to be a uniformly random leaf.
Next, traverse the data tree from the root to the leaf pos, making exactly one read and one write operation for the memory bucket associated with each of the nodes along the path. More precisely, we read the content once, and then we either write it back (unchanged), or we simply “erase it” (writing \(\perp \)) so as to implement the following task: search for a tuple of the form (b, pos, v) for the desired b, pos in any of the nodes during the traversal; if such a tuple is found, remove it from its place in the tree and set v to the found value, and otherwise take \(v=\perp \). Finally, return the ith component of v as the output of the \(\mathsf{ORead}(r)\) operation.
-
Update Position Map: Pick a uniformly random leak \(pos' \leftarrow [n/\alpha ]\) and let \(\mathsf{Pos}(b) = pos'\).
-
Put Back: Add the tuple \((b,pos',v)\) to the root \(\lambda \) of the tree. If there is not enough space left in the bucket, abort outputting overflow.
-
Flush: Pick a uniformly random leaf \(pos^* \leftarrow [n/\alpha ]\) and traverse the tree from the roof to the leaf \(pos^*\), making exactly one read and one write operation for every memory cell associated with the nodes along the path so as to implement the following task: “push down” each tuple \((b'',pos'',v'')\) read in the nodes traversed so far as possible along the path to \(pos^*\) while ensuring that the tuple is still on the path to its associated leaf \(pos''\) (that is, the tuple ends up in the node \(\gamma \) = longest common prefix of \(pos''\) and \(pos^*\).) Note that this operation can be performed trivially as long as the CPU has sufficiently many work registers to load two whole buckets into memory; since the bucket size is polylogarithmic, this is possible. If at any point some bucket is about to overflow, abort outputting \(\mathsf{overflow}\).
\(\mathsf{OWrite}(r,v)\) proceeds identically in the same steps as \(\mathsf{ORead}(r)\), except that in the “Put Back” steps, we add the tuple \((b,pos',v')\), where \(v'\) is the string v but the ith component is set to v (instead of adding the tuple \((b,pos',v)\) as in \(\mathsf{ORead}\)). (Note that, just as \(\mathsf{ORead}\), \(\mathsf{OWrite}\) also outputs the ordinal memory content of the memory cell r; this feature will be useful in the “full-fledged” construction.)
The Full-fledged Construction: ORAM with Polylog Registers. The full-fledged construction of the CP ORAM proceeds as above, except that instead of storing the position map in registers in the CPU, we now recursively store them in another ORAM (which only needs to operate on \(n/\alpha \) memory cells, but still using buckets that store \(K\) tuples). Recall that each invocation of \(\mathsf{ORead}\) and \(\mathsf{OWrite}\) requires reading one position in the position map and updating its value to a random leaf; that is, we need to perform a single recursive \(\mathsf{OWrite}\) call (recall that \(\mathsf{OWrite}\) updates the value in a memory cell, and returns the old value) to emulate the position map.
At the base of the recursion, when the position map is of constant size, we use the trivial ORAM construction which simply stores the position map in the CPU registers.
Theorem 3
([CP13]). The compiler ORAM described above is a secure Oblivious RAM compiler with \(\mathsf{polylog}(n)\) worst-case computation overhead and \(\omega (\log n)\) memory overhead, where \(n\) is the database memory size.
2.3 Sorting Networks
Our protocol will employ an n -wire sorting network, which can be used to sort values on n wires via a fixed topology of comparisons. A sorting network consists of a sequence of layers, each layer in turn consisting of one or more comparator gates, which take two wires as input, and swap the values when in unsorted order. Formally, given input values \(\mathbf {x} = (x_1, \ldots , x_n)\) (which we assume to be integers wlog), a comparator operation \(\mathsf{compare}(i,j, \mathbf {x})\) for \(i<j\) returns \(\mathbf {x}'\) where \(\mathbf {x} = \mathbf {x'}\) if \(x_i \le x_j\), and otherwise, swaps these values as \(x'_i = x_j\) and \(x'_j = x_i\) (whereas \(x'_k = x_k\) for all \(k \ne i, j\)). Formally, a layer in the sorting network is a set \(L = \{(i_1,j_1), \ldots , (i_k, j_k)\}\) of pairwise-disjoint pairs of distinct indices of [n]. A d-depth sorting network is a list \(SN = (L_1, \ldots , L_{d})\) of layers, with the property that for any input vector \(\mathbf {x}\), the final output will be in sorted order \(x_i \le x_{i+1}~\forall i < n\).
Ajtai, Komlós, and Szemerédi demonstrated a sorting network with depth logarithmic in n.
Theorem 4
([AKS83]). There exists an n-wire sorting network of depth \(O(\log n)\) and size \(O(n\log n)\).
While the AKS sorting network is asymptotically optimal, in practical scenarios one may wish to use the simpler alternative construction due to Batcher [Bat68] which achieves significantly smaller linear constants.
3 Oblivious PRAM
The definition of an Oblivious PRAM (OPRAM) compiler mirrors that of standard ORAM, with the exception that the compiler takes as input and produces as output a parallel RAM program. Namely, denote the sequence of shared memory cell accesses made during an execution of a PRAM program \(\varPi \) on input \((m,n,x)\) as \(\tilde{\varPi }(m,n,x)\). And, denote by \(\mathsf{ActivationPatterns}(\varPi ,m,n.,x)\) the (public) CPU activation patterns (i.e., number of active CPUs per timestep) of program \(\varPi \) on input (m, n, x). We present a definition of an OPRAM compiler following Chung and Pass [CP13], which in turn follows Goldreich [Gol87].
Definition 1
(Oblivious Parallel RAM). A polynomial-time algorithm O is an Oblivious Parallel RAM (OPRAM) compiler with computational overhead \(\mathsf{comp}(\cdot ,\cdot )\) and memory overhead \(\mathsf{mem}(\cdot ,\cdot )\), if O given \(m,n\in \mathbb {N}\) and a deterministic m-processor PRAM program \(\varPi \) with memory size \(n\), outputs an m-processor program \(\varPi '\) with memory size \(\mathsf{mem}(m,n)\cdot n\) such that for any input x, the parallel running time of \(\varPi '(m,n,x)\) is bounded by \(\mathsf{comp}(m,n) \cdot T\), where T is the parallel runtime of \(\varPi (m,n,x)\), and there exists a negligible function \(\mu \) such that the following properties hold:
-
Correctness: For any \(m,n\in \mathbb {N}\) and any string \(x \in \{0,1\}^*\), with probability at least \(1-\mu (n)\), it holds that \(\varPi (m,n,x) = \varPi '(m,n,x)\).
-
Obliviousness: For any two PRAM programs \(\varPi _1,\varPi _2\), any \(m,n\in \mathbb {N}\), and any two inputs \(x_1,x_2 \in \{0,1\}^*\), if \(|\varPi _1(m,n,x_1)| = |\varPi _2(m,n,x_2)|\) and \(\mathsf{ActivationPatterns}(\varPi _1,m,n,x_1)) = \mathsf{ActivationPatterns}(\varPi _2,m,n,x_2)\), then \(\tilde{\varPi }'_1(m,n,x_1)\) is \(\mu \)-close to \(\tilde{\varPi }'_2(m,n,x_2)\) in statistical distance, where \(\varPi '_i \leftarrow O(m,n,\varPi _i)\) for \(i \in \{1,2\}\).
We remark that not all m processors may be active in every time step of a PRAM program \(\varPi \), and thus its total computation cost may be significantly less than \(m \cdot T\). We wish to consider OPRAM compilers that also preserve the processor activation structure (and thus total computation complexity) of the original program up to polylogarithmic overhead. Of course, we cannot hope to do so if the processor activation patterns themselves reveal information about the secret data. We thus consider PRAMs \(\varPi \) whose activation schedules \((m_1,\ldots ,m_T)\) are a-priori fixed and public.
Definition 2
(Activation-Preserving). An OPRAM compiler O with computation overhead \(\mathsf{comp}(\cdot ,\cdot )\) is said to be activation preserving if given \(m,n \in \mathbb {N}\) and a deterministic PRAM program \(\varPi \) with memory size \(n\) and fixed (public) activation schedule \((m_1,\ldots ,m_T)\) for \(m_i \le m\), the program \(\varPi '\) output by O has activation schedule \(\big ( (m_1)_{i=1}^{t}, (m_2)_{i=1}^t,\ldots , (m_T)_{i=1}^t \big ),\) where \(t = \mathsf{comp}(m,n)\).
It will additionally be useful in applications (e.g., our construction of garbled PRAMs, and the MPC for PRAMs of [BCP15]) that the resulting oblivious PRAM is collision free.
Definition 3
(Collision-Free). An OPRAM compiler O is said to be collision free if given \(m,n \in \mathbb {N}\) and a deterministic PRAM program \(\varPi \) with memory size \(n\), the program \(\varPi '\) output by O has the property that no two processors ever access the same data address in the same timestep.
We now present our main result, which we construct and prove in the following subsections.
Theorem 5
(Main Theorem: OPRAM). There exists an activation-preserving, collision-free OPRAM compiler with \(O(\log (m) \log ^3(n))\) worst-case computational overhead and f(n) memory overhead, for any \(f \in \omega ( 1 )\), where n is the memory size and m is the number of CPUs.
3.1 Rudimentary Solution: Requiring Large Bandwidth
We first provide a solution for a simplified case, where we are not concerned with minimizing communication between CPUs or the size of required CPU local memory. In such setting, communicating and aggregating information between all CPUs is “for free.”
Our compiler \(\mathsf{Heavy}\text {-}O\), on input \(m,n\in \mathbb {N}\), fixed integer constant \(\alpha > 1\), and m-processor PRAM program \(\varPi \) with memory size \(n\), outputs a program \(\varPi '\) identical to \(\varPi \), but with each \(\mathsf{Access}(r,v)\) operation replaced by the modified procedure \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\) as defined in Fig. 2. (Here, “broadcast” means to send the specified message to all other processors).
Note that \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\) operates recursively for \(t=0,\ldots , \lceil \log _\alpha n \rceil \). This corresponds analogously to the recursion in the [SCSL11, CP13] ORAM, where in each step the size of the required “secure database memory” drops by a constant factor \(\alpha \). We additionally utilize a space optimization due to Gentry et al. [GGH+13] that applies to [CP13], where the ORAM tree used for storing data of size \(n'\) has depth \(\log n'/K\) (and thus \(n'/K\) leaves instead of \(n'\)), where K is the bucket size. This enables the overall memory overhead to drop from \(\omega (\log n)\) (i.e., K) to \(\omega (1)\) with minimal changes to the analysis.
Procedure for combining CPUs’ instructions for buckets and implementing them by a single representative CPU. (Used for correctness, not security). See Fig. 4 for a sample illustration.
Lemma 1
For any \(n,m \in \mathbb {N}\), The compiler \(\mathsf{Heavy}\text {-}O\) is a secure Oblivious PRAM compiler with parallel time overhead \(O(\log ^3n)\) and memory overhead \(\omega (1)\), assuming each CPU has \(\tilde{\varOmega }(m)\) local memory.
We will address the desired claims of correctness, security, and complexity of the \(\mathsf{Heavy}\text {-}O\) compiler by induction on the number of levels of recursion. Namely, for \(t^* \in [\log _\alpha n]\), denote by \(\mathsf{Heavy}\text {-}O_{t^*}\) the compiler that acts on memory size \(n/(\alpha ^{t^*})\) by executing \(\mathsf{Heavy}\text {-}O\) only on recursion levels \(t = t^*,(t^*+1),\ldots , \lceil \log _\alpha n\rceil \). For each such \(t^*\), we define the following property.
-
Level- \(t^*\) Heavy OPRAM: We say that \(\mathsf{Heavy}\text {-}O_{t^*}\) is a valid level- \(t^*\) heavy OPRAM if the partial-recursion compiler \(\mathsf{Heavy}\text {-}O_{t^*}\) is a secure Oblivious PRAM compiler for memory size \(n/(\alpha ^{t^*})\) with parallel time overhead \(O(\log ^2n \cdot \log (n/\alpha ^{t^*}))\) and memory overhead \(\omega (1)\), assuming each CPU has \(\tilde{\varOmega }(m)\) local memory.
Then Lemma 1 follows directly from the following two claims.
Claim
\(\mathsf{Heavy}\text {-}O_{\log _\alpha n}\) is valid level-\((\log _\alpha n)\) heavy OPRAM.
Proof
Note that \(\mathsf{Heavy}\text {-}O_{\log _\alpha n}\), acting on trivial size-1 memory, corresponds directly to the exit case (Step 0) of \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\) in Fig. 2. Namely, correctness, security, and the required efficiency trivially hold, since there is a single data item in a fixed location to access.
Claim
Suppose \(\mathsf{Heavy}\text {-}O_t\) is a valid level-t heavy OPRAM for \(t > 0\). Then \(\mathsf{Heavy}\text {-}O_{t-1}\) is a valid level-\((t-1)\) heavy OPRAM.
Proof
We first analyze the correctness, security, and complexity overhead of \(\mathsf{Heavy}\text {-}O_{t-1}\) conditioned on never reaching the event \(\mathsf{overflow}\) (which may occur in Step 5(c), or within the call to \(\mathsf{UpdateBuckets}\)). Then, we prove that the probability of \(\mathsf{overflow}\) is negligible in \(n\).
Correctness (w/o \(\mathsf{overflow}\) ). Consider the state of the memory (of the CPUs and server) in each step of \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\), assuming no \(\mathsf{overflow}\). In Step 1, each CPU learns the instruction pairs of all other CPUs; thus all CPUs agree on single representative \(\mathsf{rep}(b_i)\) for each requested block \(b_i\), and a correct aggregation of all instructions to be performed on this block. Step 2 is a recursive execution of \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\). By the inductive hypothesis, this access successfully returns the correct value \(\ell _i\) of \(\mathsf{Pos}(b_i)\) for each \(b_i\) queried, and rewrites it with the freshly sampled value \(\ell '_i\) when specified (i.e., for each \(\mathsf{rep}(b_i)\) access; the dummy accesses are read-only). We are thus guaranteed that each \(\mathsf{rep}(b_i)\) will find the desired block \(b_i\) in Step 3 when accessing the memory buckets in the path down the tree to leaf \(\ell _i\) (as we assume no \(\mathsf{overflow}\) was encountered), and so will learn the current stored data value \(v_{old}\).
In Step 4, each CPU learns the target block \(b_i\) and associated leaf \(\ell _i\) of every representative CPU \(\mathsf{rep}(b_i)\). By construction, each requested block \(b_i\) appears in some bucket B in the tree along his path, and there will necessarily be some CPU assigned as \(\mathsf{bucket\text {-}rep}(B)\) in \(\mathsf{UpdateBuckets}\), who will then successfully remove the block \(b_i\) from B. At this point, none of the requested blocks \(b_i\) appear in the tree.
In Step 5, the CPUs insert each block \(b_i\) (with updated data value \(v_i\)) into the ORAM data tree at level \(\min \{\log _\alpha n/\alpha ^t, \lfloor \log _2 (m) \rfloor \}\) along the path to its (new) leaf \(\ell '_i\).
Finally, the flushing procedure in Step 6 maintains the necessary property that each block \(b_i\) appears along the path to \(\mathsf{Pos}(b_i)\), and in Step 7 all CPUs learn the collection of all queried values \(v_{old}\) (in particular, including the value they initially requested).
Thus, assuming no \(\mathsf{overflow}\), correctness holds.
Obliviousness (w/o \(\mathsf{overflow}\) ). Consider the access patterns to server-side memory in each step of \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\), assuming no \(\mathsf{overflow}\). Step 1 is performed locally without communication to the server. Step 2 is a recursive execution of \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\), which thus yields access patterns independent of the vector of queried data locations (up to statistical distance negligible in \(n\)), by the induction hypothesis. In Step 3, each CPU accesses the buckets along a single path down the tree, where representative CPUs \(\mathsf{rep}(b_i)\) access along the path given by \(\mathsf{Pos}(b_i)\) (for distinct \(b_i\)), and non-representative CPUs each access down an independent, random path. Since the adversarial view so far has been independent of the values of \(\mathsf{Pos}(b_i)\), conditioned on this view all CPU’s paths are independent and random.
In Step 4, all data access patterns are publicly determinable based on the accesses in the previous step (that is, the complication in Step 4 is to ensure correctness without access collisions, but is not needed for security). In Step 5, each CPU i accesses his corresponding bucket i in the tree. In the flushing procedure of Step 6, each CPU selects an independent, random path down the tree, and the communication patterns to the server reveal no information beyond the identities of these paths. Finally, Step 7 is performed locally without communication to the server.
Thus, assuming no \(\mathsf{overflow}\), obliviousness holds.
Protocol Complexity (w/o \(\mathsf{overflow}\) ). First note that the server-side memory storage requirement is simply that of the [CP13] ORAM construction, together with the \(\log (2 n_t/K)\) tree-depth memory optimization of [GHL+14]; namely, \(f(n)\) memory overhead suffices for any \(f \in \omega (1)\).
Consider the local memory required per CPU. Each CPU must be able to store: \(O(\log n)\)-size requests from each CPU (due to the broadcasts in Steps 1(a), 4(a), 5(a), and 7); and the data contents of at most 3 memory buckets (due to the flushing procedure in \(\mathsf{UpdateBuckets}\)). Overall, this yields a per-CPU local memory requirement of \(\tilde{\varOmega }(m)\) (where \(\tilde{\varOmega }\) notation hides \(\log n\) factors).
Consider the parallel complexity of the OPRAM-compiled program \(\varPi ' \leftarrow \mathsf{Heavy}\text {-}O(m,n,\varPi )\). For each parallel memory access in the underlying program \(\varPi \), the processors perform: Conflict resolution (1 local communication round), Read/writing the position map (which has parallel complexity \(O(\log ^2n \cdot \log (n/\alpha ^t))\) by the inductive hypothesis), Looking up current memory values (sequential steps = depth of level-\((t-1)\) ORAM tree \(\in O(\log (n/\alpha ^{t-1}))\)), Removing old data from the ORAM tree (1 local communication round, plus depth of the ORAM tree \(\in O(\log (n/\alpha ^{t-1}))\) sequential steps), Inserting the new data in parallel (1 local communication round, plus 1 communication round to the server), Flushing the ORAM database (1 local communication round, and \(2 \times \) the depth of the ORAM tree rounds of communication with the server, since each bucket along a flush path is accessed once to receive new data items and once to flush its own data items down), and Updating CPUs with the read values (1 local communication round). Altogether, this yields parallel complexity overhead \(O(\log ^2n \cdot \log (n/\alpha ^{t-1}))\).
It remains to address the probability of encountering \(\mathsf{overflow}\).
Claim
There exists a negligible function \(\mu \) such that for any deterministic m-processor PRAM program \(\varPi \), any database size \(n\), and any input x, the probability that the \(\mathsf{Heavy}\text {-}O\)-compiled program \(\varPi '(m,n,x)\) outputs \(\mathsf{overflow}\) is bounded by \(\mu (n)\).
Proof
We consider separately the probability of overflow in each of the level-t recursive ORAM trees. Since there are \(\lceil \log n\rceil \) of them, the claim follows by a straightforward union bound.
Taking inspiration from [CP13], we analyze the ORAM-compiled execution via an abstract dart game. The game consists of black and white darts. In each round of the game, m black darts are thrown, followed by m white darts. Each dart independently hits the bullseye with probability \(p = 1/m\). The game continues until exactly \(K\) darts have hit the bullseye (recall \(K\in \omega (\log n)\) is the bucket size), or after the end of the Tth round for some fixed polynomial bound \(T=T(n)\), whichever comes first. The game is “won” (which will correspond to \(\mathsf{overflow}\) in a particular bucket) if \(K\) darts hit the bullseye, and all of them are black.
Let us analyze the probability of winning in the above dart game.
Subclaim 1: With overwhelming probability in \(n\) , no more than \(K/2\) darts hit the bullseye in any round. In any single round, associate with each of the \(2\cdot m\) darts thrown an indicator variable \(X_i\) for whether the dart strikes the target. The \(X_i\) are independent random variables each equal to 1 with probability \(p = 1/m\). Thus, the probability that more than \(K/2\) of the darts hit the target is bounded (via a Chernoff tail boundFootnote 3) by
Since there are at most \(T = \mathsf{poly}(n)\) distinct rounds of the game, the subclaim follows by a union bound.
Subclaim 2: Conditioned on no round having more than \(K/2\) bullseyes, the probability of winning the game is negligible in d. Fix an arbitrary such winning sequence s, which terminates sometime during some round r of the game. By assumption, the final partial round r contains no more than \(K/2\) bullseyes. For the remaining \(K/2\) bullseyes in rounds 1 through \(r-1\), we are in a situation mirroring that of [CP13]: for each such winning sequence s, there exist \(2^{K/2}-1\) distinct other “losing” sequences \(s'\) that each occur with the same probability, where any non-empty subset of black darts hitting the bullseye are replaced with their corresponding white darts. Further, every two distinct winning sequences \(s_1,s_2\) yield disjoint sets of losing sequences, and all such constructed sequences have the property that no round has more than \(K/2\) bullseyes (since this number of total bullseyes per round is preserved). Thus, conditioned on having no round with more than \(K/2\) bullseyes, the probability of winning the game is bounded above by \(2^{-K/2} \in e^{-\omega (\log n)}\).
We now relate the dart game to the analysis of our OPRAM compiler.
We analyze the memory buckets at the nodes in the t-th recursive ORAM tree, via three sub-cases.
Case 1: Nodes in level \(\mathsf{lev}< \log m\). Since data items are inserted to the tree in parallel directly at level \(\log m\), these nodes do not receive data, and thus will not overflow.
Case 2: Consider any internal node (i.e., a node that is not a leaf) \(\gamma \) in the tree at level \(\log m \le \mathsf{lev}< \log (L_t)\). (Recall \(L_t := 2n_t/K\) is the number of leaves in the t’th tree when applying the [GHL+14] optimization). Note that when \(m > L_t\), this case is vacuous. For purposes of analysis, consider the contents of \(\gamma \) as split into two parts: \(\gamma _L\) containing the data blocks whose leaf path continues to the left from \(\gamma \) (i.e., leaf \(\gamma || 0 || \cdot \)), and \(\gamma _R\) containing the data blocks whose leaf path continues right (i.e., \(\gamma || 1 || \cdot \)). For the bucket of node \(\gamma \) to overflow, there must be \(K\) tuples in it. In particular, either \(\gamma _L\) or \(\gamma _R\) must have \(K/2\) tuples.
For each parallel memory access in \(\varPi (m,n,x)\), in the t-th recursive ORAM tree for which \(n_t \ge m/K\), (at most) m data items are inserted, and then m independent paths in the tree are flushed. By definition, an inserted data item will enter our bucket \(\gamma _L\) (respectively, \(\gamma _R\)) only if its associated leaf has the prefix \(\gamma || 0\) (resp., \(\gamma || 1\)); we will assume the worst case in which all such data items arrive directly to the bucket. On the other hand, the bucket \(\gamma _L\) (resp., \(\gamma _R\)) will be completely emptied after any flush whose path contains this same prefix \(\gamma || 0\) (resp., \(\gamma || 1\)). Since all leaves for inserted data items and data flushes are chosen randomly and independently, these events correspond directly to the black and white darts in the game above. Namely, the probability that a randomly chosen path will have the specific prefix \(\gamma || 0\) of length \(\mathsf{lev}\) is \(2^{-\mathsf{lev}} \le 1/m\) (since we consider \(\mathsf{lev}\ge \log m\)); this corresponds to the probability of a dart hitting the bullseye. The bucket can only overflow if \(K/2\) “black darts” (inserts) hit the bullseye without any “white dart” (flush) hitting the bullseye in between. By the analysis above, we proved that for any sequence of \(K/2\) bullseye hits, the probability that all \(K/2\) of them are black is bounded above by \(2^{-K/4}\), which is negligible in \(n\). However, since there is a fixed polynomial number \(T = \mathsf{poly}(n)\) of parallel memory accesses in the execution of \(\varPi (m,n,x)\) (corresponding to the number of “rounds” in the dart game), and in particular, \(T(2m) \in \mathsf{poly}(n)\) total darts thrown, the probability that the sequence of bullseyes contains \(K/2\) sequential blacks anywhere in the sequence is bounded via a direct union bound by \((T2m) 2^{-K/4} \in e^{-\omega (\log n)}\), as desired.
Case 3: Consider any leaf node \(\gamma \). This analysis follows the same argument as in [CP13] (with slightly tweaked parameters from the [GHL+14] tree-depth optimization). We refer the reader to the full version of this work for details.
Thus, the total probability of \(\mathsf{overflow}\) is negligible in \(n\), and the theorem follows.
3.2 Oblivious Routing, Aggregation, and Multi-cast
Oblivious Parallel Insertion (Oblivious Routing).
Recall during the memory “put-back” phase, each CPU must insert its data item into the bucket at level \(\log m\) of the tree lying along a freshly sampled random path, while hiding the path.
We solve this problem by delivering data items to their target locations via a fixed-topology routing network. Namely, the m processors \(CPU_1,\ldots ,CPU_m\) will first write the relevant m data items \(\mathsf{msg}_i\) (and their corresponding destination addresses \(\mathsf{addr}_i\)) to memory in fixed order, and then rearrange them in \(\log m\) sequential rounds to the proper locations via the routing network. At the conclusion of the routing procedure, each node j will hold all messages \(\mathsf{msg}_i\) for which \(\mathsf{addr}_i = j\).
For simplicity, assume \(m = 2^\ell \) for some \(\ell \in \mathbb {N}\). The routing network has depth \(\ell \); in each level \(t=1,\ldots ,\ell \), each node communicates with the corresponding node whose id agrees in all bit locations except for the tth (corresponding to his tth neighbor in the \(\log m\)-dimensional boolean hypercube). These nodes exchange messages according to the tth bit of their destination addresses \(\mathsf{addr}_i\). This is formally described in Fig. 5. After the tth round, each message \(\mathsf{msg}_i\) is held by a party whose id agrees with the destination address \(\mathsf{addr}_i\) in the first t bits. Thus, at the conclusion of \(\ell \) rounds, all messages are properly delivered.
We demonstrate the case \(m=8 = 2^3\) below: first, CPUs exchange information along the depicted communication network in 3 sequential rounds (left); then, each CPU i inserts his resulting collection of items directly into node i of level 3 of the data tree (right).

In the full version, we show that if the destination addresses \(\mathsf{addr}_i\) are uniformly sampled, then with overwhelming probability no node will ever need to hold too many (the threshold \(K\) will be set to \(\omega (\log n)\)) messages at any point during the routing network execution:
Lemma 2
(Routing Network). If L messages begin with target destination addresses \(\mathsf{addr}_i\) distributed independently and uniformly over [L] in the L-to-L node routing network in Fig. 5, then with probability bounded by \(1-(L\log L) 2^{-K}\), no intermediate node will ever hold greater than \(K\) messages at any point during the course of the protocol execution.
Oblivious Aggregation.
To perform the “CPU-coordination” phase, the CPUs efficiently identify a single representative and aggregate relevant CPU instructions; then, at the conclusion, the representative CPU must be able to multi-cast the resulting information to all relevant requesting CPUs. Most importantly, these procedures must be done in an oblivious fashion. We discuss oblivious aggregation first.
Formally, we want to achieve the following aggregation goal, with communication patterns independent of the inputs, using only \(O(\log (m)\mathsf{polylog}(n))\) local memory and communication per CPU, in only \(O(\log (m))\) sequential time steps. An illustrative example to keep in mind is where \(\mathsf {key}_i = b_i\), \(\mathsf {data}_i = v_i\), and \(\mathsf {Agg}\) is the process that combines instructions to data items within the same data block, resolving conflicts as necessary.
Oblivious aggregation
-
Input: Each CPU \(i \in [m]\) holds \((\mathsf {key}_i, \mathsf {data}_i)\). Let \(\mathsf {K}= \bigcup \{\mathsf {key}_i \}\) denote the set of distinct keys. We assume that any (subset of) data associated with the same key can be aggregated by an aggregation function \(\mathsf {Agg}\) to a short digest of size at most \(\mathsf{poly}(\ell , \log m)\), where \(\ell = |\mathsf {data}_i|\).
-
Goal: Each CPU i outputs \(\mathsf {out}_i\) such that the following holds.
– For every \(\mathsf {key}\in \mathsf {K}\), there exists unique agent i with \(\mathsf {key}_i = \mathsf {key}\) s.t. \(\mathsf {out}_i = (\mathsf{rep}, \mathsf {key}, \mathsf {agg}_\mathsf {key})\), where \(\mathsf {agg}_\mathsf {key}= \mathsf {Agg}( \{ \mathsf {data}_j: \mathsf {key}_j = \mathsf {key}\})\).
– For every remaining agent i, \(\mathsf {out}_i = (\mathsf {dummy}, \bot , \bot )\).
At a high level, we achieve this via the following steps. (1) First, the CPUs sort their data list with respect to the corresponding key values. This can be achieved via an implementation of a \(\log (m)\)-depth sorting network, and provides the useful guarantee that all data pertaining to the same key are necessarily held by an block of adjacent CPUs. (2) Second, we pass data among CPUs in a sequence of \(\log (m)\) steps such that at the conclusion the “left-most” (i.e., lowest indexed) CPU in each key-block will learn the aggregation of all data pertaining to this key. Explicitly, in each step i, each CPU sends all held information to the CPU \(2^i\) to the “left” of him, and simultaneously accepts any received information pertaining to his key. (3) Third, each CPU will learn whether he is the “left-most” representative in each key-block, by simply checking whether his left-hand neighbor holds the same key. From here, the CPUs have succeeded in aggregating information for each key at a single representative CPU; (4) in the fourth step, they now reverse the original sorting procedure to return this aggregated information to one of the CPUs who originally requested it.
Lemma 3
(Space-Efficient Oblivious Aggregation). Suppose m processors initiate protocol \(\mathsf{OblivAgg}\) w.r.t. aggregator \(\mathsf {Agg}\), on respective inputs \(\{(\mathsf {key}_i,\mathsf {data}_i)\}_{i \in [m]}\), each of size \(\ell \). Then at the conclusion of execution, each processor \(i \in [m]\) outputs a triple \((\mathsf{rep}'_i, \mathsf {key}'_i,\mathsf {data}'_i)\) such that the following properties hold (where asymptotics are w.r.t. m):
-
1.
The protocol terminates in \(O(\log m)\) rounds.
-
2.
The local memory and computation required per processor is \(O(\log m + \ell )\).
-
3.
(Correctness). For every key \(\mathsf {key}\in \bigcup \{\mathsf {key}_i\}\), there exists a unique processor i with output \(\mathsf {key}'_i = \mathsf {key}\). For each such processor, it further holds that \(\mathsf {key}'_i = \mathsf {key}_i\), \(\mathsf{rep}'_i = ``\mathsf{rep}''\), and \(\mathsf {data}'_i = \mathsf {Agg}(\{\mathsf {data}_j : \mathsf {key}_j = \mathsf {key}_i\})\). For every remaining processor, the output tuple is \((\mathsf {dummy}, \bot ,\bot )\).
-
4.
(Obliviousness). The inter-CPU communication patterns are independent of the inputs \((\mathsf {key}_i,\mathsf {data}_i)\).
A full description of our Oblivious Aggregation procedure \(\mathsf{OblivAgg}\) is given in Fig. 6. We defer the proof of Lemma 3 to the full version of this work and provide only a high-level sketch.
Proof Sketch of Lemma 3. Property (1): The parallel complexity of \(\mathsf{OblivAgg}\) comes from Steps 1 and 4, which execute a sorting network and require \(O(\log m)\) communication rounds.
Property (2): At any given time, a processor must only store and/or communicate a constant number of CPU id’s (size \(\log m\)) and data items (size \(\ell \)), yielding total \(O(\log m + \ell )\).
Property (3): To show that the Aggregate Left phase in Step 2 is correct, it is proved (by induction) that for each pair of CPU indices \(i<j\) with the same key, \(CPU_i\) will learn \(CPU_j\)’s data after a number of rounds equal to the highest index in which the bit representations of i and j disagree.
Property (4): Both sorting network and aggregate-to-left have fixed communication topologies; thus the induced inter-CPU communications are independent of the initial CPU inputs.
Oblivious Multicasting.
Our goal for Oblivious Multicasting is dual to that of the previous section: Namely, a subset of CPUs must deliver information to (unknown) collections of other CPUs who request it. This is abstractly modeled as follows, where \(\mathsf {key}_i\) denotes which data item is requested by each CPU i.
Oblivious Multicasting
-
Input: Each CPU i holds \((\mathsf {key}_i, \mathsf {data}_i)\) with the following promise. Let \(\mathsf {K}= \bigcup \{\mathsf {key}_i \}\) denote the set of distinct keys. For every \(\mathsf {key}\in \mathsf {K}\), there exists a unique agent i with \(\mathsf {key}_i = \mathsf {key}\) such that \(\mathsf {data}_i \ne \bot \); let \(\mathsf {data}_{\mathsf {key}}\) denote such \(\mathsf {data}_i\).
-
Goal: Each agent i outputs \(\mathsf {out}_i = (\mathsf {key}_i, \mathsf {data}_{\mathsf {key}_i})\).
Oblivious Multicast can be solved in an analogous manner. We refer the reader to the full version of this work for the \(\mathsf{OblivMCast}\) construction.
3.3 Putting Things Together
We now combine the so-called “\(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\)” structure of our OPRAM formalized in Sect. 3.1 (Fig. 2) within the simplified “free CPU communication” setting, together with the (oblivious) \(\mathsf{Route}\), \(\mathsf{OblivAgg}\), and \(\mathsf{OblivMCast}\) procedures constructed in the previous subsection. For simplicity, we describe the case in which the number of CPUs m is fixed; however, it can be modified in a straightforward fashion to the more general case (as long as the activation schedule of CPUs is a-priori fixed and public).
Recall the steps in \(\mathsf{Heavy}\text {-}\mathsf{OPAccess}\) where large memory/bandwidth are required.
-
In Step 1, each \(CPU_i\) broadcasts \((r_i, v_i)\) to all CPUs. Let \(b_i = \lfloor r_i/\alpha \rfloor \). This is used to aggregate instructions to each \(b_i\) and determine its representative CPU \(\mathsf{rep}(b_i)\).
-
In Step 4, each \(CPU_i\) broadcasts \((b_i,\ell _i)\) or \((\bot , \ell _i)\). This is used to aggregate instructions to each buckets along path \(\ell _i\) about which blocks \(b_i\)’s to be removed.
-
In Step 5, each (representative) \(CPU_i\) broadcasts \((b_i,\bar{v}_i,\ell '_i)\). This is used to aggregate blocks to be inserted to each bucket in appropriate level of the tree.
-
In Step 6, each \(CPU_i\) broadcasts \(\ell _i^{\mathsf{flush}}\). This is used to aggregate information about which buckets the flush operation should perform.
-
In Step 7, each (representative) \(CPU_{\mathsf{rep}(b)}\) broadcasts the old value \(v_{\mathsf{old}}\) of block b to all CPUs, so that each CPU receives desired information.
We will use oblivious aggregation procedure to replace broadcasts in Step 1, 4, and 6; the parallel insertion procedure to replace broadcasts in Step 5, and finally the oblivious multicast procedure to replace broadcasts in Step 7.
Let us first consider the aggregation steps. For Step 1, to invoke the oblivious aggregation procedure, we set \(\mathsf {key}_i = b_i\) and \(\mathsf {data}_i = (r_i \mod \alpha , v_i)\), and define the output of \(\mathsf {Agg}( \{ (u_i, v_i)\} )\) to be a vector \(\bar{v} = \bar{v}[1]\cdots \bar{v}[\alpha ]\) of read/write instructions to each memory cell in the block, where conflicts are resolved by writing the value specified by the smallest CPU: i.e., \(\forall s \in [\alpha ]\), take \(\bar{v}[s] \leftarrow v_j\) for minimal j such that \(u_j = s\) and \(v_j \ne \bot \). By the functionality of \(\mathsf{OblivAgg}\), at the conclusion of \(\mathsf{OblivAgg}\), each block \(b_i\) is assigned to a unique representative (not necessarily the smallest CPU), who holds the aggregation of all instructions on this block.
Both Step 4 and 6 invoke \(\mathsf{UpdateBuckets}\) to update buckets along m random paths. In our rudimentary solution, the paths (along with instructions) are broadcast among CPUs, and the buckets are updated level by level. At each level, each update bucket is assigned to a representative CPU with minimal index, who performs aggregated instructions to update the bucket. Here, to avoid broadcasts, we invoke the oblivious aggregation procedure per level as follows.
-
In Step 4, each CPU i holds a path \(\ell _i\) and a block \(b_i\) (or \(\bot \)) to be removed. Also note that the buckets along the path \(\ell _i\) are stored locally by each CPU i, after the read operation in the previous step (Step 3). At each level \(\mathsf{lev}\in [\log n]\), we invoke the oblivious aggregation procedure with \(\mathsf {key}_i = \ell _i^{(\mathsf{lev})}\) (the \(\mathsf{lev}\)-bits prefix of \(\ell _i\)) and \(\mathsf {data}_i = b_i\) if \(b_i\) is in the bucket of node \(\ell _i^{(\mathsf{lev})}\), and \(\mathsf {data}_i = \bot \) otherwise. We simply define \(\mathsf {Agg}( \{ \mathsf {data}_i \} ) = \{ b: \exists \mathsf {data}_i = b\}\) to be the union of blocks (to be removed from this bucket). Since \(\mathsf {data}_i \ne \bot \) only when \(\mathsf {data}_i\) is in the bucket, the output size of \(\mathsf {Agg}\) is upper bounded by the bucket size K. By the functionality of \(\mathsf{OblivAgg}\), at the conclusion of \(\mathsf{OblivAgg}\), each bucket \(\ell _i^{(\mathsf{lev})}\) is assigned to a unique representative (not necessarily the smallest CPU) with aggregated instruction on the bucket. Then the representative CPUs can update the corresponding buckets accordingly.
-
In Step 6, each CPU i samples a path \(\ell ^{\mathsf{flush}}_i\) to be flushed and the instructions to each bucket are simply left and right flushes. At each level \(\mathsf{lev}\in [\log n]\), we invoke the oblivious aggregation procedure with \(\mathsf {key}_i = \ell _i^{^\mathsf{flush}(\mathsf{lev})}\) and \(\mathsf {data}_i = L\) (resp., R) if the \((\mathsf{lev}+1)\)-st bit of \(\ell _i^\mathsf{flush}\) is 0 (resp., 1). The aggregation function \(\mathsf {Agg}\) is again the union function. Since there are only two possible instructions, the output has O(1) length. By the functionality of \(\mathsf{OblivAgg}\), at the conclusion of \(\mathsf{OblivAgg}\), each bucket \(\ell _i^{\mathsf{flush}(\mathsf{lev})}\) is assigned to a unique representative (not necessarily the smallest CPU) with aggregated instruction on the bucket. To update a bucket \(\ell _i^{\mathsf{flush}(\mathsf{lev})}\), the representative CPU loads the bucket and its two children (if needed) into local memory from the server, performs the flush operation(s) locally, and writes the buckets back.
Note that since we update m random paths, we do not need to hide the access pattern, and thus the dummy CPUs do not need to perform dummy operations during \(\mathsf{UpdateBuckets}\). A formal description of full-fledged \(\mathsf{UpdateBuckets}\) can be found in Fig. 7.
For Step 5, we rely on the parallel insertion procedure of Sect. 3.2, which routes blocks to proper destinations within the relevant level of the server-held data tree in parallel using a simple oblivious routing network. The procedure is invoked with \(\mathsf{msg}_i = b_i\) and \(\mathsf{addr}_i = \ell '_i\).
Finally, in Step 7, each representative CPU \(\mathsf{rep}(b)\) holds information of the block b, and each dummy CPU i wants to learn the value of a block \(b_i\). To do so, we invoke the oblivious multicast procedure with \(\mathsf {key}_i = b_i\) and \(\mathsf {data}_i = v_i^{old}\) for representative CPUs and \(\mathsf {data}_i = \bot \) for dummy CPUs. By the functionality of \(\mathsf{OblivMCast}\), at the conclusion of \(\mathsf{OblivMCast}\), each CPU receives the value of the block it originally wished to learn.
The Final Compiler. For convenience, we summarize the complete protocol. Our OPRAM compiler O, on input \(m,n_t \in \mathbb {N}\) and a m-processor PRAM program \(\varPi \) with memory size \(n_t\) (which in recursion level t will be \(n_t=n/\alpha ^t\)), will output a program \(\varPi '\) that is identical to \(\varPi \), but where each \(\mathsf{Access}(r,v)\) operation is replaced by a sequence of operations defined by subroutine \(\mathsf{OPAccess}(r,v)\), which we will construct over the following subsections. The \(\mathsf{OPAccess}\) procedure begins with m CPUs, each with a requested data cell \(r_i\) (within some \(\alpha \)-block \(b_i\)) and some action to be taken (either \(\bot \) to denote read, or \(v_i\) to denote rewriting cell \(r_i\) with value \(v_i\)).
-
1.
Conflict Resolution: Run \(\mathsf{OblivAgg}\) on inputs \(\{(b_i,v_i)\}_{i \in [m]}\) to select a unique representative \(\mathsf{rep}(b_i)\) for each queried block \(b_i\) and aggregate all CPU instructions for this \(b_i\) (denoted \(\bar{v}_i\)).
-
2.
Recursive Access to Position Map: Each representative CPU \(\mathsf{rep}(b_i)\) samples a fresh random leaf id \(\ell '_i \leftarrow [n_t]\) in the tree and performs a (recursive) Read/Write access command on the position map database \(\ell _i \leftarrow \mathsf{OPAccess}(t+1,(b_i, \ell _i'))\) to fetch the current position map value \(\ell \) for block \(b_i\) and rewrite it with the newly sampled value \(\ell '_i\). Each dummy CPU performs an arbitrary dummy access (e.g., \(\mathsf{garbage} \leftarrow \mathsf{OPAccess}(t+1,(1,\emptyset ))\)).
-
3.
Look Up Current Memory Values: Each CPU \(\mathsf{rep}(b_i)\) fetches memory from the database nodes down the path to leaf \(\ell _i\); when \(b_i\) is found, it copies its value \(v_i\) into local memory. Each dummy CPU chooses a random path and make analogous dummy data fetches along it, ignoring all read values. (Recall that simultaneous data reads do not yield conflicts).
-
4.
Remove Old Data: For each level in the tree,
-
Aggregate instructions across CPUs accessing the same “buckets” of memory (corresponding to nodes of the tree) on the server side. Each representative CPU \(\mathsf{rep}(b)\) begins with the instruction of “remove block b if it occurs” and dummy CPUs hold the empty instruction. (Aggregation is as before, but at bucket level instead of the block level).
-
For each bucket to be modified, the CPU with the smallest id from those who wish to modify it executes the aggregated block-removal instructions for the bucket. Note that this aggregation step is purely for correctness and not security.
-
-
5.
Insert Updated Data into Database in Parallel : Run \(\mathsf{Route}\) on inputs \(\{(m,( \mathsf{msg}_i, \mathsf{addr}_i))\}_{i \in [m]}\), where for each \(\mathsf{rep}(b_i)\), \(\mathsf{msg}_i = (b_i,\bar{v}_i,\ell '_i)\) (i.e., updated block data) and \(\mathsf{addr}_i = [\ell '_i]_{\log m}\) (i.e., level-\(\log m\)-truncation of \(\ell '_i\)), and for each dummy CPU, \(\mathsf{msg}_i, \mathsf{addr}_i = \emptyset \).
-
6.
Flush the ORAM Database: In parallel, each CPU initiates an independent flush of the ORAM tree. (Recall that this corresponds to selecting a random path down the tree, and pushing all data blocks in this path as far as they will go). To implement the simultaneous flush commands, as before, commands are aggregated across CPUs for each bucket to be modified, and the CPU with the smallest id performs the corresponding aggregated set of commands. (For example, all CPUs will wish to access the root node in their flush; the aggregation of all corresponding commands to the root node data will be executed by the lowest-numbered CPU who wishes to access this bucket, in this case CPU 1).
-
7.
Return Output: Run \(\mathsf{OblivMCast}\) on inputs \(\{(b_i, v_i)\}_{i \in [m]}\) (where for dummy CPUs, \(b_i,\bar{v}_i := \emptyset \)) to communicate the original (pre-updated) value of each data block \(b_i\) to the subset of CPUs that originally requested it.
A few remarks regarding our construction.
Remark 2
(Truncating OPRAM for Fixed m). In the case that the number of CPUs m is fixed and known a priori, the OPRAM construction can be directly trimmed in two places.
Trimming Tops of Recursive Data Trees: Note that data items are always inserted into the OPRAM trees at level \(\log m\), and flushed down from this level. Thus, the top levels in the ORAM tree are never utilized. In such case, the data buckets in the corresponding tops of the trees, from the root node to level \(\log m\) for this bound, can simply be removed without affecting the OPRAM.
Truncating Recursion: In the t-th level of recursion, the corresponding database size shrinks to \(n_t = n/\alpha ^t\). In recursion level \(\log _\alpha n/m\) (i.e., where \(n_t = m\)), we can then achieve oblivious data accesses via local CPU communication (storing each block \(i \in [n_t]=[m]\) locally at CPU i, and running \(\mathsf{OblivAgg}, \mathsf{OblivMCast}\) directly) without needing any tree lookups or further recursion.

Remark 3
(Collision-Freeness). In the compiler above, CPUs only access the same memory address simultaneously in the (read-only) memory lookup in Step 3. However, a simple tweak to the protocol, replacing the direct memory lookups with an appropriate aggregation and multicast step (formally, the procedure \(\mathsf{UpdateBuckets}\) as described in the appendix), yields collision freeness.
Notes
- 1.
E.g., for tree-based ORAMs, the size of the root bucket.
- 2.
As previously mentioned, dealing with a variable number of processors is needed to capture standard circuit models of computation, where the circuit topology may be of varying width.
- 3.
Explicit Chernoff bound used: for \(X=X_1 + \cdots X_{2m}\) (\(X_i\) independent) and mean \(\mu \), then for any \(\delta > 0\), it holds that \(\Pr [X > (1+\delta )\mu ] \le e^{-\delta ^2\mu /(2+\delta )}\).
References
Ajtai, M.: Oblivious rams without cryptogarphic assumptions. In: STOC, pp. 181–190 (2010)
Ajtai, M., Komlós, J., Szemerédi, E.: An 0(n log n) sorting network. In: Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing, STOC 1983, pp. 1–9 (1983)
Batcher, K.E.: Sorting networks and their applications. In: Proceedings of the Spring Joint Computer Conference, AFIPS 1968 (Spring), New York, NY, USA, 30 April–2 May 1968, pp. 307–314. ACM (1968)
Boyle, E., Chung, K.-M., Pass, R.: Large-scale secure computation: multi-party computation for (parallel) RAM programs. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 742–762. Springer, Heidelberg (2015)
Bitansky, N., Garg, S., Lin, H., Pass, R., Telang, S.: Succinct randomized encodings and their applications. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, pp. 439–448 (2015)
Chen, Y.-C., Chow, S.S.M., Chung, K.-M., Lai, R.W.F., Lin, W.-K., Zhou, H.-S.: Computation-trace indistinguishability obfuscation and its applications. Cryptology ePrint Archive, Report 2015/406 (2015)
Canetti, R., Holmgren, J., Jain, A., Vaikuntanathan, V.: Succinct garbling and indistinguishability obfuscation for RAM programs. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, pp. 429–437 (2015)
Chung, K.-M., Liu, Z., Pass, R.: Statistically-secure ORAM with \(\tilde{O}(\log ^2 n)\) overhead. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 62–81. Springer, Heidelberg (2014)
Chen, B., Lin, H., Tessaro, S.: Oblivious parallel RAM: improved efficiency and generic constructions. Cryptology ePrint Archive (2015)
Chung, K.-M., Pass, R.: A simple ORAM. Cryptology ePrint Archive, Report 2013/243 (2013)
Damgård, I., Meldgaard, S., Nielsen, J.B.: Perfectly secure oblivious RAM without random oracles. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 144–163. Springer, Heidelberg (2011)
Fletcher, C.W., van Dijk, M., Devadas, S.: A secure processor architecture for encrypted computation on untrusted programs. In: Proceedings of the Seventh ACM Workshop on Scalable Trusted Computing, STC 2012, pp. 3–8 (2012)
Gentry, C., Goldman, K.A., Halevi, S., Julta, C., Raykova, M., Wichs, D.: Optimizing ORAM and using it efficiently for secure computation. In: De Cristofaro, E., Wright, M. (eds.) PETS 2013. LNCS, vol. 7981, pp. 1–18. Springer, Heidelberg (2013)
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M., Wichs, D.: Garbled RAM revisited. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 405–422. Springer, Heidelberg (2014)
Gentry, C., Halevi, S., Raykova, M., Wichs, D.: Outsourcing private RAM computation. In: Symposium on Foundations of Computer Science, FOCS 2014, pp. 404–413 (2014)
Gordon, S.D., Katz, J., Kolesnikov, V., Krell, F., Malkin, T., Raykova, M., Vahlis, Y.: Secure two-party computation in sublinear (amortized) time. In: The ACM Conference on Computer and Communications Security, CCS 2012, Raleigh, NC, USA, 16–18 October 2012, pp. 513–524 (2012)
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: How to run turing machines on encrypted data. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 536–553. Springer, Heidelberg (2013)
Garg, S., Steve, L., Ostrovsky, R., Scafuro, A.: Garbled RAM from one-way functions. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC 2015, pp. 449–458 (2015)
Goodrich, M.T., Mitzenmacher, M.: Privacy-preserving access of outsourced data via oblivious RAM simulation. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011, Part II. LNCS, vol. 6756, pp. 576–587. Springer, Heidelberg (2011)
Goodrich, M.T., Mitzenmacher, M., Ohrimenko, O., Tamassia, R.: Oblivious ram simulation with efficient worst-case access overhead. In: CCSW, pp. 95–100 (2011)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: STOC, pp. 218–229 (1987)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious RAMs. J. ACM 43(3), 431–473 (1996)
Goldreich, O.: Towards a theory of software protection and simulation by oblivious RAMs. In: STOC, pp. 182–194 (1987)
Kushilevitz, E., Lu, S., Ostrovsky, R.: On the (in)security of hash-based oblivious ram and a new balancing scheme. In: SODA, pp. 143–156 (2012)
Koppula, V., Lewko, A.B., Waters, B.: Indistinguishability obfuscation for turing machines with unbounded memory. In: Proceedings of the Forty-Seventh Annual ACM on Symposium on Theory of Computing, STOC, pp. 419–428 (2015)
Lu, S., Ostrovsky, R.: Distributed oblivious RAM for secure two-party computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 377–396. Springer, Heidelberg (2013)
Lorch, J.R., Parno, B., Mickens, J.W., Raykova, M., Schiffman, J.: Shroud: ensuring private access to large-scale data in the data center. In: FAST, pp. 199–214 (2013)
Nayak, K., Wang, X.S., Ioannidis, S., Weinsberg, U., Taft, N., Shi, E.: GraphSC: parallel secure computation made easy. In: IEEE Symposium on Security and Privacy (S&P) (2015)
Ostrovsky, R., Shoup, V.: Private information storage (extended abstract). In: STOC, pp. 294–303 (1997)
Pippenger, N., Fischer, M.J.: Relations among complexity measures. J. ACM 26(2), 361–381 (1979)
Ren, L., Fletcher, C.W., Kwon, A., Stefanov, E., Shi, E., van Dijk, M., Devadas, S.: Ring ORAM: closing the gap between small and large client storage oblivious RAM. IACR Cryptology ePrint Archive 2014:997 (2014)
Shi, E., Chan, T.-H.H., Stefanov, E., Li, M.: Oblivious RAM with O((logN)\(^\text{3 }\)) worst-case cost. In: Wang, X., Lee, D.H. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 197–214. Springer, Heidelberg (2011)
Stefanov, E., Shi, E.: ObliviStore: high performance oblivious cloud storage. In: IEEE Symposium on Security and Privacy, pp. 253–267 (2013)
Stefanov, E., van Dijk, M., Shi, E., Fletcher, C.W., Ren, L., Yu, X., Devadas, S.: Path ORAM: an extremely simple oblivious RAM protocol. In: ACM Conference on Computer and Communications Security, pp. 299–310 (2013)
Wang, X.S., Hubert Chan, T.-H., Shi, E.: Circuit ORAM: on tightness of the goldreich-ostrovsky lower bound. IACR Cryptology ePrint Archive 2014:672 (2014)
Wang, X.S., Huang, Y., Hubert Chan, T.-H., Shelat, A., Shi, E.: SCORAM: oblivious RAM for secure computation. In: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pp. 191–202 (2014)
Williams, P., Sion, R., Tomescu, A.: PrivateFS: a parallel oblivious file system. In: Proceedings of the 2012 ACM Conference on Computer and Communications Security, CCS 2012, pp. 977–988 (2012)
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd Annual Symposium on Foundations of Computer Science (FOCS), pp. 160–164 (1982)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Boyle, E., Chung, KM., Pass, R. (2016). Oblivious Parallel RAM and Applications. In: Kushilevitz, E., Malkin, T. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9563. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49099-0_7
Download citation
DOI: https://doi.org/10.1007/978-3-662-49099-0_7
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49098-3
Online ISBN: 978-3-662-49099-0
eBook Packages: Computer ScienceComputer Science (R0)





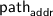 , and removes it where found.
, and removes it where found. , and is returned to the root node of the tree.
, and is returned to the root node of the tree.






