Key-Recovery Attacks on ASASA

Abstract

The $\mathsf {ASASA}$ construction is a new design scheme introduced at Asiacrypt 2014 by Biruykov, Bouillaguet and Khovratovich. Its versatility was illustrated by building two public-key encryption schemes, a secret-key scheme, as well as super S-box subcomponents of a white-box scheme. However one of the two public-key cryptosystems was recently broken at Crypto 2015 by Gilbert, Plût and Treger. As our main contribution, we propose a new algebraic key-recovery attack able to break at once the secret-key scheme as well as the remaining public-key scheme, in time complexity $2^{63}$ and $2^{39}$ respectively (the security parameter is 128 bits in both cases). Furthermore, we present a second attack of independent interest on the same public-key scheme, which heuristically reduces its security to solving an $\mathsf {LPN}$ instance with tractable parameters. This allows key recovery in time complexity $2^{56}$. Finally, as a side result, we outline a very efficient heuristic attack on the white-box scheme, which breaks an instance claiming 64 bits of security under one minute on a single desktop computer.

P.Derbez—Supported by the CORE ACRYPT project from the Fond National de la Recherche, Luxembourg.

P.Karpman—Partially supported by the Direction Générale de l’Armement and by the Singapore National Research Foundation Fellowship 2012 (NRF-NRFF2012-06).

1 Introduction

The idea of creating a public-key cryptosystem by obfuscating a secret-key cipher was proposed by Diffie and Hellman in 1976, in the same seminal paper that introduced the idea of public-key encryption [DH76]. While the RSA cryptosystem was introduced only a year later, creating a public-key scheme based on symmetric components has remained an open challenge to this day. The interest of this problem is not merely historical: beside increasing the variety of available public-key schemes, one can hope that a solution may help bridging the performance gap between public-key and secret-key cryptosystems, or at least offer new trade-offs in that regard.

Multivariate cryptography is one way to achieve this goal. This area of research dates back to the 1980’s [MI88, FD86], and has been particularly active in the late 1990’s and early 2000’s [Pat95, Pat96, RP97, FJ03, ...]. Many of the proposed public-key cryptosystems build an encryption function from a structured, easily invertible polynomial, which is then scrambled by affine maps (or similarly simple transformations) applied to its input and output to produce the encryption function.

This approach might be aptly described as an $\mathsf {ASA}$ structure, which should be read as the composition of an affine map “$\mathsf {A}$”, a nonlinear transformation of low algebraic degree “$\mathsf {S}$” (not necessarily made up of smaller S-boxes), and another affine layer “$\mathsf {A}$”. The secret key is the full description of the three maps A, S, A, which makes computing both ASA and $(ASA)^{-1}$ easy. The public key is the function ASA as a whole, which is described in a generic manner by providing the polynomial expression of each output bit in the input bits (or group of n bits if the scheme operates on $\mathbb {F}_{2^{n}}$). Thus the owner of the secret key is able to encrypt and decrypt at high speed, depending on the structure of S. The downside is slow public key operations, and a large key size.

The ${{\mathbf {\mathsf{{ASASA}}}}}$ Construction. Historically, attempts to build public-key encryption schemes based on the above principle have been ill-fated [FJ03, BFP11, DGS07, DFSS07, WBDY98, ...]¹. However several new ideas to build multivariate schemes were recently introduced by Biryukov, Bouillaguet and Khovratovich at Asiacrypt 2014 [BBK14]. The paradigm federating these ideas is the so-called $\mathsf {ASASA}$ structure: that is, combining two quadratic mappings $\mathsf {S}$ by interleaving random affine layers $\mathsf {A}$. With quadratic $\mathsf {S}$ layers, the overall scheme has degree 4, so the polynomial description provided by the public key remains of reasonable size.

This is very similar to the 2R scheme by Patarin [PG97], which fell victim to several attacks [Bih00, DFKYZD99], including a powerful decomposition attack [DFKYZD99, FP06], later developed in a general context by Faugère et al. [FvzGP10, FP09a, FP09b]. The general course of this attack is to differentiate the encryption function, and observe that the resulting polynomials in the input bits live in a “small” space entirely determined by the first $\mathsf {ASA}$ layers. This essentially allows the scheme to be broken down into its two $\mathsf {ASA}$ sub-components, which are easily analyzed once isolated. A later attempt to circumvent this and other attacks by truncating the output of the cipher proved insecure against the same technique [FP06] — roughly speaking truncating does not prevent the derivative polynomials from living in too small a space.

In order to thwart attacks including the decomposition technique, the authors of [BBK14] propose to go in the opposite direction: instead of truncating the cipher, a perturbation is added, consisting in new random polynomials of degree four added at fixed positions, prior to the last affine layer². The idea is that these new random polynomials will be spread over the whole output of the cipher by the last affine layer. When differentiating, the “noise” introduced by the perturbation polynomials is intended to drown out the information about the first quadratic layer otherwise carried by the derivative polynomials, and thus to foil the decomposition attack.

Based on this idea, two public-key cryptosystems are proposed. One uses random quadratic expanding S-boxes as nonlinear components, while the other relies on the $\chi$ function, most famous for its use in the SHA-3 winner Keccak. However the first scheme was broken at Crypto 2015 by a decomposition attack [GPT15]: the number of perturbation polynomials turned out to be too small to prevent this approach. This leaves open the question of the robustness of the other cryptosystem, based on $\chi$, to which we answer negatively.

Black-Box ${{\mathbf {\mathsf{{ASASA.}}}}}$ Besides public-key cryptosystems, the authors of [BBK14] also propose a secret-key (“black-box”) scheme based on the $\mathsf {ASASA}$ structure, showcasing its versatility. While the structure is the same, the context is entirely different. This black-box scheme is in fact the exact counterpart of the $\mathsf {SASAS}$ structure analyzed by Biryukov and Shamir [BS01]: it is a block cipher operating on 128-bit inputs; each affine layer is a random affine map on $\mathbb {Z}_{2}^{128}$, while the nonlinear layers are composed of 16 random 8-bit S-boxes. The secret key is the description of the three affine layers, together with the tables of all S-boxes.

In some sense, the “public key” is still the encryption function as a whole; however it is only accessible in a black-box way through known or chosen-plaintext or ciphertext attacks, as any standard secret-key scheme. A major difference however is that the encryption function can be easily distinguished from a random permutation because the constituent S-boxes have algebraic degree at most 7, and hence the whole function has degree at most 49; in particular, it sums up to zero over any cube of dimension 50. The security claim is that the secret key cannot be recovered, with a security parameter evaluated at 128 bits.

White-Box ${{\mathbf {\mathsf{{ASASA.}}}}}$ The structure of the black-box scheme is also used as a basis for several white-box proposals. In that setting, a symmetric (black-box) $\mathsf {ASASA}$ cipher with small block (e.g. 16 bits) is used as a super S-box in a design with a larger block. A white-box user is given the super S-box as a table. The secret information consists in a much more compact description of the super S-box in terms of alternating linear and nonlinear layers. The security of the $\mathsf {ASASA}$ design is then expected to prevent a white-box user from recovering the secret information.

1.1 Our Contribution

Algebraic attack on the secret-key and ${\mathbf {\chi {-}Based}}$ Public-Key Schemes. Despite the difference in nature between the $\chi$-based public-key scheme and the black-box scheme, we present a new algebraic key-recovery attack able to break both schemes at once. This attack does not rely on a decomposition technique. Instead, it may be regarded as exploiting the relatively low degree of the encryption function, coupled with the low diffusion of nonlinear layers. Furthermore, in the case of the public-key scheme, the attack applies regardless of the amount of perturbation. Thus, contrary to the attack of [GPT15], there is no hope of patching the scheme by increasing the number of perturbation polynomials. As for the secret-key scheme, our attack may be seen as a counterpart to the cryptanalysis of $\mathsf {SASAS}$ in [BS01], and is structural in the same sense.

While the same attack applies to both schemes, their respective bottlenecks for the time complexity come from different stages of the attack. For the $\chi$ scheme, the time complexity is dominated by the need to compute the kernel of a binary matrix of dimension $2^{13}$, which can be evaluated to $2^{39}$ basic linear operations³. As for the black-box scheme, the time complexity is dominated by the need to encrypt $2^{63}$ chosen plaintexts, and the data complexity follows.

This attack actually only peels off the last linear layer of the scheme, reducing $\mathsf {ASASA}$ to $\mathsf {ASAS}$. In the case of the black-box scheme, the remaining layers can be recovered in negligible time using Biryukov and Shamir’s techniques [BS01]. In the case of the $\chi$ scheme, removing the remaining layers poses non-trivial algorithmic challenges (such as how to efficiently recover quadratic polynomials $A, B, C \in \mathbb {Z}_{2}[X_{1},\dots ,X_{n}]/\langle X_{i}^{2}-X_{i}\rangle$, given $A+B\cdot C$), and some of the algorithms we propose may be of independent interest. Nevertheless, in the end the remaining layers are peeled off and the secret key is recovered in time complexity negligible relative to the cost of removing the first layer.

${{\mathbf {\mathsf{{LPN}}}}}$ -Based Attack on the $\chi$ scheme. As a second contribution, we present an entirely different attack, dedicated to the $\chi$ public-key scheme. This attack exploits the fact that each bit at the output of $\chi$ is “almost linear” in the input: indeed the nonlinear component of each bit is a single product, which is equal to zero with probability 3/4 over all inputs. Based on this property, we are able to heuristically reduce the problem of breaking the scheme to an $\mathsf {LPN}$-like instance with easy-to-solve parameters. By $\mathsf {LPN}$-like instance, we mean an instance of a problem very close to the Learning Parity with Noise problem ($\mathsf {LPN}$), on which typical $\mathsf {LPN}$-solving algorithms such as the Blum-Kalai-Wasserman algorithm ($\mathsf {BKW}$) [BKW03] are expected to immediately apply. The time complexity of this approach is higher than the previous one, and can be evaluated at $2^{56}$ basic operations. However it showcases a different weakness of the $\chi$ scheme, providing a different insight into the security of $\mathsf {ASASA}$ constructions. In this regard, it is noteworthy that the security of another recent multivariate scheme, presented by Huang et al. at PKC’12 [HLY12], was also reduced to an easy instance of $\mathsf {LWE}$ [Reg05], which is an extension of $\mathsf {LPN}$, in [AFF+14]⁴.

Heuristic Attack on the White-Box Scheme. Finally as a side result, we describe a key-recovery attack on white-box $\mathsf {ASASA}$. The attack technique is unrelated to the previous ones, and its motivation relies on heuristics rather than a theoretical model. On the other hand it is very effective on the smallest white-box instances of [BBK14] (with a security level of 64 bits), which we break under a minute on a laptop computer. Thus it seems that the security level offered by small-block $\mathsf {ASASA}$ is much lower than anticipated.

The same attack on white-box schemes was found independently by Dinur, Dunkelman, Kranz and Leander [DDKL15]. Their approach focuses on small-block $\mathsf {ASASA}$ instances, and is thus only applicable to the white-box scheme of [BBK14]. Section 5 of [DDKL15] is essentially the same attack as ours, minus some heuristic improvements (see [MDFK15]). On the other hand, the authors of [DDKL15] present other methods to attack small-block $\mathsf {ASASA}$ instances that are less reliant on heuristics, but as efficient as our heuristically improved variant, and thus provide a better theoretical basis for understanding small-block $\mathsf {ASASA}$, as used in the white-box scheme of [BBK14].

1.2 Structure of the Article

Section 3 provides a brief description of the three $\mathsf {ASASA}$ schemes under attack. In Sect. 4, we present our main attack, as applied to the secret-key (“black-box”) scheme. In particular, an overview of the attack is given in Sect. 4.1. The attack is then adapted to the $\chi$ public-key scheme in Sect. 5.1, while the $\mathsf {LPN}$-based attack on the same scheme is presented in Sect. 5.2. Finally, our attack on the white-box scheme is presented in Sect. 6.

1.3 Implementation and Full Version

Due to space constraints, some subordinate algorithms and proofs were removed from the print version of this article. However none of the missing material is essential to understanding the attacks. The full version is available on ePrint [MDFK15]. It is also available at the following link, together with implementations of our attacks:

https://www.dropbox.com/sh/3glwc5x181fekre/AAASeG7D-CGKM2gLmr-UVBK9a

2 Notation and Preliminaries

The sign denotes an equality by definition. |S| denotes the cardinality of a set S. The $\log ()$ function denotes logarithm in base 2.

Binary Vectors. We write $\mathbb {Z}_{2}$ as a shorthand for $\mathbb {Z}/2\mathbb {Z}$. The set of n-bit vectors is denoted interchangeably by $\{0,1\}^{n}$ or $\mathbb {Z}_{2}^{n}$. However the vectors are always regarded as elements of $\mathbb {Z}_{2}^{n}$ with respect to addition $+$ and dot product $\langle \cdot | \cdot \rangle$. In particular, addition should be understood as bitwise XOR. The canonical basis of $\mathbb {Z}_{2}^{n}$ is denoted by $e_{0}, \dots , e_{n-1}$.

For any $v \in \{0,1\}^{n}$, $v_{i}$ denotes the i-th coordinate of v. In this context, the index i is always computed modulo n, so $v_{0} = v_{n}$ and so forth. Likewise, if F is a function mapping into $\{0,1\}^{n}$, $F_{i}$ denotes the i-th bit of the output of F.

For $a \in \{0,1\}^{n}$, $\langle F | a \rangle$ is a shorthand for the function $x \mapsto \langle F(x) | a \rangle$.

For any $v \in \{0,1\}^{n}$, $\lfloor v \rfloor _{k}$ denotes the truncation $(v_{0},\dots ,v_{k-1})$ of v to its first k coordinates.

For any bit b, $\overline{b}$ stands for $b+1$.

Derivative of a Binary Function. For $F: \{0,1\}^{m} \rightarrow \{0,1\}^{n}$ and $\delta \in \{0,1\}^{m}$, we define the derivative of F along $\delta$ as . We write for the order-d derivative along $v_{0},\dots ,v_{d-1} \in \{0,1\}^{m}$. For convenience we may write $F'$ instead of $\partial F / \partial v$ when v is clear from the context; likewise for $F''$.

The degree of $F_{i}$ is its degree as an element of $\mathbb {F}_{2}[x_{0},\dots ,x_{m-1}]/\langle x_{i}^{2}-x_{i}\rangle$ in the binary input variables. The degree of F is the maximum of the degrees of the $F_{i}$’s.

Cube. A cube of dimension d in $\{0,1\}^{n}$ is simply an affine subspace of dimension d. The terminology comes from [DS09]. Note that summing a function F over a cube C of dimension d, i.e. computing $\sum _{c \in C}F(c)$, amounts to computing the value of an order-d differential of F at a certain point: it is equal to $\partial ^{d} F / \partial v_{0}\dots \partial v_{d-1}(a)$ for a, $(v_{i})$ such that $C = a + \mathrm{span}\{v_{0},\dots ,v_{d-1}\}$. In particular if F has degree d, then it sums up to zero over any cube of dimension $d+1$.

Bias. For any probability $p \in [0,1]$, the bias of p is $|2p-1|$. Note that the bias is sometimes defined as $|p-1/2|$ in the literature. Our choice of definition makes the formulation of the Piling-up Lemma more convenient [Mat94]:

Lemma 1

(Piling-up Lemma). For $X_{1}, \dots , X_{n}$ independent random binary variables with respective biases $b_{1}, \dots , b_{n}$, the bias of $X = \sum X_{i}$ is $b = \prod b_{i}$.

Learning Parity with Noise ${{\mathbf {\mathsf{{(LPN).}}}}}$ The $\mathsf {LPN}$ problem was introduced in [BKW03], and may be stated as follows: given $(A,As + e)$, find s, where:

• $s\in \mathbb {Z}_{2}^{n}$ is a uniformly random secret vector.

• $A \in \mathbb {Z}_{2}^{N \times n}$ is a uniformly random binary matrix.

• $e \in \mathbb {Z}_{2}^{N}$ is an error vector, whose coordinates are chosen according to a Bernoulli distribution with parameter p.

3 Description of $\mathsf {ASASA}$ schemes

3.1 Presentation and Notations

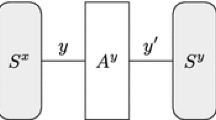
$\mathsf {ASASA}$ is a general design scheme for public or secret-key ciphers (or cipher components). An $\mathsf {ASASA}$ cipher is composed of 5 interleaved layers: the letter $\mathsf {A}$ represents an affine layer, and the letter $\mathsf {S}$ represents a nonlinear layer (not necessarily made up of smaller S-boxes). Thus the cipher may be pictured as:

We borrow the notation of [GPT15] and write the encryption function F as:

$$\begin{aligned} F = A^{z} \circ S^{y} \circ A^{y} \circ S^{x} \circ A^{x} \end{aligned}$$

Moreover, $x = (x_{0},\dots ,x_{n-1})$ is used to denote the input of the cipher; $x'$ is the output of the first affine layer $A^{x}$; and so on, as pictured above. The variables $x'_{i}$, $y_{i}$, etc., will often be viewed as polynomials over the input bits $(x_{0},\dots ,x_{n-1})$. Similarly, F denotes the whole encryption function, while $F^{y} = S^{x} \circ A^{x}$ is the partial encryption function that maps the input x to the intermediate state y, and likewise $F^{x'} = A^{x}$, $F^{y'} = A^{y}\circ S^{x} \circ A^{x}$, etc.

One secret-key (“black-box”) and two public-key $\mathsf {ASASA}$ ciphers are presented in [BBK14]. The secret-key and public-key variants are quite different in nature, even though our main attack applies to both. We now present in turn the black-box and white-box constructions and the public-key variant based on $\chi$.

3.2 Description of the Black-Box Scheme

It is worth noting that the following $\mathsf {ASASA}$ scheme is the exact counterpart of the $\mathsf {SASAS}$ structure analyzed by Biryukov and Shamir [BS01], with swapped affine and S-box layers.

Black-box $\mathsf {ASASA}$ is a secret-key encryption scheme, parameterized by m, the size of the S-boxes and k, the number of S-boxes. Let $n = km$ be the number of bits of the scheme. The overall structure of the cipher follows the $\mathsf {ASASA}$ construction, with layers as follows:

• $A^{x}, A^{y}, A^{z}$ are a random invertible affine mappings $\mathbb {Z}_{2}^{n} \rightarrow \mathbb {Z}_{2}^{n}$. Without loss of generality, the mappings can be considered purely linear, because the affine constant can be integrated into the preceding or following S-box layer. In the remainder we assume the mappings to be linear.

• $S^{x}, S^{y}$ are S-box layers. Each S-box layer consists in the application of k parallel random invertible m-bit S-boxes.

All linear layers and all S-boxes are uniformly random among invertible elements, and independent from each other.

In the concrete instance of [BBK14], each S-box layer contains $k = 16$ S-boxes over $m = 8$ bits each, so that the scheme operates on blocks of $n = 128$ bits. The secret key consists in three n-bit matrices and 2k m-bit S-boxes, so the key size is $3\cdot n^{2} + 2k\cdot m2^{m}$-bit long. With the previous parameters this amounts to 14 KB.

It should be pointed out that the scheme is not IND-CPA secure. Indeed, an 8-bit invertible S-box has algebraic degree (at most) 7, so the overall scheme has algebraic degree (at most) 49. Thus, the sum of ciphertexts on entries spanning a cube of dimension 50 is necessarily zero. As a result the security claim in [BBK14] is only that the secret key cannot be recovered, with a security parameter of 128 bits.

3.3 Description of the White-Box Scheme

As an application of the symmetric $\mathsf {ASASA}$ scheme, Biryukov et al. propose its use as a basis for designing white-box block ciphers. In a nutshell, their idea is to use $\mathsf {ASASA}$ to create small ciphers of, say, 16-bit blocks and to use them as super S-boxes in e.g. a substitution-permutation network (SPN). Users of the cipher in the white-box model are given access to super S-boxes in the form a table, which allows them to encrypt and decrypt at will. Yet if the small ciphers used in building the super S-boxes are secure, one cannot efficiently recover their keys even when given access to their whole codebook, meaning that white-box users cannot extract a more compact description of the super S-boxes from their tables. This achieves weak white-box security as defined by Biryukov et al.  [BBK14]:

Definition 1

(Key Equivalence [BBK14]). Let $E: \{0,1\}^\kappa \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a (symmetric) block cipher. $\mathbb {E}(k)$ is called the equivalent key set of k if for any $k' \in \mathbb {E}(k)$ one can efficiently compute $E'$ such that $\forall \,p~E(k,p) = E'(k',p)$.

Definition 2

(Weak White-Box T -security [BBK14]). Let $E: \{0,1\}^\kappa \times \{0,1\}^n \rightarrow \{0,1\}^n$ be a (symmetric) block cipher. $\mathbb {W}(E)(k,\cdot )$ is said to be a T-secure weak white-box implementation of $E(k,\cdot )$ if $\forall \,p~\mathbb {W}(E)(k,p) = E(k,p)$ and if it is computationally expensive to find $k' \in \mathbb {E}(k)$ of length less than T bits when given full access to $\mathbb {W}(E)(k,\cdot )$.

Example 1

If $S _{16}$ is a secure cipher with 16-bit blocks, then the full codebook of $S _{16}(k,\cdot )$ as a table is a $2^{20}$-secure weak white-box implementation of $S _{16}(k,\cdot )$.

For their instantiations, Biryukov et al. propose to use several super S-boxes of different sizes, among others:

• A 16-bit $\mathsf {ASASA} _{16}$ where the nonlinear permutations $S$ are made of the parallel application of two 8-bit S-boxes, with conjectured security of 64 bits against key recovery.

• A 20-bit $\mathsf {ASASA} _{20}$ where the nonlinear permutations $S$ are made of the parallel application of two 10-bit S-boxes, with conjectured security of 100 bits against key recovery.

• A 24-bit $\mathsf {ASASA} _{24}$ where the nonlinear permutations $S$ are made of the parallel application of three 8-bit S-boxes, with conjectured security of 128 bits against key recovery.

3.4 Description of the $\chi$-based Public-Key Scheme

The $\chi$ mapping was introduced by Daemen [Dae95] and later used for several cryptographic constructions, including the SHA-3 competition winner Keccak. The mapping $\chi : \{0,1\}^{n} \rightarrow \{0,1\}^{n}$ is defined by:

$$\begin{aligned} \chi _{i}(a) = a_{i} + \overline{a_{i+1}}a_{i+2} \end{aligned}$$

$\chi$-based $\mathsf {ASASA}$ scheme presented in [BBK14] is a public-key encryption scheme operating on 127-bit inputs, the odd size coming from the fact that $\chi$ is only invertible on inputs of odd length. The encryption function may be written as:

$$\begin{aligned} F = A^{z} \circ (P + \chi \circ A^{y} \circ \chi \circ A^{x}) \end{aligned}$$

where:

• $A^{x}, A^{y}, A^{z}$ are random invertible affine mappings $\mathbb {Z}_{2}^{127} \rightarrow \mathbb {Z}_{2}^{127}$. In the remainder we will decompose $A^{x}$ as a linear map $L^{x}$ followed by the addition of a constant $C^{x}$, and likewise for $A^{y}, A^{z}$.

• $\chi$ is as above.

• P is the perturbation. It is a mapping $\{0,1\}^{127} \rightarrow \{0,1\}^{127}$. For 24 output bits at a fixed position, it is equal to a random polynomial of degree 4. On the remaining 103 bits, it is equal to zero.

Since $\chi$ has degree only 2, the overall degree of the encryption function is 4. The public key of the scheme is the encryption function itself, given in the form of degree 4 polynomials in the input bits, for each output bit. The private key is the triplet of affine maps $(A^{x},A^{y},A^{z})$.

Due to the perturbation, the scheme is not actually invertible. To circumvent this, some redundancy is required in the plaintext, and the 24 bits of perturbation must be guessed during decryption. The correct guess is determined first by checking whether the resulting plaintext has the required redundancy, and second by recomputing the ciphertext from the tentative plaintext and checking that it matches. This is not relevant to our attack, and we refer the reader to [BBK14] for more information.

4 Structural Attack on Black-Box $\mathsf {ASASA}$

Our goal in this section is to recover the secret key of the black-box $\mathsf {ASASA}$ scheme, in a chosen-plaintext model. For this purpose, we begin by peeling off the last linear layer, $A^{z}$. Once $A^{z}$ is removed, we obtain an $\mathsf {ASAS}$ structure, which can be broken using Biryukov and Shamir’s techniques [BS01] in negligible time. Thus the critical step is the first one.

4.1 Attack Overview

Before progressing further, it is important to observe that the secret key of the scheme is not uniquely defined. In particular, we are free to compose the input and output of any S-box with a linear mapping of our choosing, and use the result in place of the original S-box, as long as we modify the surrounding linear layers accordingly. Thus, S-boxes are essentially defined up to linear equivalence. When we claim to recover the secret key, this should be understood as recovering an equivalent secret key; that is, any secret key that results in an encryption function identical to the black-box instance under attack.

In particular, in order to remove the last linear layer of the scheme, it is enough to determine, for each S-box, the m-dimensional subspace corresponding to its image through the last linear layer. Indeed, we are free to pick any basis of this m-dimensional subspace, and assert that each element of this basis is equal to one bit at the output of the S-box. This will be correct, up to composing the output of the S-box with some invertible linear mapping, and composing the input of the last linear layer with the inverse mapping; which has no bearing on the encryption output.

Thus, peeling off $A^{z}$ amounts to finding the image space of each S-box through $A^{z}$. For this purpose, we will look for linear masks $a, b \in \{0,1\}^{n}$ over the output of the cipher, such that the two dot products $\langle F | a \rangle$ and $\langle F | b \rangle$ of the encryption function F along each mask are each equal to one bit at the output of the same S-box in the last nonlinear layer $S^{y}$. Let us denote the set of such pairs (a, b) by $\mathcal {S}$ (as in “solution”).

In order to compute $\mathcal {S}$, the core property at play is that if masks a and b are as required, then the binary product $\langle F | a \rangle \langle F | b \rangle$ has degree only $(m-1)^{2}$ over the input variables of the cipher (meaning that $\langle F | a \rangle \langle F | b \rangle$ sums to zero over any cube of dimension $(m-1)^{2}+1$), whereas it has degree $2(m-1)^{2}$ in general.

We define the two linear masks a and b we are looking for as two vectors of binary unknowns. Then $f(a,b) = \langle F | a \rangle \langle F | b \rangle$ may be expressed as a quadratic polynomial over these unknowns, whose coefficients are $\langle F | e_{i} \rangle \langle F | e_{j}\rangle$ for $(e_{i})$ the canonical basis of $\mathbb {Z}_{2}^{n}$. Now, the fact that f(a, b) sums to zero over some cube C gives us a quadratic condition on (a, b), whose coefficients are $\sum _{c \in C}\langle F(c) | e_{i} \rangle \langle F(c) | e_{j}\rangle$.

By computing $n(n-1)/2$ cubes of dimension $(m-1)^{2}+1$, we thus derive $n(n-1)/2$ quadratic conditions on (a, b). The resulting system can then be solved by relinearization. This yields the linear space K spanned by $\mathcal {S}$.

However we want to recover $\mathcal {S}$, rather its linear combinations K. Thus in a second step, we compute $\mathcal {S}$ as $\mathcal {S} = K \cap P$, where P is essentially the set of elements that stem from a single product of two masks a and b. While P is not a linear space, by guessing a few bits of the masks a, b, we can get many linear constraints on the elements of P satisfying these guesses, and intersect these linear constraints with K.

The first step may be regarded as the core of the attack, and it is also the computationally most expensive: essentially we need to encrypt plaintexts spanning $n(n-1)/2$ cubes of dimension $(m-1)^{2}+1$. We recall that in the actual black-box scheme of [BBK14], we have S-boxes over $m = 8$ bits, and the total block size is $n = 128$ bits, covered by $k = 16$ S-boxes, so the complexity is dominated by the computation of the encryption function over $2^{13}$ cubes of dimension 50, i.e. $2^{63}$ encryptions.

4.2 Description of the Attack

We use the notation of Sect. 3.1: let $F = A^{z} \circ S^{y} \circ A^{y} \circ S^{x} \circ A^{x}$ denote the encryption function. We are interested in linear masks $a \in \{0,1\}^{n}$ such that $\langle F | a \rangle$ depends only on the output of one S-box. Since $\langle F | a \rangle = \langle S^{y} \circ A^{y} \circ S^{x} \circ A^{x} | (A^{z}) ^\mathrm{T} a \rangle$, this is equivalent to saying that the active bits of $(A^{z}) ^\mathrm{T}a$ span a single S-box.

In fact we are searching for the set $\mathcal {S}$ of pairs of masks (a, b) such that $(A^{z}) ^\mathrm{T}a$ and $(A^{z}) ^\mathrm{T}b$ span the same single S-box. Formally, if we let $(e_{0},\dots ,e_{n-1})$ be the canonical basis of $\mathbb {Z}_{2}^{n}$, and let $O_{t} = \mathrm{span}\{e_{i} : mt \le i < m(t+1)\}$ be the span of the output of the t-th S-box, then:

$$\begin{aligned} \mathcal {S} = \{(a,b) \in \{0,1\}^{n} \times \{0,1\}^{n} : \exists \,t, (A^{z}) ^\mathrm{T}a \in O_{t} \text { and } (A^{z}) ^\mathrm{T}b \in O_{t}\} \end{aligned}$$

The core property exploited in the attack is that if (a, b) belongs to $\mathcal {S}$, then $\langle F | a \rangle \langle F | b \rangle$ has degree at most $(m-1)^{2}$, as shown by Lemma 2 below. On the other hand, if $(a,b) \not \in \mathcal {S}$, then $\langle F | a \rangle \langle F | b \rangle$ is akin to the product of two independent random polynomials of degree $(m-1)^{2}$, and it reaches degree $2 (m-1)^{2}$ with overwhelming probability.

Lemma 2

Let G be an invertible mapping $\{0,1\}^{m} \rightarrow \{0,1\}^{m}$ for $m>2$. For any two m-bit linear masks a and b, $H = \langle G | a \rangle \langle G | b \rangle$ has degree at most $m-1$.

Proof

It is clear that the degree cannot exceed m, since we depend on only m variables (and we live in $\mathbb {F}_{2}$). What we show is that it is less than $m-1$, as long as $m > 2$. If $a=0$ or $b=0$ or $a=b$, this is clear, so we can assume that a, b are linearly independent. Note that there is only one possible monomial of degree m, and its coefficient is equal to $\sum _{x \in \{0,1\}^{m}} H(x)$. So all we have to show is that this sum is zero.

Because G is invertible, G(x) spans each value in $\{0,1\}^{m}$ once as x spans $\{0,1\}^{m}$. As a consequence, the pair $(\langle G | a \rangle , \langle G | b \rangle )$ takes each of its 4 possible values an equal number of times. In particular, it takes the value (1, 1) exactly 1 / 4 of the time. Hence $\langle G | a \rangle \langle G | b \rangle$ takes the value 1 exactly $2^{m-2}$ times, which is even for $m>2$. Thus $\sum _{x \in \{0,1\}^{m}} H(x) = 0$ and we are done.   $\square$

In the remainder, we regard two masks a and b as two sequences of n binary unknowns $(a_{0},\dots ,a_{n-1})$ and $(b_{0},\dots ,b_{n-1})$.

Step 1: Kernel Computation. If a, b are as desired, $\langle F | a \rangle \langle F | b \rangle$ has degree at most $(m-1)^{2}$. Hence the sum of this product over a cube of dimension $(m-1)^{2}+1$ is zero, as this amounts to an order-$(m-1)^{2}+1$ differential of a degree $(m-1)^{2}$ function. Let then C denote a random cube of dimension $(m-1)^{2}+1$ – that is, a random affine space of dimension $(m-1)^{2}$+1, over $\{0,1\}^{n}$. We have:

$$\begin{aligned} \sum _{c \in C}\langle F(c) | a \rangle \langle F(c) | b \rangle&= \sum _{c \in C} \sum _{i < n}a_{i}F_{i}(c) \sum _{j < n} b_{j}F_{j}(c)\\&= \sum _{i,j < n} \Big (\sum _{c \in C} F_{i}(c)F_{j}(c)\Big ) a_{i}b_{j}\\&= \sum _{i < j < n} \Big (\sum _{c \in C} F_{i}(c)F_{j}(c)\Big ) (a_{i}b_{j} + a_{j}b_{i}) \end{aligned}$$

To deduce the last line, notice that $\sum _{c \in C} F_{i}F_{i} = 0$ since F has degree less than $\dim C$. Since the equation above really only says something about $a_{i}b_{j} + a_{j}b_{i}$ rather than $a_{i}b_{j}$ (which is unavoidable, since the roles of a and b are symmetric), we define $E = \mathbb {Z}_{2}^{n(n-1)/2}$, see its canonical basis as $e_{i,j}$ for $i < j < n$, and define $\lambda (a,b) \in E$ by: $\lambda (a,b)_{i,j} = a_{i}b_{j} + a_{j}b_{i}$. By convention we set $\lambda _{j,i} = \lambda _{i,j}$ and $\lambda _{i,i} = 0$. The previous equations tells us that knowing only the $n(n-1)/2$ bits $\sum _{c \in C} F_{i}(c)F_{j}(c)$ yields a quadratic condition on (a, b), and more specifically a linear condition on $\lambda (a,b)$. Whence we proceed as follows:

Let M be a binary matrix of size $(n^{2}/2)\times (n(n-1)/2)$, whose rows are separate outputs of Algorithm 1. Let K be the kernel of this matrix. Then for all $(a,b) \in \mathcal {S}$, $\lambda (a,b)$ is necessarily in K. Thus K contains the span of the $\lambda (a,b)$’s for $(a,b) \in \mathcal {S}$. Because M contains more than $n(n-1)/2$, with overwhelming probability K contains no other vector⁵. This is confirmed by our experiments.

Complexity Analysis. Overall, the dominant cost is to compute $2^{(m-1)^{2}+1}$ encryptions per cube, for $n^{2}/2$ cubes, which amounts to a total of $n^{2}2^{(m-1)^{2}}$ encryptions. With the parameters of [BBK14], this is $2^{63}$ encryptions. In practice, we could limit ourselves to dimension-$(m-1)^{2}+1$ subcubes of a single dimension-$(m-1)^{2}+2$ cube, which would cost only $2^{(m-1)^{2}+2}$ encryptions. However we would still need to sum (pairwise bit products of) ciphertexts for each subcube, so while this approach would certainly be an improvement in practice, we believe it is cleaner to simply state the complexity as $n^{2}2^{(m-1)^{2}}$ encryption equivalents.

Beside that, we also need to compute the kernel of a matrix of dimension $n(n-1)/2$, which incurs a cost of roughly $n^{6}/8$ basic linear operations. With the parameters of [BBK14], we need to invert a binary matrix of dimension $2^{13}$, costing around $2^{39}$ (in practice, highly optimized) operations, so this is negligible compared to the required number of encryptions.

Step 2: Extracting Masks. Let:

$$\begin{aligned} P = \{\lambda \in E : \exists \,a,b \in \{0,1\}^{n}, \lambda = \lambda (a,b)\} \end{aligned}$$

Clearly we have $\lambda (\mathcal {S}) \subseteq K \cap P$. In fact, we assume $\lambda (\mathcal {S}) = K \cap P$, which is confirmed by our experiments. We now want to compute $K \cap P$.

However we do not need to enumerate the whole intersection $K \cap P$ directly: for our purpose, it suffices to recover enough elements of $\lambda (\mathcal {S})$ such that the corresponding masks span the output space of all S-boxes. Indeed, recall that our end goal is merely to find the image of all k S-boxes through the last linear layer. Thus, in the remainder, we explain how to find a random element in $K\cap P$. Once we have found km linearly independent masks in this manner, we will be done.

The general idea to find a random element of $K \cap P$ is as follows. We begin by guessing the value of a few pairs $(a_{i},b_{i})$. This yields linear constraints on the $\lambda _{i,j}$’s. As an example, if $(a_{0},b_{0}) = (0,0)$, then $\forall i, \lambda _{0,i} = 0$. Because the constraints are linear and so is the space K, finding the elements of K satisfying the constraints only involves basic linear algebra. Thus, all we have to do is guess enough constraints to single out an element of $\mathcal {S}$ with constant probability, and recover that element as the one-dimensional subspace of K satisfying the constraints.

More precisely, assume we guess 2r bits of a, b as:

$$\begin{aligned} a_{0}, \dots , a_{r-1}&= \alpha _{0}, \dots , \alpha _{r-1}\\ b_{0}, \dots , b_{r-1}&= \beta _{0}, \dots , \beta _{r-1} \end{aligned}$$

We view pairs $(\alpha _{i},\beta _{i})$ as elements of $\mathbb {Z}_{2}^{2}$. Assume there exists some linear dependency between the $(\alpha _{i},\beta _{i})$’s: that is, for some $(\mu _{i}) \in \{0,1\}^{r}$:

$$\begin{aligned} \sum _{i=0}^{r-1} \mu _{i}(\alpha _{i},\beta _{i}) = (0,0) \end{aligned}$$

Then for all $j < n$, we have:

$$\begin{aligned} \sum _{i=0}^{r-1} \mu _{i}\lambda _{i,j} = b_{j}\sum _{i=0}^{r-1} \mu _{i}a_{i} + a_{j}\sum _{i=0}^{r-1} \mu _{i}b_{i} = 0 \end{aligned}$$

(1)

Now, since $\mathbb {Z}_{2}^{2}$ has dimension only 2, we can be sure that there exist $r-2$ independent linear relations between the $(\alpha _{i},\beta _{i})$’s, from which we deduce as above $(r-2)n$ linear relations on the $\lambda _{i,j}$’s. In the full version of this article (see Sect. 1.3), we prove that at least $(r-2)(n-r)$ of these relations are linearly independent.

Now, the cardinality of $\mathcal {S}$ is $k(2^{m}-1)(2^{m}-2) \approx k2^{2m}$. Hence if we choose $r = \lfloor \log (|\mathcal {S}|)/2 \rfloor \approx m + \frac{1}{2}\log k$, and randomly guess the values of $(a_{i},b_{i})$ for $i < r$, then we can expect that with constant probability there exists exactly one element in $\mathcal {S}$ satisfying our guess. More precisely, each element has a probability (close to) $2^{-2\lfloor |\mathcal {S}|/2 \rfloor }\approx 2^{-|\mathcal {S}|}$ of fitting our guess of 2r bits, so this probability is close to $|\mathcal {S}|\big (|\mathcal {S}|^{-1}(1-|\mathcal {S}|^{-1})^{|\mathcal {S}|-1}\big ) \approx 1/e$. Thus, if we denote by T the subspace of E of vectors satisfying the linear constraints induced by our guess, with probability roughly 1 / 3, $\lambda (\mathcal {S}) \cap T$ contains a single element.

On the other hand, K is generated by pairs of masks corresponding to distinct bits for each S-box in $S^{y}$. Hence $\dim K = km(m-1)/2 = n(m-1)/2$. As shown earlier, from our 2r guesses, we deduce (at least) $(r-2)(n-r)$ linear conditions on the $(\lambda _{i,j})$’s, so $\mathrm{codim}\;T \ge (r-2)(n-r)$. Since we chose $r = m+\frac{1}{2}\log k$, this means:

$$\begin{aligned}&\mathrm{codim}\;T \ge (m - 2 + \frac{1}{2}\log k) \cdot (n-m-\frac{1}{2}\log k)\\&\quad \dim K = (m-1) \qquad \qquad \cdot (n/2) \end{aligned}$$

Thus, having $\frac{1}{2}\log k \ge 1$, i.e. $k \ge 4$, and $m+\frac{1}{2}\log k \ge n/2$, which is easily the case with concrete parameters $m=8$, $k=16$, $n=128$, we have $\mathrm{codim}\;T \ge \dim K$, and so $K \cap T$ is not expected to contain any extra vector beside the span of $\lambda (\mathcal {S}) \cap T$. This is confirmed by our experiments.

In summary, if we pick $r = m + \frac{1}{2}\log k$ and randomly guess the first r pairs of bits $(a_{i},b_{i})$, then with probability close to 1 / e, $K \cap T$ contains only a single vector, which belongs to $\lambda (\mathcal {S}) \cap T$ and in particular to $\lambda (\mathcal {S})$. In practice it may be worthwhile to guess a little less then $m + \frac{1}{2}\log k$ pairs to ensure $K \cap T$ is nonzero, then guess more as needed to single out a solution. Once we have a single element in $\lambda (\mathcal {S})$, it is easy to recover the two masks (a, b) it stems from⁶.

In the end, we recover two masks (a, b) coming from the same S-box. If we repeat this process $n=km$ times on average, the masks we recover will span the output of each S-box (indeed we recover 2 masks each time, so n tries is more than enough with high probability). Furthermore, checking whether two masks belong to the same S-box is very cheap (for two masks a, b, we only need to check whether $\lambda (a,b)$ is in K), so we recover the output space of each S-box.

Complexity Analysis. In order to get a random element in $\mathcal {S}$, each guess of 2r bits yields roughly 1 / 3 chance of recovering an element by intersecting linear spaces K and T. Since K has dimension $n(m-1)/2$, the complexity is roughly $(n(m-1)/2)^{3}$ per try, and we need 3 tries on average for one success. Then the process must be repeated n times. Thus the complexity may be evaluated to roughly $\frac{3}{8}n^{4}(m-1)^{3}$ basic linear operations. With the parameters of [BBK14], this amounts to $2^{36}$ linear operations, so this step is negligible compared to Step 1 (and quite practical besides).

Before closing this section, we note that our attack does not really depend on the randomness of the S-boxes or affine layers. All that is required of the S-boxes is that the degree of $z_{i}z_{j}$ vary depending on whether i and j belong to the same S-box. This makes the attack quite general, in the same sense as the structural attack of [BS01].

5 Attacks on the $\chi$-based Public-Key Scheme

In this section, our goal is to recover the private key of the $\chi$-based $\mathsf {ASASA}$ scheme, using only the public key. For this purpose, we peel off one layer at a time, starting with the last affine layer $A^{z}$. We actually propose two different ways to achieve this. The first attack is our main algebraic attack from Sect. 4, with some modifications to account for the peculiarity of $\chi$ and the presence of the perturbation. It is presented in Sect. 5.1. The second attack reduces the problem to an instance of $\mathsf {LPN}$, and is presented in Sect. 5.2. Once the last affine layer has been removed with either attack, we move on to attacking the remaining layers in Sect. 5.3.

5.1 Algebraic Attack on the $\chi$ Scheme

The $\chi$ scheme can be attacked in exactly the same manner as the black-box scheme in Sect. 4. Using the notations of Sect. 3.1, we have:

$$\begin{aligned} z_{i}z_{i+1}&= (y'_{i} + \overline{y'_{i+1}}y'_{i+2})\cdot (y'_{i+1} + \overline{y'_{i+2}}y'_{i+3})\\&= y'_{i}y'_{i+1} + y'_{i}\overline{y'_{i+2}}y'_{i+3} \end{aligned}$$

Here the crucial point is that $y'_{i+2}$ is shared by the only degree-4 term of both sides. Thus the degree of $z_{i}z_{i+1}$ is bounded by 6. Likewise, the degree of $z_{i+1}(z_{i}+z_{i+2}) = z_{i}z_{i+1} + z_{i+1}z_{i+2}$ is also bounded by 6, as the sum of two products of the previous form. On the other hand, any product of linear combinations $(\sum \alpha _{i}z_{i})(\sum \beta _{i}z_{i})$ not of the previous two forms does not share common $y'_{i}$’s in its higher-degree terms, so no simplification occurs, and the product reaches degree 8 with overwhelming probability.

As a result, we can proceed as in Sect. 4. Let $n = 127$ be the size of the scheme, $p = 24$ the number of perturbation polynomials. The positions of the p perturbation polynomials are not defined in the original paper; in the sequel we assume that they are next to each other. Other choices of positions increase the tedium of the attack rather than its difficulty. A brief discussion of random positions for perturbation polynomials is offered in the full version of this article (see Sect. 1.3). Due to the rotational symmetry of $\chi$, the positions of the perturbed bits is only defined modulo rotational symmetry; for convenience, we assume that perturbed bits are at positions $z_{n-p}$ to $z_{n-1}$.

The full attack presented below has been verified experimentally for small values of n.

Step 1: Kernel Computation. We fill the rows of an $n(n-1)/2 \times n(n-1)/2$ matrix with separate outputs of Algorithm 1, with the difference that the dimension of cubes in the algorithm is only 7 (instead of $(m-1)^{2}+1 = 50$ in the black-box case). Then we compute the kernel K of this matrix. Since $n(n-1)/2 \approx 2^{13}$ the complexity of this step is roughly $2^{39}$ basic linear operations.

Step 2: Extracting Masks. The second step is to intersect K with the set P of elements of the form $\lambda (a,b)$ to recover actual solutions (see Sect. 4, step 2). In Sect. 4 we were content with finding random elements of $K \cap P$. Now we want to find all of them. To do so, instead of guessing a few pairs $(a_{i},b_{i})$ as earlier, we exhaust all possibilities for $(a_{0},b_{0})$ then $(a_{1},b_{1})$ and so forth along a tree-based search. For each branch, we stop when the dimension of K intersected with the linear constraints stemming from our guesses of $(a_{i},b_{i})$’s is reduced to 1. Each branch yields a solution $\lambda (a,b)$, from which the two masks a and b can be easily recovered.

Step 3: Sorting Masks. Let $a_{i} = ((L^{z}) ^\mathrm{T})^{-1} e_{i}$ be the linear mask such that $z_{i} = \langle F | a_{i} \rangle$ (for the sake of clarity we first assume $C^{z} = 0$; this has no impact on the attack until step 4 in Sect. 5.3 where we will recover $C^{z}$). At this point we have recovered the set $\mathcal {S}$ of all (unordered) pairs of masks $\{a_{i},a_{i+1}\}$ and $\{a_{i},a_{i-1}+a_{i+1}\}$ for $i<n-p$, i.e. such that the corresponding $z_{i}$’s are not perturbed. Now we want to distinguish masks $a_{i-1}+a_{i+1}$ from masks $a_{i}$. For each i such that $z_{i-1}, z_{i}, z_{i+1}$ are not perturbed, this is easy enough, as $a_{i}$ appears exactly three times among unordered pairs in $\mathcal {S}$: namely in the pairs $\{a_{i},a_{i-1}\}$, $\{a_{i},a_{i+2}\}$ and $\{a_{i},a_{i-1}+a_{i+1}\}$; whereas masks of the form $a_{i-1}+a_{i+1}$ appear only once, in $\{a_{i-1}+a_{i+1},a_{i}\}$.

Thus we have recovered every $a_{i}$ for which $z_{i-1}, z_{i}, z_{i+1}$ are not perturbed. Since perturbed bits are next to each other, we have recovered all unperturbed $a_{i}$’s save the two $a_{i}$’s on the outer edge of the perturbation, i.e. $a_{0}$ and $a_{n-p-1}$. We can also order all recovered $a_{i}$’s simply by checking whether $\{a_{i},a_{i+1}\}$ is in $\mathcal {S}$. In other words, we look at $\mathcal {S}$ as the set of edges of a graph whose vertices are the elements of pairs in $\mathcal {S}$; then the chain $(a_{1},\dots ,a_{n-p-2})$ is simply the longest path in this graph. In fact we recover $(a_{1},\dots ,a_{n-p-2})$, minus its direction: that is, so far, we cannot distinguish it from $(a_{n-p-2},\dots ,a_{1})$. If we look at the neighbours of the end points of the path, we also recover $\{a_{0},a_{0}+a_{2}\}$ and $\{a_{n-p-1},a_{n-p-3}+a_{n-p-1}\}$. However we are not equipped to tell apart the members of each pair with only $\mathcal {S}$ at our disposal.

To find $a_{0}$ in $\{a_{0},a_{0}+a_{2}\}$ (and likewise $a_{n-p-2}$ in $\{a_{n-p-1},a_{n-p-3}+a_{n-p-1}\}$), a very efficient technique is to anticipate a little and use the distinguisher in Sect. 5.2. Namely, in short, we differentiate the encryption function F twice using two fixed random input differences $\delta _{1} \not = \delta _{2}$, and check whether for a fraction 1 / 4 of possible choices of $(\delta _{1}, \delta _{2})$, $\langle \partial ^{2}F/\partial \delta _{1} \partial \delta _{2}| x \rangle$ is equal to a constant with bias $2^{-4}$: this property holds if and only if x is one of the $a_{i}$’s. This only requires around $2^{16}$ encryptions for each choice of $(\delta _{1}, \delta _{2})$, and thus completes in negligible time. Another more self-contained approach is to move on to the next step (in Sect. 5.3), where the algorithm we use is executed separately on each recovered mask $a_{i}$, and fails for $a_{0}+a_{2}$ but not $a_{1}$. However this would be slower in practice.

We assume either solution was chosen and we now know the whole ordered chain $(a_{0},\dots ,a_{n-p-1})$ of masks corresponding to unperturbed bits. At this stage we are only missing the direction of the chain, i.e. we cannot distinguish $(a_{0},\dots ,a_{n-p-1})$ from $(a_{n-p-1},\dots ,a_{0})$. This will be corrected at the next step.

As mentioned earlier, we propose two different techniques to recover the first linear layer of the $\chi$ scheme: one algebraic technique, and another based on $\mathsf {LPN}$. We have now just completed the algebraic technique. In the next section we present the $\mathsf {LPN}$-based technique. Afterwards we will move on to the remaining steps, which are common to both techniques, and fully break the cipher with the knowledge of $(a_{0},\dots ,a_{n-p-1})$, in Sect. 5.3.

5.2 $\mathsf {LPN}$-based attack on the $\chi$ scheme

We now present a different approach to remove the last linear layer of the $\chi$ scheme. This approach relies on the fact that each output bit of $\chi$ is almost linear, in the sense that the only nonlinear component is the product of two input bits. In particular this nonlinear component is zero with probability 3 / 4. The idea is then to treat this nonlinear component as random noise. To achieve this we differentiate the encryption function F twice. So the first $\mathsf {ASA}$ layers of $F''$ yield a constant; then $\mathsf {ASAS}$ is a noisy constant due to the weak nonlinearity; and $\mathsf {ASASA}$ is a noisy constant accessed through $A^{z}$. This allows us to reduce the problem of recovering $A^{z}$ to (a close variant of) an $\mathsf {LPN}$ instance with tractable parameters.

We now describe the attack in detail. First, pick two distinct random differences $\delta _{1}, \delta _{2} \in \{0,1\}^{n}$. Then compute the order 2 differential of the encryption function along these two differences. That is, let $F'' = \partial F / \partial \delta _{1} \partial \delta _{2}$. This second-order differential is constant at the output of $F^{y'} = A^{y} \circ \chi \circ A^{x}$, since $\chi$ has degree only two:

Now if we look at a single bit at the output of $F^{z} = \chi \circ F^{y'}$, we have:

$$\begin{aligned} (F^{z})''_{i}(x) = (F^{y'})''_{i}(x)&+ \overline{F^{y'}_{i+1}}F^{y'}_{i+2}(x) + \overline{F^{y'}_{i+1}}F^{y'}_{i+2}(x+\delta _{1})\nonumber \\&+ \overline{F^{y'}_{i+1}}F^{y'}_{i+2}(x+\delta _{2}) + \overline{F^{y'}_{i+1}}F^{y'}_{i+2}(x+\delta _{1}+\delta _{2}) \end{aligned}$$

(2)

That is, a bit at the output of $(F^{z})''$ still sums up to a constant, plus the sum of four bit products. If we look at each product as an independent random binary variable that is zero with probability 3 / 4, i.e. bias $2^{-1}$, then by the Piling-up Lemma (Lemma 1) the sum is equal to zero with bias $2^{-4}$.

Experiments show that modeling the four products as independent is not quite accurate: a significant discrepancy is introduced by the fact that the four inputs of the products sum up to a constant. For the sake of clarity, we will disregard this for now and pretend that the four products are independent. We will come back to this issue later on.

Now a single linear layer remains between $(F^{z})''$ and $F''$. Let $s_{i} \in \{0,1\}^{n}$ be the linear mask such that $\langle F | s_{i} \rangle = F^{z}_{i}$ (once again we assume $C^{z} = 0$, and postpone taking $C^{z}$ into account until step 4 of the attack). Then $\langle F'' | s_{i} \rangle$ is equal to a constant with bias $2^{-4}$. Now let us compute N different outputs of $F''$ for some N to be determined later, which costs 4N calls to the encryption function F. Let us stack these N outputs in an $N \times n$ matrix A.

Then we know that $A \cdot s_{i}$ is either the all-zero or the all-one vector (depending on $(F^{y'})''_{i}$) plus a noise of bias $2^{-4}$. Thus finding $s_{i}$ is essentially an $\mathsf {LPN}$ problem with dimension $n = 127$ and bias $2^{-4}$ (i.e. noise $1/2 + 2^{-5}$). Of course this is not quite an $\mathsf {LPN}$ instance: A is not uniform, there are n solutions instead of one, and there is no output vector b (although we could isolate the last column of A and define it as the output vector). However in practice none of this should hinder the performance of a $\mathsf {BKW}$ algorithm [BKW03]. Thus we make the heuristic assumption that $\mathsf {BKW}$ performs here as it would on a standard $\mathsf {LPN}$ instance⁷.

In the end, we recover the masks $s_{i}$ such that $z_{i} = \langle F | s_{i} \rangle$. Before moving on to the next stage of the attack, we go back to the earlier independence assumption.

Dependency Between the Four Products. In the reasoning above, we have modeled the four bit products in Eq. 2 as independent binary random variables with bias $2^{-1}$. That is, we assumed the four products would behave as:

$$\begin{aligned} \varPi = W_{1}W_{2} + X_{1}X_{2} + Y_{1}Y_{2} + Z_{1}Z_{2} \end{aligned}$$

where $W_{i}, X_{i}, Y_{i}, Z_{i}$ are uniformly random independent binary variables. This yields an expectancy $\mathbb {E}[\varPi ]$ with bias $2^{-4}$. As noted above, this is not quite accurate, and we now provide a more precise model that matches with our experiments.

Since $F^{y'}$ has degree two, $(F^{y'})''$ is a constant, dependent only on $\delta _{1}$ and $\delta _{2}$. This implies that in the previous formula, we have $W_{1} + X_{1} + Y_{1} + Z_{1} = (F^{y'})''_{i+1}$ and $W_{2} + X_{2} + Y_{2} + Z_{2} = (F^{y'})''_{i+2}$. To capture this, we look at:

$$\begin{aligned} E(c_{1},c_{2}) = \mathbb {E}[\varPi \, |\, W_{1} + X_{1} + Y_{1} + Z_{1} = c_{1}, W_{2} + X_{2} + Y_{2} + Z_{2} = c_{2}] \end{aligned}$$

It turns out that E(0, 0) has a stronger bias, close to $2^{-3}$; while perhaps surprisingly, E(a, b) for $(a,b) \not = (0,0)$ has bias zero, and is thus not suitable for our attack. Since $G''$ is essentially random, this means that our technique will work for only a fraction 1/4 of output bits. However, once we have recovered these output bits, we can easily change $\delta _{1}, \delta _{2}$ to obtain a new value of $G''$ and start over to find new output bits.

After k iterations of the above process, a given bit at position $i \le 127$ will have probability $(3/4)^{k}$ of remaining undiscovered. In order for all 103 unperturbed bits to be discovered with good probability, it is thus enough to perform $k = -\log (103)/\log (3/4) \approx 16$ iterations.

In the end we recover all linear masks $a_{i}$ corresponding to unperturbed bits at the output of the second $\chi$ layer; i.e. $a_{i} = ((A^{z}) ^\mathrm{T})^{-1} e_{i}$ for $0\le i < n-p$. The $a_{i}$’s can then be ordered into a chain $(a_{0},\dots ,a_{n-p-1})$ like in Sect. 5.1: neighbouring $a_{i}$’s are characterized by the fact that $\langle F | a_{i} \rangle \langle F | a_{i+1} \rangle$ has degree 6. We postpone distinguishing between $(a_{0},\dots ,a_{n-p-1})$ and $(a_{n-p-1},\dots ,a_{0})$ until Sect. 5.3.

Complexity Analysis. According to [LF06, Theorem 2], the number of samples needed to solve an $\mathsf {LPN}$ instance of dimension 127 and bias $2^{-4}$ is $N = 2^{44}$ (attained by setting $a = 3$ and $b = 43$). This requires $4N = 2^{46}$ encryptions. Moreover the dominant cost in the time complexity is to sort the $2^{44}$ samples a times, which requires roughly $3\cdot 44\cdot 2^{44} < 2^{52}$ basic operations. Finally, as noted above, we need to iterate the process 16 times to recover all unperturbed output bits with good probability, so our overall time complexity is increased to $2^{56}$ for $\mathsf {BKW}$, and $2^{50}$ encryptions to gather samples (slightly less with a structure sharing some plaintexts between the 16 iterations).

5.3 Peeling Off the Remaining $\mathsf {ASAS}$ layers

Using either the algebraic attack from Sect. 5.1 or the $\mathsf {LPN}$-based attack from Sect. 5.2, we have recovered the ordered chain $(a_{0},\dots ,a_{n-p-1})$ of linear masks such that $z_{i} = \langle F | a_{i} \rangle$. More exactly we have recovered either $(a_{0},\dots ,a_{n-p-1})$ or $(a_{n-p-1},\dots ,a_{0})$. For simplicity assume we have recovered $(a_{0},\dots ,a_{n-p-1})$. We will be able to distinguish between the two cases later on.

Essentially, this means we have peeled off the last affine layer $A^{z}$ — or more accurately, its linear component, over the unperturbed bits. Note that we cannot hope to recover $A^{z}$ over perturbed bits, as perturbed bits are by definition uniformly random polynomials of degree 4, and a linear combination of uniformly random polynomials of degree 4 is still a uniformly random polynomial of degree 4. In other words, the perturbation is essentially defined modulo affine equivalence.

We now move on to peeling off the remaining layers one by one. We point out once again that all steps below have been verified experimentally.

Step 4: from ${{\mathbf {\mathsf{{ASAS}}}}}$ to ${{\mathbf {\mathsf{{ASA.}}}}}$ The next layer we wish to peel off is a $\chi$ layer, which is entirely public. It may seem that applying $\chi ^{-1}$ should be enough. The difficulty arises from the fact that we do not know the full output of $\chi$, but only $n-p$ bits. Furthermore, if our goal was merely to decrypt some specific ciphertext, we could use other techniques, e.g. the fact that guessing one bit at the input of $\chi$ produces a cascade effect that allows recovery of all other input bits from output bits, regardless of the fact that the function has been truncated [Dae95]. However our goal is different: we want to recover the secret key, not just be able to decrypt messages. For this purpose we want to cleanly recover the input of $\chi$ in the form of degree 2 polynomials, for every unperturbed bit. We propose a technique to achieve this below.

From the previous step, we are in possession of $(a_{0},\dots ,a_{n-p-1})$ as defined above. Since by definition $z_{i} = \langle F | a_{i} \rangle$, this means we know $z_{i}$ for $0\le i < n-p$. Note that $y'_{i}$ has degree only 2, and we know that $z_{i} = y'_{i} + \overline{y'_{i+1}}y'_{i+2}$. In order to reverse the $\chi$ layer, we set out to recover $y'_{i}, y'_{i+1}, y'_{i+2}$ from knowledge of only $z_{i}$, by using the fact that $y'_{i}, y'_{i+1}, y'_{i+2}$ are quadratic.

This reduces to the following problem: given $P = A + B\cdot C$, where A, B, C are degree-2 polynomials, recover A, B, C. A closer look reveals that this problem is not possible exactly as stated, because P can be equivalently written in four different ways as: $A + B\cdot C$, $A + B + B\cdot \overline{C}$, $A + C + \overline{B}\cdot C$, $\overline{A + B + C} + \overline{B}\cdot \overline{C}$. On the other hand, we assume that for uniformly random A, B, C, the probability that P may be written in some unrelated way, i.e. $P = C + D\cdot E$ for C, D, E distinct from the previous four cases, is overwhelmingly low. This situation has never occurred in our experiments. Thus our problem reduces to:

Problem 1

Given $P = A + B\cdot C$, where A, B, C are degree-2 polynomials, recover degree-2 polynomials $A', B', C'$ such that $P = A' + B'\cdot C'$.

Our previous assumption says $A' \in \mathrm{span}\{A,B,C,1\}$; $B', C' \in \mathrm{span}\{B,C,1\}$. A straightforward approach to tackle this problem is to write B formally as a generic degree-2 polynomial with unknown coefficients. This gives us $k = 1 + n + n(n+1)/2 \approx n^{2}/2$ binary unknowns. Then we observe that $B\cdot P$ has degree only 4 (since $B^{2}=B$). Each term of degree 5 in $B\cdot P$ must have a zero coefficient, and thus each term gives us a linear constraint on the unknown coefficients of B. Collecting the constraints takes up negligible time, at which point we have a $k \times k$ matrix whose kernel is $\mathrm{span}\{B,C,1\}$. This gives us a few possibilities for $B', C'$, which we can filter by checking that $A' = P - B'\cdot C'$ has degree 2. The complexity of this approach boils down to inverting a k-dimensional binary matrix, which costs essentially $2^{3k}$ basic linear operations. In our case this amounts to $2^{39}$ basic linear operations. In the full version of this article (cf. Sect. 1.3), we present a more elaborate, but faster algorithm to solve Problem 1.

At this point, we have essentially removed the first two $\mathsf {ASASA}$ layers (assuming $C^{z}=0$, but this actually has no impact up to this point). More work is required to fully recover the layers, and analyze the remaining $\mathsf {ASA}$ layers. However the core of the attack is over. A detailed description of the remaining steps to fully recover the remaining layers is provided in the full version of this article (see Sect. 1.3).

6 A Practical Attack on White-Box $\mathsf {ASASA}$

In this section we show that the actual security of small-block $\mathsf {ASASA}$ ciphers is much lower than was estimated by Biryukov et al. We describe a procedure that attempts to recover the secret components of the structure, thus breaking the weak white-box security notion (Definition 2). Our algorithm relies rather heavily on heuristics, and evaluating its efficiency requires actual implementation. We focused on two instance, the 16-bit $\mathsf {ASASA} _{16}$ with claimed security of 64 bits and the 20-bit $\mathsf {ASASA} _{20}$ with claimed security of 100 bits. A straightforward implementation of our algorithm is able to recover the secret components of the 16-bit instance in under a minute and of the 20-bit instance in a few hours, when running on a standard PC. We recall that the source code is publicly available (see Sect. 1.3). For the remainder of the section, we implicitly use the 16-bit instance when describing the attack.

6.1 Attack Overview

Our general black-box attack from Sect. 4 does not apply, because the block size is too small to allow computing cubes of dimension 50. On the other hand, the small block size makes it possible to compute the distribution of output differences for a single input difference in very reasonable time. For instance, one can compute and store the entire difference distribution table (DDT) of a 16-bit cipher in under a second using just a standard PC.

Remark 1

Our attack makes use of the full codebook of the ciphers, which in general may be seen as a very strong requirement. This is however only natural in the case of attacking white-box implementations, as the user is actually required to be given the full codebook of the super S-boxes as part of the implementation.

From the results of Biryukov and Shamir [BS01], it is already enough to recover only one of the external affine (or linear) layers in order to break the security of $\mathsf {ASASA}$. Indeed, this allows to reduce the cipher to either of $\mathsf {ASAS}$ or $\mathsf {SASA}$, which can then be attacked in practical time using their method. Thus we focus on removing the first linear layer. In accordance with the opening remarks of Sect. 4.1, this amounts to finding the image space of each S-box through $(A^{x})^{-1}$.

The general idea of the attack is to create an oracle able to recognize whether an input difference $\delta$ activates one or two S-boxes in the first S-box layer $S^{x}$. More accurately, we create a ranking function $\mathcal {F}$ such that $\mathcal {F}(\delta )$ is expected to be significantly higher if $\delta$ activates only one S-box rather than two. We propose two choices for $\mathcal {F}$.

Both choices begin by computing the entire output difference distribution $D(\delta )$ for the input difference $\delta$, i.e. the row corresponding to $\delta$ in the DDT. Then the value of $\mathcal {F}(\delta )$ is computed from $D(\delta )$. Choices for $\mathcal {F}$ are heuristic, but experiments show they are quite efficient. We now present our two choices for $\mathcal {F}$.

Walsh Transform. The idea behind this version of the attack is quite intuitive. If $\delta$ activates only one S-box, then after the first $\mathsf {SA}$ layers, two inner states computed from any two plaintexts with input difference $\delta$ are equal on the output of the inactive S-box. Hence after the first $\mathsf {ASA}$ layers, they are equal along $2^{8}-1$ non-zero linear masks. Since these masks only traverse a single S-box layer before the output of the cipher, linear cryptanalysis [Mat94] tells us that we can expect some linear masks to be biased at the output of the cipher. On the other hand if both S-boxes are active in the first round, no such phenomenon occurs, and linear biases on the output differences are expected to be weaker.

In order to measure this difference, we propose to compute, for every output mask a, the value $f(a) = (\sum _{x \in \{0,1\}^{16}}\langle \partial F \partial \delta (x) | a\rangle )-2^{15}$ (where the sum is computed in $\mathbb {Z}$). That is, $2^{-15}f(a)$ is the bias of the output differences $D(\delta )$ along mask a. The function f can be computed efficiently, since it is precisely the Walsh transform of the characteristic function of $D(\delta )$, and we can use a fast Fourier transform algorithm. Then as a ranking function $\mathcal {F}$ we simply choose $\max (f)$, i.e. the highest bias among all output masks.

Number of Collisions. It turns out that performing the Walsh transform is not truly necessary. Indeed, the number of collisions in $D(\delta )$ is higher when $\delta$ activates only 1 S-box; where by number of collisions we mean $2^{15}$ minus the number of distinct values in $D(\delta )$. This may be understood as a consequence of the fact that whenever $\delta$ activates a single S-box, only $2^{7}$ output differences are possible after the first $\mathsf {ASA}$ layers; and depending on the properties of the active (random) S-box, the distribution between these differences may be quite uneven. Whereas if both S-boxes are active, $2^{15}$ differences are possible and the distribution is expected to be less skewed. Thus we pick as ranking function $\mathcal {F}$ the number of collisions in $D(\delta )$ in the previous sense.

Once we have chosen a ranking function $\mathcal {F}$, we simply compute the ranking of every possible input difference, sort the differences, and choose the highest 16 linearly independent differences according to our ranking. Our hope is that these differences only activate a single S-box. In a second step, we will group together differences that activate the same S-box. A more detailed description of the attack, together with a discussion of the results, is provided in the full version of this article (see Sect. 1.3).

7 Conclusion

We presented a new algebraic attack able to efficiently break both the $\chi$-based public-key cryptosystem and the secret-key scheme of [BBK14]. In addition we proposed another attack that heuristically reduces the key-recovery problem on the $\chi$ scheme to an easy instance of $\mathsf {LPN}$. In the case of the public-key scheme, both attacks go through regardless of the amount of perturbation. For both schemes, the attacks are quite structural (in the case of the black-box scheme, it is in fact structural in the sense of [BS01]), and seem difficult to patch. Finally, although the general attack on the black-box scheme does not carry over to the small-block instances used for white-bow designs, we also showed a very efficient dedicated attack on some of the small-block instances, casting a doubt on their general suitability for that purpose.