Abstract
We introduce the notion of asymmetric programmable hash functions (APHFs, for short), which adapts Programmable Hash Functions, introduced by Hofheinz and Kiltz at Crypto 2008, with two main differences. First, an APHF works over bilinear groups, and it is asymmetric in the sense that, while only secretly computable, it admits an isomorphic copy which is publicly computable. Second, in addition to the usual programmability, APHFs may have an alternative property that we call programmable pseudorandomness. In a nutshell, this property states that it is possible to embed a pseudorandom value as part of the function’s output, akin to a random oracle. In spite of the apparent limitation of being only secretly computable, APHFs turn out to be surprisingly powerful objects. We show that they can be used to generically implement both regular and linearly-homomorphic signature schemes in a simple and elegant way. More importantly, when instantiating these generic constructions with our concrete realizations of APHFs, we obtain: (1) the first linearly-homomorphic signature (in the standard model) whose public key is sub-linear in both the dataset size and the dimension of the signed vectors; (2) short signatures (in the standard model) whose public key is shorter than those by Hofheinz-Jager-Kiltz from Asiacrypt 2011, and essentially the same as those by Yamada, Hannoka, Kunihiro, (CT-RSA 2012).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Programmable Hash Functions. Programmable Hash Functions (PHFs) were introduced by Hofheinz and Kiltz [26] as an information theoretic tool to “mimic” the behavior of a random oracle in finite groups. In a nutshell, a PHF \({\mathsf {H}}\) is an efficiently computable function that maps suitable inputs (e.g., binary strings) into a group \(\mathbb G\), and can be generated in two different, indistinguishable, ways. In the standard modality, \({\mathsf {H}}\) hashes inputs X into group elements \({\mathsf {H}}(X) \in \mathbb G\). When generated in trapdoor mode, a trapdoor allows one to express every output in terms of two (user-specified) elements \(g, h \in \mathbb G\), i.e., one can compute two integers \(a_{X}, b_{X}\) such that \({\mathsf {H}}(X) = g^{a_X} h^{b_X}\). Finally, \({\mathsf {H}}\) is programmable in the sense that it is possible to program the behavior of \({\mathsf {H}}\) so that its outputs contain (or not) g with a certain probability. More precisely, \({\mathsf {H}}\) is said (m, n)-programmable if for all disjoint sets of inputs \(\{X_1, \ldots , X_m\}\) and \(\{Z_1, \ldots , Z_n\}\), the joint probability that \(\forall i, a_{X_i}=0\) and \( \forall j, a_{Z_j} \ne 0\) is significant (e.g., \(1/\mathsf{poly}(\lambda )\)). Programmability turns out to be particularly useful in several security proofs. For instance, consider a security proof where a signature on \({\mathsf {H}}(X)\) can be simulated as long as \(a_{X}=0\) (i.e., g does not appear) while a forgery on \({\mathsf {H}}(Z)\) can be successfully used if \(a_{Z} \ne 0\) (i.e., g does appear). Then one could rely on an (m, 1)-programmability of \({\mathsf {H}}\) to “hope” that all the queried messages \(X_1, \ldots , X_m\) are simulatable, i.e., \(\forall i, a_{X_i}=0\), while the forgery message Z is not, i.e., \(a_{Z} \ne 0\). PHFs essentially provide a nice abstraction of the so-called partitioning technique used in many cryptographic proofs.
1.1 Our Contribution
Asymmetric Programmable Hash Functions. We introduce the notion of asymmetric programmable hash functions (asymmetric PHFs) which modifies the original notion of PHFs [26] in two main ways. First, an asymmetric PHF \({\mathsf {H}}\) maps inputs into a bilinear group \(\mathbb G\) and is only secretly computable. At the same time, an isomorphic copy of \({\mathsf {H}}\) can be publicly computed in the target group \(\mathbb G_T\), i.e., anyone can compute \(e({\mathsf {H}}(X), g)\).Footnote 1 Second, when generated in trapdoor mode, for two given group elements \(g, h \in \mathbb G\) such that \(h=g^{z}\), the trapdoor allows one to write every \({\mathsf {H}}(X)\) as \(g^{c_{X}(z)}\) for a degree-d polynomial \(c_{X}(z)\).
We define two main programmability properties of asymmetric PHFs. The first one is an adaptation of the original programmability notion, and it says that \({\mathsf {H}}\) is (m, n, d)-programmable if it is (m, n)-programmable as before except that, instead of looking at the probability that \(a_{X}=0\), one now looks at whether \(c_{X,0}=0\), where \(c_{X,0}\) is the coefficient of the degree-0 term of the polynomial \(c_{X}(\cdot )\) obtained using the trapdoor.Footnote 2 The second programmability property is new and is called programmable pseudo-randomness. Roughly speaking, programmable pseudo-randomness says that one can program \({\mathsf {H}}\) so that the values \(g^{c_{X,0}}\) look random to any polynomially-bounded adversary who observes the public hash key and the outputs of \({\mathsf {H}}\) on a set of adaptively chosen inputs. This functionality turns out to be useful in security proofs where one needs to cancel some random values for simulation purposes (we explain this in slightly more detail later in the introduction). In other words, programmable pseudo-randomness provides another random-oracle-like property for standard model hash functions, that is to “hide” a PRF inside the hash function. This is crucial in our security proofs, and we believe it can have further applications.
Applications. In principle, secretly computable PHFs seem less versatile than regular PHFs. In this work, however, we show that, for applications such as digital signatures, asymmetric PHFs turn out to be more powerful than their publicly computable counterparts. Specifically, we show how to use asymmetric PHFs to realize both regular and linearly-homomorphic signatures secure in the standard model. Next, we show efficient realizations of asymmetric PHFs that, when plugged in our generic constructions, yield new and existing schemes that improve the state-of-the-art in the following way. First, we obtain the first linearly homomorphic signature scheme, secure in the standard model, achieving a public key which is sub-linear in both the dataset size and the dimension of the signed vectors. Second, we obtain regular signature schemes, matching the efficiency of the ones in [31], thus providing the shortest signatures in the standard model with a public key shorter than in [25].
In the following we elaborate more on these solutions.
Linearly-Homomorphic Signatures with Short Public Key in the Standard Model. Imagine a user Alice stores one or more datasets \(D_1, D_2, \ldots , D_{\ell }\) on a cloud server. Imagine also that some other user, Bob, is allowed to perform queries over Alice’s datasets, i.e., to compute one or more functions \(F_1, \ldots , F_{m}\) over any \(D_{i}\). The crucial requirement here is that Bob wants to be ensured about the correctness of the computation’s results \(F_j(D_i)\), even if the server is not trusted. An obvious way to do this (reliably) is to ask Alice to sign all her data \(D_i = m^{(i)}_1, \ldots , m^{(i)}_N\). Later, Bob can check the validity of the computation by (1) downloading the full dataset locally, (2) checking all the signatures and (3) redoing the computation from scratch. Efficiency-wise, this solution is clearly undesirable in terms of bandwidth, storage (Bob has to download and store potentially large amount of data) and computation (Bob has to recompute everything on his own).
A much better solution comes from the notion of homomorphic signatures [9]. These allow to overcome the first issue (bandwidth) in a very elegant way. Using such a scheme, Alice can sign \(m_1, \ldots , m_N\), thus producing signatures \(\sigma _1, \ldots , \sigma _N\), which can be verified exactly as ordinary signatures. In addition, the homomorphic property provides the extra feature that, given \(\sigma _1, \ldots , \sigma _N\) and some function \(F: \mathcal{M}^{N} \rightarrow \mathcal{M}\), one can compute a signature \(\sigma _{F,y}\) on the value \(y=F(m_1,\ldots , m_N)\) without knowledge of the secret signing key \(\mathsf{sk}\). In other words, for a set of signed messages and any function F, it is possible to provide \(y=F(m_1,\ldots , m_N)\) along with a signature \(\sigma _{F,y}\) vouching for the correctness of y. The security of homomorphic signatures guarantees that creating a signature  for a
for a  is computationally hard, unless one knows \(\mathsf{sk}\).
is computationally hard, unless one knows \(\mathsf{sk}\).
To solve the second issue and allow Bob to verify efficiently such signatures (i.e., by spending less time than that required to compute F), one can use homomorphic signatures with efficient verification, recently introduced in [15].
The notion of homomorphic signature was first introduced by Johnson et al. [28]. Since then several schemes have been proposed. The first schemes were homomorphic only for linear functions over vector spaces [1–3, 8, 10, 12–14, 17, 19, 30] and have nice applications to network coding and proofs of retrievability. More recent works proposed realizations that can support more expressive functionalities such as polynomials [9, 15] or general circuits of bounded polynomial depth [11, 21].
Despite the significant research work in the area, it is striking that all the existing homomorphic signature schemes that are proven secure in the standard model [1–3, 11, 13–15, 17, 21, 30] suffer from a public key that is at least linear in the size N of the signed datasets. On one hand, the cost of storing such large public key can be, in principle, amortized since the key can be re-used for multiple datasets. On the other hand, this limitation still represents a challenging open question from both a theoretical and a practical point of view. From a practical perspective, a linear public key might be simply unaffordable by a user Bob who has limited storage capacity. From a theoretical point of view, considered the state-of-the-art, it seems unclear whether achieving a standard-model scheme with a key of length o(N) is possible at all. Technically speaking, indeed, all these schemes in the standard model somehow rely on a public key as large as one dataset for simulation purposes. This essentially hints that any solution for this problem would require a novel proof strategy.
Our Contribution. We solve the above open problem by proposing the first standard-model homomorphic signature scheme that achieves a public key whose size is sub-linear in the maximal size N of the supported datasets. Slightly more in detail, we show how to use asymmetric PHFs in a generic fashion to construct a linearly-homomorphic signature scheme based on bilinear maps that can sign datasets, each consisting of up to N vectors of dimension T. The public key of our scheme mainly consists of the public hash keys of two asymmetric PHFs. By instantiating these using (one of) our concrete realizations we obtain a linearly-homomorphic signature with a public key of length \(O(\sqrt{N} + \sqrt{T})\). We stress that ours is also the first linearly-homomorphic scheme where the public key is sub-linear in the dimension T of the signed vectors. Concretely, if one considers applications with datasets of 1 million of elements and a security parameter of 128bits, previous solutions (e.g., [2, 14]) require a public key of at least 32 MB, whereas our solution simply works with a public key below 100 KB.
On the Power of Secretly-Computable PHFs. The main technical idea nderlying this result is a new proof technique that builds on asymmetric hash functions with programmable pseudo-randomness. We illustrate the technique via a toy example inspired by our linearly-homomorphic signature scheme. The scheme works over asymmetric bilinear groups \(\mathbb G_1, \mathbb G_2\), and with an asymmetric PHF \({\mathsf {H}}: [N] \rightarrow \mathbb G_1\) that has programmable pseudo-randomness w.r.t. \(d=1\). To sign a random message \(M \in \mathbb G_1\) w.r.t. a label \({\tau }\), one creates the signature
where z is the secret key. The signature is linearly-homomorphic – \(S_1 S_2 = ({\mathsf {H}}({\tau }_1) {\mathsf {H}}({\tau }_2) M)^{1/z}\), for \(M=M_1 M_2\) – and it can be efficiently checked using a pairing – \(e(S, g_2^z) = \prod _{i} e({\mathsf {H}}({\tau }_i), g_2) e(M, g_2) \) – and by relying on that \(e({\mathsf {H}}(\cdot ), g_2)\) is publicly computable.
The first interesting thing to note is that having \({\mathsf {H}}\) secretly computable is necessary: if \({\mathsf {H}}\) is public the scheme could be easily broken, e.g., choose  . Let us now show how to prove its security assuming that we want to do a reduction to the following assumption: given \(g_1, g_2, g_2^{z}\), the challenge is to compute \(W^{1/z} \in \mathbb G_1\) for \(W\ne 1\) of adversarial choice. Missing \(g_1^{z}\) seems to make hard the simulation of signatures since \(M, S \in \mathbb G_1\). However, we can use the trapdoor generation of \({\mathsf {H}}\) for \(d=1\) (that for asymmetric pairings takes \(g_1, h_1=g_1^{y_1}, g_2, h_2=g_2^{y_2}\) and allows to express \({\mathsf {H}}(X)=g_1^{c_{X}(y_1, y_2)}\)), by plugging \(h_1=1, h_2=g_2^{z}\). This allows to write every output as \({\mathsf {H}}({\tau }) = g_1^{c_{{\tau }}(z)} = g_1^{c_{{\tau },0} + c_{{\tau },1} z}\). Every signing query with label \({\tau }\) is simulated by setting \(M_{{\tau }}=g^{-c_{{\tau },0}}\) and \(S_{{\tau }} = (g_1^{c_{{\tau },1}})\). The signature is correctly distributed since (1) \(S_{{\tau }} = ({\mathsf {H}}({\tau }) \cdot M_{{\tau }})^{1/z}\), and (2) \(M_{\tau }\) looks random thanks to the programmable pseudo-randomness of \({\mathsf {H}}\). To conclude the proof, assume that the adversary comes up with a forgery
. Let us now show how to prove its security assuming that we want to do a reduction to the following assumption: given \(g_1, g_2, g_2^{z}\), the challenge is to compute \(W^{1/z} \in \mathbb G_1\) for \(W\ne 1\) of adversarial choice. Missing \(g_1^{z}\) seems to make hard the simulation of signatures since \(M, S \in \mathbb G_1\). However, we can use the trapdoor generation of \({\mathsf {H}}\) for \(d=1\) (that for asymmetric pairings takes \(g_1, h_1=g_1^{y_1}, g_2, h_2=g_2^{y_2}\) and allows to express \({\mathsf {H}}(X)=g_1^{c_{X}(y_1, y_2)}\)), by plugging \(h_1=1, h_2=g_2^{z}\). This allows to write every output as \({\mathsf {H}}({\tau }) = g_1^{c_{{\tau }}(z)} = g_1^{c_{{\tau },0} + c_{{\tau },1} z}\). Every signing query with label \({\tau }\) is simulated by setting \(M_{{\tau }}=g^{-c_{{\tau },0}}\) and \(S_{{\tau }} = (g_1^{c_{{\tau },1}})\). The signature is correctly distributed since (1) \(S_{{\tau }} = ({\mathsf {H}}({\tau }) \cdot M_{{\tau }})^{1/z}\), and (2) \(M_{\tau }\) looks random thanks to the programmable pseudo-randomness of \({\mathsf {H}}\). To conclude the proof, assume that the adversary comes up with a forgery  for label
for label  such that
such that  was already queried, and let \(\hat{S}, \hat{M}\) be the values in the simulation of the signing query for \({\tau }^*\). Now, \(\hat{S} = ({\mathsf {H}}({\tau }^*) \cdot \hat{M})^{1/z}\) holds by correctness, while \(S^* = ({\mathsf {H}}({\tau }^*) \cdot M^*)^{1/z}\) holds for
was already queried, and let \(\hat{S}, \hat{M}\) be the values in the simulation of the signing query for \({\tau }^*\). Now, \(\hat{S} = ({\mathsf {H}}({\tau }^*) \cdot \hat{M})^{1/z}\) holds by correctness, while \(S^* = ({\mathsf {H}}({\tau }^*) \cdot M^*)^{1/z}\) holds for  by definition of forgery. Then \((M^*/ \hat{M}, S^*/\hat{S})\) is clearly a solution to the above assumption. This essentially shows that we can sign as many M’s as the number of \({\tau }\)’s, that is N. And by using our construction \({\mathsf {H}}={\mathsf {H}}_\mathsf{sqrt}\) this is achievable with a key of length \(O(\sqrt{N})\). Let us stress that the above one is an incomplete proof sketch, that we give only to illustrate the core ideas of using programmable pseudo-randomness. We defer the reader to Sect. 4 for a precise description of our signature scheme and its security proof.
by definition of forgery. Then \((M^*/ \hat{M}, S^*/\hat{S})\) is clearly a solution to the above assumption. This essentially shows that we can sign as many M’s as the number of \({\tau }\)’s, that is N. And by using our construction \({\mathsf {H}}={\mathsf {H}}_\mathsf{sqrt}\) this is achievable with a key of length \(O(\sqrt{N})\). Let us stress that the above one is an incomplete proof sketch, that we give only to illustrate the core ideas of using programmable pseudo-randomness. We defer the reader to Sect. 4 for a precise description of our signature scheme and its security proof.
Short Signatures from Bilinear Maps in the Standard Model. Hofheinz and Kiltz [26] proposed efficient realizations of PHFs, and showed how to use them to obtain black-box proofs of several cryptographic primitives. Among these applications, they use PHFs to build generic, standard-model, signature schemes from the Strong RSA problem and the Strong q-Diffie Hellman problem. Somewhat interestingly, these schemes (in particular the ones over bilinear groups) can enjoy very short signatures. The remarkable contribution of the generic construction in [26] is that signatures can be made short by reducing the size \(\rho \) of the randomness used (and included) in the signature so that \(\rho \) can go beyond the birthday bound. Precisely, by using an (m, 1)-programmable hash function, m can control the size of the randomness so that the larger is m, the smaller is the randomness. However, although this would call for (m, 1)-PHFs with a large m, the original work [26] described PHFs realizations that are only (2, 1)-programmable.Footnote 3
Later, Hofheinz, Jager and Kiltz [25] showed constructions of (m, 1)-PHFs for any \(m \ge 1\). By choosing a larger m, these new PHFs realizations yield the shortest known signatures in the standard model. On the negative side, however, this also induces much larger public keys. For instance, to obtain a signature of 302 bits from bilinear maps, they need a public key of more than 8MB. The reason of such inefficiency is that their realizations of (deterministic) (m, 1)-PHFs have keys of length \(O(m^{2} \ell )\), where \(\ell \) is the bit size of the inputs. In a subsequent work, Yamada et al. [31] improved on this aspect by proposing a signature scheme with a public key of length \(O(m \sqrt{\ell })\). Their solution followed a different approach: instead of relying on (m, 1)-PHFs they obtained the signature by applying the Naor’s transformation [7] to a new identity-based key encapsulation mechanism (IBKEM).
Our Results. Our results are mainly two. First, we revisit the generic signature constructions of [25, 26] in order to work with asymmetric (m, 1, d)-PHFs. Our generic construction is very similar to that in [25, 26], and, as such, it inherits the same property: the larger is m, the shorter can be the randomness.
Second we show the construction of an asymmetric PHF, \({\mathsf {H}}_\mathsf{acfs}\), that is (m, 1, 2)-programmable and has a hash key consisting of \(O(m \sqrt{\ell })\) group elements. By plugging \({\mathsf {H}}_\mathsf{acfs}\) into our generic construction we immediately obtain standard-model signatures that achieve the same efficiency as the scheme of Yamada et al. [31]. Namely, they are the shortest standard model signature schemes with a public key of length \(O(m \sqrt{\ell })\), that concretely allows for signatures of 302bits and a public key of 50KB. One of our two schemes recover the one in [31]. In this sense we provide a different conceptual approach to construct such signatures. While Yamada et al. obtained this result by going through an IBKEM, our solution revisits the original Hofheinz-Kiltz’s idea of applying programmable functions.
Other Related Work. Hanaoka, Matsuda and Schuldt [23] show that there cannot be any black-box construction of a \((\mathsf{poly},1)\)-PHF. The latter result has been overcome by the recent work of Freire et al. [18] who propose a \((\mathsf{poly},1)\)-PHF based on multilinear maps. The latter result is obtained by slightly changing the definition of PHFs in order to work in the multilinear group setting. Their \((\mathsf{poly},1)\)-PHF leads to several applications, notably standard-model versions (over multilinear groups) of BLS signatures, the Boneh-Franklin IBE, and identity-based non-interactive key-exchange. While the notion of PHFs in the multilinear setting of [18] is different from our asymmetric PHFs (with the main difference being that ours are secretly computable), it is worth noting that the two notions have some relation. As we discuss in the full version of our paper, our asymmetric PHFs indeed imply PHFs in the bilinear setting (though carrying the same degree of programmability).
The idea of using bilinear maps to reduce the size of public keys was used previously by Haralambiev et al. [24] in the context of public-key encryption, and by Yamada et al. [31] in the context of digital signatures. We note that our solutions use a similar approach in the construction of APHFs, which however also include the important novelty of programmable pseudorandomness, that turned out to be crucial in our proofs for the linearly-homomorphic signature.
2 Preliminaries
Bilinear Groups and Complexity Assumptions. Let \(\lambda \in \mathbb N\) be a security parameter and let \(\mathcal{G}(1^\lambda )\) be an algorithm which takes as input the security parameter and outputs the description of (asymmetric) bilinear groups \(\mathsf{bgp}= (p, \mathbb G_1, \mathbb G_2, \mathbb G_T, e, g_1, g_2)\) where \(\mathbb G_1\), \(\mathbb G_2\) and \(\mathbb G_T\) are groups of the same prime order \(p > 2^\lambda \), \(g_1 \in \mathbb G_1\) and \(g_2 \in \mathbb G_2\) are two generators, and \(e: \mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T\) is an efficiently computable, non-degenerate, bilinear map, and there is no efficiently computable isomorphism between \(\mathbb G_1\) and \(\mathbb G_2\). We call such an algorithm \(\mathcal{G}\) a bilinear group generator. In the case \(\mathbb G_1 = \mathbb G_2\), the groups are said symmetric, else they are said asymmetric.
In our work we rely on specific complexity assumptions in such bilinear groups: q-Strong Diffie-Hellman [6], q-Diffie-Hellman-Inversion [5], and External DDH in \(\mathbb G_1\). For lack of space, we defer the interested reader to the corresponding references or the full version of our paper for their definition.
Finally, we introduce the following static assumption over asymmetric bilinear groups, that we call “Flexible Diffie-Hellman Inversion” (FDHI) for its similarity to Flexible Diffie-Hellman [22]. As we discuss in the full version of our paper, FDHI is hard in the generic bilinear group model.
Definition 1
(Flexible Diffie-Hellman Inversion Assumption). Let \(\mathcal{G}\) be a generator of asymmetric bilinear groups, and let \(\mathsf{bgp}= (p,\mathbb G_1, \mathbb G_2, \mathbb G_{T}, g_1, g_2, e) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{G}(1^{\lambda })\). We say that the Flexible Diffie-Hellman Inversion (FDHI) Assumption is \(\epsilon \)-hard for \(\mathcal{G}\) if for random \(z, r, v \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) and for every PPT adversary \(\mathcal{A}\):
3 Asymmetric Programmable Hash Functions
In this section we present our new notion of asymmetric programmable hash functions.
Let \(\mathsf{bgp}= (p, \mathbb G_1, \mathbb G_2, \mathbb G_T, g_1, g_2, e)\) be a family of asymmetric bilinear groups induced by a bilinear group generator \(\mathcal{G}(1^{\lambda })\) for a security parameter \(\lambda \in \mathbb N\).Footnote 4 An asymmetric group hash function \({\mathsf {H}}: \mathcal{X}\rightarrow \mathbb G_1\) consists of three PPT algorithms \(({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval},{\mathsf {H}}.\mathsf{PubEval})\) working as follows:
-
\({\mathsf {H}}.\mathsf{Gen}(1^\lambda , \mathsf{bgp}) \rightarrow (\mathsf{sek}, \mathsf{pek})\): on input the security parameter \(\lambda \in \mathbb N\) and a bilinear group description \(\mathsf{bgp}\), the PPT key generation algorithm outputs a (secret) evaluation key \(\mathsf{sek}\) and a (public) evaluation key \(\mathsf{pek}\).
-
\({\mathsf {H}}.\mathsf{PriEval}(\mathsf{sek}, X) \rightarrow Y \in \mathbb G_1\): given the secret evaluation key \(\mathsf{sek}\) and an input \(X \in \mathcal{X}\), the deterministic evaluation algorithm returns an output \(Y={\mathsf {H}}(X) \in \mathbb G_1\).
-
\({\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek}, X) \rightarrow \hat{Y} \in \mathbb G_{T}\): on input the public evaluation key \(\mathsf{pek}\) and an input \(X \in \mathcal{X}\), the public evaluation algorithm outputs a value \(\hat{Y} \in \mathbb G_{T}\) such that \(\hat{Y} = e({\mathsf {H}}(X), g_2)\).
For asymmetric hash functions satisfying the syntax described above, we define two different properties that model their possible programmability.
The first property is a generalization of the notion of programmable hash functions of [26, 27] to our asymmetric setting (i.e., where the function is only secretly-computatble), and to the more specific setting of bilinear groups. The basic idea is that it is possible to generate the function in a trapdoor-mode that allows one to express every output of \({\mathsf {H}}\) in relation to some specified group elements. In particular, the most useful fact of programmability is that for two arbitrary disjoint sets of inputs \(\bar{X}, \bar{Z} \subset \mathcal{X}\), the joint probability that some of these group elements appear in \({\mathsf {H}}(Z), \forall Z \in \bar{Z}\) and do not appear in \({\mathsf {H}}(X), \forall X \in \bar{X}\) is significant.
Definition 2
(Asymmetric Programmable Hash Functions). An asymmetric group hash function \({\mathsf {H}}=({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval},{\mathsf {H}}.\mathsf{PubEval})\) is \((m, n, d, \gamma , \delta )\) -programmable if there exist an efficient trapdoor generation algorithm \({\mathsf {H}}.\mathsf{TrapGen}\) and an efficient trapdoor evaluation algorithm \({\mathsf {H}}.\mathsf{TrapEval}\) such that:
-
Syntax: \({\mathsf {H}}.\mathsf{TrapGen}(1^{\lambda }, \mathsf{bgp}, \hat{g}_1, \hat{h}_1, \hat{g}_2, \hat{h}_2) \rightarrow (\mathsf{td}, \mathsf{pek})\) takes as input the security parameter \(\lambda \), bilinear group description \(\mathsf{bgp}\) and group elements \(\hat{g}_1, \hat{h}_1 \in \mathbb G_1, \hat{g}_2, \hat{h}_2 \in \mathbb G_2\), and it generates a public hash key \(\mathsf{pek}\) along with a trapdoor \(\mathsf{td}\). \({\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X) \rightarrow \varvec{c}_{X}\) takes as input the trapdoor information \(\mathsf{td}\) and an input \(X \in \mathcal{X}\), and outputs a vector of integer coefficients \(\varvec{c}_X = (c_0, \ldots , c_{d'}) \in \mathbb {Z}^{d'}\) of a 2-variate polynomial \(c_{X}(y_1, y_2)\) of degree \(\le d\).
-
Correctness: For all group elements \(\hat{g}_1, \hat{h}_1 \in \mathbb G_1, \hat{g}_2, \hat{h}_2 \in \mathbb G_2\) such that \(\hat{h}_1 = \hat{g}_1^{y_1}\) and \(\hat{h}_2 = \hat{g}_2^{y_2}\) for some \(y_1, y_2 \in \mathbb {Z}_p\), for all trapdoor keys \((\mathsf{td}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{TrapGen}(1^{\lambda }, \hat{g}_1, \hat{h}_1, \hat{g}_2, \hat{h}_2)\), and for all inputs \(X \in \mathcal{X}\), if \(\varvec{c}_{X} \leftarrow {\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X)\), then
$${\mathsf {H}}(X) = \hat{g}_1^{c_X(y_1, y_2)}$$ -
Statistically-Close Trapdoor Keys: For all generators \(\hat{g}_1, \hat{h}_1 \in \mathbb G_1,\hat{g}_2, \hat{h}_2 \in \mathbb G_2\) and for all \((\mathsf{sek}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{Gen}(1^{\lambda })\), \((\mathsf{td}, \mathsf{pek}') \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{TrapGen}(1^{\lambda }, \hat{g}_1, \hat{h}_1, \hat{g}_2, \hat{h}_2)\), the distribution of the public keys \(\mathsf{pek}\) and \(\mathsf{pek}'\) is within statistical distance \(\gamma \).
-
Well Distributed Logarithms: For all \(\hat{g}_1, \hat{h}_1 \in \mathbb G_1,\hat{g}_2, \hat{h}_2 \in \mathbb G_2\), all keys \((\mathsf{td}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{TrapGen}(1^{\lambda }, \hat{g}_1, \hat{h}_1, \hat{g}_2, \hat{h}_2)\), and all inputs \(X_1, \ldots , X_m \in \mathcal{X}\) and \(Z_1, \ldots , Z_n \in \mathcal{X}\) such that \(X_i \ne Z_j\) for all i, j, we have
$$\Pr [c_{X_1, 0} = \cdots = c_{X_m, 0} = 0 \; \wedge \; c_{Z_1, 0}, \ldots , c_{Z_n, 0} \ne 0] \ge \delta $$where \(\varvec{c}_{X_i} {\leftarrow }{\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X_i)\) and \(\varvec{c}_{Z_j} {\leftarrow }{\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, Z_j)\), and \(c_{X_i, 0}\) (resp. \(c_{Z_j, 0}\)) is the coefficient of the term of degree 0.
If \(\gamma \) is negligible and \(\delta \) is noticeable we simply say that \({\mathsf {H}}\) is (m, n, d)-programmable. Furthermore, if m (resp. n) is an arbitrary polynomial in \(\lambda \), then we say that \({\mathsf {H}}\) is \((\mathsf{poly}, n, d)\)-programmable (resp. \((m, \mathsf{poly}, d)\)-programmable). Finally, if \({\mathsf {H}}\) admits trapdoor algorithms that satisfy only the first three properties, then \({\mathsf {H}}\) is said simply \((d, \gamma )\)-programmable. Note that any \({\mathsf {H}}\) that is \((m,n,d,\gamma , \delta )\)-programmable is also \((d,\gamma )\)-programmable.
Programmable Pseudo-randomness. The second main programmability property that we define for asymmetric hash functions is quite different from the previous one. It is called programmable pseudo-randomness, and very intuitively it says that, when using the hash function in trapdoor mode, it is possible to “embed” a PRF into it. More precisely, the trapdoor algorithms satisfy programmable pseudo-randomness if they allow to generate keys such that even by observing \(\mathsf{pek}\) and \({\mathsf {H}}(X)\) for a bunch of inputs X, then the elements \(g_1^{c_{X,0}}\) look random. The formal definition follows:
Definition 3
(Asymmetric Hash Functions with Programmable Pseudorandomness). An asymmetric hash function \({\mathsf {H}}= ({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval}, {\mathsf {H}}.\mathsf{PubEval})\) has \((d, \gamma , \epsilon )\)-programmable pseudorandomness if there exist efficient trapdoor algorithms \({\mathsf {H}}.\mathsf{TrapGen}, {\mathsf {H}}.\mathsf{TrapEval}\) that satisfy the properties of syntax, correctness, and \(\gamma \)-statistically-close trapdoor keys as in Definition 2, and additionally satisfy the following property with parameter \(\epsilon \):
-
Pseudorandomness: Let \(b \in \{0,1\}\) and let \(\mathbf {Exp}_{\mathcal{A}, {\mathsf {H}}}^{PRH\text{- }b}(\lambda )\) be the following experiment between an adversary \(\mathcal{A}\) and a challenger.
-
1.
Generate \(\mathsf{bgp}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{G}(1^{\lambda })\), and run \(\mathcal{A}(\mathsf{bgp})\), that outputs two generators \(h_1 \in \mathbb G_1, h_2 \in \mathbb G_2\).
-
2.
Compute \((\mathsf{td}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{TrapGen}(1^{\lambda }, g_1, h_1, g_2, h_2)\) and run \(\mathcal{A}(\mathsf{pek})\) with access to the following oracle:
-
If \(b=0\), \(\mathcal{A}\) is given \(\mathcal{O}(\cdot )\) that on input \(X \in \mathcal{X}\) returns \({\mathsf {H}}(X) = g_1^{c_{X}(y_1, y_2)}\) and \(g_1^{c_{X,0}}\), where \(\varvec{c}_{X} {\leftarrow }{\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X)\);
-
If \(b=1\), \(\mathcal{A}\) is given \(\mathcal{R}(\cdot )\) that on input \(X \in \mathcal{X}\) returns \({\mathsf {H}}(X) = g_1^{c_{X}(y_1, y_2)}\) and \( g_1^{r_X}\), for a randomly chosen \(r_{X} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) (which is unique for every \(X\in \mathcal{X}\)).
-
-
3.
At the end the adversary outputs a bit \(b'\), and \(b'\) is returned as the output of the experiment.
Then we say that \({\mathsf {H}}.\mathsf{TrapGen}, {\mathsf {H}}.\mathsf{TrapEval}\) satisfy pseudo-randomness for \(\epsilon \), if for all PPT \(\mathcal{A}\)
$$\left| \Pr [\mathbf {Exp}_{\mathcal{A},{\mathsf {H}}}^{PRH\text{- }0}(\lambda )=1] - \Pr [\mathbf {Exp}_{\mathcal{A},{\mathsf {H}}}^{PRH\text{- }1}(\lambda )=1] \right| \le \epsilon $$where the probabilities are taken over all the random choices of \(\mathsf{TrapGen}\), the oracle \(\mathcal{R}\) and the adversary \(\mathcal{A}\).
-
1.
Other Variants of Programmability. Here we define two other variants of the programmability notion given in Definition 2. Formal definitions appear in the full version of our paper.
Weak Programmability. We consider a weak version of the above programmability property in which one fixes at key generation time the n inputs \(Z_j\) on which \(c_{Z_j,0} \ne 0\).
Remark 1
We remark that for those (deterministic) functions \({\mathsf {H}}\) whose domain \(\mathcal{X}\) has polynomial size any weak programmability property for an arbitrary \(m = \mathsf{poly}\) trivially holds with \(\delta =1\).
Degree- d Programmability. In our work we also consider a variant of the above definition in which the property of well distributed logarithms is stated with respect to the degree-d coefficients of the polynomials generated by \({\mathsf {H}}.\mathsf{TrapEval}\). In this case, we say that \({\mathsf {H}}\) is \((m, n, d, \gamma , \delta )\)-degree-d-programmable.
3.1 An Asymmetric PHF Based on Cover-Free Sets
In this section we present the construction of an asymmetric hash function, \({\mathsf {H}}_\mathsf{acfs}\), based on cover-free sets. Our construction uses ideas similar to the ones used by Hofheinz, Jager and Kiltz [25] to design a (regular) programmable hash function. Our construction extends these ideas with a technique that allows us to obtain a much shorter public key. Concretely, for binary inputs of size \(\ell \), the programmable hash function \({\mathsf {H}}_\mathsf{cfs}\) in [25] is (m, 1)-programmable with a hash key of length \(O(\ell m^{2})\). In contrast, our new construction \({\mathsf {H}}_\mathsf{acfs}\) is (m, 1)-programmable with a hash key of length \(O(m \sqrt{\ell })\). While such improvement is obtained at the price of obtaining the function in the secret-key model, our results of Sect. 5 show that asymmetric programmable hash are still useful to build short bilinear-map signatures, whose efficiency, in terms of signature’s and key’s length matches that of state-of-the-art schemes [31].
Before proceeding with describing our function, below we recall the notion of cover-free sets.
Cover-Free Families. If S, V are sets, we say that S does not cover V if \(S \not \supseteq V\). Let T, m, s be positive integers, and let \(F = \{F_i\}_{i \in [s]}\) be a family of subsets of [T]. A family F is said to be m -cover-free over [T], if for any subset \(I \subseteq [s]\) of cardinality at most m, then the union \(\cup _{i \in I} F_i\) does not cover \(F_j\) for all \(j \notin I\). More formally, for any \(I \subseteq [s]\) such that \(|I| \le m\), and any \(j \notin I\), \(\cup _{i \in I} F_i \not \supseteq F_j\). Furthermore, we say that F is w-uniform if every subset \(F_i\) in the family have size w. In our construction, we use the following fact from [16, 29]:
Lemma 1
([16, 29]). There is a deterministic polynomial time algorithm that, on input integers \(s=2^{\ell }\) and m, returns w, T, F where \(F = \{F_i\}_{i \in [s]}\) is a w-uniform, m-cover-free family over [T], for \(w = T/4m\) and \(T \le 16m^2 \ell \).
The Construction of \({\mathsf {H}}_\mathsf{acfs}\). Let \(\mathcal{G}(1^{\lambda })\) be a bilinear group generator, let \(\mathsf{bgp}= (p, \mathbb G_1, \mathbb G_2, \mathbb G_T, g_1, g_2, e)\) be an instance of bilinear group parameters generated by \(\mathcal{G}\). Let \(\ell = \ell (\lambda )\) and \(m = m(\lambda )\) be two polynomials in the security parameter. We set \(s = 2^{\ell }\), \(T = 16m^{2}\ell \), and \(w = T/4m\) as for Lemma 1, and define \(t = \lceil \sqrt{T} \rceil \). Note that every integer \(k \in [T]\) can be written as a pair of integers \((i,j) \in [t] \times [t]\) using some canonical mapping. For the sake of simplicity, sometimes we abuse notation and write \((i,j) \in [T]\) where \(i, j \in [t]\).
In the following we describe the asymmetric hash function \({\mathsf {H}}_\mathsf{acfs}= ({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval}, {\mathsf {H}}.\mathsf{PubEval})\) that maps \({\mathsf {H}}_\mathsf{acfs}: \mathcal{X}\rightarrow \mathbb G_1\) where \(\mathcal{X}=\{0,1\}^{\ell }\). In particular, every input \(X \in \{0,1\}^{\ell }\) is associated to a set \(F_i\), \(i \in [2^{\ell }]\), by interpreting X as an integer in \(\{0, \ldots , 2^{\ell }-1\}\) and by setting \(i = X+1\). We call \(F_{X}\) such subset associated to X.
-
\({\mathsf {H}}.\mathsf{Gen}(1^\lambda , \mathsf{bgp})\): for \(i=1\) to t, sample \(\alpha _i, \beta _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) and compute \(A_i = g_1^{\alpha _i}, B_i = g_2^{\beta _i}\). Finally, set \(\mathsf{sek}= \{\alpha _i, \beta _i\}_{i=1}^{t}\), \(\mathsf{pek}= \{A_i, B_i \}_{i=1}^{t}\), and return \((\mathsf{sek}, \mathsf{pek})\).
-
\({\mathsf {H}}.\mathsf{PriEval}(\mathsf{sek}, X)\): first, compute the subset \(F_{X} \subseteq [T]\) associated to \(X \in \{0,1\}^{\ell }\), and then return
$$Y= g_1^{\sum _{(i,j) \in F_{X}} \alpha _i \beta _j} \in \mathbb G_1$$ -
\({\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek}, X)\): let \(F_{X} \subseteq [T]\) be the subset associated to X, and compute
$$\hat{Y} = \prod _{(i,j) \in F_{X}} e(A_i, B_j) = e({\mathsf {H}}(X), g_2)$$
Theorem 1
Let \(\mathcal{G}\) be a bilinear group generator. The hash function \({\mathsf {H}}_\mathsf{acfs}\) described above is an asymmetric \((m, n, d, \gamma , \delta )\)-programmable hash function with \(n=1\), \(d=2\), \(\gamma = 0\) and \(\delta = 1/T\).
We show a proof sketch by giving the description of the trapdoor algorithms. A full proof showing that these algorithms satisfy the desired programmability property appears in the full version.
-
\({\mathsf {H}}.\mathsf{TrapGen}(1^\lambda , \mathsf{bgp}, \hat{g}_1, \hat{h}_1, \hat{g}_2, \hat{h}_2)\): first, sample \(a_i, b_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) for all \(i \in [t]\), and pick a random index \(\tau \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}[T]\). Parse \(\tau = (i^*, j^*) \in [t] \times [t]\). Next, set
 ,
,  , \(A_i = \hat{h}_1^{a_i}\), \(\forall i \ne i^*\), and \(B_j = \hat{h}_2^{b_j}\), \(\forall j \ne j^*\). Finally, set \(\mathsf{td}= (\tau , \{a_i, b_i\}_{i=1}^{t})\), \(\mathsf{pek}= \{A_i, B_i \}_{i=1}^{t}\), and output \((\mathsf{td}, \mathsf{pek})\).
, \(A_i = \hat{h}_1^{a_i}\), \(\forall i \ne i^*\), and \(B_j = \hat{h}_2^{b_j}\), \(\forall j \ne j^*\). Finally, set \(\mathsf{td}= (\tau , \{a_i, b_i\}_{i=1}^{t})\), \(\mathsf{pek}= \{A_i, B_i \}_{i=1}^{t}\), and output \((\mathsf{td}, \mathsf{pek})\). -
\({\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X)\): first, compute the subset \(F_{X} \subseteq [T]\) associated to \(X \in \{0,1\}^{\ell }\), and then return the coefficients of the degree-2 polynomial \(c_X(y_1, y_2) = \sum _{(i,j) \in F_{X}} \alpha _i(y_1) \cdot \beta _j(y_2),\) where every \(\alpha _i(y_1)\) (resp. \(\beta _j(y_2)\)) is the discrete logarithm of \(A_i\) (resp. \(B_j\)) in base \(\hat{g}_1\) (resp. \(\hat{g}_2\)), viewed as a degree-1 polynomial in the unknown \(y_1\) (resp. \(y_2\)).
3.2 An Asymmetric PHF with Small Domain
In this section, we present the construction of an asymmetric hash function, \({\mathsf {H}}_\mathsf{sqrt}\), whose domain is of polynomial size T. \({\mathsf {H}}_\mathsf{sqrt}\) has a public key of length \(O(\sqrt{T})\), and it turns out to be very important for obtaining our linearly-homomorphic signature scheme with short public key presented in Sect. 4. Somewhat interestingly, we show that this new function \({\mathsf {H}}_\mathsf{sqrt}\) satisfies several programmability properties, that make it useful in the context of various security proofs.
Let \(\mathcal{G}(1^{\lambda })\) be a bilinear group generator, let \(T = \mathsf{poly}(\lambda )\) and \(t = \lceil \sqrt{T} \rceil \). The hash function \({\mathsf {H}}_\mathsf{sqrt}= ({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval}, {\mathsf {H}}.\mathsf{PubEval})\) that maps \({\mathsf {H}}_\mathsf{sqrt}: \mathcal{X}\rightarrow \mathbb G_1\) with \(\mathcal{X}=[T]\) is defined as follows.
-
\({\mathsf {H}}.\mathsf{Gen}(1^\lambda , \mathsf{bgp})\): for \(i=1\) to t, sample \(\alpha _i, \beta _i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) and compute \(A_i = g_1^{\alpha _i}, B_i = g_2^{\beta _i}\). Finally, set \(\mathsf{sek}= \{\alpha _i, \beta _i\}_{i=1}^{t}\), \(\mathsf{pek}= \{A_i, B_i \}_{i=1}^{t}\), and return\((\mathsf{sek}, \mathsf{pek})\).
-
\({\mathsf {H}}.\mathsf{PriEval}(\mathsf{sek}, X)\): first, write \(X \in [T]\) as a pair of integer \((i, j) \in [t] \times [t]\), and then return
$$Y= g_1^{\alpha _i \beta _j} \in \mathbb G_1$$ -
\({\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek}, X)\): let \(X = (i,j)\). The public evaluation algorithm returns
$$\hat{Y} = e(A_i, B_j) = e({\mathsf {H}}(X), g_2)$$
Here we show that \({\mathsf {H}}_\mathsf{sqrt}\) satisfies the programmable pseudo-randomness property of Definition 3.
Theorem 2
(Programmable Pseudorandomness of \({\mathsf {H}}_\mathsf{sqrt}\) ). Let \(\mathbb G_1\) be a bilinear group of order p over which the XDDH assumption is \(\epsilon '\)-hard. Then the asymmetric hash function \({\mathsf {H}}_\mathsf{sqrt}\) described above satisfies \((2, 0, \epsilon )\)-programmable pseudo-randomness with \(\epsilon = T \cdot \epsilon '\). Furthermore, in the case when \(h_1=1 \in \mathbb G_1\) or \(h_1 = g_1\), \({\mathsf {H}}_\mathsf{sqrt}\) has \((1, 0, \epsilon )\)-programmable pseudo-randomness.
Proof. First, we describe the trapdoor algorithms:
-
\({\mathsf {H}}.\mathsf{TrapGen}(1^\lambda , g_1, h_1, g_2, h_2)\): first, sample \(a_i, r_i, s_i, b_i \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p\) for all \(i \in [t]\) and then set \(A_i = h_1^{r_i} g_1^{a_i}, B_i = h_2^{s_i} g_2^{b_i}\). Finally, set \(\mathsf{td}= ( \{ a_i, r_i, s_i, b_i\}_{i=1}^{t})\), \(\mathsf{pek}= \{A_i, B_i \}_{i=1}^{t}\), and output \((\mathsf{td}, \mathsf{pek})\).
-
\({\mathsf {H}}.\mathsf{TrapEval}(\mathsf{td}, X)\): let \(X = (i,j)\), and then return the coefficients of the degree-2 polynomial
$$c_X(y_1, y_2) = (y_1 r_i + a_i )(y_2 s_j + b_j)$$
First, it is easy to see that the two algorithms satisfy the syntax and correctness properties. Also, in the case \(h_1=1\) (i.e., \(y_1=0\)) or \(h_1=g_1\) (i.e., \(y_1=1\)), we obtain a degree-1 polynomial \(c_X(y_2)\). Second, observe that each element \(A_i\) (resp. \(B_i\)) in \(\mathsf{pek}\) is a uniformly distributed group element in \(\mathbb G_1\) (resp. \(\mathbb G_2\)), as in \({\mathsf {H}}.\mathsf{Gen}\), hence \(\gamma =0\). Third, we show that the function satisfies the pseudo-randomness property under the assumption that XDDH holds in \(\mathbb G_1\). The main observation is that for every \(X = (i,j)\), we have \(c_{X,0} = a_i b_j\) where all the values \(b_i\) are uniformly distributed and information-theoretically hidden to an adversary who only sees \(\mathsf{pek}\). In particular, this holds even if \(h_1 = 1\).
To prove the pseudo-randomness we make use of Lemma 2 below, which shows that for a uniformly random choice of \(\varvec{a}, \varvec{b} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^{t}, c \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^{t \times t}\) the distributions \((g_1^{\varvec{a}}, g_1^{\varvec{a} \cdot \varvec{b}^{\top }}) \in \mathbb G_1^{t \times (t +1)}\) and \((g_1^{\varvec{a}}, g_1^{c}) \in \mathbb G_1^{t \times (t + 1)}\) are computationally indistinguishable.
Lemma 2
Let \(\varvec{a}, \mathbf {b} \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^{t}, c \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^{t \times t}\) be chosen uniformly at random. If the XDDH assumption is \(\epsilon '\)-hard in \(\mathbb G_1\), then for any PPT \(\mathcal{B}\) it holds \(|\Pr [\mathcal{B}(g_1^{\varvec{a}}, g_1^{\varvec{a} \cdot \varvec{b}^{\top }})=1] - \Pr [\mathcal{B}(g_1^{\varvec{a}}, g_1^{c})=1]| \le T \cdot \epsilon '\).
We first show how to use Lemma 2 to prove that \({\mathsf {H}}_\mathsf{sqrt}\) has programmable pseudo-randomness. The proof of Lemma 2 appears in the full version.
Let \(\mathcal{A}\) be an adversary that breaks the \(\epsilon \)-programmable pseudo-randomness of \({\mathsf {H}}_\mathsf{sqrt}\). We construct a simulator \(\mathcal{B}\) that can distinguish the two distributions \((g_1^{\varvec{a}}, g_1^{\varvec{ a} \cdot \varvec{b}^{\top }})\) and \((g_1^{\varvec{a}}, g_1^{c})\) described above with advantage greater than \(\epsilon \).
\(\mathcal{B}\)’s input is a tuple \((\mathbf {A}', C) \in \mathbb G_1^{t} \times \mathbb G_1^{t \times t}\) and its goal is to decide about the distribution of C. First, \(\mathcal{B}\) runs \(\mathcal{A}(\mathsf{bgp})\) which outputs the generators \(h_1, h_2\). \(\mathcal{B}\) then samples two random vectors \(\varvec{r}, \mathbf {\beta }\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^{t}\), computes \(\varvec{B} = g_2^{\mathbf {\beta }} \in \mathbb G_2^{t}\), \(\varvec{A} = h_1^{\varvec{r}} \cdot \mathbf {A}' \in \mathbb G_1^{t}\), sets \(\mathsf{pek}= (\varvec{A}, \varvec{B})\), and runs \(\mathcal{A}(\mathsf{pek})\) Next, for every oracle query (i, j) made by \(\mathcal{A}\), \(\mathcal{B}\) simulates the answer by returning to \(\mathcal{A}\): \({\mathsf {H}}(i,j) = A_i^{\beta _j}\) and \(C_{i,j}\). It is easy to see that if \(C = g_1^{\varvec{a} \cdot \varvec{b}^{\top }}\) then \(\mathcal{B}\) is perfectly simulating \(\mathbf {Exp}_{\mathcal{A},{\mathsf {H}}_\mathsf{sqrt}}^{PRH\text{- }0}\), otherwise, if C is random and independent, then \(\mathcal{B}\) is simulating \(\mathbf {Exp}_{\mathcal{A},{\mathsf {H}}_\mathsf{sqrt}}^{PRH\text{- }1}\). As a final note, we observe that the above proof works even in the case \(h_1=1\). \(\square \)
In the following theorems (whose proofs appear in the full version of our paper) we show that \({\mathsf {H}}_\mathsf{sqrt}\) satisfies programmability with various parameters.
Theorem 3
( \((\mathsf{poly}, 0, 2)\) -programmability of \({\mathsf {H}}_\mathsf{sqrt}\) ). The asymmetric hash function \({\mathsf {H}}_\mathsf{sqrt}\) described above is \((\mathsf{poly}, 0, d,\gamma ,\delta )\)-programmable with \(d=2\), \(\gamma =0\) and \(\delta =1\). Furthermore, in the case when either \(\hat{h}_1 = \hat{g}_1\) or \(\hat{h}_2 = \hat{g}_2\), \({\mathsf {H}}_\mathsf{sqrt}\) is \((\mathsf{poly}, 0, d,\gamma ,\delta )\)-programmable with \(d=1\), \(\gamma =0\) and \(\delta =1\).
Theorem 4
(Weak \((\mathsf{poly}, 1, 2)\) -programmability of \({\mathsf {H}}_\mathsf{sqrt}\) ). The asymmetric hash function \({\mathsf {H}}_\mathsf{sqrt}\) described above is weakly \((\mathsf{poly}, 1, d,\gamma ,\delta )\)-programmable with \(d=2\), \(\gamma =0\) and \(\delta =1\).
Theorem 5
(Weak \((\mathsf{poly}, 1, 2)\) -degree-2-programmability of \({\mathsf {H}}_\mathsf{sqrt}\) ). The asymmetric hash function \({\mathsf {H}}_\mathsf{sqrt}\) described above is weakly \((\mathsf{poly}, 1, d,\gamma ,\delta )\)-degree-2 programmable with \(d=2\), \(\gamma =0\) and \(\delta =1\).
4 Linearly-Homomorphic Signatures with Short Public Keys
In this section, we show a new linearly-homomorphic signature scheme that uses asymmetric PHFs in a generic way. By instantiating the asymmetric PHFs with our construction \({\mathsf {H}}_\mathsf{sqrt}\) given in Sect. 3, we obtain the first linearly-homomorphic signature scheme that is secure in the standard model, and whose public key has a size that is sub-linear in both the dataset size and the dimension of the signed vectors. Precisely, if the signature scheme supports datasets of maximal size N and can sign vectors of dimension T, then the public key of our scheme is of size \(O(\sqrt{N} + \sqrt{T})\). All previously existing constructions in the standard model achieved only public keys of length \(O(N + T)\). Furthermore, our scheme is adaptive secure and achieves the interesting property of efficient verification that allows to use the scheme for verifiable delegation of computation in the preprocessing model [15].
4.1 Homomorphic Signatures for Multi-Labeled Programs
First we recall the definition of homomorphic signatures as presented in [15]. This definition extends the one by Freeman in [17] in order to work with the general notion of multi-labeled programs [4, 20].
Multi-Labeled Programs. A labeled program \({\mathcal {P}}\) is a tuple \((f, {\tau }_1,...,{\tau }_n)\) such that \(f : \mathcal{M}^n \rightarrow \mathcal{M}\) is a function of n variables (e.g., a circuit) and \({\tau }_i \in \{0,1\}^*\) is a label of the i-th input of f. Labeled programs can be composed as follows: given \({\mathcal {P}}_1, \dots , {\mathcal {P}}_t\) and a function \(g: \mathcal{M}^t \rightarrow \mathcal{M}\), the composed program \({\mathcal {P}}^*\) is the one obtained by evaluating g on the outputs of \({\mathcal {P}}_1,\dots , {\mathcal {P}}_t\), and it is denoted as \({\mathcal {P}}^* = g({\mathcal {P}}_1 , \dots , {\mathcal {P}}_t )\). The labeled inputs of \({\mathcal {P}}^*\) are all the distinct labeled inputs of \({\mathcal {P}}_1 , \cdots {\mathcal {P}}_t\) (all the inputs with the same label are grouped together and considered as a unique input of \({\mathcal {P}}^*\)). Let \(f_{id} : \mathcal{M}\rightarrow \mathcal{M}\) be the identity function and \({\tau }\in \{0,1\}^*\) be any label. We refer to \(\mathcal{I}_{{\tau }}= (f_{id}, {\tau })\) as the identity program with label \({\tau }\). Note that a program \({\mathcal {P}}= (f, {\tau }_1 , \cdots , {\tau }_n) \) can be expressed as the composition of n identity programs \({\mathcal {P}}= f(\mathcal{I}_{\tau _1}, \cdots , \mathcal{I}_{\tau _1})\).
A multi-labeled program \({\mathcal {P}}_{\varDelta }\) is a pair \(({\mathcal {P}}, {\varDelta })\) in which \({\mathcal {P}}= (f, {\tau }_1 , \cdots , {\tau }_n)\) is a labeled program while \({\varDelta }\in \{0,1\}^*\) is a data set identifier. Given \(({\mathcal {P}}_1 , {\varDelta }), \dots , ({\mathcal {P}}_t , {\varDelta })\) which has the same data set identifier \({\varDelta }\), and given a function \(g : \mathcal{M}^t \rightarrow \mathcal{M}\), the composed multi-labeled program \({\mathcal {P}}^*_{\varDelta }\) is the pair \(({\mathcal {P}}^* , {\varDelta })\) where \({\mathcal {P}}^*\) = \(g({\mathcal {P}}_1, \cdots , {\mathcal {P}}_t)\), and \({\varDelta }\) is the common data set identifier for all the \({\mathcal {P}}_i\). As for labeled programs, one can define the notion of a multi-labeled identity program as \(\mathcal{I}_{({\varDelta }, {\tau })}= ((f_{id}, {\tau }), {\varDelta })\).
Definition 4
(Homomorphic Signatures). A homomorphic signature scheme \(\mathsf{HSig}\) consists of a tuple of PPT algorithms \((\mathsf{KeyGen}, \mathsf{Sign}, \mathsf{Ver}, \mathsf{Eval})\) satisfying the following four properties: authentication correctness, evaluation correctness, succinctness and security.
-
\(\mathsf{KeyGen}(1^\lambda , \mathcal{L})\) the key generation algorithm takes as input a security parameter \(\lambda \), the description of the label space \(\mathcal{L}\) (which fixes the maximum data set size N), and outputs a public key \(\mathsf{vk}\) and a secret key \(\mathsf{sk}\). The public key \(\mathsf{vk}\) defines implicitly a message space \(\mathcal{M}\) and a set \(\mathcal{F}\) of admissible functions.
-
\(\mathsf{Sign}(\mathsf{sk}, {\varDelta }, {\tau }, m)\) the signing algorithm takes as input a secret key \(\mathsf{sk}\), a data set identifier \({\varDelta }\), a label \({\tau }\in \mathcal{L}\) a message \(m \in \mathcal{M}\), and it outputs a signature \(\sigma \).
-
\(\mathsf{Ver}(\mathsf{vk}, {\mathcal {P}}_{\varDelta }, m, \sigma )\) the verification algorithm takes as input a public key \(\mathsf{vk}\), a multi-labeled program \({\mathcal {P}}_{\varDelta }= ((f, {\tau }_1, \dots , {\tau }_n), {\varDelta })\) with \(f \in \mathcal{F}\), a message \(m \in \mathcal{M}\), and a signature \(\sigma \). It outputs either 0 (reject) or 1 (accept).
-
\(\mathsf{Eval}(\mathsf{vk}, f, \mathbf {\sigma })\) the evaluation algorithm takes as input a public \(\mathsf{vk}\), a function \(f \in \mathcal{F}\) and a tuple of signatures \(\{\sigma _i \}_{i=1}^{n}\) (assuming that f takes n inputs). It outputs a new signature \(\sigma \).
Authentication Correctness. The scheme \(\mathsf{HSig}\) satisfies the authentication correctness property if for a given label space \(\mathcal{L}\), all key pairs \((\mathsf{sk}, \mathsf{vk}) \leftarrow \mathsf{KeyGen}(1^\lambda , \mathcal{L})\), any label \({\tau }\in \mathcal{L}\), data identifier \({\varDelta }\in \{0,1\}^*\), and any signature \(\sigma \leftarrow \mathsf{Sign}(\mathsf{sk}, {\varDelta }, {\tau }, m)\), \(\mathsf{Ver}(\mathsf{vk}, \mathcal{I}_{{\varDelta }, {\tau }}, m , \sigma )\) outputs 1 with all but negligible probability.
Evaluation Correctness. Fix a key pair \((\mathsf{vk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(1^\lambda , \mathcal{L})\), a function \(g: \mathcal{M}^t \rightarrow \mathcal{M}\), and any set of program/message/signature triples \(\{({\mathcal {P}}_i, m_i, \sigma _i)\}_{i=1}^t\) such that \(\mathsf{Ver}(\mathsf{vk}, {\mathcal {P}}_i, m_i, \sigma _i)=1\). If \(m^* = g(m_1, \dots , m_t)\), \({\mathcal {P}}^* = g({\mathcal {P}}_1 , \cdots , {\mathcal {P}}_t )\), and \(\sigma ^* = \mathsf{Eval}(\mathsf{vk}, g, (\sigma _1 , \dots , \sigma _t))\), then \(\mathsf{Ver}(\mathsf{vk}, {\mathcal {P}}^* , m^* , \sigma ^*)= 1\) holds with all but negligible probability.
Succintness. A homomorphic signature scheme is said to be succint if, for a fixed security parameter \(\lambda \), the size of signatures depends at most logarithmically on the data set size N.
Security. To define the security notion of homomorphic signatures we define the following experiment  between an adversary \(\mathcal{A}\) and a challenger \(\mathcal{C}\):
between an adversary \(\mathcal{A}\) and a challenger \(\mathcal{C}\):
-
Key Generation \(\mathcal{C}\) runs \((\mathsf{vk}, \mathsf{sk}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}(1^\lambda , \mathcal{L})\) and gives \(\mathsf{vk}\) to \(\mathcal{A}\).
-
Signing Queries \(\mathcal{A}\) can adaptively submit queries of the form \(({\varDelta }, {\tau }, m)\), where \({\varDelta }\) is a data set identifier, \({\tau }\in \mathcal{L}\), and \(m \in \mathcal{M}\). The challenger \(\mathcal{C}\) proceeds as follows: if \(({\varDelta }, {\tau }, m)\) is the first query with the data set identifier \({\varDelta }\), the challenger initializes an empty list \(T_{\varDelta }= \emptyset \) for \({\varDelta }\). If \(T_{\varDelta }\) does not already contain a tuple \(( {\tau }, \cdot )\), the challenger \(\mathcal{C}\) computes \(\sigma \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{Sign}(\mathsf{sk}, {\varDelta }, {\tau }, m)\), returns \(\sigma \) to \(\mathcal{A}\) and updates the list \(T_{\varDelta }\leftarrow T_{\varDelta }\cup ({\tau }, m)\). If \(({\tau }, m) \in T_{\varDelta }\) then \(\mathcal{C}\) replies with the same signature generated before. If \(T_{\varDelta }\) contains a tuple \(({\tau }, m^\prime )\) for some message \(m^\prime \ne m\), then the challenger ignores the query.
-
Forgery At the end \(\mathcal{A}\) outputs a tuple
 .
.
The experiment  outputs 1 if the tuple returned by \(\mathcal{A}\) is a forgery, and 0 otherwise. To define what is a forgery in such a game we recall the notion of well defined program with respect to a list
outputs 1 if the tuple returned by \(\mathcal{A}\) is a forgery, and 0 otherwise. To define what is a forgery in such a game we recall the notion of well defined program with respect to a list  [15].
[15].
Definition 5
A labeled program  is well defined with respect to
is well defined with respect to  if
if  s.t.
s.t.  .
.  s.t.
s.t.  and
and  does not change for all possible choices of
does not change for all possible choices of  .
.
Using this notion, it is then possible to define the three different types of forgeries that can occur in the experiment  :
:
-
Type 1:
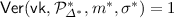 and
and 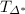 was not initialized in the game
was not initialized in the game -
Type 2:
 ,
,  is well defined w.r.t.
is well defined w.r.t. 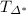 and
and 
-
Type 3:
 and
and 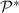 is not well defined w.r.t.
is not well defined w.r.t.  .
.
Then we say that \(\mathsf{HSig}\) is a secure homomorphic signature if for any PPT adversary \(\mathcal{A}\), we have that  where \(\epsilon (\lambda )\) is a negligible function.
where \(\epsilon (\lambda )\) is a negligible function.
Finally, we recall that, as proved by Freeman in [17], in a linearly-homomorphic signatures scheme any adversary who outputs a Type 3 forgery can be converted into one that outputs a Type 2 forgery.
Homomorphic Signatures with Efficient Verification. We recall the notion of homomorphic signatures with efficient verification introduced in [15]. Informally, the property states that the verification algorithm can be split in two phases: an offline phase where, given the verification key \(\mathsf{vk}\) and a labeled program \({\mathcal {P}}\), one precomputes a concise key \(\mathsf{vk}_{{\mathcal {P}}}\); an online phase in which \(\mathsf{vk}_{{\mathcal {P}}}\) can be used to verify signatures w.r.t. \({\mathcal {P}}\) and any dataset \({\varDelta }\). To achieve (amortized) efficiency, the idea is that \(\mathsf{vk}_{{\mathcal {P}}}\) can be reused an unbounded number of times, and the online verification is cheaper than running \({\mathcal {P}}\).
4.2 Our Construction
Let \(\Sigma ^{\prime }= (\mathsf{KeyGen}^{\prime }, \mathsf{Sign}^{\prime }, \mathsf{Ver}^{\prime })\) be a regular signature scheme, and \({ F }: \mathcal{K}\times \{0, 1\}^* \rightarrow \mathbb {Z}_p\) be a pseudorandom function with key space \(\mathcal{K}\). Our linearly-homomorphic signature scheme signs T-dimensional vectors of messages in \(\mathbb {Z}_p\), and supports datasets of size N, with both \(N=\mathsf{poly}(\lambda )\) and \(T=\mathsf{poly}(\lambda )\). Let \({\mathsf {H}}= ({\mathsf {H}}.\mathsf{Gen}, {\mathsf {H}}.\mathsf{PriEval}, {\mathsf {H}}.\mathsf{PubEval})\) and \({\mathsf {H}}' = ({\mathsf {H}}.\mathsf{Gen}', {\mathsf {H}}.\mathsf{PriEval}', {\mathsf {H}}.\mathsf{PubEval}')\) be two asymmetric programmable hash functions such that \({\mathsf {H}}: [N] \rightarrow \mathbb G_1\) and \({\mathsf {H}}':[T] \rightarrow \mathbb G_1\). We construct a homomorphic signature \(\mathsf{HSig}= (\mathsf{KeyGen}, \mathsf{Sign}, \mathsf{Ver}, \mathsf{Eval})\) as follows:
-
\(\mathsf{KeyGen}(1^{\lambda }, \mathcal{L}, T)\). Let \(\lambda \) be the security parameter, \(\mathcal{L}\) be a set of admissible labels where \(\mathcal{L}= \{1,\ldots , N\}\), and T be an integer representing the dimension of the vectors to be signed. The key generation algorithm works as follows.
-
Generate a key pair \((\mathsf{vk}^{\prime }, \mathsf{sk}^{\prime }) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathsf{KeyGen}^{\prime }(1^\lambda )\) for the regular scheme.
-
Run \(\mathsf{bgp}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{G}(1^{\lambda })\) to generate the bilinear groups parameters \(\mathsf{bgp}= (p,\mathbb G_1, \mathbb G_2, \mathbb G_{T}, g_1, g_2, e).\)
-
Choose a random seed \(K \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{K}\) for the PRF \({ F }_K : \{0,1\}^* \rightarrow \mathbb {Z}_p\).
-
Run \((\mathsf{sek}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{Gen}(1^{\lambda }, \mathsf{bgp})\) and \((\mathsf{sek}', \mathsf{pek}') \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{Gen}'(1^{\lambda }, \mathsf{bgp})\) to generate the keys of the asymmetric hash functions.
-
Return \(\mathsf{vk}= (\mathsf{vk}^{\prime }, \mathsf{bgp}, \mathsf{pek}, \mathsf{pek}')\) and \(\mathsf{sk}= ( \mathsf{sk}^{\prime } , K, \mathsf{sek}, \mathsf{sek}')\).
-
-
\(\mathsf{Sign}(\mathsf{sk}, {\varDelta }, {\tau }, \varvec{m})\). The signing algorithm takes as input the secret key \(\mathsf{sk}\), a data set identifier \({\varDelta }\in \{0,1\}^*\), a label \({\tau }\in [N]\) and a message vector \(\varvec{m} \in \mathbb {Z}_p^{T}\), and proceeds as follows:
-
1.
Derive the integer \(z \leftarrow F_K({\varDelta })\) using the PRF, and compute \(Z= g_2^z\).
-
2.
Compute \(\sigma _{\varDelta }\leftarrow \mathsf{Sign}^{\prime }(\mathsf{sk}^{\prime }, {\varDelta }| Z)\) to bind Z to the dataset identifier \({\varDelta }\).
-
3.
Choose a random \(R \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb G_1\) and compute
$$S = \left( {\mathsf {H}}.\mathsf{PriEval}(\mathsf{sek}, {\tau }) \cdot R \cdot \prod _{j=1}^{T} {\mathsf {H}}.\mathsf{PriEval}'(\mathsf{sek}', j)^{m_j}\right) ^{1/z}$$ -
4.
Return a signature \(\sigma = (\sigma _{\varDelta }, Z, R, S)\).
Essentially, the algorithm consists of two main steps. First, it uses the PRF \({ F }_K\) to derive a common parameter z which is related to the data set \({\varDelta }\), and it signs the public part, \(Z=g_2^z\), of this parameter using the signature scheme \(\Sigma ^{\prime }\). Second, it uses z to create the homomorphic component R, S of the signature, such that S is now related to all \(({\varDelta }, {\tau }, \varvec{m})\).
-
1.
-
\(\mathsf{Eval}(\mathsf{vk}, f, \mathbf {\sigma })\). The public evaluation algorithm takes as input the public key \(\mathsf{vk}\), a linear function \(f: \mathbb {Z}_p^{\ell } \rightarrow \mathbb {Z}_p\) described by its vector of coefficients \(\varvec{f} = (f_1, \ldots , f_\ell )\), and a vector \(\mathbf {\sigma }\) of \(\ell \) signatures \(\sigma _1, \ldots , \sigma _{\ell }\) where \(\sigma _i = (\sigma _{{\varDelta }, i}, Z_i, R_i, S_i)\) for \(i=1,\ldots ,\ell \). \(\mathsf{Eval}\) returns a signature \(\sigma = (\sigma _{\varDelta },, Z, R, S)\) that is obtained by setting \(Z= Z_1\), \(\sigma _{\varDelta }= \sigma _{{\varDelta }, 1}\), and by computing
$$R = \prod _{i=1}^{\ell } R_i^{f_i}, \quad S = \prod _{i=1}^{\ell } S_i^{f_i}$$ -
\(\mathsf{Ver}(\mathsf{vk}, {\mathcal {P}}_{{\varDelta }}, \varvec{m}, \sigma )\). Let \({\mathcal {P}}_{{\varDelta }}=((f, {\tau }_1, \ldots , {\tau }_\ell ), {\varDelta })\) be a multi-label ed program such that \(f: \mathbb {Z}_p^{\ell } \rightarrow \mathbb {Z}_p\) is a linear function described by coefficients \(\varvec{f} = (f_1, \ldots , f_\ell )\). Let \(\varvec{m} \in \mathbb {Z}_p^{T}\) be a message-vector and \(\sigma = (\sigma _{{\varDelta }}, Z, R, S)\) be a signature.
First, run \(\mathsf{Ver}^{\prime }(\mathsf{vk}^{\prime }, {\varDelta }| Z, \sigma _{{\varDelta }})\) to check that \(\sigma _{{\varDelta }}\) is a valid signature for Z and the dataset identifier \({\varDelta }\) taken as input by the verification algorithm. If \(\sigma _{{\varDelta }}\) is not valid, stop and return 0 (reject).
Otherwise, output 1 if and only if the following equation is satisfied
$$\begin{aligned} e(S, Z) = \left( \prod _{i=1}^{\ell } {\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek}, {\tau }_i)^{f_i}\right) \cdot e(R, g_2) \cdot \left( \prod _{j=1}^{T} {\mathsf {H}}.\mathsf{PubEval}'(\mathsf{pek}', j)^{m_j}\right) \end{aligned}$$
Finally, we describe the algorithms for efficient verification:
-
\(\mathsf{VerPrep}(\mathsf{vk}, {\mathcal {P}})\). Let \({\mathcal {P}}= (f, {\tau }_1, \ldots , {\tau }_{\ell })\) be a labeled program for a linear function \(f: \mathbb {Z}_p^\ell \rightarrow \mathbb {Z}_p\). The algorithm computes \(H = \prod _{i=1}^{\ell } {\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek}, {\tau }_i)^{f_i}\), and returns the concise verification key \(\mathsf{vk}_{{\mathcal {P}}} = (\mathsf{vk}', \mathsf{bgp}, H, \mathsf{pek}')\).
-
\(\mathsf{EffVer}(\mathsf{vk}_{\mathcal {P}}, {\varDelta }, \varvec{m},\sigma )\). The online verification is the same as \(\mathsf{Ver}\) except that in the verification equation the value H has been already computed in the off-line phase (and is included in \(\mathsf{vk}_{{\mathcal {P}}}\)).
Clearly, running the combination of \(\mathsf{VerPrep}\) and \(\mathsf{EffVer}\) gives the same result as running \(\mathsf{Ver}\), and \(\mathsf{EffVer}\)’s running time is independent of f’s complexity \(\ell \).
The following theorem states the security of the scheme. Formal proofs of correctness and security appear in the full version of our paper.
Theorem 6
Assume that \(\Sigma ^\prime \) is an unforgeable signature scheme, F is a pseudorandom function, and \(\mathcal{G}\) is a bilinear group generator such that: \({\mathsf {H}}\) has \((1,\gamma ,\epsilon )\)-programmable pseudorandomness; \({\mathsf {H}}'\) is weakly \((\mathsf{poly}, 1, 2, \gamma ', \delta ')\)-degree-2-programmable, weakly \((\mathsf{poly}, 1, 2, \gamma ', \delta ')\)-programmable and \((\mathsf{poly}, 0, 1, \gamma ', \delta ')\)- programmable; the 2-DHI and the FDHI assumptions hold. Then \(\mathsf{HSig}\) is a secure linearly-homomorphic signature scheme.
We note that our scheme \(\mathsf{HSig}\) can be instantiated by instantiating both \({\mathsf {H}}\) and \({\mathsf {H}}'\) with two different instances of our programmable hash \({\mathsf {H}}_\mathsf{sqrt}\) described in Sect. 3.2. As one can check in Sect. 3.2, \({\mathsf {H}}_\mathsf{sqrt}\) allows for the multiple programmability modes required in our Theorem 6. Let us stress that requiring the same function to have multiple programmability modes is not contradictory, as such modes do not have to hold simultaneously. It simply means that for the same function there exist different pairs of trapdoor algorithms each satisfying programmability with different parameters.Footnote 5
5 Short Signatures with Shorter Public Keys from Bilinear Maps
In this section we describe how to use asymmetric PHFs to construct in a generic fashion standard-model signature schemes over bilinear groups. We propose two constructions that are provably-secure under the q-Strong Diffie-Hellman [6] and the q-Diffie-Hellman [5] assumptions. These constructions are the analogues of the schemes in [26] and [25] respectively. The basic idea behind the constructions is to replace a standard (m, 1)-PHF with an asymmetric (m, 1, d)-PHF. In fact, in this context, having a secretly-computable \({\mathsf {H}}\) does not raise any issue when using \({\mathsf {H}}\) in the signing procedure as the signer already uses a secret key. At the same time, for verification purposes, computing the (public) isomorphic copy of \({\mathsf {H}}\) in the target group is also sufficient. Our proof confirms that the (m, 1, d)-programmability can still be used to control the size of the randomness in the same way as in [25, 26]. One difference in the security proof is that the schemes in [25, 26] are based on the q-(S)DH assumption, where q is the number of signing queries made by the adversary, whereas ours have to rely on the \((q+d-1)\)-(S)DH problem. Since our instantiations use \(d=2\), the difference (when considering concrete security) is very minor.
When plugging into these generic constructions our new asymmetric PHF, \({\mathsf {H}}_\mathsf{acfs}\), described in Sect. 3.1, which is (m, 1, 2)-programmable, we obtain schemes that, for signing \(\ell \)-bits messages, allow for public keys of length \(O(m \sqrt{\ell })\) as in [31].
Below we describe the scheme based on q-SDH. For lack of space, the one based on q-DH (which uses similar ideas) appears in the full version. As discussed in [25], the advantage of the scheme from q-DH compared to the one from q-SDH is to be based on a weaker assumption.
A q -Strong Diffie-Hellman Based Solution. Here we revisit the q-SDH based solution of [26]. The signature \(\Sigma _\mathsf{qSDH} = (\mathsf{KeyGen}, \mathsf{Sign}, \mathsf{Ver})\) is as follows:
-
\(\mathsf{KeyGen}(1^{\lambda })\). Let \(\lambda \) be the security parameter, and let \(\ell =\ell (\lambda )\) and \(\rho =\rho (\lambda )\) be arbitrary polynomials. Our scheme can sign messages in \(\{0,1\}^\ell \) using randomness in \(\{0,1\}^\rho \). The key generation algorithm works as follows:
-
Run \(\mathsf{bgp}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathcal{G}(1^{\lambda })\) to generate the bilinear groups parameters \(\mathsf{bgp}= (p,\mathbb G_1, \mathbb G_2, \mathbb G_{T}, g_1, g_2, e)\).
-
Run \((\mathsf{sek}, \mathsf{pek}) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{\mathsf {H}}.\mathsf{Gen}(1^{\lambda }, \mathsf{bgp})\) to generate the keys of the asymmetric hash function.
-
Choose a random \(x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_p^*\) and set \(X\leftarrow g_2^x\). Return \(\mathsf{vk}= (\mathsf{bgp}, \mathsf{pek}, X)\) and \(\mathsf{sk}= (\mathsf{sek},x)\).
-
-
\(\mathsf{Sign}(\mathsf{sk}, M)\). The signing algorithm takes as input the secret key \(\mathsf{sk}\), and a message \(M \in \{0,1\}^\ell \). It starts by generating a random \(r \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\{0,1\}^\rho \). Next, it computes \(\sigma ={\mathsf {H}}.\mathsf{PriEval}(\mathsf{sek}, M)^{\frac{1}{x+r}}\) and outputs \((\sigma ,r)\).
-
\(\mathsf{Ver}(\mathsf{vk}, M, (\sigma ,r))\). To check that \((\sigma ,r)\) is a valid signature, check that r is of length \(\rho \) and that \(e(\sigma ,X\cdot g_2^r)={\mathsf {H}}.\mathsf{PubEval}(\mathsf{pek},M). \)
We state the security of the scheme in the following theorem (whose proof appears in the full version). We note that for simplicity our proof assumes an asymmetric (m, 1, d)-PHF for \(d=2\), which matches our realization. A generalization of the theorem for a generic d can be immediately obtained, in which case one would rely on the \((q+d-1)\)-SDH assumption.
Theorem 7
Assume that \(\mathcal{G}\) is a bilinear group generator such that the \((q+1)\)-SDH assumption holds in \(\mathbb G_1\) and \({\mathsf {H}}\) is \((m, 1, 2, \gamma , \delta )\)-programmable, then \(\Sigma _\mathsf{qSDH}\) is a secure signature scheme. More precisely, let \(\mathcal{B}\) be an efficient (probabilistic) algorithm that runs in time t, asks (up to) q signing queries and produces a valid forgery with probability \(\epsilon \), then there exists an equally efficient algorithm \(\mathcal{A}\) that confutes the \((q+1)\)-SDH assumption with probability \(\epsilon '\ge \frac{\delta }{q} \left( \epsilon - \gamma - \frac{q}{p} - \frac{q^{m+1}}{2^{\rho m}}\right) \).
Notes
- 1.
Because of such asymmetric behavior we call these functions “asymmetric”.
- 2.
For \(d=1\), this is basically the same programmability of [26].
- 3.
[26] gives also a \((1,\mathsf{poly})\)-programmable PHF which allows for different applications.
- 4.
Our definition can be easily adapted to work in symmetric bilinear groups where \(\mathbb G_1= \mathbb G_2\).
- 5.
We also stress that, by definition, the outputs of these trapdoor algorithms are statistically indistinguishable.
References
Attrapadung, N., Libert, B.: Homomorphic network coding signatures in the standard model. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 17–34. Springer, Heidelberg (2011)
Attrapadung, N., Libert, B., Peters, T.: Computing on authenticated data: new privacy definitions and constructions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 367–385. Springer, Heidelberg (2012)
Attrapadung, N., Libert, B., Peters, T.: Efficient completely context-hiding quotable and linearly homomorphic signatures. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 386–404. Springer, Heidelberg (2013)
Backes, M., Fiore, D., Reischuk, R.M.: Verifiable delegation of computation on outsourced data. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13, pp. 863–874. ACM Press, New York (2013)
Boneh, D., Boyen, X.: Efficient selective-id secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004)
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 56–73. Springer, Heidelberg (2004)
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–239. Springer, Heidelberg (2001)
Boneh, D., Freeman, D., Katz, J., Waters, B.: Signing a linear subspace: signature schemes for network coding. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 68–87. Springer, Heidelberg (2009)
Boneh, D., Freeman, D.M.: Homomorphic signatures for polynomial functions. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 149–168. Springer, Heidelberg (2011)
Boneh, D., Freeman, D.M.: Linearly homomorphic signatures over binary fields and new tools for lattice-based signatures. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 1–16. Springer, Heidelberg (2011)
Boyen, X., Fan, X., Shi, E.: Adaptively secure fully homomorphic signatures based on lattices. Cryptology ePrint Archive, report 2014/916 (2014). http://eprint.iacr.org/2014/916
Catalano, D., Fiore, D., Gennaro, R., Vamvourellis, K.: Algebraic (Trapdoor) one-way functions and their applications. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 680–699. Springer, Heidelberg (2013)
Catalano, D., Fiore, D., Warinschi, B.: Adaptive pseudo-free groups and applications. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 207–223. Springer, Heidelberg (2011)
Catalano, D., Fiore, D., Warinschi, B.: Efficient network coding signatures in the standard model. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 680–696. Springer, Heidelberg (2012)
Catalano, D., Fiore, D., Warinschi, B.: Homomorphic signatures with efficient verification for polynomial functions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 371–389. Springer, Heidelberg (2014)
Erdös, P., Frankel, P., Furedi, Z.: Families of finite sets in which no set is covered by the union of \(r\) others. Israeli J. Math. 51, 79–89 (1985)
Freeman, D.M.: Improved security for linearly homomorphic signatures: a generic framework. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 697–714. Springer, Heidelberg (2012)
Freire, E.S.V., Hofheinz, D., Paterson, K.G., Striecks, C.: Programmable hash functions in the multilinear setting. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 513–530. Springer, Heidelberg (2013)
Gennaro, R., Katz, J., Krawczyk, H., Rabin, T.: Secure network coding over the integers. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 142–160. Springer, Heidelberg (2010)
Gennaro, R., Wichs, D.: Fully homomorphic message authenticators. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 301–320. Springer, Heidelberg (2013)
Gorbunov, S., Vaikuntanathan, V., Wichs, D.: Leveled fully homomorphic signatures from standard lattices. In: 47th ACM STOC. ACM Press (2015). To appear
Green, M., Hohenberger, S.: Practical adaptive oblivious transfer from simple assumptions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 347–363. Springer, Heidelberg (2011)
Hanaoka, G., Matsuda, T., Schuldt, J.C.N.: On the impossibility of constructing efficient key encapsulation and programmable hash functions in prime order groups. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 812–831. Springer, Heidelberg (2012)
Haralambiev, K., Jager, T., Kiltz, E., Shoup, V.: Simple and efficient public-key encryption from computational diffie-hellman in the standard model. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 1–18. Springer, Heidelberg (2010)
Hofheinz, D., Jager, T., Kiltz, E.: Short signatures from weaker assumptions. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 647–666. Springer, Heidelberg (2011)
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 21–38. Springer, Heidelberg (2008)
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. J. Cryptology 25(3), 484–527 (2012)
Johnson, R., Molnar, D., Song, D., Wagner, D.: Homomorphic signature schemes. In: Preneel, B. (ed.) CT-RSA 2002. LNCS, vol. 2271, pp. 244–262. Springer, Heidelberg (2002)
Kumar, R., Rajagopalan, S., Sahai, A.: Coding constructions for blacklisting problems without computational assumptions. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 609–623. Springer, Heidelberg (1999)
Libert, B., Peters, T., Joye, M., Yung, M.: Linearly homomorphic structure-preserving signatures and their applications. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 289–307. Springer, Heidelberg (2013)
Yamada, S., Hanaoka, G., Kunihiro, N.: Two-dimensional representation of cover free families and its applications: short signatures and more. In: Dunkelman, O. (ed.) CT-RSA 2012. LNCS, vol. 7178, pp. 260–277. Springer, Heidelberg (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 International Association for Cryptologic Research
About this paper
Cite this paper
Catalano, D., Fiore, D., Nizzardo, L. (2015). Programmable Hash Functions Go Private: Constructions and Applications to (Homomorphic) Signatures with Shorter Public Keys. In: Gennaro, R., Robshaw, M. (eds) Advances in Cryptology -- CRYPTO 2015. CRYPTO 2015. Lecture Notes in Computer Science(), vol 9216. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-48000-7_13
Download citation
DOI: https://doi.org/10.1007/978-3-662-48000-7_13
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-47999-5
Online ISBN: 978-3-662-48000-7
eBook Packages: Computer ScienceComputer Science (R0)





 ,
,  ,
,  .
.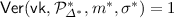 and
and 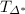 was not initialized in the game
was not initialized in the game ,
,  is well defined w.r.t.
is well defined w.r.t. 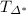 and
and 
 and
and 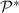 is not well defined w.r.t.
is not well defined w.r.t.  .
.