Abstract
This chapter describes the theory and techniques for modelling the electrical activity of excitable cells and tissues, along with their electrical simulation, using COMSOL. It begins with a summary of Maxwell’s equations, before moving on to electrostatics and volume conductor theory. Examples in COMSOL are presented for designing an optimal electric field stimulator for cell cultures in a Petri dish, as well as determining the current density and access resistance of an isopotential disc electrode in an infinite medium. The chapter then proceeds to cover continuum models of excitable tissues such as nerve and muscle and their electrical stimulation, expressed as classical bidomain and monodomain formulations. Examples in COMSOL are presented for modelling reentrant spiral waves in a slab of cardiac tissue and a propagating action potential in a nerve axon embedded in a nerve bundle stimulated by extracellular cuff electrodes.
1 Electrical Stimulation
Matter is composed of atoms consisting of positively-charged nuclei and negatively-charged electrons. These positive and negative charges produce and respond to electromagnetic fields , which are completely described by Maxwell’s equations.Footnote 1
1.1 Maxwell’s Equations
Maxwell’s equations, expressed in so-called “macroscopic” form which characterize electromagnetic fields in materials, are:
where \(\mathbf {E}\) denotes the electric field (SI units: V m\(^{-1}\)), \(\mathbf {B}\) the magnetic field (SI units: T), \(\mathbf {D}\) the electric displacement (SI units: C m\(^{-2}\)), \(\mathbf {H}\) the magnetization (SI units: A m\(^{-1}\)), \(\mathbf {J}\) the applied current density (SI units: A m\(^{-2}\)) and \(\rho _v\) the volume charge density (SI units: C m\(^{-3}\)). Equation 6.1 is also known as Faraday’s Law of Induction and states that a time-varying change in the local magnetic field will produce an electric field. Equation 6.2 represents an extension to Ampère’s Law , which states that a steady electric current produces a magnetic field. Maxwell’s contribution was the addition of a “displacement current” term \(\partial \mathbf {D}/\partial t\) , such that the magnetization field is also produced by a time-varying electric field in addition to a steady current. Equation 6.3 is known as Gauss’ Law , and states that an electric field is produced by electric charge. Equation 6.4 is also known as Gauss’ Law for Magnetism , and effectively states that there are no analogues of electric charge for magnetic fields (so-called “magnetic charges”).
For homogeneous linear isotropic materials, the electric displacement and magnetization fields satisfy
where \(\varepsilon \) is the permittivity , \(\mu \) is the permeability , and c is the speed of light within the material.Footnote 2 Denoting the permittivity and permeability of free space by \(\varepsilon _0\) and \(\mu _0\), we can express \(\varepsilon \) and \(\mu \) for any such material relative to their free-space values as
where \(\varepsilon _r\), \(\mu _r\) respectively denote the relative permittivity and permeability. Numerical values for \(\varepsilon _0\) and \(\mu _0\) are:
where H denotes the Henry, the unit of electrical inductance. Substituting the above expressions for \(\mathbf {D}\) and \(\mathbf {H}\) into Maxwell’s equations, we can express these equations in terms of fields \(\mathbf {E}\) and \(\mathbf {B}\) as follows:
1.2 Electrostatic Formulations
If the electric and magnetic fields are steady, then the time derivatives in Eqs. 6.5–6.8 will vanish, resulting in the following formulations:
The above equations indicate that in the static case, electricity and magnetism are distinct phenomena: only in the presence of sufficiently rapid changes will \(\mathbf {E}\) and \(\mathbf {B}\) depend on each other.
The formulation \(\nabla \times \mathbf {E} = \mathbf {0}\) states that the electrostatic electric field is curl-free . Recalling Example 4.4, such curl-free fields can be formed from the gradient of a scalar quantity. Defining this scalar as V, and letting
we can show that it has zero curl, using:
where we have used our earlier definition of the curl operator (Eq. 4.4). The scalar V in Eq. 6.9 is known as the electric potential , with SI Units of Volts or V. The SI units of electric field \(\mathbf {E} = -\nabla V\) are therefore V m\(^{-1}\) .
The second equation of electrostatics is \(\nabla \cdot \left( \varepsilon _r\varepsilon _0\mathbf {E} \right) = \rho \). Using Eq. 6.9, this formulation is equivalent to:
Equation 6.10 represents a PDE in the electric potential that can be solved for in any medium given the distributed charge density and appropriate boundary conditions .Footnote 3
1.3 Volume Conductor Theory
In this section, we derive the fundamental equations describing conservation of current in a 3DFootnote 4 conductive medium, also known as a volume conductor.
1.3.1 Electrical Conductivity
If we wish to determine the voltage distribution in a conducting medium arising from the flow of electric current within it, we can utilise Ohm’s Law .Footnote 5 In 1D, Ohm’s Law relates the voltage drop across a resistor to the current flow through it according to:
where V is the potential difference across the resistor, I is the electric current flowing through it (in SI units of Ampères, or A), and R is its resistance (in SI units of Ohms, or \(\Omega \)). The value of resistance will depend on the resistor material as well as its dimensions. For a resistor of length L and uniform cross-sectional area A, the total resistance across its ends (see Fig. 6.1) will depend on the resistivity \(\rho \) , a parameter of the material with SI units of \(\Omega \,\mathrm {m}\), in accordance with Pouillet’s Law Footnote 6:
where \(\sigma = 1/\rho \) is the conductivity of the material in SI units of Siemens per metre, or S m\(^{-1}\).
For a 3D block of material of infinitesimal length \(\Delta x\), we can substitute Eq. 6.12 into Ohm’s Law (Eq. 6.11), to obtain the voltage drop, \(\Delta V\), across it as:
On re-arranging, we obtain
and taking the limit as \(\Delta x \rightarrow 0\),
where the derivative on the right-hand side is simply the electric field in the x-direction along the infinitesimal length of the block, \(E_x\). Defining the current density along the x-direction as \(J_x = I/A\), the above becomes:
In a higher dimensional volume conductor, all components of current density and electric field will satisfy the above relationship. The equivalent expression of Ohm’s law therefore becomes
where current density \(\mathbf {J}\) has SI units of A m\(^{-2}\). Using Eq. 6.9, this expression is equivalent to
For isotropic materials, where the electrical conductivity is independent of direction, \(\sigma \) will be a scalar and \(\mathbf {J}\) and \(\mathbf {E}\) will be parallel to each other. Many physical structures however, including many biological tissues, exhibit preferential directions of conductivity whereby current flow is not in the same direction as the applied electric field. The white matter of the brain, for example, consists of numerous nerve fibres and tracts, which exhibit lower resistance along the local fibre direction than transverse to it. Such materials are said to possess anisotropic conductivity , in which \(\sigma \) in Eq. 6.14 is represented by a conductivity tensor, equivalent in 3D to a \(3\times 3\) matrix:
where the \(\sigma _{ij}\), (\(i,j = 1,2,3\)) denote the individual conductivity components. The eigenvectors of this tensor define the principle directions of conductivity, in which any applied electric field oriented in these directions will result in a current density parallel to it. For most anisotropic materials, it is possible to define three such principle directions which are orthogonal to each other. In such cases, the conductivity tensor will be symmetric and given by:
where \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\) are the scalar conductivities along the three orthogonal principle directions given by the unit vectors \(\mathbf {n}_1\), \(\mathbf {n}_2\), \(\mathbf {n}_3\) respectively .
1.3.2 Current Conservation
Now assume that an arbitrary volume \(\Omega \) in a region of space is providing a source of current with volume current density \(i_s\) (in SI units of A m\(^{3}\)) , as shown in Fig. 6.2. From conservation of current, the total current \(i_{out}\) leaving the closed surface S of \(\Omega \) must be
where \(\mathrm{d}\Omega \) denotes an infinitesimal volume element of \(\Omega \). Using the divergence theorem (Eq. 4.5), we can transform the right-hand surface integral above into
Substituting this identity into Eq. 6.17, we obtain
Since this relationship holds true for any arbitrary volume \(\Omega \), the integrands must identically be equal. That is,
Equation 6.18 represents the governing PDE for volume conductor electric current flow based on the principle of conservation of current. For most conductive media, the volumetric source current on the right-hand side will be zero, since there are no physical sources of current present. That is,
However, for electrically active biological tissue, macroscopic approximations of tissue activity incorporate a volumetric current source due to cell membrane currents flowing between the intracellular and extracellular domains. In such cases, as will be seen later in this chapter, Eq. 6.18 is used. For inactive non-biological conductive media such as saline, Eq. 6.19 is used, as in the example of the next section .
1.4 Example: Cell Culture Electric Field Stimulator
We wish to design an electric field stimulator to experimentally determine the effect of electric fields on cell cultures in a Petri dish. The electric field is to be delivered using an identical pair of wire electrodes formed from circular arcs placed at opposite ends of the dish against its walls, as shown in Fig. 6.3. Each electrode subtends an angle of \(\theta _0\) at the centre of the dish, whose overall radius is 45 mm. The right electrode is grounded whilst the left electrode has a voltage of 2 V applied to it. All other boundaries are electrically-insulating. The electrical conductivity of the saline medium in which the cells are placed is 1 S/m, and the dish is filled to a height of 10 mm.
Using COMSOL, we will determine the optimal value of electrode angle \(\theta _0\) that maximises the area in which the electric field magnitude is within \(\pm 10\)% of its value at the dish centre (see also Problem 4.10). To do this, we implement the following sequence of steps in COMSOL:
Model Wizard
-
1.
Open the Model Wizard and select the 2D spatial dimension.
-
2.
In the Select Physics panel, choose AC/DC\(\mid \)Electric Currents. Click “Add”. For the dependent variable in the settings window, leave its name as V.
-
3.
Click the Study arrow (
 ) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
Global Definitions
-
1.
Right-click the Definitions sub-node under the Global node, and select Parameters . Specify the name of the parameter as theta and in the expression column enter 60 [deg]. This will be the default electrode angle \(\theta _0\).
Geometry
-
1.
Select the Geometry 1 node in the model tree. In the settings window, change the default length unit to ‘mm’.
-
2.
Right-click Geometry 1 and select Circle. Specify the radius as 45 mm. Click Build Selected (
 ).
). -
3.
Right-click Geometry 1 again and select Circle a second time. Specify the radius as 45 mm, the sector angle as theta and the rotation angle as -theta/2. Click Build Selected (
 ).
). -
4.
Repeat the previous step and select Circle for a third time. Specify the the radius as 45 mm, the sector angle as theta|, and the rotation angle as 180-theta/2. Click Build Selected (
 ).
). -
5.
Right-click Geometry 1 and select Booleans and Partitions\(\mid \)Union. For the input objects, select all three objects in the geometry (one circle and two sectors). Uncheck the checkbox ‘Keep interior boundaries’, and select Build Selected (
 ). This will remove the interior sector lines, keeping electrode arc regions on the perimeter of the circular domain.
). This will remove the interior sector lines, keeping electrode arc regions on the perimeter of the circular domain. -
6.
Finally, right-click Geometry 1 and select Point. Leave the default x, y values to 0 and select Build Selected (
 ). This creates a geometric point at the centre of the dish.
). This creates a geometric point at the centre of the dish.
Component Definitions
-
1.
Right-click the Definitions sub-node under the Component 1 node, and select Component Couplings\(\mid \)Integration. Specify the geometric entity level as ‘point’, and select point 5 corresponding to the centre of the Petri dish. Leave the default operator name as intop1. This integration operator will simply return the value of a given expression evaluated at that point, making it available elsewhere in the model. We will use it to store the electric field magnitude at the centre of the dish.
-
2.
Right-click the Component 1 Definitions sub-node again, and select Component Couplings\(\mid \)Integration. This time, keep the geometric entity level to its default type of ‘domain’, and select domain 1 corresponding to the entire dish. Leave the default operator name as intop2. This integration operator will be used to evaluate the area in which the electric field is relatively uniform.
-
3.
Finally, right-click the Component 1 Definitions sub-node a third time and select ‘Variables’. Keep the default geometric entity selection as ‘Entire model’. Specify a variable with name Ec and expression intop1(ec.normE). This will equal the electric field magnitude at the centre of the dish. Specify a second variable with name A and expression:
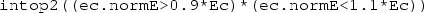
Each of the boolean expressions in the argument of intop2 will return a value of 1 if true or 0 if false.
The product
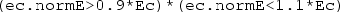 is equivalent to a logical AND operation, returning a value of 1 if
is equivalent to a logical AND operation, returning a value of 1 if  AND
AND 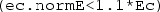 , and 0 otherwise. As a result, the domain integration operator intop2 will return the area of the dish for which the argument is true. That is, the area in which the electric field magnitude is within \(\pm 10\)% of its magnitude at the centre.
, and 0 otherwise. As a result, the domain integration operator intop2 will return the area of the dish for which the argument is true. That is, the area in which the electric field magnitude is within \(\pm 10\)% of its magnitude at the centre.
Electric Currents
-
1.
Select the Electric Currents (ec) node of the model tree, and specify the out-of-plane thickness as 0.01 m (i.e. 10 mm, corresponding to the height of saline filling the dish).
-
2.
Select the Current Conservation 1 sub-node of Electric Currents. In the settings panel, specify the electrical conductivity as ‘user-defined’ with a value of 1 S m\(^{-1}\). Similarly, specify the relative permeability as user-defined, leaving the default value of 1.
-
3.
Right-click the Current Conservation 1 sub-node and select ‘Electric Potential’. In the settings panel, select boundaries 1 and 2 (i.e. left electrode) and specify the electric potential as 2 V.
-
4.
Right-click the Current Conservation 1 sub-node again and select ‘Ground’. In the settings panel, select boundaries 7 and 8 (i.e. the right electrode) to be the grounded boundaries.
Study
-
1.
Right-click the Study 1 node and select ‘Parametric Sweep’ . In the settings panel, click the ‘Add’ button (
 ) to add parameter theta. To specify the parameter value list, click the ‘Range’ button (
) to add parameter theta. To specify the parameter value list, click the ‘Range’ button ( ) and specift the start, step and stop values as 5, 5, 175 respectively. Click add to insert this range of parameter values. For the parameter unit, enter deg. This will setup a parameter sweep on the electrode angle from \(5\,^{\circ }\) to \(175\,^{\circ }\) in steps of \(5\,^{\circ }\).
) and specift the start, step and stop values as 5, 5, 175 respectively. Click add to insert this range of parameter values. For the parameter unit, enter deg. This will setup a parameter sweep on the electrode angle from \(5\,^{\circ }\) to \(175\,^{\circ }\) in steps of \(5\,^{\circ }\). -
2.
To solve the model, right-click Study 1 and select Compute (
 ). This will compute the solution for the specified range of parameter values of theta.
). This will compute the solution for the specified range of parameter values of theta.
Results
-
1.
Under the Results node of the model tree, select the Electric Potential (ec) sub-node. In the Settings window, specify the Parameter value of theta as \(60\,^{\circ }\). Click the Plot button (
 ) to display the electric potential variable V for this parameter value, as shown in Fig. 6.4.
) to display the electric potential variable V for this parameter value, as shown in Fig. 6.4. -
2.
Right-click the Result node and select ‘1D Plot Group’. Right-click the newly-created 1D Plot Group 2 sub-node and select ‘Global’. In the settings panel, click the ‘Add’ button (
 ) followed by Component 1\(\mid \)Definitions\(\mid \)Variables\(\mid \)A to add expression A to the y-axis data for plotting. Specify the y-axis data unit as
) followed by Component 1\(\mid \)Definitions\(\mid \)Variables\(\mid \)A to add expression A to the y-axis data for plotting. Specify the y-axis data unit as 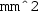 . For the data set, specify ‘Study 1/Parametric Solutions 1’. For the x-axis data, leave the default entry as ‘Parameter value’. Click the Plot button (
. For the data set, specify ‘Study 1/Parametric Solutions 1’. For the x-axis data, leave the default entry as ‘Parameter value’. Click the Plot button ( ) to display the plot of uniform electric field area versus electrode angle, as shown in Fig. 6.4.
) to display the plot of uniform electric field area versus electrode angle, as shown in Fig. 6.4.
Top COMSOL-generated voltage distribution in Petri-dish for an electrode angle theta (i.e. \(\theta _0\)) of \(60\,^{\circ }\) (\(\approx \) \(1.0472\) rad). Bottom COMSOL-generated plot of uniform electric field area (variable A) against electrode angle theta. As can be seen, the maximum uniform electric field area is \(\approx \) \(4000\) mm\(^{2}\) for \(\theta _0 \approx \pi /2\) rad, or \(90\,^{\circ }\)
1.5 Example: Access Resistance of Electrode Disc
Consider a 2D circular disc electrode embedded in a 3D hemispherical infinite medium of conductivity \(\sigma = 1\,\mathrm {S}\,\mathrm {m}^{-1}\) as shown in Fig. 6.5. The radius of the disc electrode is \(R_e = 5\,\mathrm {mm}\), and the potential at the infinite boundary of the hemisphere is taken to be ground (i.e. \(V=0\)). Outside the electrode, the x-y plane boundary surounding the electrode is assumed to be electrically-insulating. Assuming the surface of the disc electrode is at an isopotential value of \(V_s = 1\,\mathrm {V}\), plot the normal component of inward current density as a function of radial position across the electrode and determine the total electrode current \(I_s\). Compare the normal component of current density in the disc with the theoretical solution (see Example 4.12):
where r is the radial distance from the centre of the disc. Find also the access resistance Z of the electrode, defined as the ratio \(V_s/I_s\), comparing this with the theoretical value of
To solve this model in COMSOL, we can use a 2D axisymmetric geometry due to the rotational symmetry about the z-axis (Fig. 6.5). COMSOL also provides the option of adding an infinite domain to represent regions with boundaries infinitely far away.Footnote 7 To implement this model in COMSOL, we can utilise the following steps:
Model Wizard
-
1.
Open the Model Wizard and select the 2D Axisymmetric spatial dimension.
-
2.
In the Select Physics panel, choose AC/DC\(\mid \)Electric Currents. Click “Add”. For the dependent variable in the settings window, leave its name as V.
-
3.
Click the Study arrow (
 ) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
Global Definitions
-
1.
Right-click the Definitions sub-node under the Global node, and select Parameters . Specify the name of the parameter as Vs and in the expression column enter 1 [V]. This will be the electrode voltage. Specify a second parameter with name sigma and expression 1 [S/m] to define the conductivity. Specify a third parameter Re with expression 5 mm. This is the electrode disc radius. Finally, specify a fourth parameter Zth with expression 1/(4*sigma*Re): this is the theoretical access resistance. COMSOL evaluates this expression in terms of the other specified parameters, displaying its value as 50 \(\Omega \).
Geometry
-
1.
Select the Geometry 1 node in the model tree. In the settings window, change the default length unit to ‘mm’.
-
2.
Right-click Geometry 1 and select Circle. Specify the radius as 10 mm and the sector angle as \(90\,^{\circ }\). Click Build Selected (
 ).
). -
3.
Right-click Geometry 1 again and select Circle a second time. Specify the radius as 15 mm and the sector angle as \(90\,^{\circ }\). Click Build Selected (
 ). To zoom out to the entire geometry, click the Zoom Extents button (
). To zoom out to the entire geometry, click the Zoom Extents button ( ).
). -
4.
Right-click Geometry 1 and select Polygon. In the settings window, specify the r coordinate values as 0 Re (insert a space between these two entries), and for the z coordinate, specify 0 0 (again with a space). Click Build Selected (
 ) to draw the electrode as a line interval of length 5 mm on the lower boundary. Once complete, the geometry and model tree will look like that shown in Fig. 6.6.
) to draw the electrode as a line interval of length 5 mm on the lower boundary. Once complete, the geometry and model tree will look like that shown in Fig. 6.6.
Component Definitions
-
1.
Right-click the Definitions sub-node under the Component 1 node, and select Component Couplings\(\mid \)Integration. Specify the geometric entity level as ‘boundary’, and select boundary 2 corresponding to the electrode. Leave the default operator name as intop1. This integration operator will return the integral of its argument over the electrode. We will use it to determine the total inward current \(i_s\) by integrating the normal component of current density as
$$\begin{aligned} i_s = \int _0^{R_e} 2\pi r J_n\,\mathrm{d}r \end{aligned}$$(6.20) -
2.
Right-click the Component 1 Definitions sub-node again, and select ‘Variables’. Keep the default geometric entity selection as ‘Entire model’. Specify a variable with name Is and expression intop1(2*pi*r*ec.Jn). This will equal return the total electrode current, according to Eq. 6.20. Specify a second variable with name Jth and expression
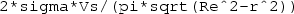 to specify the theoretical current density.
to specify the theoretical current density.Finally, specify an access resistance variable with name Z and expression Vs/Is.
-
3.
Right-click the Component 1 Definitions sub-node a third time and select ‘Infinite Element Domain’. Specify domain 2 in the settings panel.
Electric Currents
-
1.
Select the Current Conservation 1 sub-node of Electric Currents. In the settings panel, specify the electrical conductivity as ‘user-defined’ with a value of sigma. Similarly, specify the relative permeability as user-defined, leaving the default value of 1.
-
2.
Right-click the Current Conservation 1 sub-node and select ‘Electric Potential’. In the settings panel, select boundary 2 (i.e. electrode disc) and specify the electric potential as Vs.
-
3.
Right-click the Current Conservation 1 sub-node again and select ‘Ground’. In the settings panel, select boundary 7 (i.e. infinite boundary) to be the ground.
Mesh
-
1.
Right-click the Mesh 1 node and select ‘Distribution’. In the settings panel, select boundary 2 and specify 100 as the number of elements.
-
2.
Right-click the Mesh 1 node again and select ‘Free Triangular’, leaving the geometric entity level to its default value of ‘Remaining’. Click the Build all button (
 ) to build and display the mesh. A view of the resulting mesh is shown in Fig. 6.7.
) to build and display the mesh. A view of the resulting mesh is shown in Fig. 6.7.
Study
-
1.
To solve the model, right-click Study 1 and select Compute (
 ). This will compute the solution and display the default plot of voltage, as shown in Fig. 6.8.
). This will compute the solution and display the default plot of voltage, as shown in Fig. 6.8.
Results
-
1.
Right-click the Results node of the model tree, and select ‘1D Plot Group’. Right-click the 1D Plot Group 3 sub-node and select ‘Line Graph’. In the Settings window, select boundary 2 in the boundary selection list. Under the y-Axis Data tab, specify ec.nJ as the expression to plot. For the x-Axis Data under Parameter, select ‘Expression’ and specify r. Under the Legends tab, check the ‘Show legends’ checkbox and specify the ‘Manual’ option. In the Legends table, enter the text ‘Computed’.
-
2.
Right-click the 1D Plot Group 3 sub-node and select ‘Line Graph’ again. In the Settings window, select boundary 2 and specify J_th as the expression to plot. For the x-Axis Data under Parameter, select ‘Expression’ and specify r. Under the Legends tab, check the ‘Show legends’ checkbox and specify the ‘Manual’ option. In the Legends table, enter the text ‘Theoretical’. Click the Plot button (
 ) to display the current density plots, as shown in Fig. 6.9. As can be seen from the plots, the computed and theoretical solutions for current density across the electrode agree closely.
) to display the current density plots, as shown in Fig. 6.9. As can be seen from the plots, the computed and theoretical solutions for current density across the electrode agree closely. -
3.
Right-click the Derived Values sub-node under Results and select ‘Global Evaluation’. In the settings panel, specify Z as the expression to evaluate. Click the Evaluate button (
 ) to display the value of the access resistance in a table below the graphics window. COMSOL determines this value to be 52.65 \(\Omega \) which is slightly higher that the 50 \(\Omega \) theoretical value. The discrepancy is due to the mesh resolution not being able to capture the theoretical infinite current density at the edge of the disc. An even finer mesh resolution would improve the estimate of this resistance value
.
) to display the value of the access resistance in a table below the graphics window. COMSOL determines this value to be 52.65 \(\Omega \) which is slightly higher that the 50 \(\Omega \) theoretical value. The discrepancy is due to the mesh resolution not being able to capture the theoretical infinite current density at the edge of the disc. An even finer mesh resolution would improve the estimate of this resistance value
.
2 Modelling Electrical Activity of Tissues
This section will describe macroscopic approximations of excitable tissue electrical activity, and how these can be used to formulate models of tissue electrical stimulation. An example of such an approach may be found in the model of cardiac defibrillation described in Appendix B.
2.1 Continuum Models of Excitable Tissues
As described in Sect. 6.1.3.2, the electrostatic PDE describing voltage distribution in a volume conductor is Eq. 6.18:
This equation is the basis of continuum formulations of the electrical activity of excitable tissues and their modulation by extracellular stimulation. We begin with the formulation of nerve axon membrane current proposed by Hodgkin and Huxley (see Sect. 2.3.2), which we will generalise to any excitable tissue:
where \(i_m\) is the total cell membrane current per unit membrane area, \(C_m\), \(i_{Na}\), \(i_K\), \(i_L\) are the membrane capacitance, sodium, potassium and leakage currents per unit membrane area respectively, and \(V_m\) is the transmembrane voltage, defined as
where \(V_i\), \(V_e\) are the intracellular and extracellular voltages. Equation 6.21 describes total membrane current as consisting of capacitive and ionic components. The equation may be generalised for any excitable cell type (neural, muscular, sensory) by substituting in a generic ionic current, \(i_{ion}\) as:
where \(i_{ion}\) is particular to the cell type in question. Rather than model every individual cell in the tissue, we can employ a macroscopic approximation by assuming the tissue consists of two interpenetrating domains: the intracellular and extracellular spaces. That is, at every point in the excitable tissue, we can define coupled variables \(V_i\), \(V_e\) corresponding to the intracellular and extracellular voltages. Using Eq. 6.18, we can write the equations for both domains as:
where \(\beta \) is the tissue surface-to-volume ratio (in SI units of m\(^{-1}\)). In these equations, the extracellular volume current source \(i_s\) (Eq. 6.18) has been replaced with \(\beta i_m\), and the corresponding current source for the intracellular domain has been replaced with an equal and opposite magnitude, \(-\beta i_m\). The factor \(\beta \) is a parameter of the tissue representing the total cell membrane surface area per unit volume.
Substituting Eq. 6.22 into Eqs. 6.23 and 6.24, we obtain the bidomain equations :
Furthermore, substituting the expression \(V_m = V_i-V_e\), and incorporating extracellular and intracellular volume stimulus current sources \(i_{se}\) and \(i_{si}\) , we obtain the full-form of the bidomain equations:
where \(i_{si}\) and \(i_{se}\) are external stimulus currents per unit volume for the intracellular and extracellular domains respectively. External intracellular stimulus currents include stimuli delivered directly to the cell interiors through inserted microelectrodes. External extracellular stimulus currents are delivered directly to the extracellular space, but are not typically specified as a volume current source as above, but rather as boundary conditions on the electrode boundaries of the extracellular volume .
By fixing the extracellular potential everywhere to ground (i.e. \(V_e = 0\)), the bidomain equations reduce to the simpler monodomain formulation:
where \(\sigma \) denotes the intracellular conductivity of the tissue. Although much simpler than the bidomain equations, the monodomain Eq. 6.29 cannot be used to simulate the effects of an applied extracellular stimulus, or to simulate extracellular voltage signals such as the ECG arising from the electrical activity of tissue .
2.2 Example: Modelling Spiral-Wave Reentry in Cardiac Tissue
In this example, we will simulate spiral-wave reentry in cardiac tissue using a modified bidomain formulation of the Rogers-McCulloch PDE formulations [8] for the cardiac action potential:
with
where u is an auxiliary ‘recovery’ variable, \(\varvec{\sigma }_i\) and \(\varvec{\sigma }_e\) are the intra- and extracellular conductivity tensors , with principle conductivities along the global x, y axes given by \(\sigma _{ix}\), \(\sigma _{ex}\), \(\sigma _{iy}\), \(\sigma _{ey}\), \(\beta \) is the tissue surface to volume ratio, \(C_m\) is cell membrane capacitance per unit area, \(i_{ion}\) is the ionic current per unit cell membrane area, \(i_{stim}\) is the applied extracellular stimulus current per unit tissue volume, and A, B, a, b, d, e, \(c_1\) and \(c_2\) are parameters describing the active electrical activity of the atria, as given in Table 6.1. Initial values at \(t=0\) throughout the tissue are \(V_e = 0\,\mathrm {mV}\), \(V_i = -85\,\mathrm {mV}\) and \(u=0\).
The cardiac tissue domain is a 2D square of side-length 10 cm, with the left-hand corner located at \(x=0\), \(y=0\), where x, y represent the 2D spatial coordinates. Zero-flux boundary conditions for \(V_e\) , \(V_i\) apply on all four external boundaries of the domain. Furthermore, the extracellular potential at the top right-hand corner at \(x=10\,\mathrm {cm}\), \(y=10\,\mathrm {cm}\) is held at ground (i.e. \(V_e=0\,\mathrm {V}\)). The stimulus current is given by:
To setup and solve this model in COMSOL, we implement the following steps:
Model Wizard
-
1.
Open the Model Wizard and select the 2D spatial dimension.
-
2.
In the Select Physics panel, choose Mathematics\(\mid \)PDE Interfaces\(\mid \)General Form PDE, and click “Add”. In the Review Physics panel at right, specify V as the Field name and 2 as the number of dependent variables. In the dependent variables list, enter the names of these variables as Ve and Vi. For the dependent variable quantity, specify the units as Electric potential (V) , and the source term quantity as Current source (
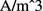 )
.
)
. -
3.
Next, select again Mathematics\(\mid \)PDE Interfaces\(\mid \)General Form PDE, and click “Add”. This will insert a second General Form PDE into the model. In the Review Physics panel, leave the field name as u and the number of dependent variables as 1. Leave the units of the dependent variable as Dimensionless, but enter the source term units manually as 1/s.
-
4.
Click the Study arrow (
 ) to open the Select Study panel. Select Time Dependent, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Time Dependent, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
Global Definitions
-
1.
Right-click Global Definitions in the model tree and select Parameters . Enter the following details in the Parameters table of the Settings window:
Name
Expression
Description
A
55 [mV]
Model parameter
B
-85 [mV]
Model parameter
a
-66.8 [mV]
Model parameter
b
-85 [mV]
Model parameter
d
140 [mV]
Model parameter
e
285.7 [1/(V*s)]
Model parameter
c_1
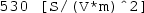
Model parameter
c_2
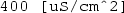
Model parameter
C_m
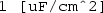
Membrane capacitance
beta
100[1/m]
Surface to volume ratio
s_ex
0.1 [mS/cm]
Extracellular x conductivity
s_ey
0.025 [mS/cm]
Extracellular y conductivity
s_ix
0.2 [mS/cm]
Intracellular x conductivity
s_iy
0.1 [mS/cm]
Intracellular y conductivity
I_stim

Stimulus amplitude
T1_on
10 [ms]
Stimulus 1 onset
T2_on
110 [ms]
Stimulus 2 onset
T_dur
1 [ms]
Stimulus duration
-
2.
Right-click Global Definitions and select Functions\(\mid \)Rectangle. Specify the lower limit as T1_on and the upper limit as T1_on+T_dur. In the Smoothing tab, specify the size of the transition zone as T_dur/10. Leave the function name to its default (rect1).
-
3.
Right-click Global Definitions again and select Functions\(\mid \)Rectangle. Specify the lower limit as T2_on and the upper limit as T2_on+T_dur. In the Smoothing tab, specify the size of the transition zone as T_dur/10. Leave the function name to its default (rect2).
Geometry
-
1.
Select the Geometry 1 node in the model tree. In the settings window, change the length unit to ‘cm’.
-
2.
Right-click Geometry 1 and select Square. Specify the side length as 10 cm and click Build Selected (
 ).
). -
3.
Right-click Geometry 1 again and select Rectangle. Specify the width as 1 cm and the height as 10 cm. Click Build Selected (
 ).
). -
4.
Right-click Geometry 1 a third time and select Rectangle again. In the settings window, specify the width as 10 cm and the height as 1 cm. Click Build Selected (
 ).
). -
5.
Right-click Geometry 1 a fourth time and select Rectangle again. In the settings window, specify the width as 10 cm, the height as 1 cm, and the corner at \(x=0\,\mathrm {cm},\,y=9\,\mathrm {cm}\). Click Build Selected (
 ).
). -
6.
Right-click Geometry 1 a fifith time and select Rectangle again. In the settings window, specify the width as 1 cm, the height as 10 cm, and the corner at \(x=9\,\mathrm {cm},\,y=0\,\mathrm {cm}\). Click Build Selected (
 ). Once complete, the geometry and model tree will look like that shown in Fig. 6.10.
). Once complete, the geometry and model tree will look like that shown in Fig. 6.10.
Component Definitions
-
1.
Right-click the Definitions sub-node of Component 1 and select Variables. Leave the geometric entity level to its default as ‘Entire model’, and enter the following variables in the settings table:
Name
Expression
Vm
Vi-Ve
i_ion
c_1*(Vm-a)*(Vm-A)*(Vm-B)+c_2*u*(Vm-B)
i_stim_1
I_stim*rect1(t [1/s])
i_stim_2
I_stim*rect2(t [1/s])
-
2.
Right-click the Definitions sub-node of Component 1 a second time and select Variables again. This time, specify the geometric entity level as ‘Domain’, and select domain 1 corresponding to the small square region in the the lower left-hand corner. Define a variable with name stim and expression i_stim_1+i_stim_2.
This specifies domain 1 as a region in which both stimuli are delivered, albeit at different times.
-
3.
Right-click the Definitions sub-node of Component 1 a third time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and select domain 2 corresponding to the mid-rectangular sub-domain on the left-hand edge of the tissue. Define a variable with the same name as above, stim, but this time with expression i_stim_2. This specifies domain 2 as the region in which the second stimulus is delivered.
-
4.
Right-click the Definitions sub-node of Component 1 a fourth time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 3 corresponding to the small square sub-domain at top-left of the tissue. Define another variable with the name stim and expression -i_stim_1+i_stim_2. This specifies domain 3 as the region in which a negative first stimulus is delivered followed by a positive second stimulus.
-
5.
Right-click the Definitions sub-node of Component 1 a fifth time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 4 corresponding to the mid-rectangular sub-domain on the bottom edge of the tissue. Define a variable with name stim and expression i_stim_1. This specifies domain 4 as the region in which the first stimulus is delivered.
-
6.
Right-click the Definitions sub-node of Component 1 a sixth time and select Variables. Again, specify the geometric entity level as ‘Domain’, and select domain 5 corresponding to the larger square sub-domain occupying the central portion of the tissue. Define another variable with the name stim and expression 0. This specifies domain 5 as the region in which no stimulus is delivered.
-
7.
Right-click the Definitions sub-node of Component 1 a seventh time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 6 corresponding to the mid-rectangular sub-domain on the top edge of the tissue. Define a variable with name stim and expression -i_stim_1. This specifies domain 6 as the region in which the negative of the first stimulus is delivered.
-
8.
Right-click the Definitions sub-node of Component 1 an eighth time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 7 corresponding to the small square sub-domain at the bottom-right corner of the tissue. Define another variable with the name stim and expression i_stim_1-i_stim_2. This specifies domain 7 as the region in which the first stimulus is delivered followed by a negative second stimulus.
-
9.
Right-click the Definitions sub-node of Component 1 a ninth time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 8 corresponding to the mid-rectangular sub-domain on the right edge of the tissue. Define a variable with name stim and expression -i_stim_2. This specifies domain 8 as the region in which the negative of the second stimulus is delivered.
-
10.
Finally, right-click the Definitions sub-node of Component 1 a tenth time and select Variables again. As above, specify the geometric entity level as ‘Domain’, and now select domain 9 corresponding to the small square sub-domain at the top-right corner of the tissue. Define another variable with the name stim and expression -i_stim_1-i_stim_2. This specifies domain 9 as the region in which the negative of the first stimulus is delivered followed by the negative of the second stimulus.
General Form PDE
-
1.
Select the General Form PDE 1 sub-node of General Form PDE, and enter the following expressions for the conservative flux \(\varGamma \) components for variables \(V_e\) and \(V_i\) respectively:
Component
Expression
x
-s_ex*Vex
y
-s_ey*Vey
x
-s_ix*Vix
y
-s_iy*Viy
Enter the following expressions for the source term f corresponding to variables \(V_e\) and \(V_i\) respectively:
beta*i_ion + stim
-beta*i_ion
Finally, enter the following terms for the damping coefficient matrix \(d_a\):
beta*C_m -beta*C_m
-beta*C_m beta*C_m
Leave the mass coefficient matrix \(e_a\) entries to their default value of 0.
-
2.
Right-click General Form PDE again and select Points\(\mid \)Pointwise Constraint. In the settings panel, specify point 16 corresponding to the upper right-hand corner of the square domain. Under the Constraint expression tab in the settings panel, specify Ve. The constraint expression is held to a value of 0: in this case, this is equivalent to specifying \(V_e=0\) at point 16.
-
3.
Select the Initial Values 1 sub-node of the General Form PDE node . Leave the initial value of Ve to its default value of 0. For Vi however, enter the initial value expression −85 [mV].
General Form PDE 2
-
1.
Select the General Form PDE 1 sub-node of General Form PDE 2, and enter a value of 0 for each of the two components of conservative flux \(\varGamma \), since there are no spatial derivatives in the equation for u. For the source term f , enter the expression e*(Vm-d*u-b) and for the damping and mass coefficients \(d_a\) and \(e_a\), leave their value as 1 and 0 respectively.
Study
-
1.
Select the Step1: Time Dependent sub-node of the Study 1 node. In the Settings window, Click the Range button (
 ) adjacent to the Times field. Leave the entry method as ‘Step’ and enter Start, Step and Stop values of 0, 0.001 and 0.6 respectively. Click Replace. This will create a range of output time values from 0 to 0.6 s in time steps of 0.001 s.
) adjacent to the Times field. Leave the entry method as ‘Step’ and enter Start, Step and Stop values of 0, 0.001 and 0.6 respectively. Click Replace. This will create a range of output time values from 0 to 0.6 s in time steps of 0.001 s. -
2.
Right-click the Study 1 node and select Show Default Solver . Select the Study 1\(\mid \)Solver Configurations\(\mid \)Solver 1\(\mid \)Time-Dependent Solver 1 node. In the Settings window, expand the Time Stepping tab and specify ‘Strict’ for the steps taken by solver option. Expand the Advanced tab, and for the ‘Singular mass matrix’ option , select ‘Yes’.
-
3.
To solve the model, right-click Study 1 and select Compute (
 ). Select the Progress tab in the Information window to see the solver progress.
). Select the Progress tab in the Information window to see the solver progress.
Results
-
1.
When the model has completed solving,Footnote 8 the Graphics window will display a default plot of the extracellular potential (variable \(V_e\)) at \(t=0.6\,\mathrm {s}\), as shown in Fig. 6.11.
-
2.
To plot the membrane potential at this time, select the Surface 1 sub-node of 2D Plot Group 1. In the settings panel, type the expression to plot as Vm. Specify the unit as ‘mV’ and click the Plot button (
 ). Selecting the parent 2D Plot Group 1 node, the required time can be selected from the list of times stored in the solution output. Figure 6.12 shows the plot of membrane potential at \(t=0.54\,\mathrm {s}\). The solution for \(V_m\) consists of a spiral wavefront rotating counter-clockwise in the tissue, also referred to as reentrant activation.
). Selecting the parent 2D Plot Group 1 node, the required time can be selected from the list of times stored in the solution output. Figure 6.12 shows the plot of membrane potential at \(t=0.54\,\mathrm {s}\). The solution for \(V_m\) consists of a spiral wavefront rotating counter-clockwise in the tissue, also referred to as reentrant activation. -
3.
To plot the \(V_m\) and \(V_e\) waveforms at a given point in the tissue, right-click the Data Sets sub-node under Results and select ‘Cut Point 2D’. In the settings panel, specify the Point Data coordinates as \(x=5\,\mathrm {cm}\), \(y=5\,\mathrm {cm}\).
-
4.
Right-click the Results node of the model tree, and select ‘1D Plot Group’. Right-click the 1D Plot Group 3 sub-node and select ‘Point Graph’. In the Settings window, select Cut Point 2D 1 for the Data set. Under the y-Axis Data tab, specify Vm as the expression to plot, with units of ‘mV’ . Under the Legends tab, check the ‘Show legends’ checkbox and specify the ‘Manual’ option. In the Legends table, overwrite the default text of ‘(5,5)’ with the text ‘Membrane Potential’.
-
5.
Right-click the 1D Plot Group 3 sub-node and select ‘Point Graph’ again. In the Settings window, select Cut Point 2D 1 for the Data set and specify Ve as the expression to plot in units of ‘mV’. Under the Legends tab, check the ‘Show legends’ checkbox and specify the ‘Manual’ option. In the Legends table, enter the text ‘Extracellular Potential’.
-
6.
Select the 1D Plot Group 3 sub-node and in the settings window, expand the Title tab and select ‘Manual’ for the Title type. Enter the text ‘Ve and Vm at Point (5,5) cm (in mV)’. Under the Axis tab, check the Manual axis limits checkbox and enter the following values: x minimum (−0.01), x maximum (0.61), y minimum (-100), y maximum (100). Click the Plot button (
 ) to display the point plots, as shown in Fig. 6.13.
) to display the point plots, as shown in Fig. 6.13.
2.3 Modelling PDEs/ODEs on Boundaries, Edges and Points
Many models require the formulation of PDEs/ODEs on lower-dimensional boundaries, edges or points, in addition to any PDEs that may be specified in the main spatial domain. For example, to simulate the 3D electrical activity of cardiac atrial tissue, the atria can be modelled as 2D surfaces embedded in 3D space owing to the small thickness of their walls. A 2D PDE such as Eq. 6.29 can then be employed to simulate electrical activity on these surfaces. To implement such equations in COMSOL, we can utilise use the Lower Dimensions PDE application modes (boundary, edge or point) of COMSOL’s Mathematics Physics interface.
For a COMSOL variable u defined only on a lower dimensional boundary, edge or point, the standard COMSOL spatial derivative variables ux, uy, uz are not defined on this boundary, and cannot be used to specify the components of flux \(\varGamma \) in COMSOL’s PDE General form:
To specify the components of \(\varGamma \), we instead utilise COMSOLs tangential derivative in-built variables uTx, uTy, and uTz, which are available on the boundary. To understand the concept of tangential derivatives, consider a variable u which is defined everywhere in the higher-dimensional domain of a model. If \(\nabla u\) is the gradient of u , then on a lower-dimensional boundary with outward unit normal \(\mathbf {n}\), the tangential gradient, \((\nabla u)_t\), is defined as the projection of \(\nabla u\) onto the boundary, as shown in Fig. 6.14. Referring to this figure, we can determine the tangential gradient according to:
For variables u defined only on a lower-dimensional boundary, the tangential derivatives define the components of flux tangential to the surface itself, analogous to Eq. 6.31.
2.4 Example: Axonal Stimulation Using Nerve Cuff Electrodes
Consider a 10 mm length nerve bundle of radius 1 mm containing an embedded edge element along its central axis representing a single axon fibre as shown in Fig. 6.15. The two small surface patches represent external cuff electrodes to stimulate the axon, and are squares of sidelength 1 mm ‘wrapped around’ the bundle, with a centre-centre spacing of 7 mm along the main axis. To stimulate the axon, the active left cuff electrode delivers an outward square-wave current of 1 mA over 1 ms and acts as a cathode, whilst the right electrode is held at ground.
To derive the underlying PDE governing the intra- and extracellular potentials on the 1D neural edge, we can use a process similar to Example 4.15, whereby we discretize the axon into segments of length \(\Delta s\), where s is the arclength along the axon. The electrical equivalent circuit of three adjacent intracellular nodes is shown in Fig. 6.16.
Axon cable discretization showing three adjacent nodes for intracellular potential \(V_i\): \(V_{i,k-1}\), \(V_{i,k}\), and \(V_{i,k+1}\). The extracellular potential at node k is \(V_{e,k}\), and the internodal separation is given by \(\Delta s\), r denotes the radius of the axon, and \(\rho _i\) is the axoplasmic resistivity . Membrane capacitance \(C_m\) and ionic current \(i_{ion}\) are given per unit membrane area
The axoplasmic resistance between two nodes may be determined from Pouillet’s law, \(\rho L/A\) which evaluates to \(\rho _i\Delta s/\pi r^2\), as shown in Fig. 4.16 between the nodes. Furthermore, the total membrane capacitance of a cylindrical nerve segment of length \(\Delta s\) is given by \(C_m\) multiplied by the area of its curved surface, or \(C_m2\pi r\Delta s\). A similar argument follows for the total membrane ionic current of the segment, namely \(i_{ion}2\pi r\Delta s\). These values are also shown in Fig. 4.16. From Kirchhoff’s current law, the total current entering node k must equal the current leaving through the parallel membrane capacitance and ionic pathways. This can be expressed by the equation
On re-arranging, this becomes:
where \(V_{m,k}\) is the membrane potential at node k, equal to \(V_{i,k}-V_{e,k}\). The left-hand side of this equation is simply the FD approximation of the second-order derivative of \(V_i\) (see Eq. 4.35). Hence, in the limit as \(\Delta s \rightarrow 0\), Eq. 6.32 becomes
where \(C_m\), \(\rho _i\) and r are assumed to be fixed along the axon. Using \(V_i = V_m+V_e\), Eq. 6.33 may also be expressed as:
Re-arranging all terms of this equation, we can express it in terms of the COMSOL PDE general form Eq. 6.30 in 1D as
where the flux \(\varGamma \), source term f and damping coefficient \(d_a\) are given by:
To express the flux , we make use COMSOL’s tangential derivative variables:
where Vm, Ve, rho_i are the COMSOL variables/parameters corresponding to \(V_m\), \(V_e\) and \(\rho _i\) respectively. For the ionic current \(i_ion\) in Eq. 6.34, we can use the Hodgkin-Huxley formulation of axonal electrical activity (see Sect. 2.3.2):
with
where \(V_m\) in these equations is in units of mV. All Hodgkin-Huxley model parameter values are as given earlier in Table 2.2.
To determine the extracellular potential \(V_e\) in Eq. 6.30, we utilise COMSOL’s current conservation physics mode for determining electric potential in a volume conductor. To account for the influence of nerve axon excitation on the extracellular potential, we utilise COMSOL’s line current source to specify outward nerve membrane current per unit length along the axon as
To implement this model in COMSOL, we implement the following steps:
Model Wizard
-
1.
Select the 3D dimension. Under Select Physics, choose Mathematics\(\mid \)PDE Interfaces\(\mid \)Lower Dimensions\(\mid \)General Form Edge PDE. Click Add to add the physics application. Specify 1 dependent variable with name Vm, units of Electric potential (V), and source term quantity as Current source in units of A/m\(^{3}\) .
-
2.
Select the General Form Edge PDE again, and click Add a second time to add another Edge PDE physics node. This time, specify 3 dependent variables with names N, M and H. Note that COMSOL variables are case-sensitive, and that lower-case h is a reserved variable denoting mesh size. Leave the units of these three variables as dimensionless, and specify the source term units as 1/s.
-
3.
Finally, select AC/DC\(\mid \)Electric Currents, and click Add to add the physics. Specify the name of the dependent variable as Ve.
-
4.
For the study type, select ‘Time Dependent’, then click ‘Done’.
Geometry
-
1.
Right click the Geometry 1 node of the model tree and specify a cylinder with radius = 1 mm, height = 10 mm, position (0, 0, 0) and axis type to x-axis in order to make the cylinder align along the x-axis. Click ‘Build Selected’.
-
2.
Right click the Geometry 1 node again to define a work plane as a quick yz-plane located at x = 0. Select the Plane Geometry sub-node of this work plane and click the Zoom to Extents tool button at the top of the graphics window. Right click the Plane Geometry work plane sub-node node and specify a point at (0, 0). Click ‘Build Selected’.
-
3.
Right click the Geometry 1 node a third time and select Extrude. Specify the input object as the point in the work plane array, with the distance to extrude as 10 mm. Click ‘Build Selected’: this defines a line element in 3D. Click the transparency tool button (
 ) to see the edge element within the nerve.
) to see the edge element within the nerve. -
4.
Right click the Geometry 1 node again to define a second work plane as a quick-zx plane located at y = 0. Select the Plane Geometry sub-node of this work plane and click the Zoom to Extents tool button.
-
5.
Right click the Plane Geometry sub-node and select Polygon. Specify its type as Open curve with x coordinates: −1 mm, −1 mm and y coordinates: 1 mm, 2 mm. Click ‘Build Selected’.
-
6.
Right click the Plane Geometry sub-node node again and reselect Polygon. Again specify its type as Open curve with x coordinates: −1 mm, −1 mm and y coordinates: 8 mm, 9 mm. Click ‘Build Selected’.
-
7.
Return to the Geometry 1 node and right click to select Revolve. Specify the input objects as ‘wp2’ (i.e. Work Plane 2), start angle: (pi [rad] +1 [rad]) and end angle: pi [rad]. Leave the points on the revolution axis and the revolution axis direction to their default values and click ‘Build Selected’. This defines the two cuff electrodes. The resulting COMSOL model tree and geometry are shown in Fig. 6.17.
Global Definitions
-
1.
Right click Global Definitions and define the following Parameters:
Name
Expression
g_Na
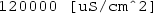
g_K
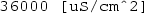
g_L
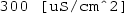
V_Na
55 [mV]
V_K
-72 [mV]
V_L
-49.387 [mV]
Cm

rho_i
60 [ohm*cm]
sigma_e
1 [S/m]
r
0.00025 [cm]
I_stim
1 [mA]
-
2.
Right click Global Definitions again and select Functions\(\mid \)Rectangle. Specify the upper and lower limits as 0.001 and 0.002 respectively. In the Smoothing tab, specify the size of the transition zone as \(1\text {e}-5\). Leave the name rect1 as the default function name. This defines the stimulus current waveform.
Definitions
-
1.
Right click the Definitions sub-node of Component 1 to specify Variables, and select Edge as the geometric entity level. Specify edge 6 and define variables as shown below. Note that ‘...’ is used for convenience whenever relevant expressions continue to the next line - it would be omitted when typing in COMSOL:
Name
Expression
i_Na
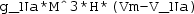
i_K
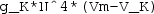
i_L
g_L*(Vm-V_L)
i_ion
i_Na+i_K+i_L
alpha_N
(10 [1/(mV*s)])*(Vm+(50 [mV]))/...
(1-exp(-(Vm+(50 [mV]))/(10 [mV])))
beta_N
(125 [1/s])*exp(-(Vm+(60 [mV]))/(80 [mV]))
alpha_M
(100 [1/(mV*s)])*(Vm+(35 [mV]))/...
(1-exp(-(Vm+(35 [mV]))/(10 [mV])))
beta_M
(4000 [1/s])*exp(-(Vm+(60 [mV]))/(18 [mV]))
alpha_H
(70 [1/s])*exp(-(Vm+(60 [mV]))/(20 [mV]))
beta_H
(1000 [1/s])/...
(1+exp(-(Vm+(30 [mV]))/(10 [mV])))
General Form Edge PDE
-
1.
Select the General Form Edge PDE node and remove all edges except edge 6 which corresponds to the axon fibre.
-
2.
Select the General Form PDE 1 sub-node and enter the following into the flux (\(\varGamma \)) fields:
-
-VmTx/rho_i - VeTx/rho_i
-
-VmTy/rho_i - VeTy/rho_i
-
-VmTz/rho_i - VeTz/rho_i
Specify the source term (f) as -(2/r)*i_ion , and the damping coefficient (da) as (2*Cm/r).
-
-
3.
Under the Initial Values node, specify −60 [mV] .
-
4.
Right click the General Form PDE Edge node and select ‘Dirichlet boundary condition’. Add points 3 and 16 to the selection corresponding to the end points of the axon edge. Specify a prescribed value for Vm of −60 [mV].
General Form Edge PDE 2
-
1.
Select the General Form Edge PDE 2 node and remove all edges except edge 6 which corresponds to the axon fibre.
-
2.
Select the General Form PDE 1 sub-node and enter 0 into all of the flux (\(\varGamma \)) fields, since there are no spatial derivatives in the PDEs for variables N, M, H. Enter the following into the source term components (f):
-
N: alpha_N*(1-N)-beta_N*N
-
M: alpha_M*(1-M)-beta_M*M
-
H: alpha_H*(1-H)-beta_H*H
-
-
3.
Select the Initial Values node and specify initial values for the gating variables as N: 0.3177, M: 0.0529, H: 0.5961
Electric Currents
-
1.
Select the Current Conservation 1 node. Set the conductivity \(\sigma \) to the user-defined value of sigma_e, and the relative permittivity to the user-defined value of 1.
-
2.
Right click the Electric Currents node and add a Ground boundary condition for boundary 7, which corresponds to the right cuff electrode.
-
3.
Right click the Electric Currents node again and add a Normal Current Density boundary condition. Specify boundary 6 (i.e. the active left cuff electrode) and set the inward current density \(J_n\) to
 . Note that the (
. Note that the (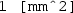 ) term denotes the area of the \(1\times 1\) mm cuff electrode, and the negative sign up front specifies cathodic stimulation.
) term denotes the area of the \(1\times 1\) mm cuff electrode, and the negative sign up front specifies cathodic stimulation. -
4.
Right click the Electric Currents node again and select Edges\(\mid \)Line Current Source . Specify edge 6 and enter the expression for \(Q_j\) corresponding to Eq. 6.35 as: 2*pi*r*(Cm*Vmt+i_ion).
Mesh
-
1.
Right click the Mesh node and select ‘Distribution’. Specify the geometric entity level as Edge, and select edge 6. Specify the number of elements as 100 to specify this amount of edge elements along the axon.
-
2.
Right click the Mesh node again and add a Free Tetrahedral sub-node to mesh the remaining geometry .
Study 1
-
1.
Under the Step 1: Time-Dependent node, specify the time range from 0 to 0.01 s in steps of 0.0001 s.
-
2.
Right click the Study 1 node and select ‘Show default solver’. Under Solver Configurations\(\mid \)Solver 1\(\mid \)Time-Dependent Solver 1, select the Time Stepping tab. Specify the time steps taken by solver to be ‘Strict’ .
-
3.
Right click the Time-Dependent Solver 1 sub-node, and select ‘Fully Coupled’. Right click the ‘Direct’ solver greyed-out sub-node and select ‘enabled’.
-
4.
Right click the Study 1 node again and select Compute.
Results
-
1.
When the model has completed solving,Footnote 9 the Graphics window will display a default plot of the membrane potential (variable \(V_m\)) along the axon at \(t=0.01\,\mathrm {s}\).
-
2.
To plot the membrane potential along the axon at various times, right-click Results and select ‘1D Plot Group’. Right-click the 1D Plot Group 4 sub-node and select ‘Line Graph’. In the Settings window, select edge 6 corresponding to the axon.
-
3.
Select the 1D Plot Group 4 sub-node and in the settings window, select ‘From list’ for the Time selection, and choose times of 0.001, 0.003, 0.005, 0.007 and 0.009 s. Under the Plot Settings Tab, check the x-axis label checkbox and enter ‘Axon position (mm)’.
-
4.
Click the Line Graph 1 sub-node. Leave Vm as the default expression to plot, but specify the units as ‘mV’ . Under the Legends tab, click the ‘Show legends’ check box.
-
5.
Finally, click the Plot button (
 ) to display the line plots, as shown in Fig. 6.18
.
) to display the line plots, as shown in Fig. 6.18
.
3 Further Reading
An good overview of the theory of electromagnetism and Maxwell’s equations may be found in the very short and readable text of Fleisch [3]. Electromagnetism applied to physiology and biology is covered in the texts of Malmivuo and Plonsey [5], Plonsey and Barr [6], and Barnes and Greenebaum [2]. More comprehensive treatments of the electrophysiology of excitable cells and tissues, including nerve and muscle, is provided in the texts of Hille [4] and Aidley [1]. Further examples of electromagnetics modelling using COMSOL, albeit in a non-biological context, may be found in the text of Pryor [7].
Notes
- 1.
James Clerk Maxwell (1831–1879), Scottish mathematical physicist whose contributions to physics, along with those of Einstein and Newton, are regarded as greatest in the history of science.
- 2.
The relationship between \(\mathbf {D}\) and \(\mathbf {E}\) is known as the electric constitutive relation of the material .
- 3.
COMSOL provides the electrostatics module under its AC/DC physics application interface to solve such formulations. Equation 6.10 is specifically implemented using COMSOL’s charge conservation domain setting in the electrostatics module .
- 4.
The subsequent analysis may also be generalised to lower dimensions.
- 5.
Named after the German physicist Georg Simon Ohm (1789–1854).
- 6.
French physicist Claude Pouillet (1790–1868).
- 7.
Available in the AC/DC module. Infinite domains are implemented by applying a coordinate transformation within the domain such that the transformed coordinate tends to infinity on the appropriate boundary, whilst the spatial coordinate remains finite.
- 8.
Using a MacBook Air 2013 with 8GB RAM and OS X 10.8.5, it took 47 s to solve this model.
- 9.
Using a MacBook Air 2013 with 8GB RAM and OS X 10.8.5, it took 4 min, 23 s to solve this model.
References
Aidley DJ (1978) The physiology of excitable cells, 2nd edn. Cambridge University Press, Cambridge
Barnes FS, Greenebaum B (eds) (2007) Handbook of biological effects of electromagnetic fields: bioengineering and biophysical aspects of electromagnetic fields, 3rd edn. CRC Press, Boca Raton
Fleisch D (2008) A student’s guide to Maxwell’s equations. Cambridge University Press, Cambridge
Hille B (2001) Ion channels of excitable membranes, 3rd edn. Sinauer, Sunderland
Malmivuo J, Plonsey R (1995) Bioelectromagnetism: principles and applications of bioelectric and biomagnetic fields. Oxford University Press, Oxford
Plonsey R, Barr RC (2007) Bioelectricity: a quantitative approach. Springer, New York
Pryor RW (2011) Multiphysics modeling using COMSOL: a first principles approach. Jones and Bartlett, Sudbury
Rogers JM, McCulloch AD (1994) A collocation-Galerkin finite element model of cardiac action potential propagation. IEEE Trans Biomed Eng 41:743–757
Author information
Authors and Affiliations
Corresponding author
Problems
Problems
6.1
Two platinum spherical stimulating electrodes of radius 0.5 mm are placed 2 mm apart centre-centre in an infinite saline solution of conductivity 1 S m\(^{-1}\). Assuming the surface of each electrode lies at an isopotential state, use COMSOL to determine the resistance between the electrodes.
6.2
Consider a 2D square slab of excised cardiac tissue of sidelength 1 cm, as shown below. Electrical stimulating electrodes are placed on its left and right boundaries such that the left boundary is held at a potential of 1 V whilst the right is at ground. All other boundaries are assumed to be electrically insulated. The tissue consists of parallel muscle fibres oriented at an angle \(\theta \) relative to the x-axis, with longitudinal conductivity (i.e. along the fibre) of 0.2 mS cm\(^{-1}\) and transverse conductivity 0.1 mS cm\(^{-1}\). Plot the potential distribution and current streamlines for fibre angles \(\theta = 0^{\circ }\), \(\theta = 45^{\circ }\) and \(\theta = 90^{\circ }\).

6.3
A platinum disc electrode of radius 1 mm is injecting current into a hemispherical infinite saline domain of conductivity 1 S m\(^{-1}\), similar to the geometry shown in Fig. 6.5. At the junction between the saline and the platinum, there is a liquid-metal interface, represented by a distributed resistance of \(0.001\,\Omega \,\mathrm {m}^2\). If the platinum electrode is at a steady-state equipotential level of 1 V, the local potential in the saline adjacent to the electrode will be less, owing to the voltage drop across the distributed resistance. Using COMSOL, plot the inward current density as a function of radial position along the disc, comparing against the theoretical solution with no distributed resistance .
Rights and permissions
Copyright information
© 2017 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Dokos, S. (2017). Modelling Electrical Stimulation of Tissue. In: Modelling Organs, Tissues, Cells and Devices. Lecture Notes in Bioengineering. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-54801-7_6
Download citation
DOI: https://doi.org/10.1007/978-3-642-54801-7_6
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-54800-0
Online ISBN: 978-3-642-54801-7
eBook Packages: EngineeringEngineering (R0)





 ) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface. ).
). ).
). ).
). ). This will remove the interior sector lines, keeping electrode arc regions on the perimeter of the circular domain.
). This will remove the interior sector lines, keeping electrode arc regions on the perimeter of the circular domain. ). This creates a geometric point at the centre of the dish.
). This creates a geometric point at the centre of the dish.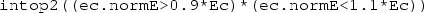
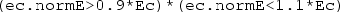 is equivalent to a logical AND operation, returning a value of 1 if
is equivalent to a logical AND operation, returning a value of 1 if  AND
AND 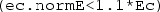 , and 0 otherwise. As a result, the domain integration operator intop2 will return the area of the dish for which the argument is true. That is, the area in which the electric field magnitude is within
, and 0 otherwise. As a result, the domain integration operator intop2 will return the area of the dish for which the argument is true. That is, the area in which the electric field magnitude is within  ) to add parameter
) to add parameter  ) and specift the start, step and stop values as 5, 5, 175 respectively. Click add to insert this range of parameter values. For the parameter unit, enter
) and specift the start, step and stop values as 5, 5, 175 respectively. Click add to insert this range of parameter values. For the parameter unit, enter  ). This will compute the solution for the specified range of parameter values of
). This will compute the solution for the specified range of parameter values of  ) to display the electric potential variable V for this parameter value, as shown in Fig.
) to display the electric potential variable V for this parameter value, as shown in Fig.  ) followed by Component 1
) followed by Component 1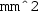 . For the data set, specify ‘Study 1/Parametric Solutions 1’. For the x-axis data, leave the default entry as ‘Parameter value’. Click the Plot button (
. For the data set, specify ‘Study 1/Parametric Solutions 1’. For the x-axis data, leave the default entry as ‘Parameter value’. Click the Plot button ( ) to display the plot of uniform electric field area versus electrode angle, as shown in Fig.
) to display the plot of uniform electric field area versus electrode angle, as shown in Fig. 

 ) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Stationary, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface. ).
). ). To zoom out to the entire geometry, click the Zoom Extents button (
). To zoom out to the entire geometry, click the Zoom Extents button ( ).
). ) to draw the electrode as a line interval of length 5 mm on the lower boundary. Once complete, the geometry and model tree will look like that shown in Fig.
) to draw the electrode as a line interval of length 5 mm on the lower boundary. Once complete, the geometry and model tree will look like that shown in Fig. 
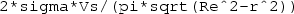 to specify the theoretical current density.
to specify the theoretical current density. ) to build and display the mesh. A view of the resulting mesh is shown in Fig.
) to build and display the mesh. A view of the resulting mesh is shown in Fig. 
 ). This will compute the solution and display the default plot of voltage, as shown in Fig.
). This will compute the solution and display the default plot of voltage, as shown in Fig. 
 ) to display the current density plots, as shown in Fig.
) to display the current density plots, as shown in Fig.  ) to display the value of the access resistance in a table below the graphics window. COMSOL determines this value to be 52.65
) to display the value of the access resistance in a table below the graphics window. COMSOL determines this value to be 52.65 
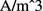 )
.
)
. ) to open the Select Study panel. Select Time Dependent, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.
) to open the Select Study panel. Select Time Dependent, and click “Done”. This will exit the Model Wizard, displaying the main COMSOL interface.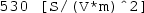
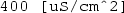
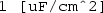

 ).
). ).
). ).
). ).
). ). Once complete, the geometry and model tree will look like that shown in Fig.
). Once complete, the geometry and model tree will look like that shown in Fig. 
 ) adjacent to the Times field. Leave the entry method as ‘Step’ and enter Start, Step and Stop values of 0, 0.001 and 0.6 respectively. Click Replace. This will create a range of output time values from 0 to 0.6 s in time steps of 0.001 s.
) adjacent to the Times field. Leave the entry method as ‘Step’ and enter Start, Step and Stop values of 0, 0.001 and 0.6 respectively. Click Replace. This will create a range of output time values from 0 to 0.6 s in time steps of 0.001 s. ). Select the Progress tab in the Information window to see the solver progress.
). Select the Progress tab in the Information window to see the solver progress.

 ). Selecting the parent 2D Plot Group 1 node, the required time can be selected from the list of times stored in the solution output. Figure
). Selecting the parent 2D Plot Group 1 node, the required time can be selected from the list of times stored in the solution output. Figure  ) to display the point plots, as shown in Fig.
) to display the point plots, as shown in Fig. 



 ) to see the edge element within the nerve.
) to see the edge element within the nerve.
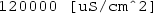
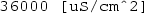
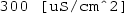

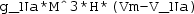
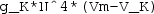
 . Note that the (
. Note that the ( ) term denotes the area of the
) term denotes the area of the  ) to display the line plots, as shown in Fig.
) to display the line plots, as shown in Fig. 