Abstract
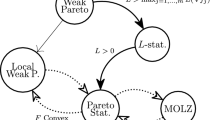
In multiple criteria optimization an important research topic is the topological structure of the set X e of efficient solutions. Of major interest is the connectedness of X e , since it would allow the determination of X e without considering non-efficient solutions in the process. We review general results on the subject, including the connectedness result for efficient solutions in multiple criteria linear programming. This result can be used to derive a definition of connectedness for discrete optimization problems. We present a counterexample to the connectivity conjecture, namely that the sets of efficient solutions of the shortest path problem and the minimal spanning tree problem are connected. We will also present a general method to construct non-connected efficiency graphs for these problems.
partially supported by the Deutsche Forschungsgemeinschaft (DFG) and grant ERBCHRXCT930087 of the European HC&M Programme
supported by the Deutsche Forschungsgemeinschaft (DFG)
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
K.A. Andersen, K. Joernsten, and M. Lind. On bicriterion minimal spanning trees: An approximation. Technical Report 95/13, Department of Operations Research, University of Aarhus, 1995.
E.U. Choo and A.D. Atkins. Connectedness in multiple linear fractional programming. Management Science, 29: 250–255, 1983.
J.G. Ecker and I.A. Kouada. Finding efficient points for linear multiple objective programs. Mathematical Programming, 8: 375–377, 1975.
M. Ehrgott. On matroids with multiple objectives. To appear in Opimization, 1996.
M. Ehrgott and K. Klamroth. Connectedness of efficient solutions in multiple criteria combinatorial optimization. European Journal of Operational Research, 97, 1997.
J.P. Evans and R.E. Steuer. A revised simplex method for linear multiple objective programs. Mathematical Programming, 5: 375–377, 1973.
H.W. Hamacher. Matroid intersections with several objectives. Presented at ECCO VII, Milan, February 21.-23., 1994, 1994.
H.W. Hamacher and G. Ruhe. On spanning tree problems with multiple objectives. Annals of Operations Research, 52: 209–230. 1994.
S. Helbig. On the connectedness of the set of weakly efficient points of a vector optimization problem in locally convex spaces. Journal of Optimization Theory and Applications, 65: 257–271, 1990.
H. Isermann. The enumeration of the set of all efficient solutions for a linear multiple objective program. Operational Research Quarterly, 28 (3): 711–725, 1977.
M. Lind. Neighbourhood search for the bicriterion spanning tree problem. Program implemented at University of Aarhus and Universität Kaiserslautern, February 1995, 1995.
M. Lind. On bicriterion spanning tree problems. Presented at the Twelfth International Conference on MCDM, Hagen, June 18.-23., 1995. 1995.
E.Q.V. Martins. On a multicriteria shortest path problem. European Journal of Operational Research, 16: 236–245, 1984.
P.H. Naccache. Connectedness of the set of nondominated outcomes in multicriteria optimization. Journal of Optimization Theory and Applications, 25: 459–467, 1978.
A.R. Warburton. Quasiconcave vector maximization: Connectedness of the sets of Pareto-optimal and weak Pareto-optimal alternatives. Journal of Optimization Theory and Applications, 40: 537–557, 1983.
P.L. Yu. Cone convexity, cone extreme points and nondominated solutions in decision problems with multiobjectives. Journal of Optimization Theory and Applications, 14: 319–377, 1974.
P.L. Yu and M. Zeleny. The set of all nondominated solutions in linear cases and a multicriteria simplex method. Journal of Mathematical Analysis and Applications, 49: 430–468, 1975.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1997 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Ehrgott, M., Klamroth, K. (1997). Non-connected Efficiency Graphs in Multiple Criteria Combinatorial Optimization. In: Caballero, R., Ruiz, F., Steuer, R. (eds) Advances in Multiple Objective and Goal Programming. Lecture Notes in Economics and Mathematical Systems, vol 455. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-46854-4_15
Download citation
DOI: https://doi.org/10.1007/978-3-642-46854-4_15
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-63599-4
Online ISBN: 978-3-642-46854-4
eBook Packages: Springer Book Archive