Abstract
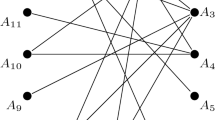
Many research problems are extremely complex, making interdisciplinary knowledge a necessity; consequently cooperative work in mixed teams is a common and increasing research procedure. In this paper, we evaluated information-theoretic network measures on publication networks. For the experiments described in this paper we used the network of excellence from the RWTH Aachen University, described in [1]. Those measures can be understood as graph complexity measures, which evaluate the structural complexity based on the corresponding concept. We see that it is challenging to generalize such results towards different measures as every measure captures structural information differently and, hence, leads to a different entropy value. This calls for exploring the structural interpretation of a graph measure [2] which has been a challenging problem.
Chapter PDF
Similar content being viewed by others
Keywords
References
Calero Valdez, A., Schaar, A.K., Ziefle, M., Holzinger, A., Jeschke, S., Brecher, C.: Using mixed node publication network graphs for analyzing success in interdisciplinary teams. In: Huang, R., Ghorbani, A.A., Pasi, G., Yamaguchi, T., Yen, N.Y., Jin, B. (eds.) AMT 2012. LNCS, vol. 7669, pp. 606–617. Springer, Heidelberg (2012)
Dehmer, M.: Information theory of networks. Symmetry 3(4), 767–779 (2011)
Merton, R.: The Matthew Effect in Science: The reward and communication systems of science are considered. Science 159(3810), 56–63 (1968)
Wuchty, S., Jones, B., Uzzi, B.: The increasing dominance of teams in production of knowledge. Science 316(5827), 1036–1039 (2007)
Holzinger, A.: Successful Management of Research Development. BoD–Books on Demand (2011)
Dehmer, M.: Information processing in complex networks: Graph entropy and information functionals. Appl. Math. Comput. 201(1-2), 82–94 (2008)
Dehmer, M., Varmuza, K., Borgert, S., Emmert-Streib, F.: On entropy-based molecular descriptors: Statistical analysis of real and synthetic chemical structures. Journal of Chemical Information and Modeling 49, 1655–1663 (2009)
Dehmer, M., Mowshowitz, A.: A history of graph entropy measures. Inf. Sci. 181(1), 57–78 (2011)
Holzinger, A., Stocker, C., Bruschi, M., Auinger, A., Silva, H., Gamboa, H., Fred, A.: On Applying Approximate Entropy to ECG Signals for Knowledge Discovery on the Example of Big Sensor Data. In: Huang, R., Ghorbani, A.A., Pasi, G., Yamaguchi, T., Yen, N.Y., Jin, B. (eds.) AMT 2012. LNCS, vol. 7669, pp. 646–657. Springer, Heidelberg (2012)
Calero Valdez, A., Ziefle, M., Alagöz, F., Holzinger, A.: Mental models of menu structures in diabetes assistants. In: Miesenberger, K., Klaus, J., Zagler, W., Karshmer, A. (eds.) ICCHP 2010, Part II. LNCS, vol. 6180, pp. 584–591. Springer, Heidelberg (2010)
Salotti, J., Plantevit, M., Robardet, C., Boulicaut, J.F.: Supporting the Discovery of Relevant Topological Patterns in Attributed Graphs (December 2012), Demo Session of the IEEE International Conference on Data Mining (IEEE ICDM 2012)
Shannon, C.E.: A mathematical theory of communication. Bell System Technical Journal 27 (1948)
Mowshowitz, A.: Entropy and the complexity of graphs: I. An index of the relative complexity of a graph 30, 175–204 (1968)
Holzinger, A., Stocker, C., Peischl, B., Simonic, K.M.: On using entropy for enhancing handwriting preprocessing. Entropy 14(11), 2324–2350 (2012)
Mowshowitz, A., Dehmer, M.: Entropy and the complexity of graphs revisited. Entropy 14(3), 559–570 (2012)
Solé, R., Valverde, S.: Information Theory of Complex Networks: On Evolution and Architectural Constraints. In: Ben-Naim, E., Frauenfelder, H., Toroczkai, Z. (eds.) Complex Networks. Lecture Notes in Physics, vol. 650, pp. 189–207. Springer, Heidelberg (2004)
Ji, L., Bing-Hong, W., Wen-Xu, W., Tao, Z.: Network entropy based on topology configuration and its computation to random networks. Chinese Physics Letters 25(11), 4177 (2008)
Jooss, C., Welter, F., Leisten, I., Richert, A., Schaar, A., Calero Valdez, A., Nick, E., Prahl, U., Jansen, U., Schulz, W., et al.: Scientific cooperation engineering in the cluster of excellence integrative production technology for high-wage countries at rwth aachen university. In: ICERI 2012 Proceedings, pp. 3842–3846 (2012)
Schaar, A.K., Calero Valdez, A., Ziefle, M.: Publication network visualisation as an approach for interdisciplinary innovation management. In: IEEE Professional Communication Conference (IPCC) (2013)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 IFIP International Federation for Information Processing
About this paper
Cite this paper
Holzinger, A. et al. (2013). On Graph Entropy Measures for Knowledge Discovery from Publication Network Data. In: Cuzzocrea, A., Kittl, C., Simos, D.E., Weippl, E., Xu, L. (eds) Availability, Reliability, and Security in Information Systems and HCI. CD-ARES 2013. Lecture Notes in Computer Science, vol 8127. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-40511-2_25
Download citation
DOI: https://doi.org/10.1007/978-3-642-40511-2_25
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-40510-5
Online ISBN: 978-3-642-40511-2
eBook Packages: Computer ScienceComputer Science (R0)