Abstract
This chapter is an introduction to conformal field theory (CFT) which is the basic tool for studying world-sheet properties of string theory. First, we discuss CFT defined on the complex plane, which is relevant for closed strings at tree level. As an application, we then discuss the CFT of a free boson, i.e. string theory in flat space. Finally, we discuss boundary conformal field theory relevant for describing open strings ending on D-branes and non-oriented strings in orientifolds.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
\(\phi ^\prime(z^\prime,\overline{z}^\prime)\,{(dz^\prime)}^{h}\,{(d\overline{z}^\prime)}^{\overline{h}} = \phi (z,\overline{z})\,{(dz)}^{h}\,{(d\overline{z})}^{\overline{h}}\)
- 2.
On the Riemann sphere \(\mathbb{C} \cup \infty \)the only analytic functions are the constants. When we speak about infinitesimal conformal transformations, we mean that ξ(z) is analytic and small in the region where the operators are inserted. Outside this region, they are also small but not necessarily analytic.
- 3.
With indices made explicit, the conserved currents are \({\xi }^{z}(z){T}_{zz}(z)\).
- 4.
In analogy, Lie algebras cannot be classified, but finite dimensional semi-simple Lie algebras allow for the so-called Cartan classification.
- 5.
Alternatively, take the vacuum state and n = 2, then \(\langle 0\vert {L}_{2}{L}_{-2}\vert 0\rangle ={ c \over 2}\), which is the two-point function of the energy-momentum tensor.
- 6.
In quantum field theory, locality and causality demand that operators at space-like separation commute. It follows that an operator which does not depend on position commutes with all other operators and is therefore a c-number.
- 7.
We will see examples of this later.
- 8.
As we remarked above, \(SL(2, \mathbb{C})\)transformations map the Riemann sphere to itself. More general conformal transformations change the geometry.
- 9.
The r.h.s. can be written as \({ 4\pi \over \sqrt{h}} {h}^{\alpha \beta }{ \delta \over \delta {h}^{\alpha \beta }} \left ({ c \over 96\pi } \int olimits olimits \sqrt{h}R{ 1 \over \square } R\,{d}^{2}\sigma \right )\), where the action in parenthesis is the non-local effective action for the external metric, also called Polyakov action, which one obtains if one integrates out the CFT. The fact that the trace is the variation of a non-local action means that it cannot be removed by the addition of local counter terms, i.e. we have a true anomaly.
- 10.
One way to see this is as follows: \(\partial \bar{\partial }\log \vert z\vert ={ 1 \over 2} \partial { 1 \over \overline{z}} ={ 1 \over 2} \partial { z \over \vert z{\vert }^{2}} ={{ 1 \over 2} \lim }_{\epsilon \rightarrow 0}\partial { z \over \vert z{\vert }^{2}+{\epsilon }^{2}} ={{ 1 \over 2} \lim }_{\epsilon \rightarrow 0}{ {\epsilon }^{2} \over {(\vert z{\vert }^{2}+{\epsilon }^{2})}^{2}} = \pi {\delta }^{(2)}(z)\). An alternative way is to integrate with a test function, e.g. \({e}^{-\alpha z\overline{z}}\). The normalization is such that \(\int olimits olimits {d}^{2}z\,{\delta }^{(2)}(z) = 1\). For \(z = {\sigma }^{1} + i{\sigma }^{2},\overline{z} = {\sigma }^{1} - i{\sigma }^{2}\), i.e. \({d}^{2}z = 2\,d{\sigma }^{1}d{\sigma }^{2}\), \({\delta }^{(2)}(z) ={ 1 \over 2} {\delta }^{(2)}(\sigma )\)with \(\int olimits olimits {d}^{2}\sigma {\delta }^{(2)}(\sigma ) = 1\).
- 11.
Great care is required when dealing with normal ordered products of more than two fields. If they are not free fields, the product is not associative and Wick’s theorem cannot be applied straightforwardly. An example will be the Sugawara form of the energy-momentum tensor which we will discuss in Chap. 11.
- 12.
Note that the field conjugate to \({e}^{ipX(z)}\)is \({e}^{-ipX(z)}\).
- 13.
The discussion here is limited to string tree level amplitudes since there the world-sheet is the (Riemann) sphere which is conformally equivalent to \(\mathbb{C} \cup \infty \).
- 14.
Recall Wick’s theorem which reads schematically:

and use
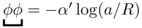
.
- 15.
More generally, \(z^\prime = {e}^{i\alpha }{ z-{z}_{0} \over z-{\overline{z}}_{0}} \,,\alpha \in \mathbb{R},\,\mathrm{Im}({z}_{0}) >0\).
- 16.
The mode expansion on the z-plane would be \(T(z) = \sum olimits {L}_{n}\,{z}^{-n-2}\), where the L n ’s are not the same as the \({L}_{n}^{(\zeta )}\). Below we will drop the superscript ζ.
- 17.
We will discuss one-loop diagrams in detail in Chap. 6.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Berlin Heidelberg
About this chapter
Cite this chapter
Blumenhagen, R., Lüst, D., Theisen, S. (2012). Introduction to Conformal Field Theory. In: Basic Concepts of String Theory. Theoretical and Mathematical Physics. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-29497-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-642-29497-6_4
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-29496-9
Online ISBN: 978-3-642-29497-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)