Abstract
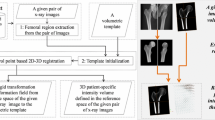
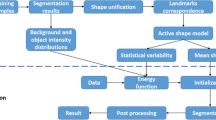
Low-dose CT-like imaging systems offer numerous perspectives in terms of clinical application, in particular for osteoarticular diseases. In this paper, we address the challenging problem of 3D femur modeling and estimation from bi-planar views. Our contributions are threefold. First, we propose a non-uniform hierarchical decomposition of the shape prior of increasing clinical-relevant precision which is achieved through curvature driven unsupervised clustering acting on the geodesic distances between vertices. Second, we introduce a graphical-model representation of the femur which can be learned from a small number of training examples and involves third-order and fourth-order priors, while being similarity and mirror-symmetry invariant and providing means of measuring regional and boundary supports in the bi-planar views. Last but not least, we adopt an efficient dual-decomposition optimization approach for efficient inference of the 3D femur configuration from bi-planar views. Promising results demonstrate the potential of our method.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Cootes, T.F., Taylor, C.J., Cooper, D.H., Graham, J.: Active shape models - their training and application. CVIU 61(1), 38–59 (1995)
Glocker, B., Komodakis, N., Tziritas, G., Navab, N., Paragios, N.: Dense image registration through mrfs and efficient linear programming. Medical Image Analysis 12(6), 731–741 (2008)
Gottschling, H., Roth, M., Schweikard, A., Burgkart, R.: Intraoperative, fluoroscopy-based planning for complex osteotomies of the proximal femur. Int. J. Med. Robotics Comput. Assist. Surg. 1, 67–73 (2005)
Heimann, T., Meinzer, H.P.: Statistical shape models for 3d medical image segmentation: A review. Medical Image Analysis 13(4), 543–563 (2009)
Kadoury, S., Cheriet, F., Laporte, C., Labelle, H.: A versatile 3d reconstruction system of the spine and pelvis for clinical assessment of spinal deformities. Med. Biol. Engineering and Computing 45(6), 591–602 (2007)
Komodakis, N., Paragios, N., Tziritas, G.: MRF optimization via dual decomposition: Message-passing revisited. In: ICCV (2007)
Komodakis, N., Paragios, N., Tziritas, G.: Clustering via lp-based stabilities. In: NIPS (2009)
Kurazume, R., Nakamura, K., Okada, T., Sato, Y., Sugano, N., Koyama, T., Iwashita, Y., Hasegawa, T.: 3d reconstruction of a femoral shape using a parametric model and two 2d fluoroscopic images. CVIU 113(2), 202–211 (2009)
Laporte, S., Skalli, W., de Guise, J.A., Lavaste, F., Mitton, D.: A biplanar reconstruction method based on 2d and 3d contours: Application to the distal femur. Computer Methods in Biomechanics and Biomedical Engineering 6(1), 1–6 (2003)
Mitton, D., Deschenes, S., Laporte, S., Godbout, B., Bertrand, S., de Guise, J.A., Skalli, W.: 3d reconstruction of the pelvis from bi-planar radiography. Computer Methods in Biomechanics and Biomedical Engineering 9(1), 1–5 (2006)
Varshney, K.R., Paragios, N., Deux, J.F., Kulski, A., Raymond, R., Hernigou, P., Rahmouni, A.: Postarthroplasty examination using x-ray images. IEEE Trans. Med. Imaging 28(3), 469–474 (2009)
Wang, C., Teboul, O., Michel, F., Essafi, S., Paragios, N.: 3d knowledge-based segmentation using pose-invariant higher-order graphs. In: Jiang, T., Navab, N., Pluim, J.P., Viergever, M.A. (eds.) MICCAI 2010, Part III. LNCS, vol. 6363, pp. 189–196. Springer, Heidelberg (2010)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2011 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Wang, C., Boussaid, H., Simon, L., Lazennec, JY., Paragios, N. (2011). Pose-Invariant 3D Proximal Femur Estimation through Bi-planar Image Segmentation with Hierarchical Higher-Order Graph-Based Priors. In: Fichtinger, G., Martel, A., Peters, T. (eds) Medical Image Computing and Computer-Assisted Intervention – MICCAI 2011. MICCAI 2011. Lecture Notes in Computer Science, vol 6893. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-23626-6_43
Download citation
DOI: https://doi.org/10.1007/978-3-642-23626-6_43
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-23625-9
Online ISBN: 978-3-642-23626-6
eBook Packages: Computer ScienceComputer Science (R0)