Abstract
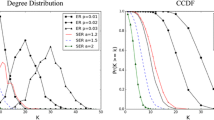
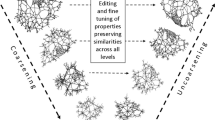
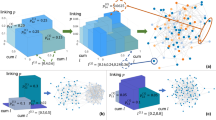
Creating ensembles of random but “realistic” topologies for complex systems is crucial for many tasks such as benchmark generation and algorithm analysis. In general, explanatory models are preferred to capture topologies of technological and biological complex systems, and some researchers claimed that it is largely impossible to capture any nontrivial network structure while ignoring domain-specific constraints. We study topology models of specific spatial networks, and show that a simple descriptive model, the generalized random graph model (GRG) which only reproduces the degree sequence of complex networks, can closely match the topologies of a variety of real-world spatial networks including electronic circuits, brain and neural networks and transportation networks, and outperform some plausible and explanatory models which consider spatial constraints.
Chapter PDF
Similar content being viewed by others
References
Wang, J., Provan, G.M.: Generating application-specific benchmark models for complex systems. In: AAAI, pp. 566–571 (2008)
Li, L., Doyle, J.C., Willinger, W.: Towards a theory of scale-free graphs: Definition, properties, and implications. Internet Mathematics 2(4), 431–523 (2006)
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., Hwang, D.U.: Complex networks: Structure and dynamics. Physics Reports 424(4-5), 175–308 (2006)
Hansen, M.C., Yalcin, H., Hayes, J.P.: Unveiling the iscas-85 benchmarks: A case study in reverse engineering. IEEE Des. Test 16(3), 72–80 (1999)
He, Y., Chen, Z.J.J., Evans, A.C.C.: Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex (2007)
Kaiser, M., Hilgetag, C.C.: Spatial growth of real-world networks. Phys. Rev. E 69(3), 036103 (2004)
Dambre, J.: Prediction of interconnect properties for digital circuit design and technology exploration. Ph.D. dissertation: Ghent University, Faculty of Engineering (2003)
Amaral, L.A., Scala, A., Barthelemy, M., Stanley, H.E.: Classes of small-world networks. Proc. Natl. Acad. Sci. USA 97(21), 11149–11152 (2000)
Mahadevan, P., Krioukov, D.V., Fall, K.R., Vahdat, A.: Systematic topology analysis and generation using degree correlations. In: SIGCOMM, pp. 135–146 (2006)
Middendorf, M., Ziv, E., Wiggins, C.H.: Inferring network mechanisms: the drosophila melanogaster protein interaction network. Proc. Natl. Acad. Sci. USA 102(9), 3192–3197 (2005)
Sporns, O., Chialvo, D.R., Kaiser, M., Hilgetag, C.C.: Organization, development and function of complex brain networks. Trends in Cognitive Sciences 8, 418–425 (2004)
Kaiser, M.: Brain architecture: a design for natural computation. Philosophical Transactions of the Royal Society A 365, 3033–3045 (2007)
Chklovskii, D.B.: Exact solution for the optimal neuronal layout problem. Neural Comput. 16(10), 2067–2078 (2004)
Kaiser, M., Hilgetag, C.C.: Nonoptimal component placement, but short processing paths, due to long-distance projections in neural systems. PLoS Computational Biology 2(7), e95+ (2006)
Costa, L., Kaiser, M., Hilgetag, C.: Predicting the connectivity of primate cortical networks from topological and spatial node properties. BMC Systems Biology 1, 16 (2007)
Cancho, R.F.i., Janssen, C., Solé, R.V.: Topology of technology graphs: Small world patterns in electronic circuits. Physical Review E 64(4), 046119 (2001)
Dorogovtsev, S.N., Mendes, J.F., Samukhin, A.N.: Structure of growing networks with preferential linking. Phys. Rev. Lett. 85(21), 4633–4636 (2000)
Guimera, R., Amaral, L.: Modeling the world-wide airport network. The European Physical Journal B - Condensed Matter 38(2), 381–385 (2004)
Li, W., Cai, X.: Statistical analysis of airport network of china. Phys. Rev. E 69(4), 046106 (2004)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2009 ICST Institute for Computer Science, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Wang, J., Provan, G. (2009). A Comparative Analysis of Specific Spatial Network Topological Models. In: Zhou, J. (eds) Complex Sciences. Complex 2009. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 5. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-02469-6_31
Download citation
DOI: https://doi.org/10.1007/978-3-642-02469-6_31
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-642-02468-9
Online ISBN: 978-3-642-02469-6
eBook Packages: Computer ScienceComputer Science (R0)