Abstract
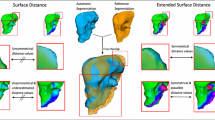
This paper presents the first segmentation operation defined within the 3D topological map framework. Firstly we show how a traditional segmentation algorithm, found in the literature, can be transposed on a 3D image represented by a topological map. We show the consistency of the results despite of the modifications made to the segmentation algorithm and we study the complexity of the operation. Lastly, we present some experimental results made on 3D medical images. These results show the process duration of this method and validate the interest to use 3D topological map in the context of image processing.
Partially supported by the ANR program ANR-06-MDCA-008-05/FOGRIMMI.
Chapter PDF
Similar content being viewed by others
References
Rosenfeld, A.: Adjacency in digital pictures. Information and Control 26, 24–33 (1974)
Kropatsch, W.G., Macho, H.: Finding the structure of connected components using dual irregular pyramids. In: Discrete Geometry for Computer Imagery, pp. 147–158 (September 1995) (invited lecture)
Bertrand, Y., Damiand, G., Fiorio, C.: Topological map: Minimal encoding of 3d segmented images. In: Workshop on Graph-Based Representations in Pattern Recognition, Ischia, Italy, IAPR-TC15, pp. 64–73 (May 2001)
Braquelaire, J.P., Domenger, J.P.: Representation of segmented images with discrete geometric maps. Image and Vision Computing 17(10), 715–735 (1999)
Damiand, G., Bertrand, Y., Fiorio, C.: Topological model for two-dimensional image representation: definition and optimal extraction algorithm. Computer Vision and Image Understanding 93(2), 111–154 (2004)
Fiorio, C.: A topologically consistent representation for image analysis: the frontiers topological graph. In: Miguet, S., Ubéda, S., Montanvert, A. (eds.) DGCI 1996. LNCS, vol. 1176, pp. 151–162. Springer, Heidelberg (1996)
Braquelaire, J.P., Brun, L.: Image segmentation with topological maps and inter-pixel representation. Journal of Visual Communication and Image Representation 9(1), 62–79 (1998)
Haxhimusa, Y., Ion, A., Kropatsch, W.G., Brun, L.: Hierarchical image partitioning using combinatorial maps. In: Hanbury, A., Bischof, H. (eds.) 10th Computer Vision Winter Workshop, pp. 43–52 (February 2005)
Damiand, G., Resch, P.: Split and merge algorithms defined on topological maps for 3d image segmentation. Graphical Models 65(1-3), 149–167 (2003)
Felzenszwalb, P.F., Huttenlocher, D.P.: Image segmentation using local variation. In: Computer Vision and Pattern Recognition, 1998. Proceedings. IEEE Computer Society Conference on, June 1998, pp. 98–104 (1998)
Lienhardt, P.: Topological models for boundary representation: a comparison with n-dimensional generalized maps. Computer-Aided Design 23, 59–82 (1991)
Khalimsky, E., Kopperman, R., Meyer, P.R.: Boundaries in digital planes. Journal of Applied Mathematics and Stochastic Analysis 3(1), 27–55 (1990)
Damiand, G.: Définition et étude d’un modèle topologique minimal de représentation d’images 2d et 3d. Thèse de doctorat, Université Montpellier II (Décembre 2001)
Dupas, A., Damiand, G.: Comparison of local and global region merging in the topological map. In: BrimKov, V.E., et al. (eds.) IWCIA 2008, vol. 4958, pp. 420–431. Springer, Heidelberg (2008)
Cormen, T.H., Leiserson, C.E., Rivest, R.: Introduction to Algorithms. MIT Press, Cambridge (1990)
Tarjan, R.: Efficiency of a good but not linear set union algorithm. Journal of the ACM 22, 215–225 (1975)
Felzenszwalb, P.F., Huttenlocher, D.P.: Efficient graph-based image segmentation. International Journal of Computer Vision 59(2), 167–181 (2004)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Dupas, A., Damiand, G. (2008). First Results for 3D Image Segmentation with Topological Map. In: Coeurjolly, D., Sivignon, I., Tougne, L., Dupont, F. (eds) Discrete Geometry for Computer Imagery. DGCI 2008. Lecture Notes in Computer Science, vol 4992. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-79126-3_45
Download citation
DOI: https://doi.org/10.1007/978-3-540-79126-3_45
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-79125-6
Online ISBN: 978-3-540-79126-3
eBook Packages: Computer ScienceComputer Science (R0)