Abstract
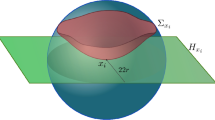
We give a method to generate polynomial approximations to constant mean curvature surfaces with prescribed boundary. We address this problem by finding triangular Bézier extremals of the CMC-functional among all polynomial surfaces with a prescribed boundary. Moreover, we analyze the \(\mathcal{C}^1\) problem, we give a procedure to obtain solutions once the tangent planes for the boundary curves are also given.
Chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
References
Arnal, A., Lluch, A., Monterde, J.: Triangular Bézier Surfaces of Minimal Area. In: Kumar, V., Gavrilova, M.L., Tan, C.J.K., L’Ecuyer, P. (eds.) ICCSA 2003. LNCS, vol. 2669, pp. 366–375. Springer, Heidelberg (2003)
Struwe, M.: Plateau’s problem and the calculus of variations. Mathematical Notes. Princeton University Press, Princeton (1988)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2008 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Arnal, A., Lluch, A., Monterde, J. (2008). Triangular Bézier Approximations to Constant Mean Curvature Surfaces. In: Bubak, M., van Albada, G.D., Dongarra, J., Sloot, P.M.A. (eds) Computational Science – ICCS 2008. ICCS 2008. Lecture Notes in Computer Science, vol 5102. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-69387-1_11
Download citation
DOI: https://doi.org/10.1007/978-3-540-69387-1_11
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-69386-4
Online ISBN: 978-3-540-69387-1
eBook Packages: Computer ScienceComputer Science (R0)