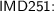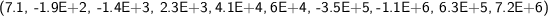Keywords

1 Introduction

The interaction between a medical doctor and a smart machine must respect at least two requirements: Fast action and good integration with the human operator. As far as mere morphology is concerned, deep learning has already reached performances comparable with the ones of a dermatologist [6]. In real practice, the number of (hidden or evident, formal or intuitive) parameters in a diagnostic task is so high, that a good synthesis in short times is, at least for the moment, the field of a human expert; the machine can anyway offer a reliable, stable, powerful assistance. It is necessary that the medical doctor understands what’s going on in his/her interaction with the machine: This is a primary issue in the design of “explainable” AI systems [15]. A way out of the “black box” frustration is to accept a feedback from the user, so that the system adapts more and more to his/her viewpoint.

This is the case of a system currently developed by Ca-Mi srl, an Italian company producing biomedical devices, in collaboration with the Universities of Bologna and Parma and with the Romagna Institute for Study and Cure of Tumors (IRST). The machine acquires the image of a dermatological lesion and retrieves a set of most similar images out of a database with sure diagnoses. The similarity is assessed by a relatively recent geometric-topological technique: Persistent homology. This tool is very effective above all on data of natural origin [8], but the main tool for classification and (dis)similarity assessment—the bottleneck distance between persistence diagrams—is computationally heavy. We are then experimenting a different coding of the same information contained in a persistence diagram, through a complex polynomial; the coding is then “shortened” in that we just use the first few coefficients, so that comparison and search becomes much faster; it appears that these first coefficients contain most of the relevant information.

While the first experiments are very promising [10], there is still a wide gap between what the system and the doctor see as “similar”. Therefore it is an active area of research, to study a relevance feedback method for drawing the machine’s formalization of similarity near the doctor’s skilled view.

In this paper we present a preliminary study on a small public database (\(PH^2\)) of nevi and melanomas; our goal is to combine two relevance feedback methods expressly designed for persistent homology, with a new coding of one of its main tools, persistence diagrams.

Content Based Image retrieval (CBIR) is a ripe and challenging research area [11]. Apart from annotation-based systems, much of the success of CBIR is tied with the use of histograms (of colours, directions, etc.). Topological descriptors have entered the game but are not yet fully employed [19]. On the other hand, we are aware of the incredible flourishing of Deep Learning in the areas of image understanding and of medical diagnosis; our interest in the techniques proposed here depends on the needs to work with a rather limited database, and to be able to control step-by-step how the system adapts to the user. Still we plan, as a future step, to combine persistent homology with Deep Learning—as several researchers already do—by feeding a neural net with persistence diagrams. There are at least two reasons for wishing such a development: The importance of the user’s viewpoint (or taste, or goal) formalized by the choice of filtering functions; and the fact that whatever the kind of input, persistence diagrams have always the same structure, so that a learning network trained on persistence diagrams becomes immediately a much more versatile tool. A step in this direction has already been done [14].

2 Persistent Homology

Persistent homology is a branch of computational topology, of remarkable success in shape analysis and pattern recognition. Its key idea is to analyze data through filtering functions, i.e. continuous functions f defined on a suitable topological space X with values e.g. in \({\mathbb {R}}\) (but sometimes in \({\mathbb {R}}^n\) or in a circle). Given a pair (X, f), with \(f:X \rightarrow {\mathbb {R}}\) continuous, for each \(u\in {\mathbb {R}}\) the sublevel set \(X_u\) is the set of elements of X whose value through f is less than or equal to u.

For each \(X_u\) one can compute the homology modules \(H_r(X_u)\), vector spaces which summarize the presence of “voids” of dimension r, with \(r\in \mathbb {N}\) (connected components in the case \(r=0\)) and their relations. As there exist various homology theories, some additional hypotheses might be requested on f depending on the choice of the homology.

Of course, if \(u<v\) then \(X_u \subseteq X_v\). There corresponds a linear map \(\iota ^r_{(u, v)}: H_r(X_u)\rightarrow H_r(X_v)\). On \(\varDelta ^+ = \{(u, v)\in {\mathbb {R}}^2 \, | \, u<v\}\) we can then define the r-Persistent Betti Number (r-PBN) function

$$\begin{array}{cccc} \beta ^r_{(X,f)}: &{}\varDelta ^+ &{} \rightarrow &{} \mathbb {Z}\\ &{} (u, v) &{} \mapsto &{}\dim \text {Im}(\iota ^r_{(u, v)}) \end{array}$$

All information carried by r-PBN’s is condensed in some points (dubbed proper cornerpoints) and some half-lines (cornerlines); cornerlines are actually thought of as cornerpoints at infinity. Cornerpoints (proper and at infinity) build what is called the persistence diagram relative to dimension r. Figure 1 shows a letter “M” as space X, ordinate as function f on the left, its 0-PBN function at the center and the corresponding persistence diagram on the right.

Fig. 1.
figure 1

Letter M, its 0-PBM function and the corresponding persistence diagram, relative to filtering function ordinate.

Full size image

Remark 1

The theory also contemplates a multiplicity for cornerpoints (proper and at infinity); multiplicity higher than one is generally due to symmetries. We don’t care about it in the present research, since all cornerpoints in our experiments have multiplicity one, as usual in diagrams coming from natural images.

Classification and retrieval of persistence diagrams (and consequently of the object they represent) is usually performed by the following distance, where persistence diagrams are completed by all points on the “diagonal” \(\varDelta =\{(u, v)\in {\mathbb {R}}\, | \, u=v\}\).

Definition 1

Bottleneck (or matching) distance.

Let \(\mathcal {D}_{k}\) and \(\mathcal {D'}_{k}\) be two persistence diagrams with a finite number of cornerpoints, the bottleneck distance \(d_{B}(\mathcal {D}_{k},\mathcal {D'}_{k})\) is defined as

$$\begin{aligned} d_{B}(\mathcal {D}_{k},\mathcal {D'}_{k})=\min _{\sigma }\max _{P\in \mathcal {D}_{k}}\hat{d}(P,\sigma (P)) \end{aligned}$$

where \(\sigma \) varies among all the bijections between \(\mathcal {D}_{k}\) and \(\mathcal {D'}_{k}\) and

$$\begin{aligned} \hat{d}((u,v),(u',v'))=\min \left\{ \max \left\{ |u-u'|,|v-v'|\right\} ,\max \left\{ \frac{v-u}{2},\frac{v'-u'}{2}\right\} \right\} \end{aligned}$$

given \((u,v)\in \mathcal {D}_{k}\) and \((u',v')\in \mathcal {D'}_{k}\).

For homology theory one can consult any text on algebraic topology, e.g. [13]. For persistent homology, two good references are [4, 5].

3 Symmetric Functions of Warped Persistence Diagrams

There are two main difficulties in comparing persistence diagrams. One is the fact that the diagonal \(\varDelta \) has a special role: For a persistence diagram, the diagonal \(\varDelta \) is a sort of “blown up” point, in the sense that points close to it are seen as close to each other by the bottleneck distance; moreover cornerpoints close to \(\varDelta \) generally represent noise, and it would be desirable to diminish their contribution. A second difficulty consists in the coding of a set of points in the plane, in a form suited for comparison and processing: E.g. an intuitive coding like making a 2M vector out of a set of M points is highly unstable and is not the solution to the problem of avoiding the permutations required by the bottleneck distance; a distance computed component by component might be very far from the optimal one. In [1]—which also contains a comparison with the bottleneck distance— we have tried to overcome both difficulties.

Fig. 2.
figure 2

The action of transformations T (left) and R (right) on some segments (above).

Full size image

Following [3, 9], we have faced the first problem by two different transformations T (designed by Barbara Di Fabio) and R which “warp” the plane, so that all \(\varDelta \) is sent to (0, 0), seen here as the complex number zero (Fig. 2):

  • \(T:\bar{\varDelta }^+\rightarrow \mathbb {C}\),    \(T(u,v)=\frac{v-u}{2}(\cos (\alpha )-\sin (\alpha )+i(\cos (\alpha )+\sin (\alpha )))\)

where \(\alpha =\sqrt{u^2+v^2}\).

  • \(R:\bar{\varDelta }^+\rightarrow \mathbb {C}\),    \(R(u,v)=\frac{v-u}{\sqrt{2}}(\cos (\theta )+i\sin (\theta ))\)

where \(\theta =\pi (u+v)\).

The main ideas behind T and R are: For the reasons mentioned at the beginning of this section, cornerpoints close to \(\varDelta \) ought to be considered close to each other. Therefore T and R (and other maps under study) take \(\varDelta \) to zero. Moreover they wrap the strip adjacent to \(\varDelta \) around zero itself, so that the contributions of noise cornerpoints should balance away in Viète’s symmetric functions. We are still looking for the best wrapping function. Both T and R are continuous maps. See Fig. 3 for a persistent diagram and its two images through T and R.

Fig. 3.
figure 3

A persistence diagram (above) and its images through T (left) and R.

Full size image

As for the second problem, following an idea of Claudia Landi [3, 9] we decided to encode each (transformed) persistence diagram \(\mathcal{D}\) as the polynomial having the complex numbers, images of the cornerpoints, as roots. We can then design distances built on the pairs of coefficients of equal position in the polynomials representing two diagrams, avoiding a combinatorial explosion. Actually, for a given diagram we form the vector having as components the elementary symmetric functions of the transformed cornerpoints (which, through Viète’s formulas, equal the coefficients of the polynomial up to the sign) [16, Sect. IV.8]. So, the first component of the vector is the sum of all those numbers, the second one is the sum of all pairwise products, and so on. In order to take also cornerpoints at infinity into account, we have performed the following substitution. Given a cornerpoint at infinity (i.e. a cornerline) with abscissa w of a persistence diagram \(\mathcal{D}\), we substitute it with the point

$$\begin{aligned} \big (w, \max \{v \, | \, (u,v) \ \text {is a proper cornerpoint of} \ \mathcal{D} \}\big ) \end{aligned}$$

Remark 2

Since cornerpoints near \(\varDelta \) generally represent noise, the two transformations were designed to wrap them around zero, so that the symmetric functions be scarcely affected by them. To this goal, transformation R fits better in our case, since our filtering functions (hence the cornerpoint coordinates) are bounded between 0 and 1.

For a fixed filtering function, for a fixed transformation (T or R), the same elementary symmetric function computed on two persistence diagrams may show a difference of several orders of magnitude, when there are many cornerpoints. This might consistently alter the comparisons, so we actually formed, for each persistence diagram \(\mathcal{D}\), the complex vector \(a_\mathcal{D}\) whose i-th component \(a_\mathcal{D}(i)\) is the i-th root of the i-th elementary symmetric function of the transformed cornerpoints, divided by the number of cornerpoints. As an example, these are the (approximated) real parts of the first 10 symmetric functions for images IMD251 and IMD423, fitering function “Light intensity 2”, transformation T:

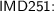
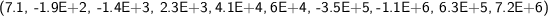
  • which, by taking the i-th root of the ith symmetric function, become:

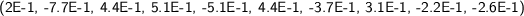
  • and division by the number of cornerpoints (here 257 and 1408 respectively) yields:

  • whose differences finally make sense.

The advantage of using the vectors \(a_\mathcal{D}\) instead of the original diagrams is that one can directly design a distance between complex vectors component-by-component (e.g. the \(L^1\) distance we used), instead of considering all bijections between cornerpoint sets. Still, the computation of all the elementary symmetric functions would be too time consuming, so we performed in [1] some experiments by reducing the computation to the first k components, \(k\in \{5, 10, 20, 50\}\), a small number compared with the hundreds of cornerpoints commonly found in the persistence diagrams of the examined images. Classification and retrieval of dermatological images using such “shortened” vectors was quite satisfactory with a dramatic time reduction.

4 Modifying Distances

One of the major advantages of persistent homology is its modularity: By changing filtering function we change point of view on the shape of the objects under study and on the comparison criteria. Therefore the same data can be transformed into several pairs (X, f), and for each pair we obtain a distance reflecting the features of X captured by filtering function f. Both for classification and for retrieval, we need a single distance, so we have to blend the distances we have into one. There are two rather natural choices for that: either the maximum or the arithmetic average.

Maximum is the initial choice of [12]. An ongoing research, by some of the authors of the present paper, prefers the average instead [17]; this agrees with the idea of cooperation of the different filtering functions (like in [2, 7]), versus one of them prevailing. We make the “neutral” choice of equal weights in the starting average for initializing the subsequent optimization process. As hinted in the Introduction, the research is aimed at enhancing a device of acquisition and retrieval of dermatological images. The concept of “similarity” is (and has to remain!) highly subjective in the medical domain: We want to adapt the system to the physician, not the other way around. This can be done by modifying the weights of the different distances when building a single distance, to approximate the (pseudo)distance \(\delta \) representing the dissimilarity as perceived by the user.

Our setting is: We have a set \(X =\{x_1, \ldots , x_N\}\) of objects (in our case dermatological images) and J descriptors \(d^{(1)}, \ldots , d^{(J)}\) which give rise to an initial distance \(D^{IN}\) between the objects in X. In our study, \(D^{IN}\) is one of these two:

$$ D^{MAX} = \max \{d^{(1)},\ldots ,d^{(J)}\}, \ \ \ D^{AVG} = \frac{d^{(1)}+\cdots +d^{(J)}}{J} $$

Given a query q (i.e. an acquired image), the system retrieves the L objects closest to q with respect to \(D^{IN}\), i.e. an L-tuple \(X_q=(x_{i_1}, \ldots , x_{i_L})\) such that \(D^{IN}(q, x_{i_1}) \le \cdots \le D^{IN}(q, x_{i_L})\). The user is shown these objects and expresses his/her relevance feedback by assessing the perceived dissimilarities as numbers \(\delta (q, x_{i_1}), \ldots , \delta (q, x_{i_L})\).

While the Multilevel Relevance Feedback (MLRF) method proposed in [12] starts from \(D^{MAX}\), then rescales the distances \(d^{(i)}\) and takes the maximum, our Least Squares Relevance Feedback (LSRF) scheme start from \(D^{AVG}\) and computes a new distance \(D^{OUT}\) as

$$\begin{aligned} D^{OUT} = \sum _{j=1}^J \lambda _j d^{(j)}, \ \ \lambda _j\ge 0 \end{aligned}$$

by minimizing the objective function

$$\begin{aligned} g(\mathbf {\lambda }) = \Vert \mathbf {d\lambda } - \mathbf {\delta }\Vert ^2_2 \end{aligned}$$

i.e. by looking for \(\lambda =\) argmin\(\Vert \mathbf {d\lambda } - \mathbf {\delta }\Vert ^2_2\), where the t-th row of matrix \(\mathbf {d}\) is formed by the distances \(d^{(j)}(q, x_{i_t})\), \(\mathbf {\lambda }\) is the column matrix of the \(\lambda _j\) and \(\mathbf {\delta }\) is the column matrix formed by \(\delta (q, x_{i_t})\) for \(t= 1, \ldots , L\) and \(j=1, \ldots , J\).

Since this minimization problem might have multiple solutions, the vector of weights \(\lambda _j\) in \(D^{OUT}\) is obtained by iterating the Projected Gradient method. \(D^{OUT}\) is the best possible distance approximating the user’s similarity distance \(\delta \) from the given data in a least-square sense. More details on this procedure will be given in an article to come.

5 Experimental Results

As a preliminary study, we have tried to combine the modularity of persistent homology with the fast computation of the short vectors of symmetric functions of the transformed cornerpoints, with the adapting weights of relevance feedback.

We experimented with a small public database, \(PH^2\) [18], containing 8-bit RGB, \(768 \times 560\) pixels images of 80 common nevi, 80 atypical nevi, and 40 melanomas. We used 19 distances: 8 coming from simple morphological parameters, 11 coming from as many filtering functions; see Table 1 for a description of these features [1, 10]. It should be mentioned that the 11 distances coming from persistent homology already yield very good results, but the simple (and very fast computable) ones, obtained from morphological parameters, refine the general performance. For each image, we built the 11 persistence diagrams, performed one of the transformations T and R (see Sect. 3), and computed the 11 corresponding vectors, limited to length \(k=20\).

Table 1. Features.
Full size table

In normal operation, the user will give his/her feedback as follows. For \(j = 1, \ldots , L\), the user is asked to assign a similarity judgement (where 0 stands for “dissimilar” and 1 for “similar”) to the pair \((q, x_{i_j})\) with respect to three different aspects of the skin lesion (boundary/shape, colours, texture). This results in a similarity vote \(v_{i_j}\) in the range \(\{0, 1, 2, 3\}\) which is transformed into \(\delta (q, x_{i_j})\) by the following formula:

\(\delta (q, x_{i_j})= \max \Big \{ 0, \ \ D^{IN}(q, x_{i_1})+ \frac{4(3-v_{i_j})-1}{10}\big (D^{IN}(q, x_{i_1}) - D^{IN}(q, x_{i_L})\big ) \Big \}\)

The formula assigns the values of \(\delta \) in such a way that if the similarity vote \(v_{i_j}\) is maximal (3/3), then the corresponding \(\delta \) is lower than the lowest value of the distances of the database images from the query and, conversely, if \(v_{i_j}\) is minimal, then \(\delta \) is higher then the distance of the image which is farthest from it.

We finally retrieve again the L closest objects according to the modified distance (see Sect. 4).

Table 2. Sums of scores with the two considered methods of relevance feedback.
Full size table

In the present research \(L=10\) and the retrieval is performed by the “leave one out” scheme. Not having a real relevance feedback by a physician, we assign a retrieved image the maximal similarity vote \(v = 3\) if it shares the same histological diagnosis of the query, and the minimal similarity vote \(v = 0\) otherwise.

Assessment of the retrieval is performed by counting how many, of the retrieved lesions, have the same diagnosis of the query before and after the feedback. This is summarized in Table 2 by summing these scores for all images of the database as queries, starting from \(D^{MAX}\) and then applying the MLRF scheme, starting from \(D^{AVG}\) and applying our LSRF method.

As we can see, transformations R and T yield similar results. \(D^{AVG}\) performs better than \(D^{MAX}\) and LSRF produces a better improvement than MLRF.

6 Conclusions

We have compared—on a small public database of nevi and melanomas—two relevance feedback methods, conceived for a retrieval system based on persistent homology, combined with a computation reduction based on elementary symmetric functions of warped persistence diagrams. A weighted average of distances, with weights obtained by a standard optimization method, seems to perform better. The experiment will be extended to larger databases and with real feedback from expert dermatologists.