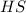Abstract
An algorithm for splitting permutation representations of a finite group over fields of characteristic zero into irreducible components is described. The algorithm is based on the fact that the components of the invariant inner product in invariant subspaces are operators of projection into these subspaces. An important part of the algorithm is the solution of systems of quadratic equations. A preliminary implementation of the algorithm splits representations up to dimensions of hundreds of thousands. Examples of computations are given in the appendix.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
A Las Vegas algorithm is a randomized algorithm, each iteration of which either produces the correct result, or reports a failure. An algorithm of this type always gives the correct answer, but the run time is indeterminate.
- 2.
The solution is always algorithmically realizable, since the problem involves only polynomial equations with abelian Galois groups.
- 3.
It is well known that any solution of the matrix equation
 can be represented as
can be represented as  where
where  is an arbitrary invertible
is an arbitrary invertible  .
.
References
Holt, D.F., Eick, B., O’Brien, E.A.: Handbook of Computational Group Theory. Chapman & Hall/CRC, Boca Raton (2005)
Parker, R.: The computer calculation of modular characters (the Meat-Axe). In: Atkinson, M.D. (ed.) Computational Group Theory, pp. 267–274. Academic Press, London (1984)
Kornyak, V.V.: Quantum models based on finite groups. J. Phys.: Conf. Ser. 965, 012023 (2018). http://stacks.iop.org/1742-6596/965/i=1/a=012023
Kornyak, V.V.: Modeling quantum behavior in the framework of permutation groups. EPJ Web Conf. 173, 01007 (2018). https://doi.org/10.1051/epjconf/201817301007
Cameron, P.J.: Permutation Groups. Cambridge University Press, Cambridge (1999)
Bosma, W., Cannon, J., Playoust, C., Steel, A.: Solving Problems with Magma. University of Sydney. http://magma.maths.usyd.edu.au/magma/pdf/examples.pdf
Wilson, R., et al.: Atlas of finite group representations. http://brauer.maths.qmul.ac.uk/Atlas/v3
Acknowledgments
I am grateful to Yu.A. Blinkov, V.P. Gerdt and R.A. Wilson for fruitful discussions and valuable advice.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Examples of Computations
A Examples of Computations
-
Generators of representations are taken from the section “Sporadic groups” of the Atlas [7].
-
For a group

-
 denotes the Schur multiplier, the
denotes the Schur multiplier, the  nd homology group
nd homology group  ,
, -
 denotes the outer automorphism group of
denotes the outer automorphism group of  ,
, -
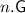 denotes a covering group of
denotes a covering group of  , a central extension of
, a central extension of  by
by 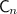 .
.
-
-
The results presented below assume the following ordering for the centralizer ring basis matrices

The matrices within the first sublist are ordered by the rule:
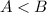 if
if 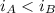 , where
, where  . The same rule is applied to the first elements of the pairs of asymmetric matrices.
. The same rule is applied to the first elements of the pairs of asymmetric matrices. -
Representations are denoted by their dimensions in bold (possibly with some signs added to distinguish different representations of the same dimension). Permutation representations are underlined. Multiple subrepresentations are underbraced in the decompositions.
-
We omit the irreducible projectors related to the trivial subrepresentation: these projectors have the standard form
 .
. -
All timing data refer to a PC with 3.30 GHz Intel Core i3 2120 CPU.
1.1 A.1 Higman–Sims Group 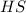
Main properties:



\(\varvec{11200}\)-dimensional Representation of \(\varvec{2.HS}\)
Rank:  . Suborbit lengths:
. Suborbit lengths: 



Time C:  s. Time Maple:
s. Time Maple:  h
h  min
min  s.
s.
1.2 A.2 Held Group 
Main properties:



\(\varvec{29155}\)-dimensional Representation of \({\varvec{He}}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.


Time C:  s. Time Maple:
s. Time Maple:  s.
s.
1.3 A.3 Suzuki Group 
Main properties:



\(\varvec{65520}\)-dimensional Representation of \(\varvec{2.Suz}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.
Time C:  min
min  s. Time Maple:
s. Time Maple:  s.
s.
\(\varvec{98280}\)-dimensional Representation of \(\varvec{3.Suz}\)
Rank:  . Suborbit lengths:
. Suborbit lengths:  .
.

 is the basic primitive
is the basic primitive  rd root of unity.
rd root of unity.
Time C:  min
min  s. Time Maple:
s. Time Maple:  min
min  s.
s.
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Kornyak, V.V. (2018). Splitting Permutation Representations of Finite Groups by Polynomial Algebra Methods. In: Gerdt, V., Koepf, W., Seiler, W., Vorozhtsov, E. (eds) Computer Algebra in Scientific Computing. CASC 2018. Lecture Notes in Computer Science(), vol 11077. Springer, Cham. https://doi.org/10.1007/978-3-319-99639-4_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-99639-4_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-99638-7
Online ISBN: 978-3-319-99639-4
eBook Packages: Computer ScienceComputer Science (R0)


 can be represented as
can be represented as  where
where  is an arbitrary invertible
is an arbitrary invertible  .
.
 denotes the Schur multiplier, the
denotes the Schur multiplier, the  nd homology group
nd homology group  ,
, denotes the outer automorphism group of
denotes the outer automorphism group of  ,
,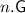 denotes a covering group of
denotes a covering group of  , a central extension of
, a central extension of  by
by 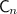 .
.
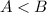 if
if 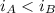 , where
, where  . The same rule is applied to the first elements of the pairs of asymmetric matrices.
. The same rule is applied to the first elements of the pairs of asymmetric matrices. .
.