Keywords

1 Introduction

The concept of function played a central role in Felix Klein’s vision of secondary school mathematics. His Elementary Mathematics from an Advanced Standpoint (1932) developed a concept of function that mathematized a sketched graph, “restructuring school in the direction of giving more emphasis to geometrical aspects of meaning (intuition, Anschauung)” (Biehler 2005, p. 63). Biehler also noted that Klein (1932) wrote his “Elementary Mathematics from an Advanced Standpoint” book with the understanding that teachers already had a firm knowledge of the secondary mathematics curriculum. Klein’s intention was to connect ideas in this curriculum to their brethren in higher mathematics. He pointed to a “double discontinuity” in the preparation of high school mathematics teachers: the discontinuity that high school students experience when they first meet higher mathematics in college, and then the discontinuity they experience when going from studying higher mathematics to teaching school mathematics (Buchholtz and Kaiser 2013; Kaiser et al. 2017; Kilpatrick 2008). We will return to the issue of double discontinuity in our concluding section.

2 A Focus on Meanings Instead of on Knowledge

We focus on teachers’ mathematical meanings for teaching for a number of reasons. First, the word “knowledge” in “teachers’ mathematical knowledge” is used largely as a primitive (undefined) term in researching teachers’ mathematical knowledge for teaching. Second, “knowledge” is used most commonly as justified true belief, with an emphasis on “true”. From this perspective, one cannot “know” something that is incorrect. We believe, as argued in Thompson (2013), that teachers operate mostly with ideas formulated for themselves in terms that could not be called true or justified from an expert perspective. We therefore cast aside concern with whether teachers “know” a concept and focus instead on meanings and ways of thinking teachers bring to mind in their moments of acting—interacting with students, planning instruction, or implementing their plan.

To this end, we designed an instrument called Mathematical Meanings for Teaching secondary mathematics (MMTsm; Thompson 2016). The MMTsm is a 46-item instrument containing items addressing teachers’ meanings for function (definition and properties, notation, and modelling), variation and covariation, proportionality, rate of change, frames of reference, and structure sense. In this paper, we focus on teachers’ meanings for functions.

3 Our Perspective on Productive Meanings for Function

We take it as axiomatic that students profit when their teachers hold rich, coherent meanings and ways of thinking regarding ideas they teach. Also, different types of coherence are more or less appropriate to help different levels of students in learning those ideas. Figure 4.1 illustrates two teachers’ images of function as mapping. Both images capture essential features of the common definition of function: every element of the domain is paired with a unique element of the range. The left image illustrates a teacher’s strong focus on the idea of function as mapping elements of the domain to unique elements of the range. It also expresses the teacher’s inattention to the nature of the domain and an inattention to how one might think about the independent variable’s values varying. The right image illustrates a teacher who aims for students to think that a function’s domain is a continuum of values. This teacher’s image entails the action of “moving through” the continuum, so that every value of the continuum is mapped to one and only one value in the range. (Unfortunately, a static diagram cannot capture the dynamism of the teacher’s image.) The left image could be productive for a teacher of higher-level mathematics, where domains can have arbitrary elements and structures. The right image could be productive for a high school teacher who hopes that students be able to envision functions as mapping continuous intervals to intervals.

Fig. 4.1
figure 1

Two images of functions as mappings—static (left) and dynamic (right)

Full size image

Any design of items that probe teachers’ meanings for a concept must be grounded in a scheme of meanings that the designers take as a target understanding of the concept. For our purposes, we emphasize two aspects: (1) That a function is a named relation between two sets of elements such that the relation constitutes a rule of association between them, and (2) that one understands all the features of the relation being packed into the notation f(u), so that “f(u)” means “The value in f’s range that is associated with the value u in f’s domain.” Figure 4.2 illustrates a common way that this way of understanding function is depicted in textbooks.

Fig. 4.2
figure 2

Image of a function as a relation between values of A and B according to a rule of association

Full size image

U.S. students commonly experience function notation with the attitude that “f(x)” is an unnecessarily complicated way to say “y”. This is understandable when we consider the density of meanings that are packed into function notation in relation to the concept of function. Figure 4.3 illustrates a coherent way in which one can understand a function f defined using function notation as denoting the same scheme of meanings as in Fig. 4.2.

Fig. 4.3
figure 3

Connections between function concept and components of function notation

Full size image

In the sequel, we discuss several items in the MMTsm, and results from 619 teachers from U.S. or South Korea, that probe ways they thought about function and function notation. We discuss this with the assumption that the meanings teachers have regarding functions and function notation influence the ways students understand these ideas.

4 Method

The study included 366 South Korean mathematics teachers (264 high school, 102 middle school) and 253 U.S. high school mathematics teachers. South Korean (SK) teachers constituted a geographic national sample; US teachers were from one state in the Southwest and one state from the Midwest. Teachers sat for the MMTsm in groups of varying size in summer 2013 and summer 2014. SK teachers taught a mean of 3.99 years (s.d. = 1.97); US teachers taught a mean of 4.35 years (s.d. = 4.22). SK teachers congregated for their required recertification examination; US teachers participated voluntarily in government-funded summer professional development programs. Teachers sat for the MMTsm in groups of sizes ranging from 40 to 150.

Items on the MMTsm were validated and refined over a three year period as described in Thompson (2016). Scoring rubrics assigned levels to teachers’ responses according to the criterion productivity of conveyed meaning for student learning. For example, we deemed a meaning for variable that might convey to students that a variable stands for one number at a time as less productive for students’ learning than a meaning that conveyed that a variable stands for the value of a quantity whose value varies.

5 Results

The MMTsm includes 18 items on functions (6 on definitions and properties, 8 on function notation, and 4 on functions as models). We present results from three items, one in each category, that exemplify the overall results. The items reported here were also reported in Musgrave and Thompson (2014) with data collected during item development.

Item 1: Function Notation

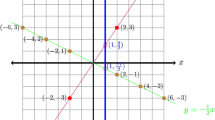
The function notation item display in Fig. 4.4 was designed to see the extent to which teachers thought of the left-hand side as a name for the rule on the right-hand side. A similar item, given prior to the MMTsm to calculus students, showed that many students thought that they should use the same letter as appeared in the original definition in any re-use of the function with function notation. They thought that the letter within parentheses was part of the function name.

Fig. 4.4
figure 4

MMTsm item addressing teachers’ meanings for function notation. © 2016 Arizona Board of Regents. Used with permission

Full size image

We considered teachers who placed t and s in the blanks as having thought of “w(t)” and “q(s)” as names and not in terms of a scheme of meanings as depicted in Fig. 4.3.

Results for this function notation item are given in Table 4.1.

Table 4.1 Results from function notation item. Cell entries are count (% of row total)
Full size table

Calculus is a standard part of the high school curriculum in South Korea but not in the United States. We therefore disaggregated US teachers into teachers who never taught calculus and teachers who taught calculus at least once.

In many respects, the entries in Table 4.1 speak for themselves. SK high school teachers were the most sensitive to the role that s and t played in the definitions of w and q (77%) and the least likely to think of s and t as part of a function name (5%). US high school teachers who never taught calculus were the least sensitive to the role of s and t (30%) and the most likely to think that s and t were part of a function name (41%). It struck us that South Korean middle school teachers were 50% more likely to understand the role of s and t in their respective function definitions than were US high school teachers who taught calculus as a subject at least once.

Item 2: Function Definition

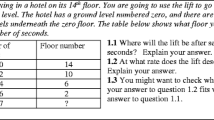
Part of a holistic meaning of function is that its definition is relative to a domain of values. The item in Fig. 4.5 was designed to address this issue.

Fig. 4.5
figure 5

MMTsm item addressing the extent to which teachers’ meanings for function definition entails attention to a domain of definition. © 2016 Arizona Board of Regents. Used with permission

Full size image

Highest level responses explained that w is defined only for input values greater than 0, and therefore the graph of y = w(x) + w(x − 10) + w(x − 20), x > 0, exists only for values of x greater than 20.

The first two columns of Table 4.2 contain valid answers. The distinction is that responses in the first column explained why y was undefined for values of x less than or equal to 20 whereas responses in the second column gave an example or were given without explanation. The third column contains two different types of responses. The first type (“time cannot be negative”) explained that the value of the input to w is time, and there is no such thing as negative time. The second type (“w(t) < 0”) explained that there actually is a graph, but it is below the horizontal axis, off the viewing pane shown on the page. The fourth column contains responses that explained the missing segments in Billy’s graph in terms of pumps’ behaviour, such as they malfunctioned and did not start until 20 min had elapsed (Fig. 4.6).

Table 4.2 Results from MMTsm item on function domain as part of function definition
Full size table
Fig. 4.6
figure 6

MMTsm item for function as model (using function notation representationally)

Full size image

Sixty-three percent (63%) of SK high school teachers related the function definition to the domain of w by noting that the value of x in y = w(x) + w(x − 10) + w(x − 20) had to be greater than 20 for y to be defined, whereas 44% of SK middle school teachers, 11% of US precalculus teachers, and 12% of US calculus teachers said this. While we were not surprised by US precalculus teachers’ non-normative responses, we were quite surprised that US calculus teachers responded at essentially the same levels as precalculus teachers.

One might think that Item 2 is heavily reliant on teachers’ meanings for function notation since it involves function notation in the definition of w and its use in defining y. However, the Kendall’s tau statistic for these items is 0.07, so performance on the two seems unrelated.

Item 3: Function as Model (Using Function Notation Representationally)

An important aspect of using functions to model situations is to use function notation representationally. For example, one could define the function d as the distance from Earth to Mars at each number of years since 00 CE. Then d(1999.7) − d(1998.2) would represent the net change in distance from Earth to Mars from 1998.2 years CE to 1999.7 years CE. We can do this meaningfully even without a rule of association for d that would allow us to compute these distances.

We anticipated that many teachers would use function notation on the left side of a function definition because this is customary when defining a function using function notation. We judged teachers to use function notation representationally when they used function notation on the right side of the function definition, defining the circle’s radius as a function of time within the formula for area of a circle. A response using function notation on both sides of the function definition was scored at the highest level.

We scored responses according to whether they used function notation on both sides, right side only, or left side only. We were forced to include two additional categories of responses: Level 0 (could not interpret) and inconsistent use of variables (using different letters on either side of the definition).

Table 4.3 gives examples of responses in four categories. The first “both sides” example is quite impressive. This teacher used the Fundamental Theorem of Calculus to define the length of the radius as an integral of its velocity. The second example was the most common for “both sides” responses. The “right side only” example is straightforward. As we explained, we judged teachers to use function notation representationally when they used it on the right side, to represent the circle’s radius as a function of time.

Table 4.3 Examples of responses to Item 3 in selected categories
Full size table

The example for “left side only” typifies responses in this category. Teachers responding with function notation on left side only wrote a formula on the right side. The example of “inconsistent variables” has a large intersection with “left side only” responses in that they used function notation only on the left side, but used different letters in the function’s argument and in the defining formula.

Table 4.4 presents results for Item 3. We categorized teachers’ responses according to the scheme presented in Table 4.3.

Table 4.4 Results for MMTsm item on function as model (using function notation representationally)
Full size table

The first two columns in Table 4.4 represent teachers who have richer and more accurate meanings for function notation and the use of functions as models than teachers included in the other columns. As in the previous examples, teachers from SK’s high schools are 83% more likely than their U.S. counterparts (understood as those who taught calculus at least once) to have answered with function notation on the right-hand side or both sides (61.8% compared with 33.8%), the latter being more comparable to SK’s middle school teachers.

The disparity becomes much larger when comparing SK’s middle school teachers with those from U.S. high schools who had not taught calculus. SK’s teachers’ likelihood of having answered with function notation on the right-hand side or both sides is essentially double that of U.S. teachers in the comparison group. On the positive side for U.S. teachers who had taught calculus, when looking at the first column of Table 4.4, we see that they are only 21.1% less likely than SK’s high school teachers to give such answers. This may be partly a consequence of the fact that high school calculus classes (just like those in college) include a fairly large number of modelling problems.

However, the larger disparity in response rates with function notation on the left-hand side only (34.7% for US teachers with calculus compared with 7.6% for SK’s high school teachers) possibly reflects a rather weak meaning of function notation in the case of US teachers. The majority of teachers and calculus students interviewed prior to item development had the schema shown in line three of Table 4.3. “Using function notation”, to them, meant writing “f(x)” instead of y. They also felt that function notation by itself was meaningless, that a statement with function notation required an explicit rule of association on the definition’s right side. Such an explicit representation is impossible in Item 3 because we only know that the rate of change of the radius of the circular ripples with respect to time is not constant—that the radius is not a linear function of time. But we do not know what function it is.

Also, when we compare all teachers from SK who participated in the study with all those from the U.S., we see the percentage in the first column (FN on both sides) being almost twice for SK (30.0%) compared with the US (16.2%). Even more extreme is the comparison for column three (FN left side only), where the percentage for the US (35.3%) is 3.6 times as large as for the SK teachers collectively (9.8%).

The statistics for these three sample items, because they are representative of the 18 items in the MMTsm on functions, indicate unequivocally that high school teachers in SK have more productive meanings for function definitions and properties, function notation, and for functions as models than their US counterparts. Future research will be required to investigate ways that these differences play out in teachers’ instruction and students’ learning.

6 Discussion

Results from TIMSS and other studies (Judson and Nishimori 2005; Tarr et al. 2000) indicate that U.S. students use calculators more frequently than their foreign counterparts. Possibly, by analogy, U.S. teachers may rely more on calculator use than their counterparts in South Korea and thus become more focused on how to input data on the calculator than on the correct notation to write intended formulas on paper. Also, given the gender bias in TIMSS Advanced (end of high school) in favour of boys, we should check for gender differences in the MMTsm study.

We suspect, however, that deeper, cultural differences might be at play. Our experience is that the meanings and ways of thinking exhibited by a preponderance of US teachers are common among US school students, too. If teachers’ meanings shape students’ meanings by way of intersubjective operations of negotiation of meaning, then many of these teachers’ students will pass through university with those meanings largely untouched only to become future high school mathematics teachers. This is the process Lortie (1975) described as a way that schools regenerate themselves. The evidence for the “Lortie hypothesis” is that US teachers we tested were school students before they were teachers, and their study of university mathematics evidently left the meanings they developed as school students (as shaped by their teachers) largely untouched. To study this hypothesis requires evolutionary and sociological research methods that, at this moment, do not exist in mathematics education.

We hasten to note that what we described above is not Klein’s double discontinuity. Rather, for a majority of US teachers in our sample, it seems there was a continuity of mathematical meanings that teachers carried from school to university and back to school. They seem to have maintained these meanings despite their experiences in higher mathematics courses.

The problem we face in the US is to enrich future teachers’ school mathematical meanings so that they are truly foundational, instead of irrelevant, for higher mathematics. Thompson (2013) outlines a number of long-term strategies that address this problem. One effort that is central to all of them is that university mathematics programs must take into account the mathematical meanings that students (not just future teachers) bring to their university studies. Again, this will require a long-term effort. Culturally embedded meanings and ways of thinking are difficult to dislodge among university instructors as well as high school instructors.