Fully Online Matching with Advice on General Bipartite Graphs and Paths

Abstract

We consider the problem of finding a maximum-size matching in a fully online setting, where the vertices of a bipartite graph are given one after the other in discrete time steps, together with all edges to previously revealed vertices. In each time step, an online algorithm has to irrevocably decide which of the newly presented edges is going to be part of the matching.

It is known that this problem admits a 2-competitive online algorithm in the case of general graphs. We prove a tight lower bound that even holds for bipartite graphs, and tight bounds of $\frac{3}{2}$ for paths.

In the main part of the paper, we consider the model of advice complexity which contributes to a more fine-grained complexity analysis. Within this model, one asks how much information about the yet missing parts of the input is needed to compute an optimal or near-optimal solution. We prove almost tight linear upper and lower bounds on the amount of advice that is necessary for computing an optimal solution for paths. We complement these results by bounding the sufficient amount of advice for computing sub-optimal matchings. We furthermore prove that a single bit of advice does not help to improve over deterministic algorithms.

1 Introduction

Finding a maximum-size matching in a graph is one of the fundamental algorithmic tasks in graph theory with numerous practical applications. The classical offline version of the problem, where the whole graph is known in advance, can be solved in polynomial time (see, e.g., [19, 29, 30]). This problem has been widely investigated, an overview of matching theory can be found in [31].

In contrast to this, the online version of the problem is hard even for bipartite graphs. Most attention has been paid to the so-called one-sided matching in bipartite graphs, where the vertices from one shore of the bipartite graph are given beforehand, and the vertices from the other shore appear one after the other in an online fashion [26]. An online algorithm then has to irrevocably decide which of the edges incident to the newly presented vertex, if any, will be included in the matching. The performance of an online algorithm is classically analyzed using the competitive ratio, i.e., by comparing the cost of the computed solution to the optimal cost of a solution computed by an exact offline algorithm knowing the complete instance beforehand. This competitive analysis was introduced by Sleator and Tarjan [33], for an introduction, see the textbooks by Komm [27] or Borodin and El-Yaniv [12]. For the one-sided matching problem, Karp et al. [26] have shown that a simple greedy strategy reaches a competitive ratio of 2, i.e., that this strategy computes a matching of at least half the size of a maximum matching, and they have further proven that this is the best possible for any deterministic online algorithm.

In this paper, we consider the fully online version of the matching problem, where all vertices appear online. More precisely, in each time step, one vertex of the graph appears, together with all edges incident to already presented vertices. Thus, the problem is not limited to bipartite graphs. This version of the problem is less studied, but also very well motivated. Consider, for example, the work of a job center that receives job offers daily from companies and, independent from these offers, job applications of candidates with a certain profile. Clearly, the job center cannot wait infinitely long to find the best candidate for an open position.

Not much is known about the fully online matching problem besides a greedy algorithm by Favrholdt and Vatshelle [21] achieving a competitive ratio of 2 on general graphs and of 3/2 on paths. We show in this paper that this is the best possible ratio, even if we restrict the set of inputs to bipartite graphs. This result points to how coarse-grained classical competitive analysis can be. In terms of competitive ratio, the fully online matching problem is as hard on bipartite graphs as it is on general graphs.

As a means for a more fine-grained analysis of online algorithms, we use the concept of advice complexity of online problems. The idea behind this approach is to measure the information content of an online problem, i.e., the amount of information about the yet unknown parts of the input that is needed to compute an optimal solution or a solution with a certain competitive ratio. The advice complexity was introduced by Dobrev et al. [17] and refined by Emek et al. [20] and by Böckenhauer et al. [10, 11]; see also Hromkovič et al. [25]. It has been successfully used for many online problems since then, including the k-server problem [8, 9, 16, 20, 24], the knapsack problem [6, 7], bin packing [14], disjoint path allocation [1, 10, 11, 23], set cover [18, 28], coloring problems [2, 3, 15, 22, 32], and many others. For a comprehensive overview, see the textbook by Komm [27] and a recent survey by Boyar et al. [13].

The paper is organized as follows. In Sect. 2, we fix our notation and give a formal definition of online algorithms with advice and the fully online bipartite matching problem. We further review the known results on online computation without advice. In Sect. 3, we consider lower and upper bounds on the advice complexity for computing optimal solutions in general and bipartite graphs. In Sects. 4 and 5, we deal with restricting the problem to online paths. We consider online algorithms with advice computing optimal solutions in Sect. 4 and approximate solutions in Sect. 5, where we in particular prove the same lower bound for algorithms using a single advice bit as for those working without advice. In Sect. 6, we conclude the paper.

2 Preliminaries and Algorithms Without Advice

In this section, we formally define the notions used in the following. All logarithms in this paper are taken to be binary, unless stated otherwise.

Definition 1

(Online Maximization Problem). An online maximization problem consists of a set $\mathcal {I}$ of inputs and a gain function. Every input $I\in \mathcal {I}$ is a sequence of requests $I=(x_1,\dots ,x_n)$. Furthermore, a set of feasible outputs (or solutions) is associated with every I; every output is a sequence of answers $O=(y_1,\dots ,y_n)$. The gain function assigns a positive real value $\mathrm {gain}(I,O)$ to every input I and any feasible output O. If the input is clear from the context, we omit I and denote the gain of O as $\mathrm {gain}(O)$. For every input I, we call any output O that is feasible for I and has largest possible gain an optimal solution of I, denoted by $\text {Opt} (I)$.

We now formally define online algorithms with advice for online maximization problems, and their competitive ratios.

Definition 2

(Online Algorithm with Advice). Consider an input I of an online maximization problem. An online algorithm A with advice computes the output sequence $A^{\phi }(I)=(y_1,\ldots ,y_n)$ such that $y_i$ is computed from $\phi ,x_1,\ldots ,x_i$, where $\phi$ is the content of the advice tape, i.e., an infinite binary sequence. We denote the gains of the computed output by $\mathrm {gain}(A^{\phi }(I))$. The algorithm A is c-competitive with advice complexity b(n) if there exists a constant $\alpha$ such that, for every n and for each I of length at most n, there exists some $\phi$ such that $\mathrm {gain}(A^{\phi }(I))\ge \frac{1}{c}\cdot \mathrm {gain}(\mathrm {Opt}(I))-\alpha$ and at most the first b(n) bits of $\phi$ have been accessed during the computation of $A^{\phi }(I)$. If A is c-competitive for $\alpha =0$, we call it strictly c-competitive.

Definition 2 follows the advice complexity model from Böckenhauer et al. [10, 11]. A motivation and discussion of this model is found in [25].

We use the standard notions for dealing with graphs in this paper; an introduction to graph theory can, e.g., be found in [34]. Let $G=(V,E)$ be a graph. A subset $M\subseteq E$ is called a matching if the edges in M are pairwise not adjacent, i.e., if no two edges have a common end vertex. The size of a matching is measured by the number of edges in the matching. We call a vertex v matched in a matching M if there is an edge $e\in M$ such that v is incident to e. A maximum matching is a matching of maximum cardinality.

An online graph instance $G^\prec =(G,\prec )$ consists of a graph $G=(V,E)$ and a linear ordering $\prec$ on the vertex set $V=\{v_1,v_2,\dots ,v_n\}$ with $v_i\prec v_j$ for $i<j$. In the online presentation $G^\prec$ of the graph G, the vertices of V appear in the order determined by $\prec$, together with the edges adjacent to already present vertices. Let $V_i=\{v_1,\ldots ,v_i\}$. Then we denote by $G^\prec [V_i]$ the online subgraph of $G^\prec$ induced by $V_i$.

Definition 3

(Fully Online Matching Problem). The fully online matching problem is the following online maximization problem: Given an online graph $G^\prec = (G,\prec )$ with $G=(V,E)$ and $V=\{v_1,v_2,\dots ,v_n\}$, the goal is to compute a sequence $(M_1,M_2,\dots ,M_n)$ such that $M_i\subseteq E$ is a matching on $G^\prec [V_i]$ and $M_i\subseteq M_j$ for all $i<j$ with $i\in \{1,2,\dots ,n-1\}$ and $j\in \{2,3,\dots ,n\}$ such as to maximize the size $\vert M_n\vert$ of the computed matching for $G^\prec$.

We will use the following notation in the figures throughout this paper: a matching edge will be drawn as a wavy line, whereas all other edges are drawn as straight lines.

The following results are known for the classical online setting without advice. The lower bound of 2 on the competitive ratio for the one-sided online matching problem in general graphs from Karp et al. [26] carries over to the fully online matching problem. In [21], Favrholdt and Vatshelle complemented this result with a tight upper bound for the fully online matching problem on general graphs.

In [21], the authors moreover showed a matching lower and upper bound of $\frac{3}{2}$ on the competitive ratio of the fully online matching problem on paths. The upper bound can be achieved by a simple greedy strategy that takes every presented edge into the matching as long as both endpoints are not yet matched.

3 Optimality on General and Bipartite Graphs

In this section, we investigate how much advice is necessary and sufficient to compute an optimal matching in a general or bipartite graph. An upper bound for general graphs is easy to see: A vertex in a general online graph on n vertices has at most $n-1$ neighbors, i.e., it has a vertex degree of at most $n-1$. For every vertex, at most one incident edge can be a matching edge. Therefore, if an algorithm asks, for every of the n vertices, which of the neighboring edges should be a matching edge, it finds a maximum matching.

Theorem 1

There exists an online algorithm with advice that reads at most $n\cdot (\log (n)-\log (\mathrm {e})+1)$ advice bits in order to find a maximum matching in a general online graph $G^\prec _n$ on n vertices.

Proof

For each presented vertex $v_k$, except for the first one, the algorithm reads advice telling it which of the edges to the already presented vertices $v_1,\ldots ,v_{k-1}$ should be included in the matching, if any. This advice can be encoded by some number from $\{0,\ldots ,k-1\}$, where 0 stands for not choosing any edge in this time step. No self-delimiting is needed for encoding these numbers in binary since the algorithm knows the number of the current time step. Thus, the number of advice bits can be bounded by

Although this algorithm is very simple, we will see in the following that no essentially better online algorithm with advice is possible, not even for bipartite graphs. The following lower bound is of the same order of magnitude $\varTheta (n\log (n))$ as the upper bound from Theorem 1.

Theorem 2

Any deterministic online algorithm for the problem of finding a maximum matching in an online bipartite graph instance with n vertices needs to read at least $\log \left( \left( \frac{n}{2}\right) !\right) \in \varTheta (n\log (n))$ advice bits in order to find a maximum matching.

Proof

In order to prove the claim, we describe a class of (n/2)! online instances in which each two of the instances need a different advice string.

Let $n=2k$ with be the number of vertices in the instances from this class, containing two shores of size k, $S_1=\{w_1, w_2, \dots , w_k\}$ and $S_2=\{w_{k}, w_{k+1}, \dots , w_{2k}\}$; see Fig. 1 for an example.

Fig. 1.

Pattern of the online bipartite graphs used in the proof of Theorem 2. Here, we have $n=12$. The adversary shows first a permutation of the vertices $w_1, w_2, \dots , w_6$. Then, the vertices $w_7, w_8, \dots , w_{12}$ are given in this order.

The edge set E is defined as

$$\begin{aligned} E = \left\{ \{w_i,w_j\} \mid 1\le i\le k\text { and } k+1\le j \le k+i \right\} , \end{aligned}$$

leading to a unique perfect matching in these types of bipartite graphs since the only possibility for all vertices $w_{2i}$ being matched is that they are matched by the edges $\{w_{i},w_{2i}\}$, for $1\le i\le k$.

The online presentation of one of these bipartite graphs starts with any permutation of isolated vertices $w_1, w_2, \dots , w_k$. Then, the adversary presents the vertices $w_{k+1}, w_{k+2}, \dots , w_{2k}$ in this order. In every time step i, for any $k+1\le i \le 2k$, the algorithm encounters the same prefix but it has to choose one of the $2k-i+1$ edges incident to $w_i$ to be a matching edge, and only one of these possibilities is correct. Therefore, the algorithm has to distinguish

$$\begin{aligned} \prod _{i=k+1}^{2k} \left( 2k-i+1\right) = \prod _{i=1}^{k} i =k!= \left( \frac{n}{2}\right) ! \end{aligned}$$

different possible online representations of this bipartite graph, leading to

$$\begin{aligned} \log \left( \left( \frac{n}{2}\right) !\right) \in \varTheta (n\log (n)) \end{aligned}$$

advice bits that every online algorithm with advice needs to read at least in order to be optimal.    $\square$

We see that the class of hard instances as used in the proof of Theorem 2 has some nice additional properties. For example, none of these graphs contains an induced path on 5 vertices. Thus, the proof of Theorem 2 also shows that at least $\varOmega (n\log (n))$ advice bits are necessary to compute an optimal matching in online $P_5$-free graphs. Moreover, the graphs from this instance class have a diameter of 3. Thus the same lower bound also holds for online graphs with a diameter bounded by 3.

Although the problem thus appears to be quite hard on very restricted classes of graphs, we will analyze a graph class in the subsequent sections, where less advice is sufficient, namely paths.

4 Optimality on Paths

In this section, we will show how much advice is necessary and sufficient in order to solve the online matching problem on paths optimally. For this, we will mostly focus on matchings which match all inner vertices.

In the online setting of a path $P_n$, the isolated edges play a special role. Since, at a certain time step i, they are not appended to any other subpath, the algorithm does not get any information from the neighborhood about whether they are matching or non-matching edges. Therefore, intuitively, an online algorithm for solving the online matching problem on a path should get some advice on these edges in order to be optimal. We show that there cannot appear too many isolated edges in an online path instance. By $\mathcal {P}_n$ we denote the set of all online paths on n vertices.

Theorem 3

There exists an online algorithm with advice for finding a maximum matching in a path $P^\prec \in \mathcal {P}_n$ on n vertices which uses at most $\lceil \frac{n}{3} \rceil$ advice bits.

Proof

If n is even, the maximum matching is unique and matches all inner vertices. If n is odd, there also exists a matching that matches all inner vertices. Algorithm 1 always constructs such a matching. The idea behind this algorithm is as follows. It asks advice for every new vertex if necessary and applies the answer of this bit to the adjacent edges. The intuition is that the algorithm has no information from the neighborhood for isolated edges or for an isolated path of length 2 that arises in time step i by connecting two isolated vertices by a new vertex $v_i$. Therefore, the advice bits can also be directly associated with the edges. In all other cases, the algorithm uses a greedy strategy.

For the correctness of Algorithm 1, note that, due to the greedy strategy and since the advice is given in such a way as to force the algorithm to choose a matching that does not leave any inner vertex unmatched, a vertex $v_i$ cannot be connected to two non-isolated unmatched vertices $v_{j_1}$ and $v_{j_2}$. In this case, one of the two inner vertices $v_{j_1}$ and $v_{j_2}$ would remain unmatched. Moreover, $v_i$ also cannot be connected to two matched non-isolated vertices, since it would remain unmatched in this case.

The number of advice bits used by the algorithm depends on the number of isolated edges or isolated subpaths of length 2. These isolated subpaths need to be separated by at least one vertex in order to ensure that the algorithm has to ask for an advice bit for each of these subpaths. In the worst case, the online path $P^\prec$ consists of subpaths of length 1, i.e., isolated edges, and each two consecutive subpaths will be separated by a single vertex. Such a presentation of the online path on n vertices contains $\lceil \frac{n}{3} \rceil$ isolated edges. Thus, $\lceil \frac{n}{3} \rceil$ advice bits suffice for any online path of length n.    $\square$

In the following, we prove asymptotically matching lower bounds for the online matching problem on paths.

Theorem 4

Any deterministic online algorithm for the problem of finding a maximum matching in an online path instance $P^\prec \in \mathcal {P}_n$ needs to read at least

$$ \left\lfloor \frac{1}{3}n - \frac{1}{2}\log (n)+\log \left( \sqrt{\frac{3}{2\pi }}\right) \right\rfloor $$

advice bits in order to be optimal.

Proof

We give a proof by contradiction, based on the following idea. We assume that there exists an algorithm $A_<$ that uses less than

$$b(n)=\frac{1}{3}n - \frac{1}{2}\log (n) + \log \left( \sqrt{\frac{3}{2\pi }}\right) $$

advice bits to find a maximum matching in any online path instance with n vertices. Then, we describe a special set of pairwise different instances with pairwise different optimal solutions. The number of these instances will be at least $2^{b(n)}$. Therefore, by the pigeonhole principle, there exists a pair of instances such that $A_<$ has to use the same advice string to solve them both optimally. The set of instances will be constructed in such a way that they all have a long common prefix and so any online algorithm can perform differently on this long prefix if and only if the advice is different. Moreover, any optimal algorithm is forced to behave differently already in a time step when it cannot distinguish between them, because they have the same prefix. Therefore, the algorithm cannot use the same advice string to solve them both optimally.

For the proof, we will assume that $n=6k$ is an even number such that all the instances contain exactly one maximum matching. The special instances all start with a common prefix, namely with $\frac{n}{3}=2k$ isolated edges

$$ \left\{ \{w_{3i+1},w_{3i+2}\} \mid i\in \{0,1,2,\dots ,2k-1\}\right\} $$

given in all possible orders. Note that each online algorithm has to decide immediately which of these edges are part of the matching and which are not. In the second step, each two of those edges are connected by one of the vertices in $\left\{ w_{3i} \mid i\in \{1,2,\dots ,2k\}\right\}$ in order to get a path (see Fig. 2).

Fig. 2.

Structure of the online instances for the lower bound on the advice bits used for solving the online matching problem on an online path. In this example, we have $n=12$ and therefore $k=2$.

The described instances only differ in the presentation order of the edge set $\{\{w_{3i+1},w_{3i+2}\} \mid i\in \{0,1,2,\dots ,2k-1\}\}$ containing 2k vertices. Thereby, it does not matter whether the vertex $w_{3i+1}$ or the vertex $w_{3i+2}$ appears first.

Note that the k edges $\{w_1,w_2\},\dots ,\{w_{6k-5},w_{6k-4}\}$ have to be matching edges and the remaining k edges $\{w_4,w_5\},\dots ,\{w_{6k-2},w_{6k-1}\}$ are non-matching edges. The solution only depends on the order in which the matching and the non-matching edges appear. This divides the set of all instances that can be reached with the described construction in equivalence classes, and for each of these classes, there is exactly one unique optimal solution. The unique solution is determined by a string $x_1x_2x_3\dots x_{2k}$ with $x_i\in \{0,1\}$ for all $i\in \{1,2,\dots ,2k\}$ with

$$\begin{aligned} x_i = {\left\{ \begin{array}{ll} 1 &{} \text {if the } i\text {th isolated edge is a matching edge},\\ 0 &{} \text {else}. \end{array}\right. } \end{aligned}$$

These strings contain exactly k zeros and k ones. This leads to $\left( {\begin{array}{c}2k\\ k\end{array}}\right)$ equivalence classes. Using a well-known bound on the central binomial coefficient, we get

$$\begin{aligned} \left( {\begin{array}{c}2k\\ k\end{array}}\right)&> \frac{1}{2}\cdot \frac{4^k}{\sqrt{\pi k}} = \frac{1}{2}\cdot \frac{4^{\frac{n}{6}}}{\sqrt{\pi \cdot \frac{n}{6}}} = \frac{1}{2}\cdot \frac{2^{\frac{n}{3}}}{\sqrt{\frac{\pi }{6}}\cdot \sqrt{n}}\\&=\sqrt{\frac{3}{2\pi }}\cdot \frac{2^\frac{n}{3}}{\sqrt{n}}, \end{aligned}$$

for any $k=\frac{n}{6}$. We claimed that $A_<$ uses less than

$$\begin{aligned} \log \left( \sqrt{\frac{3}{2\pi }}\cdot \frac{2^\frac{n}{3}}{\sqrt{n}}\right) = \frac{1}{3}n - \frac{1}{2}\log (n)+\log \left( \sqrt{\frac{3}{2\pi }}\right) < \log \left( {\begin{array}{c}2k\\ k\end{array}}\right) \end{aligned}$$

advice bits. Therefore, there are two equivalence classes which get the same advice string. This means that the algorithm makes the same decisions on the first $\frac{n}{3}$ isolated edges on both instance classes. But since these equivalence classes are different, there is a first isolated edge e such that, w.l.o.g., e is a matching edge in the first instance but a non-matching edge in the second instance. Thus, the matching chosen by $A_<$ will not be optimal for one of these instances, which is a contradiction to the assumption.    $\square$

5 Tradeoffs on Paths

Until now, we have seen bounds on how much advice is needed to be optimal on general graphs or paths. In this section, we want to analyze what happens in the case when the algorithm has less advice bits at disposal.

We want to discuss some tradeoffs between the available amount of advice bits and the achievable competitive ratio. We know from Theorems 3 and 4 that approximately n/3 advice bits are necessary and sufficient for computing a maximal matching. On the other hand, as proven in [21], without advice, no competitive ratio better than $\frac{3}{2}-\varepsilon$ can be reached, for any $\varepsilon >0$.

First, we want to show that, for one bit of advice, we can prove the same lower bound as for deterministic algorithms without advice on paths.

Theorem 5

No online algorithm using one bit of advice for finding a maximum matching in a path on n vertices with $n\ge \frac{3(\alpha +1)}{\varepsilon } -2$ can be better than $\left( \frac{3}{2}-\varepsilon \right)$-competitive (with additive constant $\alpha$), for arbitrary non-negative constants $\alpha$ and $\varepsilon$.

Fig. 3.

The four possibilities how a pair of algorithms $A_1$ and $A_2$ can decide about an isolated edge.

Proof

One bit of advice can be used to decide which of two given deterministic algorithms should be used in order to find a maximum matching in paths on n vertices. This makes the work of the adversary more involved since he has to provide a class of lower-bound instances for all pairs of algorithms. To cover all these pairs, we distinguish the algorithms with respect to the behavior on the isolated edges for a given online path instance $P^\prec \in \mathcal {P}_n$. Let $A_1$ and $A_2$ be two arbitrary online algorithms. There are four possibilities how these two algorithms can treat an isolated edge e (see Fig. 3):

• Group 1: Both $A_1$ and $A_2$ assign e to the matching.

• Group 2: Only $A_1$ takes e into the matching.

• Group 3: Only $A_2$ takes e into the matching.

• Group 4: Neither $A_1$ nor $A_2$ allocates e to the matching.

This gives us a classification of the isolated edges. Note that the adversary fights against two arbitrary deterministic algorithms. Therefore, some of these groups of edges can be empty. The algorithm with advice has to handle all subsets of these four groups.

It is easy to see that a matching with k unmatched vertices has $\left\lfloor \frac{k}{2}\right\rfloor$ less matching-edges than a maximum matching on this instance. Therefore, it suffices if we count the minimum number of unmatched vertices on the instances of this special instance class in order to calculate a lower bound on the competitive ratio for algorithms reading one bit of advice.

The construction is done as follows. Let $n=6k+4$ be the number of vertices in the online path $P^\prec$ for a . The adversary starts with $\frac{n-1}{3}$ isolated edges which belong to one of the above-described edge groups. In order to reach a high number of unmatched vertices, the adversary arranges the isolated edges group by group to build four subpaths, connecting the isolated edges inside a group by single vertices. Note that, in each group, the neighboring isolated edges are either both matching or both non-matching edges. Therefore, if the algorithms act best possible, any of the four subpaths built by any of the two algorithms is of one of the two forms as shown in Fig. 4.

Fig. 4.

The algorithm chooses, inside each group, one of the two patterns if it acts best possible connecting the isolated edges to a path. The marked vertices are the unmatched vertices within each group (ignoring the end vertices for type 2 subpaths). Note that we can assume w.l.o.g. that the algorithm always assigns the right edge to the matching when connecting the isolated edges in a subpath of type 2.

In both types of subpaths containing i isolated edges, the adversary forces the algorithms to leave at least $i-1$ vertices unmatched. Therefore, we can guarantee $i-1$ unmatched vertices in each group. In type-2 subpaths, we have possibly further unmatched vertices at the left and the right end. But we will count these possibly unmatched vertices in a second step, when the adversary connects the subpaths such that the two algorithms are forced to leave many vertices unmatched in between the at most four groups. Note that connecting two edges that are both matching or both non-matching forces the algorithms to leave one vertex unmatched. On the other hand, connecting two different edges enables the algorithms to construct at least locally a good matching (see Fig. 5).

Fig. 5.

Connecting two isolated edges. The adversary can only force the algorithms to leave a vertex unmatched when connecting two edges of the same type.

The end edges of possibly four subpaths are depicted in Fig. 3. Therefore, these pairs of edges will symbolize the whole subpaths in the following figures. We will make a case distinction with respect to the subset of the groups that arise in the solution of a given pair of algorithms:

• Groups 1, 2, 3, 4. If all the edge groups are present in a solution, we arrange the subpaths in the order 2, 1, 3, 4, as shown in Fig. 6.

  Both algorithms, $A_1$ and $A_2$, have to leave 3 vertices unmatched. Since in a subpath on i vertices, both algorithms leave at least $i-1$ vertices unmatched, we have $\frac{n-1}{3}-4$ unmatched vertices within the four subpaths. Therefore, overall, the adversary can force both algorithms to leave at least

  $$\begin{aligned} \frac{n-1}{3}-4+3 =\frac{n-1}{3}-1 = 2k \end{aligned}$$

  vertices unmatched, leading to a loss of k matching edges.

Fig. 6.

All of the edge groups are present in the solution.

Fig. 7.

The edge groups 1, 2 and 3 are present in the solution.

If we can show the same for all other subgroups, we are done, since in this case we get the same lower bound as in the deterministic case.

• Groups 1, 2, 3. If no edges from group 4 appear in the solution, the adversary arranges the remaining groups as shown in Fig. 7.

  Within the three subpaths, there are at least $\frac{n-1}{3}-3$ unmatched vertices and together with the two additional unmatched vertices between the paths, we have again $\frac{n-1}{3}-1$ unmatched vertices.

• Groups 2, 3, 4. In this case, the adversary provides the order of Fig. 8, leading to at least $\frac{n-1}{3}-1$ unmatched vertices.

• Groups 1, 2, 4 or groups 1, 3, 4. In these two equivalent cases, the order of Fig. 9 leads to $\frac{n-1}{3}-1$ unmatched vertices.

• Groups 1, 4 or groups 2, 4 or groups 3, 4. If only two edge groups appear in the solution, there are $\frac{n-1}{3}-2$ unmatched vertices within the two subpaths. Therefore, one unmatched vertex between the two subpaths or at one end would be enough to reach the bound of $\frac{n-1}{3}-1$ unmatched vertices in total. We see in Fig. 10 that this is given for all pairs of groups containing group 4, since the adversary can force the algorithms to leave at least the right end vertex unmatched.

• Groups 1, 2 or groups 1, 3. Also in these two cases, the adversary can force the algorithms to leave $\frac{n-1}{3}-1$ vertices unmatched (see Fig. 11).

• Groups 2, 3. Also in this case, one of the end vertices will stay unmatched (see Fig. 11) and therefore the adversary can guarantee $\frac{n-1}{3}$ unmatched vertices.

• Group 1 or 2 or 3 or 4. If only one group of edges is present in the solution, any algorithm leaves at least $\frac{n-1}{3}$ vertices unmatched within the path.

Fig. 8.

The edge groups 2, 3 and 4 are present in the solution.

Fig. 9.

The edge groups 1 and 4 and either group 2 or group 3 are present in the solution.

Summarizing, in all possible subsets of isolated edges, the solution has to contain at least $\frac{n-1}{3}$ unmatched vertices. A simple calculation shows that this leads to a competitive ratio of $\frac{3}{2}-\varepsilon$ on paths on n vertices with $n\ge \frac{3(\alpha +1)}{\varepsilon } -2$, for arbitrary non-negative constants $\alpha$ and $\varepsilon$.    $\square$

We already mentioned above that, given the decision on the isolated edges whether to take them into the matching or not as advice, an algorithm solves the online matching problem on paths optimally. In the following, we investigate which competitive ratio an algorithm can reach for the online matching problem on paths if the given information about the decisions on isolated edges is only partially correct. To this end, we use the so-called string guessing problem with known history as introduced in [4, 5].

In the string guessing problem with known history, the algorithm has to guess a bit string $b=b_1b_2b_3\dots b_n$ of a given length n, one bit in each time step, and gets an immediate reply in the next time step, whether the guess was correct or not. With the first request, it additionally learns the length n of the sequence to be guessed. With the request $n+1$, the last bit $b_n$ is revealed, and the algorithm does not have to respond in this last round. The goal of the online algorithm is to minimize the number of wrongly guessed bits. This very generic online problem has been proven very useful for providing both upper and lower bounds on the advice complexity of many different online problems. In particular, the following upper bound for the string guessing problem with known history is known.

Fig. 10.

All pairs of edge groups containing group 4 in the solution.

Fig. 11.

All remaining pairs of two edge groups.

Lemma 1

(Böckenhauer et al. [4]). Let b be a bit string of length m. There is an online algorithm reading at most

$$\begin{aligned} \left\lceil \left( 1+(1-\alpha )\log (1-\alpha )+\alpha \log (\alpha )\right) m+ \frac{3}{2}\log (m)+\frac{1}{2}+\log (\ln (2))\right\rceil \end{aligned}$$

advice bits in order to guess $\alpha m$ bits of b correctly, for some $\frac{1}{2}\le \alpha <1$.

This result can be used to design an algorithm for the online matching problem on paths.

Theorem 6

There exists an online algorithm that finds a matching on

$$\left\lfloor \frac{n}{2}\right\rfloor - (1-\alpha )\left\lceil \frac{n}{3}\right\rceil $$

edges on a path on n vertices using at most

$$\left\lceil \left( 1+(1-\alpha )\log (1-\alpha )+ \alpha \log (\alpha )\right) \left\lceil \frac{n}{3}\right\rceil + \frac{3}{2}\log \left( \left\lceil \frac{n}{3}\right\rceil \right) + \frac{1}{2}+\log (\ln (2))\right\rceil $$

advice bits, for some $\frac{1}{2}\le \alpha <1$.

Proof

Let $P^\prec \in \mathcal {P}_n$ be an online path instance for the online matching problem and let $M^*$ be a fixed maximum matching that matches all inner vertices. Algorithm 2 works greedily on the non-isolated edges and computes its decisions on the isolated edges using an algorithm solving the string guessing problem with known history.

Recall that an online path instance on n vertices contains at most $\left\lceil \frac{n}{3}\right\rceil$ isolated edges. Let

$$\begin{aligned} e_1, e_2, \dots , e_k \text {, for some } k\in \left\{ 1,2,\dots ,\left\lceil \frac{n}{3}\right\rceil \right\} , \end{aligned}$$

be these isolated edges. The algorithm transforms the decision on these isolated edges to the problem of finding a bit string $b=b_1b_2\dots b_{\lceil \frac{n}{3}\rceil }$ with

$$\begin{aligned} b_i = {\left\{ \begin{array}{ll} 1 &{}\text {if } e_i \text { is an edge in } M^*,\\ 0 &{}\text {if } e_i \text { is not present in } M^*, \end{array}\right. } \end{aligned}$$

for all $i\in \{1,2,\dots , k\}$ and $b_i = 0$ for all non-relevant bits $b_{k+1}, \dots , b_{\lceil \frac{n}{3}\rceil }$; see Fig. 12 for an example.

Fig. 12.

This online path instance on 16 vertices contains the isolated edges $e_1$, $e_2$, $e_3$, and $e_4$. The maximum matching corresponds to the bit string $b=b_1b_2b_3b_4b_5b_6 = 100100$ in the bit string guessing problem with known history. $b_1$ to $b_4$ correspond to the decision on the edges $e_1$ to $e_4$, and $b_5$ and $b_6$ are non-relevant bits that occur since this online path does not contain the maximum possible number of isolated edges, which would be 6.

Guessing $\alpha m$ bits correctly means guessing $(1-\alpha )m$ bits wrongly, implying $(1-\alpha )m$ wrongly set isolated edges of the online path on n vertices with $m=\left\lceil \frac{n}{3}\right\rceil$ with respect to $M^*$.

It can easily be seen that every wrongly set isolated edge leads to exactly two unmatched vertices if the adversary can arrange the isolated edges such that every correctly set edge lies between two wrongly set edges. This directly implies that every wrongly set isolated edge leads to exactly one edge less in the matching computed by the algorithm, with respect to the fixed maximum matching $M^*$. Arranging the isolated edges in this way is possible as long as less than half of the isolated edges is set wrong, i.e., if $\alpha \ge \frac{1}{2}$ holds.

Therefore, we can use Lemma 1 and the fact that a path on n vertices has a matching containing $\left\lfloor \frac{n}{2}\right\rfloor$ matching edges to show that Algorithm 2 finds a matching of size

$$\begin{aligned} \left\lfloor \frac{n}{2}\right\rfloor - (1-\alpha )m = \left\lfloor \frac{n}{2}\right\rfloor - (1-\alpha )\left\lceil \frac{n}{3}\right\rceil , \end{aligned}$$

for some $\frac{1}{2}\le \alpha <1$, using

$$\begin{aligned} \left\lceil \left( 1+(1-\alpha )\log (1-\alpha )+ \alpha \log (\alpha )\right) \left\lceil \frac{n}{3}\right\rceil + \frac{3}{2}\log \left( \left\lceil \frac{n}{3}\right\rceil \right) + \frac{1}{2}+\log (\ln (2))\right\rceil \end{aligned}$$

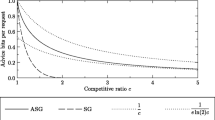
advice bits. This function is visualized in Fig. 13.

Fig. 13.

Minimum number of edges found by Algorithm 2 on an arbitrary online path on n edges with respect to the number of advice bits that are at disposal.

   $\square$

6 Conclusion

We considered the fully online matching problem mainly on general bipartite graphs and paths. For general graphs, we constructed a deterministic online algorithm with advice that solves the problem optimally using $\mathcal {O}(n\log (n))$ advice bits. We complemented this result with a matching lower bound that holds already for $P_5$-free bipartite graphs with diameter 3.

For paths, we showed an almost tight upper and lower bound of approximately $\frac{n}{3}$ advice bits for optimality. These results can be quite easily generalized also to the case of cycles.

For paths, we also investigated the tradeoff between the number of advice bits and the competitive ratio using a reduction from string guessing. Moreover, we showed that one single advice bit does not help at all. It is open which ratio can be reached with two or a few more advice bits. Also the tradeoff for other graph classes would be of interest.